• Основное уравнение
кинетической теории газов
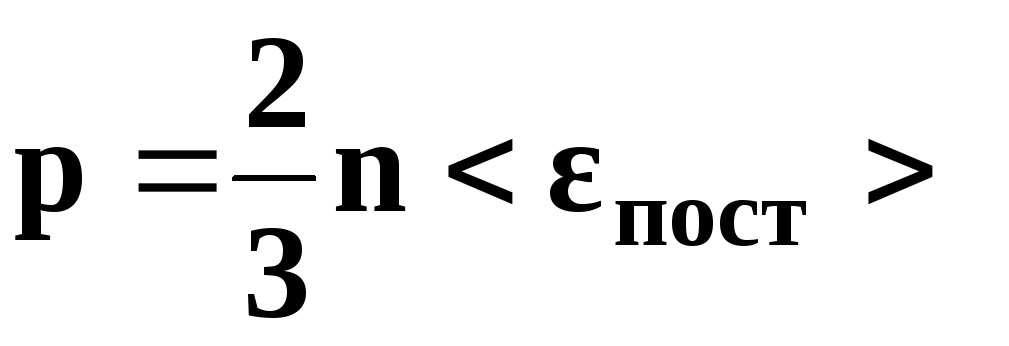 ,
,
где
р – давление
газа, n
– концентрация
молекул (число молекул в единице объема),
![]() –
–
средняя кинетическая энергия
поступательного движения одной молекулы,
угловые скобки обозначают осреднение
по
большому
ансамблю частиц, m0
– масса
молекулы,
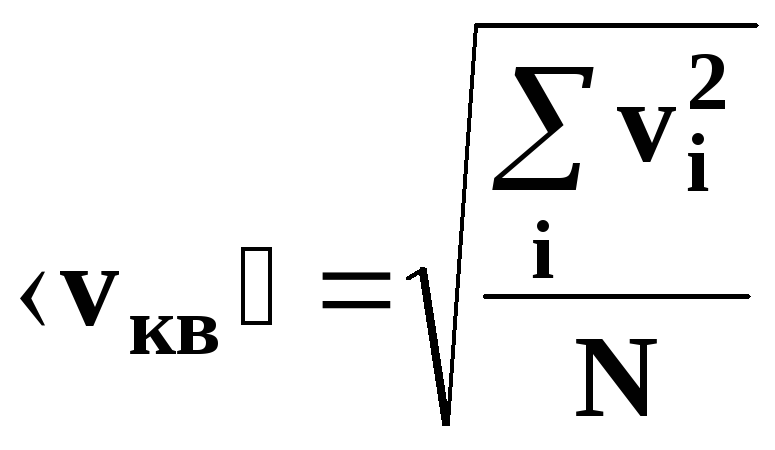 –
–
средняя квадратичная скорость движения
молекул.
• Средняя
кинетическая энергия поступательного
движения одной молекулы
![]()
![]() ,
,
где
k
=
1,38·10-23
Дж/К –
постоянная Больцмана, Т
– абсолютная температура.
•
Энергия теплового
движения молекул (внутренняя энергия
идеального газа):
![]() ,
,
где
i
– число степеней свободы молекулы, m
– масса газа, М
– молярная
масса данного вещества, R
= 8,31 Дж/(кг·К) –
универсальная газовая постоянная, Т
– абсолютная
температура.
• Числом степеней
свободы называется число независимых
координат полностью определяющих
положение тела в пространстве. Любая
молекула имеет 3 поступательных степени
свободы (iпост=3).
Молекулы,
кроме одноатомных, имеют еще вращательные
степени свободы (у двухатомных молекул
iвр
= 2, у
многоатомных iвр
= 3) и
колебательные степени свободы, которые
при невысоких (комнатных) температурах
не учитываются.
• В соответствии
с законом Больцмана о равномерном
распределении энергии по степеням
свободы, в
среднем на каждую степень свободы
молекулы приходится одинаковая энергия,
равная
![]() .
.
• Средняя
кинетическая энергия вращательного
движения одной молекулы:
![]()
![]()
•
Средняя суммарная
кинетическая энергия одной молекулы:
![]() ,
,
где
i
– число степеней свободы молекулы
(i=iпост+
iвр).
• Средняя
квадратичная скорость молекулы:
![]()
• Средняя
арифметическая скорость (средняя
скорость теплового движения)молекулы:
![]() ,
,
где m0
– масса одной молекулы, М
– молярная масса вещества, причем
![]()
![]() ,
,
NA=
6,023·1023
1/моль –
число Авогадро.
• Барометрическая
формула характеризует изменение давления
газа с высотой в поле сил тяжести:![]()
![]() или
или
![]() ,
,
где
p
– давление
на высоте h
над уровнем
моря, p0
– давление на высоте h
= 0,
g
– ускорение
свободного падения. Эта формула
приближенная, так как температуру нельзя
считать постоянной для большой разности
высот.
•
Распределение
Больцмана для концентрации частиц в
силовом поле имеет вид:
![]()
![]() ,
,
где
n
– концентрация частиц, обладающих
потенциальной энергией Wп
, n0
– концентрация
частиц в точках поля с Wп
= 0.
Примеры
решения задач
Задача
1. Найти
среднюю кинетическую энергию
![]() вращательного движения одной молекулы
вращательного движения одной молекулы
кислорода при температуреТ
= 350 К, а также среднюю кинетическую
энергию
![]() вращательного движения всех молекул
вращательного движения всех молекул
кислорода массойm
= 4 г.
Решение.
Согласно закону Больцмана о равном
распределении энергии по степеням
свободы на каждую степень свободы
приходится энергия равная
![]() ,
,
гдеk
– постоянная Больцмана, Т
– абсолютная
температура.
Так
как молекула кислорода двухатомная, у
нее две вращательных степени свободы,
поэтому средняя кинетическая энергия
вращательного движения выразится
формулой:
![]()
Подставим
в полученную формулу значения k
= 1,38·10-23
Дж/К, и Т
= 350 К, получим
![]()
Кинетическая
энергия всех N
молекул, содержащихся в 4 г кислорода
равна:
![]()
Число
всех молекул газа можно вычислить по
формуле:
![]() ,
,
где NA
– число
Авогадро,
![]() –
–
количество вещества,m
– масса газа, М
– молярная
масса. Учтя приведенные выражения,
получим:
![]()
Подставляем
числовые значения: NA
= 6,023·1023
1/моль ; m
= 4 г = 4·10-3
кг ; М
= 32·10-3
кг/моль;
![]() =
=
4,83·10-21
Дж:
![]()
![]()
![]() Выведем
Выведем
размерность полученной величины:
![]()
Задача
2. В
воздухе при нормальных условиях взвешены
одинаковые частицы. Известно, что
концентрация частиц уменьшается в два
раза на высоте h
= 20 м. Определить массу частицы.
Решение.
Воспользуемся формулой распределения
Больцмана:
![]() ,
,
где
Wп
= m0gh
– потенциальная
энергия частицы в поле сил тяжести.
Подставив
это выражение в формулу распределения
Больцмана, получим:
![]()
Логарифмируем
обе части уравнения по основанию е,
тогда:![]()
![]() ,
,
откуда

Подставив
числовые значения в полученную формулу,
найдем
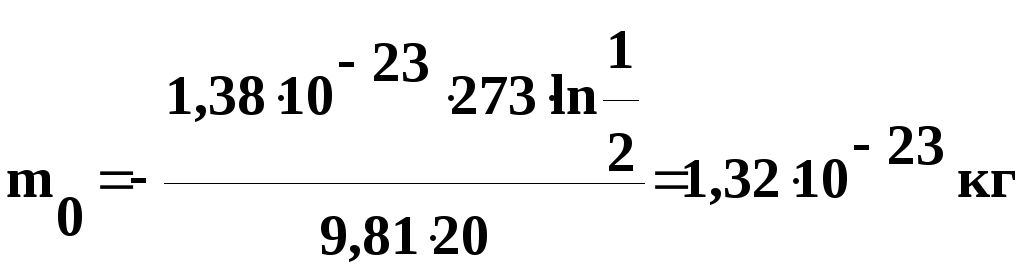
Выведем
размерность полученной величины:
![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Повседневный опыт показывает, что недвижимые тела можно привести в движение, а движимые остановить. Мы с вами постоянно что-то делаем, мир вокруг суетится, светит солнце… Но откуда у человека, животных, да и у природы в целом берутся силы для выполнения этой работы? Исчезает ли механическое движение бесследно? Начнет ли двигаться одно тело без изменения движения другого? Обо всем этом мы расскажем в нашей статье.
Понятие энергии
Для работы двигателей, которые придают движение автомобилям, тракторам, тепловозам, самолетам, нужно топливо, которое является источником энергии. Электродвигатели придают движение станкам при помощи электроэнергии. За счет энергии воды, падающей с высоты, оборачиваются гидротурбины, соединенные с электрическими машинами, производящими электрический ток. Человеку для того, чтобы существовать и работать, также нужна энергия. Говорят, что для того, дабы выполнять какую-нибудь работу, необходима энергия. Что же такое энергия?
- Наблюдение 1. Поднимем над землей мяч. Пока он пребывает в состоянии спокойствия, механическая работа не выполняется. Отпустим его. Под действием силы тяжести мяч падает на землю с определенной высоты. Во время падения мяча выполняется механическая работа.
- Наблюдение 2. Сомкнем пружину, зафиксируем ее нитью и поставим на пружину гирьку. Подожжем нить, пружина распрямится и поднимет гирьку на некую высоту. Пружина выполнила механическую работу.
- Наблюдение 3. На тележку закрепим стержень с блоком в конце. Через блок перекинем нить, один конец которой намотан на ось тележки, а на другом висит грузик. Отпустим грузик. Под действием силы тяжести он будет опускаться книзу и придаст тележке движение. Грузик выполнил механическую работу.

После анализа всех вышеперечисленных наблюдений можно сделать вывод, что если тело или несколько тел во время взаимодействия выполняют механическую работу, то говорят, что они имеют механическую энергию, либо энергию.
Понятие энергии
Энергия (от греч. слова энергия – деятельность) – это физическая величина, которая характеризирует способность тел выполнять работу. Единицей энергии, а также и работы в системе СИ является один Джоуль (1 Дж). На письме энергия обозначается буквой Е. Из вышеуказанных экспериментов видно, что тело выполняет работу тогда, когда переходит из одного состояния в другое. Энергия тела при этом меняется (уменьшается), а выполненная телом механическая работа равна результату изменения ее механической энергии.
Виды механической энергии. Понятие потенциальной энергии

Различают 2 вида механической энергии: потенциальную и кинетическую. Сейчас подробнее рассмотрим потенциальную энергию.
Потенциальная энергия (ПЭ) – это энергия, определяющаяся взаимным положением тел, которые взаимодействуют, либо частями того самого тела. Поскольку любое тело и земля притягивают друг друга, то есть взаимодействуют, ПЭ тела, поднятого над землей, будет зависеть от высоты поднятия h. Чем выше поднято тело, тем больше его ПЭ. Экспериментально установлено, что ПЭ зависит не только от высоты, на которую оно поднято, но и от массы тела. Если тела были подняты на одинаковую высоту, то тело, имеющее большую массу, будет иметь и большую ПЭ. Формула данной энергии выглядит следующим образом: Eп = mgh, где Eп – это потенциальна энергия, m – масса тела, g = 9,81 Н/кг, h – высота.
Потенциальная энергия пружины
Потенциальной энергией упруго деформированного тела называют физическую величину Eп, которая при изменении скорости поступательного движения под действием сил упругости уменьшается ровно на столько, на сколько растет кинетическая энергия. Пружины (как и другие упруго деформированные тела) имеют такую ПЭ, которая равна половине произведения их жесткости k на квадрат деформации: x = kx2: 2.
Энергия кинетическая: формула и определение
Иногда значение механической работы можно рассматривать без употребления понятий силы и перемещения, акцентировав внимание на том, что работа характеризует изменение энергии тела. Все, что нам может потребоваться, – это масса некоего тела и его начальная и конечная скорости, что приведет нас к кинетической энергии. Кинетическая энергия (КЭ) – это энергия, принадлежащая телу вследствие собственного движения.

Кинетическую энергию имеет ветер, ее используют для придания движения ветряным двигателям. Движимые массы воздуха оказывают давление на наклонные плоскости крыльев ветряных двигателей и заставляют их оборачиваться. Вращательное движение при помощи систем передач передается механизмам, выполняющим определенную работу. Движимая вода, оборачивающая турбины электростанции, теряет часть своей КЭ, выполняя работу. Летящий высоко в небе самолет, помимо ПЭ, имеет КЭ. Если тело пребывает в состоянии покоя, то есть его скорость относительно Земли равна нулю, то и его КЭ относительно Земли равна нулю. Экспериментально установлено, что чем больше масса тела и скорость, с которой оно движется, тем больше его КЭ. Формула кинетической энергии поступательного движения в математическом выражении следующая:

Где К – кинетическая энергия, m – масса тела, v – скорость.
Изменение кинетической энергии
Поскольку скорость движения тела является величиной, зависящей от выбора системы отсчета, значение КЭ тела также зависит от ее выбора. Изменение кинетической энергии (ИКЭ) тела происходит вследствие действия на тело внешней силы F. Физическую величину А, которая равна ИКЭ ΔЕк тела вследствие действия на него силы F, называют работой: А = ΔЕк. Если на тело, которое движется со скоростью v1, действует сила F, совпадающая с направлением, то скорость движения тела вырастет за промежуток времени t к некоторому значению v2. При этом ИКЭ равно:
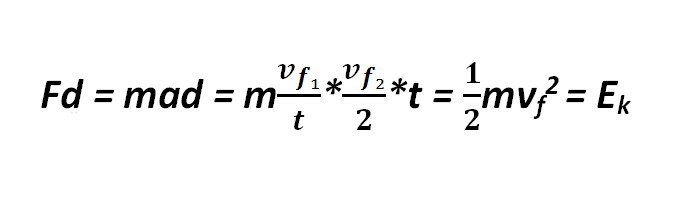
Где m – масса тела; d – пройденный путь тела; Vf1 = (V2 – V1); Vf2 = (V2 + V1); a = F : m. Именно по этой формуле высчитывается, на сколько изменяется энергия кинетическая. Формула также может иметь следующую интерпретацию: ΔЕк = Flcosά, где cosά является углом между векторами силы F и скорости V.
Средняя кинетическая энергия
Кинетическая энергия представляет собой энергию, определяемую скоростью движения разных точек, которые принадлежат этой системе. Однако следует помнить, что необходимо различать 2 энергии, характеризующие разные виды движения: поступательное и вращательное. Средняя кинетическая энергия (СКЭ) при этом является средней разностью между совокупностью энергий всей системы и ее энергией спокойствия, то есть, по сути, ее величина – это средняя величина потенциальной энергии. Формула средней кинетической энергии следующая:

где k – это константа Больцмана; Т – температура. Именно это уравнение является основой молекулярно-кинетической теории.
Средняя кинетическая энергия молекул газа
Многочисленными опытами было установлено, что средняя кинетическая энергия молекул газа в поступательном движении при заданной температуре одна и та же, и не зависит от рода газа. Кроме того, было установлено также, что при нагревании газа на 1 оС СКЭ увеличивается на одно и то же самое значение. Сказать точнее, это значение равно: ΔЕк = 2,07 х 10-23Дж/оС. Для того чтобы вычислить, чему равна средняя кинетическая энергия молекул газа в поступательном движении, необходимо, помимо этой относительной величины, знать еще хотя бы одно абсолютное значение энергии поступательного движения. В физике достаточно точно определены эти значения для широкого спектра температур. К примеру, при температуре t = 500 оС кинетическая энергия поступательного движения молекулы Ек = 1600 х 10-23Дж. Зная 2 величины (ΔЕк и Ек), мы можем как вычислить энергию поступательного движения молекул при заданной температуре, так и решить обратную задачу – определить температуру по заданным значениям энергии.
Напоследок можно сделать вывод, что средняя кинетическая энергия молекул, формула которой приведена выше, зависит только от абсолютной температуры (причем для любого агрегатного состояния веществ).
Закон сохранения полной механической энергии
Изучение движения тел под действием силы тяжести и сил упругости показало, что существует некая физическая величина, которую называют потенциальной энергией Еп; она зависит от координат тела, а ее изменение приравнивается ИКЭ, которая взята с противоположным знаком: ΔЕп = –ΔЕк. Итак, сумма изменений КЭ и ПЭ тела, которые взаимодействуют с гравитационными силами и силами упругости, равна 0: ΔЕп + ΔЕк = 0. Силы, которые зависят только от координат тела, называют консервативными. Силы притяжения и упругости являются консервативными силами. Сумма кинетической и потенциальной энергий тела является полной механической энергией: Еп + Ек = Е.

Этот факт, который был доказан наиболее точными экспериментами,
называют законом сохранения механической энергии. Если тела взаимодействуют силами, которые зависят от скорости относительного движения, механическая энергия в системе взаимодействующих тел не сохраняется. Примером сил такого типа, которые называются неконсервативными, являются силы трения. Если на тело действуют силы трения, то для их преодоления необходимо затратить энергию, то есть ее часть используется на выполнение работы против сил трения. Однако нарушение закона сохранения энергии здесь только мнимое, потому что он является отдельным случаем общего закона сохранения и преобразования энергии. Энергия тел никогда не исчезает и не появляется вновь: она лишь преобразуется из одного вида в другой. Этот закон природы очень важен, он выполняется повсюду. Его еще иногда называют общим законом сохранения и преобразования энергии.
Связь между внутренней энергией тела, кинетической и потенциальной энергиями
Внутренняя энергия (U) тела – это его полная энергия тела за вычетом КЭ тела как целого и его ПЭ во внешнем поле сил. Из этого можно сделать вывод, что внутренняя энергия состоит из КЭ хаотического движения молекул, ПЭ взаимодействия между ними и внутремолекулярной энергии. Внутренняя энергия – это однозначная функция состояния системы, что говорит о следующем: если система находится в данном состоянии, ее внутренняя энергия принимает присущие ему значения, независимо от того, что происходило ранее.
Релятивизм
Когда скорость тела близка к скорости света, кинетическую энергию находят по следующей формуле:

Кинетическая энергия тела, формула которой была написана выше, может также рассчитываться по такому принципу:

Примеры задач по нахождению кинетической энергии
1. Сравните кинетическую энергию шарика массой 9 г, летящего со скоростью 300 м/с, и человека массой 60 кг, бегущего со скоростью 18 км/час.
Итак, что нам дано: m1 = 0,009 кг; V1 = 300 м/с; m2 = 60 кг, V2 = 5 м/с.
Решение:
- Энергия кинетическая (формула): Ек = mv2 : 2.
- Имеем все данные для расчета, а поэтому найдем Ек и для человека, и для шарика.
- Ек1 = (0,009 кг х (300 м/с)2) : 2 = 405 Дж;
- Ек2 = (60 кг х (5 м/с)2) : 2= 750 Дж.
- Ек1 < Ек2.
Ответ: кинетическая энергия шарика меньше, чем человека.
2. Тело с массой 10 кг было поднято на высоту 10 м, после чего его отпустили. Какую КЭ оно будет иметь на высоте 5 м? Сопротивлением воздуха разрешается пренебречь.
Итак, что нам дано: m = 10 кг; h = 10 м; h1 = 5 м; g = 9,81 Н/кг. Ек1 – ?
Решение:
- Тело определенной массы, поднятое на некую высоту, имеет потенциальную энергию: Eп = mgh. Если тело падает, то оно на некоторой высоте h1 будет иметь пот. энергию Eп = mgh1 и кин. энергию Ек1. Чтобы была правильно найдена энергия кинетическая, формула, которая была приведена выше, не поможет, а поэтому решим задачу по нижеследующему алгоритму.
- В этом шаге используем закон сохранения энергии и запишем: Еп1 + Ек1 = Еп.
- Тогда Ек1 = Еп – Еп1 = mgh – mgh1 = mg(h-h1).
- Подставив наши значения в формулу, получим: Ек1 = 10 х 9,81(10-5) = 490,5 Дж.
Ответ: Ек1 = 490,5 Дж.
3. Маховик, имеющий массу m и радиус R, оборачивается вокруг оси, проходящей через его центр. Угловая скорость оборачивания маховика – ω. Дабы остановить маховик, к его ободу прижимают тормозную колодку, действующей на него с силой Fтрения. Сколько оборотов сделает маховик до полной остановки? Учесть, что масса маховика сосредоточена по ободу.
Итак, что нам дано: m; R; ω; Fтрения. N – ?
Решение:
- При решении задачи будем считать обороты маховика подобными оборотам тонкого однородного обруча с радиусом R и массой m, который оборачивается с угловой скоростью ω.
- Кинетическая энергия такого тела равна: Ек = (Jω2) : 2, где J = mR2.
- Маховик остановится при условии, что вся его КЭ истратится на работу по преодолению силы трения Fтрения, возникающей между тормозной колодкой и ободом: Ек = Fтрения*s, где s – это тормозной путь, который равен 2πRN.
- Следовательно, Fтрения*2πRN = (mR2ω2) : 2, откуда N = (mω2R) : (4πFтр).
Ответ: N = (mω2R) : (4πFтр).
В заключение
Энергия – это важнейшая составляющая во всех аспектах жизни, ведь без нее никакие тела не смогли бы выполнять работу, в том числе и человек. Думаем, статья вам внятно дала понять, что собой представляет энергия, а развернутое изложение всех аспектов одной из ее составляющих – кинетической энергии – поможет вам осознать многие процессы, происходящих на нашей планете. А уж о том, как найти кинетическую энергию, вы можете узнать из приведенных выше формул и примеров решения задач.
Молекулярная физика Основные формулы
1. Основы молекулярно-кинетической теории. Газовые законы
1.1 Количество вещества

m — масса;
μ — молярная масса вещества;
N — число молекул;
NA = 6,02·1023 моль-1 — число Авогадро
1.2 Основное уравнение молекулярно-кинетической теории идеального газа

p — давление идеального газа;
m — масса одной молекулы;
n = N/V — концентрация молекул;
V — объем газа;
N — число молекул;
 — среднее значение квадрата скорости молекул.
— среднее значение квадрата скорости молекул.
1.3 Средняя квадратичная скорость молекул идеального газа

k = 1,38·10-23 Дж/К — постоянная Больцмана;
R = kNA = 8,31 Дж/(моль·К) — универсальная газовая постоянная;
T = t+273 — абсолютная температура;
t — температура по шкале Цельсия.
1.4 Средняя кинетическая энергия молекулы одноатомного газа

1.5 Давление идеального газа

n — концентрация молекул;
k — постоянная Больцмана;
T — абсолютная температура.
1.6 Закон Бойля-Мариотта

p — давление;
V — объем газа.
1.7 Закон Шарля
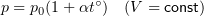
p0 — давление газа при 0 °С;
α = 1/273 °C-1 — температурный коэффициент давления.
1.8 Закон Гей-Люссака

V0 — объем газа при 0 °С.
1.9 Уравнение Менделеева-Клапейрона

1.10 Объединенный закон газового состояния (уравнение Клапейрона)

1.11 Закон Дальтона

pi — парциальное давление i-й компоненты смеси газов.
2. Основы термодинамики
2.1 Внутренняя энергия идеального одноатомного газа

ν — количество вещества;
R = 8,31 Дж/(моль·К) — универсальная газовая постоянная;
T — абсолютная температура.
2.2 Элементарная работа, совершаемая газом,
при изменении объема на бесконечно малую величину dV

p — давление газа.
При изменении объема от V1 до V2

2.3 Первый закон термодинамики

ΔQ — количество подведенной теплоты;
ΔA — работа, совершаемая веществом;
ΔU — изменение внутренней энергии вещества.
2.4 Теплоемкость идеального газа

ΔQ — количество переданной системе теплоты на участке процесса;
ΔT — изменение температуры на этом участке процесса.
Физика, 10 класс
Урок 18. Основное уравнение МКТ
Перечень вопросов, рассматриваемых на уроке:
1) средняя кинетическая энергия молекулы;
2) давление газа;
3) основное уравнение МКТ;
Глоссарий по теме:
Давление идеального газа пропорционально произведению концентрации молекул и средней кинетической энергии поступательного движения молекул.
Средняя кинетическая энергия молекул – усреднённая величина, равная половине произведения массы молекулы на среднюю величину квадрата её скорости.
Концентрация – число молекул в единице объёма.
Масса молекулы (или атома) – чрезвычайно маленькая величина в макроскопических масштабах (граммах и килограммах), вычисляется через отношение массы вещества к количеству содержащихся в ней молекул (или атомов).
Изменение импульса тела – произведение силы на время действия силы. Импульс силы всегда показывает, как изменяется импульс тела за данное время.
Основная и дополнительная литература по теме урока:
- Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. С. 188 – 192.
- Кирик Л.А., Генденштейн Л.Э., Гельфгат И.М.. Задачи по физике. 10-11 классы для профильной школы. – М.: Илекса, 2010. С. 111.
- Рымкевич А.П. Физика. Задачник. 10-11 классы. – М.: Дрофа, 2013. С. 65 – 67.
Открытые электронные ресурсы по теме урока:
- http://kvant.mccme.ru/1991/09/idealnyj_gaz_-_universalnaya_f.htm
- http://kvant.mccme.ru/1983/10/davlenie_idealnogo_gaza.htm
- http://kvant.mccme.ru/1987/09/davlenie_gaza_v_sosude.htm
Теоретический материал для самостоятельного изучения
Основная задача молекулярно-кинетической теории газа заключается в том, чтобы установить соотношение между давлением газа и его микроскопическими параметрами – массой молекул, их средней скоростью и концентрацией. Это соотношение называется основным уравнением молекулярно-кинетической теории газа.
Давление газа на стенку сосуда обусловлено ударами молекул, давление газа пропорционально концентрации молекул: чем больше молекул в единице объема, тем больше ударов молекул о стенку за единицу времени. Каждая молекула при ударе о стенку передает ей импульс, пропорциональный импульсу молекулы m0v.
Давление пропорционально второй степени скорости, так как, чем больше скорость молекулы, тем чаще она бьется о стенку сосуда. Расчеты показывают, что основное уравнение молекулярно-кинетической теории идеального газа имеет вид:
 , где m0 – масса одной молекулы газа,
, где m0 – масса одной молекулы газа,
n– концентрация молекул,
 – среднее значение квадрата скорости молекул.
– среднее значение квадрата скорости молекул.

Коэффициент  обусловлен трёхмерностью пространства – во время хаотического движения молекул все три направления равноправны.
обусловлен трёхмерностью пространства – во время хаотического движения молекул все три направления равноправны.
Средняя кинетическая энергия поступательного движения

тогда уравнение примет вид:

Давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.
Примеры и разбор решения заданий.
1. К каждой позиции первого столбца подберите соответствующую позицию второго:
|
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ |
ФОРМУЛЫ |
|
1) импульс тела |
А) |
|
2) средняя кинетическая энергия молекул |
Б) |
|
3) давление газа на стенку сосуда |
В) |
|
4) концентрация молекул |
Г) |
Правильный ответ: вспомнив формулы величин, устанавливаем соответствие:
|
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ |
ФОРМУЛЫ |
|
1) импульс тела |
В) |
|
2) средняя кинетическая энергия молекул |
А) |
|
3) давление газа на стенку сосуда |
Г) |
|
4) концентрация молекул |
Б) |
2. Кислород находится при нормальных условиях. Средняя квадратичная скорость молекул кислорода в этом случае равна ___ м/с.
Решение:


Ответ: 460 м/с.
Формулы молекулярной физики
Формула концентрации молекул
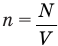
Здесь n — концентрация  , N — количество молекул (безразмерное), V — объем
, N — количество молекул (безразмерное), V — объем  .
.
Формула плотности
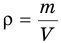
Здесь  — плотность вещества
— плотность вещества  , m — масса вещества (кг), V — объем
, m — масса вещества (кг), V — объем  .
.
Формула относительной молекулярной массы
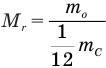
Здесь 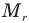 — относительная молекулярная масса (безразмерная),
— относительная молекулярная масса (безразмерная),  — масса одной молекулы (кг),
— масса одной молекулы (кг), 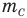 — масса атома углерода (кг).
— масса атома углерода (кг).
Формула количества вещества (количества молей)
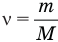
Здесь v — количество вещества (количество молей) (моль), m — масса вещества (кг), М — молярная масса (кг/моль).
Формулы массы одной молекулы
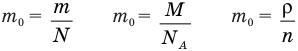
Здесь 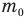 — масса одной молекулы (кг), т — масса вещества (кг), N — количество молекул (безразмерное), М — молярная масса (кг/моль),
— масса одной молекулы (кг), т — масса вещества (кг), N — количество молекул (безразмерное), М — молярная масса (кг/моль), 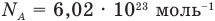 — число Авогадро,
— число Авогадро,  — плотность вещества
— плотность вещества  , n — концентрация молекул
, n — концентрация молекул  .
.
Формулы количества молекул
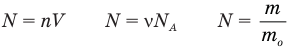
Здесь A — количество молекул (безразмерное), п — концентрация молекул  , V— объем
, V— объем  , v — количество вещества (количество молей) (моль),
, v — количество вещества (количество молей) (моль), 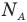 — число Авогадро
— число Авогадро 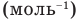 , m — масса вещества (кг),
, m — масса вещества (кг),  — масса одной молекулы.
— масса одной молекулы.
Формулы средней квадратичной скорости молекул
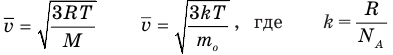
Здесь 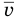 — средняя квадратичная скорость молекул (м/с), R = 8,31 Дж/(моль • К) — молярная газовая постоянная, Т — абсолютная температура (К), М — молярная масса (кг/моль),
— средняя квадратичная скорость молекул (м/с), R = 8,31 Дж/(моль • К) — молярная газовая постоянная, Т — абсолютная температура (К), М — молярная масса (кг/моль), 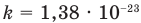 Дж/К — постоянная Больцмана,
Дж/К — постоянная Больцмана,  — масса одной молекулы (кг).
— масса одной молекулы (кг).
Основное уравнение кинетической теории идеального газа

Здесь р — давление газа (Па),  — масса одной молекулы (кг), n — концентрация молекул
— масса одной молекулы (кг), n — концентрация молекул  ,
, 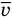 — средняя квадратичная скорость молекул (м/с),
— средняя квадратичная скорость молекул (м/с),  — средняя кинетическая энергия молекул (Дж).
— средняя кинетическая энергия молекул (Дж).
Формула средней кинетической энергии молекул
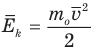
Здесь 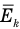 — средняя кинетическая энергия молекул (Дж),
— средняя кинетическая энергия молекул (Дж), 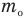 — масса одной молекулы (кг),
— масса одной молекулы (кг), 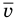 — средняя квадратичная скорость молекул (м/с).
— средняя квадратичная скорость молекул (м/с).
Связь шкал Цельсия и Кельвина
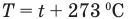
Здесь Т — абсолютная температура (К), t — температура по шкале Цельсия.
Связь средней кинетической энергии молекул идеального газа с абсолютной температурой
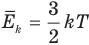
Здесь  — средняя кинетическая энергия молекул (Дж), k — постоянная Больцмана (Дж/К), Т — абсолютная температура (К).
— средняя кинетическая энергия молекул (Дж), k — постоянная Больцмана (Дж/К), Т — абсолютная температура (К).
У равнение состояния идеального газа — уравнение Клапейрона — Менделеева
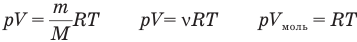
Здесь р — давление газа (Па), V — объем  , т — масса газа (кг), М — молярная масса (кг/моль), R — молярная газовая постоянная (ДжДмоль • К), Т — абсолютная температура (К), v — количество вещества (количество молей) (моль),
, т — масса газа (кг), М — молярная масса (кг/моль), R — молярная газовая постоянная (ДжДмоль • К), Т — абсолютная температура (К), v — количество вещества (количество молей) (моль), 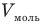 — объем моля
— объем моля 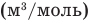 .
.
Объединенный газовый закон — уравнение Клапейрона
при 
Здесь 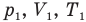 — давление (Па), объем
— давление (Па), объем  и абсолютная температура (К) газа в первом состоянии,
и абсолютная температура (К) газа в первом состоянии, 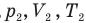 — давление (Па), объем
— давление (Па), объем  и абсолютная температура (К) газа во втором состоянии.
и абсолютная температура (К) газа во втором состоянии.
Закон Бойля — Мариотта (изотермический процесс)
при 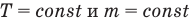
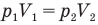
Здесь Т — абсолютная температура газа (К), m — масса газа (кг), 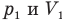 — давление (Па) и объем газа
— давление (Па) и объем газа  в первом состоянии,
в первом состоянии, 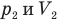 — давление (Па) и объем
— давление (Па) и объем  газа во втором состоянии.
газа во втором состоянии.
Закон Гей-Люссака (изобарный процесс)
при 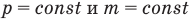
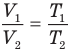
Здесь р — давление газа (Па), m — масса газа (кг), 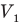 и
и 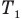 — объем
— объем  и абсолютная температура (К) газа в первом состоянии,
и абсолютная температура (К) газа в первом состоянии, 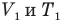 — объем
— объем  и абсолютная температура (К) газа во втором состоянии.
и абсолютная температура (К) газа во втором состоянии.
Закон Шарля
при 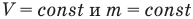
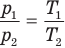
Здесь V — объем газа  , m — масса газа (кг),
, m — масса газа (кг), 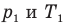 — давление (Па) и абсолютная температура (К) газа в первом состоянии,
— давление (Па) и абсолютная температура (К) газа в первом состоянии, 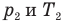 — давление (Па) и абсолютная температура (К) газа во втором состоянии.
— давление (Па) и абсолютная температура (К) газа во втором состоянии.
Связь давления идеального газа с концентрацией его молекул и температурой
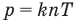
Здесь р — давление газа (Па), к — постоянная Больцмана (Дж/К), п — концентрация молекул газа  , абсолютная температура Т (К).
, абсолютная температура Т (К).
Формулы относительной влажности
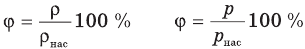
Здесь 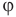 — относительная влажность (безразмерная или в %), р — плотность водяного пара в воздухе при данной температуре
— относительная влажность (безразмерная или в %), р — плотность водяного пара в воздухе при данной температуре 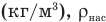 — плотность насыщенного водяного пара при той же температуре
— плотность насыщенного водяного пара при той же температуре 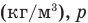 — давление водяного пара в воздухе при данной температуре (Па),
— давление водяного пара в воздухе при данной температуре (Па), 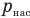 — давление насыщенного водяного пара в воздухе при той же температуре (Па).
— давление насыщенного водяного пара в воздухе при той же температуре (Па).
Работа при изобарном изменении объема газа
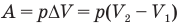
Здесь А — работа (Дж), р — давление газа (Па), 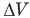 — изменение объема газа
— изменение объема газа 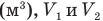 — соответственно начальный и конечный объемы газа
— соответственно начальный и конечный объемы газа  .
.
Внутренняя энергия идеального одноатомного газа
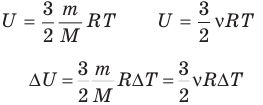
Здесь U — внутренняя энергия газа (Дж), m — масса газа (кг), М — молярная масса газа (кг/моль), R — молярная газовая постоянная (Дж/(моль • К), Т — абсолютная температура (К), v — количество вещества или число молей (моль), 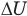 — изменение внутренней энергии (Дж),
— изменение внутренней энергии (Дж), 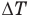 — изменение температуры (К).
— изменение температуры (К).
Первый закон термодинамики
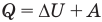
Здесь Q — количество теплоты, переданное термодинамической системе (Дж),  — изменение внутренней энергии системы (Дж), А — работа против внешних сил (Дж)
— изменение внутренней энергии системы (Дж), А — работа против внешних сил (Дж)
Применение первого закона термодинамики к термодинамическим процессам
к изотермическому: при 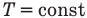
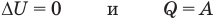
к изохорному: при V = const
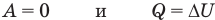
к изобарному: при р = const
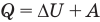
к адиабатному: при Q = 0

Здесь Т — абсолютная температура (К),  — изменение внутренней энергии (Дж), Q — количество теплоты (Дж), А — работа (Дж), V — объем
— изменение внутренней энергии (Дж), Q — количество теплоты (Дж), А — работа (Дж), V — объем 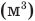 , р — давление (Па).
, р — давление (Па).
Формулы количества теплоты при нагревании или охлаждении тел
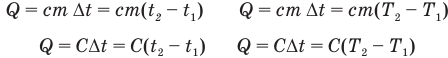
Здесь Q — количество теплоты, переданное телу при нагревании или отданное им при охлаждении (Дж), с — удельная теплоемкость вещества (Дж/(кг • К), т — масса тела (кг), 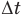 — изменение температуры тела по шкале Цельсия,
— изменение температуры тела по шкале Цельсия, 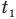 и
и 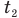 — температуры тела в начале и в конце процесса передачи теплоты по шкале Цельсия,
— температуры тела в начале и в конце процесса передачи теплоты по шкале Цельсия, 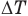 — изменение абсолютной температуры тела (К),
— изменение абсолютной температуры тела (К), 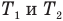 — абсолютные температуры тела в начале и в конце процесса передачи теплоты (К),
— абсолютные температуры тела в начале и в конце процесса передачи теплоты (К), 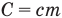 — теплоемкость тела (Дж/К).
— теплоемкость тела (Дж/К).
Формула количества теплоты при плавлении или кристаллизации
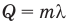
Здесь Q — количество теплоты (Дж), т — масса тела (кг), 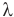 — удельная теплота плавления вещества (Дж/кг).
— удельная теплота плавления вещества (Дж/кг).
Формула количества теплоты при парообразовании или конденсации
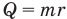
Здесь Q — количество теплоты (Дж), m — масса тела (кг), r — удельная теплота парообразования (Дж/кг).
Формула количества теплоты при сгорании топлива
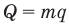
Здесь Q — количество выделившейся теплоты, m — масса топлива (кг), q — удельная теплота сгорания (Дж/кг).
Коэффициент полезного действия теплового двигателя
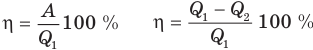
Здесь  — коэффициент полезного действия (безразмерный или в %),
— коэффициент полезного действия (безразмерный или в %), 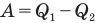 — работа, совершенная двигателем (Дж),
— работа, совершенная двигателем (Дж), 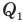 — количество теплоты, полученное рабочим веществом от нагревателя (Дж),
— количество теплоты, полученное рабочим веществом от нагревателя (Дж), 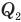 — количество теплоты, отданное рабочим веществом холодильнику (Дж).
— количество теплоты, отданное рабочим веществом холодильнику (Дж).
Коэффициент полезного действия идеального теплового двигателя
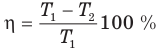
Здесь  — коэффициент полезного действия идеального теплового двигателя (безразмерный или в %),
— коэффициент полезного действия идеального теплового двигателя (безразмерный или в %), 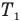 — абсолютная температура нагревателя (К),
— абсолютная температура нагревателя (К), 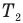 — абсолютная температура холодильника(К).
— абсолютная температура холодильника(К).
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Задачи по физике с решением
Возможно вам будут полезны эти страницы:









