2018-07-08
Найти кинетическую энергию нейтрона, возникшего при распаде остановившегося $Sigma^{-}$ – гиперона ($Sigma^{-} rightarrow n + pi^{-}$).
Решение:
$O = vec{p}_{n} + vec{p}_{ pi}$
$m_{ Sigma}c^{2} = E_{n} + E_{ pi}$
или $(m_{ Sigma}c^{2} – E_{n} )^{2} = E_{ pi}^{2}$
или $m_{ Sigma}^{2}c^{4} – 2m_{ Sigma}c^{2} E_{n} = E_{ pi}^{2} – E_{n}^{2} =c^{4}m_{ pi}^{2} – c^{4} m_{n}^{2}$
потому что (1) подразумевает $E_{ pi}^{2} – E_{n}^{2} = m_{ pi}^{2}c^{4} – m_{n}^{2}c^{4}$
Следовательно $E_{n} = frac{m_{ Sigma}^{2} + m_{n}^{2} – m_{ pi}^{2} }{2m_{ Sigma} }c^{2} $
и $T_{n} = left ( frac{m_{ Sigma}^{2} + m_{n}^{2} – m_{ pi}^{2} }{2m_{ Sigma} } – m_{n} right )c^{2} = frac{(m_{ Sigma} – m_{n} )^{2} – m_{ pi}^{2} }{2m_{ Sigma} }c^{2} $.
Подстановка дает $T_{n} = 19,55 МэВ$.
В
ядерном реакторе функционируют свободные
нейтроны широкого диапазона кинетических
энергий – от 10-3
эВ до десятков МэВ. Для удобства их
различий они классифицируются на:
–
быстрые нейтроны
(с кинетическими энергиями выше 0.1 МэВ);
–
промежуточные нейтроны (с
энергиями 0.625эВ <
E <
0.1МэВ);
–
медленные нейтроны (с
энергиями ниже 0.625 эВ).
Необходимость
такой классификации обусловлена тем,
что нейтроны различных кинетических
энергий обладают
различной
склонностью к вступлению в различные
нейтронные реакции с ядрами одних
веществ.
*)
По этой причине, говоря о плотности
нейтронов, следует всегда указывать, о
нейтронах какой энергии идет речь.
Математическая форма записи – n(E) –
полностью отвечает этому: указывается
и величина плотности нейтронов, и
величина их кинетической энергии.
Ибо, поскольку в рассматриваемом
единичном объёме, кроме нейтронов с
энергией Е, обязательно есть ещё нейтроны
самых различных энергий очень широкого
диапазона, суммарная (интегральная)
плотность нейтронов всех возможных
энергий будет:
¥
n
= ò
n(E) .
dE
(2.3.2)
0
Особую
часть медленных нейтронов составляют
тепловые
нейтроны
– то есть нейтроны, находящиеся в
кинетическом равновесии с ядрами среды,
в которой они движутся. Поскольку
энергетическое распределение молекул
(а следовательно, и атомов, и ядер атомов)
в их тепловом движении имеет вид спектра
Л.Больцмана:
N(E)
= Nо
.C
.E
exp(-E / kT),
-
аналогичное
распределение должны иметь
в непоглощающей среде
и тепловые нейтроны: раз они находятся
в кинетическом равновесии с ядрами
атомов среды, то каждой группе ядер,
имеющих определенную энергию Е, должна
соответствовать пропорциональная по
численности группа нейтронов той
же энергии. Поэтому энергетический
спектр тепловых нейтронов – спектр
Максвелла (Maxwell) –
в непоглощающих средах формально
описывается тем же выражением:
n(E)
= no
C
E exp(-E / kT) (2.3.3)
где:
n(E) – плотность тепловых нейтронов,
имеющих энергии в элементарном
интервале dE вблизи значения Е;
no
–
интегральная плотность тепловых
нейтронов всех возможных энергий в
среде с термодинамической температурой
Т;
k
= 8.62 .10-5
эВ/К – постоянная Больцмана;
С
– постоянный сомножитель нормировки.
В
реальной (поглощающей нейтроны) среде
максвелловское распределение тепловых
нейтронов по энергиям, конечно, нарушается.
Однако, компактное математическое
удобство этого выражения настолько
велико, что условились считать, что и в
поглощающей тепловые нейтроны среде
энергетическое распределение тепловых
нейтронов сохраняет
ту же (гауссову) форму, что и в непоглощающей
среде:
n(E)
= no
C
E exp(-E / kTн),
(2.3.4)
с
той лишь разницей, что в показателе
экспоненциала стоит не термодинамическая
температура среды Т, а так называемая
температура нейтронов
Тн.
Максвелловский
спектр тепловых нейтронов (рис.2.9)
характеризуется следующими присущими
ему энергиями тепловых нейтронов:
Рис.
2.9. Энергетический спектр тепловых
нейтронов Максвелла.
а)
Наиболее
вероятной энергией
Енв
=
kTн,
соответствующей максимуму распределения
тепловых нейтронов по энергиям при
данной температуре нейтронов Тн.
Это означает, что тепловых нейтронов с
кинетической энергией Енв
в среде
больше, чем тепловых нейтронов любых
других энергий
(до 36% от общего числа всех тепловых
нейтронов).
б)
Средней
энергией тепловых нейтронов:
¥
Еср
= (1/no)
ò
E n(E) dE (2.3.5)
0
Подстановка
в (2.3.5) выражения (2.3.4) приводит к величине:
Eср
= 4kTн
/
p
»
1.273 kTн
= 1.273 Енв
(2.3.6)
В
частности при температуре нейтронов
Тн
= 293К (или 20оС),
называемой стандартной
температурой,
наиболее вероятная и средняя энергии
тепловых нейтронов соответственно
равны:
Eнв
= 0.0253 эВ Еср
= 0.0322 эВ
Заметим
одно
счастливое
свойство максвелловского спектра:
Отношение
средней и наиболее вероятной энергий
нейтронов
в
спектре Максвелла при постоянной
температуре нейтронов
есть
величина постоянная, равная Еср/Енв
= 4/p
»
1.273.
Cледовательно,
отношение
скоростей нейтронов,
соответствующих средней и наиболее
вероятной энергиям тепловых нейтронов:
____
__
vср/vнв
= Ö4/p
= 2/Öp
»
1.128, (2.3.7)
–
то есть
также
является постоянной величиной.
Запомним это. Понятие средней энергии
тепловых нейтронов понадобилось нам
для того, чтобы поведение и взаимодействия
всей совокупности
различных по энергиям тепловых нейтронов
заменить
эквивалентным их взаимодействием с
ядрами среды так, словно
все они одинаковы по энергиям,
а значит – и по
своим свойствам.
Суммирование кинетической энергии всех
тепловых нейтронов и раздел этой суммы
поровну между всеми тепловыми нейтронами
– см. формулу (2.3.5) – как раз и приводит к
понятию “среднего теплового
нейтрона”, подобно понятию “среднего
нейтрона деления”, с которым мы уже
имели дело, говоря о спектре Уатта.
Итак,
спектр нейтронов, то есть их энергетическое
распределение в среде, является второй
характеристикой нейтронного поля.
К
сожалению, теория реакторов до сих пор
не располагает компактным аналитическим
выражением для спектра всех
нейтронов в реакторе, и поэтому задачу
по выяснению реакторного спектра
приходится решать путём громоздких
вычислений с помощью ЭВМ. Частные же
задачи теории решаются на базе
трёх энергетических спектров:
спектр нейтронов деления (Уатта); спектр
тепловых нейтронов (Максвелла) и спектр
замедляющихся нейтронов (Ферми), с
которым мы познакомимся позже.
2.3.3.
Плотность потока нейтронов.
Третья из основных характеристик
нейтронных полей –
плотность потока нейтронов
(Ф) – является попросту
произведением первых двух:
плотности нейтронов на их скорость:
Ф
= n .
v
(2.3.8)
По
физическому смыслу эта величина –
суммарный секундный путь всех нейтронов
в 1 см3
среды.
Однако размерность плотности потока
– нейтр/см2
с
–
может привести к путанице в попытках
обнаружить физический смысл этой
величины в самой размерности: сразу
воображается некая плоская площадка
размером в 1 см2,
через которую ежесекундно проходит
определённое число нейтронов. Такому
представлению способствует прошлый
опыт изучения сходным образом звучащих
величин иной физической природы:
плотности потока жидкости (из
гидродинамики), плотности магнитного
потока и плотности потока электронов
в проводнике (из электродинамики),
плотности теплового потока на теплоотдающей
поверхности (из теплотехники) и
другими. Аналогия плотности потока
нейтронов с перечисленными величинами
(увы!) несостоятельна, так как все эти
величины характеризуют направленный
перенос энергии, а нейтроны в единичном
объёме среды движутся не направленно,
а
хаотично
по всем возможным направлениям.
На
первый взгляд эта характеристика вообще
кажется
лишней,
т.к. она – простая комбинация двух других
характеристик нейтронных полей –
плотности (n) и скорости (v) нейтронов.
Однако, самое простое рассуждение о
том, что секундное количество актов
любой нейтронной реакции в 1 см3
среды должно быть
прямо
пропорционально
величинам и плотности нейтронов (n), и
скорости их переноса (v), а, следовательно,
– величине
плотности потока нейтронов
(Ф), даёт этой характеристике право на
существование. Действительно, чем больше
плотность нейтронов
n
и чем больше скорость их перемещения
v,
тем больше шансов имеют все эти нейтроны
в 1см3
среды
провзаимодействовать
с ядрами среды в течение 1 с и вызвать
те или иные нейтронные реакции.
В
этих рассуждениях, как видим, не содержится
ни малейшего намёка на привязку к
какому-либо конкретному направлению
движения нейтронов в единичном объёме
среды. Но зададим себе вопрос: а важно
ли вообще направление, по которому
нейтрон перед взаимодействием приближается
к ядру, если разговор в конечном счёте
сводится к ответу на другой вопрос:
произойдет
ядерное взаимодействие или не произойдет?
–
Ведь нас в конце концов интересует
секундное количество конкретных
взаимодействий каждого вида в единичном
объёме среды. И если нам не известно о
какой-либо
анизотропии
свойств ядер по отношению к взаимодействующим
с ними с разных направлений нейтронам,
то проще предположить, что
ядру
безразлично,
ударит ли его нейтрон “в лоб” или
“по затылку”, – результат должен
быть
одинаковым!
А это значит, что для удовлетворения
нашего интереса, касающегося
только
скоростей нейтронных реакций, нам
достаточно
скалярной
характеристики нейтронного поля (каковой
Ф и является).
Но
отметим всё-таки, что представляя ядро
в виде сферы, даже предполагая
изотропность действия ядерных сил в
пределах этой сферы, говоря о
вероятности взаимодействия нейтрона
с ядром, невозможно
обойтись в рассуждениях без величины
поверхности
этой сферы: ведь для нейтронной
реакции
необходимо,
чтобы приближающийся извне нейтрон
пересёк
поверхность этой сферы. И чем больше
величина этой поверхности, тем больше
ограничивающий её объём, тем больше
нейтронов имеют возможность попасть
в этот объём, инициируя ту или иную
нейтронную реакцию.
Поэтому
вероятность взаимодействия ядра с
нейтронами, пересекающими извне
поверхность сферы действия ядерных сил
ядра, должна быть пропорциональна
плотности потока нейтронов вблизи ядра,
подразумевая под последней
отношение
числа падающих за 1 с на поверхность
сферы нейтронов к величине поверхности
этой сферы. Та же размерность – нейтр/см2с;
та же
скалярность
величины (ведь поверхность сферы в целом
не направлена никуда и в то же время
направлена куда угодно).
А
теперь сравним это определение со
строгим определением плотности
потока нейтронов, которое дает Стандарт:
Плотность
потока нейтронов – это отношение числа
нейтронов,
ежесекундно
падающих на поверхность элементарной
сферы, к
величине
диаметрального
сечения этой сферы.
Та
же размерность
–
нейтр./см2с.
Та же скалярность: диаметральных
сечений в любой сфере можно указать
бесчисленное множество, и каждое из
них имеет
своё
направление нормали. И если допустить,
что элементарная сфера имеет размер
сферы действия ядерных сил ядра, то её
поверхность Sсф
= 4pR2,
а величина любого диаметрального сечения
этой сферы SD
= pR2
– величина в 4 раза меньшая, чем поверхность
сферы. То есть в определении, появившемся
из приведенных выше рассуждений,
фигурировала бы вчетверо меньшая
величина, чем в стандартном определении.
Что
касается
элементарности
сферы, отмеченной в стандартном
определении, необходимость её
обусловлена той же причиной, что и в
определении плотности нейтронов:
желанием сделать плотность потока
нейтронов Ф
непрерывной
величиной
с целью использования при исследовании
нейтронных полей компактного аппарата
непрерывных функций.
И
последнее. Говоря о плотности потока
нейтронов Ф, нельзя говорить о ней
вообще;
следует обязательно оговаривать и
указывать, о нейтронах какой
кинетической энергии идет речь. В
противном случае возникает уже не
просто неопределённость, о которой
упоминалось в п.2.3.2, а бессмыслица, суть
которой ясна из простого примера. Если
просто сказать, что Ф = 60 нейтр/см2с,
то это все равно, что
ничего не сказать,
так как такая величина плотности потока
может обеспечиваться:
–
одним нейтроном со скоростью v = 60 см/с;
–
двумя нейтронами со скоростями v = 30
см/с;
–
тремя нейтронами со скоростями v = 20
см/с;
–
четырьмя нейтронами со скоростями v =
15 см/с;
–
пятью нейтронами со скоростями v = 12
см/с;
–
шестью нейтронами со скоростями v = 10
см/с;
–
десятью нейтронами со скоростями v = 6
см/с и т.д.
А
результаты взаимодействия этих комбинаций
нейтронов с ядрами среды во всех этих
случаях будут
различными.
Вот
почему, указывая значение Ф, важно для
определённости всегда указывать энергию
нейтронов: Ф(Е).
2.3.4.
Плотность тока нейтронов.
В отличие от первых трёх характеристик
нейтронного поля, в определениях которых
игнорируется понятие направления
перемещения нейтронов, плотность тока
нейтронов – величина векторная.
Она даёт представление о
генеральном направлении
перемещения больших количеств
хаотично движущихся нейтронов и об
интенсивности
перемещения нейтронов в этом направлении.
Нейтроны
в среде, подобно молекулам воды в горной
реке, перемещаются во всех мыслимых
направлениях. Но как в реке существует
генеральное направление перемещения
воды (по руслу), так подобное направление
существует и для перемещения нейтронов.
В задачах теории реакторов об утечке
нейтронов из активной зоны, об эффективности
работы отражателя и многих других как
раз требуется знание направления и
интенсивности диффузии нейтронов.
Существо
плотности тока нейтронов нетрудно
понять, отталкиваясь от более простого
частного случая
её проекции на координатную ось.
В
точке с координатами (x,y,z), где нам
желательно знать величину и направление
вектора плотности тока нейтронов
I(x,y,z),
мысленно выделим единичную плоскую
площадку, перпендикулярную к оси OX, и
подсчитаем количества нейтронов,
ежесекундно пересекающих эту площадку
под всеми возможными углами слева
направо (в положительном направлении
оси OX) и справа налево (в отрицательном
направлении OX). Пусть в результате
подсчетов оказалось, что первая величина
равна I+x
нейтр/см2с,
а вторая – I-x
нейтр/см2с.
Тогда их разница
Ix
= I+x
– I-x,
являясь
по смыслу нашего рассуждения
скалярной
величиной, уже своим
знаком
должна показать направление
преимущественного перемещения нейтронов:
если Ix
> 0, то это означает, что больше нейтронов
вдоль OX перемещается в
положительном
направлении, а если Ix
< 0, то больше нейтронов перемещается
в
отрицательном
направлении. Сама же эта разностная
величина Ix
определяет интенсивность переноса
нейтронов вдоль оси OX в преимущественном
направлении.
Аналогичные
рассуждения можно проделать и относительно
перемещений той же совокупности
хаотично движущихся нейтронов вдоль
других координатных осей OY и OZ и
получить величины двух других проекций
вектора
I
– Iy
и Iz.
Зная величины проекций вектора на
координатные оси, можно записать
выражение и для самого вектора:
I(x,y,z)
= Ixi
+ Iyj
+ Izk,
(2.3.9)
Примеры
3.1. a-частица с
кинетической энергией МэВ упруго рассеялась на
покоившемся ядре . Определить кинетические энергии
-частицы
и ядра
отдачи , если угол между направлениями разлета
обеих частиц θ = 120˚.
|
Дано |
Решение |
|
a-частица:
___________ |
Так как кинетическая энергия Закон сохранения импульса:
Закон сохранения энергии:
Учтем, что кинетическая энергия
Запишем и решим систему из двух
Из второго уравнения системы (5) выразим
Преобразуя первое уравнение
Кинетические энергии a-частицы и ядра лития после рассеяния соответственно равны
|
|
Ответ: |
3.2. Литиевую мишень облучают пучком протонов с кинетической энергией, в 1,5 раза превышающей ее пороговое
значение (). Найти кинетическую энергию нейтронов,
вылетающих в результате реакции 7Li(p,n)7Be с энергией реакции МэВ под углом θ = 90˚
к пучку протонов.
|
Дано |
Решение |
|
7Li(p,n)7Be
|
Значение пороговой кинетической
Т. к.
(причем Закон Закон
Учтем, что кинетическая энергия
Запишем и решим систему из двух
Из второго уравнения системы
Найдем кинетическую энергию
|
|
Ответ: |
Контрольные вопросы
1. Как найти скорость
движения c-системы относительно л-системы?
2. Как связаны между
собой импульсы частиц в c-системе и в л-системе?
3. Можно ли, исходя
только из законов сохранения импульса и энергии, найти cosc, где c – угол разлета продуктов реакции относительно
направления движения сталкивающихся частиц в с-системе?
4. Как будут связаны величины
импульсов частиц до и после реакции
в c-системе при упругом рассеянии?
5. Проанализируйте
формулы (3.13) и (3.14) для случая упругого рассеяния. Что Вы можете сказать о
случае, когда масса налетающей частицы больше массы частицы, покоящейся в
л-системе?
Задачи
1. Найдите кинетическую энергию ядра отдачи,
возникшего в результате упругого рассеяния частицы с массой m и
кинетической энергией Е на первоначально покоившемся ядре с массой M(Z, A), если его импульс составляет
угол θ к направлению движения налетающей частицы. Какие выводы
из решения данной задачи можно сделать о величине средних потерь энергии
налетающей частицы по направлениям вылета ядер отдачи? Примените полученное
решение к задаче об упругом рассеянии 1) нейтронов на протонах, дейтронах, ядрах
9Be, 12С и 238U; 2) a-частиц – на электронах,
протонах, дейтронах, ядрах 238U.
Нерелятивистская частица с массой и кинетической энергией
упруго рассеивается на первоначально покоившемся ядре с массой
. Найти в ц-системе величины импульсов каждой частицы и их суммарную кинетическую энергию до и после рассеяния.
Нерелятивистская частица с массой и кинетической энергией
испытала упругое лобовое соударение с первоначально покоившейся частицей массы
. Найти кинетическую энергию налетающей частицы после соударения.
Нерелятивистская частица массы рассеивается на первоначально покоившейся частице массы
. Найти максимальные углы отклонения частиц, а также максимально возможную относительную потерю энергии падающей частицы при различных соотношениях между массами сталкивающихся частиц. Описать качественную картину рассеяния электронов электронами, электронов ядрами, нейтронов ядрами.
Нейтрон с кинетической энергией МэВ рассеивается на первоначально неподвижном ядре
. Найти возможные значения кинетических энергий рассеянных частиц.
Построить векторные диаграммы импульсов для упругого рассеяния -частицы на первоначально покоившемся ядре а)
; б)
; в)
. В каком случае связь между энергией рассеянной
-частицы и ее углом рассеяния неоднозначна? Найти для этих трех случаев значения максимально возможного угла рассеяния налетающей частицы, а также диапазон изменения кинетических энергий рассеянных частиц (энергию налетающей
-частицы принять равной
МэВ).
Определить значение максимального угла упругого рассеяния дейтрона покоящимся протоном.
Дейтроны с кинетической энергией МэВ упруго рассеиваются на протонах. Найти кинетическую энергию дейтронов, рассеянных на максимально возможных угол.
Нерелятивистский дейтрон упруго рассеялся под углом на первоначально покоившемся ядре
. Найти этот угол, если известно, что соответствующий угол в ц-системе а)
; б)
.
Нерелятивистская -частица упруго рассеялась на ядре
. Определить угол рассеяния
-частицы: а) в л-системе, если в ц-системе
; б) в ц-системе, если в л-системе
.
Выразить косинус угла отклонения падающей частицы с массой в ц-системе чрез ее угол рассеяния в л-системе на первоначально неподвижной частице массы
.
Найти связь углов рассеяния одинаковых по массе частиц, одна из которых до рассеяния покоится.
Нерелятивистский нейтрон упруго рассеялся под углом на покоящемся ядре
, в результате чего последнее отлетело под углом а)
; б)
относительно направления движения налетающего нейтрона. Определить угол
.
Нерелятивистский дейтрон упруго рассеялся на покоившемся ядре под углом . Под таким же углом к направлению движения налетающего дейтрона отлетело и ядро отдачи. Какому атому принадлежит это ядро?
Угол рассеяния -частицы на ядре
оказался равным
. Чему равен при этом угол вылета ядра
?
Определить угол рассеяния первоначально покоившегося ядра с массой
по известному значению угла рассеяния
падающей частицы с массой
. Рассмотреть случай рассеяния протона на ядре
, если
.
Нерелятивистская частица с массой упруго рассеивается на первоначально неподвижной частице массы
. Найти угол разлета частиц
, если частица мишени отлетела на угол
. Какие значения может принимать угол
при разных соотношениях масс сталкивающихся частиц?
Нерелятивистская частица с массой и импульсом
рассеивается на первоначально покоившейся частице с массой
. Найти величины импульсов рассеянных частиц и их углы вылета относительно л-системы как функции импульса налетающей частицы до рассеяния и угла рассеяния частиц в их системе центра масс
.
Какую долю кинетической энергии теряет нерелятивистская -частица при упругом рассеянии под углом
(в ц-системе) на покоившемся ядре
?
Нерелятивистская частица с массой и кинетической энергией
упруго рассеялась на угол
в системе центра масс на первоначально покоившейся частице массы
. Чему равны кинетические энергии частиц после рассеяния в лабораторной системе отсчета и системе центра масс?
Альфа-частица с кинетической энергией МэВ упруго рассеялась на покоившемся ядре
. Определить кинетическую энергию ядра отдачи, отлетевшего под углом
к первоначальному направлению движения
-частицы.
Фотоэмульсии нередко используются в качестве детектора нейтронов. Быстрые нейтроны регистрируются обычно по протонам отдачи. Какие характеристики рассеяния надо измерять, чтобы определить энергию нейтронов? Направление потока нейтронов в эксперименте известно.
При упругом рассеянии нейтрона на ядре массы последнее отлетело на угол
с кинетической энергией
. Найти кинетическую энергию нейтрона до столкновения и его угол рассеяния.
При рассеянии -частицы с кинетической энергией
МэВ на покоившемся ядре
последнее отлетело на
. Чему равны при этом угол рассеяния
-частицы и кинетические энергии рассеянных частиц?
Частица с массой и кинетической энергией
рассеивается на первоначально неподвижной частице с массой
. Чему равна кинетическая энергия падающей частицы, рассеянной на угол
?
Протон с кинетической энергией МэВ упруго рассеивается на неподвижном ядре
на угол
. Найти кинетическую энергию и угол рассеяния ядра отдачи.
Дейтроны с кинетической энергией МэВ испытывают упругое соударение с первоначально неподвижными ядрами
. Под какими углами вылетают ядра отдачи, если дейтроны рассеиваются под углом а)
; б)
? Какую энергию при этом имеют протоны?
Протоны с кинетической энергией МэВ упруго рассеиваются на покоящихся ядрах
. Под каким углом к первоначальному падению вылетят протоны с энергиями
МэВ?
Найти кинетическую энергию налетающей -частицы, если в результате упругого рассеяния ее на дейтроне угол между направлениями разлета обеих частиц
и энергия, которую приобрел дейтрон,
МэВ.
bindushewin
Вопрос по физике:
Найти импульс, полную и кинетическую энергию нейтрона, движущегося со скоростью 0,6 с.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 1
zlwaraisem935
Импульс тела – произведение массы на его скорость.

Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Физика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Физика — область естествознания: естественная наука о простейших и вместе с тем наиболее общих законах природы, о материи, её структуре и движении.
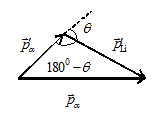 Построим векторную
Построим векторную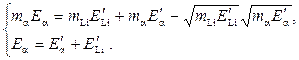 (5)
(5)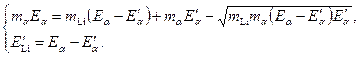 (6)
(6)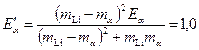 МэВ,
МэВ,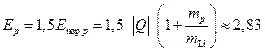 МэВ
МэВ Построим векторную диаграмму для импульсов
Построим векторную диаграмму для импульсов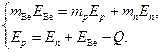 (5)
(5)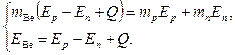 (6)
(6)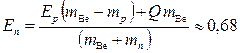 МэВ.
МэВ.