Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 3 октября 2015 года; проверки требуют 5 правок.
Кинетическая энергия вращательного движения — энергия тела, связанная с его вращением.
Основные кинематические характеристики вращательного движения тела — его угловая скорость (
Основные динамические характеристики вращательного движения — момент импульса 

и кинетическая энергия
где  — момент инерции тела относительно оси вращения.
— момент инерции тела относительно оси вращения.
Похожий пример можно найти при рассмотрении вращающейся молекулы с главными осями инерции I1, I2 и I3. Вращательная энергия такой молекулы задана выражением
где ω1, ω2, и ω3 — главные компоненты угловой скорости.
В общем случае, энергия при вращении с угловой скоростью 
, где
— тензор инерции.
В термодинамике[править | править код]
Точно по тем же самым рассуждениям, как и в случае поступательного движения, равнораспределение подразумевает, что при тепловом равновесии средняя вращательная энергия каждой частицы одноатомного газа: (3/2)kBT. Аналогично, теорема о равнораспределении позволяет вычислить среднеквадратичную угловую скорость молекул.
См. также[править | править код]
- Угловая скорость
- Теорема Кёнига
Определим
кинетическую энергию твёрдого тела,
вращающегося вокруг неподвижной оси.
Разобьем это тело на n
материальных точек. Каждая точка движется
с линейной скоростью υi=ωri,
тогда кинетическая энергия точки
или
Полная
кинетическая энергия вращающегося
твердого тела равна сумме кинетических
энергий всех его материальных точек:
(3.22)
(J
– момент инерции тела относительно оси
вращения)
Если
траектории всех точек лежат в параллельных
плоскостях (как у цилиндра, скатывающегося
с наклонной плоскости, каждая точка
перемещается в своей плоскости рис ),
это плоское
движение.
В соответствии с принципом Эйлера
плоское движение всегда можно бесчисленным
количеством способов разложить на
поступательное и вращательное движение.
Если шарик падает или скользит вдоль
наклонной плоскости, он двигается только
поступательно; когда же шарик катится
– он ещё и вращается.
Если
тело совершает поступательное и
вращательное движения одновременно,
то его полная кинетическая энергия
равна
(3.23)
Из
сопоставления формул кинетической
энергии для поступательного и
вращательного движений видно, что мерой
инертности при вращательном движении
служит момент инерции тела.
§ 3.6 Работа внешних сил при вращении твёрдого тела
При
вращении твёрдого тела его потенциальная
энергия не изменяется, поэтому элементарная
работа внешних сил равна приращению
кинетической энергии тела:
dA
= dE
или
Учитывая,
что Jβ
= M,
ωdr
= dφ,
имеем α
тела на конечный угол φ
равна
(3.25)
При
вращении твёрдого тела вокруг неподвижной
оси работа внешних сил определяется
действием момента этих сил относительно
данной оси. Если момент сил относительно
оси равен нулю, то эти силы работы не
производят.
Примеры решения задач
Пример
2.1. Маховик
массой m
=5кг и радиусом r
= 0,2 м вращается вокруг горизонтальной
оси с частотой ν0=720
мин-1
и при торможении останавливается за t
=20 с. Найти тормозящий момент и число
оборотов до остановки.
Решение
Для
определения тормозящего момента применим
основное уравнение динамики вращательного
движения
IΔω
= MΔt
где
I=mr2–
момент инерции диска; Δω
=ω
– ω0,
причём ω
=0 конечная угловая скорость, ω0=2πν0
– начальная. М –тормозящий момент сил,
действующих на диск.
Зная
все величины, можно определить тормозящий
момент
-mr2
2πν0=МΔt
(1)
откуда
(2)
Из
кинематики вращательного движения угол
поворота за время вращения диска до
остановки может быть определён по
формуле
(3)
где β–угловое ускорение.
По условию задачи: ω =ω0
– βΔt, так как ω=0, ω0
= βΔt
Тогда выражение (2) может быть записано
в виде:
Пример 2.2. Два
маховика в виде дисков одинаковых
радиусов и масс были раскручены до
скорости вращения n=
480 об/мин и предоставили самим себе. Под
действием сил трения валов о подшипники
первый остановился через t
=80 с, а второй сделал N=
240 оборотов до остановки. У какого и
маховика момент сил трения валов о
подшипники был больше и во сколько раз.
Решение:
Момент сил терния М1
первого маховика найдём, воспользовавшись
основным уравнением динамики вращательного
движения
M1Δt
= Iω2–
Iω1
где Δt
– время действия момента сил трения,
I=mr2
– момент инерции
маховика , ω1=
2πν и ω2=
0– начальная и конечная угловые скорости
маховиков
Тогда
Момент сил трения М2
второго маховика выразим через связь
между работой А сил трения и изменением
его кинетической энергии ΔEк:
где Δφ = 2πN
– угол поворота, N
-число оборотов маховика.
Тогда , откуда
Отношение
будет равно
Момент сил трения второго маховика в
1.33 раза больше.
Пример
2.3. Масса
однородного сплошного диска m, массы
грузов m1
и m2
(рис.15). Скольжения и трения нити в оси
цилиндра нет. Найти ускорение грузов и
отношение натяжений нити
в процессе движения.
Решение
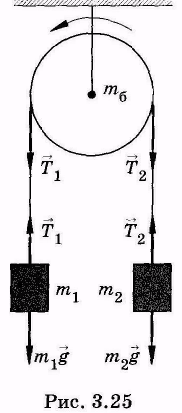
поэтому, когда m1
и m2
будут совершать поступательное движение,
цилиндр будет совершать вращение
относительно оси, проходящей через
точку О. Положим для определённости,
что m2
> m1
.
Тогда груз m2
опускается и цилиндр вращается по
часовой стрелке. Запишем уравнения
движения тел, входящих в систему
Первые два
уравнения записаны для тел с массами
m1
и m2
, совершающих поступательное движение,
а третье уравнение – для вращающегося
цилиндра. В третьем уравнении слева
стоит суммарный момент сил, действующих
на цилиндр (момент силы T1
взят
со знаком минус, так как сила T1
стремится
повернуть цилиндр против часовой
стрелки). Справа I – момент инерции
цилиндра относительно оси О, который
равен
где R – радиус цилиндра; β –
угловое ускорение цилиндра.
Так как
проскальзывания нити нет, то
. С учётом выражений для I и β получим:
Складывая уравнения системы, приходим
к уравнению
Отсюда находим
ускорение a
грузов
Далее легко
найти T1
и T2
и их отношение
Из полученного
уравнения видно, что натяжения нитей
будут одинаковы, т.е. =1,
если масса цилиндра будет гораздо меньше
массы грузов.
Пример
2.4. Полый
шар массой m = 0,5 кг имеет внешний радиус
R = 0,08м и внутренний r = 0,06м. Шар вращается
вокруг оси, проходящей через его центр.
В определённый момент на шар начинает
действовать сила, в результате чего
угол поворота шара изменяется по закону
.
Определить момент приложенной силы.
Решение
Решаем задачу,
используя основное уравнение динамики
вращательного движения .
Основная трудность – определить момент
инерции полого шара, а угловое ускорение
β находим как .
Момент инерции I полого шара равен
разности моментов инерции шара радиуса
R и шара радиуса r:
где ρ – плотность материала шара. Находим
плотность, зная массу полого шара
Отсюда определим плотность материала
шара
Так как
Для момента силы M получаем следующее
выражение:
Пример
2.5. Тонкий
стержень массой 300г и длиной 50см вращается
с угловой скоростью 10с-1
в
горизонтальной плоскости вокруг
вертикальной оси, проходящей через
середину стержня. Найдите угловую
скорость, если в процессе вращения в
той же плоскости стержень переместится
так, что ось вращения пройдёт через
конец стержня.
Решение
Используем
закон сохранения момента импульса
(1)
(Ji-момент
инерции стержня относительно оси
вращения).
Для
изолированной системы тел векторная
сумма моментов импульса остаётся
постоянной. Вследствие того, что
распределение массы стержня относительно
оси вращения изменяется момент инерции
стержня также изменяется в соответствии
с (1):
J0ω1
=
J2ω2.
(2)
Известно,
что момент инерции стержня относительно
оси, проходящей через центр масс и
перпендикулярной стержню, равен
J0
=
mℓ2/12.
(3)
По
теореме Штейнера
J
=J0
+mа2
(J-момент
инерции стержня относительно произвольной
оси вращения; J0
–
момент инерции относительно параллельной
оси, проходящей через центр масс; а–
расстояние от центра масс до выбранной
оси вращения).
Найдём
момент инерции относительно оси,
проходящей через его конец и перпендикулярной
стержню:
J2
=J0
+mа2,
J2
= mℓ2/12
+m(ℓ/2)2
=
mℓ2/3.
(4)
Подставим
формулы (3) и (4) в (2):
mℓ2
ω1/12
=
mℓ2
ω2/3
откуда
ω2
=
ω1/4
ω2
=10с-1/4=2,5с-1
Пример
2.6.
Человек массой m=60кг,
стоящий на краю платформы массой М=120кг,
вращающейся по инерции вокруг неподвижной
вертикальной оси с частотой ν1=12мин-1,
переходит к её центру. Считая платформу
круглым однородным диском, а человека
– точечной массой, определите, с какой
частотой ν2
будет
тогда вращаться платформа.
Дано:
m=60кг,
М=120кг, ν1=12мин-1
= 0,2с-1.
Найти:
ν1
Решение:
Согласно
условию задачи, платформа с человеком
вращается по инерции, т.е. результирующий
момент всех сил, приложенных к вращающейся
системе, равен нулю. Поэтому для системы
«платформа-человек» выполняется закон
сохранения момента импульса
I1ω1=
I2ω2
где
–
момент инерции системы, когда человек
стоит на краю платформы (учли, что момент
инерции платформы, равен(R
– радиус п
момент инерции человека на краю платформы
равенmR2).
–
момент инерции системы, когда человек
стоит в центре платформы (учли, что
момент человека, стоящего в центре
платформы, равен нулю). Угловая скорость
ω1=
2π ν1
и
ω1=
2π ν2.
Подставив
записанные выражения в формулу (1),
получаем
откуда
искомая частота вращения
Ответ:
ν2=24мин-1.
Соседние файлы в папке Физика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Кинетическая энергия вращательного движения

4.6
Средняя оценка: 4.6
Всего получено оценок: 231.
4.6
Средняя оценка: 4.6
Всего получено оценок: 231.
Энергия – это способность к совершению работы. Поскольку существует много способов совершения работы, существуют разные виды энергии. Рассмотрим один из таких видов – кинетическую энергию вращательного движения.
Баланс энергии при совершении работы
Если тело имеет некоторую энергию, то существуют возможности передачи этой энергии другим телам. В частности, если тело обладает потенциальной энергией (например, пружина в сжатом состоянии), то оно может передать эту энергию другим телам, изменяя их положение, и совершая работу.
Согласно законам сохранения энергии, общая сумма энергии в изолированной системе остается постоянной. А значит, если вся энергия тела уйдет на совершение работы, то, определив эту работу, мы можем вычислить энергию, которой обладало тело перед совершением работы.
Формула кинетической энергии при вращении
Кинетической называют энергию движения.
Найдем кинетическую энергию вращающейся материальной точки.
Пусть изначально материальная точка с моментом инерции $J = mR^2$ вращается по траектории радиусом $R$ c угловой скоростью $omega$. Начнем равномерно тормозить вращение, чтобы до полной остановки точка повернулась на угол $alpha$.
При равномерном торможении сила торможения $F$ и момент этой силы $M=FR$ будут постоянными. А значит, согласно Второму Закону Ньютона, угловое ускорение, получаемое материальной точкой, тоже будет постоянным, и равным:
$$varepsilon = {M over J}$$
Для равноускоренного вращения угол поворота и угловая скорость и угловое ускорение связаны соотношением:
$$alpha ={omega_2^2-omega_1^2over 2varepsilon}$$
Учитывая полную остановку вращения, и формулу ускорения, получаем:
$$alpha ={omega^2over 2varepsilon}={omega^2 J over 2M}$$
Во время поворота на этот угол на тело постоянно действовал момент силы торможения $M$, а значит была совершена работа:
$$A = alpha M={omega^2 J over 2}$$
Поскольку материальная точка остановилась – то вся первоначальная кинетическая энергия $E_k$ была направлена на совершение работы, и, таким образом, эта энергия равна совершенной работе.
В итоге мы получили формулу полной кинетической энергий вращательного движения материальной точки:
$$E_k ={omega^2 J over 2}={omega^2 mR^2over 2}$$
Особенности кинетической энергии при вращении
Сравним формулу кинетической энергии при вращении с формулой кинетической энергии тела для прямолинейного движения:
$$E_k ={v^2 m over 2}$$
Можно видеть их близость. Но, в формуле для вращения для материальной точки присутствует дополнительный множитель – радиус. Его необходимость объясняется тем, что при повороте на один и тот же угол, материальная точка, расположенная на более далеком расстоянии от центра вращения, проходит больший путь, по сравнению с более близкой точкой. Поэтому и ее мгновенная линейная скорость, а значит, и кинетическая энергия получается больше. Для твердых тел различной формы радиус вращения также учитывается при определении момента инерции.
В том, что у материальной точки с большим радиусом вращения кинетическая энергия больше, легко убедиться, раскручивая груз на шнуре. Если раскручивать груз с постоянной частотой (скажем, один оборот в секунду), то при малой длине шнура это сделать легко, однако, чем длиннее шнур, тем приходится прилагать больше усилий, хотя масса шнура остается постоянной.
Именно поэтому с помощью пращи камень можно метнуть дальше, чем просто рукой. Больший радиус вращения позволяет сообщить камню большую энергию.
Что мы узнали?
Формула кинетической энергии вращающейся материальной точки аналогична формуле кинетической энергии поступательного движения материальной точки. Вместо линейной скорости используется угловая скорость, а вместо массы – момент инерции. Поскольку момент инерции материальной точки зависит от радиуса вращения, кинетическая энергия вращения материальной точки зависит не только от угловой скорости, но и от радиуса вращения.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 231.
А какая ваша оценка?
Кинематика и динамика вращательного движения твердого тела. Кинематика
движения материальной точки по окружности
Кинетическая энергия вращающегося тела
При вращательном движении работа внешних
сил идет на приращение кинетической энергии вращающегося тела. Она может быть найдена как сумма кинетических энергий всех материальных точек тела
.
Выражая линейные скорости материальных точек тела через угловую скорость
, получим выражение
.
где – момент инерции тела относительно оси вращения. Таким образом, кинетическая энергия тела, вращающегося вокруг неподвижной оси, выражается формулой
. (4.22)
Если центр масс тела перемещается со скоростью и тело вращается вокруг центра масс (участвует в плоском движении), то его полная кинетическая энергия выражается как сумма кинетической энергии центра масс и вращательного движения вокруг центра масс
. (4.23)