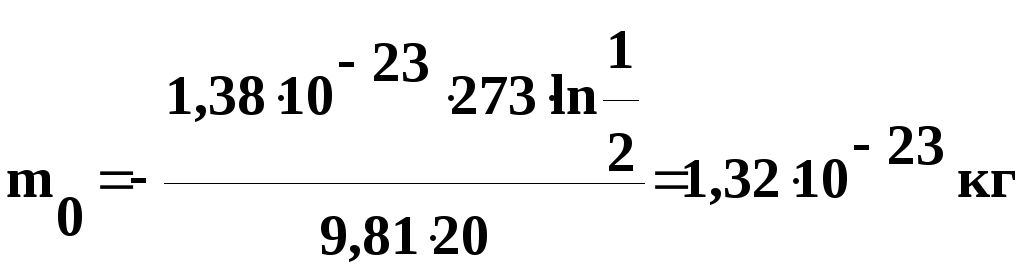Как найти кинетическую энергию вращательного движения молекулы

Как найти кинетическую энергию вращательного движения молекулы

• Основное уравнение
кинетической теории газов

,

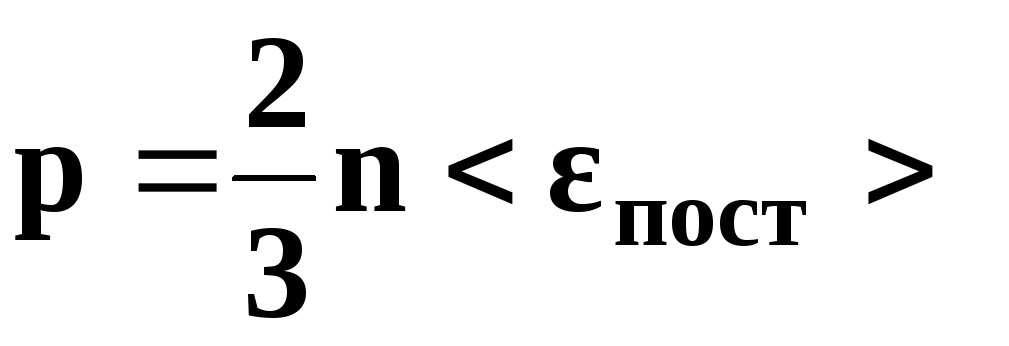
где
р – давление
газа, n
– концентрация
молекул (число молекул в единице объема),
–
средняя кинетическая энергия
поступательного движения одной молекулы,
угловые скобки обозначают осреднение
по

большому
ансамблю частиц, m0
– масса
молекулы,
–
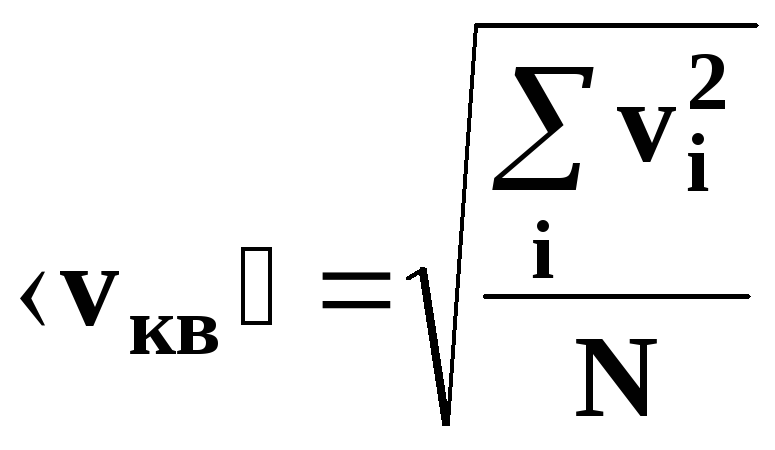
средняя квадратичная скорость движения
молекул.

• Средняя
кинетическая энергия поступательного
движения одной молекулы

,

где
k
=
1,38·10-23
Дж/К –
постоянная Больцмана, Т
– абсолютная температура.

•
Энергия теплового
движения молекул (внутренняя энергия
идеального газа):

,

где
i
– число степеней свободы молекулы, m
– масса газа, М
– молярная
масса данного вещества, R
= 8,31 Дж/(кг·К) –
универсальная газовая постоянная, Т
– абсолютная
температура.

• Числом степеней
свободы называется число независимых
координат полностью определяющих
положение тела в пространстве. Любая
молекула имеет 3 поступательных степени
свободы (iпост=3).
Молекулы,
кроме одноатомных, имеют еще вращательные
степени свободы (у двухатомных молекул
iвр
= 2, у
многоатомных iвр
= 3) и
колебательные степени свободы, которые
при невысоких (комнатных) температурах
не учитываются.

• В соответствии
с законом Больцмана о равномерном
распределении энергии по степеням
свободы, в
среднем на каждую степень свободы
молекулы приходится одинаковая энергия,
равная
.

• Средняя
кинетическая энергия вращательного
движения одной молекулы:

•
Средняя суммарная
кинетическая энергия одной молекулы:

,

где
i
– число степеней свободы молекулы
(i=iпост+
iвр).

• Средняя
квадратичная скорость молекулы:

• Средняя
арифметическая скорость (средняя
скорость теплового движения)молекулы:

,

где m0
– масса одной молекулы, М
– молярная масса вещества, причем
,

NA=
6,023·1023
1/моль –
число Авогадро.

• Барометрическая
формула характеризует изменение давления
газа с высотой в поле сил тяжести:

или
,

где
p
– давление
на высоте h
над уровнем
моря, p0
– давление на высоте h
= 0,
g
– ускорение
свободного падения. Эта формула
приближенная, так как температуру нельзя
считать постоянной для большой разности
высот.

•
Распределение
Больцмана для концентрации частиц в
силовом поле имеет вид:

,

где
n
– концентрация частиц, обладающих
потенциальной энергией Wп
, n0
– концентрация
частиц в точках поля с Wп
= 0.

Примеры
решения задач

Задача
1. Найти
среднюю кинетическую энергию
вращательного движения одной молекулы
кислорода при температуреТ
= 350 К, а также среднюю кинетическую
энергию
вращательного движения всех молекул
кислорода массойm
= 4 г.

Решение.
Согласно закону Больцмана о равном
распределении энергии по степеням
свободы на каждую степень свободы
приходится энергия равная
,
гдеk
– постоянная Больцмана, Т
– абсолютная
температура.

Так
как молекула кислорода двухатомная, у
нее две вращательных степени свободы,
поэтому средняя кинетическая энергия
вращательного движения выразится
формулой:

Подставим
в полученную формулу значения k
= 1,38·10-23
Дж/К, и Т
= 350 К, получим

Кинетическая
энергия всех N
молекул, содержащихся в 4 г кислорода
равна:

Число
всех молекул газа можно вычислить по
формуле:

,
где NA
– число
Авогадро,
–
количество вещества,m
– масса газа, М
– молярная
масса. Учтя приведенные выражения,
получим:

Подставляем
числовые значения: NA
= 6,023·1023
1/моль ; m
= 4 г = 4·10-3
кг ; М
= 32·10-3
кг/моль;
=
4,83·10-21
Дж:

Выведем
размерность полученной величины:

Задача
2. В
воздухе при нормальных условиях взвешены
одинаковые частицы. Известно, что
концентрация частиц уменьшается в два
раза на высоте h
= 20 м. Определить массу частицы.

Решение.
Воспользуемся формулой распределения
Больцмана:

,

где
Wп
= m0gh
– потенциальная
энергия частицы в поле сил тяжести.

Подставив
это выражение в формулу распределения
Больцмана, получим:

Логарифмируем
обе части уравнения по основанию е,
тогда:

,
откуда

Подставив
числовые значения в полученную формулу,
найдем

Выведем
размерность полученной величины:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Решение.
Т = (273 + 27) К = 300 К.
Температура газа связана с средней кинетической энергией движения молекулы соотношением:

[ {{E}_{K}}=frac{i}{2}cdot kcdot T (1). ]

Где: к – постоянная Больцмана, к = 1,38∙10-23 Дж/К, i – количество степеней свободы.
Определим среднее значение кинетической энергии вращательного движения всех молекул водорода (вращательному движению для двухатомной молекулы водорода соответствует количество степеней свободы i = 2)

[ begin{align}
  & {{E}_{K}}({{H}_{2}})=Ncdot frac{2}{2}cdot kcdot T(2),N=frac{m}{M}cdot {{N}_{A}}(3),{{E}_{K}}({{H}_{2}})=frac{m}{M}cdot {{N}_{A}}cdot kcdot T(4). \
 & {{E}_{K}}({{H}_{2}})=frac{0,2cdot {{10}^{-3}}}{2cdot {{10}^{-3}}}cdot 6,02cdot {{10}^{23}}cdot 1,38cdot {{10}^{-23}}cdot 300=249,228. \
end{align} ]

Где: N – количество всех молекул, M – молярная масса молекулы водорода, М(Н2) = 2∙10-3 кг/моль, NА число Авогадро, NА = 6,02∙1023 моль-1.
Ответ: 249,228 Дж.

Источник

С помощью какой формулы можно определить энергию вращательного движения одной молекулы водорода? Заранее спасибо.



Ученик

(98),
закрыт



15 лет назад

Пользователь удален

Мастер

(1087)


15 лет назад

Рано говорите “спасибо”. Во-первых в формуле, которую Вам предлагают, ошибка: между k и T должен быть знак умножения, а не сложения. А, во-вторых, для чего такая формула, когда известен закон равнораспределения энергии по степеням свободы. Известно, что на каждую степень свободы приходится энергия kT/2. У любой молекулы всегда 3 поступательные степени свободы, вращательных: у одноатомной – нет, у двухатомной – 2 (это Ваш случай) , если в молекуле 3 и более атомов – 3, про колебательные степени умолчим (если интересно, пишите) . Следовательно Ваш ответ – kT, где k – постоянная Больцмана, T – абсолютная температура. Успехов!

LordG

Высший разум

(109572)


15 лет назад

Средняя кинетическая энергия вращательного движения молекулы:
[(i – 3) / 2] * k + T,
где
i – число степеней свободы, для двухатомного газа (водород) равно 5
k – постоянная Больцмана, равна 1,38∙10 в степени -23 Дж/К
T – абсолютная температура, в кельвинах

andy

Гуру

(4916)


15 лет назад

Если позволите, поправлю LordG. Следует найти энергию ВРАЩАТЕЛЬНОГО движения. Следовательно Нужно убрать три степери свободы, которые описывают поступательное движение. Остаются две степени свободы – вращение в плоскости oxy и вращение в плоскости oxz. Любое другое вращение будет учтено, как сумма вращений в этих плоскостях.
i=2
Удачи!

LordGВысший разум (109572)

15 лет назад

А не надо поправлять !!!
Формулу видим ???
А что там стоит ???
(i-3) !!!
Так что i все-таки равно 5 !

Источник
Автор статьи

Виктор Матвеевич Скоков

Эксперт по предмету «Физика»

Задать вопрос автору статьи

Количество независимых переменных, которыми определяется состояние системы, называют числом степеней свободы. Для полной характеристики энергетического состояния движения материальной точки в момент времени t требуется задать три компоненты скорости для того, чтобы определить кинетическую энергию и три координаты, чтобы определить потенциальную энергию, получается всего необходимо шесть переменных. В случае динамического рассмотрения движения материальной точки эти переменные являются зависимыми. Статистическая система, которая состоит из n точек, имеет 6n степеней свободы. Из них 3n степеней свободы — носители кинетической энергии и 3n — носители потенциальной энергии, если система находится в поле внешних сил или частицы взаимодействуют между собой.

Степени свободы

Степени свободы делят на: поступательные, вращательные и колебательные. Три степени свободы материальной точки – поступательные. Система из n материальных точек, между которыми нет жестких связей имеет 3 n степени свободы. Каждая жесткая связь уменьшает число степеней свободы на единицу. Рассмотрим молекулу, состоящую из двух атомов, если считать, что между атомами существует одна жесткая связь, то такая молекула имеет пять степеней свободы, три поступательные и две вращательные. Если связь квазиупругая, то степеней свободы будет шесть, причем из них три поступательные, две вращательные и одна колебательная. Трехатомной нелинейной молекуле с жесткой связью между атомами нужно приписать шесть степеней свободы – три поступательные, три вращательные. Поступательные степен свободы не имеют преимуществ друг перед другом.

Средняя энергия молекулы

Согласно закону равномерного распределения энергии по степеням свободы на каждую степень свободы в среднем приходится одинаковая кинетическая энергия равная $leftlangle {varepsilon }_irightrangle =frac{1}{2}kT$. В таком случае можно сказать, что средняя энергия молекулы $leftlangle {varepsilon } rightrangle$ равна:

где $i=m_{post}+m_{vr}+2m_{kol}$- сумма числа поступательных, вращательных и удвоенного количества колебательных степеней свободы, $k$ — постоянная Больцмана, T- термодинамическая температура. Возникновение коэффициента 2 при подсчёте энергии колебаний объясняется просто: При колебаниях частица имеет как кинетическую, так и потенциальную энергии. Если колебания гармонические, то эти энергии в среднем равны друг другу. Соответственно, $leftlangle {varepsilon }_{kol}rightrangle =kT$.

Закон равномерного распределения энергии по степеням свободы является приближенным, так как получен на основе классической механики и нарушается, если существенными становятся квантовые эффекты.

«Энергия молекул» 👇

Необходимо отметить, что поступательно могут двигаться только молекулы газов.

Из(1) следует, что одноатомные молекулы имеют среднюю кинетическую энергию:

Полную энергию i частицы можно представить:

[{varepsilon }_i=frac{1}{2}m_i{v_i}^2+frac{1}{2}left(J_{i1}{w_{i1}}^2+J_{i2}{w_{i2}}^2+J_{i3}{w_{i3}}^2right)+sumlimits_j{frac{m_{ij}{{eta }_{ij}}^2}{2}}+sumlimits_j{frac{k_{ij}{{xi }_{ij}}^2}{2}}+U_ileft(x_i,y_i,z_iright) left(3right),]

где $U_ileft(x_i,y_i,z_iright)$- потенциальная энергия сложной частицы во внешних полях, ${xi }_{ij}$- отклонение от положения равновесия частицы при колебаниях, ${eta }_{ij}$- скорость колебательных движений частицы, первый индекс обозначает номер сложной частицы, второй определяет номер частицы внутри сложной, $v_i$ — скорость центра масс сложной частицы, $m_i$- масс частицы, $J_1,J_2,J_3$- моменты инерции вращения частицы, $w_1,w_2,w_3$ — угловые скорости вращения частицы относительно ее главных осей. Индекс j принимает столько значений, сколько необходимо, чтобы исчерпать все степени свободы сложной частицы.

Пример 1

Задание: Сравните средние энергии молекул кислорода и азота при одинаковых температурах.

Решение:

Кислород имеет двухатомную молекулу ($O_2)$, предположим, что связь между атомами жесткая, следовательно, молекула кислорода обладает пятью степенями свободы (тремя поступательными и двумя вращательными). Из закона равномерного распределения энергии по степеням свободы имеем средняя энергия молекулы:

[leftlangle varepsilon rightrangle =frac{i}{2}kTto leftlangle {varepsilon }_{O_2}rightrangle =frac{5}{2}kT left(1.1right)]

Азот имеет двухатомную молекулу ($N_2)$, предположим, что связь между атомами жесткая, следовательно, молекула азота также обладает пятью степенями свободы. Соответственно:

[leftlangle {varepsilon }_{N_2}rightrangle =frac{5}{2}kTleft(1.2right).]

Ответ: Средние энергии молекул кислорода и азота при одинаковых температурах одинаковы.

Пример 2

Задание: Водород находится в сосуде при температуре T=300K. Определите среднюю энергию вращательного движения молекул.

Решение:

Основой для решения задачи является закон равномерного распределения энергии по степеням свободы. Из него известно, что на каждую степень свободы приходится в среднем энергия $leftlangle {varepsilon }_irightrangle $, равная:

[leftlangle {varepsilon }_irightrangle =frac{1}{2}kT left(2.1right).]

Следовательно, чтобы решить задачу, осталось определить, сколько вращательных степеней свободы имеет молекула водорода. Для этого вспомним химическую формулу водорода:

[H_2.]

В молекуле имеется два атома, если молекула жесткая, то общее число степеней свободы такой молекулы будет равно пяти. Из них три приходятся на поступательные степени свободы, на вращательные степени свободы остается две степени. Соответственно:

[leftlangle {varepsilon }_{vr}rightrangle =frac{2}{2}kT=kTleft(2.2right)]

Проведем расчет:

[leftlangle {varepsilon }_{vr}rightrangle =1,38cdot {10}^{-23}cdot 300=4,14cdot {10}^{-21}(Дж)]

Ответ: Средняя энергия вращательного движения молекул водорода при заданных условиях равна $4,14cdot {10}^{-21}Дж$.

Пример 3

Задание: Чему равна суммарная средняя кинетическая энергия молекул двухатомного газа, заключенного в объеме 4 л при давлении 1,47 $cdot {10}^5$Па? Молекулы считать жесткими.

Решение:

Жесткие двухатомные молекулы имеют пять степеней свободы. Средняя энергия движения молекулы определяет формула:

[leftlangle varepsilon rightrangle =frac{i}{2}kTto leftlangle varepsilon rightrangle =frac{5}{2}kTleft(3.1right).]

Следовательно кинетическая энергия всех N молекул газа может быть найдена, как:

[leftlangle Erightrangle =frac{5}{2}NkT left(3.2right).]

Из уравнения состояния идеального газа:

[p=nkT, где n=frac{N}{V}to pV=NkTleft(3.3right).]

Подставим в (3.2) уравнение из (3.3), получим:

[leftlangle Erightrangle =frac{5}{2}pV left(3.4right).]

Переведем данные в СИ: V=4 л=4$cdot {10}^{-3}м^3$

Проведем расчет:

[leftlangle Erightrangle =frac{5}{2}1,47 cdot {10}^5cdot 4cdot {10}^{-3}=1470 (Дж)]

Ответ: Суммарная средняя кинетическая энергия молекул двухатомного газа при заданных условиях равна $1470 Дж.$

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 3 октября 2015 года; проверки требуют 5 правок.

Кинетическая энергия вращательного движения — энергия тела, связанная с его вращением.

Основные кинематические характеристики вращательного движения тела — его угловая скорость (omega ) и угловое ускорение.

Основные динамические характеристики вращательного движения — момент импульса L относительно оси вращения z, а именно:

L_{z}=I_{z}omega

и кинетическая энергия

{displaystyle E_{k}={frac {I_{z}omega ^{2}}{2}}}
где {displaystyle I_{z}} — момент инерции тела относительно оси вращения.

Похожий пример можно найти при рассмотрении вращающейся молекулы с главными осями инерции I1, I2 и I3. Вращательная энергия такой молекулы задана выражением

H^{{{mathrm {rot}}}}={tfrac {1}{2}}(I_{{1}}omega _{{1}}^{{2}}+I_{{2}}omega _{{2}}^{{2}}+I_{{3}}omega _{{3}}^{{2}}),

где ω1, ω2, и ω3 — главные компоненты угловой скорости.

В общем случае, энергия при вращении с угловой скоростью vecomega находится по формуле:

{displaystyle T={frac {1}{2}}{vec {omega }}^{T}cdot Icdot {vec {omega }}}, где I — тензор инерции.

В термодинамике[править | править код]

Точно по тем же самым рассуждениям, как и в случае поступательного движения, равнораспределение подразумевает, что при тепловом равновесии средняя вращательная энергия каждой частицы одноатомного газа: (3/2)kBT. Аналогично, теорема о равнораспределении позволяет вычислить среднеквадратичную угловую скорость молекул.

См. также[править | править код]

  • Угловая скорость
  • Теорема Кёнига
Источник

Добавить комментарий