Энергия связи атомных ядер
Важнейшую роль во всей ядерной физике играет понятие энергии связи ядра. Энергия связи позволяет объяснить устойчивость ядер, выяснить, какие процессы ведут к выделению ядерной энергии. Нуклоны в ядре прочно удерживаются ядерными силами. Для того чтобы удалить нуклон из ядра, надо совершить довольно большую работу, т. е. сообщить ядру значительную энергию.
Под энергией связи ядра понимают ту энергию, которая необходима для полного расщепления ядра на отдельные нуклоны. На основе закона сохранения энергии можно также утверждать, что энергия связи ядра равна той энергии, которая выделяется при образовании ядра из отдельных частиц.
Энергия связи атомных ядер очень велика. Но как ее определить?
В настоящее время рассчитать энергию связи теоретически, подобно тому как это можно сделать для электронов в атоме, не удается. Выполнить соответствующие расчеты можно, лишь применяя соотношение Эйнштейна между массой и энергией:
Точнейшие измерения масс ядер показывают, что масса покоя ядра Мя всегда меньше суммы масс входящих в его состав протонов и нейтронов:
Существует, как говорят, дефект масс: разность масс
положительна. В частности, для гелия масса ядра на 0,75% меньше суммы масс двух протонов и двух нейтронов. Соответственно для гелия в количестве вещества один моль ΔM = 0,03 г.
Уменьшение массы при образовании ядра из нуклонов означает, что при этом уменьшается энергия этой системы нуклонов на значение энергии связи Есв:
Но куда при этом исчезают энергия Есв и масса ΔM?
При образовании ядра из частиц последние за счет действия ядерных сил на малых расстояниях устремляются с огромным ускорением друг к другу. Излучаемые при этом γ-кванты как раз обладают энергией Есв и массой
Энергия связи — это энергия, которая выделяется при образовании ядра из отдельных частиц, и соответственно это та энергия, которая необходима для расщепления ядра на составляющие его частицы.
О том, как велика энергия связи, можно судить по такому примеру: образование 4 г гелия сопровождается выделением такой же энергии, что и при сгорании 1,5—2 вагонов каменного угля.
Важную информацию о свойствах ядер содержит зависимость удельной энергии связи от массового числа А.
Удельной энергией связи называют энергию связи, приходящуюся на один нуклон ядра. Ее определяют экспериментально. Из рисунка 13.11 хорошо видно, что, не считая самых легких ядер, удельная энергия связи примерно постоянна и равна 8 МэВ/нуклон. Отметим, что энергия связи электрона и ядра в атоме водорода, равная энергии ионизации, почти в миллион раз меньше этого значения. Кривая на рисунке 13.11 имеет слабо выраженный максимум. Максимальную удельную энергию связи (8,6 МэВ/нуклон) имеют элементы с массовыми числами от 50 до 60, т. е. железо и близкие к нему по порядковому номеру элементы. Ядра этих элементов наиболее устойчивы.
У тяжелых ядер удельная энергия связи уменьшается за счет возрастающей с увеличением Z кулоновской энергии отталкивания протонов. Кулоновские силы стремятся разорвать ядро.
Частицы в ядре сильно связаны друг с другом. Энергия связи частиц определяется по дефекту масс.
Ядерные реакции
Атомные ядра при взаимодействиях испытывают превращения. Эти превращения сопровождаются увеличением или уменьшением кинетической энергии участвующих в них частиц.
Ядерными реакциями называют изменения атомных ядер при взаимодействии их с элементарными частицами или друг с другом. С примерами ядерных реакций вы уже ознакомились в § 103. Ядерные реакции происходят, когда частицы вплотную приближаются к ядру и попадают в сферу действия ядерных сил. Одноименно заряженные частицы отталкиваются друг от друга. Поэтому сближение положительно заряженных частиц с ядрами (или ядер друг с другом) возможно, если этим частицам (или ядрам) сообщена достаточно большая кинетическая энергия. Эта энергия сообщается протонам, ядрам дейтерия — дейтронам, α-частицам и другим более тяжелым ядрам с помощью ускорителей.
Для осуществления ядерных реакций такой метод гораздо эффективнее, чем использование ядер гелия, испускаемых радиоактивными элементами. Во-первых, с помощью ускорителей частицам может быть сообщена энергия порядка 105 МэВ, т. е. гораздо большая той, которую имеют α-частицы (максимально 9 МэВ). Во-вторых, можно использовать протоны, которые в процессе радиоактивного распада не появляются (это целесообразно потому, что заряд протонов вдвое меньше заряда α-частиц, и поэтому действующая на них сила отталкивания со стороны ядер тоже в 2 раза меньше). В-третьих, можно ускорить ядра более тяжелые, чем ядра гелия.
Первая ядерная реакция на быстрых протонах была осуществлена в 1932 г. Удалось расщепить литий на две α-частицы:
Как видно из фотографии треков в камере Вильсона (рис. 13.12), ядра гелия разлетаются в разные стороны вдоль одной прямой согласно закону сохранения импульса (импульс протона много меньше импульса возникающих α-частиц; на фотографии треки протонов не видны).
Энергетический выход ядерных реакций. В описанной выше ядерной реакции кинетическая энергия двух образующихся ядер гелия оказалась больше кинетической энергии вступившего в реакцию протона на 7,3 МэВ. Превращение ядер сопровождается изменением их внутренней энергии (энергия связи). В рассмотренной реакции удельная энергия связи в ядрах гелия больше удельной энергии связи в ядре лития. Поэтому часть внутренней энергии ядра лития превращается в кинетическую энергию разлетающихся α-частиц.
Изменение энергии связи ядер означает, что суммарная энергия покоя участвующих в реакциях ядер и частиц не остается неизменной. Ведь энергия покоя ядра Мя*с2 согласно формуле (13.5) непосредственно выражается через энергию связи. В соответствии с законом сохранения энергии изменение кинетической энергии в процессе ядерной реакции равно изменению энергии покоя участвующих в реакции ядер и частиц.
Энергетическим выходом ядерной реакции называется разность энергий покоя ядер и частиц до реакции и после реакции. Согласно вышесказанному энергетический выход ядерной реакции равен также изменению кинетической энергии частиц, участвующих в реакции.
Если суммарная кинетическая энергия ядер и частиц после реакции больше, чем до реакции, то говорят о выделении энергии. В противном случае реакция идет с поглощением энергии.
Выделяющаяся при ядерных реакциях энергия может быть огромной. Но использовать ее при столкновениях ускоренных частиц (или ядер) с неподвижными ядрами мишени практически нельзя. Ведь бо́льшая часть ускоренных частиц пролетает мимо ядер мишени, не вызывая реакцию.
Ядерные реакции на нейтронах. Открытие нейтрона было поворотным пунктом в исследовании ядерных реакций. Так как нейтроны не имеют заряда, то они беспрепятственно проникают в атомные ядра и вызывают их изменения. Например, наблюдается следующая реакция:
Великий итальянский физик Энрико Ферми первым начал изучать реакции, вызываемые нейтронами. Он обнаружил, что ядерные превращения обусловлены не только быстрыми, но и медленными нейтронами. Причем эти медленные нейтроны оказываются в большинстве случаев даже гораздо более эффективными, чем быстрые. Поэтому быстрые нейтроны целесообразно предварительно замедлять. Замедление нейтронов до тепловых скоростей происходит в обыкновенной воде. Этот эффект объясняется тем, что в воде содержится большое число ядер водорода — протонов, масса которых почти равна массе нейтронов. Следовательно, нейтроны после соударений движутся со скоростью теплового движения. При центральном соударении нейтрона с покоящимся протоном он целиком передает протону свою кинетическую энергию.
Реакции, в которые вступают атомные ядра, очень разнообразны. Нейтроны не отталкиваются ядрами и поэтому особенно эффективно вызывают превращения ядер.
Тест
Напомним, что кинематикой
называют раздел механики, посвященный
изучению геометрических свойств движения
тел без учета действующих на тела сил.
Движение любого тела в кинематике
изучают по отношению к некоторой системе
координат, позволяющей задать относительное
положение движущегося объекта в любой
момент времени. В ядерной физике обычно
используют две системы координат:
лабораторную (ЛСК), связанную с
ядром-мишенью, и систему центра инерции
(СЦИ), определение которой будет
дано ниже.
Кинематическая схема ядерной
реакции и связь между энергиями,
импульсами и углами вылета частиц в ЛСК
и СЦИ имеет наглядное графическое
представление и может быть проанализирована
с помощью импульсной диаграммы
(векторной диаграммы импульсов).
Построение импульсной диаграммы основано
на применении законов сохранения энергии
и импульса.
Рассмотрение
выполним для случая, когда скорости
движения объектов существенно меньше
скорости света, т.е. когда массы
частиц m >> T
– их кинетической энергии, и можно
использовать законы классической
механики.
Пусть
имеется произвольная инерциальная
система координат К’, которая движется
относительно ЛСК со скоростью
![]()
.
Тогда скорость
![]()
любой
из i = 1,
2, 3, . . . , N частиц в ЛСК
и скорость
![]()
в К’‑системе связаны следующим
образом (принцип относительности
Галилея):
|
|
(4.5.1) |
Закон
сохранения импульса для выбранной
совокупности частиц записывается
следующим образом:
|
|
(4.5.2) |
Первое слагаемое в правой части есть
суммарный импульс
![]()
частиц
в К’-системе, а второе – определяет
импульс движения К’-системы как
целого относительно ЛСК, который
носит название переносного импульса.
Соответствующим выбором вектора скорости
можно
добиться, чтобы суммарный импульс частиц
в К’-системе был равен нулю:
|
|
(4.5.3) |
Система
координат, в которой суммарный импульс
![]()
частиц
равен нулю, называется системой центра
инерции (СЦИ). Условимся величины,
относящиеся к СЦИ, обозначать сверху
значком “~” (тильда). Положив в (4.5.2)
= 0,
найдем скорость движения СЦИ
относительно ЛСК:
|
|
(4.5.4) |
Обратимся
к рассмотрению процесса (4.1.1). Пусть в
ЛСК
частица а
движется со скоростью
![]()
,
а ядро-мишень А
– покоится. Используя (4.5.4) найдем
скорость движения центра инерции системы
(или составного ядра, если таковое
образуется) относительно ЛСК:
|
|
(4.5.5) |
Из сотношения
(4.5.2) и (4.5.5) следует, что переносной
импульс СЦИ
относительно ЛСК
равен импульсу частицы а
в ЛСК:
|
|
(4.5.6) |
Поместим ядро-мишень
А в начале координат (рис. 4.5.1). Если
частица а движется параллельно оси
Х навстречу частице А, то из
(4.5.5) следует, что координата центра
инерции
![]()
на
оси Х в любой момент времени связано
следующим образом с координатой ха
частицы а:
|
|
(4.5.7) |
т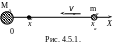
.к.
скорость движения вдоль оси Х есть
dx/dt.
На рисунке показано, что центр инерции
всегда располагается между частицами
а и А,
двигаясь вдоль оси Х со скоростью
![]()
,
относительно ядра-мишени А.
Найдем с помощью
(4.5.1) и (4.5.5) скорости движения частицы а
и ядра-мишени А в СЦИ и
соответствующие им импульсы:
|
|
(4.5.8) |
|
|
(4.5.9) |
Таким
образом, импульсы частиц а и А
в СЦИ равны друг другу и противоположно
направлены, как и должно быть.
Используя
(4.5.8) и (4.5.9), выразим суммарную
кинетическую энергию
![]()
частиц a и А в СЦИ
через кинетическую энергию Тa
частицы a
в ЛСК
|
|
(4.5.10) |
Кинетическая
энергия
есть энергия взаимного движения частиц
а и А и она меньше суммарной
кинетической энергии Т1 =
Та
на величину
|
|
(4.5.11) |
которая есть ничто иное, как кинетическая
энергия движения центра инерции системы
(или составного ядра) относительно ЛСК.
Действительно, кинетическая энергия
движения частиц а и А относительно
ЛСК равна
|
|
(4.5.12) |
Очевидно,
что кинетическая энергия (4.5.12) движения
центра инерции системы не может перейти
во внутреннюю энергию частиц и не может
быть использована в ядерной реакции.
На
этом закончим рассмотрение входного
канала процесса (4.1.1) и перейдем к
рассмотрению выходного канала.
В ЛСК
сумма импульсов частиц b
и В, образовавшихся в результате
ядерной реакции, по закону сохранения
импульса равна импульсу налетающей
частицы а:
|
|
(4.5.13) |
Н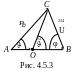
а
рис. 4.5.2 представлена схема одного из
возможных вариантов разлета продуктов
реакции, а на рис. 4.5.3 графический аналог
векторного уравнения (4.5.13). На этих
рисунках
и
φ – углы вылета частиц b
и B относительно
направления движения частицы а.
Очевидно, что отрезок СВ на рис.
4.5.3 равен импульсу![]()
на рис. 4.5.2. Остальные величины совпадают
с рис. 4.5.2. Поэтому в дальнейшем будем
рассматривать векторный треугольник
АСВ (рис. 4.5.3).
Так
как сумма импульсов частиц b
и В относительно ЛСК согласно
(4.5.6) должна быть равна импульсу
![]()
,
т.е. (см. (4.5.6))
|
|
(4.5.14) |
то отношение
|
|
(4.5.15) |
и в соответствии с (4.5.15) точка О
на рис. 4.5.3 делит отрезок АВ =![]()
на отрезки АО =
![]()
и
ОВ =
![]()
,
т.е. АО/ОВ = ma/MA.
Очевидно,
что ОС =![]()
,
так как
|
|
(4.5.16) |
а угол
![]()
на рис. 4.5.3 – есть угол вылета частицы b
в СЦИ.
Вектор
![]()
,
согласно свойствам СЦИ, равен вектору
![]()
по абсолютной величине:
|
|
(4.5.17) |
и направлен в
противоположную сторону, т.е. частицы
b и B
в СЦИ разлетаются с равными и
противоположными импульсами.
Вычислим величину
![]()
.
Из формулы (4.4.6):
|
|
(4.5.18) |
Или, учитывая
(4.5.10),
|
|
(4.5.19) |
Из последнего
уравнения находим
|
|
(4.5.20) |
где
|
|
(4.5.21) |
– есть приведенная
масса частиц b и B.
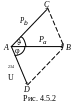
П
олученные
результаты можно использовать для
построения векторной диаграммы импульсов,
графически связывающей импульсы в ЛСК
и СЦИ. Для этого отрезок АВ,
изображающий импульс Ра
(рис. 4.5.4), надо разделить точкой
О в отношении
![]()
.
Затем из этой точки радиусом
![]()
(4.5.20)
следует провести окружность, которая
является геометрическим местом точек
С для любого угла
вылета частицы b.
Тогда, если известна хотя бы одна из
величин Рb
, РB
,
,
φ,
![]()
,
![]()
,
то из диаграммы можно определить
графически все остальные.
В
случае упругого рассеяния (Q
= 0) состав выходного канала тождественен
составу входного канала и из (4.5.20)
следует, что
|
|
(4.5.22) |
Далее построение
векторной диаграммы импульсов для
упругого рассеяния не имеет особенностей
и выполняется аналогичным образом.
Приведем
теперь несколько примеров применения
законов сохранения в ядерных реакциях.
Определим
энергетический порог для
эндоэнергетической реакции. В СЦИ
из формулы (4.4.6) имеем
|
|
(4.5.22) |
и, следовательно, минимальное значение
![]()
(когда
![]()
–
продукты реакции неподвижны)
составит
|
|
(4.5.23) |
Используя (4.5.10) найдем
минимальную кинетическую энергию
частицы а в лабораторной системе
координат (ЛСК):
|
|
(4.5.24) |
Полученное
значение кинетической энергии
бомбардирующей частицы в ЛСК, при
котором становится возможным протекание
эндоэнергетической реакции, называется
порогом реакции.
Получим формулу
(4.2.2) для вычисления возможной энергии
Wc
возбуждения составного ядра. По
определению
|
|
(4.5.25) |
где массы
основного и возбужденного состояний
составного ядра выражены в энергетических
единицах.
Пусть
ядро-мишень А покоится. Запишем
законы сохранения энергии и импульса
для первой стадии реакции
|
a + A |
(4.5.26) |
стадии образования составного ядра С*
(звездочка означает возбужденное
состояние):
|
|
(4.5.27) |
Рассмотрение
проведем для нерелятивистского случая,
когда кинетическая энергия налетающей
частицы Та
≤ 10 МэВ << ma.
Тогда
|
|
(4.5.28) |
Подставляя
(4.5.28) в (4.5.27), получим
квадратное уравнение для нахождения
![]()
:
|
|
(4.5.29) |
В
(4.5.29) последнее слагаемое составляет
ничтожную долю от первых двух, так как
![]()
.
Поэтому в качестве первого приближения
принимаем
![]()
.
Для получения второго приближения
подставляем это выражение в (4.5.29).
Получаем
|
|
(4.5.30) |
Подставив
(4.5.30) в (4.5.25), получим формулу
|
|
(4.5.31) |
Первый
член в этом выражении есть ни что иное,
как энергия отделения
![]()
частицы а
от составного ядра (см., например,
(1.4.17)). Второй член
– суммарная кинетическая энергия
частиц
a
и А до реакции в системе центра
инерции. Итак,
|
|
(4.5.32) |
На
рис. 4.5.5а приведена энергетическая
диаграмма для экзоэнергетической
реакции (Q > 0),
а на рис. 4.5.5б – для эндоэнергетической
реакции (Q < 0).
На диаграммах изображен процесс
образования составного возбужденного
ядра
![]()
и его распад с образованием част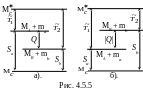
иц
B и b
для обоих типов реакций. Sа = MA
+ ma – Mc
– есть энергия связи частицы а,
а Sb = MB
+ mb – Mc
– частицы b
относительно составного ядра Мс
соответственно.
![]()
![]()
Примеры
3.1. a-частица с
кинетической энергией ![]() МэВ упруго рассеялась на
МэВ упруго рассеялась на
покоившемся ядре ![]() . Определить кинетические энергии
. Определить кинетические энергии
![]() -частицы
-частицы ![]() и ядра
и ядра
отдачи ![]() , если угол между направлениями разлета
, если угол между направлениями разлета
обеих частиц θ = 120˚.
|
Дано |
Решение |
|
a-частица:
___________
|
Так как кинетическая энергия Закон сохранения импульса:
Закон сохранения энергии:
Учтем, что кинетическая энергия
Запишем и решим систему из двух
Из второго уравнения системы (5) выразим
Преобразуя первое уравнение
Кинетические энергии a-частицы и ядра лития после рассеяния соответственно равны
|
|
Ответ: |
3.2. Литиевую мишень облучают пучком протонов с кинетической энергией, в 1,5 раза превышающей ее пороговое
значение (![]() ). Найти кинетическую энергию нейтронов,
). Найти кинетическую энергию нейтронов,
вылетающих в результате реакции 7Li(p,n)7Be с энергией реакции ![]() МэВ под углом θ = 90˚
МэВ под углом θ = 90˚
к пучку протонов.
|
Дано |
Решение |
|
7Li(p,n)7Be
|
Значение пороговой кинетической
Т. к.
(причем Закон Закон
Учтем, что кинетическая энергия
Запишем и решим систему из двух
Из второго уравнения системы
Найдем кинетическую энергию
|
|
Ответ: |
Контрольные вопросы
1. Как найти скорость
движения c-системы относительно л-системы?
2. Как связаны между
собой импульсы частиц в c-системе и в л-системе?
3. Можно ли, исходя
только из законов сохранения импульса и энергии, найти cosc, где c – угол разлета продуктов реакции относительно
направления движения сталкивающихся частиц в с-системе?
4. Как будут связаны величины
импульсов частиц до и после реакции
в c-системе при упругом рассеянии?
5. Проанализируйте
формулы (3.13) и (3.14) для случая упругого рассеяния. Что Вы можете сказать о
случае, когда масса налетающей частицы больше массы частицы, покоящейся в
л-системе?
Задачи
1. Найдите кинетическую энергию ядра отдачи,
возникшего в результате упругого рассеяния частицы с массой m и
кинетической энергией Е на первоначально покоившемся ядре с массой M(Z, A), если его импульс составляет
угол θ к направлению движения налетающей частицы. Какие выводы
из решения данной задачи можно сделать о величине средних потерь энергии
налетающей частицы по направлениям вылета ядер отдачи? Примените полученное
решение к задаче об упругом рассеянии 1) нейтронов на протонах, дейтронах, ядрах
9Be, 12С и 238U; 2) a-частиц – на электронах,
протонах, дейтронах, ядрах 238U.
2018-07-08 ![]()
Найти кинетическую энергию ядра отдачи при позитронном распаде ядра $N^{13}$ в том случае, когда энергия позитрона максимальна.
Решение:
Кинетическая энергия позитрона максимальна, когда энергия нейтрино равна нулю. Поскольку энергия отдачи ядра довольно мала, его можно вычислить последовательным приближением. Реакция
$N^{13} rightarrow C^{13} + e^{+} + nu_{e}$.
Максимальная энергия, доступная для позитрона (включая его энергию покоя), равна
$c^{2} (масса : ядра : N^{13} – масса : ядра : C^{13}) = c^{2} (масса : атома : N^{13} – масса : атома : C^{13} – m_{e}) = 0,00239c^{2} – m_{e}c^{2} = (0,00239 cdot 931 – 0,511) МэВ = 1,71 МэВ$
Импульс, соответствующий этой энергии, составляет $1,636 МэВ / с$. Энергия отдачи ядра тогда
$E = frac{p^{2} }{2M} = frac{1,636^{2}}{2 cdot 13 cdot 931} = 0,111 кэВ$
При использовании $Mc^{2} = 13 cdot 931 МэВ$
|
|
Макеты страниц
1. Направление радиоактивных превращений (сопоставление изобарных ядер). Пользуясь поясненной в предыдущем параграфе формулой  и положением, что самопроизвольное
и положением, что самопроизвольное
превращение ядра возможно только в направлении уменьшения массы покоя (§ 110, стр. 548), нетрудно ответить на следующие вопросы:
1) Почему при одинаковом притяжении между нейтроном и протоном, а также нейтроном и нейтроном не наблюдается ядер, состоящих из одних нейтронов, без протонов?
2) Почему одни ядра устойчивы, а другие неустойчивы и как предугадать тип радиоактивности неустойчивого ядра: будет ли она электронной, позитронной или альфа-распадом?
3) Почему в стабильных (не слишком тяжелых ядрах) число протонов и нейтронов близко к равенству?
Отсутствие ядер, состоящих из одних нейтронов, объясняется весьма просто — неустойчивостью самого нейтрона, который в свободном (внеядерном) состоянии имеет массу, превышающую сумму масс протона и электрона на  В связи с этим в превращении
В связи с этим в превращении  освобождается энергия
освобождается энергия 
Очевидно, что если бы произошло соединение двух нейтронов в «бинейтрон» или большего их числа в один комплекс, радиоактивный распад в нем нейтронов быстро превратил бы его в обычное атомное ядро.
Допустим, например, как бы это ни было маловероятно, что вследствие большой концентрации нейтронов и их взаимного притяжения случайно возник комплекс из семи нейтронов. Ничто не препятствует немедленному превращению одного из нейтронов этого комплекса в протон, что должно было бы привести к возникновению ядра  Для превращения нейтрона в протон нужно, чтобы энергия исходного ядра превышала энергию образующегося не менее чем на
Для превращения нейтрона в протон нужно, чтобы энергия исходного ядра превышала энергию образующегося не менее чем на  Применяя формулу (34), нетрудно убедиться, что возможно превращение еще одного и даже еще двух нейтронов в протоны, так что вместо ядер
Применяя формулу (34), нетрудно убедиться, что возможно превращение еще одного и даже еще двух нейтронов в протоны, так что вместо ядер  в итоге получится ядро
в итоге получится ядро  Такой же подсчет по формуле (34) показывает, что в ядре
Такой же подсчет по формуле (34) показывает, что в ядре  превращение еще одного, четвертого нейтрона в протон без сообщения дополнительной энергии извне уже невозможно; и действительно, ядро
превращение еще одного, четвертого нейтрона в протон без сообщения дополнительной энергии извне уже невозможно; и действительно, ядро  является стабильным. Для ядра с тем же общим числом нуклонов, равным семи, но с четырьмя протонами, т. е. для ядра
является стабильным. Для ядра с тем же общим числом нуклонов, равным семи, но с четырьмя протонами, т. е. для ядра  [применяя все ту же формулу (34) или же просто сопоставляя массу этого ядра 7,01915 с массой ядра
[применяя все ту же формулу (34) или же просто сопоставляя массу этого ядра 7,01915 с массой ядра  равной 7,018221, мы обнаруживаем энергетическую возможность уже обратного превращения одного из ядерных протонов в нейтрон; и действительно, изотоп бериллия
равной 7,018221, мы обнаруживаем энергетическую возможность уже обратного превращения одного из ядерных протонов в нейтрон; и действительно, изотоп бериллия  неустойчив — в нем происходит захват ближайшего к ядру электрона
неустойчив — в нем происходит захват ближайшего к ядру электрона  -слоя с превращением в ядро
-слоя с превращением в ядро 
Аналогичная картина получается при сопоставлении масс и для всех других групп изобарных ядер: соотношение факторов, влияющих на энергию ядра, таково, что для заданного значения
 всегда имеется определенное значение
всегда имеется определенное значение  при котором анергия и масса ядра минимальны (рис. 415). На рис. 415 кривая выражает изменение массы при
при котором анергия и масса ядра минимальны (рис. 415). На рис. 415 кривая выражает изменение массы при  рассчитанное по формуле (34), а точки указывают фактическое значение масс изобарных атомов (кривизна линии различна для разных А).
рассчитанное по формуле (34), а точки указывают фактическое значение масс изобарных атомов (кривизна линии различна для разных А).
При  -превращениях масса ядра немного уменьшается — на величину массы выброшенного электрона или позитрона и массы, сопряженной с выделяемой энергией. Стабильное ядро
-превращениях масса ядра немного уменьшается — на величину массы выброшенного электрона или позитрона и массы, сопряженной с выделяемой энергией. Стабильное ядро  имеет меньшую массу, чем нестабильные ядра
имеет меньшую массу, чем нестабильные ядра  причем в диаграмме, представленной на рис. 415,
причем в диаграмме, представленной на рис. 415,  -превращения соответствуютлевой ветви кривой, а
-превращения соответствуютлевой ветви кривой, а  -превращения — правой ветви кривой. Таким образом, простое сопоставление масс позволяет предсказать, каше из изобарных ядер устойчивы, а какие радиоактивны. Пример такого сопоставления масс дан в приведенной таблице:
-превращения — правой ветви кривой. Таким образом, простое сопоставление масс позволяет предсказать, каше из изобарных ядер устойчивы, а какие радиоактивны. Пример такого сопоставления масс дан в приведенной таблице:
(см. скан)

Рис. 415. Характерное для изобарных ядер изменение атомной массы в зависимости от числа протонов в ядре.
Минимуму энергии и массы ядра при  соответствует состав устойчивого ядра. Равенство чисел нейтронов и протонов, т. е. соотношение
соответствует состав устойчивого ядра. Равенство чисел нейтронов и протонов, т. е. соотношение  только приблизительно отвечает условию минимума энергии и массы ядра (для легких ядер). Более точное соотношение между числами нейтронов и протонов в стабильных
только приблизительно отвечает условию минимума энергии и массы ядра (для легких ядер). Более точное соотношение между числами нейтронов и протонов в стабильных
ядрах может быть получено из полуэмпирической формулы для масс (34), если, руководствуясь этой формулой, рассматривать массу ядра как непрерывную функцию  и отвлечься от ступенчатого влияния спиновых поправок (т. е. не учитывать поправочный член 6). Тогда число протонов в стабильном ядре должно определяться из уравнения
и отвлечься от ступенчатого влияния спиновых поправок (т. е. не учитывать поправочный член 6). Тогда число протонов в стабильном ядре должно определяться из уравнения 

Отсюда для стабильных элементов получается действительно хорошо согласующееся с опытом отношение числа протонов к числу нейтронов

или

В частности, для малых А получается 
Если число протонов  в ядре (при общем числе нуклонов А) меньше
в ядре (при общем числе нуклонов А) меньше  то в
то в  -превращении
-превращении  возрастает до
возрастает до  хотя это приводит к увеличению кулоновской энергии отталкивания протонов в ядре, тем не менее суммарная энергия (а соответственно, и масса) ядра уменьшается. Это объясняется тем (как пояснено ниже, в п. 2), что кинетическая энергия нуклонов в ядре резко возрастает при отступлениях от (35).
хотя это приводит к увеличению кулоновской энергии отталкивания протонов в ядре, тем не менее суммарная энергия (а соответственно, и масса) ядра уменьшается. Это объясняется тем (как пояснено ниже, в п. 2), что кинетическая энергия нуклонов в ядре резко возрастает при отступлениях от (35).
2. Энергия внутриядерного движения нуклонов. Действительные массы нейтрона и протона в ядре отличаются от их массы в изолированном состоянии на величину энергии каждой из этих частиц в ядре, деленную на квадрат скорости света. Массы нейтрона и протона не равные, когда эти частицы изолированы и находятся в покое, в ядре могут оказаться и часто оказываются равными.
Чтобы пояснить взаимосвязь между составом ядра и его энергией (или массой), рассмотрим условия движения нуклонов в ядре. Это позволит попутно ответить на следующие вопросы:
1) Почему в тяжелых ядрах число нейтронов превышает число протонов?
2) Почему ряд ядер с возрастающей массой обрывается при числе нуклонов порядка 240?
3) Почему при сочетании нечетного числа протонов с нечетным числом нейтронов ядра (за редким исключением) неустойчивы?
4) Почему большинство наиболее устойчивых ядер состоит из четного числа нейтронов и четного числа протонов, когда при этом общее число нуклонов кратно четырем?
Нуклоны, как и вообще все частицы с полуцелыми значениями спинов, подчиняются статистике Ферми, основанной на принципе Паули. По принципу Паули, две одинаковые частицы или большее их число не могут находиться в тождественных квантовых состояниях (§ 60). Так как для нуклонов, подобно электронам, возможны две противоположные ориентации спинов, то на каждом квантовом энергетическом уровне может находиться максимально два одноименных нуклона. Чтобы, руководствуясь этим принципом, вычислить, следуя Ферми, энергию движения нуклонов в основном состоянии ядра, отложим на осях координат значения компонент количества движения (импульса) нуклона  Состояние движения каждой частицы в любой момент (в любую «фазу») изображается точкой в таком фазовом пространстве. Все изображающие движение частиц точки («фазовые точки») — по числу частиц в системе — будут все вемя находиться внутри сферического объема
Состояние движения каждой частицы в любой момент (в любую «фазу») изображается точкой в таком фазовом пространстве. Все изображающие движение частиц точки («фазовые точки») — по числу частиц в системе — будут все вемя находиться внутри сферического объема  , описанного в фазовом пространстве из начала координат радиусом, равным максимально возможному импульсу частицы
, описанного в фазовом пространстве из начала координат радиусом, равным максимально возможному импульсу частицы  который связан с максимально возможной кинетической энергией частицы
который связан с максимально возможной кинетической энергией частицы  обычным соотношением (из
обычным соотношением (из 

Согласно одному из основных положений квантовой статистики, которое учитывает принцип Паули и которое можно рассматривать как следствие соотношения неопределенностей [§ 65, формула (19)], состояния движения (импульсы) частиц, отличающиеся друг от друга менее чем на  неразличимы (здесь
неразличимы (здесь  планковская постоянная и
планковская постоянная и  пределы изменения координат частицы, т. е. в нашем случае линейный размер атомного ядра). Поэтому каждому квантовому состоянию в фазовом пространстве соответствует ячейка, объем которой равен
пределы изменения координат частицы, т. е. в нашем случае линейный размер атомного ядра). Поэтому каждому квантовому состоянию в фазовом пространстве соответствует ячейка, объем которой равен  где
где  геометрический объем, занимаемый системой частиц, т. е. в нашем случае объем ядра. Объем интересующей нас части фазового пространства равен:
геометрический объем, занимаемый системой частиц, т. е. в нашем случае объем ядра. Объем интересующей нас части фазового пространства равен:

Число ячеек (число различных по энергии квантовых состояний)
мы найдем, разделив этот объем на объем одной фазовой ячейки, т. е.

В основном состоянии ядра все нуклоны находятся на своих низших энергетических уровнях вплоть до некоторого максимального, причем на каждом энергетическом уровне может находиться только два протона (или два нейтрона) с противоположными ориентациями спинов. Поэтому, обозначая максимальную кинетическую энергию протонов в ядре через  макс, а максимальную кинетическую энергию нейтронов через
макс, а максимальную кинетическую энергию нейтронов через  макс, получаем два уравнения, связывающих число протонов в ядре
макс, получаем два уравнения, связывающих число протонов в ядре  и число нейтронов
и число нейтронов  с их максимальными энергиями внутриядерного движения в основном состоянии:
с их максимальными энергиями внутриядерного движения в основном состоянии:

Определяя отсюда максимальные энергии через числа частиц находим:

Средние энергии движения протонов и нейтронов в ядре, как показывает аналогичное вычисление, получаются равными 3/5 их максимальных энергий.
Таким образом, суммарные энергии движения в ядре протонов и нейтронов, равные их средним энергиям, умноженным на число частиц, определяются выражениями:

Если мы прибавили бы к этим энергиям движения нуклонов их энергию (тоже положительную) кулоновского отталкивания

и определили бы, при каком соотношении между  энергия движения и взаимодействия минимальна, то получили бы формулу, совпадающую с формулой (35). Далее, если бы мы поставили себе задачу определить, как возрастает энергия движения нуклонов в ядре, когда соотношение
энергия движения и взаимодействия минимальна, то получили бы формулу, совпадающую с формулой (35). Далее, если бы мы поставили себе задачу определить, как возрастает энергия движения нуклонов в ядре, когда соотношение  отклоняется от того, которое [по формуле
отклоняется от того, которое [по формуле  обеспечивает минимум энергии, то получили бы выражение, аналогичное пятому члену в полуэмпирической формуле для энергии атомного ядра [формула (д) § 114].
обеспечивает минимум энергии, то получили бы выражение, аналогичное пятому члену в полуэмпирической формуле для энергии атомного ядра [формула (д) § 114].
В-отличие от частиц максвелловского газа суммарная энергия движения нуклонов пропорциональна не первой степени числа частиц, а почти квадрату числа частиц. Только по этой причине энергия внутриядерного движения в основном состоянии оказывается минимальной при приблизительном равенстве числа разнородных нуклонов; здесь сказывается арифметический закон, что сумма квадратов чисел, из которых можно составить число  является наименьшей при тождестве слагаемых (например,
является наименьшей при тождестве слагаемых (например,  В конечном счете именно этот арифметический закон и квантовый принцип заполнения энергетических уровней нуклонами и являются основой наблюдаемых закономерностей строения стабильных ядер и превращения неустойчивых ядер.
В конечном счете именно этот арифметический закон и квантовый принцип заполнения энергетических уровней нуклонами и являются основой наблюдаемых закономерностей строения стабильных ядер и превращения неустойчивых ядер.
Уравнения  и (38) показывают, что при равенстве чисел нейтронов и протонов в ядре равны (если считать их массы
и (38) показывают, что при равенстве чисел нейтронов и протонов в ядре равны (если считать их массы  равными) также и их кинетические энергии
равными) также и их кинетические энергии  (максимальные и средние). Но каждый протон в ядре имеет еще положительную кулоновскую энергию отталкивания В тяжелых ядрах она значительна, и поэтому полная энергия наиболее быстрых протонов в ядре (находящихся на высшем энергетическом уровне) и их фактическая масса
(максимальные и средние). Но каждый протон в ядре имеет еще положительную кулоновскую энергию отталкивания В тяжелых ядрах она значительна, и поэтому полная энергия наиболее быстрых протонов в ядре (находящихся на высшем энергетическом уровне) и их фактическая масса  могут оказаться больше энергии и массы наиболее быстрых нейтронов в ядре. Это неравенство масс
могут оказаться больше энергии и массы наиболее быстрых нейтронов в ядре. Это неравенство масс  обратное тому, которое наблюдается для свободных нуклонов, ведет к одностороннему превращению протонов, находящихся на высших энергетических уровнях, в нейтроны, что и создает в тяжелом ядре некоторое превышение числа нейтронов над числом протонов. Но по (37) при
обратное тому, которое наблюдается для свободных нуклонов, ведет к одностороннему превращению протонов, находящихся на высших энергетических уровнях, в нейтроны, что и создает в тяжелом ядре некоторое превышение числа нейтронов над числом протонов. Но по (37) при  максимальная кинетическая энергия у нейтронов больше, чем у протонов. В итоге устанавливается такое отношение
максимальная кинетическая энергия у нейтронов больше, чем у протонов. В итоге устанавливается такое отношение  когда полные энергии на верхних уровнях оказываются для протона и нейтрона одинаковыми или отличающимися менее чем на
когда полные энергии на верхних уровнях оказываются для протона и нейтрона одинаковыми или отличающимися менее чем на  , где
, где  — масса электрона (т. е. на
— масса электрона (т. е. на 
Чем тяжелее ядро, тем большая доля его энергии определяется отталкиванием протонов, которые плотно сконцентрированы ядерными силами в весьма малом объеме ядра. Поэтому, в частности, чем тяжелее ядро, тем сильнее обнаруживается тенденция его к делению, как это было уже пояснено в § 95. «Разрыхлением» ядерной структуры при чрезмерном возрастании заряда ядра и объясняется обрыв периодической системы элементов в области  превышающих 100.
превышающих 100.
Уже при  порядка 30—50 влияние кулоновского отталкивания протонов в ядре (конкурируя с выравнивающим влиянием энергии движения) смещает отношение
порядка 30—50 влияние кулоновского отталкивания протонов в ядре (конкурируя с выравнивающим влиянием энергии движения) смещает отношение  в сторону уменьшения числа протонов на один-два
в сторону уменьшения числа протонов на один-два
протона по сравнению с числом нейтронов. При А порядка 100 число нейтронов в стабильных ядрах на 8—10 нейтронов больше числа протонов, а при  число нейтронов в стабильных ядрах примерно в полтора раза превышает число протонов. При таком большом отступлении от равенства чисел разноименных нуклонов (что связано с увеличением их энергии движения) и вследствие большого заряда, ядра становятся неустойчивыми в отношении альфа-распада.
число нейтронов в стабильных ядрах примерно в полтора раза превышает число протонов. При таком большом отступлении от равенства чисел разноименных нуклонов (что связано с увеличением их энергии движения) и вследствие большого заряда, ядра становятся неустойчивыми в отношении альфа-распада.
В начале периодической системы устойчивость ядра более всего зависит от того, являются ли числа нейтронов и протонов в ядре четными или нечетными. Это существенно влияет, как будет сейчас пояснено, на энергию внутриядерного движения нуклонов.
При выводе формулы (38) мы считали, что все протонные и нейтронные энергетические уровни заполнены парами нуклонов с противоположной ориентацией спинов. Но это возможно только в четно-четных ядрах, т. е. в ядрах с четным числом протонов  четным числом нейтронов
четным числом нейтронов  При нечетности
При нечетности  на верхних энергетических уровнях для протоков и нейтронов имеется только по одному нуклону, а не по два. Обозначим число энергетических уровней протонов через
на верхних энергетических уровнях для протоков и нейтронов имеется только по одному нуклону, а не по два. Обозначим число энергетических уровней протонов через  а нейтронов через
а нейтронов через  При выводе формулы (38) для четно-четных ядер мы могли принять, что
При выводе формулы (38) для четно-четных ядер мы могли принять, что  Но при нечетности
Но при нечетности  на верхнем протонном уровне имеется только один протон, и поэтому
на верхнем протонном уровне имеется только один протон, и поэтому

При нечетности  аналогичное соотношение получается и для нейтронов. Это сказывается, как нетрудно проследить, повторяя вывод формулы (38), в некотором увеличении средней энергии движения нуклонов в ядре. Поэтому средняя энергия связи, в которую энергия движения нуклонов входит с отрицательным знаком, в четно-четных ядрах имеет наибольшую величину, а в нечетно-нечетных ядрах (когда
аналогичное соотношение получается и для нейтронов. Это сказывается, как нетрудно проследить, повторяя вывод формулы (38), в некотором увеличении средней энергии движения нуклонов в ядре. Поэтому средняя энергия связи, в которую энергия движения нуклонов входит с отрицательным знаком, в четно-четных ядрах имеет наибольшую величину, а в нечетно-нечетных ядрах (когда  оба нечетные, а стало быть,
оба нечетные, а стало быть,  -четное) наименьшую величину, чем отчасти и объясняется устойчивость первых и неустойчивость вторых. Проведя вычисления, мы пришли бы к обоснованию поправки А в формуле (32).
-четное) наименьшую величину, чем отчасти и объясняется устойчивость первых и неустойчивость вторых. Проведя вычисления, мы пришли бы к обоснованию поправки А в формуле (32).

Рис. 416. Энергетическая диаграмма ядра 
На рис. 416 схематически представлена энергетическая диаграмма нечетно-нечетного ядра  здесь стрелки символизируют ориентацию спинов. В энергетической диаграмме высота уровней показывает величину суммы энергии движения и потенциальной энергии отталкивания нуклонов. Поэтому уровни протонов расположены выше уровней нейтронов в среднем на величину потенциальной энергии
здесь стрелки символизируют ориентацию спинов. В энергетической диаграмме высота уровней показывает величину суммы энергии движения и потенциальной энергии отталкивания нуклонов. Поэтому уровни протонов расположены выше уровней нейтронов в среднем на величину потенциальной энергии
отталкивания протонов, отнесенной к одному протону  Вследствие кулоновского отталкивания связь протонов в ядре слабее, чем нейтронов? и соответственно глубина потенциальной ямы от уровня энергии свободных частиц для протонов получается меньшей, чем для нейтронов, на Но верхний край потенциальной ямы протонов возвышается над уровнем энергии свободных частиц на высоту потенциального кулоновского барьера
Вследствие кулоновского отталкивания связь протонов в ядре слабее, чем нейтронов? и соответственно глубина потенциальной ямы от уровня энергии свободных частиц для протонов получается меньшей, чем для нейтронов, на Но верхний край потенциальной ямы протонов возвышается над уровнем энергии свободных частиц на высоту потенциального кулоновского барьера  поэтому и для протонов и для нейтронов глубина потенциальных ям от их верхних краев приблизительно одинакова.
поэтому и для протонов и для нейтронов глубина потенциальных ям от их верхних краев приблизительно одинакова.
В стабильном ядре высота верхнего уровня протонов, как уже было пояснено, не может превосходить высоту верхнего уровня нейтронов более чем на  Различие высот низших протонных и нейтронных уровней не нарушает стабильности ядра, так как эти уровни заполнены, и поэтому одностороннее превращение нуклонов здесь невозможно.
Различие высот низших протонных и нейтронных уровней не нарушает стабильности ядра, так как эти уровни заполнены, и поэтому одностороннее превращение нуклонов здесь невозможно.
Поскольку верхние уровни у нечетно-нечетных ядер не заполнены, небольшое различие в высоте этих уровней для нейтронов и протонов вызывает превращение одного из нуклонов. Кроме того, как уже упоминалось, энергия связи в этих ядрах несколько уменьшена. Поэтому нечетно-нечетные ядра редко являются стабильными; подавляющее большинство их радиоактивно; исключение составляют  Наибольшую устойчивость и наибольшее распространение в природе имеют четно-четные ядра.
Наибольшую устойчивость и наибольшее распространение в природе имеют четно-четные ядра.
Если сопоставлять наиболее стабильные и не слишком тяжелые ядра сходного строения, например четно-четные или же только четно-нечетные, то средняя на нуклон энергия внутриядерного движения в основных состояниях этих ядер оказывается приблизительно одинаковой. Это видно из выведенных выше формул (37) для максимальных энергий нуклонов. Действительно, в формулы (37) входит объем ядра, а он пропорционален числу нуклонов, которое в стабильных и не слишком тяжелых ядрах приблизительно равно удвоенному числу протонов; вследствие этого для ядер сходного строения максимальные энергии нейтрона и протона не зависят от А, а поэтому приблизительно равны и средние энергии движения, которые, как уже было отмечено в связи с обоснованием формулы (38), составляют  Если подставить в формулу
Если подставить в формулу  где
где  то нетрудно вычислить, что максимальная энергия движения нуклона в не слишком тяжелых четно-четных ядрах равна приблизительно
то нетрудно вычислить, что максимальная энергия движения нуклона в не слишком тяжелых четно-четных ядрах равна приблизительно  и поэтому средняя кинетическая энергия нуклона равна
и поэтому средняя кинетическая энергия нуклона равна  Средняя энергия связи у многих четно-четных ядер составляет
Средняя энергия связи у многих четно-четных ядер составляет  а так как она, взятая с обратным знаком, равна сумме средней потенциальной энергии ядерных сил и средней кинетической энергии нуклона, то, стало быть, средняя потенциальная энергия нуклонов в стабильных ядрах составляет —
а так как она, взятая с обратным знаком, равна сумме средней потенциальной энергии ядерных сил и средней кинетической энергии нуклона, то, стало быть, средняя потенциальная энергия нуклонов в стабильных ядрах составляет —  Для нуклонов, находящихся на высшем энергетическом уровне,
Для нуклонов, находящихся на высшем энергетическом уровне,  имеющих кинетическую энергию около
имеющих кинетическую энергию около  энергия связи не сильно отличается от энергии связи других нуклонов. Если ее принять равной для «верхнего» нуклона
энергия связи не сильно отличается от энергии связи других нуклонов. Если ее принять равной для «верхнего» нуклона  то глубина потенциальной ямы нуклонов в ядре получается равной
то глубина потенциальной ямы нуклонов в ядре получается равной  (рис. 359, § 94).
(рис. 359, § 94).
Давно было замечено, что наиболее устойчивы ядра, имеющие число нейтронов или же протонов, равное одному из следующих «магических» чисел:

Многие из таких ядер широко распространены в природе. Их полные энергии минимальны в сравнении с энергиями ядер, имеющих близкое к ним число нейтронов или протонов. Для всех
этих ядер весьма характерна также малая (в сравнении с «соседними» ядрами) вероятность радиационного захвата нейтронов.
Если рассматривать движение нуклона происходящим в некотором эффективном поле остальных нуклонов (например, в прямоугольной потенциальной яме), то можно ввести представление об энергетических нуклонных оболочках, заполнение которых при увеличении числа нуклонов в ядре подчинено принципу Паули, как это имеет место для электронных оболочек атомов (§ 60). Приведенные выше магические числа соответствуют как раз таким (наиболее устойчивым) конфигурациям, когда энергетические оболочки нейтронов и протонов в ядре полностью заполнены.
Каждому значению орбитального момента количества движения нуклона I (кроме  соответствуют два значения полного момента
соответствуют два значения полного момента 
(Для обозначения энергетических уровней нуклонов применяют обычную спектроскопическую запись:  для
для  для
для  )
)
Состояния нуклона  несколько различаются по энергии. Расчет и эксперимент показывают, что уровень с
несколько различаются по энергии. Расчет и эксперимент показывают, что уровень с  расположен ниже, чем уровень с
расположен ниже, чем уровень с  а расстояния между уровнями, отвечающими одному и тому же значению
а расстояния между уровнями, отвечающими одному и тому же значению  растут с ростом
растут с ростом  Если
Если  число вырожденных
число вырожденных
Оболочное строение ядер
(см. скан)
состояний в оболочке, то по принципу Паули эта оболочка может содержать не более  нейтронов и не более
нейтронов и не более  протонов.
протонов.
Таким образом, получается распределение, указанное в помещенной выше таблице.
Полные моменты отдельных нуклонов складываются в результирующий спин ядра, причем суммарные моменты полностью заполненных оболочек равны нулю.
Считают, что на любом уровне (при каждом значении  нуклоны, если число их на этом уровне четное, всегда располагаются так, что их результирующий момент количества движения оказывается равным нулю. Поэтому полный спин ядра
нуклоны, если число их на этом уровне четное, всегда располагаются так, что их результирующий момент количества движения оказывается равным нулю. Поэтому полный спин ядра  равен значению
равен значению  нечетного нуклона на внешней, еще полностью не заполненной оболочке (моменты же всех остальных нуклонов попарно компенсируются).
нечетного нуклона на внешней, еще полностью не заполненной оболочке (моменты же всех остальных нуклонов попарно компенсируются).
Например, в ядре  протонов заполняют оболочки I, II и На; их результирующий момент равен нулю, и спин ядра определяется значением
протонов заполняют оболочки I, II и На; их результирующий момент равен нулю, и спин ядра определяется значением  для низшего состояния оболочки
для низшего состояния оболочки  занятого
занятого  протоном, т. е.
протоном, т. е.  По той же причине спин ядра
По той же причине спин ядра  с 15 нейтронами также равен
с 15 нейтронами также равен  Ядро
Ядро  имеет один нечетный протон в оболочке IV, где низшее состояние
имеет один нечетный протон в оболочке IV, где низшее состояние  и поэтому спин этого ядра
и поэтому спин этого ядра 
Одновременно с определением спина по приведенной таблице легко установить и значение результирующего орбитального момента ядра  которое равно орбитальному моменту нечетного нуклона. Так, для ядер
которое равно орбитальному моменту нечетного нуклона. Так, для ядер  будет
будет  для
для  имеем
имеем 
Спин и орбитальный момент в совокупности определяют магнитный момент ядра 
Спины и магнитные моменты некоторых ядер
(см. скан)
Из сказанного следует, что у ядер с четным числом протонов и нейтронов спин и магнитный момент равны нулю. Спины всех ядер с нечетным числом протонов или нейтронов (т. е. при А нечетном) имеют полуцелые значения, от  до
до  Спины ядер при четном А целочисленны.
Спины ядер при четном А целочисленны.
Оглавление
- ЧАСТЬ ЧЕТВЕРТАЯ. ОПТИКА
- § 2. Электромагнитная теория света
- § 3. Скорость света
- § 4. Опыт Майкельсона
- § 5. Отрицательный результат опыта Майкельсона и теория относительности
- § 6. Некоторые замечания о теории относительности
- § 7. Явление Доплера для световых волн
- ГЛАВА II. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- § 8. Законы отражения и преломления света
- § 9. Линза
- § 10. Оптические системы
- § 11. Глаз как оптическая система
- § 12. Приборы, вооружающие глаз
- § 13. Фотоаппарат и проекционный аппарат
- § 14. Принцип Ферма
- § 15. Электронная оптика
- ГЛАВА III. ИНТЕРФЕРЕНЦИЯ СВЕТА
- § 16. Принцип суперпозиции. Когерентность
- § 17. Зеркала Френеля
- § 18. Цвета тонких пленок. Полосы равной толщины
- § 19. Полосы равного наклона. Просветленная оптика
- § 20. Интерферометры
- § 21. Интерференционное измерение технических мер длины
- § 22. Интерференция многих колебаний
- § 23. Интерференционная спектроскопия
- ГЛАВА IV. ДИФРАКЦИЯ СВЕТА
- § 24. Явление дифракции. Опыт Френеля
- § 25. Принцип Гюйгенса-Френеля
- § 26. Метод зон Френеля
- § 27. Дифракция от узкой щели
- § 28. Дифракционная решетка
- § 29. Дифракционный спектр. Решетки Роуланда и эшелон Майкельсона
- § 30. Плоскостные решетки. Пространственная решетка
- § 31. Структурный рентгеновский анализ
- § 32. Дифракция света на ультразвуковых волнах
- § 33. Дифракция от мелких частиц
- § 34. Разрешающая способность оптических инструментов. Звездный интерферометр
- ГЛАВА V. ПОЛЯРИЗАЦИЯ СВЕТА
- § 35. Поляризация света
- § 36. Двойное лучепреломление
- § 37. Интерференция поляризованного света
- § 38. Оптический метод исследования упругих натяжений. Эффект Керра
- § 39. Вращение плоскости поляризации. Эллиптическая поляризация
- ГЛАВА VI. ДИСПЕРСИЯ, ПОГЛОЩЕНИЕ И ИЗЛУЧЕНИЕ СВЕТА
- § 40. Отражение света
- § 41. Давление света. Опыты Лебедева
- § 42. Дисперсия. Опыты Ньютона
- § 43. Молекулярная теория дисперсии
- § 44. Хроматическая аберрация. Спектрограф
- § 45. Поглощение света
- § 46. Закон Бугера. Опыты Вавилова
- § 47. Атом как элементарный излучатель света
- § 48. Эффект Вавилова — Черенкова
- ГЛАВА VII. ТЕРМОДИНАМИКА ИЗЛУЧЕНИЯ И СВЕТОВОЙ ПОТОК
- § 49. Излучение черного тела. Формула Планка. Закон Вина
- § 50. Излучение нечерных тел. Законы Кирхгофа
- § 51. Приемники излучения
- § 52. Световые величины и их измерения
- § 53 Температурные излучатели как источники света
- ЧАСТЬ ПЯТАЯ. АТОМНАЯ ФИЗИКА
- ГЛАВА VIII. СТРОЕНИЕ АТОМА И ТЕОРИЯ БОРА
- § 55. Опыты, обнаружившие ядерное строение атомов
- § 56. Противоречие между фактическим строением атомов и выводами классической электродинамики. Строение линейчатых спектров
- § 57. Опытные основания теории квантов в первые годы ее развития
- § 58. Теория Бора. Происхождение спектра водорода
- § 59. Квантовые числа
- § 60. Принцип Паули. Строение электронных оболочек атомов
- § 61. Общая картина возникновения спектров
- ГЛАВА IX. ОСНОВЫ КВАНТОВОЙ (ВОЛНОВОЙ) МЕХАНИКИ
- § 62. Волновые свойства частиц. Формула де Бройля. Дифракция электронов
- § 63. Уравнение Шредингера. Просачивание через энергетический барьер. Нулевая энергия
- § 64. Волномеханическая теория атома водорода
- § 65. Соотношение неопределенностей и его разные трактовки
- ГЛАВА X. КВАНТОВАЯ ОПТИКА
- § 66. Развитие квантовой оптики
- § 67. Спектр щелочных металлов. Спин электрона
- § 68. Спектр гелия. Символика спектральных термов
- § 69. Сверхтонкая структура спектральных линий
- § 70. Атом в силовом поле
- § 71. Молекулярные спектры и строение молекул
- § 72. Комбинационное рассеяние света
- § 73. Квантовая картина испускания света атомами и молекулами
- § 74. Люминесценция
- § 75. Возбуждение люминесценции ударами частиц вещества
- § 76. Применения люминесценции
- § 77. Фотохимические реакции
- ГЛАВА XI. ЗАКОН ПРОПОРЦИОНАЛЬНОСТИ МАССЫ И ЭНЕРГИИ И РЕЛЯТИВИСТСКИЕ СООТНОШЕНИЯ
- § 78. Закон пропорциональности массы и энергии
- § 79. Предварительные замечания о релятивистских эффектах. Зависимость массы от скорости
- § 80. Корпускулярные свойства фотонов. Явление Комптона
- § 81. Вывод закона Эйнштейна сложения скоростей из закона пропорциональности массы и энергии и законов сохранения энергии или количества движения
- § 82. Две трактовки закона пропорциональности массы и энергии и уточнение закона тяготения
- § 83. Красное смещение спектральных линий. Поперечный эффект Доплера
- § 84. Влияние гравитационного поля на скорость света в вакууме и показатель преломления вакуума
- ЧАСТЬ ШЕСТАЯ. ЯДЕРНАЯ ФИЗИКА
- § 85. Заряд и масса ядра. Масс-спектральный анализ
- § 86. Состав ядер. Изотопы. Атомные единицы массы и энергии
- § 87. Радиоактивный распад ядер. Закон радиоактивного смещения. Изомеры
- § 88. Альфа-лучи. Потери энергии на ионизацию. Квантовомеханическое объяснение альфа-радиоактивности
- § 89. Бета- и гамма-лучи
- § 90. Искусственное расщепление ядер. Открытие нейтрона
- § 91. Открытие позитрона. Взаимопревращение фотонов определенной энергии и электронно-позитронных пар
- § 92. Индуцированная позитронная и электронная радиоактивность. Фоторасщепление ядер, K-захват
- § 93. Энергетические уровни ядер. Внутренняя конверсия. Нейтрино
- § 94. Капельная теория строения ядер
- § 95. Деление ядер и развитие капельной теории строения ядер
- ГЛАВА XIII. КОСМИЧЕСКИЕ ЛУЧИ
- § 96. Методы исследования и первые итоги изучения космических лучей
- § 97. Каскадное образование электронно-позитронных пар в космических лучах. Потери энергии электронами на тормозное излучение
- § 98. «мю»-мезоны. Зависимость времени жизни неустойчивых частиц от скорости движения
- § 99. «пи»-мезоны
- § 100. Взрывные ядерные ливни и их каскадное развитие в космических лучах
- § 101. Корпускулярный и энергетический спектр космических лучей. Происхождение космического излучения
- ГЛАВА XIV. ЭКСПЕРИМЕНТАЛЬНЫЕ СРЕДСТВА ЯДЕРНОЙ ФИЗИКИ
- § 102. Циклотроны
- § 103. Фазотроны
- § 104. Бетатроны
- § 105. Синхротроны и синхрофазотроны
- § 106. Линейные ускорители электронов и ионов
- § 107. Лабораторные источники нейтронов. Замедлители нейтронов в ядерных реакторах
- § 108. Усовершенствование методов наблюдения и счета частиц
- ГЛАВА XV. ЯДЕРНЫЕ РЕАКЦИИ И АТОМНАЯ ЭНЕРГИЯ
- § 109. Основные виды и обозначения ядерных реакций. Конкурирующие процессы в ядерных реакциях
- § 110. Энергетический эффект, энергия возбуждения и порог ядерных реакций
- § 111. Превращения элементарных частиц
- § 112. Ядерные силы
- § 113. Энергия связи ядер и средняя энергия связи нуклона
- § 114. Полуэмпирическая формула для энергии ядерной связи и для атомных энергий и масс
- § 115. Взаимосвязь энергии и строения ядер. Внутриядерное движение нуклонов и нуклонные оболочки. Спины и магнитные моменты ядер
- § 116. Энергия отделения частиц и анализ возможного хода ядерной реакции
- § 117. Выход продуктов ядерной реакции. Эффективные сечения. Резонансные явления
- § 118. Цепной процесс деления ядер. Активно делящиеся вещества. Ядерные реакторы
- § 119. Термоядерные реакции
- § 120. Применение ядерных реакций
- § 121. Ядерные реакции в звездах
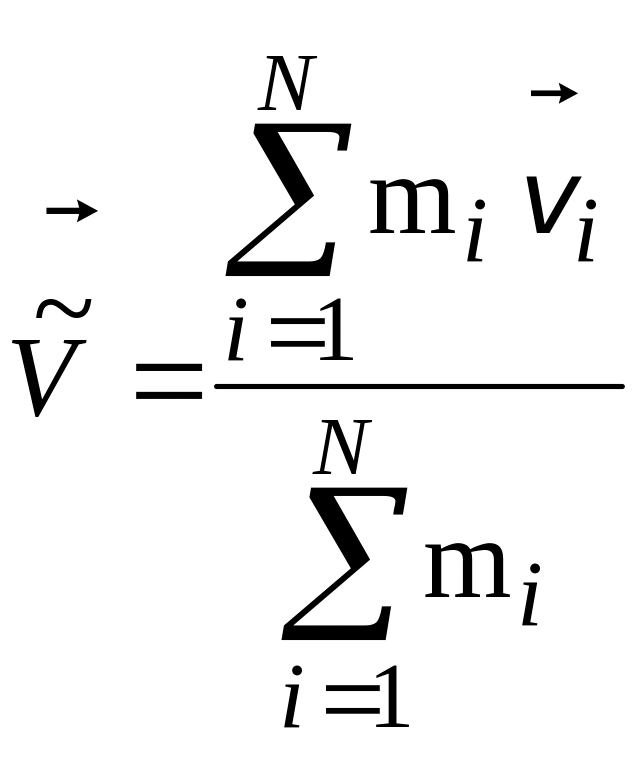
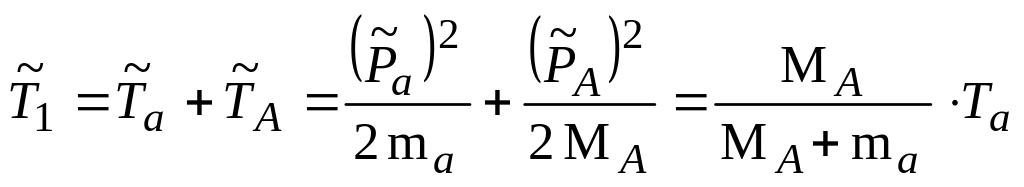
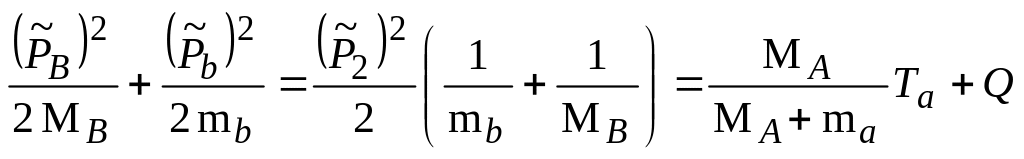

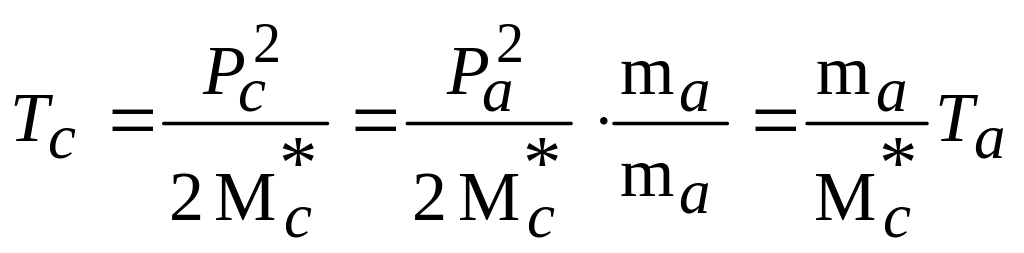

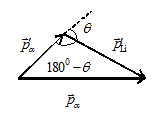 Построим векторную
Построим векторную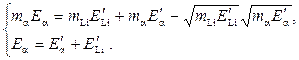 (5)
(5)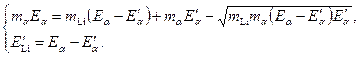 (6)
(6)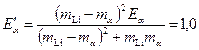 МэВ,
МэВ,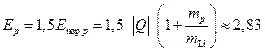 МэВ
МэВ Построим векторную диаграмму для импульсов
Построим векторную диаграмму для импульсов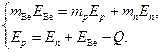 (5)
(5)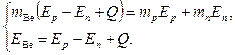 (6)
(6)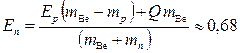 МэВ.
МэВ.
