Как найти класс эквивалентности элемента

Отношение эквивалентности. Классы эквивалентности

Классы эквивалентных элементов и их свойства

Пусть %%R%% — отношение эквивалентности на множестве %%M%% и %%a%% — некоторый элемент из %%M%%. Рассмотрим множество всех элементов из %%M%%, находящихся в отношении %%R%% к элементу %%a%%.

Классом эквивалентности %%M_a%%

называется множество всех элементов %%M%%, находящихся в отношении %%R%% к элементу %%a%%, то есть множество

$$
M_a = {x in M : x~R~a}.
$$

Пример

Пусть %%M%% — множество всех жителей России и %%R%% — отношение эквивалентности «проживать в одном городе». Найти классы эквивалентных элементов %%M_a%% для %%a in M%%.

Класс элементов, эквивалентных элементу %%a%%, имеет вид:
$$
M_a = {x in M : x text{ проживает в одном городе с человеком } a}
$$

В зависимости от элемента %%a%% получаем несколько классов эквивалентности. Например, класс эквивалентности жителей Москвы или Санкт-Петербурга.

Свойства классов эквивалентности

Пусть %%R%% — отношение эквивалентности на множестве %%M%% и %%M_a, M_b, dotsc, M_z, dotsc%% — все классы эквивалентности для отношения %%R%%. Тогда эти классы имеют следующие свойства.

Свойство 1

Для любого элемента %%a in M%% выполняется условие
$$
a in M_a
$$

Действительно, по определению, класс %%M_a = {x in M : x~R~a}%%. Тогда для элемента %%a%% должно выполняться условие %%a in M_a leftrightarrow a~R~a%%, которое выполняется в связи с тем, что отношение %%R%% рефлексивно по определению отношения эквивалентности. Следовательно, %%a in M_a%%.

Как следствие этого свойства можно сказать, что всякий класс %%M_a%% является непустым множеством.

Свойство 2

Пусть %%M_a%% и %%M_b%% классы эквивалентности для отношения %%R%%. Классы %%M_a%% и %%M_b%% равны тогда и только тогда, когда элемент %%a%% находится в отношении %%R%% к элементу %%b%%.
$$
M_a = M_b leftrightarrow a~R~b.
$$

Свойство 3

Пусть %%M_a%% и %%M_b%% классы эквивалентности для отношения %%R%%. Тогда классы %%M_a%% и %%M_b%% не имеют общих элементов.
$$
M_a neq M_b rightarrow M_a cap M_b = varnothing
$$

Свойство 4

Объединение всех классов эквивалентности множества %%M%% равно множеству %%M%%.
$$
bigcup_{ain M}{M_a} = M.
$$

Разбиение множества

Совокупностью подмножеств %%M_i%%, где %%i in I%% (множеству индексов), множества %%M%% называется разбиением множества %%M%% если выполняются следующие условия:

Каждое из подмножеств %%M_i%% непусто.
Объединение всех подмножеств %%M_i%% равно множеству %%M%%.
Два различных подмножества %%M_i%% и %%M_j%%, где %%i neq j%%, не имеют общих элементов.

Теорема. Пусть %%R%% — отношение эквивалентности на множестве %%M%%. Тогда совокупность классов эквивалентности множества %%M%% образует его разбиение.

Действительно, если в качестве подмножеств %%M_i%% взять классы эквивалентности %%M_a%%, то все три условия выполняются:

Каждый класс эквивалентности является непустым множеством, согласно свойству 1.
Объединение всех классов эквивалентности есть множество %%M%%, согласно свойству 4.
Два различных класса эквивалентности не имеют общих элементов, согласно свойству 3.

Все условия определения разбиения выполнены. Следовательно классы эквивалентности есть разбиение множества %%M%%.

Примеры

Пусть дано множество %%M = {1, 2, 3, 4, 5, 6, 7, 8, 9, 0 }%%, тогда разбиением этого множества могут быть следующие совокупности множеств:

%%A_1 = {1, 2, 3}, A_2 = {4, 5, 6, 7}, A_3 = {8, 9, 0 }%%.
%%B_1 = {0, 7, 2}, B_2 = {1, 3, 5 }, B_3 = {4, 6, 8, 9}%%.

Но следующие совокупности не являются разбиением:

%%C_1 = {1, 2, 3}, C_2 = {4, 5, 6, 7}, C_3 = {8, 9, 0, 3}%%.
%%D_1 = {0, 7, 2}, D_2 = {1, 3, 5 }, D_3 = {4, 6, 8, 9}, D_4 = varnothing%%.
%%E_1 = {0, 1, 2}, E_2 = {3, 4, 5}, E_3 = {6, 7, 8}%%.

Совокупность множеств %%C_i%% не является разбиением, т.к. оно не удовлетворяет условию 3 разбиения множеств: множества %%C_1%% и %%C_3%% имеют общий элемент %%3%%.

Совокупность множеств %%D_i%% не является разбиением, т.к. оно не удовлетворяет условию 1 разбиения множеств: множество %%D_4%% пусто.

Совокупность множеств %%E_i%% не является разбиением, т.к. оно не удовлетворяет условию 2 разбиения множеств: объединение множеств %%E_1, E_2%% и %%E_3%% не образует множество %%M%%.

Источник

У этого термина существуют и другие значения, см. Эквивалентность.

Отношение эквивалентности — бинарное отношение между элементами данного множества,
свойства которого сходны со свойствами отношения равенства.

Определение[править | править код]

Отношение эквивалентности ( sim ) на множестве — это бинарное отношение, для которого при любых a,b,c из выполнены следующие условия:

рефлексивность: ;
симметричность: если , то ;
транзитивность: если и , то .

Запись вида «» читается как « эквивалентно ».

Связанные определения[править | править код]

Классом эквивалентности элемента ain X называется подмножество элементов, эквивалентных ; то есть,

Из вышеприведённого определения немедленно следует, что если , то .

Фактормножество — множество всех классов эквивалентности заданного множества по заданному отношению sim , обозначается .

Для класса эквивалентности элемента используются следующие обозначения: [a] , , .

Множество классов эквивалентности по отношению sim является разбиением множества.

Примеры[править | править код]

Равенство («»), тривиальное отношение эквивалентности на любом множестве, в частности, вещественных чисел.
Сравнение по модулю: а ≡ b (mod n).
В евклидовой геометрии
Эквивалентность функций в математическом анализе:

Говорят, что функция эквивалентна функции при $xrightarrow x_{0}$ , если она допускает представление вида , где при $xrightarrow x_{0}$ . В этом случае пишут , напоминая при необходимости, что речь идёт о сравнении функций при $xrightarrow x_{0}$ . Если при ${displaystyle xneq x_{0}}$ , эквивалентность функций и при $xrightarrow x_{0}$ , очевидно, равносильна соотношению $lim _{{xrightarrow x_{0}}}{{frac {f(x)}{g(x)}}}=1$ .
Эквивалентность норм на векторном пространстве.
Отношение равномощности множеств.
Изоморфизм групп, колец, векторных пространств
Эквивалентность категорий.
Изоморфизм в некоторой категории задаёт отношение эквивалентности на этой категории.
Эквивалентность гладких атласов гладкого многообразия.

Классы эквивалентности[править | править код]

Множество всех классов эквивалентности, отвечающее отношению эквивалентности sim , обозначается символом и называется фактормножеством относительно sim .
При этом сюръективное отображение

называется естественным отображением (или канонической проекцией) на фактормножество .

Пусть и — множества, — отображение, тогда бинарное отношение , определённое правилом

{displaystyle xsim yiff f(x)=f(y),quad x,yin X}

является отношением эквивалентности на .
При этом отображение индуцирует отображение , определяемое правилом

или, что то же самое,

При этом получается факторизация отображения на сюръективное отображение и инъективное отображение .

См. также[править | править код]

Отношение толерантности — ослабленная форма эквивалентности.
Эквиваленция — логическая операция.
Знак равенства.

Литература[править | править код]

А. И. Кострикин, Введение в алгебру. М.: Наука, 1977, 47—51.
А. И. Мальцев, Алгебраические системы, М.: Наука, 1970, 23—30.
Отношение типа равенства (отношение эквивалентности) // Большая Советская энциклопедия (в 30 т.) / А. М. Прохоров (гл. ред.). — 3-е изд. — М.: Сов. энциклопедия, 1974. — Т. XVIII. — С. 629. — 632 с.

Источник

From Wikipedia, the free encyclopedia

This article is about equivalency in mathematics. For equivalency in music, see equivalence class (music).

Congruence is an example of an equivalence relation. The leftmost two triangles are congruent, while the third and fourth triangles are not congruent to any other triangle shown here. Thus, the first two triangles are in the same equivalence class, while the third and fourth triangles are each in their own equivalence class.

In mathematics, when the elements of some set have a notion of equivalence (formalized as an equivalence relation), then one may naturally split the set into equivalence classes. These equivalence classes are constructed so that elements and belong to the same equivalence class if, and only if, they are equivalent.

Formally, given a set and an equivalence relation ,sim, on the equivalence class of an element in denoted by ^[1] is the set^[2]

of elements which are equivalent to It may be proven, from the defining properties of equivalence relations, that the equivalence classes form a partition of This partition—the set of equivalence classes—is sometimes called the quotient set or the quotient space of by and is denoted by .

When the set has some structure (such as a group operation or a topology) and the equivalence relation ,sim, is compatible with this structure, the quotient set often inherits a similar structure from its parent set. Examples include quotient spaces in linear algebra, quotient spaces in topology, quotient groups, homogeneous spaces, quotient rings, quotient monoids, and quotient categories.

Examples[edit]

Let be the set of all rectangles in a plane, and the equivalence relation “has the same area as”, then for each positive real number there will be an equivalence class of all the rectangles that have area ^[3]
Consider the modulo 2 equivalence relation on the set of integers, such that if and only if their difference is an even number. This relation gives rise to exactly two equivalence classes: one class consists of all even numbers, and the other class consists of all odd numbers. Using square brackets around one member of the class to denote an equivalence class under this relation, and all represent the same element of ^[4]
Let be the set of ordered pairs of integers with non-zero and define an equivalence relation on such that if and only if then the equivalence class of the pair can be identified with the rational number and this equivalence relation and its equivalence classes can be used to give a formal definition of the set of rational numbers.^[5] The same construction can be generalized to the field of fractions of any integral domain.
If consists of all the lines in, say, the Euclidean plane, and means that and are parallel lines, then the set of lines that are parallel to each other form an equivalence class, as long as a line is considered parallel to itself. In this situation, each equivalence class determines a point at infinity.

Definition and notation[edit]

An equivalence relation on a set is a binary relation ,sim, on satisfying the three properties:^[6]^[7]

The equivalence class of an element is often denoted [a] or ${displaystyle [a]_{sim },}$ and is defined as the set of elements that are related to by ^[2] The word “class” in the term “equivalence class” may generally be considered as a synonym of “set”, although some equivalence classes are not sets but proper classes. For example, “being isomorphic” is an equivalence relation on groups, and the equivalence classes, called isomorphism classes, are not sets.

The set of all equivalence classes in with respect to an equivalence relation is denoted as and is called modulo (or the quotient set of by ).^[8] The surjective map from onto which maps each element to its equivalence class, is called the canonical surjection, or the canonical projection.

Every element of an equivalence class characterizes the class, and may be used to represent it. When such an element is chosen, it is called a representative of the class. The choice of a representative in each class defines an injection from to X. Since its composition with the canonical surjection is the identity of such an injection is called a section, when using the terminology of category theory.

Sometimes, there is a section that is more “natural” than the other ones. In this case, the representatives are called canonical representatives. For example, in modular arithmetic, for every integer m greater than 1, the congruence modulo m is an equivalence relation on the integers, for which two integers a and b are equivalent—in this case, one says congruent —if m divides this is denoted Each class contains a unique non-negative integer smaller than and these integers are the canonical representatives.

The use of representatives for representing classes allows avoiding to consider explicitly classes as sets. In this case, the canonical surjection that maps an element to its class is replaced by the function that maps an element to the representative of its class. In the preceding example, this function is denoted and produces the remainder of the Euclidean division of a by m.

Properties[edit]

Every element of is a member of the equivalence class Every two equivalence classes [x] and [y] are either equal or disjoint. Therefore, the set of all equivalence classes of forms a partition of : every element of belongs to one and only one equivalence class.^[9] Conversely, every partition of comes from an equivalence relation in this way, according to which xsim y if and only if and belong to the same set of the partition.^[10]

It follows from the properties of an equivalence relation that

if and only if

In other words, if ,sim, is an equivalence relation on a set and and are two elements of then these statements are equivalent:

Graphical representation[edit]

Graph of an example equivalence with 7 classes

An undirected graph may be associated to any symmetric relation on a set where the vertices are the elements of and two vertices and are joined if and only if Among these graphs are the graphs of equivalence relations; they are characterized as the graphs such that the connected components are cliques.^[4]

Invariants[edit]

If ,sim, is an equivalence relation on and P(x) is a property of elements of such that whenever P(x) is true if P(y) is true, then the property is said to be an invariant of or well-defined under the relation

A frequent particular case occurs when is a function from to another set ; if ${displaystyle fleft(x_{1}right)=fleft(x_{2}right)}$ whenever ${displaystyle x_{1}sim x_{2},}$ then is said to be class invariant under or simply invariant under This occurs, for example, in the character theory of finite groups. Some authors use “compatible with ,sim, ” or just “respects ,sim, ” instead of “invariant under ,sim, “.

Any function f:Xto Y is class invariant under according to which if and only if ${displaystyle fleft(x_{1}right)=fleft(x_{2}right).}$ The equivalence class of is the set of all elements in which get mapped to f(x), that is, the class [x] is the inverse image of f(x). This equivalence relation is known as the kernel of

More generally, a function may map equivalent arguments (under an equivalence relation ${displaystyle sim _{X}}$ on ) to equivalent values (under an equivalence relation ${displaystyle sim _{Y}}$ on ). Such a function is a morphism of sets equipped with an equivalence relation.

Quotient space in topology[edit]

In topology, a quotient space is a topological space formed on the set of equivalence classes of an equivalence relation on a topological space, using the original space’s topology to create the topology on the set of equivalence classes.

In abstract algebra, congruence relations on the underlying set of an algebra allow the algebra to induce an algebra on the equivalence classes of the relation, called a quotient algebra. In linear algebra, a quotient space is a vector space formed by taking a quotient group, where the quotient homomorphism is a linear map. By extension, in abstract algebra, the term quotient space may be used for quotient modules, quotient rings, quotient groups, or any quotient algebra. However, the use of the term for the more general cases can as often be by analogy with the orbits of a group action.

The orbits of a group action on a set may be called the quotient space of the action on the set, particularly when the orbits of the group action are the right cosets of a subgroup of a group, which arise from the action of the subgroup on the group by left translations, or respectively the left cosets as orbits under right translation.

A normal subgroup of a topological group, acting on the group by translation action, is a quotient space in the senses of topology, abstract algebra, and group actions simultaneously.

Although the term can be used for any equivalence relation’s set of equivalence classes, possibly with further structure, the intent of using the term is generally to compare that type of equivalence relation on a set either to an equivalence relation that induces some structure on the set of equivalence classes from a structure of the same kind on or to the orbits of a group action. Both the sense of a structure preserved by an equivalence relation, and the study of invariants under group actions, lead to the definition of invariants of equivalence relations given above.

Notes[edit]

^ “7.3: Equivalence Classes”. Mathematics LibreTexts. 2017-09-20. Retrieved 2020-08-30.
^ ^a ^b Weisstein, Eric W. “Equivalence Class”. mathworld.wolfram.com. Retrieved 2020-08-30.
^ Avelsgaard 1989, p. 127
^ ^a ^b Devlin 2004, p. 123
^ Maddox 2002, pp. 77–78
^ Devlin 2004, p. 122
^ Weisstein, Eric W. “Equivalence Relation”. mathworld.wolfram.com. Retrieved 2020-08-30.
^ Wolf 1998, p. 178
^ Maddox 2002, p. 74, Thm. 2.5.15
^ Avelsgaard 1989, p. 132, Thm. 3.16

References[edit]

Avelsgaard, Carol (1989), Foundations for Advanced Mathematics, Scott Foresman, ISBN 0-673-38152-8
Devlin, Keith (2004), Sets, Functions, and Logic: An Introduction to Abstract Mathematics (3rd ed.), Chapman & Hall/ CRC Press, ISBN 978-1-58488-449-1
Maddox, Randall B. (2002), Mathematical Thinking and Writing, Harcourt/ Academic Press, ISBN 0-12-464976-9
Wolf, Robert S. (1998), Proof, Logic and Conjecture: A Mathematician’s Toolbox, Freeman, ISBN 978-0-7167-3050-7

External links[edit]

Media related to Equivalence classes at Wikimedia Commons

Источник

Прочие статьи цикла

Отношения. Часть I
Отношения. Часть II
Количественные характеристики отношений

Формальная теория моделирования использует алгебраические отношения, включая их в сигнатуры моделей алгебраических структур, которыми описывает реальные физические, технические объекты и процессы их функционирования. Эта публикация является продолжением предшествующей, прочтение которой желательно, так как многие понятия и термины, используемые здесь, описываются там.

Предлагается изложение не в традиционном (стрелочном) стиле, а так, как мне самому пришлось всю эту кухню представлять и осваивать и по учебникам/пособиям, и по журнальным статьям. Особенно полезной вещью считаю созданный мной каталог, он позволяет выделить практически любое пространство и представить его элементы в удобном виде: матрицей, графом и др. Сразу видишь с чем имеешь дело и свойства (они уже выписаны) проверять часто не требуется.

Понятие отношения

Думаю, что термин отношение знаком каждому читателю, но просьба дать определение поставит большинство в тупик. Причин для этого много. Они чаще всего в преподавателях, которые, если и использовали отношения в процессе преподавания, внимания на этом термине не заостряли, запоминающихся примеров не приводили. Некоторые комментаторы статьи отнесли замечания на свой счет и насыпали минусов. Но шила в мешке не утаишь. Серьезных публикаций как не было, так и нет. Задайте себе вопрос, работали ли Вы с каким-либо пространством отношений? И честно себе ответьте. Что об этом пространстве можете миру поведать, для начала хотя-бы перечислить его элементы и указать свойства. Даже на СУБД Вы смотрите глазами их создателей, а они ведь тоже не все видят, или не все показывают, как, например, в микросхемах.

Здесь сделаю небольшой повтор. Начинать следует с абстрактного множества А ={a1,a2,a3,…, an}. О нем почитать можно здесь. Для лучшего понимания сократим множество до 3 элементов, т.е. А ={a1, a2, a3}. Теперь выполним декартово умножение А×А =А² и явно перечислим все элементы декартова квадрата
А×А={(a1, a1),(a1, а2),(a1, a3),(a2, а1),(a2, a2),(a2, a3),(a3, a1),(a3, a2),(a3, a3)}.
Получили 9 упорядоченных пар элементов из А×А, в паре первый элемент из первого сомножителя, второй — из второго. Теперь попробуем получить все подмножества из декартова квадрата А×А. Подмножества будут содержать разное количество пар: одну, две, три и так до всех 9 пар, включаем в этот список и пустое множество ∅. Сколько же получилось подмножеств? Много, а именно 2⁹ = 512 элементов.

Определение. Подмножество декартова квадрата множества называется бинарным отношением. Если декартов квадрат из двух сомножителей отношение бинарное, если из 3-х -тернарное, из 4-х — тетрарное, из n — n-арное. Арность — число мест в элементе отношения.
Определение. Множество всех подмножеств множества А называется булеаном. Булеан состоит из 2^|A| элементов, здесь |A| — мощность множества.

Отношения можно задавать в разном представлении:

перечислением элементов; R1 ={(a2,a2),(a2,a3),(a3,a1)}; R2 ={(a3,a3)}
двоичным вектором; <000011100>; <000000001>
матрицей;
графом и др. способами.

Далее переходим к рассмотрению пространств отношений, считая, что понятие, свойства отношений и операции с ними, читателю знакомы хотя бы в объеме нашей публикации в ссылке.

Пространства бинарных отношений

Предварительно уточним, что отношения могут быть строгими (это все антирефлексивные отношения) или нестрогими (все остальные). Внимание сосредоточим на отношениях безразличия и предпочтения, последние подразделяются на слабые предпочтения и строгие предпочтения (почему-то не сильные). Вообще в науке с терминологией нет порядка и скорее всего не будет. В криптографии, например, снятие шифра с криптограммы при наличии ключа -расшифрование, а без ключа — дешифрование. Казалось бы, дешифратор — дешифрует, но нет.

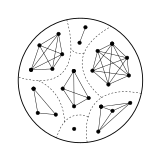
Пространством бинарных отношений с множеством-носителем называется произвольное подмножество множества бинарных отношений заданных на. Рассмотрим основные пространства для отношений предпочтений (рис. 2.15).

Р – пространство всех отношений слабого предпочтения, удовлетворяют условию рефлексивности и полноты.
QT – слабые предпочтения, удовлетворяющие условию квазитранзитивности.
QO – пространство линейных квазипорядков, т. е. отношения из QT, которые являются транзитивными.
ТО – пространство всех совершенных порядков, т. е. отношения из QO, которые являются антисимметричными.
SP – пространство всех отношений строгого предпочтения, удовлетворяют свойствам антирефлексивности и антисимметричности.
РО – отношения строгого частичного порядка, или транзитивные строгие предпочтения. Так как отношения строгого частичного порядка транзитивны, естественно пользоваться, для их представления сокращенными графами, то есть такими, в которых опущены дуги, реализующие транзитивность. Такие сокращенные графы называются диаграммами Хассе.
QS – пространство квазисерий, т. е. строгие частичные порядки, для которых отношение I=¬(PUP^-1) – эквивалентность.
TSO – пространство строгих линейных порядков, т. е. тех частичных порядков, для которых выполняется свойство полноты.
Необходимо отметить, всего таких отношений n!.. Например, для n = 3, число совершенных отношений равно 6 и все они приведены на рис. 2.13.
Т – пространство всех отношений толерантности (безразличия), они обладают свойствами симметричности и рефлексивности.
ТОТ – пространство транзитивно ориентируемых отношений толерантности, т. е. такие отношения, что дополнение к I представляется в виде объединения взаимно обратных транзитивных отношений, т. е.
¬I =R∩R^-1.
I – пространство всех отношений эквивалентности, т. е. симметричных, рефлексивных и транзитивных отношений.
Е – пространство отношений равенства, состоит из одного отношения представленного диагональной матрицей. Между пространствами R, P и I имеется взаимно-однозначная связь, определяемая отображением отношений предпочтения.

Рисунок 2.15 Схема пространств бинарных отношений

Выявленные связи между пространствами используются для переноса задач принятия решений (ЗПР) из одних пространств в другие, где они могут быть решены более простым путем, а затем полученное решение возвращают в исходное пространство, где была сформулирована ЗПР.
Эти отношения представлены диаграммой на рис. 2.14. Пространства бинарных отношений (типы отношений) представлены рис. 2.15.

Отношения эквивалентности

Определение. Бинарное отношение σ ⊆ А×А, обладающее тремя свойствами рефлексивности, симметричности, транзитивности, называется, бинарным отношением эквивалентности (БОЭ). Обозначается отношение эквивалентности σ(х, у), (х, у)∊σ, хσу, х≈у. Удобно использовать матричное (табличное) представление отношения. Ниже на рис 2.24 приведено как раз матричное представление. Над множеством из 4-х элементов существует 15 БОЭ, которые все изображены.

Представление и анализ структуры отношений эквивалентности (n = 4)
Эквивалентность из бинарных отношений, пожалуй, самое распространенное БО. Редкая наука обходится без этого понятия, но даже тогда, когда эквивалентности используются в изложении каких-либо вопросов, бывает трудно понять, что в виду имел автор. Даже при корректном определении и перечислении свойств, присущих этому бинарному отношению – трудности восприятия остаются.

Начнем с примера об эквивалентностях, который иллюстрирует ограниченность их количества.

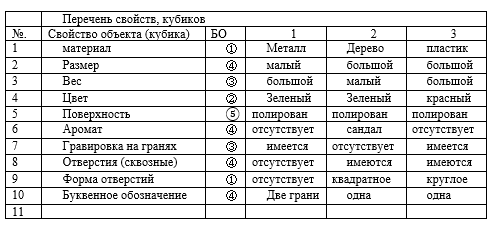
Пример 1. Пусть имеется три кубика. Составим список свойств, которыми наделены кубики и практическое использование которых (свойств кубиков) делает их как бы взаимозаменяемыми. Кубикам присвоим номера, а их свойства представим таблицей 1.

По каждому из свойств возникает БОЭ и классы эквивалентности. Продолжая список свойств, мы новых отношений эквивалентности не получим. Будут только повторы уже построенных, но для других признаков. Покажем связь БОЭ с множествами.

Рассмотрим множество из трех элементов А ={1,2,3} и получим для него все возможные разбиения на все части. ①1|2|3; ②12|3; ③13|2; ④ 1|23; ⑤123. Последнее разбиения на одну часть. Номера разбиений и БО в кружках.

Определение. Разбиением множества А называют семейство Аi, i = 1(1)I, непустых попарно непересекающихся подмножеств из А, объединение которых образует все исходное множество А=UАi, Аi∩Аj =∅, ∀ i ≠ j. Под-множества Аi называют классами эквивалентности разбиения исходного множества.

Это все разбиения множества (5 штук). Анализ БО показывает, что различных отношений эквивалентности тоже только 5 штук. Случайно ли это совпадение? Мы можем каждому разбиению сопоставить матрицу из девяти ячеек (3×3 = 9), в каждой из которых либо размещается упорядоченная пара элементов из множества А, либо ячейка остается пустой, если для соответствующей пары нет объекта. Строки и столбцы матрицы размечаются элементами множества А, а пересечению строка – столбец соответствует упорядоченная пара (i, j). В ячейку матрицы вписывается не пара, а просто единица или нуль, впрочем, нуль часто не пишут совсем.

Нет, совпадение не случайное. Оказывается, каждому разбиению множества взаимно однозначно соответствует БОЭ, при этом мощность множества может быть любой |A| = n.

Это отношение едва ли не самое частое по использованию в научном обороте, но совокупность свойств, реализуемых в этом отношении, сильно ограничивает его распространенность.
Так среди всех абстрактных бинарных отношений над множеством из трех элементов (всего их 2⁹ = 512 отношений) только пять являются эквивалентностями — носителями требуемых свойств, менее одного процента.

Для |A| = 4 отношений существует 2¹⁶ = 65536, но эквивалентностей лишь 15 штук. Это весьма редкий тип отношений. С другой стороны, отношения эквивалентности широко распространены в прикладных задачах. Везде, где имеются и рассматриваются множества самых различных объектов и различные разбиения таких множеств (не чисел) на части возникают отношения эквивалентности. Их можно назвать математическими (алгебраическими) моделями таких разбиений, классифицирующими множества объектов по различным признакам.

Минимальное разбиение множества А, образованное из одноэлементных подмножеств А= U{a} и разбиение А, состоящее из самого множества {А}, называются тривиальными (несобственными) разбиениями.

Решетка Р(4): все разбиения множества А = {a1,a2,a3,a4} = {1,2,3,4}

Минимальному разбиению соответствует отношение эквивалентности П15, которое называется равенством или единичным отношением. В каждом классе эквивалентности — единственный элемент. Разбиению множества А, включающему лишь само множество А, соответствует отношение эквивалентности, содержащее все элементы декартова квадрата А×А.

Ближайший тип к отношениям эквивалентности – отношения толерантности. Множество отношений толерантности содержит в себе все отношения эквивалентности. Для носителя А из трех элементов толерантностей 8. Все они обладают свойствами рефлексивности и симметричности.

При выполнении свойства транзитивности пять из восьми толерантностей преобразует в эквивалентности (рис. 2.24 и 2.25).

Определение. Совокупность классов [a]σ эквивалентности элементов множества А называется фактор-множеством (обозначается А/σ) множества А по эквивалентности σ.

Определение. Естественным (каноническим) отображением f: A→ А/σ называется такое отображение f, при котором f(а) = [a]σ.

Отношения толерантности и их анализ

Об этих БО ранее уже упоминалось, а здесь рассмотрим их подробнее. Всем известны понятия сходство, похожесть, одинаковость, неразличимость, взаимозаменяемость объектов. Они кажутся близкими по содержанию, но при этом не одно и то же. Когда для объектов указано только сходство, то невозможно разбить их на четкие классы так, что внутри класса объекты похожи, а между объектами разных классов сходства нет. В случае сходства возникает размытая ситуация без четких границ. С другой стороны, накапливание несущественных различий у сходных объектов может привести к совершенно непохожим объектам.

В предыдущей части мы обсудили содержательный смысл отношения одинаковости (эквивалентности) объектов. Не менее важной является ситуация, когда приходится устанавливать сходство объектов.

Пусть изучается форма геометрических тел. Если одинаковость формы объектов, например, кубиков, означает их полную взаимозаменяемость в определенной ситуации обучения, то сходство – это частичная взаимозаменяемость, (когда среди кубиков встречаются очень похожие на них параллелепипеды) т. е. возможность взаимной замены с некоторыми (допустимыми в данной ситуации) потерями.

Наибольшая мера для сходства – неразличимость, а вовсе не одинаковость, как может показаться на первый взгляд. Одинаковость – свойство качественно иное. Одинаковость можно рассматривать только как частный случай неразличимости и сходства.

Все дело в том, что неразличимые объекты (так же, как и сходные, похожие) не удается разбить на классы так, чтобы в каждом классе элементы не различались, а элементы разных классов заведомо различались.

В самом деле, будем рассматривать множество точек (х, у) на плоскости. Пусть величина d имеет значение меньшее порога разрешимости глаза, т. е. d – такое расстояние, при котором две точки, находящиеся на этом расстоянии, сливаются в одну, т.е. визуально неразличимы (при выбранном удалении плоскости от наблюдателя). Рассмотрим теперь n точек, лежащих на одной прямой и отстоящих (каждая от соседних) на расстоянии d. Каждая пара
соседних точек неразличима, но, если n достаточно велико, первая и последняя точки будут отстоять друг от друга на большое расстояние и заведомо будут различимы.

Традиционный подход к изучению сходства или неразличимости состоит в том, чтобы сначала определить меру сходства, а затем исследовать взаимное расположение сходных объектов. Английский математик Зиман, изучая модели зрительного аппарата, предложил аксиоматическое определение сходства. Тем самым свойства сходства стало возможным изучать независимо от того, как конкретно оно задано в той или иной ситуации: расстоянием между объектами, совпадением каких-то признаков или субъективным мнением наблюдателя.
Введем экспликацию понятия сходства или неразличимости.

Определение. Отношение Т на множестве M называется отношением толерантности или толерантностью, если оно рефлексивно и симметрично.

Корректность такого определения видна из того, что объект заведомо неразличим сам с собой и, конечно, похож на себя (это задает рефлексивность отношения). Порядок рассмотрения двух объектов не влияет на окончательный вывод об их сходстве или несходстве (симметричность).
Из примера со зрительной неразличимостью точек плоскости видим, что транзитивность толерантности выполняется не для всех пар объектов.

Ясно также, что поскольку одинаковость есть частный случай сходства, то эквивалентность должна быть частным случаем толерантности. Сравнивая определения эквивалентности и толерантности, убеждаемся, что так оно и есть. Философский принцип: «частное богаче общего» наглядно подтверждается. Дополнительное свойство – транзитивности делает часть отношений толерантности эквивалентностями. Двое близнецов бывают настолько одинаковыми, что без риска могут сдавать экзамены друг за друга. Однако если два студента только похожи, то такая проделка, хотя и осуществима, но рискованна.

Каждый элемент множества несет определенную информацию о похожих на него элементах. Но не всю информацию, как в случае одинаковых элементов. Здесь возможны разные степени информации, которую один элемент содержит относительно другого.

Рассмотрим примеры, где толерантность задается разными способами.

Пример 2. Множество M состоит из четырехбуквенных русских слов — нарицательных существительных в именительном падеже. Будем называть такие слова сходными, если они отличаются не более чем на одну букву. Известная задача «Превращение мухи в слона» в точных терминах формулируется так. Найти последовательность слов, начинающуюся словом «муха» и кончающуюся словом «слон», любые два соседних слова в которой сходны в смысле только что данного определения. Решение этой задачи:

муха — мура — тура — тара — кара — каре — кафе — кафр — каюр — каюк — крюк — крок — срок — сток — стон — слон.

Пример 3. Пусть p — натуральное число. Обозначим через Sp совокупность всех непустых подмножеств множества М = {1, 2, …, p}. Отношение «иметь хотя бы один общий элемент» на множестве Sp – это отношение толерантности. Тогда два таких подмножества назовем толерантными, если у них есть хотя бы один общий элемент. Легко видеть, что рефлексивность и симметричность отношения выполнены.

Множество Sp называется (p –1) -мерным симплексом. Это понятие обобщает понятие отрезка, треугольника и тетраэдра на многомерный случай. Числа 1, 2, 3, …, p интерпретируются как вершины симплекса. Двухэлементные подмножества – как ребра, трехэлементные – как плоские (двумерные) грани, прочие k-элементные подмножества – как (k –1)-мерные грани. Число всех элементов (подмножеств) из Sp равно 2^р −1.

Толерантность подмножеств (граней) означает наличие у них общих вершин.

Определение. Множество M с заданным на нем отношением толерантности τ называется пространством толерантности. Таким образом, пространство толерантности есть пара (M, τ).

Пример 4. Пространство толерантности Sp допускает обобщение на бесконечный случай. Пусть H — произвольное множество. Если SH – совокупность всех непустых подмножеств множества H, то отношение толерантности Т на SH задается условием: X Т Y, если X∩Y ≠ ∅. Симметричность и рефлексивность этого отношения очевидны. Пространство SH обозначается <Н, Т> и называется «универсальным» пространством толерантности.

Пример 5. Пусть p — натуральное число. Обозначим Bp множество всех точек p-мерного пространства, координаты которых равны 0 или 1. Толерантность в Bp задается правилом: xτy, если x и y содержат хотя бы одну совпадающую компоненту (координату). Общее количество элементов в Bp равно 2^р. Для каждого элемента x = (a1, a2, …,ap) из множества Bp существует только один не толерантный ему элемент y = (1−a1, 1−a2, …, 1−ap ).
Очевидно, что Bp состоит из всех вершин p-мерного куба.

Пример 6. Рассмотрим пространство толерантности, компоненты которого принимают любые действительные значения.

В частности, это множество всех точек x = (a1, a2) декартовой плоскости. Толерантность двух точек означает совпадение у них хотя бы одной координаты. Значит, две толерантные точки находятся либо на общей вертикали, либо на общей горизонтали.

При других значениях p пространство можно интерпретировать как множество точек p-мерного пространства. В частности, каждый элемент x можно считать числовой функцией, заданной на множестве натуральных чисел {1, 2, 3, …}, которая каждому натуральному числу i: 1 ≤ i ≤ p сопоставляет действительное число ai (конечная числовая последовательность). Тогда толерантность двух функций x и y означает, что они хотя бы в одной точке равны.

Отношения частичного порядка и их анализ

Упорядоченные множества – это множества с введенным на нем отношением порядка. Определение. Множество А и бинарное отношение порядка R на нем (≤) называется частично упорядоченным, если для отношения выполнены (как и в БОЭ) три условия (одно условие другое):

рефлексивность ∀ х ∊ А (хRx); (антирефлексивность ∀ х ∊ А ¬(хRx));
антисимметричность ∀ х, y ∊ А (хRy yRx→x = y);
транзитивность ∀ х, у, z ∊ А (хRy& yRz →xRz).

При антирефлексивном отношении возникает строгий частичный порядок. Множество В(А) всех подмножеств множества А, упорядоченное по включению элементов является частично упорядоченным множеством (ЧУМ). Частично упорядоченное множество (В(А), ⊆) часто называют булеаном.

Элемент х∊А ЧУМ А покрывает элемент у∊А, если х > y и не существует z∊А такого, что х > z > y. Пара элементов х, у∊А называется сравнимой, если х ≥ у или х ≤ у.

Если в ЧУМ А всякая пара его элементов является сравнимой, то А называют линейно упорядоченным множеством или цепью.

Если же некоторое ЧУМ В состоит лишь из несравнимых друг с другом элементов, то множество В называют антицепью. Цепь в ЧУМ А называется насыщенной, если она не может быть вложена ни в какую другую цепь, отличную от себя.

Аналогично определяется насыщенная антицепь. Максимальной цепью (антицепью) называется цепь (антицепь), содержащая максимальное количество элементов.

Элемент m ЧУМ А называется минимальным, если в А нет элемента х∊А, отличного от m и такого, что х≤m. Элемент M ЧУМ А называется максимальным, если в А нет элемента х «большего», чем M, отличного от M и такого, что х ≥ M.

Элемент у∊А ЧУМ А называется наибольшим, если ∀ х∊ А х ≤ у. Элемент у∊ А ЧУМ А называется наименьшим, если ∀ х∊А х ≥ у. Для наибольшего и наименьшего элементов принято использовать обозначения 1 и 0 соответственно. Их называют универсальными границами. Всякое ЧУМ А имеет не более одного наименьшего и не более одного наибольшего элементов. В ЧУМ А допустимо несколько минимальных и несколько максимальных элементов
Изображать конечное ЧУМ А удобно диаграммой Хассе, которая представляет собой ориентированный граф, его вершины распределены по уровням диаграммы и соответствуют элементам из А, а каждая дуга направляется вниз и рисуется тогда и только тогда, когда элемент х∊А покрывает элемент у∊А.

Транзитивные дуги не изображаются. Уровни диаграммы Хассе содержат элементы одинакового ранга, т.е. связанные с минимальными элементами ЧУМ путями равной длины (по числу дуг).
Пусть В непустое подмножество ЧУМ А, тогда элемент х∊А называется точной верхней гранью (обозначается sup_AB) множества В, если х ≥ у для всех у∊В и, если из истинности соотношения z ≥ у для всех у∊В вытекает, что z ≥ х.

Точной нижней гранью (обозначается inf_AB) множества В называется элемент х∊А, если х ≤ у для всех у∊В и, если из условия z ≤ у для всех у∊ В вытекает, что z ≤ х.

Пример 7. Заданы два конечных числовых множества
А = {0,1,2,…,21} и B = {6,7,10,11}.

ЧУМ (А, ≤) представлено рис. 2.26.

Совокупность В^Δ всех верхних граней для В называется верхним конусом для множества В. Совокупность В^∇ всех нижних граней для В называется нижним конусом для В.

Всякое подмножество ЧУМ также является ЧУМ относительно наследованного порядка. Если в множестве существуют наибольший и/или наименьший элементы, то они являются максимальным (минимальным соответственно). Обратное неверно. Булеан обладает единственным наименьшим (Ø) и единственным наибольшим элементами.

В приведенном множестве наименьший элемент нуль (0) и он совпадает с единственным минимальным элементом, а наибольшего элемента не существует. Максимальными элементами являются {19, 20, 21}. Точная верхняя грань для B = {6,7,10,11} есть элемент 21 (это наименьший элемент в верхнем конусе).

Общая ситуация. Пусть задано множество, мощность которого*******. Из всех бинарных отношений, возможных на этом множестве, выделим бинарные отношения предпочтения и связанные с ними отношения строгих частичных порядков.

Частичные порядки отличаются от строгих частичных порядков только тем, что содержат в своем составе дополнительные элементы (в матричном представлении – диагональные) (аi, ai ) = 1, i = 1(1)n, а число тех и других порядков в полном множестве отношений одинаково. До настоящего времени не найдены зависимости (формула, алгоритм), которые позволяли бы подсчитывать и перечислять при любом n число частичных порядков.

Разными авторами непосредственным подсчетом определены и опубликованы следующие результаты (табл. 2.12).

Вычислительные эксперименты автора позволили получить не только число, но и вид (представление) частичных порядков при разных мощностях множителя-носителя отношений. Принтер задыхался печатая такие огромные списки, но не только красота требует жертв, наука тоже не отказывается от них.

В таблице 2.12 показаны: n = |A| – мощность множества-носителя; вторая строка – количество всех бинарных отношений на множестве А; и далее

|Ин(n)| – количество классов неизоморфных отношений;
|Г(n)| – количество отношений частичного порядка;
|Гн(n)| – количество классов неизоморфны отношений частичного порядка;
|Гл(n)| = n! – количество отношений линейного порядка.

Как видим, в таблице для небольших n, например, Г(n=4) имеется всего 219, приводятся данные, значения которых с увеличением n очень быстро растут, что существенно усложняет их количественный (и качественный) непосредственный анализ даже с помощью ЭВМ.

Таблица ниже иллюстрирует возможность порождения Г(n=4) всех частичных порядков из пересечения каждого с каждым линейных частичных порядков. Но в этой ситуации возникают избыточные (повторяющиеся), которые при малых n можно отсечь вручную (пересчитать). Получаются 300 матриц, но ЧУМ среди них лишь 219. Общие формулы так и не были получены. На мировом уровне ситуация аналогичная, хотя мне не довелось видеть публикаций о перечислениях ЧУМ западных авторов. Наши алгоритмы вполне оригинальны и пионерские.

Приведу возможную схему решения задачи перечисления элементов пространства частичных порядков (n=4).

Множество строгих частичных порядков при лексикографическом упорядочении линейных порядков (n=4) порождается при их взаимном пересечении.

Несколько важных определений математики, для встречающихся часто в текстах понятий.

Определение. Замкнутый интервал – это множество вида {x: a ≤ x ≤ b}; открытый интервал не замкнут, и полуоткрытый интервал, т. е. множество вида {x: a < x ≤ b}, где а < b, или вида {x: a ≤ x < b} не открыт и не замкнут.

Определение. Граница произвольного интервала вещественной прямой в обычной топологии вещественных чисел состоит лишь из концов этого интервала, независимо от того, открыт этот интервал, замкнут или полуоткрыт. Границей множества рациональных чисел, так же, как и границей множества всех иррациональных чисел, служит все множество вещественных чисел.

Определение. Каждое линейно упорядоченное множество, в любом непустом подмножестве которого есть наименьший элемент, называется вполне упорядоченным.

Определение. Семейство R называется цепью (иногда башней, гнездом) тогда и только тогда, когда для любых его элементов А и В либо А ⊂ В, либо В ⊂ А. Это условие равносильно утверждению, что семейство R линейно упорядочено по включению или – в принятой терминологии – что семейство R вместе с отношением включения является цепью.

П р и н ц и п м а к с и м а л ь н о с т и Х а у с д о р ф а. Для любого семейства множеств A и любого гнезда R, образованного элементами семейства A существует максимальное гнездо M в A, содержащее R.

Важная теорема о множествах и их семействах (Дж.Л.Kелли «Общая топология» стр.55).
Теорема. (а) П р и н ц и п м а к с и м а л ь н о г о э л е м е н т а. Максимальный элемент в семействе A множества существует, если для каждого гнезда, лежащего в A, в A найдется элемент, который содержит произвольный элемент этого гнезда.

(б) П р и н ц и п м и н и м а л ь н о г о э л е м е н т а. Минимальный элемент в семействе A существует, если для каждого гнезда, лежащего в A, в A найдется элемент, содержащийся в каждом элементе этого гнезда.

(в) Л е м м а Т ь ю к и. В каждом семействе множеств конечного характера есть максимальный элемент.

(г) Л е м м а К у р а т о в с к о г о. Каждая цепь в (частично) упорядоченном множестве содержится в некоторой максимальной цепи.

(д) Л е м м а Ц о р н а. Если каждая цепь некоторого частично упорядоченного множества ограничена сверху, то в этом множестве есть максимальный элемент.

(е) А к с и о м а в ы б о р а. Пусть Хα – непустое множество для каждого элемента а из множества индексов А. Тогда на А существует функция с такая, что с(а)∊ Хα для каждого а из А.

(ж) П о с т у л а т Ц е р м е л о. Для любого семейства A непересекающихся непустых множеств существует такое множество С, что АUС для каждого А из A состоит ровно из одной точки.

(з) П р и н ц и п в п о л н е у п о р я д о ч е н и я. Каждое множество можно вполне упорядочить.

Источник

Отношение эквивалентности – это обобщение понятия равенства. Эквивалентные элементы не различимы для теории в каком-то фиксированном смысле.

Определение

Пусть дано множество и на нём задано бинарное отношение . Тогда называется отношением эквивалентности, если оно

Классы эквивалентности

Подмножество элементов эквивалентных данному называется его классом эквивалентности. Пишут:

Пусть Тогда либо либо Таким образом отношение эквивалентности порождает разбиение множества на непересекающиеся классы эквивалентности. Семейство таких классов образует множество, называемое фактор-множеством и обозначаемое

Примеры

Источник

Отношение эквивалентности. Классы эквивалентности

Классы эквивалентных элементов и их свойства

Пример

Свойства классов эквивалентности

Свойство 1

Свойство 2

Свойство 3

Свойство 4

Разбиение множества

Примеры

Определение[править | править код]

Связанные определения[править | править код]

Примеры[править | править код]

Классы эквивалентности[править | править код]

См. также[править | править код]

Литература[править | править код]

Examples[edit]

Definition and notation[edit]

Properties[edit]

Graphical representation[edit]

Invariants[edit]

Quotient space in topology[edit]

See also[edit]

Notes[edit]

References[edit]

Further reading[edit]

External links[edit]

Понятие отношения

Пространства бинарных отношений

Отношения эквивалентности

Отношения толерантности и их анализ

Отношения частичного порядка и их анализ

Определение

Классы эквивалентности

Примеры

Добавить комментарий Отменить ответ

Отношение эквивалентности. Классы эквивалентности

Классы эквивалентных элементов и их свойства

Пример

Свойства классов эквивалентности

Свойство 1

Свойство 2

Свойство 3

Свойство 4

Разбиение множества

Примеры

Определение[править | править код]

Связанные определения[править | править код]

Примеры[править | править код]

Классы эквивалентности[править | править код]

См. также[править | править код]

Литература[править | править код]

Examples[edit]

Definition and notation[edit]

Properties[edit]

Graphical representation[edit]

Invariants[edit]

Quotient space in topology[edit]

See also[edit]

Notes[edit]

References[edit]

Further reading[edit]

External links[edit]

Понятие отношения

Пространства бинарных отношений

Отношения эквивалентности

Отношения толерантности и их анализ

Отношения частичного порядка и их анализ

Определение

Классы эквивалентности

Примеры

Вам также может понравиться

Как найти массу нитриде магния

Как составить бизнес план по открытию магазина образец

Как найти девушку на ночь фото

Добавить комментарий Отменить ответ