Как найти код элемента python

Введение

Поиск информации, хранящейся в различных структурах данных, является важной частью практически каждого приложения.

Существует множество различных алгоритмов, которые можно использовать для поиска. Каждый из них имеет разные реализации и напрямую зависит от структуры данных, для которой он реализован.

Умение выбрать нужный алгоритм для конкретной задачи является ключевым навыком для разработчиков. Именно правильно подобранный алгоритм отличает быстрое, надежное и стабильное приложение от приложения, которое падает от простого запроса.

В этой статье:

• Операторы членства (Membership Operators)
• Линейный поиск
• Бинарный поиск
• Улучшенный линейный поиск — Jump Search
• Поиск Фибоначчи
• Экспоненциальный поиск
• Интерполяционный поиск

Операторы членства (Membership Operators)

Алгоритмы развиваются и оптимизируются в результате постоянной эволюции и необходимости находить наиболее эффективные решения для основных проблем в различных областях.

Одной из наиболее распространенных проблем в области компьютерных наук является поиск в коллекции и определение того, присутствует ли данный объект в коллекции или нет.

Почти каждый язык программирования имеет свою собственную реализацию базового алгоритма поиска. Обычно — в виде функции, которая возвращает логическое значение True или False, когда элемент найден в данной коллекции элементов.

В Python самый простой способ поиска объекта — использовать операторы членства. Их название связано с тем, что они позволяют нам определить, является ли данный объект членом коллекции.

Эти операторы могут использоваться с любой итерируемой структурой данных в Python, включая строки, списки и кортежи.

• in — возвращает True, если данный элемент присутствует в структуре данных.
• not in — возвращает True, если данный элемент не присутствует в структуре данных.

>>> 'apple' in ['orange', 'apple', 'grape']
True
>>> 't' in 'pythonist'
True
>>> 'q' in 'pythonist'
False
>>> 'q' not in 'pythonist'
True

Операторов членства достаточно, если нам нужно только определить, существует ли подстрока в данной строке, или пересекаются ли две строки, два списка или кортежа с точки зрения содержащихся  в них объектов.

В большинстве случаев помимо определения, наличествует ли элемент в последовательности, нам нужна еще и позиция (индекс) элемента. Используя операторы членства, мы не можем получить ее.

Существует множество алгоритмов поиска, которые не зависят от встроенных операторов и могут использоваться для более быстрого и/или эффективного поиска значений. Кроме того, они могут дать больше информации (например, о позиции элемента в коллекции), а не просто определить, есть ли в коллекции этот элемент.

Линейный поиск

Линейный поиск — это один из самых простых и понятных алгоритмов поиска. Мы можем думать о нем как о расширенной версии нашей собственной реализации оператора in в Python.

Суть алгоритма заключается в том, чтобы перебрать массив и вернуть индекс первого вхождения элемента, когда он найден:

def LinearSearch(lys, element):
    for i in range (len(lys)):
        if lys[i] == element:
            return i
    return -1

Итак, если мы используем функцию для вычисления:

>>> print(LinearSearch([1,2,3,4,5,2,1], 2))

То получим следующий результат:

1

Это индекс первого вхождения искомого элемента, учитывая, что нумерация элементов в Python начинается с нуля.

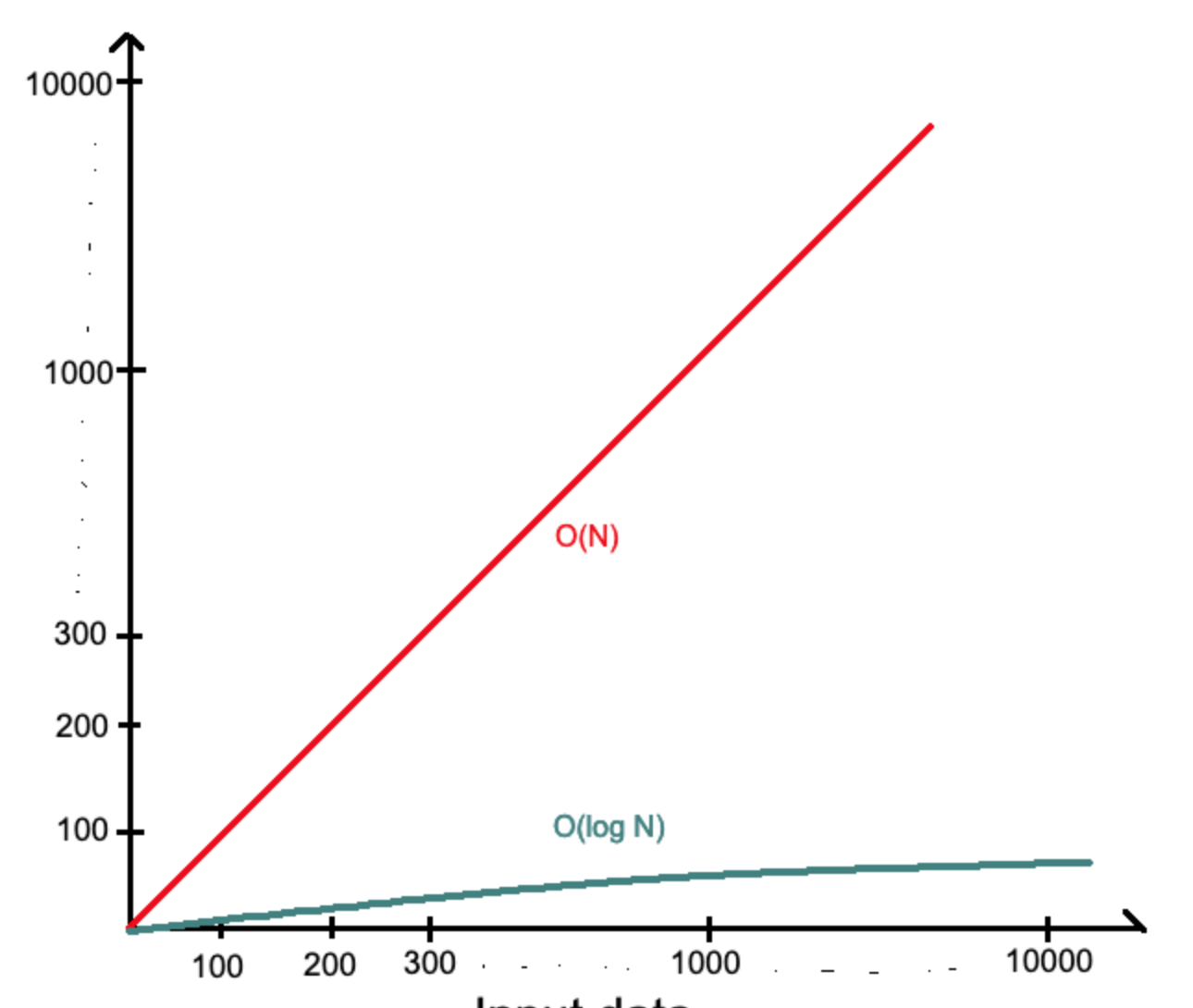
Временная сложность линейного поиска равна O(n). Это означает, что время, необходимое для выполнения, увеличивается с увеличением количества элементов в нашем входном списке lys.

Линейный поиск не часто используется на практике, потому что такая же эффективность может быть достигнута с помощью встроенных методов или существующих операторов. К тому же, он не такой быстрый и эффективный, как другие алгоритмы поиска.

Линейный поиск хорошо подходит для тех случаев, когда нам нужно найти первое вхождение элемента в несортированной коллекции. Это связано с тем, что он не требует сортировки коллекции перед поиском (в отличие от большинства других алгоритмов поиска).

Бинарный поиск

Бинарный поиск работает по принципу «разделяй и властвуй». Он быстрее, чем линейный поиск, но требует, чтобы массив был отсортирован перед выполнением алгоритма.

Предполагая, что мы ищем значение val в отсортированном массиве, алгоритм сравнивает val со значением среднего элемента массива, который мы будем называть mid.

• Если mid — это тот элемент, который мы ищем (в лучшем случае), мы возвращаем его индекс.
• Если нет, мы определяем, в какой половине массива мы будем искать val дальше, основываясь на том, меньше или больше значение val значения mid, и отбрасываем вторую половину массива.
• Затем мы рекурсивно или итеративно выполняем те же шаги, выбирая новое значение для mid, сравнивая его с val и отбрасывая половину массива на каждой итерации алгоритма.

Алгоритм бинарного поиска можно написать как рекурсивно, так и итеративно. В Python рекурсия обычно медленнее, потому что она требует выделения новых кадров стека.

Поскольку хороший алгоритм поиска должен быть максимально быстрым и точным, давайте рассмотрим итеративную реализацию бинарного поиска:

def BinarySearch(lys, val):
    first = 0
    last = len(lys)-1
    index = -1
    while (first <= last) and (index == -1):
        mid = (first+last)//2
        if lys[mid] == val:
            index = mid
        else:
            if val<lys[mid]:
                last = mid -1
            else:
                first = mid +1
    return index

Если мы используем функцию для вычисления:

>>> BinarySearch([10,20,30,40,50], 20)

То получим следующий результат, являющийся индексом искомого значения:

1

На каждой итерации алгоритм выполняет одно из следующих действий:

• Возврат индекса текущего элемента.
• Поиск в левой половине массива.
• Поиск в правой половине массива.

Мы можем выбрать только одно действие на каждой итерации. Также на каждой итерации наш массив делится на две части. Из-за этого временная сложность двоичного поиска равна O(log n).

Одним из недостатков бинарного поиска является то, что если в массиве имеется несколько вхождений элемента, он возвращает индекс не первого элемента, а  ближайшего к середине:

>>> print(BinarySearch([4,4,4,4,4], 4))

После выполнения этого фрагмента кода будет возвращен индекс среднего элемента:

2

Для сравнения: выполнение линейного поиска по тому же массиву вернет индекс первого элемента:

0

Однако мы не можем категорически утверждать, что двоичный поиск не работает, если массив содержит дубликаты. Он может работать так же, как линейный поиск, и в некоторых случаях возвращать первое вхождение элемента. Например:

>>> print(BinarySearch([1,2,3,4,4,4,5], 4))
3

Бинарный поиск довольно часто используется на практике, потому что он эффективен и быстр по сравнению с линейным поиском. Однако у него есть некоторые недостатки, такие как зависимость от оператора //. Существует много других алгоритмов поиска, работающих по принципу «разделяй и властвуй», которые являются производными от бинарного поиска. Некоторые из них мы рассмотрим далее.

Jump Search

Jump Search похож на бинарный поиск тем, что он также работает с отсортированным массивом и использует аналогичный подход «разделяй и властвуй» для поиска по нему.

Его можно классифицировать как усовершенствованный алгоритм линейного поиска, поскольку он зависит от линейного поиска для выполнения фактического сравнения при поиске значения.

В заданном отсортированном массиве мы ищем не постепенно по элементам массива, а скачкообразно. Если у нас есть размер прыжка, то наш алгоритм будет рассматривать элементы входного списка lys в следующем порядке: lys[0], lys[0+jump], lys[0+2jump], lys[0+3jump] и так далее.

С каждым прыжком мы сохраняем предыдущее значение и его индекс. Когда мы находим множество значений (блок), где lys[i] < element < lys[i + jump], мы выполняем линейный поиск с lys[i] в качестве самого левого элемента и lys[i + jump] в качестве самого правого элемента в нашем множестве:

import math

def JumpSearch (lys, val):
    length = len(lys)
    jump = int(math.sqrt(length))
    left, right = 0, 0
    while left < length and lys[left] <= val:
        right = min(length - 1, left + jump)
        if lys[left] <= val and lys[right] >= val:
            break
        left += jump;
    if left >= length or lys[left] > val:
        return -1
    right = min(length - 1, right)
    i = left
    while i <= right and lys[i] <= val:
        if lys[i] == val:
            return i
        i += 1
    return -1

Поскольку это сложный алгоритм, давайте рассмотрим пошаговое вычисление для следующего примера:

>>> print(JumpSearch([1,2,3,4,5,6,7,8,9], 5))

• Jump search сначала определит размер прыжка путем вычисления math.sqrt(len(lys)). Поскольку у нас 9 элементов, размер прыжка будет √9 = 3.
• Далее мы вычисляем значение переменной right. Оно рассчитывается как минимум из двух значений: длины массива минус 1 и значения left + jump, которое в нашем случае будет 0 + 3 = 3. Поскольку 3 меньше 8, мы используем 3 в качестве значения переменной right.
• Теперь проверим, находится ли наш искомый элемент 5 между lys[0] и lys[3]. Поскольку 5 не находится между 1 и 4, мы идем дальше.
• Затем мы снова делаем расчеты и проверяем, находится ли наш искомый элемент между lys[3] и lys[6], где 6 — это 3 + jump. Поскольку 5 находится между 4 и 7, мы выполняем линейный поиск по элементам между lys[3] и lys[6] и возвращаем индекс нашего элемента:

4

Временная сложность jump search равна O(√n), где √n — размер прыжка, а n — длина списка. Таким образом, с точки зрения эффективности jump search находится между алгоритмами линейного и бинарного поиска.

Единственное наиболее важное преимущество jump search по сравнению с бинарным поиском заключается в том, что он не опирается на оператор деления (/).

В большинстве процессоров использование оператора деления является дорогостоящим по сравнению с другими основными арифметическими операциями (сложение, вычитание и умножение), поскольку реализация алгоритма деления является итеративной.

Стоимость сама по себе очень мала, но когда количество искомых элементов очень велико, а количество необходимых операций деления растет, стоимость может постепенно увеличиваться. Поэтому jump search лучше бинарного поиска, когда в системе имеется большое количество элементов: там даже небольшое увеличение скорости имеет значение.

Чтобы ускорить jump search, мы могли бы использовать бинарный поиск или какой-нибудь другой алгоритм для поиска в блоке вместо использования гораздо более медленного линейного поиска.

Поиск Фибоначчи

Поиск Фибоначчи — это еще один алгоритм «разделяй и властвуй», который имеет сходство как с бинарным поиском, так и с jump search. Он получил свое название потому, что использует числа Фибоначчи для вычисления размера блока или диапазона поиска на каждом шаге.

Числа Фибоначчи  — это последовательность чисел 0, 1, 1, 2, 3, 5, 8, 13, 21 …, где каждый элемент является суммой двух предыдущих чисел.

Алгоритм работает с тремя числами Фибоначчи одновременно. Давайте назовем эти три числа fibM, fibM_minus_1 и fibM_minus_2. Где fibM_minus_1 и fibM_minus_2 — это два числа, предшествующих fibM в последовательности:

fibM = fibM_minus_1 + fibM_minus_2

Мы инициализируем значения 0, 1, 1 или первые три числа в последовательности Фибоначчи. Это поможет нам избежать  IndexError в случае, когда наш массив lys содержит очень маленькое количество элементов.

Затем мы выбираем наименьшее число последовательности Фибоначчи, которое больше или равно числу элементов в нашем массиве lys, в качестве значения fibM. А два числа Фибоначчи непосредственно перед ним — в качестве значений fibM_minus_1 и fibM_minus_2. Пока в массиве есть элементы и значение fibM больше единицы, мы:

• Сравниваем val со значением блока в диапазоне до fibM_minus_2 и возвращаем индекс элемента, если он совпадает.
• Если значение больше, чем элемент, который мы в данный момент просматриваем, мы перемещаем значения fibM, fibM_minus_1 и fibM_minus_2 на два шага вниз в последовательности Фибоначчи и меняем индекс на индекс элемента.
• Если значение меньше, чем элемент, который мы в данный момент просматриваем, мы перемещаем значения fibM, fibM_minus_1 и fibM_minus_2 на один шаг вниз в последовательности Фибоначчи.

Давайте посмотрим на реализацию этого алгоритма на Python:

def FibonacciSearch(lys, val):
    fibM_minus_2 = 0
    fibM_minus_1 = 1
    fibM = fibM_minus_1 + fibM_minus_2
    while (fibM < len(lys)):
        fibM_minus_2 = fibM_minus_1
        fibM_minus_1 = fibM
        fibM = fibM_minus_1 + fibM_minus_2
    index = -1;
    while (fibM > 1):
        i = min(index + fibM_minus_2, (len(lys)-1))
        if (lys[i] < val):
            fibM = fibM_minus_1
            fibM_minus_1 = fibM_minus_2
            fibM_minus_2 = fibM - fibM_minus_1
            index = i
        elif (lys[i] > val):
            fibM = fibM_minus_2
            fibM_minus_1 = fibM_minus_1 - fibM_minus_2
            fibM_minus_2 = fibM - fibM_minus_1
        else :
            return i
    if(fibM_minus_1 and index < (len(lys)-1) and lys[index+1] == val):
        return index+1;
    return -1

Используем функцию FibonacciSearch для вычисления:

>>> print(FibonacciSearch([1,2,3,4,5,6,7,8,9,10,11], 6))

Давайте посмотрим на пошаговый процесс поиска:

• Присваиваем переменной fibM наименьшее число Фибоначчи, которое больше или равно длине списка. В данном случае наименьшее число Фибоначчи, отвечающее нашим требованиям, равно 13.
• Значения присваиваются следующим образом:

           fibM = 13

           fibM_minus_1 = 8

           fibM_minus_2 = 5

           index = -1

• Далее мы проверяем элемент lys[4], где 4 — это минимум из двух значений — index + fibM_minus_2 (-1+5) и длина массива минус 1 (11-1). Поскольку значение lys[4] равно 5, что меньше искомого значения, мы перемещаем числа Фибоначчи на один шаг вниз в последовательности, получая следующие значения:

           fibM = 8

           fibM_minus_1 = 5

           fibM_minus_2 = 3

           index = 4

• Далее мы проверяем элемент lys[7], где 7 — это минимум из двух значений: index + fibM_minus_2 (4 + 3) и длина массива минус 1 (11-1). Поскольку значение lys[7] равно 8, что больше искомого значения, мы перемещаем числа Фибоначчи на два шага вниз в последовательности, получая следующие значения: 

           fibM = 3

           fibM_minus_1 = 2

           fibM_minus_2 = 1

           index = 4

• Затем мы проверяем элемент lys[5], где 5 — это минимум из двух значений: index + fibM_minus_2 (4+1) и длина массива минус 1 (11-1) . Значение lys[5] равно 6, и это наше искомое значение!

Получаем ожидаемый результат:

5

Временная сложность поиска Фибоначчи равна O(log n). Она такая же, как и у бинарного поиска. Это означает, что алгоритм в большинстве случаев работает быстрее, чем линейный поиск и jump search.

Поиск Фибоначчи можно использовать, когда у нас очень большое количество искомых элементов и мы хотим уменьшить неэффективность, связанную с использованием алгоритма, основанного на операторе деления.

Дополнительным преимуществом использования поиска Фибоначчи является то, что он может вместить входные массивы, которые слишком велики для хранения в кэше процессора или ОЗУ, потому что он ищет элементы с увеличивающимся шагом, а не с фиксированным.

Экспоненциальный поиск

Экспоненциальный поиск — это еще один алгоритм поиска, который может быть достаточно легко реализован на Python, по сравнению с jump search и поиском Фибоначчи, которые немного сложны. Он также известен под названиями galloping search, doubling search и Struzik search.

Экспоненциальный поиск зависит от бинарного поиска для выполнения окончательного сравнения значений. Алгоритм работает следующим образом:

1. Определяется диапазон, в котором, скорее всего, будет находиться искомый элемент.
2. В этом диапазоне используется двоичный поиск для нахождения индекса элемента.

Реализация алгоритма экспоненциального поиска на Python:

def ExponentialSearch(lys, val):
    if lys[0] == val:
        return 0
    index = 1
    while index < len(lys) and lys[index] <= val:
        index = index * 2
    return BinarySearch( lys[:min(index, len(lys))], val)

Используем функцию, чтобы найти значение:

>>> print(ExponentialSearch([1,2,3,4,5,6,7,8],3))

Рассмотрим работу алгоритма пошагово.

• Проверяем, соответствует ли первый элемент списка искомому значению: поскольку lys[0] равен 1, а мы ищем 3, мы устанавливаем индекс равным 1 и двигаемся дальше.
• Перебираем все элементы в списке, и пока элемент с текущим индексом меньше или равен нашему значению, умножаем  значение индекса на 2:

1. index = 1, lys[1] равно 2, что меньше 3, поэтому значение index умножается на 2 и переменной index присваивается значение 2.
2. index = 2, lys[2] равно 3, что равно 3, поэтому значение index умножается на 2 и переменной index присваивается значение 4.
3. index = 4, lys[4] равно 5, что больше 3. Условие выполнения цикла больше не соблюдается и цикл завершает свою работу.

• Затем выполняется двоичный поиск в полученном диапазоне (срезе) lys[:4]. В Python это означает, что подсписок будет содержать все элементы до 4-го элемента, поэтому мы фактически вызываем функцию следующим образом:

>>> BinarySearch([1,2,3,4], 3)

Функция вернет следующий результат:

2

Этот результат является индексом искомого элемента как в исходном списке, так и в срезе, который мы передаем алгоритму бинарного поиска.

Экспоненциальный поиск выполняется за время O(log i), где i — индекс искомого элемента. В худшем случае временная сложность равна O(log n), когда искомый элемент — это последний элемент в массиве (n — это длина массива).

Экспоненциальный поиск работает лучше, чем бинарный, когда искомый элемент находится ближе к началу массива. На практике мы используем экспоненциальный поиск, поскольку это один из наиболее эффективных алгоритмов поиска в неограниченных или бесконечных массивах.

Интерполяционный поиск

Интерполяционный поиск — это еще один алгоритм «разделяй и властвуй», аналогичный бинарному поиску. В отличие от бинарного поиска, он не всегда начинает поиск с середины. Интерполяционный поиск вычисляет вероятную позицию искомого элемента по формуле:

index = low + [(val-lys[low])*(high-low) / (lys[high]-lys[low])]

В этой формуле используются следующие переменные:

• lys — наш входной массив.
• val — искомый элемент.
• index — вероятный индекс искомого элемента. Он вычисляется как более высокое значение, когда значение val ближе по значению к элементу в конце массива (lys[high]), и более низкое, когда значение val ближе по значению к элементу в начале массива (lys[low]).
• low — начальный индекс массива.
• high — последний индекс массива.

Алгоритм осуществляет поиск путем вычисления значения индекса:

• Если значение найдено (когда lys[index] == val), возвращается индекс.
• Если значение val меньше lys[index], то значение индекса пересчитывается по формуле для левого подмассива.
• Если значение val больше lys[index], то значение индекса пересчитывается по формуле для правого подмассива.

Давайте  посмотрим на реализацию интерполяционного поиска на Python:

def InterpolationSearch(lys, val):
    low = 0
    high = (len(lys) - 1)
    while low <= high and val >= lys[low] and val <= lys[high]:
        index = low + int(((float(high - low) / ( lys[high] - lys[low])) * ( val - lys[low])))
        if lys[index] == val:
            return index
        if lys[index] < val:
            low = index + 1;
        else:
            high = index - 1;
    return -1

Если мы используем функцию для вычисления:

>>> print(InterpolationSearch([1,2,3,4,5,6,7,8], 6))

Наши начальные значения будут следующими:

val = 6,

low = 0,

high = 7,

lys[low] = 1,

lys[high] = 8,

index = 0 + [(6-1)*(7-0)/(8-1)] = 5

Поскольку lys[5] равно 6, что является искомым значением, мы прекращаем выполнение и возвращаем результат:

5

Если у нас большое количество элементов и наш индекс не может быть вычислен за одну итерацию, то мы продолжаем пересчитывать значение индекса после корректировки значений high и low.

Временная сложность интерполяционного поиска равна O(log log n), когда значения распределены равномерно. Если значения распределены неравномерно, временная сложность для наихудшего случая равна O(n) — так же, как и для линейного поиска.

Интерполяционный поиск лучше всего работает на равномерно распределенных, отсортированных массивах. В то время как бинарный поиск начинает поиск с середины и всегда делит массив на две части, интерполяционный поиск вычисляет вероятную позицию элемента и проверяет индекс, что повышает вероятность нахождения элемента за меньшее количество итераций.

Python очень удобочитаемый и эффективный по сравнению с такими языками программирования, как Java, Fortran, C, C++ и т. д. Одним из ключевых преимуществ использования Python для реализации алгоритмов поиска является то, что вам не нужно беспокоиться о приведении или явной типизации.

В Python большинство алгоритмов поиска, которые мы обсуждали, будут работать так же хорошо, если мы ищем строку. Имейте в виду, что понадобится внести изменения в код для алгоритмов, которые используют искомый элемент для числовых вычислений, например алгоритм интерполяционного поиска.

Python также подходит, если вы хотите сравнить производительность различных алгоритмов поиска для вашего dataset’а. Создание прототипа на Python проще и быстрее, потому что вы можете сделать больше с меньшим количеством строк кода.

Чтобы сравнить производительность наших реализованных алгоритмов, в Python мы можем использовать библиотеку time:

import time

start = time.time()
# вызовите здесь функцию
end = time.time()
print(start-end)

Заключение

Существует множество возможных способов поиска элемента в коллекции. В этой статье мы обсудили несколько алгоритмов поиска и их реализации на Python.

Выбор используемого алгоритма зависит от данных, с которыми вы будете работать. Это ваш входной массив, который мы называли lys во всех наших реализациях.

• Если вы хотите выполнить поиск в несортированном массиве или найти первое вхождение искомой переменной, то лучшим вариантом будет линейный поиск.
• Если вы хотите выполнить поиск в отсортированном массиве, есть много вариантов, из которых самый простой и быстрый — это бинарный поиск.
• Если у вас есть отсортированный массив, в котором вы хотите выполнить поиск без использования оператора деления, вы можете использовать либо jump search, либо поиск Фибоначчи.
• Если вы знаете, что искомый элемент, скорее всего, находится ближе к началу массива, вы можете использовать экспоненциальный поиск.
• Если ваш отсортированный массив равномерно распределен, то самым быстрым и эффективным будет интерполяционный поиск.

Если вы не уверены, какой алгоритм использовать для отсортированного массива, просто протестируйте каждый из них при помощи библиотеки time и выберите тот, который лучше всего работает с вашим dataset’ом.