Ирина Песцова
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
Десятичное и двоичное представление чисел
Определение 1
Для работы с числовой информацией мы пользуемся системой счисления, содержащей десять цифр: от $0$ до $9$. Эта система называется десятичной.
Кроме цифр, в десятичной системе большое значение имеют разряды. Подсчитывая количество чего-нибудь и дойдя до самой большой из доступных нам цифр (до $9$), мы вводим второй разряд и дальше каждое последующее число формируем из двух цифр. Дойдя до $99$, мы вынуждены вводить третий разряд. В пределах трех разрядов мы можем досчитать уже до $999$ и т.д.
Таким образом, используя всего десять цифр и вводя дополнительные разряды, мы можем записывать и проводить математические операции с любыми, даже самыми большими числами.
Компьютер ведет подсчет аналогичным образом, но имеет в своем распоряжении всего две цифры – логический ноль (отсутствие у бита какого-то свойства) и логическую единицу (наличие у бита этого свойства).
Определение 2
Система счисления, использующая только две цифры, называется двоичной. При подсчете в двоичной системе добавлять каждый следующий разряд приходится гораздо чаще, чем в десятичной.
Вот таблица первых десяти чисел в каждой из этих систем счисления:
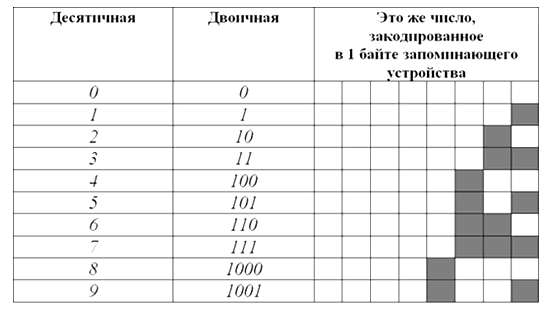
Рисунок 1.
Как видите, в десятичной системе счисления для отображения любой из первых десяти цифр достаточно $1$ разряда. В двоичной системе для тех же целей потребуется уже $4$ разряда.
«Кодирование числовой информации» 👇
Соответственно, для кодирования этой же информации в виде двоичного кода нужен носитель емкостью как минимум $4$ бита ($0,5$ байта).
Человеческий мозг, привыкший к десятичной системе счисления, плохо воспринимает систему двоичную. Хотя обе они построены на одинаковых принципах и отличаются лишь количеством используемых цифр. В двоичной системе точно так же можно осуществлять любые арифметические операции с любыми числами. Главный ее минус – необходимость иметь дело с большим количеством разрядов.
Так, самое большое десятичное число, которое можно отобразить в 8 разрядах двоичной системы – $255$, в $16$ разрядах – $65535$, в $24$ разрядах – $16777215$.
Алгоритмы кодирования чисел в двоичной системе счисления
Компьютер, кодируя числа в двоичный код, основывается на двоичной системе счисления. Но, в зависимости от особенностей чисел, может использовать разные алгоритмы:
-
Небольшие целые числа без знака.
Для сохранения каждого такого числа на запоминающем устройстве, как правило, выделяется $1$ байт ($8$ битов). Запись осуществляется в полной аналогии с двоичной системой счисления.
Целые десятичные числа без знака, сохраненные на носителе в двоичном коде, будут выглядеть примерно так:
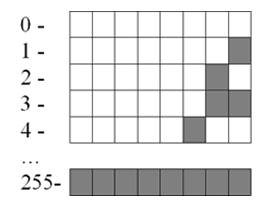
Рисунок 2.
-
Большие целые числа и числа со знаком.
Для записи каждого такого числа на запоминающем устройстве, как правило, отводится $2$-байтний блок ($16$ битов).
Старший бит блока (тот, что крайний слева) отводится под запись знака числа и в кодировании самого числа не участвует. Если число со знаком “плюс”, этот бит остается пустым, если со знаком “минус” – в него записывается логическая единица. Число же кодируется в оставшихся 15 битах.
Например, алгоритм кодирования числа $+2676$ будет следующим:- Перевести число $2676$ из десятичной системы счисления в двоичную. В итоге получится $101001110100$;
- Записать полученное двоичное число в первые $15$ бит $16$-битного блока (начиная с правого края). Последний, $16$-й бит, должен остаться пустым, поскольку кодируемое число имеет знак $+$.
В итоге $+2676$ в двоичном коде на запоминающем устройстве будет выглядеть так:
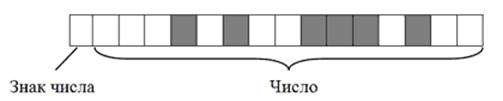
Рисунок 3.
Примечательно, что в двоичном коде присвоение числу отрицательного значения предусматривает не только изменение старшего бита. Осуществляется также инвертирование всех остальных его битов.
Чтобы было понятно, рассмотрим алгоритм кодирования числа $-2676$:
- Перевести число $2676$ из десятичной системы счисления в двоичную. Получим все тоже двоичное число $101001110100$;
- Записать полученное двоичное число в первые $15$ бит $16$-битного блока. Затем инвертировать, то есть, изменить на противоположное, значение каждого из $15$ битов;
- Записать в $16$-й бит логическую единицу, поскольку кодируемое число имеет отрицательное значение.
В итоге $-2676$ на запоминающем устройстве в двоичном коде будет иметь следующий вид:
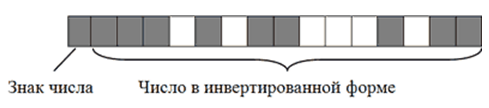
Рисунок 4.
Запись отрицательных чисел в инвертированной форме позволяет заменить все операции вычитания, в которых они участвуют, операциями сложения. Это необходимо для нормальной работы компьютерного процессора.
Максимальным десятичным числом, которое можно закодировать в $15$ битах запоминающего устройства, является $32767$. Иногда для записи чисел по этому алгоритму выделяются $4$-байтные блоки. В таком случае для кодирования каждого числа будет использоваться $31$ бит плюс $1$ бит для кодирования знака числа. Тогда максимальным десятичным числом, сохраняемым в каждую ячейку, будет $2147483647$ (со знаком плюс или минус).
-
Дробные числа со знаком.
Дробные числа на запоминающем устройстве в двоичном коде кодируются в виде так называемых чисел с плавающей запятой (точкой). Алгоритм их кодирования сложнее, чем рассмотренные выше. Тем не менее, попытаемся разобраться.
Для записи каждого числа с плавающей запятой компьютер чаще всего выделяет $4$-байтную ячейку ($32$ бита):
- в старшем бите этой ячейки (тот, что крайний слева) записывается знак числа. Если число отрицательное, в этот бит записывается логическая единица, если оно со знаком “плюс” – бит остается пустым.
- во втором слева бите аналогичным образом записывается знак порядка (что такое порядок поймете позже);
- в следующих за ним $7$ битах записывается значение порядка.
- в оставшихся $23$ битах записывается так называемая мантисса числа.

Рисунок 5.
Чтобы стало понятно, что такое порядок, мантисса и зачем они нужны, переведем в двоичный код десятичное число $6,25$.
Порядок кодирования будет примерно следующим:
- Перевести десятичное число в двоичное (десятичное $6,25$ равно двоичному $110,01$);
- Определить мантиссу числа. Для этого в числе необходимо передвинуть запятую в нужном направлении, чтобы слева от нее не осталось ни одной единицы. В нашем случае запятую придется передвинуть на три знака влево. В итоге, получим мантиссу, $11001$;
- Определить значение и знак порядка.
Значение порядка – это количество символов, на которое была сдвинута запятая для получения мантиссы. В нашем случае оно равно $3$ (или $11$ в двоичной форме);
Знак порядка – это направление, в котором пришлось двигать запятую: влево – “плюс”, вправо – “минус”. В нашем примере запятая двигалась влево, поэтому знак порядка – “плюс”.
Таким образом, порядок двоичного числа $110,01$ будет равен $+11$, а его мантисса, $11001$. В результате в двоичном коде на запоминающем устройстве это число будет записано следующим образом

Рисунок 6.
Замечание 1
Обратите внимание, что мантисса в двоичном коде записывается, начиная с первого после запятой знака, а сама запятая упускается.
Числа с плавающей запятой, кодируемые в $32$ битах, называю числами одинарной точности.
Когда для записи числа $32$-битной ячейки недостаточно, компьютер может использовать ячейку из $64$ битов. Число с плавающей запятой, закодированное в такой ячейке, называется числом двойной точности.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Код Хэмминга. Пример работы алгоритма
Время на прочтение
4 мин
Количество просмотров 511K
Вступление.
Прежде всего стоит сказать, что такое Код Хэмминга и для чего он, собственно, нужен. На Википедии даётся следующее определение:
Коды Хэмминга — наиболее известные и, вероятно, первые из самоконтролирующихся и самокорректирующихся кодов. Построены они применительно к двоичной системе счисления.
Другими словами, это алгоритм, который позволяет закодировать какое-либо информационное сообщение определённым образом и после передачи (например по сети) определить появилась ли какая-то ошибка в этом сообщении (к примеру из-за помех) и, при возможности, восстановить это сообщение. Сегодня, я опишу самый простой алгоритм Хемминга, который может исправлять лишь одну ошибку.
Также стоит отметить, что существуют более совершенные модификации данного алгоритма, которые позволяют обнаруживать (и если возможно исправлять) большее количество ошибок.
Сразу стоит сказать, что Код Хэмминга состоит из двух частей. Первая часть кодирует исходное сообщение, вставляя в него в определённых местах контрольные биты (вычисленные особым образом). Вторая часть получает входящее сообщение и заново вычисляет контрольные биты (по тому же алгоритму, что и первая часть). Если все вновь вычисленные контрольные биты совпадают с полученными, то сообщение получено без ошибок. В противном случае, выводится сообщение об ошибке и при возможности ошибка исправляется.
Как это работает.
Для того, чтобы понять работу данного алгоритма, рассмотрим пример.
Подготовка
Допустим, у нас есть сообщение «habr», которое необходимо передать без ошибок. Для этого сначала нужно наше сообщение закодировать при помощи Кода Хэмминга. Нам необходимо представить его в бинарном виде.
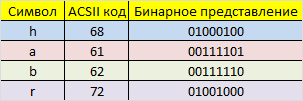
На этом этапе стоит определиться с, так называемой, длиной информационного слова, то есть длиной строки из нулей и единиц, которые мы будем кодировать. Допустим, у нас длина слова будет равна 16. Таким образом, нам необходимо разделить наше исходное сообщение («habr») на блоки по 16 бит, которые мы будем потом кодировать отдельно друг от друга. Так как один символ занимает в памяти 8 бит, то в одно кодируемое слово помещается ровно два ASCII символа. Итак, мы получили две бинарные строки по 16 бит:
 и
и 
После этого процесс кодирования распараллеливается, и две части сообщения («ha» и «br») кодируются независимо друг от друга. Рассмотрим, как это делается на примере первой части.
Прежде всего, необходимо вставить контрольные биты. Они вставляются в строго определённых местах — это позиции с номерами, равными степеням двойки. В нашем случае (при длине информационного слова в 16 бит) это будут позиции 1, 2, 4, 8, 16. Соответственно, у нас получилось 5 контрольных бит (выделены красным цветом):
Было:

Стало:

Таким образом, длина всего сообщения увеличилась на 5 бит. До вычисления самих контрольных бит, мы присвоили им значение «0».
Вычисление контрольных бит.
Теперь необходимо вычислить значение каждого контрольного бита. Значение каждого контрольного бита зависит от значений информационных бит (как неожиданно), но не от всех, а только от тех, которые этот контрольных бит контролирует. Для того, чтобы понять, за какие биты отвечает каждых контрольный бит необходимо понять очень простую закономерность: контрольный бит с номером N контролирует все последующие N бит через каждые N бит, начиная с позиции N. Не очень понятно, но по картинке, думаю, станет яснее:
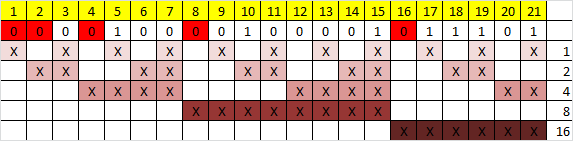
Здесь знаком «X» обозначены те биты, которые контролирует контрольный бит, номер которого справа. То есть, к примеру, бит номер 12 контролируется битами с номерами 4 и 8. Ясно, что чтобы узнать какими битами контролируется бит с номером N надо просто разложить N по степеням двойки.
Но как же вычислить значение каждого контрольного бита? Делается это очень просто: берём каждый контрольный бит и смотрим сколько среди контролируемых им битов единиц, получаем некоторое целое число и, если оно чётное, то ставим ноль, в противном случае ставим единицу. Вот и всё! Можно конечно и наоборот, если число чётное, то ставим единицу, в противном случае, ставим 0. Главное, чтобы в «кодирующей» и «декодирующей» частях алгоритм был одинаков. (Мы будем применять первый вариант).
Высчитав контрольные биты для нашего информационного слова получаем следующее:

и для второй части:

Вот и всё! Первая часть алгоритма завершена.
Декодирование и исправление ошибок.
Теперь, допустим, мы получили закодированное первой частью алгоритма сообщение, но оно пришло к нас с ошибкой. К примеру мы получили такое (11-ый бит передался неправильно):

Вся вторая часть алгоритма заключается в том, что необходимо заново вычислить все контрольные биты (так же как и в первой части) и сравнить их с контрольными битами, которые мы получили. Так, посчитав контрольные биты с неправильным 11-ым битом мы получим такую картину:

Как мы видим, контрольные биты под номерами: 1, 2, 8 не совпадают с такими же контрольными битами, которые мы получили. Теперь просто сложив номера позиций неправильных контрольных бит (1 + 2 + 8 = 11) мы получаем позицию ошибочного бита. Теперь просто инвертировав его и отбросив контрольные биты, мы получим исходное сообщение в первозданном виде! Абсолютно аналогично поступаем со второй частью сообщения.
Заключение.
В данном примере, я взял длину информационного сообщения именно 16 бит, так как мне кажется, что она наиболее оптимальная для рассмотрения примера (не слишком длинная и не слишком короткая), но конечно же длину можно взять любую. Только стоит учитывать, что в данной простой версии алгоритма на одно информационное слово можно исправить только одну ошибку.
Примечание.
На написание этого топика меня подвигло то, что в поиске я не нашёл на Хабре статей на эту тему (чему я был крайне удивлён). Поэтому я решил отчасти исправить эту ситуацию и максимально подробно показать как этот алгоритм работает. Я намеренно не приводил ни одной формулы, дабы попытаться своими словами донести процесс работы алгоритма на примере.
Источники.
1. Википедия
2. Calculating the Hamming Code
Современные компьютеры могут обрабатывать только дискретную информацию, поэтому любой вид информации преобразуется в числовую форму, которая затем кодируется в двоичном виде.
Кодированием данных называется представление данных с помощью условных знаков. Система двоичного кодирования заключается в представлении данных произвольного типа двоичным кодом, в виде последовательности нулей и единиц.
В настоящей главе рассматриваются методы двоичного кодирования целых и действительных чисел, а также текстовой информации.
В сокращенном виде двоичный код представляется в шестнадцатеричном формате, для этого используются таблицы тетрад. Шестнадцатеричный формат обозначается hex, от hexadecimal, десятичный – dec или decimal.
Кодирование целых чисел
Рассмотрим способы кодирования целых чисел. Для кодирования используется не менее 1 байта, или 8 двоичных разрядов. Типы данных, в которых хранятся целые числа, обычно состоят из 1, 2, 4 или 8 байт.
Кодирование целых неотрицательных чисел
Рассмотрим типы данных, в которых хранятся целые неотрицательные, или беззнаковые, числа. С помощью k двоичных разрядов может быть представлено 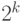 различных значений, с кодами от 00dots0 до 11dots1, поэтому в них хранятся целые числа в пределах от 0 до
различных значений, с кодами от 00dots0 до 11dots1, поэтому в них хранятся целые числа в пределах от 0 до  . Диапазоны целых беззнаковых чисел для таких типов данных, а также максимальные числа, которые в них представлены, показаны в табл. 2.1.
. Диапазоны целых беззнаковых чисел для таких типов данных, а также максимальные числа, которые в них представлены, показаны в табл. 2.1.
Пример 1. В четырех байтах число 33 кодируется в виде:  , или 00000021 (hex).
, или 00000021 (hex).
Кодирование целых чисел со знаком
Рассмотрим типы данных, которые используются для хранения положительных и отрицательных целых чисел, или целых чисел со знаком. Диапазоны чисел для этих типов данных, которые можно закодировать с помощью 1, 2, 4 или 8 байт, а также минимальные и максимальные числа показаны в таблице 2.2. В первом столбце указывается число байт.
Если количество разрядов в типе данных равно k, то диапазон кодируемых чисел составляет от 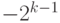 до
до 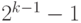 . Неотрицательные числа кодируются так же, как и в случае беззнаковых чисел, коды этих чисел начинаются с 0 (см. диапазон). Соответственно, коды отрицательных чисел начинаются с 1. Множество отрицательных чисел так же, как и множество положительных, представляется множеством двоичных кодов, упорядоченных по возрастанию.
. Неотрицательные числа кодируются так же, как и в случае беззнаковых чисел, коды этих чисел начинаются с 0 (см. диапазон). Соответственно, коды отрицательных чисел начинаются с 1. Множество отрицательных чисел так же, как и множество положительных, представляется множеством двоичных кодов, упорядоченных по возрастанию.
Рассмотрим, например, тип данных, в котором для кодирования целых чисел со знаком используется 2 разряда. В нем могут быть закодированы числа – 2, – 1, 0, 1 с помощью кодов 10, 11, 00, 01, соответственно. Если тип данных содержит 3 разряда, то в нем могут быть представлены числа – 4, – 3, – 2, – 1, 0, 1, 2, 3 соответственно с помощью кодов 100, 101, 110, 111, 000, 001, 010, 011.
В общем случае левая граница диапазона кодируется двоичным словом 100dots0, а правая – двоичным словом 011dots1.
Итак, если двоичный код числа начинается с 1, то он представляет отрицательное целое число, а если с 0, – то неотрицательное. Старший разряд двоичного кода называется знаковым разрядом. Код, который используется для кодирования неотрицательных целых чисел, называется прямым, а для кодирования отрицательных – дополнительным. Дополнительные коды позволяют заменить операцию вычитания операцией сложения и сделать возможной реализацию операций сложения и вычитания одинаковыми для знаковых и беззнаковых чисел (см. ниже).
Рассмотрим понятия прямого и дополнительного кода в общем случае для системы счисления с основанием p, где p – целое, p> 1.
Пусть для p-ичного кодирования , т. е. для представления целого числа в системе счисления с основанием p, используется k разрядов, и диапазон кодируемых чисел составляет от 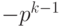 до
до  .
.
Для целого числа x, такого что 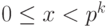 , выполняется разложение
, выполняется разложение
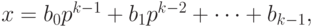
где 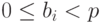 , для i = 0, 1, dots, k – 1.
, для i = 0, 1, dots, k – 1.
Прямым кодом числа x называется его представление в p-ичном виде с помощью слова длины k:
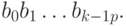
Обратным кодом числа (-x) называется код
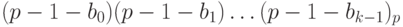
Обозначим через 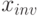 число, которое представляет этот код. Имеем:
число, которое представляет этот код. Имеем:
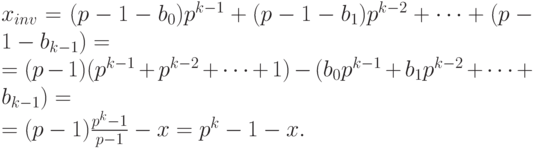
Дополнительным кодом отрицательного числа (– x) называется p-ичное представление положительного числа
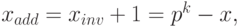
или p-ичное представление суммы
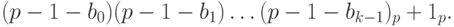
Отсюда, в частности, следует, что  и
и 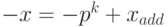 .
.
Например, найдем дополнительный код числа 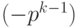 – левой границы диапазона. Прямой код числа
– левой границы диапазона. Прямой код числа 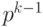 равен
равен 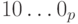 . Поэтому обратный код числа –
. Поэтому обратный код числа – 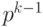 имеет вид:
имеет вид: 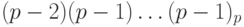 . Соответственно, дополнительный код выглядит следующим образом:
. Соответственно, дополнительный код выглядит следующим образом:
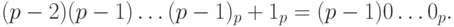
Аналогично, найдем дополнительный код числа (- 1). Число 1 имеет прямой код 00dots1, следовательно, обратный код для (- 1) имеет вид: 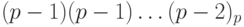 . Поэтому дополнительным кодом числа (- 1) является
. Поэтому дополнительным кодом числа (- 1) является 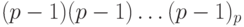 . Найдем также дополнительный код числа 0. Это число имеет прямой код
. Найдем также дополнительный код числа 0. Это число имеет прямой код  и, соответственно, обратный код
и, соответственно, обратный код 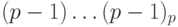 . Следовательно, дополнительный код равен 1
. Следовательно, дополнительный код равен 1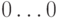 , так что
, так что 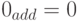 . Отметим, что в k-разрядной целочисленной арифметике полагают
. Отметим, что в k-разрядной целочисленной арифметике полагают 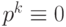 , т. е. все числа рассматриваются как остатки от деления на
, т. е. все числа рассматриваются как остатки от деления на 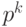 .
.
Пример 2. Найдем дополнительный код числа (- 127) при двоичном кодировании в 1 байте. Имеем:
прямой код числа 127: 01111111;
обратный код: 10000000;
дополнительный код: 10000000 + 1 = 10000001;
Пример 3. Найдем дополнительный код числа (- 12) при двоичном кодировании в 4 байтах типа данных integer. Имеем:
прямой код числа 12: 00000000 00000000 00000000 00001100;
обратный код: 11111111 11111111 11111111 11110011;
дополнительный код: 11111111 11111111 11111111 11110100,
или fffffff4 (hex).
Пример 4. Пусть p = 10. Тогда с помощью 4 разрядов можно закодировать целые числа в пределах от 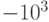 до
до 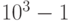 , т. е. от – 1000 до 999. Найдем дополнительный код при десятичном кодировании числа (- 812). Имеем:
, т. е. от – 1000 до 999. Найдем дополнительный код при десятичном кодировании числа (- 812). Имеем:
прямой код для 812: 0812;
обратный код: 9187;
дополнительный код: 9188 (= 10000 – 812).
Пример 5. Пусть p = 16. Тогда с помощью 3 разрядов можно закодировать числа в пределах от – 256 до 255. Найдем дополнительный код при 16-ричном кодировании числа (- 50). Имеем:
прямой код числа 50: 032;
обратный код: fcd;
дополнительный код: fce.
Все курсы > Анализ и обработка данных > Занятие 11
Алгоритмы машинного обучения, как мы знаем, не умеют работать с категориальными данными, выраженными с помощью строковых значений. Для этого строки необходимо закодировать (encode) числами. Сегодня мы рассмотрим основные способы такой кодировки.
Откроем ноутбук к этому занятию⧉
Подготовим простые учебные данные кредитного скоринга.
|
scoring = { ‘Name’ : [‘Иван’, ‘Николай’, ‘Алексей’, ‘Александра’, ‘Евгений’, ‘Елена’], ‘Age’ : [35, 43, 21, 34, 24, 27], ‘City’ : [‘Москва’, ‘Нижний Новгород’, ‘Санкт-Петербург’, ‘Владивосток’, ‘Москва’, ‘Екатеринбург’], ‘Experience’ : [7, 13, 2, 8, 4, 12], ‘Salary’ : [95, 135, 73, 100, 78, 110], ‘Credit_score’ : [‘Good’, ‘Good’, ‘Bad’, ‘Medium’, ‘Medium’, ‘Good’], ‘Outcome’ : [1, 1, 0, 1, 0, 1] } df = pd.DataFrame(scoring) df |

Про категориальные переменные
Вначале в целом повторим как выявлять и исследовать категориальные переменные.
Методы .info(), .unique(), value_counts()
Начать исследование категориальных переменных можно с изучения типа данных. Для этого подойдут метод .info() или атрибут dtypes.
|
<class ‘pandas.core.frame.DataFrame’> RangeIndex: 6 entries, 0 to 5 Data columns (total 7 columns): # Column Non-Null Count Dtype — —— ————– —– 0 Name 6 non-null object 1 Age 6 non-null int64 2 City 6 non-null object 3 Experience 6 non-null int64 4 Salary 6 non-null int64 5 Credit_score 6 non-null object 6 Outcome 6 non-null object dtypes: int64(3), object(4) memory usage: 464.0+ bytes |
|
Name object Age int64 City object Experience int64 Salary int64 Credit_score object Outcome object dtype: object |
При этом категориальные признаки часто могут «прятаться» в типах int и float. В этом случае для их выявления можно изучить распределение данных.
Отдельные категории можно посмотреть с помощью метода .unique().
|
array([‘Москва’, ‘Нижний Новгород’, ‘Санкт-Петербург’, ‘Владивосток’, ‘Екатеринбург’], dtype=object) |
С помощью методов .values_counts() библиотеки Pandas и np.unique() библиотеки Numpy можно посмотреть и количество объектов в каждой категории.
|
# метод .value_counts() сортирует категории по количеству объектов # в убывающем порядке df.City.value_counts() |
|
Москва 2 Нижний Новгород 1 Санкт-Петербург 1 Владивосток 1 Екатеринбург 1 Name: City, dtype: int64 |
|
np.unique(df.City, return_counts = True) |
|
(array([‘Владивосток’, ‘Екатеринбург’, ‘Москва’, ‘Нижний Новгород’, ‘Санкт-Петербург’], dtype=object), array([1, 1, 2, 1, 1])) |
Последовательное применение методов .value_counts() и .count() выведет общее количество уникальных категорий.
|
# посмотрим на общее количество уникальных категорий df.City.value_counts().count() |
Выведем категории на графике.
|
score_counts = df.Credit_score.value_counts() sns.barplot(x = score_counts.index, y = score_counts.values) plt.title(‘Распределение данных по категориям’) plt.ylabel(‘Количество наблюдений в категории’) plt.xlabel(‘Категории’); |

Тип данных category
Хорошая практика — перевести категориальную переменную в тип данных category. Зачастую (но не всегда, например, если много категорий) это ускоряет работу с категориями и уменьшает использование памяти.
Можно воспользоваться уже знакомым нам методом .astype().
|
df = df.astype({‘City’ : ‘category’, ‘Outcome’ : ‘category’}) |
Функция pd.Categorical() позволяет прописать, в частности, сами категории, а также указать, есть ли в переданных категориях порядок или нет.
|
df.Credit_score = pd.Categorical(df.Credit_score, categories = [‘Bad’, ‘Medium’, ‘Good’], ordered = True) |
Воспользуемся атрибутами categories и dtype.
|
df.Credit_score.cat.categories |
|
Index([‘Bad’, ‘Medium’, ‘Good’], dtype=’object’) |
|
CategoricalDtype(categories=[‘Bad’, ‘Medium’, ‘Good’], ordered=True) |
Атрибут codes выводит коды каждой из категорий (мы воспользуемся этим в дальнейшем при кодировании).
|
df.Credit_score.cat.codes |
|
0 2 1 2 2 0 3 1 4 1 5 2 dtype: int8 |
Категории можно переименовать.
|
df.Outcome = df.Outcome.cat.rename_categories(new_categories = {‘Вернул’: ‘Yes’, ‘Не вернул’: ‘No’}) df |
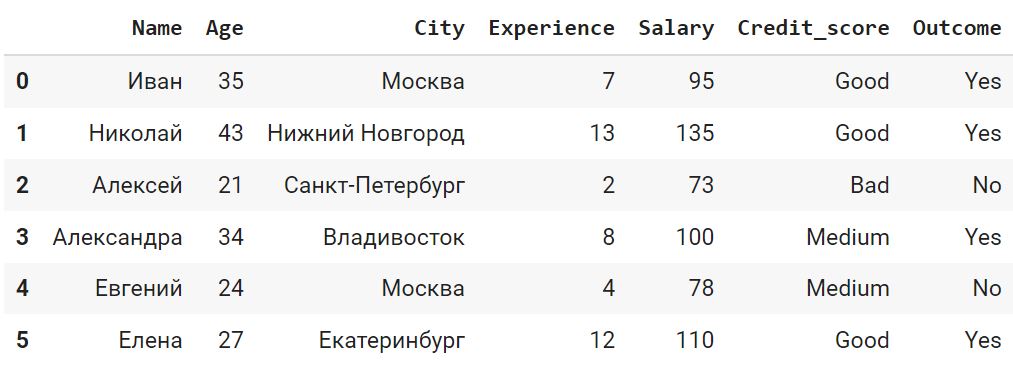
Убедимся, что нужные нам признаки преобразованы в тип category.
|
<class ‘pandas.core.frame.DataFrame’> RangeIndex: 6 entries, 0 to 5 Data columns (total 7 columns): # Column Non-Null Count Dtype — —— ————– —– 0 Name 6 non-null object 1 Age 6 non-null int64 2 City 6 non-null category 3 Experience 6 non-null int64 4 Salary 6 non-null int64 5 Credit_score 6 non-null category 6 Outcome 6 non-null category dtypes: category(3), int64(3), object(1) memory usage: 806.0+ bytes |
Кардинальность данных
Большое количество уникальных категорий в столбце называется высокой кардинальностью (high cardinality) признака. В частности, потенциально (если бы у нас было больше данных) признак City мог бы обладать высокой кардинальностью.
Ниже мы рассмотрим в каких случаях это может стать нежелательной особенностью данных. Одним из решений могло бы быть создание нового признака, например, региона группирующего несколько городов.
|
region = np.where(((df.City == ‘Екатеринбург’) | (df.City == ‘Владивосток’)), 0, 1) df.insert(loc = 3, column= ‘Region’, value = region) df |

Дополнительным полезным свойством нового признака будет то, что на основе изначальных данных алгоритм бы не увидел разницы между Москвой и Владивостоком и Москвой и Екатеринбургом (а вполне вероятно, что в данных она есть). В новом же признаке, по сути делящем города по принадлежности к европейской и азиатской частям России, такую разницу выявить получится.
Базовые методы кодирования
Кодирование через cat.codes
Как уже было сказано выше, кодировать категориальную переменную можно через атрибут cat.codes.
|
df_cat = df.copy() df_cat.Credit_score.cat.codes |
|
0 2 1 2 2 0 3 1 4 1 5 2 dtype: int8 |
|
df_cat.Credit_score = df_cat.Credit_score.astype(‘category’).cat.codes df_cat |
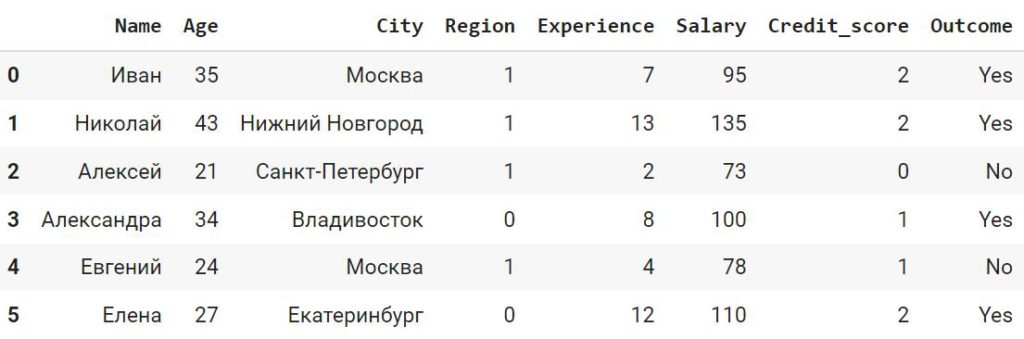
Mapping
Этот способ мы уже применяли на прошлых занятиях. Суть его заключается в том, чтобы передать схему кодирования в виде словаря в функцию map() и применить к соответствующему столбцу.
|
df_map = df.copy() # ключами будут старые значения признака # значениями словаря – новые значения признака map_dict = {‘Bad’ : 0, ‘Medium’ : 1, ‘Good’: 2} df_map[‘Credit_score’] = df_map[‘Credit_score’].map(map_dict) df_map |

Словарь в функцию map() можно передать и так.
|
# сделаем еще одну копию датафрейма df_map = df.copy() df_map.Credit_score = df_map.Credit_score.map(dict(Bad = 0, Medium = 1, Good = 2)) df_map |

Label Encoder
Рассмотрим класс LabelEncoder библиотеки sklearn. Этот класс преобразует n категорий в числа от 1 до n. Применим его к целевой переменной (бинарная категориальная переменная).
На вход LabelEncoder принимает только одномерные массивы (например, Series)
|
from sklearn.preprocessing import LabelEncoder labelencoder = LabelEncoder() df_le = df.copy() df_le.loc[:, ‘Outcome’] = labelencoder.fit_transform(df_le.loc[:, ‘Outcome’]) df_le |

Для категорий, в которых больше двух классов, но нет внутренней иерархии (номинальные данные), этот encoder подходит хуже, потому что построенная на основе преобразованных данных модель может подумать, что между категориями есть иерархия, когда в действительности ее нет.
|
# применим LabelEncoder к номинальной переменной City df_le.loc[:, ‘City’] = labelencoder.fit_transform(df_le.loc[:, ‘City’]) df_le |

Но даже для порядковых категориальных данных этот способ вряд ли подойдет, потому что LabelEncoder не видит порядка в данных.
|
# применим LabelEncoder к номинальной переменной Credit_score df_le.loc[:, ‘Credit_score’] = labelencoder.fit_transform(df_le.loc[:, ‘Credit_score’]) df_le |
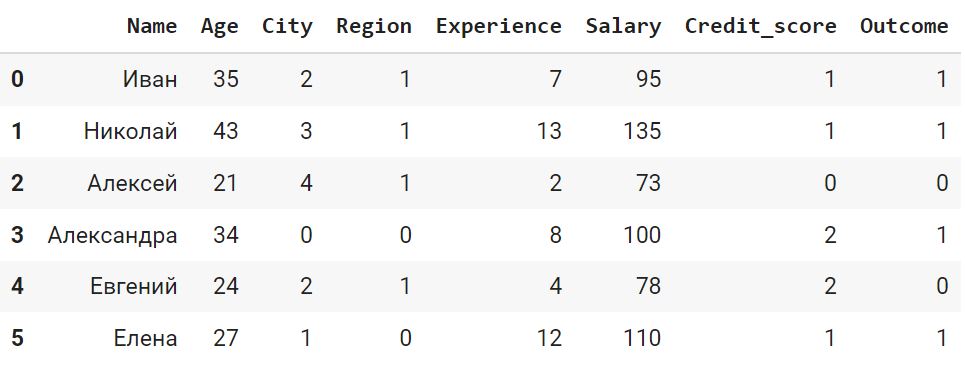
|
array([‘Bad’, ‘Good’, ‘Medium’], dtype=object) |
Как вы видите, на второе место в иерархии LabelEncoder поместил класс Good, что конечно является ошибкой. Таким образом, можно сказать, что LabelEncoder лучше всего справляется с бинарными категориальными данными.
Ordinal Encoder
С порядковыми категориальными данными справится OrdinalEncoder, которому при создании объекта класса можно передать иерархию категорий.
На вход OrdinalEncoder принимает только двумерные массивы.
|
from sklearn.preprocessing import OrdinalEncoder ordinalencoder = OrdinalEncoder(categories = [[‘Bad’, ‘Medium’, ‘Good’]]) df_oe = df.copy() # используем метод .to_frame() для преобразования Series в датафрейм df_oe.loc[:, ‘Credit_score’] = ordinalencoder.fit_transform(df_oe.loc[:, ‘Credit_score’].to_frame()) df_oe |

Убедимся, что иерархия категорий не нарушена.
|
ordinalencoder.categories_ |
|
[array([‘Bad’, ‘Medium’, ‘Good’], dtype=object)] |
OneHotEncoding
Как уже было сказано, номинальные данные нельзя заменять числами 1, 2, 3,…, так как алгоритм ML на этапе обучения подумает, что речь идет о порядковых данных. Нужно использовать one-hot encoder. С этим инструментом мы уже познакомились, когда рассматривали основы нейронных сетей.
Класс OneHotEncoder
Вначале применим класс OneHotEncoder библиотеки sklearn.
|
df_onehot = df.copy() from sklearn.preprocessing import OneHotEncoder # создадим объект класса OneHotEncoder # параметр sparse = True выдал бы результат в сжатом формате onehotencoder = OneHotEncoder(sparse = False) encoded_df = pd.DataFrame(onehotencoder.fit_transform(df_onehot[[‘City’]])) encoded_df |
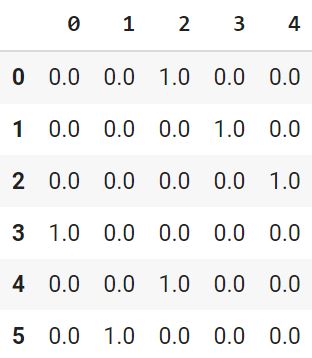
|
import sklearn # в версии sklearn, установленной в Colab, параметр называется sparse # начиная с версии 1.2 он будет называться sparse_out sklearn.__version__ |
Выведем новые признаки с помощью метода .get_feature_names_out().
|
onehotencoder.get_feature_names_out() |
|
array([‘City_Владивосток’, ‘City_Екатеринбург’, ‘City_Москва’, ‘City_Нижний Новгород’, ‘City_Санкт-Петербург’], dtype=object) |
Используем вывод этого метода, чтобы добавить названия столбцов.
|
encoded_df.columns = onehotencoder.get_feature_names_out() encoded_df |
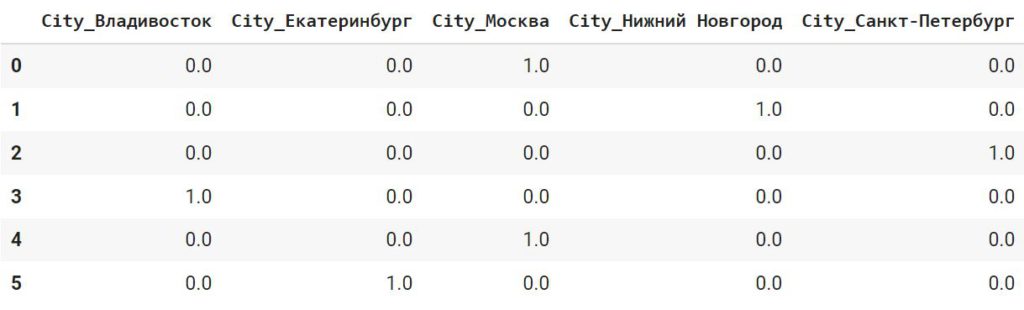
Присоединим новые признаки к исходному датафрейму, удалив, разумеется, признак City.
|
df_onehot = df_onehot.join(encoded_df) df_onehot.drop(‘City’, axis = 1, inplace = True) |
Обратите внимание, на самом деле нам не нужен первый признак (в данном случае, Владивосток). Если его убрать, при «срабатывании» этого признака (наблюдение с индексом три) все остальные признаки будут иметь нули (так мы поймем, что речь идет именно об этом отсутствующем признаке).
|
df_onehot = df.copy() # чтобы удалить первый признак, используем параметр drop = ‘first’ onehot_first = OneHotEncoder(drop = ‘first’, sparse = False) encoded_df = pd.DataFrame(onehot_first.fit_transform(df_onehot[[‘City’]])) encoded_df.columns = onehot_first.get_feature_names_out() df_onehot = df_onehot.join(encoded_df) df_onehot.drop(‘Outcome’, axis = 1, inplace = True) df_onehot |

Функция pd.get_dummies()
Еще один способ — использовать функцию pd.get_dummies() библиотеки Pandas. Применим функцию к столбцу City.
|
df_dum = df.copy() pd.get_dummies(df_dum, columns = [‘City’]) |

Уменьшить длину новых столбцов можно через параметры prefix и prefix_sep.
|
pd.get_dummies(df_dum, columns = [‘City’], prefix = ”, prefix_sep = ”) |

Опять же, можно не использовать первую dummy-переменную.
|
pd.get_dummies(df_dum, columns = [‘City’], prefix = ”, prefix_sep = ”, drop_first = True) |

Библиотека category_encoders
Рассмотрим еще один способ выполнить one-hot encoding через соответствующий инструмент⧉ очень полезной библиотеки category_encoders.
|
# установим библиотеку !pip install category_encoders |
Импортируем библиотеку и применим класс OneHotEncoder.
|
df_catenc = df.copy() import category_encoders as ce # в параметр cols передадим столбцы, которые нужно преобразовать ohe_encoder = ce.OneHotEncoder(cols = [‘City’]) # в метод .fit_transform() мы передадим весь датафрейм целиком df_catenc = ohe_encoder.fit_transform(df_catenc) df_catenc |
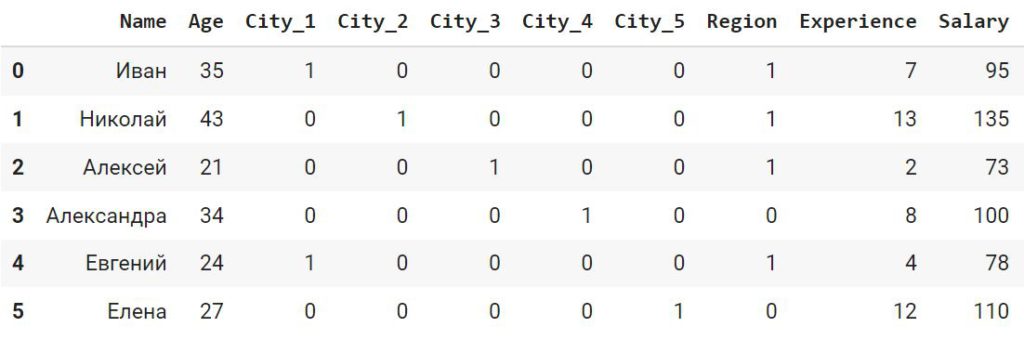
Что очень удобно, класс OneHotEncoder библиотеки category_encoders вставил новые столбцы сразу в исходный датафрейм и удалил исходный признак.
Сравнение инструментов
Создадим два очень простых датасета из одного признака: один обучающий, второй — тестовый. В первом в этом признаке (назовем его recom) будет три категории: yes, no, maybe. Во втором, только две, yes и no.
|
train = pd.DataFrame({‘recom’ : [‘yes’, ‘no’, ‘maybe’]}) train |

|
test = pd.DataFrame({‘recom’ : [‘yes’, ‘no’, ‘yes’]}) test |

Теперь применим каждый из приведенных выше инструментов к этим датасетам (напомню, что обучать кодировщик мы должны на обущающей выборке, чтобы избежать утечки данных).
pd.get_dummies()
Функция pd.get_dummies() не «запоминает» категории при обучении.


При попытке обучить модель будет ошибка.
OHE sklearn
Посмотрим, как с этим справится класс OneHotEncoder библиотеки sklearn.
|
ohe = OneHotEncoder() ohe_model = ohe.fit(train) ohe_model.categories_ |
|
[array([‘maybe’, ‘no’, ‘yes’], dtype=object)] |
|
train_arr = ohe_model.transform(train).toarray() pd.DataFrame(train_arr, columns = [‘maybe’, ‘no’, ‘yes’]) |
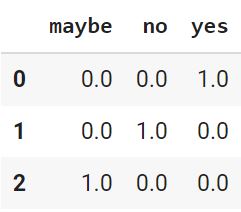
|
test_arr = ohe_model.transform(test).toarray() pd.DataFrame(test_arr, columns = [‘maybe’, ‘no’, ‘yes’]) |
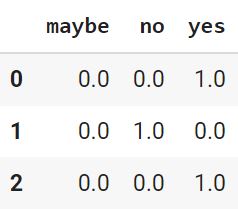
Мы видим, что этот кодировщик учел отсутствующую в тестовой выборке категорию. Впрочем, в обратном случае, когда категория отсутствует в обучающей выборке, OneHotEncoder не будет иметь возможности правильно закодировать датасеты.
|
ohe = OneHotEncoder() ohe_model = ohe.fit(test) ohe_model.categories_ |
|
[array([‘no’, ‘yes’], dtype=object)] |
OHE category_encoders
Попробуем инструмент из библиотеки category_encoders.
|
ohe_encoder = ce.OneHotEncoder() ohe_encoder.fit(train) |
|
OneHotEncoder(cols=[‘recom’]) |
|
# категория maybe стоит на последнем месте ohe_encoder.transform(test) |

|
# убедимся в этом, добавив названия столбцов test_df = ohe_encoder.transform(test) test_df.columns = ohe_encoder.category_mapping[0][‘mapping’].index[:3] test_df |

Проблема OHE
У OneHotEncoding есть одна проблема. При высокой кардинальности признака, создается очень много новых столбцов, а сама матрица становится разреженной.
|
# закодируем признак с высокой кардинальностью cities = pd.DataFrame([‘Москва’, ‘Екатеринбург’, ‘Нижний Новгород’, ‘Челябинск’, ‘Владивосток’, ‘Архангельск’, ‘Выборг’, ‘Сочи’, ‘Астрахань’, ‘Тюмень’, ‘Томск’, ‘Краснодар’]) pd.get_dummies(cities) |

Способы преодоления этой проблемы будут рассмотрены на курсе ML для продолжающих.
Binning
Некоторые (в частности, мультимодальные) количественные распределения не поддаются трансформации и приведению, например, к нормальному распределению.
Для того чтобы извлечь ценную информацию из таких признаков можно попробовать сделать переменные категориальными, разбив данные на интервалы, которые и будут классами нового признака. Такой подход называется binning или bucketing.
Вновь обратимся к датасету о недвижимости в Бостоне и, в частности, рассмотрим переменную TAX.
|
boston = pd.read_csv(‘/content/boston.csv’) boston.TAX.hist(); |
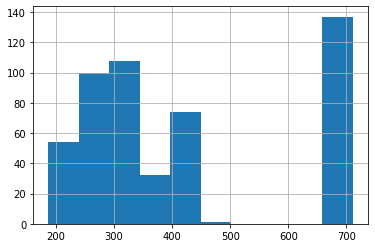
Как мы видим, распределение вряд ли можно трансформировать, используя какое-либо преобразование. Применим binning.
На равные интервалы
Подход binning на равные интервалы (binning with equally spaced boundaries) предполагает, что мы берем диапазон от минимального до максимального значений и делим его на нужное нам количество равных частей (если мы хотим получить три интервала, то нам нужно четыре границы).
|
min_value = boston.TAX.min() max_value = boston.TAX.max() bins = np.linspace(min_value, max_value, 4) bins |
|
array([187. , 361.66666667, 536.33333333, 711. ]) |
Создадим названия категорий.
|
labels = [‘low’, ‘medium’, ‘high’] |
Применим функцию pd.cut(). В параметр bins мы передадим интервалы, в labels — названия категорий.
|
boston[‘TAX_binned’] = pd.cut(boston.TAX, bins = bins, labels = labels, # уточним, что первый интервал должен включать # нижнуюю границу (значение 187) include_lowest = True) |
Посмотрим на результат.
|
boston[[‘TAX’, ‘TAX_binned’]].sample(5, random_state = 42) |

Границы и количество элементов в них можно получить с помощью метода .value_counts().
|
boston.TAX.value_counts(bins = 3, sort = False) |
|
(186.475, 361.667] 273 (361.667, 536.333] 96 (536.333, 711.0] 137 Name: TAX, dtype: int64 |
Результат этого метода позволяет выявить недостаток подхода binning на равные интервалы. Количество объектов внутри интревалов сильно различается. Преодолеть эту особенность можно с помощью деления по квантилям.
По квантилям
Binning по квантилям (quantile binning) позволяет разделить наблюдения не по значениям признака, а по количеству объектов в интервале. Например, выберем разделение на три части.
|
# для наглядности вначале найдем интересующие нас квантили np.quantile(boston.TAX, q = [1/3, 2/3]) |
Применим функцию pd.qcut().
|
boston[‘TAX_qbinned’], boundaries = pd.qcut(boston.TAX, q = 3, # precision определяет округление precision = 1, labels = labels, retbins = True) boundaries |
|
array([187., 300., 403., 711.]) |
|
boston.TAX_qbinned.value_counts() |
|
low 172 high 168 medium 166 Name: TAX_qbinned, dtype: int64 |
Как вы видите, в данном случае количество объектов примерно одинаковое. Наглядную иллюстрацию двух подходов можно посмотреть здесь⧉.
KBinsDiscretizer
Эти же задачи можно решить с помощью класса KBinsDiscretizer⧉ библиотеки sklearn. Рассмотрим три основных параметра класса:
- параметр strategy определяет как будут делиться интервалы
- на равные части (uniform)
- по квантилям (quantile) или
- так, чтобы значения в каждом кластере относились к центроиду (kmeans)
- параметр encode определяет как закодировать интервалы
- ordinal, т.е. числами от 1 до n интервалов
- one-hot encoding
- количество интервалов n_bins
Применим каждую из стратегий. Так как в категориях заложен порядок, выберем ordinal кодировку.
|
from sklearn.preprocessing import KBinsDiscretizer |
strategy = uniform
|
est = KBinsDiscretizer(n_bins=3, encode = ‘ordinal’, strategy = ‘uniform’) est.fit(boston[[‘TAX’]]) est.bin_edges_ |
|
array([array([187. , 361.66666667, 536.33333333, 711. ])], dtype=object) |
|
np.unique(est.transform(boston[[‘TAX’]]), return_counts = True) |
|
(array([0., 1., 2.]), array([273, 96, 137])) |
strategy = quantile
|
est = KBinsDiscretizer(n_bins=3, encode = ‘ordinal’, strategy = ‘quantile’) est.fit(boston[[‘TAX’]]) est.bin_edges_ |
|
array([array([187., 300., 403., 711.])], dtype=object) |
|
np.unique(est.transform(boston[[‘TAX’]]), return_counts = True) |
|
(array([0., 1., 2.]), array([165, 143, 198])) |
strategy = kmeans
|
est = KBinsDiscretizer(n_bins = 3, encode = ‘ordinal’, strategy = ‘kmeans’) est.fit(boston[[‘TAX’]]) est.bin_edges_ |
|
array([array([187. , 338.7198937 , 535.07350433, 711. ])], dtype=object) |
|
np.unique(est.transform(boston[[‘TAX’]]), return_counts = True) |
|
(array([0., 1., 2.]), array([262, 107, 137])) |
Еще одно сравнение стратегий разделения на интервалы можно посмотреть здесь⧉.
С помощью статистических показателей
Дополнительно замечу, что интервалы можно заполнить каким-либо статистическим показателем. Например, медианой. Для наглядности снова создадим только три интервала и найдем мединное значение внутри каждого из них.
Воспользуемся функцией binned_statistic()⧉ модуля scipy.stats. Функция возвращает медианы каждого из интервалов, границы интервалов, а также к какому из интервалов относится каждое из наблюдений.
Нас будут интересовать метрики и границы интервалов.
|
from scipy.stats import binned_statistic medians, bin_edges, _ = binned_statistic(boston.TAX, np.arange(0, len(boston)), statistic = ‘median’, bins = 3) medians, bin_edges |
|
(array([216. , 147.5, 424. ]), array([187. , 361.66666667, 536.33333333, 711. ])) |
Подставим эти значения в функцию pd.cut().
|
boston[‘TAX_binned_median’] = pd.cut(boston.TAX, bins = bin_edges, labels = medians, include_lowest = True) boston[‘TAX_binned_median’].value_counts() |
|
216.0 273 424.0 137 147.5 96 Name: TAX_binned_median, dtype: int64 |
Алгоритм Дженкса
Алгоритм естественных границ Дженкса (Jenks natural breaks optimization) делит данные на группы (кластеры) таким образом, чтобы минимизировать отклонение наблюдений от среднего каждого класса (дисперсию внутри классов) и максимизировать отклонение среднего каждого класса от среднего других классов (дисперсию между классами).
Этот алгоритм также можно использовать для определения границ интервалов. Установим библиотеку jenkspy⧉.
Найдем оптимальные границы. Количество интервалов (n_classes) нужно по-прежнему указывать вручную.
|
import jenkspy breaks = jenkspy.jenks_breaks(boston.TAX, n_classes = 3) breaks |
|
[187.0, 337.0, 469.0, 711.0] |
Подставим интервалы в функцию pd.cut().
|
boston[‘TAX_binned_jenks’] = pd.cut(boston.TAX, bins = breaks, labels = labels, include_lowest = True) boston[‘TAX_binned_jenks’].value_counts() |
|
low 262 high 137 medium 107 Name: TAX_binned_jenks, dtype: int64 |
Подведем итог
Сегодня мы рассмотрели базовые методы кодирования категориальных переменных, а также стратегии binning/bucketing.
Кодирование чисел
Бит – наименьшая единица информации, которая выражает логическое «Да» или «Нет» и обозначается 1 или 0. Компьютер преобразует цифровую информацию, представленную в десятичной системе счисления в последовательность 0 и 1, а дальше уже работает с ними.
Системой счисления называют совокупность символов (цифр) и правил их использования для представления чисел.
Пример 1. Число 29 перевести из десятичной системы счисления в двоичную. Перевод осуществляется последовательным делением числа 29 на 2 и записью остатков от деления справа налево, как показано на схеме (рис. 3).

 29 : 2 = 14 + 1
29 : 2 = 14 + 1

 14 : 2 = 7 + 0
14 : 2 = 7 + 0

 7 : 2 = 3 + 1
7 : 2 = 3 + 1

 3 : 2 = 1 + 1
3 : 2 = 1 + 1

 1 = 1
1 = 1
Рис. 3. Схема перевода числа из десятичной системы счисления в двоичную
Двоичная система исчисления является позиционной.
Читается: 20 – 1; 21 – 0; 22 – 1; 23 – 1; 24 – 1;
1х20 +0х21 +1х22 + 1х23 +1х24 =1+0+4+8+16=29.
Пример 2. Число 1011, заданное в двоичной системе, перевести в десятичную систему счисления.
1011 a одна единица, одна двойка, нуль четверок и одна восьмерка.
1х20 + 1х21 + 0х22 + 1х23 = 11.
Байт– группа из 8 битов.
Если учесть, что важны не только нули и единицы, но и позиции, в которых они стоят, то с помощью одного байта можно выразить 28 = 256 единиц информации:
0000 0000 = 0
0000 0001 = 1
0000 0010 = 2
0000 0011 = 3
0000 0100 = 4
0000 0101 = 5
………………
1111 1100 = 252
1111 1101 = 253
1111 1110 = 254
11111111 = 255 Писать (или набирать на клавиатуре компьютера) длинные цепочки единиц и нулей при задании чисел в двоичном формате довольно утомительно. Так же неудобно просматривать содержимое памяти компьютера, представленное в двоичном формате. Поэтому был разработан такой метод представления двоичных данных, когда каждый байт разбивается пополам и каждая 4-битовая его половина записывается в 16-ричной системе счисления. Для ее осуществления цифровой алфавит 10-тичной системы счисления дополнили шестью цифрами, условившись, что: 10 – это A, 11 – это B, 12 – это C, 13 – это D, 14 – это E, 15 – это F. Пример 3. Десятичное число 42936 в двоичном формате имеет вид 1010011110111000. После записи полубайтов 1010 0111 1011 1000 16-ричными цифрами получаем компактную запись представленного числа – A7B8.
Кодирование текста
С помощью одного байта, как было показано, можно кодировать 256 значений. Первые 128 кодов (с 0 до 127) – стандартные и обязательные для всех стран. Эту половину таблицы кодов называют таблицей ASCII (стандартный код информационного обмена США) – ввел ее американский институт стандартизации ANSI. В этой части таблицы размещаются прописные и строчные буквы английского алфавита, символы чисел от 0 до 9, все знаки препинания, символы арифметических операций, специальные коды. Коды читают а-эс-цэ-и (аски- коды). Первых 32 кода – управляющие, которые не используются для представления информации (от 0 до 31), а 32 символ – пробел.
33 – 47 – специальные символы, знаки препинания.
48 – 57 – цифры.
58 – 64 – математические символы и знаки препинания.
65 – 90 – прописные буквы английского алфавита.
91 – 96 – специальные символы.
97 – 122 – строчные буквы английского алфавита.
123 – 127 – специальные символы.
Остальные 128 кодов используются для специальных символов и букв национальных алфавитов (в том числе русского). И поскольку общепринятого стандарта для этого не было, возникло много различных кодировок, в том числе, несколько для кириллицы. Для кириллицы используют следующие кодировки: Кириллица (Windows), Кириллица (ISO), Кириллица (KOI8–R). Кириллица (ISO) используется редко. Кириллица (Windows) используется на ПК, работающих на платформе Windows. Де-факто Кириллица(Windows) стала стандартной в российском секторе World Wide Web. Кириллица (KOI8–R) де-факто является стандартной в сообщениях электронной почты и телеконференций.
В такой ситуации, когда используются различные кодировки кириллицы, на помощь приходят программы – конверторы. Они заменяют двоичный код каждого символа на код, которым такой символ представляется в другой кодировке. Это соответствие определяется таблицей перекодировки. Пользователь должен указать, из какой кодировки в какую идет преобразование, однако есть программы, автоматически определяющие кодировку исходного текста.
Следует отметить, что все рассмотренные кодировки текста ограничены набором кодов (256). Более широкими возможностями обладает система кодировки текста UNICODE, основанная на 16-разрядном кодировании символов. Шестнадцать разрядов обеспечивают кодирование 216 =65536 символов.
Чтобы рисунок буквы был виден на экране, его цвет должен отличаться от цвета фона, на котором он изображается. Поэтому коды символов (порядковые номера в таблице кодирования) необходимо дополнить кодами цвета фона и цвета рисунков. Для этих кодов цветов добавили еще один байт памяти и разделили его пополам – младшую (левую) половину из четырех битов отвели для кодирования цвета рисунка, а старшую для кодирования цвета фона. Этот байт назвали байтом атрибутов символа. Он всегда присутствует вместе с кодом символа в двух байтовых кодах символов, передаваемых в видеопамять для отображения на экране.
Четырьмя байтами можно закодировать 16 цветов, а при необходимости кодирования большего количества цветов применяют многоступенчатую систему кодирования. Содержимое байта атрибутов удобно записывать в 16-ричном формате, у которого первая цифра в этом случае обозначает цвет фона, а вторая – цвет рисунка символа. Например, 16-ричное число 4E кодирует желтые (код желтого цвета Е или 14 в 10-й системе) буквы на красном (код красного цвета равен 4) фоне.
Двухбайтовые кодовые группы каждой буквы текста, содержащие код символа и код атрибутов его изображения для вывода на экран, записываются в память устройства управления, которое называют дисплейным адаптером, а саму память – видеопамятью или видеобуфером.
Последнее название подсказывает, что для постоянного обновления изображения на экране из этого буфера с частотой примерно 25 (или более) раз в секунду считываются коды символов и преобразуются в рисунки букв на экране. Чтобы такое преобразование стало возможным, приходится закодировать и разместить в памяти компьютера и сами рисунки букв. Для изображения символов обычно отводится в зависимости от типа видеосистемы от 8 до 16 строк по 8 пикселов в строке. О каждом пикселе в изображении символа дисплейный адаптер должен знать, относится он к фону или рисунку – то есть достаточно одного бита с двумя состояниями. Если бит содержит 0, то это пиксел фона, а если 1 – то это пиксел рисунка.
256 кодовых групп символов текста хранятся в памяти для рисунков всех изображаемых символов, и вся эта область памяти называется буфером знакогенератора. Адаптер дисплея «узнает» начальный адрес этого буфера (порядковый номер его начального байта, отсчитанный от начала памяти), берет из видеопамяти код символа, означающий порядковый номер его кодовой группы в буфере знакогенератора, умножает на число пиксельных строк в изображении символа и прибавляет полученное число к начальному адресу буфера знакогенератора. Полученное число есть начальный адрес кодовой группы изображения символа. Далее видеоадаптер берет каждый байт кодовой группы изображения и работает уже с отдельными битами байта – для нулевых битов выводит пиксел цветом фона, а для единичных – цветом рисунка (коды цвета фона и рисунка он тоже берет из видеопамяти – из байта атрибутов). Вот так появляются на экране дисплея рисунки букв, как и все в компьютере, закодированные двоичными числами. При выводе изображений символов на печать коды изображений символов и их порядковые номера хранятся в памяти печатающего устройства либо постоянно, либо заносятся туда из памяти компьютера перед началом печати.
Статьи к прочтению:
- Кодирование и тестирование сверху вниз
- К оформлению семестровой контрольной работы
Кодирование текстовой информации
Похожие статьи:
-
Отображение чисел и текста с помощью компонентов tlabel, tedit
Простая кнопка. Для этого в панели инструмментов ищем на вкладке Standard компонент Button и щелкаем по нему левой кнопкой мыши. Далее щелкаем той же…
-
Двоичное кодирование звука
Лабораторная работа №5 Тема: Дискретное (цифровое) представление текстовой, графической, звуковой информации и видеоинформации Цель работы:научиться…
