Как найти коэффициент амплитуды

Переменный электрический ток

Переменный ток (AC – Alternating Current) – электрический ток, меняющий свою величину и направление с течением времени.

Часто в технической литературе переменным называют ток, который меняет только величину, но не меняет направление, например, пульсирующий ток.
Необходимо помнить при расчётах, что переменный ток в этом случае является лишь составляющей частью общего тока.
Такой вариант можно представить как переменный ток AC с постоянной составляющей DC.
Либо как постоянный ток с переменной составляющей, в зависимости от того, какая составляющая наиболее важна в контексте.

DC – Direct Current – постоянный ток, не меняющий своей величины и направления.

В реальности постоянный ток не может сохранять свою величину постоянной, поэтому существует условно в тех случаях, где можно пренебречь изменениями его постоянной величины, либо в качестве составляющей (DC) для периодически меняющегося электрического тока любой формы. Тогда величина DC будет равна среднему значению тока за период, и будет являться нулевой линией для переменной составляющей AC.

При синусоидальной форме тока, например в электросети, постоянная составляющая DC равна нулю.

Постоянный ток с переменной составляющей в виде пульсаций показан синей линией на верхнем графике рисунка.
Запись AC+DC в данном случае не является математической суммой, а лишь указывает на две составляющие тока. Суммируются мощности.

Величина тока будет равна квадратному корню из суммы квадратов двух величин – значения постоянной составляющей DC и среднеквадратичного значения переменной составляющей AC.

Термины AC и DC применимы как для тока, так и для напряжения.

Параметры переменного тока и напряжения

Величина переменного тока, как и напряжения, постоянно меняется во времени. Количественными показателями для измерений и расчётов применяются их следующие параметры:

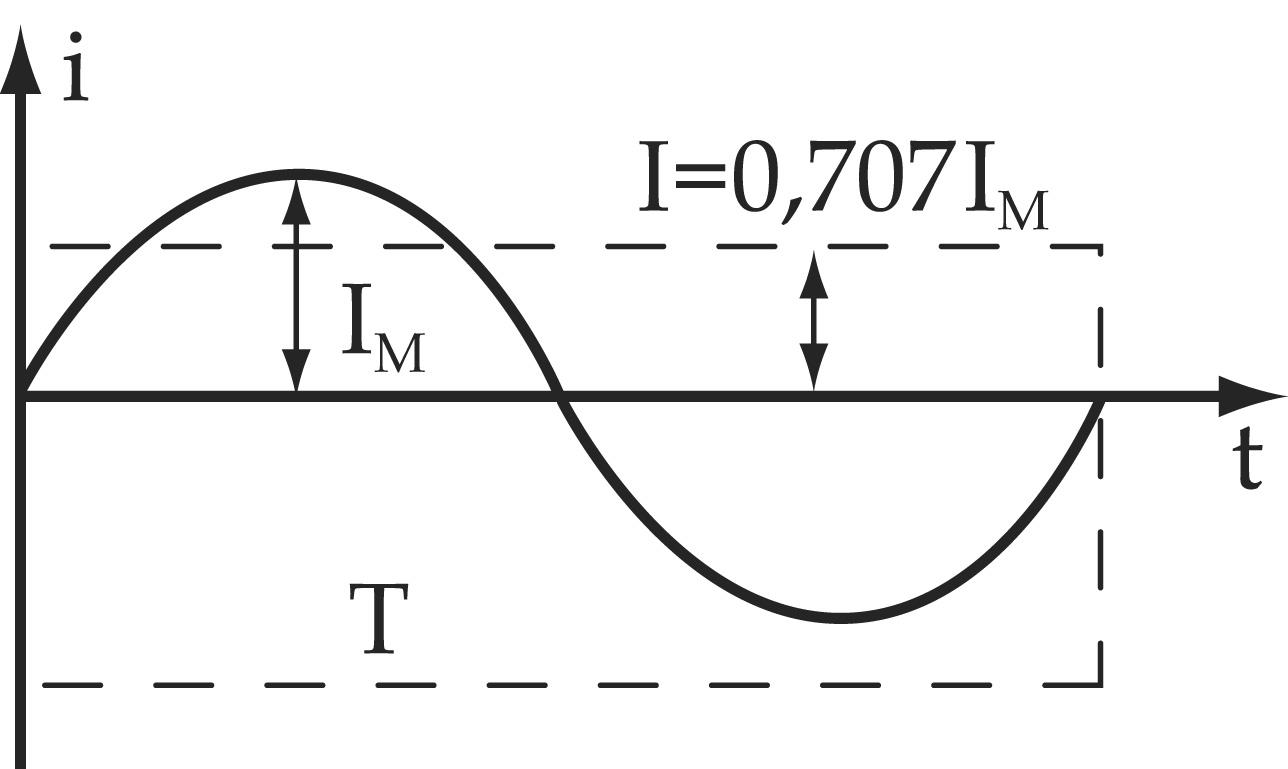
Период T – время, в течении которого происходит один полный цикл изменения тока в оба направления относительно нуля или среднего значения.

Частота  f – величина, обратная периоду, равная количеству периодов за одну секунду.

Один период в секунду это один герц (1 Hz). Частота f = 1/T

Циклическая частота  ω – угловая частота, равная количеству периодов за 2π секунд.

ω = 2πf = 2π/T

Обычно используется при расчётах тока и напряжения синусоидальной формы. Тогда в пределах периода можно не рассматривать частоту и время, а исчисления производить в радианах или градусах. T = 2π = 360°

Начальная фаза  ψ – величина угла от нуля (ωt = 0) до начала периода.
Измеряется в радианах или градусах. Показана на рисунке для синего графика синусоидального тока.

Начальная фаза может быть положительной или отрицательной величиной, соответственно справа или слева от нуля на графике.

Мгновенное значение – величина напряжения или тока измеренная относительно нуля в любой выбранный момент времени t.

i = i(t);   u = u(t)

Последовательность всех мгновенных значений в любом интервале времени можно рассмотреть как функцию изменения тока или напряжения во времени.
Например, синусоидальный ток или напряжение можно выразить функцией:

i = I_ampsin(ωt);   u = U_ampsin(ωt)

С учётом начальной фазы:

i = I_ampsin(ωt + ψ);   u = U_ampsin(ωt + ψ)

Здесь I_amp и U_amp – амплитудные значения тока и напряжения.

Амплитудное значение – максимальное по модулю мгновенное значение за период.

I_amp = max|i(t)|;   U_amp = max|u(t)|

Может быть положительным и отрицательным в зависимости от положения относительно нуля.

Часто вместо амплитудного значения применяется термин амплитуда тока (напряжения) – максимальное отклонение от нулевого значения.

Среднее значение (avg) – определяется как среднеарифметическое всех мгновенных значений за период T.

Среднее значение является постоянной составляющей DC напряжения и тока.
Для синусоидального тока (напряжения) среднее значение равно нулю.

Средневыпрямленное значение – среднеарифметическое модулей всех мгновенных значений за период.

Для синусоидального тока или напряжения средневыпрямленное значение равно среднеарифметическому за положительный полупериод.

Среднеквадратичное значение (rms) – определяется как квадратный корень из среднеарифметического квадратов всех
мгновенных значений за период.

Для синусоидального тока и напряжения амплитудой I_amp (U_amp)
среднеквадратичное значение определится из расчёта:

---

Коэффициент амплитуды и коэффициент формы

---

Действующее и среднее значения переменного тока

Действующее
значение переменного тока численно
равно такому постоянному току, который,
проходя через то же сопротивление, что
и переменный ток, выделяет за время,
равное 1 периоду, одинаковое количество
тепла. Все приборы показывают действующее
значение
.

Если левые части
уравнения равны, то и правые будут тоже
равны. Приравняв правые части и выполнив
операцию интегрирования, получим:

Среднее арифметическое
значение переменного тока определяется
в течении полупериода; если через
поперечное сечение проводника в течении
1 полупериода будет протекать один и
тот же заряд при постоянном и переменном
токе, то такое значение постоянного
тока будет равно среднему значению
переменного тока
.

Среднее значение
тока за период равно нулю.

Коэффициенты формы и амплитуды

Отношение
действующего значения переменного тока
(напряжения или ЭДС) к среднему значению
называется коэффициентом формы,
а отношение амплитудного значения к
действующему –коэффициентом
амплитуды.

Для синусоидального
тока:

,
а
.

Для кривых, имеющих
более острую форму, чем синусоида:
;.

Начальная фаза. Сдвиг фаз

Предположим, что в магнитном поле генератора находится два одинаковых витка, сдвинутых в пространстве друг относительно друга на угол . При вращении в них буду находится ЭДС одинаковой частоты и амплитуды.

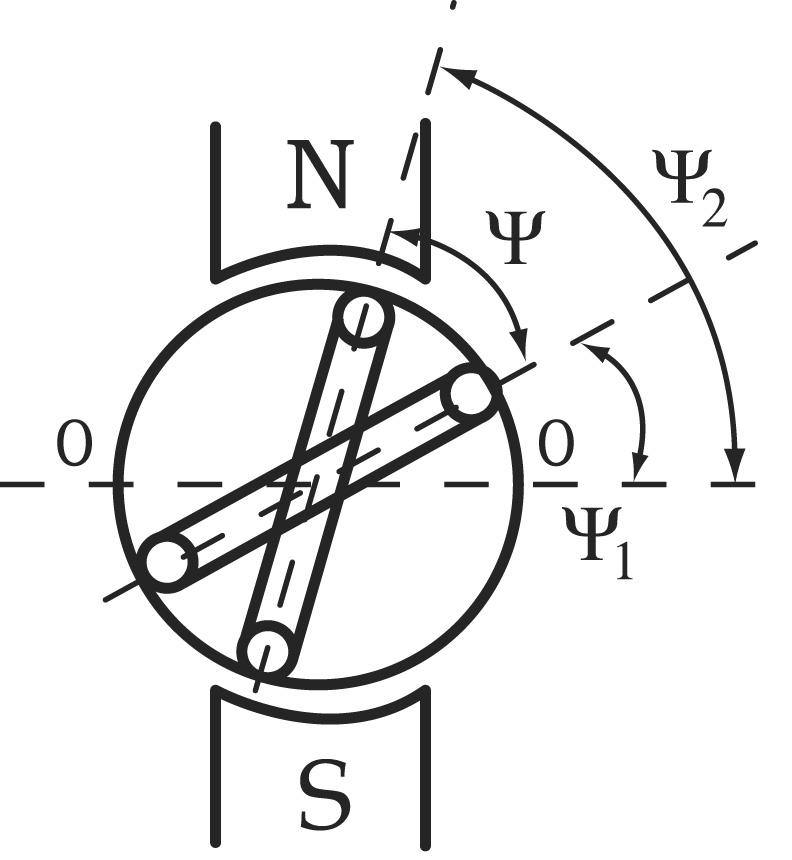
Но т.к. витки
сдвинуты в пространстве, то наводимая
в них ЭДС будет достигать амплитудных
и нулевых значений не одновременно.

В начальный момент
времени
ЭДС витка будет:

В этих выражениях
углы
иназываютсяфазными, илифазой.
Углыиназываютсяначальной фазой.
Фазный угол определяет значение ЭДС в
любой момент времени, а начальная фаза
определяет значение ЭДС в начальный
момент времени.

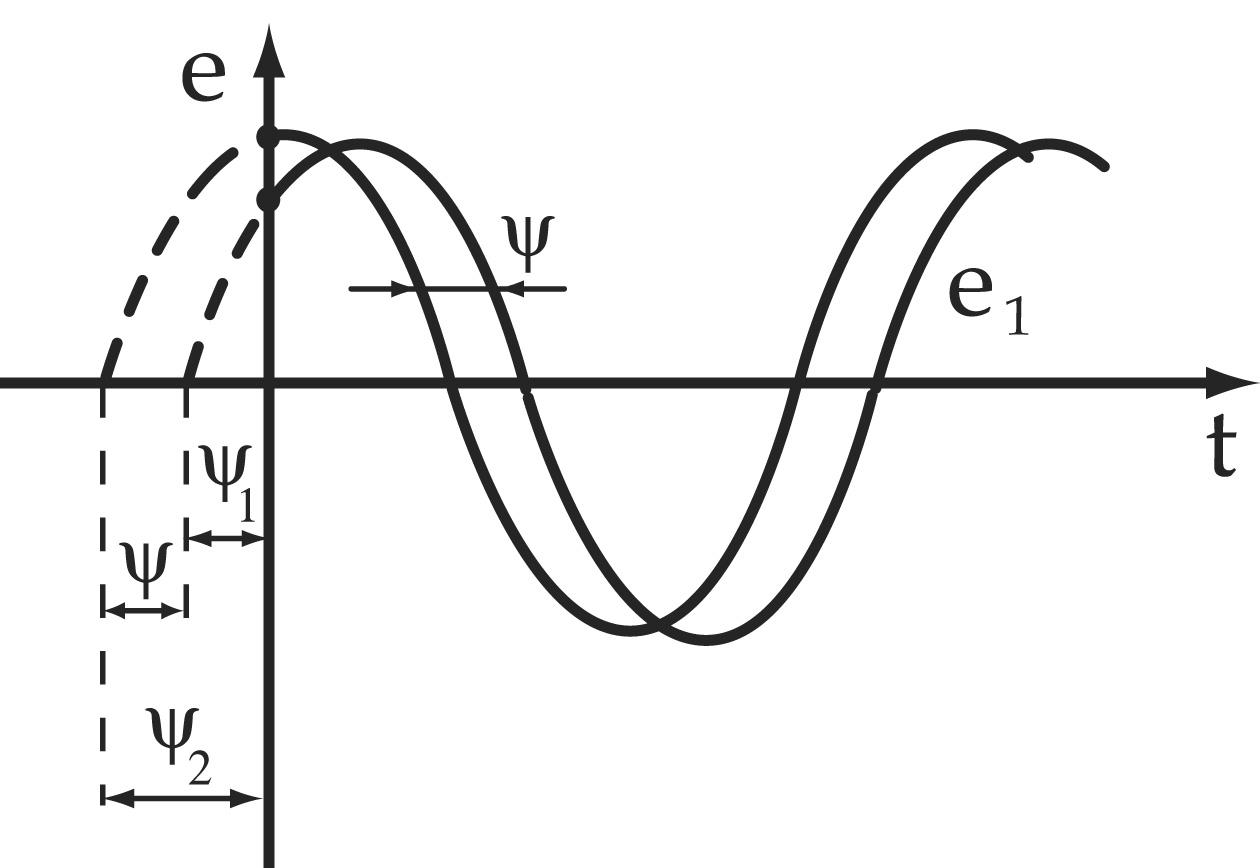
Разность начальных
фаз двух синусоидальных величин
одинаковой частоты и амплитуды называется
углом сдвига фаз

Разделив угол
сдвига фаз на угловую частоту, получим
время, прошедшее с начала периода:

Если угол сдвига фаз составляет 1800, то такие ЭДС находятся в противофазе

Графическое изображение синусоидальных величин

Синусоидальные
величины можно изображать графически
при помощи синусоид или вращающихся
векторов.

Любая синусоидальная
величина характеризуется:

1. амплитудой;

2. угловой частотой;

3. начальной фазой.

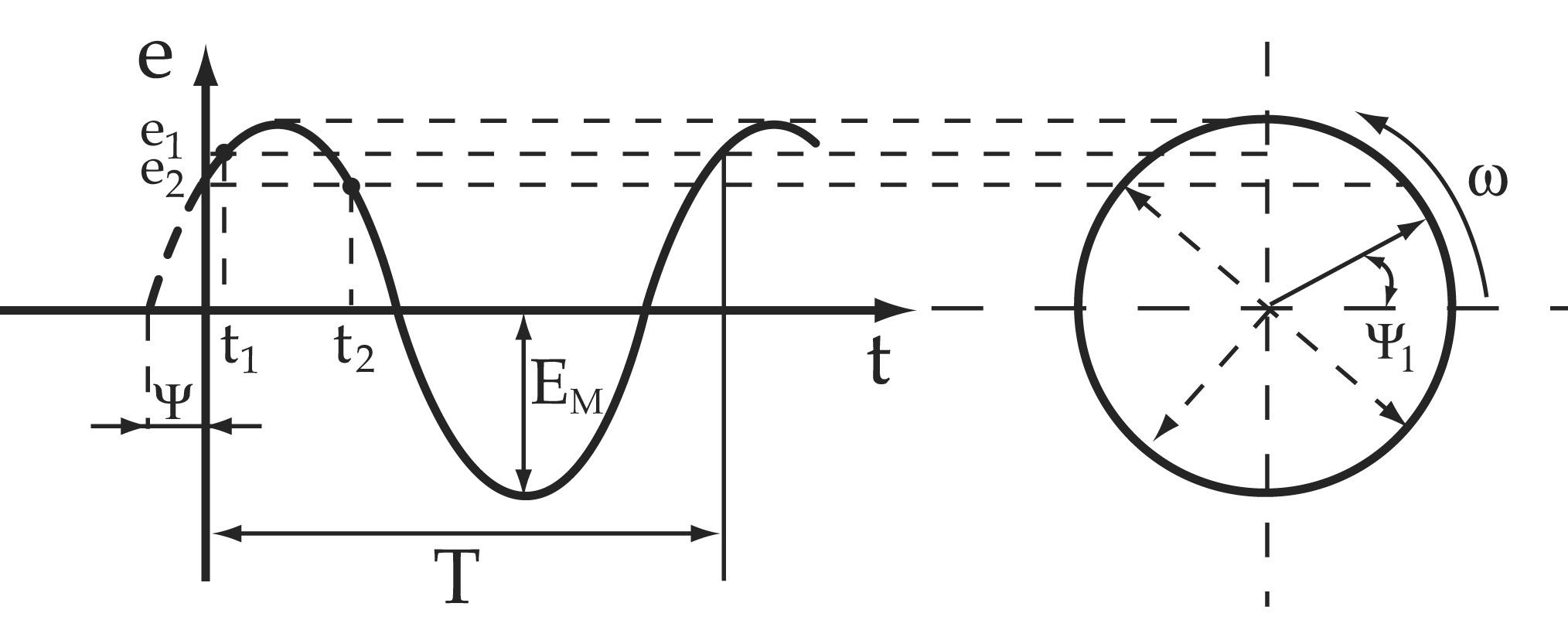
При изображении
величины с помощью синусоиды ординаты
синусоиды в масштабе представляют собой
мгновенное значение, абсциссы –
промежутки времени.

При этом длина
вектора равна амплитудному значению
величины, угол
между положительным направлением оси
абсцисс и векторов даст начальную фазу.
Вектор вращается против часовой стрелки
с угловой скоростью.
Проекция конца вектора на ось ординат
даст мгновенное значение синусоидальной
величины.

Совокупность
нескольких синусоид называется
синусоидальной (волновой) диаграммой.

Совокупность
нескольких векторов называется векторной
диаграммой.

Сложение и вычитание синусоидальных величин

.

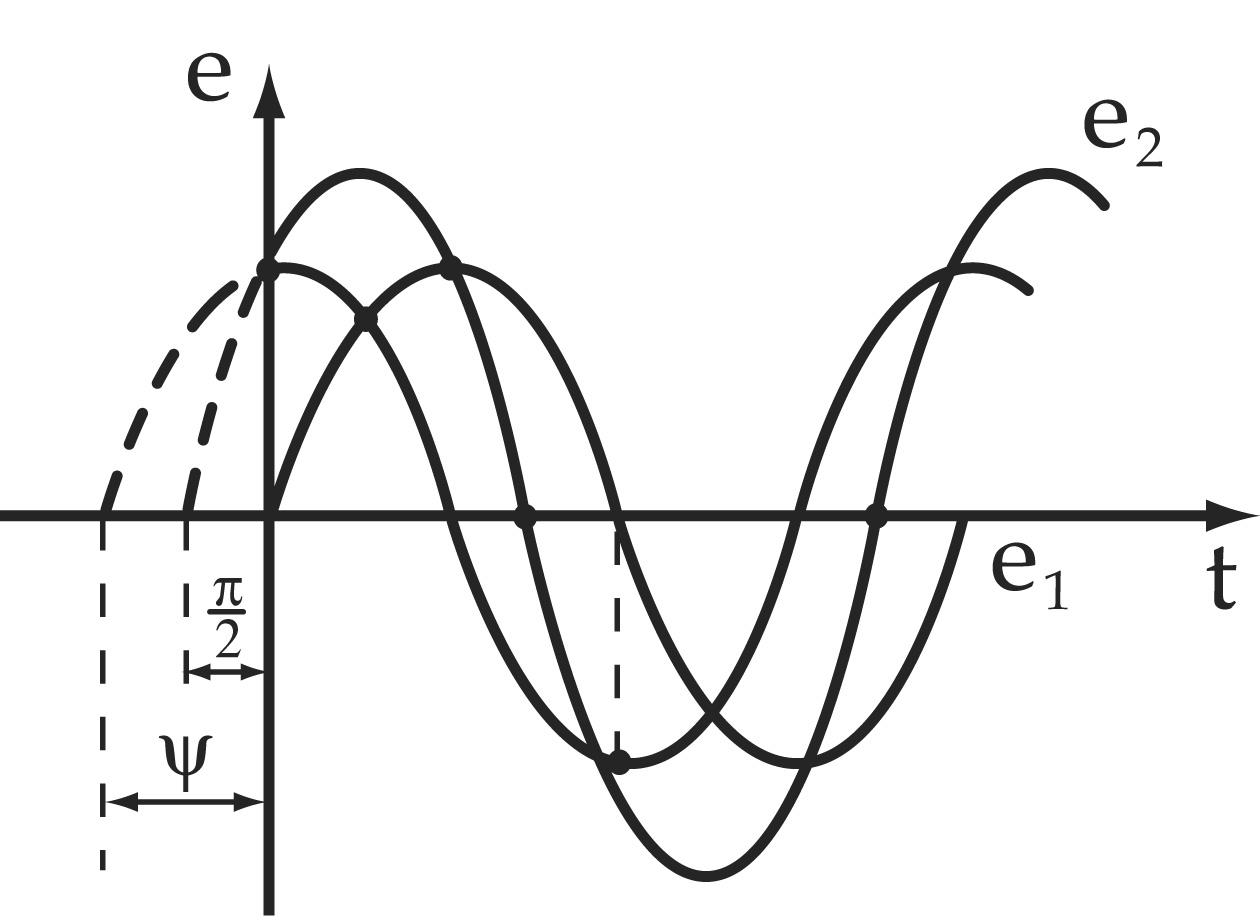
Для сложения двух
синусоидальных величин с помощью
синусоид необходимо сложить их ординаты
в каждый момент времени.

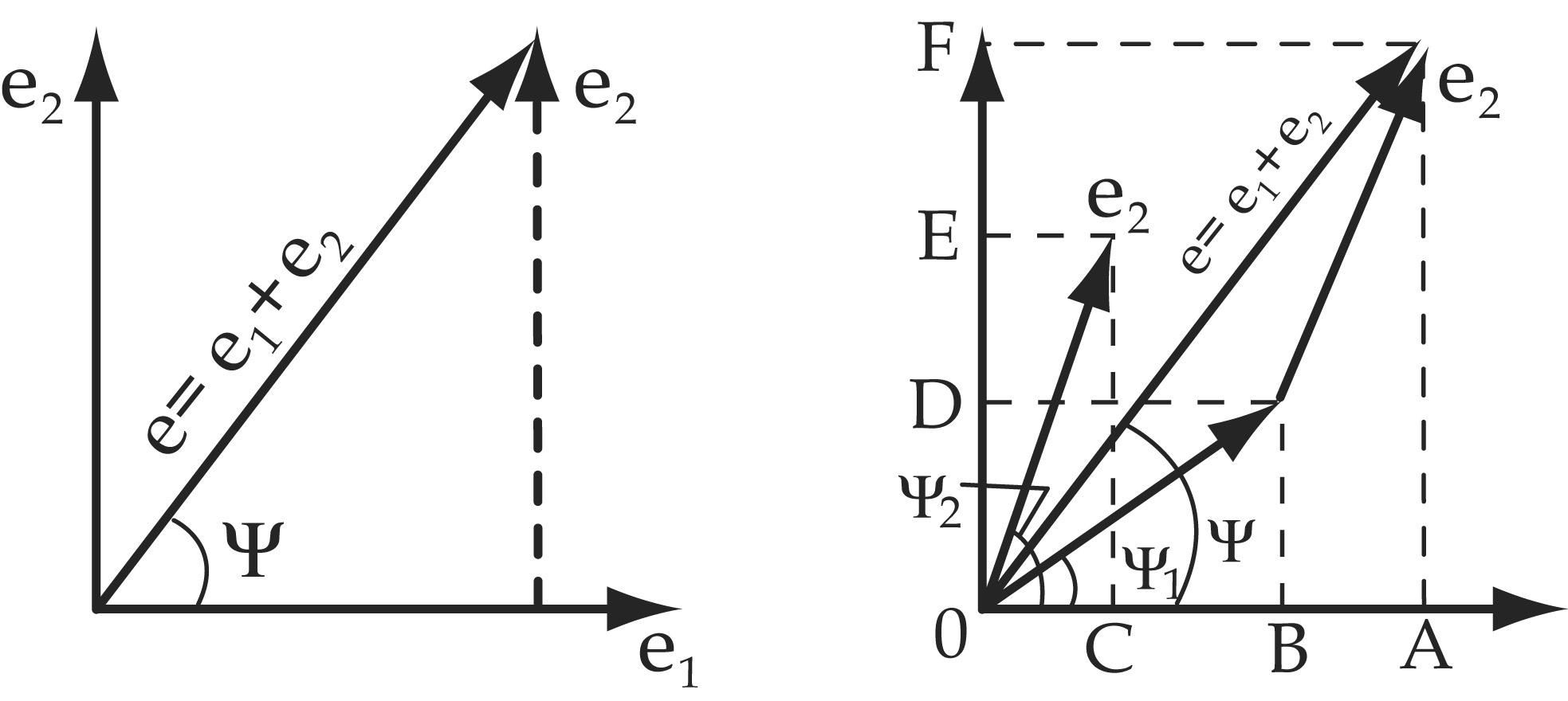
Для того, чтобы
сложить две величины с помощью векторов,
необходимо к концу первого вектора
добавить второй, не изменяя его величины
и направления. Соединив начало первого
вектора с концом второго, получим
суммарный вектор.

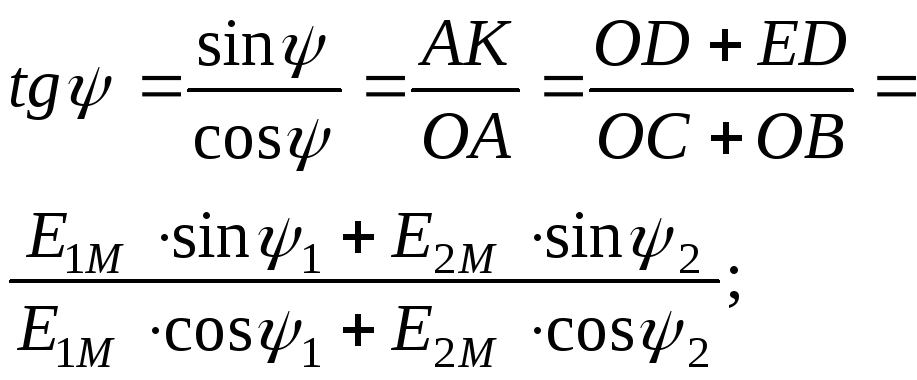
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #

  30.04.2019207.36 Кб8k1.doc
• #
• #
• #
• #
• #
• #
• #

Коэффициент амплитуды — это отношение амплитуды периодически изменяющейся функции к ее действующему значению. Для синусоидального тока

Под коэффициентом формы понимают отношение действующего значения периодически изменяющейся функции к ее среднему за полпериода значению. Для синусоидального тока

Всем доброго времени суток! В прошлой статье я рассказал, как рассчитать индуктивность катушки выполненной на разомкнутом сердечнике (например, ферритовой антенны, контурных катушек радиоприёмников, катушек с построечными сердечниками и т. д.). Сегодняшняя статья посвящена переменному напряжению и параметрам, которые его характеризуют.

Что такое переменное напряжение?

Как известно электрическим током называется упорядоченное движение заряженных частиц, которое возникает под действием разности потенциалов или напряжения. Одной из основных характеристик любого типа напряжения является его зависимость от времени. В зависимости от данной характеристики различают постоянной напряжение, значение которого с течением времени практически не изменяется и переменное напряжение, изменяющееся во времени.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Переменное напряжение в свою очередь бывает периодическим и непериодическим. Периодическим называется такое напряжение, значения которого повторяются через равные промежутки времени. Непериодическое напряжение может изменять своё значение в любой период времени. Данная статья посвящена периодическому переменному напряжению.

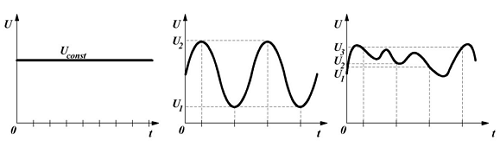
Постоянное (слева), периодическое (в центре) и непериодическое (справа) переменное напряжение.

Минимальное время, за которое значение переменного напряжения повторяется, называется периодом. Любое периодическое переменное напряжение можно описать какой-либо функциональной зависимостью. Если время обозначить через t, то такая зависимость будет иметь вид F(t), тогда в любой период времени зависимость будет иметь вид

где Т – период.

Величина обратная периоду Т, называется частотой f. Единицей измерения частоты является Герц, а единицей измерения периода является Секунда

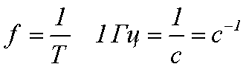
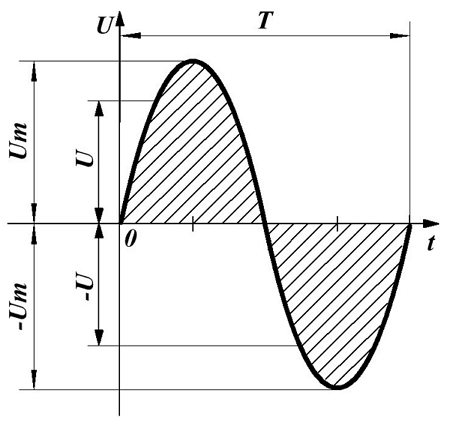
Наиболее часто встречающаяся функциональная зависимость периодического переменного напряжения является синусоидальная зависимость, график которой представлен ниже

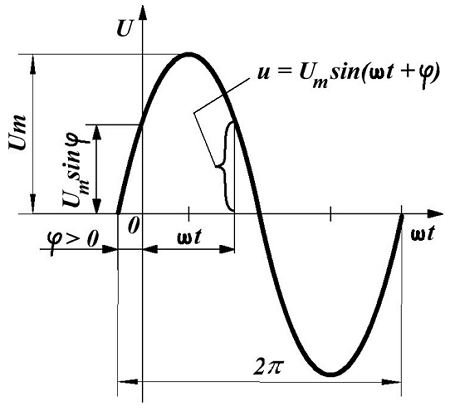Синусоидальное переменное напряжение.

Из математики известно, что синусоида является простейшей периодической функцией, и все другие периодические функции, возможно, представить в виде некоторого количества таких синусоид, имеющих кратные частоты. Поэтому необходимо изначально рассмотреть особенности синусоидального напряжения.

Таким образом, синусоидальное напряжение в любой момент времени, мгновенное напряжение, описывается следующим выражением

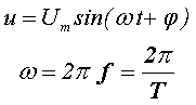
где U_m – максимальное значение напряжения или амплитуда,

ω –угловая частота, скорость изменения аргумента (угла),

φ – начальная фаза, определяемая смещением синусоиды относительно начала координат, определяется точкой перехода отрицательной полуволны в положительную полуволну.

Величина (ωt + φ) называется фазой, характеризующая значение напряжения в данный момент времени.

Таким образом, амплитуда U_m, угловая частота ω и начальная фаза φ являются основными параметрами переменного напряжения и определяют его значение в каждый момент времени.

Обычно, при рассмотрении синусоидального напряжения считают, что начальная фаза равна нулю, тогда

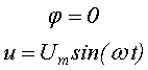
В практической деятельности, довольно часто, используют ещё ряд параметров переменного напряжения, такие как, действующее напряжение, среднее напряжение и коэффициент формы, которые мы рассмотрим ниже.

Что такое действующее напряжение переменного тока?

Как я писал выше, одним из основных параметров переменного напряжения является амплитуда U_m, однако использовать в расчётах данную величину не удобно, так как временной интервал в течение, которого значение напряжения u равно амплитудному U_m ничтожно мал, по сравнению с периодом Т напряжения. Использовать мгновенное значение напряжения u, также не очень удобно, вследствие больших объёмов расчётов. Тогда возникает вопрос, какое значение переменного напряжения использовать при расчётах?

Для решения данного вопроса необходимо обратиться к энергии, которая выделяется под воздействием переменного напряжения, и сравнить её с энергией, которая выделяется под воздействием постоянного напряжения. Для решения данного вопроса обратимся к закону Джоуля – Ленца для постоянного напряжения

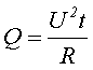
Для переменного напряжения мгновенное значение выделяемой энергии составит

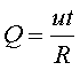
где u – мгновенное значение напряжения

Тогда количество энергии за полный период от t₀ = 0 до t₁ = T составит

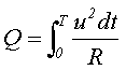
Приравняв выражения для количества энергии при переменном напряжении и постоянном напряжении и выразив полученное выражение через постоянное напряжение, получим действующее значение переменного напряжения

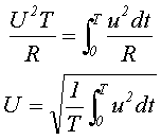
Получившееся выражение, позволяет вычислить действующее значение напряжение U для периодического переменного напряжения любой формы. Из выше изложенного можно сделать вывод, что действующее значение переменного напряжения называется такое постоянное напряжение, которое за такое же время и на таком же сопротивлении выделяет такую же энергию, которая выделяется данным переменным напряжением.

Действующее значение синусоидального напряжения.

Вычислим действующее значение синусоидального напряжения

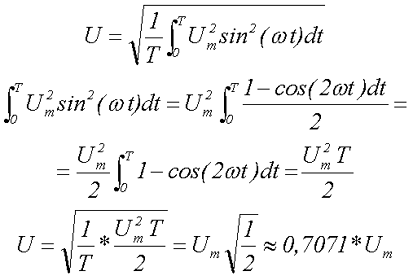
Стоит отметить, все напряжения электротехнических устройств определяются, как правило, действующим значением напряжения.

Для определения амплитудного значения синусоидального напряжения необходимо преобразовать полученное выражение

Таким образом если в розетке у нас U = 230 В, следовательно, амплитудное значение данного напряжения

Действующее напряжение также имеет название эффективного напряжения и среднеквадратичного напряжения.

С действующим напряжением разобрались, теперь рассмотрим среднее значение напряжение.

Что такое среднее значение переменного напряжения?

Ещё одним параметром переменного напряжения, который его характеризует, является средним значением переменного напряжения. В отличие от действующего значения переменного напряжения, которое характеризует работу переменного напряжения, среднее значение напряжения характеризует количество электричества, которое перемещается из одной точки цепи в другую, под действием переменного напряжения. Среднее значение напряжения за период определяется следующим выражением

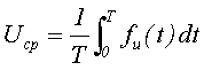
где Т – период переменного напряжения,

f_u(t) – функциональная зависимость напряжения от времени.

Таким образом, среднее значение переменного напряжения численно будет равно высоте прямоугольника с основанием T, площадь которого равна площади, ограниченной функцией f_u(t) и осью Ox за период Т.

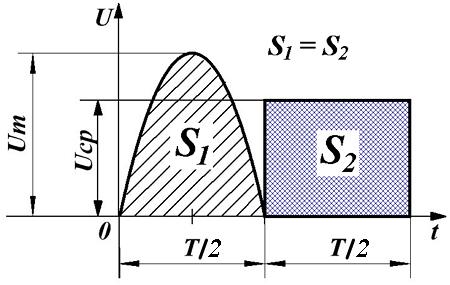
Среднее значение переменного напряжения.

В случае синусоидальной функции, можно говорить только о среднем значении за полупериод, так как в течение всего периода положительная полуволна компенсируется отрицательной полуволной, и тогда среднее за период напряжение будет равно нулю.

Таким образом, среднее за полупериод Т/2 значение переменного напряжения синусоидальной формы будет равно

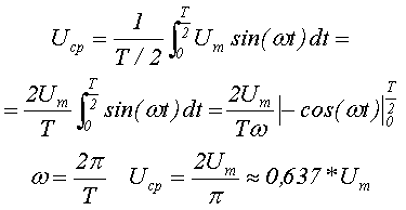
где U_m – максимальное значение напряжения или амплитуда,

ω –угловая частота, скорость изменения аргумента (угла).

Какие коэффициенты, характеризуют переменное напряжение?

Иногда возникает необходимость охарактеризовать форму переменного напряжения. Для этой цели существует ряд параметров данного переменного напряжения:

1. Коэффициент формы переменного напряжения k_ф – показывает как относится действующее значение переменного напряжения U к его среднему значению U_cp.

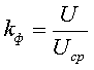
Так для синусоидального напряжения коэффициент формы составит

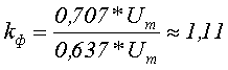
2. Коэффициент амплитуды переменного напряжения k_а – показывает как относится амплитудное значение переменного напряжения U_m к его действующему значению U

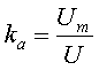
Так для синусоидального напряжения коэффициент амплитуды составит

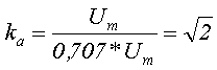
На сегодня всё, в следующей статье я рассмотрю прохождение переменного напряжения через сопротивление, индуктивность и емкость.

При оценке несинусоидальных периодических кривых в электроэнергетике, где кривые преимущественно симметричны относительно оси абсцисс, пользуются коэффициентом формы кривой , коэффициентом амплитуды , коэффициентом искажения .
Коэффициент формы определяется как отношение действующего значения к среднему по модулю значению:

Для синусоиды
Коэффициент амплитуды равен отношению максимального значения к действующему значению:

Для синусоиды
Коэффициент искажения определяется как отношение действующего значения основной гармоники к действующему значению всей кривой:

Для синусоиды .
В электронике и радиотехнике для оценки искажений пользуются коэффициентом гармоник; который определяется как отношение действующего значения высших гармоник к действующему значению основной гармоники:

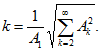
При отсутствии постоянной составляющей

Для синусоиды k=0.

Пример 12.6. Определить коэффициенты для кривых, изображенных на рис. 12.8, а и б.
Решение. Для кривой на рис. 12.8, а по известным действующему и среднему по модулю значениям находим, что , и по разложению функции на гармоники (см. приложение 3, п. 4)

Аналогично для кривой на рис. 12.8,6 получаем
Кривые напряжения промышленных сетей обычно отличаются от идеальной синусоиды. В электроэнергетике вводят понятие о практически синусоидальной кривой. По стандарту напряжение промышленной сети считается практически синусоидальным, если действующее значение всех высших гармоник не превышает 5 % действующего значения напряжения основной частоты. Коэффициент искажения такой кривой с точностью до долей процента равен единице.
Значения простейших кривых приведены в приложении 3. Сопоставляя значения коэффициентов первых четырех кривых, можно установить, что чем острее кривая, тем больше значения .
Измерение несинусоидальных токов и напряжений приборами различных систем может давать неодинаковые результаты.
Приборы электродинамической, электромагнитной и тепловой систем реагируют на действующее значение измеряемой величины. Магнитоэлектрические приборы сами по себе измеряют постоянную составляющую, а с выпрямителями — среднее по модулю значение. Амплитудные электронные вольтметры реагируют на максимальные значения. Так как обычно этими приборами пользуются для измерения действующих значений синусоидальных величин, то их шкалы часто градуируют на в приборе выпрямительной системы и на в амплитудном электронном.
Отношения U к и при несинусоидальных напряжениях нередко сильно отличаются от коэффициентов 1,11 и , и соответственно приборы выпрямительной системы и амплитудные электронные приборы дают большую погрешность при измерении действующих значений таких несинусоидальных величин.

Пример 12.7. Найти показания вольтметров различных систем, подключенных к источнику ЭДС с максимальным значением напряжения 100 В, для различных случаев формы кривой, представленных на рис. 12.8.
Решение. В первых двух случаях магнитоэлектрический прибор, реагирующий на постоянную составляющую, покажет нуль. Показания же приборов остальных систем будут различными.
В случае кривой на рис. 12.8, а электродинамический прибор покажет 100 В, прибор выпрямительной системы 111 В, а амплитудный электронный прибор
В случае кривой на рис. 12.8, б электродинамический прибор покажет , прибор выпрямительной системы , а амплитудный электронный прибор
В случае кривой на рис. 12.8, в при электродинамический прибор покажет , прибор выпрямительной системы , а амплитудный электронный прибор 71 В. Магнитоэлектрический прибор покажет постоянную составляющую
Таким образом, вольтметры разных систем могут показывать совершенно различные значения напряжений и зависимости от формы кривой напряжения.