Как найти коэффициент асимметрии случайной величины

Коэффициент асимметрии. Эксцесс распределения

Краткая теория

---

При изучении распределений, отличных от нормального,
возникает необходимость количественно оценить это различие. С этой целью вводят
специальные характеристики, в частности асимметрию и эксцесс. Для нормального
распределения эти характеристики равны нулю. Поэтому если для изучаемого
распределения асимметрия и эксцесс имеют небольшие значения, то можно
предположить близость этого распределения к нормальному.
Наоборот, большие значения асимметрии и эксцесса указывают на значительное
отклонение от нормального.

Асимметрией теоретического распределения называют отношение
центрального момента третьего порядка к кубу среднего квадратического
отклонения:

Коэффициент асимметрии характеризует скошенность
распределения по отношению к математическому ожиданию. Асимметрия положительна,
если «длинная часть» кривой распределения расположена справа от математического
ожидания; асимметрия отрицательна, если «длинная часть» кривой расположена слева
от математического ожидания.

На рисунке показаны две кривые распределения: I и II. Кривая I имеет
положительную (правостороннюю) асимметрию

,
а кривая II – отрицательную (левостороннюю)

.

Кроме вышеописанного коэффициента, для характеристики асимметрии
рассчитывают также показатель асимметрии Пирсона:

Коэффициент асимметрии Пирсона характеризует асимметрию только в
центральной части распределения, поэтому более распространенным и более точным
является коэффициент асимметрии, рассчитанный на основе центрального момента третьего
порядка.

Для оценки «крутости», т. е. большего или меньшего подъема кривой
теоретического распределения по сравнению с нормальной кривой, пользуются
характеристикой – эксцессом.

Эксцессом (или коэффициентом эксцесса) случайной величины
называется число:

Число 3 вычитается из отношения

 потому, что для наиболее часто встречающегося
нормального распределения отношение

.

Кривые, более островершинные, чем нормальная,
обладают положительным эксцессом, более плосковершинные – отрицательным
эксцессом.

Примеры решения задач

---

Задача 1

Для заданного
вариационного ряда вычислить коэффициенты асимметрии и эксцесса.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Составим расчетную
таблицу

Средняя:

Найдем моду – варианту, которой соответствует наибольшая частота.

Дисперсия:

Среднее квадратическое
отклонение:

Коэффициент асимметрии Пирсона:

Коэффициент асимметрии можно найти по формуле:

Центральный момент
3-го порядка:

Получаем:

Эксцесс можно найти по формуле:

Центральный момент
4-го порядка:

Получаем:

---

Задача 2

Для заданного
вариационного ряда (см. условие задачи 1) вычислить коэффициенты асимметрии и
эксцесса методом произведений, используя условные моменты.

Решение

Составим расчетную таблицу

Перейдем к условным вариантам

В качестве ложного нуля возьмем
3-ю варианту

0

Условные варианты вычислим по
формуле:

где

4
(разность между соседними вариантами)

Условный момент 1-го порядка:

Средняя:

Условный момент 2-го порядка:

Дисперсия:

Среднее квадратическое
отклонение:

Коэффициент асимметрии можно найти
по формуле:

Условный момент 3-го порядка:

Центральный момент 3-го порядка:

Получаем:

Эксцесс можно найти по формуле:

Условный момент 4-го порядка:

Центральный момент 4-го порядка:

Получаем:

Коэффицие́нт асимметри́и — в теории вероятностей величина, характеризующая асимметрию распределения данной случайной величины.

Определение[править | править код]

Пусть задана случайная величина , такая что . Пусть обозначает третий центральный момент: , а  — стандартное отклонение . Тогда коэффициент асимметрии задаётся формулой^[1]:

.

Замечания[править | править код]

• Неформально говоря, коэффициент асимметрии положителен, если правый хвост распределения длиннее левого, и отрицателен в противном случае.
• Если распределение симметрично относительно математического ожидания, то его коэффициент асимметрии равен нулю^[2].

См. также[править | править код]

• Коэффициент эксцесса

Примечания[править | править код]

Литература[править | править код]

• Дерр, В. Я. Теория вероятностей и математическая статистика: учебное пособие для вузов. — СПб.: Лань, 2021. — 596 с. — ISBN 978-5-8114-6515-6.

Математическое
ожидание
непрерывной случайной величины
вычисляется по формуле:

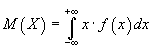
В
частности, если с.в. задана своей
плотностью вероятности на каком-либо
отрезке, то и интеграл вычисляем на этом
отрезке.

Дисперсия
непрерывной случайной величины
вычисляется по формуле:

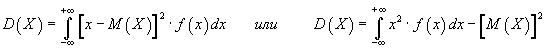
Относительно
пределов интегрирования – то же самое.

Среднее
квадратическое отклонение
непрерывной случайной величины, оно же
стандартное отклонение или среднее
квадратичное отклонение есть корень
квадратный из дисперсии:

σ(X) = √D(X)

Мода
непрерывной случайной величины Mo(X) –
значение с.в., имеющее наибольшую
вероятность. Если в задаче требуется
определить моду – находим экстремум
(максимум) плотности вероятности f(x).

Коэффициент
вариации
непрерывной случайной величины
вычисляется по той же формуле, что и для
дискретной с.в.:

V(X) = |σ(X)/M(X)| · 100%

Асимметрия
(коэффициент асимметрии) случайной
величины As(X) – величина, характеризующая
степень асимметрии распределения
относительно математического ожидания.
Коэффициент асимметрии непрерывной
случайной величины вычисляется по
формуле:

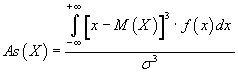
Если
коэффициент асимметрии отрицателен,
то либо большая часть значений случайной
величины, либо мода находятся левее
математического ожидания, и наоборот,
если As(X)>0, то правее.

Эксцесс
(коэффициент эксцесса) случайной величины
Ex(X) – величина, характеризующая степень
островершинности или плосковершинности
распределения. Коэффициент эксцесса
непрерывной случайной величины
вычисляется по формуле:

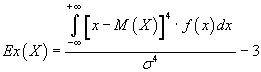
6. Примеры некоторых непрерывных распределений

6.1 Нормальное распределение

Нормальное
распределение имеет плотность вероятности
1/[σ√2π]·e^-(x-a)2/2σ2,
где a – математическое ожидание, σ –
среднее квадратическое отклонение.

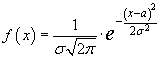
Значения
плотности нормального распределения
для конкретного числового значения x
можно вычислить в Excel с помощью формулы
=НОРМРАСП(x;a;σ;0). Если a = 0, σ = 1, то такое
нормальное распределение называется
стандартным. Значения
плотности стандартного нормального
распределения
можно посмотреть в таблице или вычислить
в Excel с помощью формулы =НОРМРАСП(x;0;
1;0)

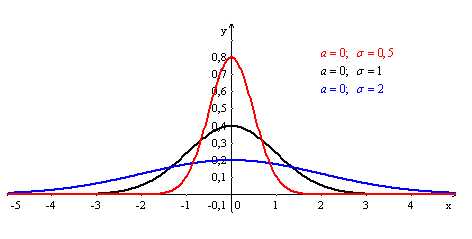
График нормального распределения
имеет куполообразную форму, он симметричен
относительно своего математического
ожидания, а на степень его островершинности
влияет величина среднего квадратичного
отклонения σ.

Асимметрия,
эксцесс, мода и медиана нормального
распределения равны:

As(X) = 0; Ex(X) = 0;
Mo(X) = a; Me(X) = a, где а – математическое
ожидание.

Интегральная функция
нормального распределения вероятностей:

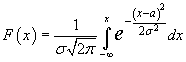
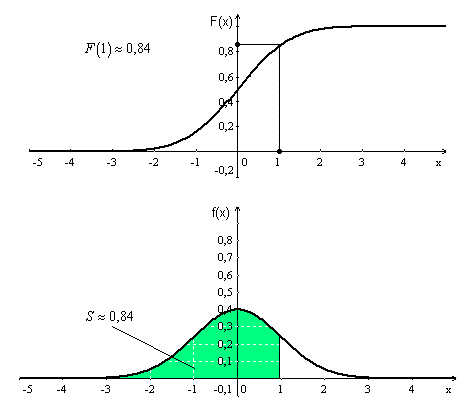
Интегральная
функция распределения вероятностей
показывает вероятность того, что с.в.
примет значение меньшее, чем x: F(x) = P(ξ <
x). Численно она равна площади криволинейной
трапеции, ограниченной сверху графиком
плотности вероятности, снизу осью OX, на
интервале от -∞ до x. Ниже дана иллюстрация.

Цепи Маркова

Формулы
и определения

Обобщая
этот пример, можно представить себе
“систему” со счетным числом возможных
“фазовых” состояний, которая с
течением дискретного времени t = 0, 1, …
случайно переходит из состояния в
состояние. Пусть ξ(t) есть ее положение
в момент t в результате цепочки случайных
переходов

ξ(0)
– ξ(1) – … – ξ(t) – … … (1)

Формально
обозначим все возможные состояния
целыми i = 0, ±1, … Предположим, что при
известном состоянии ξ(t) = k на следующем
шаге система переходит в состояние
ξ(t+1) = j с условной вероятностью

p_kj
= P(ξ(t+1) = j|ξ(t) = k) … (2)

независимо
от ее поведения в прошлом, точнее,
независимо от цепочки переходов (1) до
момента t:

P(ξ(t+1)
= j|ξ(0) = i, …, ξ(t) = k) = P(ξ(t+1) = j|ξ(t) = k) при всех
t, k, j … (3) – марковское
свойство.

Такую
вероятностную схему называют однородной
цепью Маркова со счетным числом состояний
– ее однородность состоит в том, что
определенные в (2) переходные
вероятности p_kj,
∑_j
p_kj
= 1, k = 0, ±1, …, не зависят от времени, т.е.
P(ξ(t+1) = j|ξ(t) = k) = P_ij –
матрица вероятностей
перехода за один шаг
не зависит от n. Ясно, что P_ij
– квадратная матрица с неотрицательными
элементами и единичными суммами по
строкам. Такая матрица (конечная или
бесконечная) называется стохастической
матрицей. Любая стохастическая матрица
может служить матрицей переходных
вероятностей.

Неравенство
Чебышёва

Формулировка

Для
случайной величины ξ = ξ(ω) с конечными
математическим ожиданием Eξ и дисперсией
Dξ неравенство
Чебышёва
имеет вид: для любого

вероятность
события

не
превосходит

,
или

В
таком виде неравенство было независимым
образом открыто И.Бьенеме
(I.Bienayme)
(1853)
и П.Л.Чебьшёвым
(1867),используется
при отсеве грубых погрешностей. В
современной литературе это неравенство
чаще называют неравенством
Чебышёва,
возможно и потому, что с именем П.Л.Чебышёва
связано использование его при
доказательстве обобщения закона больших
чисел (теоремы
Чебышёва).

[редактировать]

Об
однотипных неравенствах

Неравенство
Чебышёва
служит представителем класса однотипных
неравенств, простейшее из которых
утверждает, что для неотрицательной
случайной величины ξ с конечным
математическим ожиданием Eξ

Это
неравенство иногда называется неравенством
Маркова,
из него вытекают неравенства для
произвольных случайных величин, зависящие
от моментов:

(при
r
= 2 — само неравенство
Чебышёва),
а также ещё более общее неравенство

для
неотрицательной четной неубывающей
при положительных значениях x
функции f(x).
Последнее неравенство указывает путь
получения новых неравенств того же
типа, например экспоненциального
неравенства:

Обычно
все эти неравенства относят к чебышёвскому
типу и даже называют неравенствами
Чебышёва.

Теорема
Ляпунова.

   Часто приходится иметь
дело с такими случайными величинами,
которые являются суммами большого числа
независимых случайных величин. При
некоторых весьма общих условиях
оказывается, что эта сумма имеет
распределение, близкое к нормальному,
хотя каждое из слагаемых может не
подчиняться нормальному закону
распределения вероятностей. Эти условия
были найдены Ляпуновым * и составляют
содержание теоремы, названной его
именем.

   Приведем без
доказательства только следствие из
теоремы Ляпунова.

   Пусть

последовательность
попарно независимых. случайных величин
с математическими ожиданиями

и
дисперсиями

,
причем эти величины обладают следующими
двумя свойствами:

   1)
Cуществует
такое число L, что для любого i имеет
место неравенство

,
т, е. все значения случайных величин,
как говорят, равномерно ограничены,
относительно математических ожиданий;

   2)
Cумма


неограниченно
растет при

.

   Тогда при достаточно
большом n сумма

имеет
распределение, близкое к нормальному.

   Пусть a и

–
математическое ожидание и дисперсия
случайной величины

.
Тогда

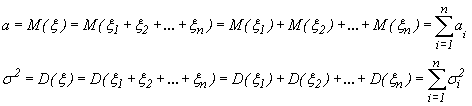
   Так
как по следствию из теоремы Ляпунова
случайная величина

для
больших значений n имеет распределение,
близкое к нормальному, то согласно
формуле (32)
имеет место соотношение

(56)

   где
Ф(х) – интеграл вероятностей.

Нулевая
гипотеза
– это
основное
проверяемое предположение, которое
обычно формулируется как отсутствие
различий, отсутствие влияние фактора,
отсутствие эффекта, равенство нулю
значений выборочных характеристик и
т.п. Примером нулевой гипотезы в педагогике
является утверждение о том, что различие
в результатах выполнения двумя группами
учащихся одной и той же контрольной
работы вызвано лишь случайными причинами.

Другое
проверяемое предположение (не всегда
строго противоположное или обратное
первому) называется конкурирующей
или
альтернативной
гипотезой.
Так, для упомянутого выше примера
гипотезы Н₀
в педагогике одна из возможных альтернатив
Н₁

будет определена как: уровни выполнения
работы в двух группах учащихся различны
и это различие определяется влиянием
неслучайных факторов, например, тех или
других методов обучения.

Выдвинутая
гипотеза может быть правильной или
неправильной, поэ­тому возникает
необходимость проверить ее. Так как
проверку произво­дят статистическими
методами, то данная проверка называется
статистической.

При
проверке статистических гипотез возможны
ошибки
(ошибочные
суждения) двух видов:

— можно
отвергнуть нулевую гипотезу, когда она
на самом деле верна (так называемая
ошибка
первого рода);

— можно
принять нулевую гипотезу, когда она на
самом деле не верна (так называемая
ошибка
второго рода).

Ошибка,
состоящая в принятии нулевой гипотезы,
когда она ложна, качественно отличается
от ошибки, состоящей в отвержении
гипотезы, когда она истинна. Эта разница
очень существенна вследствие того, что
различна значимость этих ошибок.
Проиллюстрируем вышесказанное на
следующем примере.[2]

СЛУЧАЙНЫЕ
ВЕЛИЧИНЫ

   Понятие случайной
величины является основным в теории
вероятностей и ее приложениях. Случайными
величинами, например, являются число
выпавших очков при однократном бросании
игральной кости, число распавшихся
атомов радия за данный промежуток
времени, число вызовов на телефонной
станции за некоторый промежуток времени,
отклонение от номинала некоторого
размера детали при правильно налаженном
технологическом процессе и т. д.

   Таким
образом, случайной
величиной
называется переменная величина, которая
в результате опыта может принимать то
или иное числовое значение.

   В
дальнейшем мы рассмотрим два типа
случайных величин — дискретные и
непрерывные.

   1.
Дискретные случайные величины.

   Рассмотрим случайную
величину *

,
возможные значения которой образуют
конечную или бесконечную последовательность
чисел x1,
x2,
…, xn,
… .
Пусть задана функция p(x),
значение которой в каждой точке x=xi
(i=1,2, …)
равно вероятности того, что величина

примет
значение xi

(16)

   Такая
случайная величина

называется
дискретной
(прерывной).
Функция р(х)
называется законом
распределения вероятностей случайной
величины,
или кратко, законом
распределения.
Эта функция определена в точках
последовательности x1,
x2,
…, xn,
… .
Так как в каждом из испытаний случайная
величина

принимает
всегда какое-либо значение из области
ее изменения, то

   Пример
1.
Случайная величина

—
число очков, выпадающих при однократном
бросании игральной кости. Возможные
значения

—
числа 1, 2, 3, 4, 5 и 6. При этом вероятность
того, что

примет
любое из этих значений, одна и та же и
равна 1/6. Какой будет закон распределения
? (Решение)

   Пример
2.
Пусть случайная величина

–
число наступления события A
при одном испытании, причем P(A)=p.
Множество возможных значений

состоит
из 2-х чисел 0 и 1:

=0,
если событие A
не произошло, и

=1,
если событие A
произошло. Таким образом,

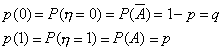
   Предположим,
что производится n
независимых испытаний, в результате
каждого из которых может наступить или
не наступить событие A.
Пусть вероятность наступления события
A
при каждом испытании равна p.
Рассмотрим случайную величину

—
число наступлений события A
при n
независимых испытаниях. Область изменения

состоит
из всех целых чисел от 0
до n
включительно. Закон распределения
вероятностей р(m)
определяется формулой Бернулли (13′):

   Закон
распределения вероятностей по формуле
Бернулли часто называют биномиальным,
так как Pn(m)
представляет собой m-й
член разложения бинома

.

   Пусть случайная величина

может
принимать любое целое неотрицательное
значение, причем

(17)

   где

—
некоторая положительная постоянная. В
этом случае говорят, что случайная
величина

распределена
по закону
Пуассона,
Заметим, что при k=0
следует положить 0!=1.

   Как мы знаем, при больших
значениях числа n
независимых испытаний вероятность
Pn(m)
наступления m
раз события A
удобнее находить не по формуле Бернулли,
а по формуле Лапласа [см.
формулу (15)].
Однако последняя дает большие погрешности
при малой вероятности р
появления события А
в одном испытании. В этом случае для
подсчета вероятности Pn(m)
удобно пользоваться формулой Пуассона,
в которой следует положить

.

   Формулу Пуассона можно
получить как предельный случай формулы
Бернулли при неограниченном увеличении
числа испытаний n
и при стремлении к нулю вероятности

.

   Пример
3.
На завод прибыла партия деталей в
количестве 1000 шт. Вероятность того, что
деталь окажется бракованной, равна
0,001. Какова вероятность того, что среди
прибывших деталей будет 5 бракованных?
(Решение)

   Распределение Пуассона
часто встречается и в других задачах.
Так, например, если телефонистка в
среднем за один час получает N
вызовов, то, как можно показать, вероятность
Р(k)
того, что в течение одной минуты она
получит k
вызовов, выражается формулой Пуассона,
если положить

.

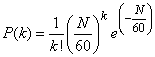
   Если
возможные значения случайной величины

образуют
конечную последовательность x1,
x2,
…, xn,
то закон распределения вероятностей
случайной величины задают в виде
следующей таблицы, в которой

и

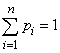
Значения	x1	x2	…	xn
Вероятности p(xi)	p1	p2	…	pn

   
Эту таблицу называют рядом
распределения
случайной величины

.
Наглядно функцию р(х)
можно изобразить в виде графика. Для
этого возьмем прямоугольную систему
координат на плоскости.

   По
горизонтальной оси будем откладывать
возможные значения случайной величины

,
а по вертикальной оси – значения функции

.
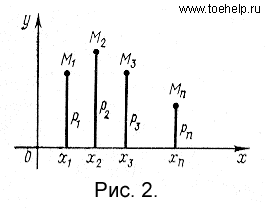
График функции р(х)
изображен на рис. 2. Если соединить точки
этого графика прямолинейными отрезками,
то получится фигура, которая называется
многоугольником
распределения.

   Пример
4.
Пусть событие А
— появление одного очка при бросании
игральной кости; Р(A)=1/6.
Рассмотрим случайную величину

—
число наступлений события А
при десяти бросаниях игральной кости.
Значения функции р(х)
(закона распределения) приведены в
следующей таблице:

 

Значения	0	1	2	3	4	5	6	7	8	9	10
Вероятности p(xi)	0,162	0,323	0,291	0,155	0,054	0,013	0,002	0	0	0	0

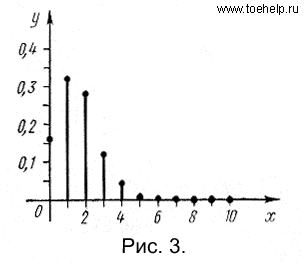
   Вероятности
p(xi)
вычислены по формуле Бернулли при n=10.
Для x>6
они практически равны нулю. График
функции p(x) изображен на рис. 3.

Нормальное
распределение.

   Говорят, что случайная
величина

нормально
распределена
или подчиняется закону
распределения Гаусса,
если ее плотность распределения

имеет
вид

(28)

   где
a
– любое действительное число, а

>0.
Смысл параметров a
и

будет
установлен в
дальнейшем (см.
§4, п. 2).
Исходя из связи между плотностью
распределения

и
функцией распределения F(x)
[см.
формулу (22)],
имеем

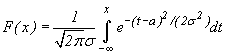
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Материал из MachineLearning.

Перейти к: навигация, поиск

Коэффицие́нт асимметри́и (skewness) — числовая характеризующая степени несимметричности распределения данной случайной величины.

Определение

Пусть задана случайная величина , такая что .

Коэффициент асимметрии распределения случайной величины определяется формулой:

где

— третий центральный момент случайной величины ;

— стандартное отклонение случайной величины ;

— дисперсия или второй центральный момент случайной величины ;

Если плотность распределения симметрична, то .

Если левый хвост распределения тяжелее, то .

Если правый хвост распределения тяжелее, то .

Иногда вместо используется обозначение .

Выборочный коэффициент асимметрии

Пусть задана случайная выборка наблюдений .

Выборочный коэффициент асимметрии определяется формулой:

где

— выборочный центральный момент k-го порядка;

— несмещённая оценка центрального момента второго порядка;

— несмещённая оценка центрального момента третьего порядка.

Проверка гипотезы симметричности

Выборочный коэффициент асимметрии используется для проверки распределения на симметричность, а также для грубой предварительной проверки на нормальность.
Он позволяет отвергнуть, но не позволяет принять гипотезу нормальности.

Проверка основана на формуле для дисперсии выборочного коэффициента асимметрии:

Распределение довольно быстро стремится к нормальному.

Литература

1. Вероятность и математическая статистика: Энциклопедия / Под ред. Ю.В.Прохорова. — М.: Большая российская энциклопедия, 2003. — 912 с.
2. Кобзарь А. И. Прикладная математическая статистика. — М.: Физматлит, 2006.

Ссылки

• Моменты случайной величины.
• Статистика (функция выборки).
• Коэффициент эксцесса.
• Коэффициент асимметрии (Википедия).
• Skewness (Wikipedia).

В прикладных задачах, например в математической ста­тистике, при теоретическом изучении Эмпирических распре­делений, отличающихся от нормального распределения, воз­никает необходимость количественных оценок этих различий. Для этой цели введены специальные безразмерные характеристики.

Определение 6. Асимметрией теоретического распределения называется отношение центрального момента третьего поряд­ка к кубу среднего квадратического отклонения:

Определение 7. Эксцессом теоретического распределения на­зывается величина, определяемая равенством

Где μ4 — центральный момент четвертого порядка.

Для нормального распределения As = Еk = 0. При отклоне­нии от нормального распределения асимметрия положительна, если “длинная” и более пологая часть кривой распределения расположена справа от точки на оси абсцисс, соответствую­щей моде; если эта часть кривой расположена слева от моды, то асимметрия отрицательна (рис. 18.7, А, б).

Эксцесс характеризует “крутизну” подъема кривой распре­деления по сравнению с нормальной кривой: если эксцесс поло­жителен, то кривая имеет более высокую и острую вершину; в случае отрицательного эксцесса сравниваемая кривая имеет более низкую и пологую вершину (рис. 18.7, В).

Следует иметь в виду, что при использовании указанных характеристик сравнения опорными являются предположения об одинаковых величинах математического ожидания и дис­персии для нормального и теоретического распределений.

Пример 5. Пусть дискретная случайная величина Х задана законом следующего распределения:

Найти асимметрию и эксцесс теоретического распределения.

Решение. Найдем сначала математическое ожидание слу­чайной величины:

Затем вычисляем начальные и центральные моменты 2, 3 и 4-го порядков и среднее квадратическое отклонение (см. фор­мулы (18.27)-(18.31)):

Теперь по формулам (18.45) и (18.46) находим искомые вели­чины:

В данном случае “длинная” часть кривой распределения рас­положена справа от моды, причем сама кривая является не­сколько более островершинной, чем нормальная кривая с теми же величинами математического ожидания и дисперсии.

< Предыдущая		Следующая >