Имеются условные данные об объемах потребления электроэнергии yt жителями региона за 16 кварталов.
| t | yt | t | yt |
|---|---|---|---|
| 1 | 5,6 | 9 | 8,2 |
| 2 | 4,7 | 10 | 5,6 |
| 3 | 5,2 | 11 | 6,4 |
| 4 | 9,1 | 12 | 10,8 |
| 5 | 7,0 | 13 | 9,1 |
| 6 | 5,1 | 14 | 6,7 |
| 7 | 6,0 | 15 | 7,5 |
| 8 | 10,2 | 16 | 11,3 |
Требуется:
1. Построить автокорреляционную функцию и сделать вывод о наличии сезонных колебаний.
2. Построить аддитивную модель временного ряда.
3. Сделать прогноз на 2 квартала вперед.
Решение:
1. Рассчитаем коэффициент автокорреляции уровней ряда первого порядка, то есть между соседними уровнями ряда yt и yt-1 (лаг = 1), и измерим тесноту связи между объёмом потребления электроэнергии в текущем и предыдущем году.
Для этого составим таблицу расчётных данных.
Расчёт коэффициента автокорреляции первого порядка для временного ряда объемов потребления электроэнергии жителями региона:
| t | yt | yt-1 |  |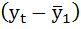
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|
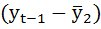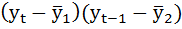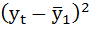| 1 | 5,6 | – | – | – | – | – | – |
| 2 | 4,7 | 5,6 | -2,827 | -1,547 | 4,371911 | 7,990044 | 2,392178 |
| 3 | 5,2 | 4,7 | -2,327 | -2,447 | 5,692578 | 5,413378 | 5,986178 |
| 4 | 9,1 | 5,2 | 1,573 | -1,947 | -3,06276 | 2,475378 | 3,789511 |
| 5 | 7 | 9,1 | -0,527 | 1,953 | -1,02876 | 0,277378 | 3,815511 |
| 6 | 5,1 | 7 | -2,427 | -0,147 | 0,355911 | 5,888711 | 0,021511 |
| 7 | 6 | 5,1 | -1,527 | -2,047 | 3,124578 | 2,330711 | 4,188844 |
| 8 | 10,2 | 6 | 2,673 | -1,147 | -3,06542 | 7,146711 | 1,314844 |
| 9 | 8,2 | 10,2 | 0,673 | 3,053 | 2,055911 | 0,453378 | 9,322844 |
| 10 | 5,6 | 8,2 | -1,927 | 1,053 | -2,02942 | 3,712044 | 1,109511 |
| 11 | 6,4 | 5,6 | -1,127 | -1,547 | 1,742578 | 1,269378 | 2,392178 |
| 12 | 10,8 | 6,4 | 3,273 | -0,747 | -2,44409 | 10,71471 | 0,557511 |
| 13 | 9,1 | 10,8 | 1,573 | 3,653 | 5,747911 | 2,475378 | 13,34684 |
| 14 | 6,7 | 9,1 | -0,827 | 1,953 | -1,61476 | 0,683378 | 3,815511 |
| 15 | 7,5 | 6,7 | -0,027 | -0,447 | 0,011911 | 0,000711 | 0,199511 |
| 16 | 11,3 | 7,5 | 3,773 | 0,353 | 1,333244 | 14,23804 | 0,124844 |
| Итого | 112,9 | 107,2 | – | – | 11,19133 | 65,06933 | 52,37733 |
Рассчитаем выборочные средние:
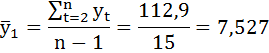
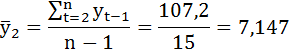
Определим коэффициент автокорреляции уровней ряда первого порядка:
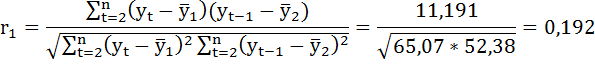
Полученное значение свидетельствует об очень слабой зависимости текущих уровней ряда от непосредственно им предшествующих уровней.
Рассчитаем коэффициент автокорреляции 2-го порядка.
| t | yt | yt-2 |  |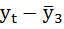
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|
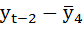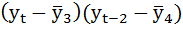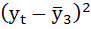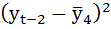| 1 | 5,6 | – | – | – | – | – | – |
| 2 | 4,7 | – | – | – | – | – | – |
| 3 | 5,2 | 5,6 | -2,529 | -1,521 | 3,847041 | 6,393673 | 2,314745 |
| 4 | 9,1 | 4,7 | 1,371 | -2,421 | -3,32082 | 1,880816 | 5,863316 |
| 5 | 7 | 5,2 | -0,729 | -1,921 | 1,399898 | 0,530816 | 3,691888 |
| 6 | 5,1 | 9,1 | -2,629 | 1,979 | -5,20082 | 6,909388 | 3,914745 |
| 7 | 6 | 7 | -1,729 | -0,121 | 0,209898 | 2,987959 | 0,014745 |
| 8 | 10,2 | 5,1 | 2,471 | -2,021 | -4,99582 | 6,107959 | 4,086173 |
| 9 | 8,2 | 6 | 0,471 | -1,121 | -0,52867 | 0,222245 | 1,257602 |
| 10 | 5,6 | 10,2 | -2,129 | 3,079 | -6,55296 | 4,530816 | 9,477602 |
| 11 | 6,4 | 8,2 | -1,329 | 1,079 | -1,43296 | 1,765102 | 1,163316 |
| 12 | 10,8 | 5,6 | 3,071 | -1,521 | -4,67296 | 9,433673 | 2,314745 |
| 13 | 9,1 | 6,4 | 1,371 | -0,721 | -0,98939 | 1,880816 | 0,520459 |
| 14 | 6,7 | 10,8 | -1,029 | 3,679 | -3,78367 | 1,057959 | 13,53189 |
| 15 | 7,5 | 9,1 | -0,229 | 1,979 | -0,45224 | 0,052245 | 3,914745 |
| 16 | 11,3 | 6,7 | 3,571 | -0,421 | -1,5051 | 12,7551 | 0,177602 |
| Итого | 108,2 | 99,7 | – | – | -27,9786 | 56,50857 | 52,24357 |
Выборочные средние:
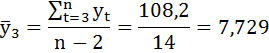
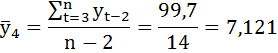
Коэффициент автокорреляции уровней ряда первого порядка:
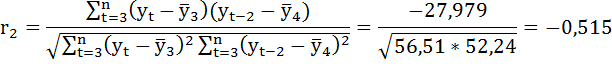
Продолжив расчёты аналогичным образом, получим автокорреляционную функцию этого ряда. Её значения приведены в таблице:
| Лаг | Коэффициент автокорреляции уровней |
|---|---|
| 1 | 0,1917 |
| 2 | -0,5149 |
| 3 | 0,1272 |
| 4 | 0,9862 |
| 5 | 0,1448 |
| 6 | -0,6487 |
| 7 | -0,00647 |
| 8 | 0,9632 |
Анализ значений автокорреляционной функции позволяет сделать вывод о наличии в изучаемом временном ряде линейной тенденции и сезонных колебаний периодичностью в 4 квартала.
2. Построим аддитивную модель временного ряда.
Общий вид аддитивной модели следующий:
Y = T + S + E
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (T), сезонной (S) и случайной (E) компонент.
Рассчитаем компоненты аддитивной модели временного ряда.
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:
1) просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени и определим условные годовые объёмы потребления электроэнергии (гр. 3);
2) разделив полученные суммы на 4, найдём скользящие средние (гр. 4). Отметим, что полученные таким образом выравненные значения уже не содержат сезонной компоненты;
3) приведём эти значения в соответствие с фактическими моментами времени, для чего найдём средние значения из двух последовательных скользящих средних – центрированные скользящие средние (гр.5).
Расчёт оценок сезонной компоненты в аддитивной модели
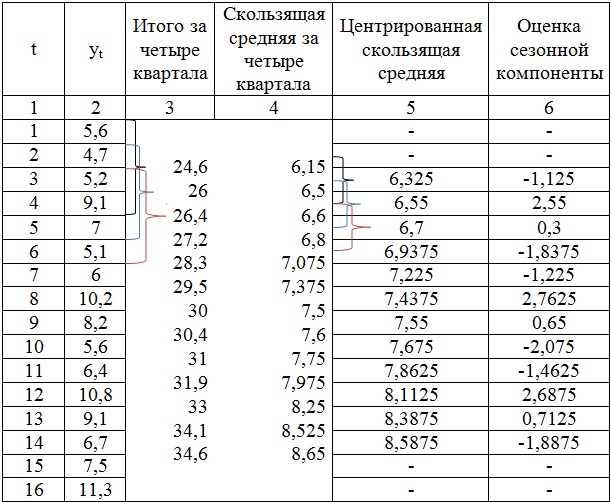
Шаг 2. Рассчитаем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними (гр. 6). Используем эти оценки для расчета значений сезонной компоненты S. Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты Si. В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.
Расчёт значений сезонной компоненты:
| Показатели | Год | № квартала, i | |||
|---|---|---|---|---|---|
| I | II | III | IV | ||
| 1 | – | – | -1,125 | 2,55 | |
| 2 | 0,3 | -1,8375 | -1,225 | 2,7625 | |
| 3 | 0,65 | -2,075 | -1,4625 | 2,6875 | |
| 4 | 0,7125 | -1,8875 | – | – | |
| Итого за i-й квартал | 1,6625 | -5,8 | -3,8125 | 8 | |
Средняя оценка сезонной компоненты для i-го квартала,  |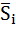
0,554167 | -1,93333 | -1,27083 | 2,666667 | |
| Скорректированная сезонная компонента, Si | 0,55 | -1,9375 | -1,275 | 2,6625 |
Для данной модели имеем:
0,554167 + ( -1,93333) + (-1,27083) + 2,666667 = 0,016667
Определим корректирующий коэффициент:
k = 0,016667 / 4 = 0,004167
Рассчитаем скорректированные значения сезонной компоненты как разность между её средней оценкой и корректирующим коэффициентом k:
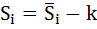
Проверим условие равенство нулю суммы значений сезонной компоненты:
0,55 + (-1,9375) + (-1,275) + 2,6625 = 0
Таким образом, получены следующие значения сезонной компоненты:
I квартал: S1 = 0,55;
II квартал: S2 = -1,9375;
III квартал: S3 = -1,275;
IV квартал: S4 = 2,6625.
Занесём полученные значения в таблицу для соответствующих кварталов каждого года (гр. 3).
| t | yt | Si | T + E = yt – Si | T | T + S | E = yt – (T + S) | E2 |
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 5,6 | 0,55 | 5,05 | 5,8588235 | 6,408824 | -0,80882 | 0,654196 |
| 2 | 4,7 | -1,9375 | 6,6375 | 6,0651471 | 4,127647 | 0,572353 | 0,327588 |
| 3 | 5,2 | -1,275 | 6,475 | 6,2714706 | 4,996471 | 0,203529 | 0,041424 |
| 4 | 9,1 | 2,6625 | 6,4375 | 6,4777941 | 9,140294 | -0,04029 | 0,001624 |
| 5 | 7 | 0,55 | 6,45 | 6,6841176 | 7,234118 | -0,23412 | 0,054811 |
| 6 | 5,1 | -1,9375 | 7,0375 | 6,8904412 | 4,952941 | 0,147059 | 0,021626 |
| 7 | 6 | -1,275 | 7,275 | 7,0967647 | 5,821765 | 0,178235 | 0,031768 |
| 8 | 10,2 | 2,6625 | 7,5375 | 7,3030882 | 9,965588 | 0,234412 | 0,054949 |
| 9 | 8,2 | 0,55 | 7,65 | 7,5094118 | 8,059412 | 0,140588 | 0,019765 |
| 10 | 5,6 | -1,9375 | 7,5375 | 7,7157353 | 5,778235 | -0,17824 | 0,031768 |
| 11 | 6,4 | -1,275 | 7,675 | 7,9220588 | 6,647059 | -0,24706 | 0,061038 |
| 12 | 10,8 | 2,6625 | 8,1375 | 8,1283824 | 10,79088 | 0,009118 | 8,31E-05 |
| 13 | 9,1 | 0,55 | 8,55 | 8,3347059 | 8,884706 | 0,215294 | 0,046352 |
| 14 | 6,7 | -1,9375 | 8,6375 | 8,5410294 | 6,603529 | 0,096471 | 0,009307 |
| 15 | 7,5 | -1,275 | 8,775 | 8,7473529 | 7,472353 | 0,027647 | 0,000764 |
| 16 | 11,3 | 2,6625 | 8,6375 | 8,9536765 | 11,61618 | -0,31618 | 0,099968 |
Шаг 3. Исключим влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины T + E = Y – S (гр. 4 табл.). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.
Шаг 4. Определим компоненту T данной модели. Для этого проведем аналитическое выравнивание ряда (T + E) с помощью линейного тренда. Результаты аналитического выравнивания следующие:
T = 5,6525 + 0,206 * t
Подставляя в это уравнение значения t = 1,…,16, найдем уровни T для каждого момента времени (гр. 5 табл.).
Шаг 5. Найдем значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к уровням T значения сезонной компоненты для соответствующих кварталов (гр. 6 табл.).
Для оценки качества построенной модели применим сумму квадратов полученных абсолютных ошибок.
Коэффициент детерминации.
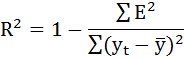
| t | yt | Е2 |  |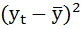
|---|---|---|---|
| 1 | 5,6 | 0,654196 | 3,262539 |
| 2 | 4,7 | 0,327588 | 7,323789 |
| 3 | 5,2 | 0,041424 | 4,867539 |
| 4 | 9,1 | 0,001624 | 2,868789 |
| 5 | 7 | 0,054811 | 0,165039 |
| 6 | 5,1 | 0,021626 | 5,318789 |
| 7 | 6 | 0,031768 | 1,977539 |
| 8 | 10,2 | 0,054949 | 7,805039 |
| 9 | 8,2 | 0,019765 | 0,630039 |
| 10 | 5,6 | 0,031768 | 3,262539 |
| 11 | 6,4 | 0,061038 | 1,012539 |
| 12 | 10,8 | 8,31E-05 | 11,51754 |
| 13 | 9,1 | 0,046352 | 2,868789 |
| 14 | 6,7 | 0,009307 | 0,498789 |
| 15 | 7,5 | 0,000764 | 0,008789 |
| 16 | 11,3 | 0,099968 | 15,16129 |
| Итого | 118,5 | 1,457029 | 68,549 |
Рассчитаем коэффициент детерминации.
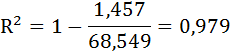
Следовательно, можно сказать, что аддитивная модель объясняет 97,9% общей вариации уровней временного ряда.
Далее необходимо провести проверку адекватности модели данным наблюдения. Воспользуемся F-критерием Фишера:
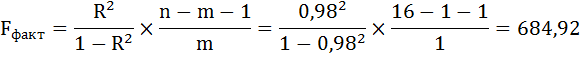
где m – количество факторов в уравнении тренда (m=1).
Табличное значение F-критерия Фишера при уровне значимости α = 0,05,
k1 = m = 1, k2 = n – m – 1 = 14,
Fтабл = 4,60
Поскольку F > Fтабл, то уравнение статистически значимо, надёжно.
Шаг 6. Прогнозирование по аддитивной модели.
Прогнозное значение Ft уровня временного ряда в аддитивной модели есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда:
T = 5,6525 + 0,206 × t
Прогноз на 1 период:
T17 = 5,6525 + 0,206 × 17 = 9,16
Значение сезонного компонента за соответствующий период равно:
S1 = 0,55
Таким образом,
F17 = T17 + S1 = 9,16 + 0,55 = 9,71
Прогноз на 2 период:
T18 = 5,6525 + 0,206 × 18 = 9,366
Значение сезонной компоненты за соответствующий период равно:
S2 = – 1,9375
Таким образом, прогнозное значение на 2 квартала вперёд составит:
F18 = T18 + S2 = 9,366 – 1,9375 = 7,429
§ 5.1 Основные элементы временного ряда
Временной
ряд (ряд динамики) –
это совокупность значений какого-либо
показателя за несколько последовательных
моментов или периодов времени. Каждый
уровень временного ряда формируется
под воздействием большого числа факторов,
которые условно можно подразделить на
три группы:
-
факторы, формирующие
тенденцию ряда; -
факторы, формирующие
циклические колебания ряда; -
случайные факторы.
При различных
сочетаниях в изучаемом явлении или
процессе этих факторов зависимость
уровней ряда от времени может принимать
различные формы.
В
о-первых,
большинство временных рядов экономических
показателей имеют тенденцию, характеризующую
совокупное долговременное воздействие
множества факторов на динамику изучаемого
показателя. Очевидно, что эти факторы,
взятые в отдельности, могут оказывать
разнонаправленное воздействие на
исследуемый показатель. Однако в
совокупности они формируют его
возрастающую или убывающую тенденцию.
В
о-вторых,
изучаемый показатель может быть подвержен
циклическим колебаниям. Эти колебания
могут носить сезонный характер, поскольку
экономическая деятельность ряда отраслей
экономики зависит от времени года
(например, цены на сельскохозяйственную
продукцию в летний период выше, чем в
зимний; уровень безработицы в курортных
городах в зимний период выше по сравнению
с летним). При наличии больших массивов
данных за длительные промежутки времени
можно выявить циклические колебания,
связанные с общей динамикой конъюнктуры
рынка, а также с фазой бизнес-цикла, в
которой н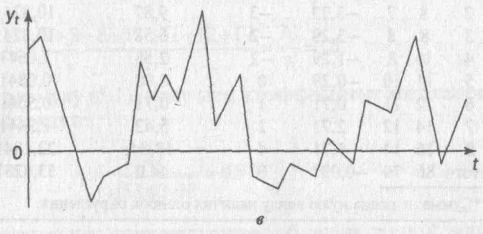
аходится
экономика страны.
Некоторые
временные ряды не содержат тенденции
и циклической компоненты, а каждый
следующий их уровень образуется как
сумма среднего уровня ряда и некоторой
(положительной или отрицательной)
случайной компоненты.
Очевидно, что
реальные данные не следуют целиком и
полностью из каких-либо описанных выше
моделей. Чаще всего они содержат все
три компоненты. Каждый их уровень
формируется под воздействием тенденции,
сезонных колебаний и случайной компоненты.
В
большинстве случаев фактический уровень
временного ряда можно представить как
сумму или произведение трендовой,
циклической и случайной компонент.
Модель, в которой временной ряд представлен
как сумма перечисленных компонент,
называется аддитивной
моделью
временного ряда. Модель, в которой
временной ряд представлен как произведение
перечисленных компонент, называется
мультипликативной
моделью
временного ряда. Основная задача
отдельного временного ряда – выявление
и придание количественного выражения
каждой из перечисленных выше компонент
с тем, чтобы использовать полученную
информацию для прогнозирования будущих
значений ряда или при построении моделей
взаимосвязи двух или более временных
рядов.
§ 5.2. Автокорреляция уровней временного ряда и выявление его структуры
При
наличии во временном ряде тенденции и
циклических колебаний значения каждого
последующего уровня ряда зависят от
предыдущих. Корреляционную зависимость
между последовательными уровнями
временного ряда называют автокорреляцией
уровней ряда.
Количественно ее
можно измерить с помощью линейного
коэффициента корреляции между уровнями
исходного временного ряда и уровнями
этого ряда, сдвинутыми на несколько
шагов во времени. Рассмотрим пример.
Пример
1.
Расчет
коэффициентов автокорреляции уровней
для временного ряда расходов на конечное
потребление.
Пусть
имеются следующие условные данные о
средних расходах на конечное потребление
(
,
д. е.) за 8 лет (таблица 1).
Таблица 1
Расчет
коэффициента автокорреляции первого
порядка для временного ряда расходов
на конечное потребление, д. е.
|
|
|
|
|
|
|
|
|
|
1 |
7 |
||||||
|
2 |
8 |
7 |
-3,29 |
-3,00 |
9,86 |
10,7959 |
9 |
|
3 |
8 |
8 |
-3,29 |
-2,00 |
6,57 |
10,7959 |
4 |
|
4 |
10 |
8 |
-1,29 |
-2,00 |
2,57 |
1,6531 |
4 |
|
5 |
11 |
10 |
-0,29 |
0,00 |
0,00 |
0,0816 |
0 |
|
6 |
12 |
11 |
0,71 |
1,00 |
0,71 |
0,5102 |
1 |
|
7 |
14 |
12 |
2,71 |
2,00 |
5,43 |
7,3673 |
4 |
|
8 |
16 |
14 |
4,71 |
4,00 |
18,86 |
22,2245 |
16 |
|
Итого |
86 |
70 |
0 |
0 |
44 |
53,4286 |
38 |
Разумно предположить,
что расходы на конечное потребление в
текущем году зависят от расходов на
конечное потребление предыдущих лет.
Определим
коэффициент корреляции между рядами
и
и измерим тесноту связи между расходами
на конечное потребление текущего и
предыдущего годов. Добавим в табл. 1
временной ряд
.
Одна из рабочих
формул для расчета коэффициента
корреляции имеет вид:
.
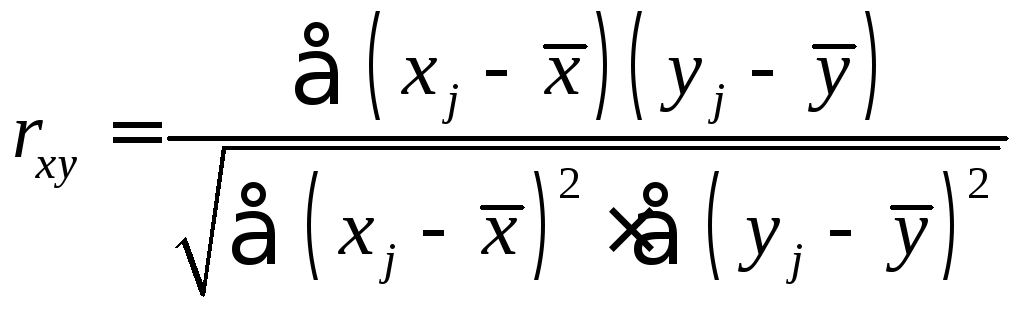В
качестве переменной
мы рассмотрим ряд
,
в качестве переменной
– ряд
.
Тогда приведенная выше формула примет
вид
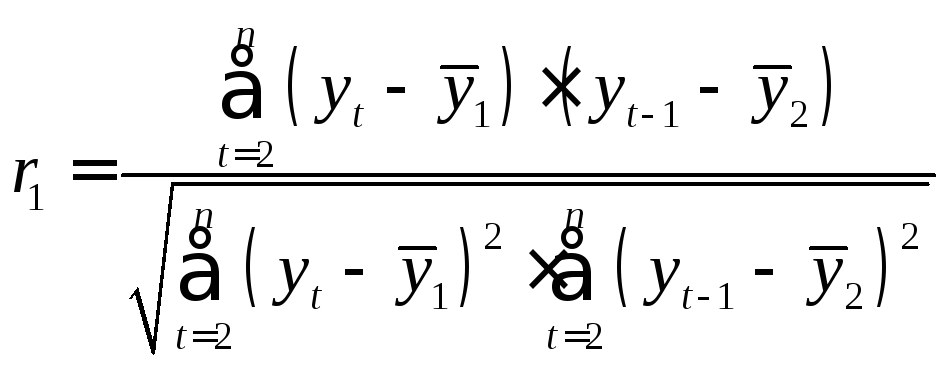
где
,
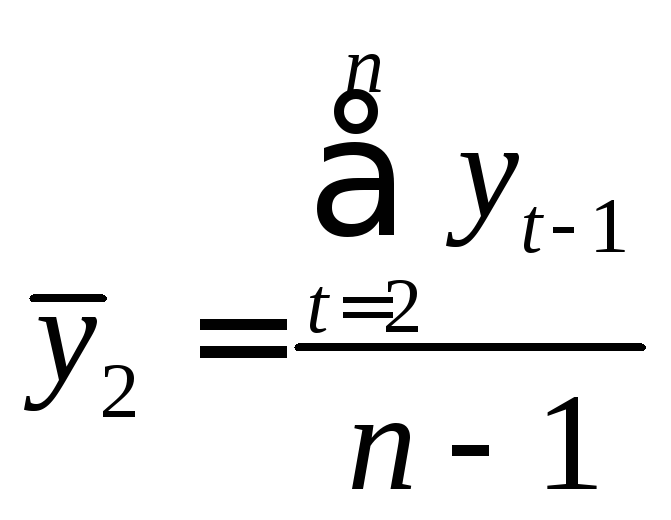
Эту
величину называют коэффициентом
автокорреляции уровней ряда первого
порядка,
так как он измеряет зависимость между
соседними уровнями ряда
и
,
т. е. при лаге 1.
Для
данных примера 1 соотношения (2) составят:
,
.
Используя
формулу (1), получаем коэффициент
автокорреляции первого порядка:
.
Полученное значение
свидетельствует об очень тесной
зависимости между расходами на конечное
потребление текущего и непосредственно
предшествующего годов и, следовательно,
о наличии во временном ряде расходов
на конечное потребление сильной линейной
тенденции.
Аналогично
можно определить коэффициенты
автокорреляции второго и более высоких
порядков. Так, коэффициент автокорреляции
второго порядка характеризует тесноту
связи между уровнями
и
и определяется по формуле
,
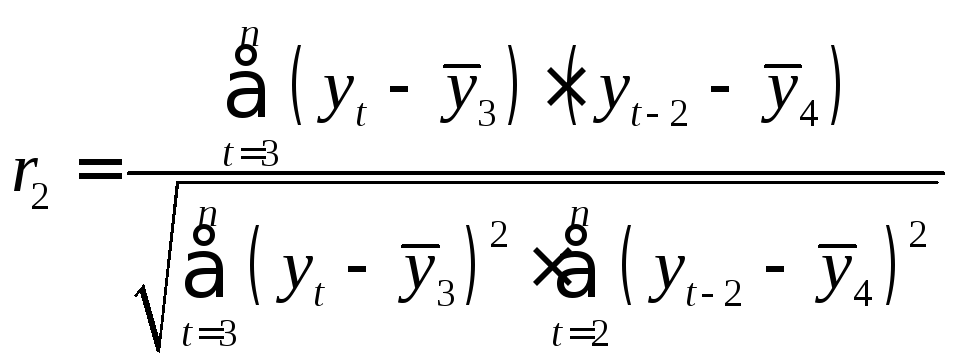где
,
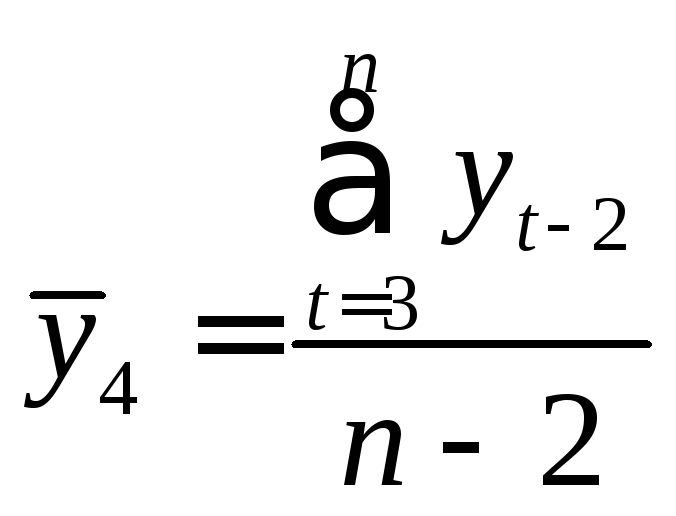
Для
данных из примера 1 получим:
,
Построим
табл. 2.
Полученные
результаты еще раз подтверждают вывод
о том, что ряд расходов на конечное
потребление содержит линейную тенденцию.
Число
периодов, по которым рассчитывается
коэффициент автокорреляции, называют
лагом.
С увеличением лага число пар значений,
по которым рассчитывается коэффициент
автокорреляции, уменьшается. Некоторые
авторы считают целесообразным для
обеспечения статистической достоверности
коэффициентов автокорреляции использовать
правило – максимальный лаг должен быть
не больше
.
Подставив полученные
значения в формулу (3), имеем:
.
Таблица
2
Расчет
коэффициента автокорреляции второго
порядка для временного ряда расходов
на конечное потребление, д. е.
|
|
|
|
|
|
|
|
|
|
1 |
7 |
||||||
|
2 |
8 |
||||||
|
3 |
8 |
7 |
-3,83 |
-2,33 |
8,9444 |
14,6944 |
5,4444 |
|
4 |
10 |
8 |
-1,83 |
-1,33 |
2,4444 |
3,3611 |
1,7778 |
|
5 |
11 |
8 |
-0,83 |
-1,33 |
1,1111 |
0,6944 |
1,7778 |
|
6 |
12 |
10 |
0,17 |
0,67 |
0,1111 |
0,0278 |
0,4444 |
|
7 |
14 |
11 |
2,17 |
1,67 |
3,6111 |
4,6944 |
2,7778 |
|
8 |
16 |
12 |
4,17 |
2,67 |
11,1111 |
17,3611 |
7,1111 |
|
Итого |
86 |
56 |
0 |
-4E-15 |
27,3333 |
40,8333 |
19,3333 |
Отметим
два
важных свойства коэффициента
автокорреляции:
Во-первых, он
строится по аналогии с линейным
коэффициентом корреляции и таким образом
характеризует тесноту только линейной
связи текущего и предыдущего уровней
ряда. Поэтому по коэффициенту автокорреляции
можно судить о наличии линейной (или
близкой к линейной) тенденции. Для
некоторых временных рядов, имеющих
сильную нелинейную тенденцию (например,
параболу второго порядка или экспоненту),
коэффициент автокорреляции уровней
исходного ряда может приближаться к
нулю.
Во-вторых, по знаку
коэффициента автокорреляции нельзя
делать вывод о возрастающей или убывающей
тенденции в уровнях ряда. Большинство
временных рядов экономических данных
содержит положительную автокорреляцию
уровней, однако при этом могут иметь
убывающую тенденцию.
Последовательность
коэффициентов автокорреляции уровней
первого, второго и т.д. порядков называют
автокорреляционной
функцией временного ряда.
График зависимости ее значений от
величины лага (порядка коэффициента
автокорреляции) называется коррелограммой.
Анализ
автокорреляционной функции и коррелограммы
позволяет определить лаг, при котором
автокорреляция наиболее высокая, а
следовательно, и лаг, при котором связь
между текущим и предыдущими уровнями
ряда наиболее тесная, т.е. при помощи
анализа автокорреляционной функции и
коррелограммы можно выявить структуру
ряда.
Если
наиболее высоким оказался коэффициент
автокорреляции первого порядка,
исследуемый ряд содержит только
тенденцию. Если наиболее высоким оказался
коэффициент автокорреляции порядка
,
ряд содержит циклические колебания с
периодичностью в
моментов времени. Если ни один из
коэффициентов автокорреляции не является
значимым, можно сделать одно из двух
предположений относительно структуры
этого ряда: либо ряд не содержит тенденции
и циклических, либо ряд содержит сильную
нелинейную тенденцию, для выявления
которой нужно провести дополнительный
анализ. Поэтому коэффициент автокорреляции
уровней и автокорреляционную функцию
целесообразно использовать для выявления
во временном ряде наличия или отсутствия
трендовой компоненты (
)
и циклической (сезонной) компоненты
(
).
Временной ряд
расходов на конечное потребление,
рассмотренный нами в примере 1, содержит
только тенденцию, так как коэффициенты
автокорреляции его уровней высокие.
Пример
2
Автокорреляционная
функция и выявление структуры ряда.
Пусть имеются
условные данные об объемах потребления
электроэнергии жителями региона за 16
кварталов (табл. 3).
Таблица 3
Потребление
электроэнергии жителями региона, млн.
кВт ч
|
|
|
|
|
|
|
|
1 |
6,0 |
||||
|
2 |
4,4 |
6,0 |
|||
|
3 |
5,0 |
4,4 |
6,0 |
||
|
4 |
9,0 |
5,0 |
4,4 |
6,0 |
|
|
5 |
7,2 |
9,0 |
5,0 |
4,4 |
6,0 |
|
6 |
4,8 |
7,2 |
9,0 |
5,0 |
4,4 |
|
7 |
6,0 |
4,8 |
7,2 |
9,0 |
5,0 |
|
8 |
10,0 |
6,0 |
4,8 |
7,2 |
9,0 |
|
9 |
8,0 |
10,0 |
6,0 |
4,8 |
7,2 |
|
10 |
5,6 |
8,0 |
10,0 |
6,0 |
4,8 |
|
11 |
6,4 |
5,6 |
8,0 |
10,0 |
6,0 |
|
12 |
11,0 |
6,4 |
5,6 |
8,0 |
10,0 |
|
13 |
9,0 |
11,0 |
6,4 |
5,6 |
8,0 |
|
14 |
6,6 |
9,0 |
11,0 |
6,4 |
5,6 |
|
15 |
7,0 |
6,6 |
9,0 |
11,0 |
6,4 |
|
16 |
10,8 |
7,0 |
6,6 |
9,0 |
11,0 |
Нанесем эти значения
на график:
Определим
коэффициент корреляции первого порядка.
Он составит:
.
Отметим, что расчет этого коэффициента
производился по 15, а не по 16 парам
наблюдений. Это значение свидетельствует
о слабой зависимости текущих уровней
ряда от непосредственно им предшествующих
уровней. Однако, как следует из графика,
структура этого ряда такова, что каждый
следующий уровень
зависит от уровня
и
в гораздо большей степени, чем от уровня
.
Рассчитаем коэффициенты автокорреляции
до порядка 8. Получим автокорреляционную
функцию этого ряда. Ее значения и
коррелограмма приведены в таблице 4.
Таблица 4
Коррелограмма
временного ряда потребления электроэнергии
|
Лаг |
Коэффициент |
Коррелограмма |
|
1 |
0,165154 |
** |
|
2 |
0,566873 |
******* |
|
3 |
0,113558 |
* |
|
4 |
0,983025 |
************ |
|
5 |
0,118711 |
* |
|
6 |
0,722046 |
********* |
|
7 |
0,003367 |
|
|
8 |
0,973848 |
************ |
Анализ
значений автокорреляционной функции
позволяет сделать вывод о наличии в
изучаемом временном ряде, во-первых,
линейной тенденции, во-вторых,
сезонных колебаний периодичностью в
четыре квартала. Данный вывод подтверждается
и графическим анализом структуры ряда
(см. график).
Аналогично,
если, например, при анализе временного
ряда наиболее высоким оказался коэффициент
автокорреляции уровней второго порядка,
ряд одержит циклические колебания в
два периода времени, т.е. имеет пилообразную
структуру.
Соседние файлы в папке 17-09-2014_11-49-43
- #
- #
- #
- #
- #
- #
При изучении развития явления во времени часто возникает необходимость оценить степень взаимосвязи в изменениях уровней 2-х или более рядов динамики различного содержания, но связанных между собой. Эта задача решается методами коррелирования:
- уровней ряда динамики
- отклонений фактических уровней от тренда
- последовательных разностей
Коррелирование уровней динамических рядов с применением парного коэффициента корреляции правильно показывает тесноту связи лишь в том случае, если в каждом из них отсутствует автокорреляция . Наличие зависимости между последующими и предшествующими уровнями динамического ряда в статистической литературе называют автокорреляцией .
Поэтому прежде, чем коррелировать ряды динамики по уровням, необходимо проверить каждый из рядов на наличие или отсутствие в них автокорреляции . Применение методов классической теории корреляции в динамических рядах связано с некоторыми особенностями. Прежде всего, это наличие для большинства динамических рядов зависимости последующих уровней от предыдущих.
Коэффициент автокорреляции вычисляется по непосредственным данным рядов динамики, когда фактические уровни одного ряда рассматриваются как значения факторного признака, а уровни этого же ряда со сдвигом на один период, принимаются в качестве результативного признака (этот сдвиг называется лагом). Коэффициент автокорреляции рассчитывается на основе формулы коэффициента корреляции для парной зависимости:
где:
- yt – фактические уровни ряда,
- yt+1– уровни того же ряда со сдвигом на 1 период (коэффициент автокорреляции первого порядка).
Примечание: во избежание путаницы, следует обратить внимание на порядок, по которому будет производиться сдвиг уровней, а именно, вниз или вверх. Соответственно и в формулах по разным источникам, ряд со сдвигом отображают либо так yt-1 либо yt+1
Формула для расчета коэффициента автокорреляции уровней ряда 1-го порядка:
Формула для расчета коэффициента автокорреляции уровней ряда 2-го порядка:
Для суждения о наличии или отсутствии автокорреляции в исследуемом ряду, фактическое значение коэффициента автокорреляции сопоставляют с табличным для 5% или 1% уровня значимости (т. е. по величине вероятности допустить ошибку при принятии гипотезы о независимости уровней ряда). Если расчетное значение меньше табличного, то гипотеза об отсутствии автокорреляции принимается и, наоборот, в противном случае, отвергается.
Последовательность коэффициентов автокорреляции 1, 2 и т.д. порядков называют автокорреляционной функцией временного ряда. График зависимости значений коэффициентов автокорреляции от величины лага (порядка коэффициента автокорреляции ) называют коррелограммой.
Анализ автокорреляционной функции и коррелограммы позволяет выявить структуру ряда, т. е. определить присутствие в ряде той или иной компоненты. Так, если наиболее высоким оказался коэффициент автокорреляции первого порядка, то исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка m, то ряд содержит циклические колебания с периодичностью в m моментов времени. Если же ни один из коэффициентов автокорреляции не является значимым, то можно сделать одно из двух предположений:
- либо ряд не содержит тенденции и циклических колебаний, а его уровень определяется только случайной компонентой;
- либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ.
Необходимо подчеркнуть, что линейные коэффициенты автокорреляции характеризуют тесноту только линейной связи текущего и предыдущих уровней ряда. Поэтому, по коэффициентам автокорреляции можно судить только о наличии или отсутствии линейной зависимости (или близкой к линейной). Для некоторых временных рядов, имеющих сильную нелинейную тенденцию (например, параболу второго порядка или экспоненту), коэффициент автокорреляции уровней исходного ряда может приближаться к нулю. По знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда. Большинство временных рядов экономических данных содержат положительную автокорреляцию уровней, однако, при этом могут иметь убывающую тенденцию.
Для проверки ряда на наличие нелинейной тенденции рекомендуется вычислить линейные коэффициенты автокорреляции для временного ряда, состоящего из логарифмов исходных уровней. Отличные от нуля значения коэффициентов автокорреляции будут свидетельствовать о наличии нелинейной тенденции.
Пример расчета:
Коэффициент автокорреляции 1 порядка
Расчет коэффициента автокорреляции 1-го порядка
Сдвигаем исходный ряд на 1 уровень. Следует учитывать, что с увеличением лага на единицу, число пар значений, по которым рассчитывается коэффициент автокорреляции , уменьшается на 1. Считается целесообразным для обеспечения статистической достоверности коэффициентов автокорреляции использовать правило: максимальный лаг не должен превышать n : 4 (n-число уровней ряда). Исходный ряд состоял из 8 уровней. Расчет производится не по 8, а по 7 парам наблюдений. Получаем следующие данные:
|
yt |
14017 |
14909 |
15333.5 |
15381.1 |
15548.8 |
22214.2 |
32267.6 |
|
yt — 1 |
14909 |
15333.5 |
15381.1 |
15548.8 |
22214.2 |
32267.6 |
42597.5 |
Для расчета коэффициента автокорреляции , необходимо рассчитать параметры уравнения авторегрессии:
Линейный коэффициент автокорреляции (L=1):
|
yt |
yt-1 |
yt 2 |
yt-1 2 |
yt • yt-1 |
|
14017 |
14909 |
196476289 |
222278281 |
208979453 |
|
14909 |
15333.5 |
222278281 |
235116222.25 |
228607151.5 |
|
15333.5 |
15381.1 |
235116222.25 |
236578237.21 |
235846096.85 |
|
15381.1 |
15548.8 |
236578237.21 |
241765181.44 |
239157647.68 |
|
15548.8 |
22214.2 |
241765181.44 |
493470681.64 |
345404152.96 |
|
22214.2 |
32267.6 |
493470681.64 |
1041198009.76 |
716798919.92 |
|
32267.6 |
42597.5 |
1041198009.76 |
1814547006.25 |
1374519091 |
|
129671.2 |
158251.7 |
2666882902.3 |
4284953619.55 |
3349312512 |
Так как коэффициент автокорреляции первого порядка оказался высоким, то исследуемый ряд содержит только тенденцию. Проверка значимости коэффициента автокорреляции дает следующий результат:
По таблице распределения Стьюдента (двусторонняя критическая область) с уровнем значимости α=0.05 и степенями свободы k=5 находим: tкрит (n-m-1; α/2) > (5; 0.025) = 2.571. Поскольку 2,16<2,571 (tнабл < tкрит), то принимаем гипотезу о равенстве коэффициента автокорреляции =0, что, в свою очередь, подтверждает наличие сильной нелинейной тенденции. Другими словами, коэффициент автокорреляции статистически — не значим.
Коэффициент автокорреляции 2 порядка
Расчет коэффициента автокорреляции 2-го порядка
Теперь cдвигаем исходный ряд на 2 уровня. Исходный ряд состоял из 8 уровней. Расчет производится не по 8, а уже по 6 парам наблюдений. Получаем следующую таблицу:
|
yt |
14017 |
14909 |
15333.5 |
15381.1 |
15548.8 |
22214.2 |
|
yt — 2 |
15333.5 |
15381.1 |
15548.8 |
22214.2 |
32267.6 |
42597.5 |
Проведя аналогичные расчеты, как при сдвиге исходного ряда на 1 уровень, получаем:
Линейный коэффициент автокорреляции (L=2):
|
yt |
yt-2 |
yt 2 |
yt-2 2 |
yt • yt-2 |
|
14017 |
15333.5 |
196476289 |
235116222.25 |
214929669.5 |
|
14909 |
15381.1 |
222278281 |
236578237.21 |
229316819.9 |
|
15333.5 |
15548.8 |
235116222.25 |
241765181.44 |
238417524.8 |
|
15381.1 |
22214.2 |
236578237.21 |
493470681.64 |
341678831.62 |
|
15548.8 |
32267.6 |
241765181.44 |
1041198009.76 |
501722458.88 |
|
22214.2 |
42597.5 |
493470681.64 |
1814547006.25 |
946269384.5 |
|
97403.6 |
143342.7 |
1625684892.54 |
4062675338.55 |
2472334689.2 |
Коэффициент автокорреляции второго порядка также оказался высоким — исследуемый ряд содержит только тенденцию. Но проверка значимости коэффициента автокорреляции опять не подтверждает значимость коэффициента автокорреляции :
По таблице распределения Стьюдента (двусторонняя критическая область) с уровнем значимости α=0.05 и степенями свободы k=4 находим: tкрит (n-m-1; α/2) > (4; 0.025) = 2.776. Поскольку 1,73<2,776 (tнабл < tкрит), то принимаем гипотезу о равенстве коэффициента автокорреляции =0, тем самым подтверждая наличие сильной нелинейной тенденции. Другими словами, коэффициент автокорреляции статистически — не значим.
Коэффициенты автокорреляции в MS Excel
Для расчета значений автокорреляционной функции в MS Excel целесообразно использовать функцию КОРРЕЛ (массив1; массив2). Так, если уровни исходного временного ряда располагаются в ячейках А1:А20, то для расчета коэффициентов автокорреляции можно вводить функции:
r1: =КОРРЕЛ (А1:А19; А2:А20)
r2: =КОРРЕЛ (А1:А18; А3:А20)
r3: =КОРРЕЛ (А1:А17; А4:А20)
r4:=КОРРЕЛ (А1:А16; А5:А20)
И т. д., постоянно сдвигая диапазон ячеек массива 1-вверх, массива 2- вниз, в зависимости от количества уровней в ряду динамики.
Остальные коэффициенты автокорреляции рассчитаем в MS Excel:
|
Лаг |
Коэффициент автокорреляции уровней |
Коррелограмма |
|
1 |
0,96538 |
********** |
|
2 |
0,86291 |
******** |
|
3 |
0,74906 |
******* |
|
4 |
0,88313 |
********* |
При анализе наиболее высоким оказался коэффициент автокорреляции уровней первого и четвертого порядков. Следовательно, исследуемый ряд содержит тенденцию и циклические колебания.
Проверка значимости коэффициентов
Существует другая методика проверки значимости коэффициентов автокорреляции , что, в свою очередь, дает основания подтвердить (отклонить) наличие в ряду динамики автокорреляции .
Значимость каждого в отдельности коэффициента автокорреляции принято проверять с помощью критерия стандартной ошибки. С его помощью удается выявить среди запаздывающих переменных те, которые необходимо включить в модель. Коэффициент автокорреляции можно считать значимым, если не выполняется неравенство с принятым уровнем надежности (95%):
![[- 1.96frac{1}{{sqrt n }}; le ;{r_k}; le 1.96frac{1}{{sqrt n }}]](https://helpstat.ru/wp-content/ql-cache/quicklatex.com-d1332b7d1520d28c7c9421a1ca33acca_l3.png "Rendered by QuickLaTeX.com")
где n – число пар наблюдений временного ряда, k – лаг (смещение данных ряда). Если рассчитанное значение автокорреляции попадает в этот интервал, то можно сделать вывод, что данные не показывают наличие автокорреляции k-го порядка с 95% уровнем надежности:
Для r1 объем выборки составляет (n-1)=(8-1)=7 пар наблюдений:
![[- 1.96frac{1}{{sqrt 7 }}; le ;{r_1}; le 1.96frac{1}{{sqrt 7 }}; Rightarrow ; - 0.7408; le ;0.9654; le ;0.7405]](https://helpstat.ru/wp-content/ql-cache/quicklatex.com-c412650e9a7b89609f69e975e000aeb3_l3.png "Rendered by QuickLaTeX.com")
Неравенство не выполняется – наличие автокорреляции .
Для r2 объем выборки составляет (n-2)=(8-2)=6 пар наблюдений:
![[- 1.96frac{1}{{sqrt 6 }}; le ;{r_2}; le 1.96frac{1}{{sqrt 6 }}; Rightarrow ; - 0.8001; le ;0.8629; le ;0.8001]](https://helpstat.ru/wp-content/ql-cache/quicklatex.com-2de31988efc78fc0e09e8e4c053e8800_l3.png "Rendered by QuickLaTeX.com")
Неравенство не выполняется – наличие автокорреляции .
Для r3 объем выборки составляет (n-3)=(8-3)=5 пар наблюдений:
![[- 1.96frac{1}{5}; le ;{r_3}; le 1.96frac{1}{{sqrt 5 }}; Rightarrow ; - 0.8765; le ;0.7491; le ;0.8756]](https://helpstat.ru/wp-content/ql-cache/quicklatex.com-a8a473d13826dcc34c96e948b06bc821_l3.png "Rendered by QuickLaTeX.com")
Неравенство выполняется – автокорреляция отсутствует.
Для r4 объем выборки составляет (n-4)=(8-4)=4 пары наблюдений:
![[- 1.96frac{1}{4}; le ;{r_4}; le 1.96frac{1}{{sqrt 4 }}; Rightarrow ; - 0.98; le ;0.8831; le ;0.98]](https://helpstat.ru/wp-content/ql-cache/quicklatex.com-cae44309ee57e7bcec2ff657e1993cae_l3.png "Rendered by QuickLaTeX.com")
Неравенство выполняется – автокорреляция отсутствует.
Данный анализ подтвердил наличие автокорреляции в ряду динамики, что дало основание отклонить применение парного линейного коэффициента корреляции при коррелировании уровней. В этом случае необходимо коррелировать отклонения или последовательные разности (см. ниже корреляция взаимосвязанных рядов динамики). Статистическая недостоверность коэффициентов корреляции подтвердила наличие в ряду динамики сильной нелинейной тенденции, для выявления которой необходимо провести дополнительный анализ, а также циклические колебания с периодичностью в k моментов времени. Конечно же, важным моментом анализа является сама содержательная характеристика исследуемого показателя (в данном примере он обезличен, но на практике этот показатель подвержен сильному влиянию конъюнктуры рынка по объему его производства и международных цен, что, в свою очередь, дает основание утверждать о присутствии циклической компоненты).
Аналитическое выравнивание по параболе 2-го порядка и анализ коррелированности отклонений исходного уровня (yi) от выравненного (yt) с использованием статистики Дарбина-Уотсона, дает следующие результаты:
|
yi |
yt= 1048.72t2 -5775.81t+20782.31 |
ei = yi-yt |
e2 |
(ei — ei-1)2 |
|
14017 |
16055.22 |
-2038.22 |
4154344.17 |
0 |
|
14909 |
13425.58 |
1483.42 |
2200547.96 |
12401985.18 |
|
15333.5 |
12893.38 |
2440.12 |
5954201.3 |
915272.61 |
|
15381.1 |
14458.62 |
922.48 |
850961.22 |
2303254.3 |
|
15548.8 |
18121.32 |
-2572.52 |
6617851.19 |
12214983.39 |
|
22214.2 |
23881.46 |
-1667.26 |
2779752.33 |
819494.81 |
|
32267.6 |
31739.05 |
528.55 |
279369.51 |
4821595.15 |
|
42597.5 |
41694.08 |
903.42 |
816169.2 |
140525.02 |
|
23653196.89 |
33617110.46 |
Критические значения d1(dL) и d2 (dU) определяются на основе специальных таблиц для требуемого уровня значимости (α) и числа наблюдений n = 8, где количество объясняющих переменных m=1. Автокорреляция отсутствует, если выполняется следующее условие: d1 < DW и d2 < DW < 4 — d2. По таблице распределений Дарбина-Уотсона для n=8 и k=1 (уровень значимости 5%) находим: d1 = 1.08; d2 = 1.36. Поскольку 1.08 < 1.42 и 1.36 < 1.42 < 4 — 1.36, то автокорреляция остатков отсутствует.
В зависимости от величины и знака расчетного значения статистики Дарбина-Уотсона, возможны следующие ситуации.
Возможные варианты:
1. Если коэффициент автокорреляции является положительной величиной (DW>0), то при проверке гипотез возможно возникновение следующих ситуаций:
- Если наблюдаемое значение критерия Дарбина-Уотсона меньше критического значения его нижней границы DW<d1, то нулевая гипотеза (H0) об отсутствии автокорреляции первого порядка между остатками модели регрессии отклоняется.
- Если наблюдаемое значение критерия Дарбина-Уотсона больше критического значения его верхней границы DW>d2, то нулевая гипотеза (H0) об отсутствии автокорреляции первого порядка между остатками модели регрессии принимается.
- Если наблюдаемое значение критерия Дарбина-Уотсона находится между верхней и нижней критическими границами d1<DW< d2 нет достаточных оснований для принятия единственно правильного решения, необходимы дополнительные исследования.
2. Если коэффициент автокорреляции является отрицательной величиной (DW<0), то при проверке гипотез возможно возникновение следующих ситуаций:
- Если наблюдаемое значение критерия Дарбина-Уотсона больше критической величины (4–d1) DW>4–d1, то нулевая гипотеза (H0) об отсутствии автокорреляции первого порядка между остатками модели регрессии отклоняется
- Если наблюдаемое значение критерия Дарбина-Уотсона меньше критической величины (4–d2) DW<4–d2, то нулевая гипотеза (H0) об отсутствии автокорреляции первого порядка между остатками модели регрессии принимается.
- Если наблюдаемое значение критерия Дарбина-Уотсона находится в критическом интервале между величинами (4–d1) и (4–d2) 4–d1<DW<4–d2, то достаточных оснований для принятия единственно правильного решения нет, необходимы дополнительные исследования.
Данный временной ряд наилучшим образом аппроксимируется параболой 3-го порядка, нежели параболой 2-го порядка, тем самым, подтверждая сильную нелинейную тенденцию ряда (R2=0.9898).
Далее, для анализа второго временного ряда, который будет выбран в качестве взаимосвязанного с рассмотренным выше, так же необходимо провести анализ на наличие (отсутствие) автокорреляции . Затем произвести расчет и анализ коэффициента корреляции 2-х взаимосвязанных рядов динамики по нижеприведенным формулам.
Взаимосвязанные ряды динамики
Применение корреляции в динамических рядах имеет ряд особенностей, недоучет которых не позволяет получить правильной оценки взаимосвязи между рядами динамики, которые, в свою очередь, рассматриваются как результативный и факторный признаки.
В рядах динамики из-за автокорреляции (влияние изменений уровней предыдущих рядов на последующие), необходимо из уровней каждого ряда исключить тренд — основную тенденцию, налагаемую на ряд развитием во времени и найти корреляцию отклонений от тренда по формулам:
где: dy (dx) — остаточные отклонения фактических уровней ряда от выровненных, соответственно, для уровней временного ряда, принятого в качестве результативного (dy) и в качестве факторного (dx) признаков, либо использовать последовательные разности уровней взаимосвязанных рядов динамики (цепные абсолютные приросты) — (Δx, Δy).
Коррелируя отклонения или последовательные разности взаимосвязанных динамических рядов, при переходе от самих уровней к их отклонениям от выровненных значений, исключается влияние общей тенденции на колеблемость (изменчивость) самих уровней.
Смотри также:
- Корреляция и регрессия
- Компоненты и сезонная декомпозиция временного ряда
- Сезонная корректировка временного ряда
- Проверка выполнимости предпосылок МНК
- Метод наименьших квадратов
Автокорреляционная функция и аддитивная модель временного ряда
Краткая теория
При
наличии во временном ряде тенденции и циклических колебаний значения каждого
последующего уровня ряда зависят от предыдущих.
Корреляционную зависимость между последовательными уровнями временного ряда
называют автокорреляцией уровней ряда. Количественно ее можно измерить с
помощью линейного коэффициента корреляции между уровнями исходного временного ряда
и уровнями этого ряда, сдвинутыми на несколько шагов во времени.
Число
периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом.
С увеличением лага число пар значений, по которым рассчитывается коэффициент
автокорреляции, уменьшается. Некоторые авторы считают целесообразным для
обеспечения статистической достоверности коэффициентов автокорреляции
использовать правило – максимальный лаг должен быть не больше
.
Отметим
два важных свойства коэффициента автокорреляции. Во-первых, он строится по аналогии
с линейным коэффициентом корреляции и таким образом характеризует тесноту
только линейной связи текущего и предыдущего уровней ряда. Поэтому по
коэффициенту автокорреляции можно судить о наличии линейной (или близкой к
линейной) тенденции. Для некоторых временных рядов, имеющих сильную нелинейную
тенденцию (например, параболу второго порядка или экспоненту), коэффициент
автокорреляции уровней исходного ряда может приближаться к нулю.
Во-вторых,
по знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или
убывающей тенденции в уровнях ряда. Большинство временных рядов экономических
данных содержит положительную автокорреляцию уровней, однако при этом могут
иметь убывающую тенденцию.
Последовательность
коэффициентов автокорреляции уровней первого, второго и т. д. порядков называют
автокорреляционной функцией временного рада. График зависимости ее значений от
величины лага (порядка коэффициента автокорреляции) называется коррелограммой.
Анализ
автокорреляционной функции и коррелограммы позволяет
определить лаг, при котором автокорреляция наиболее высокая, а
следовательно, и лаг, при котором связь между текущим и предыдущими уровнями
ряда наиболее тесная, т. е. при помощи анализа автокорреляционной функции и коррелограммы можно выявить структуру ряда.
Если
наиболее высоким оказался коэффициент автокорреляции первого порядка,
исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался
коэффициент автокорреляции порядка
, ряд содержит
циклические колебания с периодичностью в
моментов времени.
Если ни один из коэффициентов автокорреляции не является значимым, можно
сделать одно из двух предположений относительно структуры этого ряда: либо ряд
не содержит тенденции и циклических колебаний, либо ряд содержит сильную
нелинейную тенденцию, для выявления которой нужно провести дополнительный
анализ. Поэтому коэффициент автокорреляции уровней и автокорреляционную функцию
целесообразно использовать для выявления во временном ряде наличия или
отсутствия трендовой компоненты (
)
и
циклической (сезонной) компоненты (
).
Существует несколько подходов к
анализу структуры временных рядов, содержащих сезонные или циклические
колебания. Простейший подход – расчет значений сезонной компоненты методом
скользящей средней и построение аддитивной или мультипликативной модели
временного ряда. Общий вид аддитивной модели следующий:
Эта модель
предполагает, что каждый уровень временного ряда может быть представлен как
сумма трендовой
,
сезонной
и случайной
компонент. Общий вид
мультипликативный модели выглядит так:
Эта модель
предполагает, что каждый уровень временного ряда может быть представлен как
произведение трендовой
,
сезонной
и случайной
компонент. Выбор одной из двух моделей
осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда
колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в
которой значения сезонной компоненты предполагаются постоянными для различных
циклов. Если амплитуда сезонных колебаний возрастает или уменьшается, строят
мультипликативную модель временного ряда, которая ставит уровни ряда в
зависимость от значений сезонной компоненты.
Построение аддитивной и
мультипликативной моделей сводится к расчету значений
и
для каждого уровня ряда.
Процесс построения
модели включает в себя следующие шаги.
1. Выравнивание
исходного ряда методом скользящей средней.
2. Расчет значений
сезонной компоненты
.
3. Устранение сезонной
компоненты из исходных уровней ряда и получение выравненных данных
в аддитивной или
в мультипликативной модели.
4. Аналитическое
выравнивание уровней
или
и расчет значений
с использованием полученного уравнения тренда.
5. Расчет полученных по
модели значений
или
.
6. Расчет абсолютных
и/или относительных ошибок.
Если полученные
значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни
ряда и в дальнейшем использовать временной ряд ошибок
для анализа взаимосвязи исходного ряда и
других временных рядов.
Пример решения задачи
Задача
Имеются
условные данные об объемах потребления электроэнергии
жителями региона за 16 кварталов.
Требуется:
1.
Построить автокорреляционную функцию и сделать вывод о наличии сезонных
колебаний.
2.
Построить аддитивную модель временного ряда (для нечетных вариантов) или
мультипликативную модель временного ряда (для четных вариантов).
3.
Сделать прогноз на 2 квартала вперед.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
1) Построим поле корреляции:
Поле корреляции
Уже
исходя из графика видно, что значения
образуют пилообразную фигуру. Рассчитаем несколько
последовательных коэффициентов автокорреляции. Для этого составляем первую
вспомогательную таблицу:
Следует
заметить. что среднее
значение получается путем деления не на 16, а на 15, так как у нас теперь на
одно наблюдение меньше.
Коэффициент
автокорреляции первого порядка:
Составляем
вспомогательную таблицу для расчета коэффициента автокорреляции второго
порядка:
Следовательно:
Аналогично
находим коэффициенты автокорреляции более высоких порядков, а все полученные
значения заносим в сводную таблицу:
Коэффициенты автокорреляции
| Лаг |
Коэффициент автокорреляции уровней |
| 1 | 0.180 |
| 2 | -0.542 |
| 3 | 0.129 |
| 4 | 0.980 |
| 5 | 0.987 |
| 6 | -0.686 |
| 7 | 0.019 |
| 8 | 0.958 |
| 9 | 0.117 |
| 10 | -0.707 |
| 11 | -0.086 |
| 12 | 0.937 |
Коррелограмма
Анализ
коррелограммы и графика исходных уровней временного
ряда позволяет сделать выводы о наличии в изучаемом временном ряде сезонных
колебаний периодичностью в четыре квартала.
2) Проведем выравнивание исходных уровней ряда
методом скользящей средней. Для этого:
Просуммируем
уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент
времени и определим условные годовые объемы потребления электроэнергии.
Разделив
полученные суммы на 4, найдем скользящие средние. Полученные таким образом
выровненные значения уже не содержат сезонной компоненты.
Приведем
эти значения в соответствие с фактическими моментами времени, для чего найдем
средние значения из двух последовательных скользящих средних – центрированные
скользящие средние.
Расчет сезонной компоненты
|
|
|
Итого за четыре квартала |
Скользящая средняя за четыре квартала |
Центрированая скользящая средняя |
Оценка сезонной компоненты |
| 1 | 5.5 | — | — | — | — |
| 2 | 4.8 | 24.4 | 6.1 | — | — |
| 3 | 5.1 | 26 | 6.5 | 6.300 | -1.200 |
| 4 | 9 | 26.1 | 6.525 | 6.513 | 2.488 |
| 5 | 7.1 | 27.1 | 6.775 | 6.650 | 0.450 |
| 6 | 4.9 | 28.1 | 7.025 | 6.900 | -2.000 |
| 7 | 6.1 | 29.2 | 7.3 | 7.163 | -1.063 |
| 8 | 10 | 29.8 | 7.45 | 7.375 | 2.625 |
| 9 | 8.2 | 30.2 | 7.55 | 7.500 | 0.700 |
| 10 | 5.5 | 31.2 | 7.8 | 7.675 | -2.175 |
| 11 | 6.5 | 31.9 | 7.975 | 7.888 | -1.388 |
| 12 | 11 | 32.9 | 8.225 | 8.100 | 2.900 |
| 13 | 8.9 | 33.7 | 8.425 | 8.325 | 0.575 |
| 14 | 6.5 | 33.9 | 8.475 | 8.450 | -1.950 |
| 15 | 7.3 | — | — | — | — |
| 16 | 11.2 | — | — | — | — |
Найдем
оценки сезонной компоненты как разность между фактическими уровнями ряда и
центрированными скользящими среднеми. Используем эти оценки для расчета
значений сезонной компоненты
. Для этого найдем средние
за каждый квартал (по всем годам) оценки сезонной компоненты
:
В моделях
с сезонной компонентой обычно предполагается, что сезонные воздействия за
период взаимопогашаются. В аддитивной модели это выражается в том, что сумма
значений сезонной компоненты по всем кварталам должны быть равна нулю.
Для данной
модели имеем:
Корректирующий
коэффициент:
Рассчитываем
скорректированные значения сезонной компоненты
и заносим полученные данные в таблицу.
Проверим
равенство нулю суммы значений сезонной компоненты:
Исключим влияние сезонной компоненты, вычитая ее
значения из каждого уровня исходного временного ряда. Получим величины
. Эти значения
рассчитываются за каждый момент времени и содержат только тенденцию и случайную
компоненту.
Определим
компоненту
данной модели. Для этого проведем
аналитическое выравнивание ряда
с помощью линейного тренда. Результаты
аналитического выравнивания следующие:
Подставляя
в это уравнение значения
, найдем уровни
для каждого момента времени
Найлем
значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к
уровням
значения сезонной компоненты для
соответствующих кварталов.
На одном
графике отложим фактические значения уровней временного ряда и теоретические,
полученные по аддитивной модели.
Фактические и теоретические уровни
Для оценки
качества построенной модели применим сумму квадратов полученных абсолютных
ошибок:
Следовательно,
можно сказать, что аддитивная модель объясняет 99.3% общей вариации уровней
временного ряда.
3)
Прогнозное значение
уровня временного ряда в аддитивной модели
есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты
воспользуемся уравнением тренда:
Получим:
Значения
сезонных компонент за соответствующие кварталы равны:
Таким
образом:
Автокорреляция, Коэффициент автокорреляции
При наличии во временном ряде тренда и сезонных колебаний значения любого последующего уровня ряда зависят от предыдущих. Корреляционная зависимость между последовательными уровнями временного ряда в эконометрике называется автокорреляцией уровней рада.
Количественно ее можно найти с помощью коэффициента корреляции между уровнями начального временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов по времени.
Определим коэффициент корреляции между рядами уt и yt-1.
Формула для расчета коэффициента корреляции можно представить в виде:
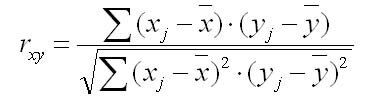
Коэффициент автокорреляции
В качестве переменной X рассматривают ряд у2, у3, …, у6 в качестве переменной у — ряд у1, у2, …, у5. Тогда приведенная формула для расчета коэффициента корреляции примет вид
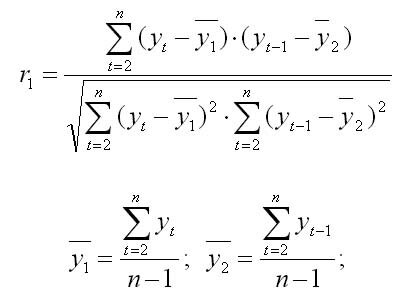
Эта величина — коэффициент автокорреляции первого порядка, так как он определяет зависимость между соседними уровнями ряда t и t-1
Аналогично определяют коэффициенты автокорреляции второго и более высоких порядков.
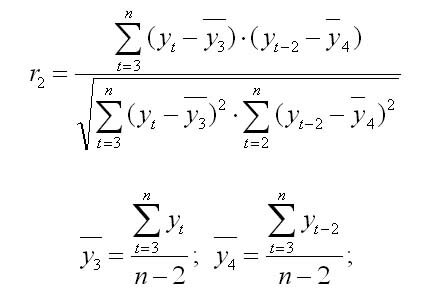
Число периодов, по которым определяется коэффициент автокорреляции, называют лаг автокорреляции. С ростом лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается. Считается что лаг должен определяться отношением n/4 — количество наблюдений деленных на 4.
Свойства коэффициента автокорреляции
По коэффициенту автокорреляции судят о наличии линейной тенденции. Для некоторых временных рядов, имеющих сильную нелинейную тенденцию (степенную функцию или экспоненту), коэффициент автокорреляции может быть меньше 0,7.
По знаку коэффициента автокорреляции нельзя делать судить о возрастающем или убывающем направлении связи в ряду.
Коррелограмма
Последовательность коэффициентов автокорреляции уровней первого, второго и других порядков называется автокорреляционной функцией временного ряда. График значений коэффициентов автокорреляции разных порядков называют коррелограммой.
Анализ автокорреляционной функции и коррелограммы позволяет найти лаг, при котором автокорреляция наиболее высокая, а следовательно, и лаг, при котором связь между текущим и предыдущими уровнями временного ряда наиболее тесная.
Анализ коэффициентов автокорреляции
Если максимальным оказался коэффициент автокорреляции первого порядка, временной ряд содержит только тенденцию (тренд).
Если максимальным оказался коэффициент автокорреляции порядка n, ряд содержит циклические колебания с периодичностью в n моментов времени.
Если ни один из коэффициентов автокорреляции не является значимым (близок к 0), можно сказать, что либо ряд не содержит тенденции и циклических колебаний, либо ряд содержит нелинейную тенденцию, для выявления которой проводят дополнительный анализ.
Источник: Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М: Финансы и статистика, 2002. – 344 с.
Для перехода на страницу выполнения контрольных по эконометрике жмите сюда
