Как найти коэффициент давления

From Wikipedia, the free encyclopedia

In fluid dynamics, the pressure coefficient is a dimensionless number which describes the relative pressures throughout a flow field. The pressure coefficient is used in aerodynamics and hydrodynamics. Every point in a fluid flow field has its own unique pressure coefficient, C_p.

In many situations in aerodynamics and hydrodynamics, the pressure coefficient at a point near a body is independent of body size. Consequently, an engineering model can be tested in a wind tunnel or water tunnel, pressure coefficients can be determined at critical locations around the model, and these pressure coefficients can be used with confidence to predict the fluid pressure at those critical locations around a full-size aircraft or boat.

Definition[edit]

The pressure coefficient is a parameter for studying both incompressible/compressible fluids such as water and air. The relationship between the dimensionless coefficient and the dimensional numbers is
^[1][2]

where:

is the static pressure at the point at which pressure coefficient is being evaluated

is the static pressure in the freestream (i.e. remote from any disturbance)

is the stagnation pressure in the freestream (i.e. remote from any disturbance)

is the freestream fluid density (Air at sea level and 15 °C is 1.225 )

is the freestream velocity of the fluid, or the velocity of the body through the fluid

Incompressible flow[edit]

Using Bernoulli’s equation, the pressure coefficient can be further simplified for potential flows (inviscid, and steady):^[3]

where u is the flow speed at the point at which pressure coefficient is being evaluated, and Ma is the Mach number: the flow speed is negligible in comparison with the speed of sound. For a case of an incompressible but viscous fluid, this represents the profile pressure coefficient, since it is associated with the pressure hydrodynamic forces rather than the viscous ones.

This relationship is valid for the flow of incompressible fluids where variations in speed and pressure are sufficiently small that variations in fluid density can be neglected. This is a reasonable assumption when the Mach number is less than about 0.3.

of minus one is significant in the design of gliders because this indicates a perfect location for a “Total energy” port for supply of signal pressure to the Variometer, a special Vertical Speed Indicator which reacts to vertical movements of the atmosphere but does not react to vertical maneuvering of the glider.

In the fluid flow field around a body there will be points having positive pressure coefficients up to one, and negative pressure coefficients including coefficients less than minus one, but nowhere will the coefficient exceed plus one because the highest pressure that can be achieved is the stagnation pressure.

Compressible flow[edit]

In the flow of compressible fluids such as air, and particularly the high-speed flow of compressible fluids, (the dynamic pressure) is no longer an accurate measure of the difference between stagnation pressure and static pressure. Also, the familiar relationship that stagnation pressure is equal to total pressure does not always hold true. (It is always true in isentropic flow but the presence of shock waves can cause the flow to depart from isentropic.) As a result, pressure coefficients can be greater than one in compressible flow.^[4]

• greater than one indicates the freestream flow is compressible.

Perturbation theory[edit]

The pressure coefficient can be estimated for irrotational and isentropic flow by introducing the potential and the perturbation potential , normalized by the free-stream velocity

Using Bernoulli’s equation,

which can be rewritten as

where is the sound speed.

The pressure coefficient becomes

where is the far-field sound speed.

Local piston theory[edit]

The classical piston theory is a powerful aerodynamic tool. From the use of the momentum equation and the assumption of isentropic perturbations, one obtains the following basic piston theory formula for the surface pressure:

where is the downwash speed and is the sound speed.

The surface is defined as

The slip velocity boundary condition leads to

The downwash speed is approximated as

Pressure distribution[edit]

An airfoil at a given angle of attack will have what is called a pressure distribution. This pressure distribution is simply the pressure at all points around an airfoil. Typically, graphs of these distributions are drawn so that negative numbers are higher on the graph, as the for the upper surface of the airfoil will usually be farther below zero and will hence be the top line on the graph.

Relationship with aerodynamic coefficients[edit]

All the three aerodynamic coefficients are integrals of the pressure coefficient curve along the chord.
The coefficient of lift for a two-dimensional airfoil section with strictly horizontal surfaces can be calculated from the coefficient of pressure distribution by integration, or calculating the area between the lines on the distribution. This expression is not suitable for direct numeric integration using the panel method of lift approximation, as it does not take into account the direction of pressure-induced lift. This equation is true only for zero angle of attack.

where:

is pressure coefficient on the lower surface

is pressure coefficient on the upper surface

is the leading edge location

is the trailing edge location

When the lower surface is higher (more negative) on the distribution it counts as a negative area as this will be producing down force rather than lift.

See also[edit]

• Lift coefficient
• Drag coefficient
• Pitching moment coefficient

References[edit]

• Abbott, I.H. and Von Doenhoff, A.E. (1959) Theory of Wing Sections, Dover Publications, Inc. New York, Standard Book No. 486-60586-8
• Anderson, John D (2001) Fundamentals of Aerodynamic 3rd Edition, McGraw-Hill. ISBN 0-07-237335-0

Коэффициент давления – это безразмерное число, которое описывает относительное давление во всем дюйме гидродинамика. Коэффициент давления используется в аэродинамике и гидродинамике. Каждая точка в поле потока жидкости имеет свой уникальный коэффициент давления, C p { displaystyle C_ {p}}.

Во многих ситуациях в аэродинамике и гидродинамике коэффициент давления в точке рядом с телом не зависит от размер тела. Следовательно, инженерная модель может быть протестирована в аэродинамической трубе или в водяной трубе, коэффициенты давления могут быть определены в критических точках вокруг модели, и эти коэффициенты давления можно с уверенностью использовать для спрогнозируйте давление жидкости в этих критических точках вокруг полноразмерного самолета или лодки.

Содержание

• 1 Определение
• 2 Несжимаемый поток
• 3 Сжимаемый поток
  • 3.1 Теория возмущений
  • 3.2 Локальная теория поршня
• 4 Распределение давления
• 5 Связь с аэродинамическими коэффициентами
• 6 См. Также
• 7 Ссылки

Определение

Коэффициент давления – это параметр для изучения как несжимаемых / сжимаемых жидкостей, таких как вода и воздух. Связь между безразмерным коэффициентом и размерными числами:

C p = p – p ∞ 1 2 ρ ∞ V ∞ 2 = p – p ∞ p 0 – p ∞ { displaystyle C_ {p} = {p-p_ { infty} over { frac {1} {2}} rho _ { infty} V _ { infty} ^ {2}} = {p-p _ { infty} over p_ {0} -p_ { infty}}}

где:

p { displaystyle p}– статическое давление в точке, в которой оценивается коэффициент давления

p ∞ { displaystyle p _ { infty}}– статическое давление в набегающем потоке (т.е. удаленном от любых помех)

p 0 { displaystyle p_ {0}}– давление торможения в набегающем потоке (т.е. удаленном от любого возмущения)

ρ ∞ { displaystyle rho _ { infty}}– набегающий поток плотность жидкости (воздух на уровне моря и 15 ° C составляет 1,225 кг / м 3 { displaystyle { rm {кг / м ^ { 3}}}})

V ∞ { displaystyle V _ { infty}}– скорость набегающего потока жидкости или скорость тела, проходящего через жидкость.

Incompressib le flow

Используя уравнение Бернулли, коэффициент давления можно дополнительно упростить для потенциальных потоков (невязких и устойчивых):

C p 0 = C p | M a ≈ 0 = 1 – (uu ∞) 2 { displaystyle C_ {p} 0 = C_ {p} | _ {Ma , приблизительно , 0} = {1 – { bigg (} { frac { u} {u _ { infty}}} { bigg)} ^ {2}}}

где u – скорость потока в точке, в которой оценивается коэффициент давления, а Ma – число Маха : скорость потока незначительна по сравнению со скоростью звука. Для случая несжимаемой, но вязкой жидкости это представляет собой коэффициент профильного давления, поскольку он связан с гидродинамическими силами давления, а не с вязкими.

Эта взаимосвязь действительна для потока несжимаемой жидкости, где изменения скорости и давления достаточно малы, чтобы отклонениями плотности жидкости можно пренебречь. Это разумное предположение, когда число Маха меньше примерно 0,3.

C p { displaystyle C_ {p}}минус один имеет важное значение в конструкции планеров, потому что это указывает на идеальное место для порта «Полная энергия» для подачи сигнального давления на Вариометр, специальный индикатор вертикальной скорости, который реагирует на вертикальные движения атмосферы, но не реагирует на вертикальное маневрирование планера.

В поле потока жидкости вокруг тела будут точки с коэффициентами положительного давления до единицы и коэффициентами отрицательного давления, включая коэффициенты меньше минус единицы, но нигде коэффициент не будет превышать плюс один, потому что наибольшее давление, которое может быть достигнуто давление торможения.

Сжимаемый поток

В потоке сжимаемых текучих сред, таких как воздух, и особенно в высокоскоростных потоках сжимаемых текучих сред, ρ v 2/2 { displaystyle { rho v ^ {2}} / 2}(динамическое давление ) больше не является точным показателем разницы между давлением застоя и статическое давление. Кроме того, не всегда верно известное соотношение, что давление торможения равно общему давлению. (Это всегда верно в изэнтропическом потоке, но присутствие ударных волн может привести к отклонению потока от изоэнтропического.) В результате коэффициенты давления могут быть больше единицы в сжимаемом потоке..

• C p { displaystyle C_ {p}}больше единицы означает, что набегающий поток является сжимаемым.

Теория возмущений

Коэффициент давления C p { displaystyle C_ {p}}можно оценить для безвихревого и изэнтропического потока, введя потенциал Φ { displaystyle Phi}и возмущение потенциал ϕ { displaystyle phi}, нормализованный скоростью набегающего потока u ∞ { displaystyle u _ { infty}}

Φ = u ∞ x + ϕ ( x, y, z) { displaystyle Phi = u _ { infty} x + phi (x, y, z)}

Использование уравнения Бернулли,

∂ Φ ∂ t + ∇ Φ ⋅ ∇ Φ 2 + γ γ – 1 п ρ = константа { Displaystyle { begin {align} { frac { partial Phi} { partial t}} + { frac { nabla Phi cdot nabla Phi} {2}} + { frac { gamma} { gamma -1}} { frac {p} { rho}} = { text {constant}} end {align}}}

, который можно переписать как

∂ Φ ∂ t + ∇ Φ ⋅ ∇ Φ 2 + a 2 γ – 1 = константа { displaystyle { begin {align} { frac { partial Phi} { partial t}} + { frac { nabla Phi cdot nabla Phi} {2}} + { frac {a ^ {2}} { gamma -1}} = { text {constant}} end {align}}}

здесь w { displaystyle w}– a { displaystyle a}– скорость звука.

Коэффициент давления становится

C p = p – p ∞ γ 2 p ∞ M 2 = 2 γ M 2 [(aa ∞) 2 γ γ – 1 – 1] = 2 γ M 2 [ (γ – 1 a ∞ 2 (u ∞ 2 2 – Φ t – ∇ Φ ⋅ ∇ Φ 2) + 1) γ γ – 1 – 1] ≈ 2 γ M 2 [(1 – γ – 1 a ∞ 2 (ϕ t + u ∞ ϕ x)) γ γ – 1 – 1] ≈ – 2 ϕ tu ∞ 2 – 2 ϕ xu ∞ { displaystyle { begin {align} C_ {p} = { frac {p-p_ { infty}} {{ frac { gamma} {2}} p _ { infty} M ^ {2}}} = { frac {2} { gamma M ^ {2}}} left [ left ({ frac {a} {a _ { infty}}} right) ^ { frac {2 gamma} { gamma -1}} – 1 right] \ = { frac {2} { gamma M ^ {2}}} left [ left ({ frac { gamma -1} {a _ { infty} ^ {2}}} ({ frac {u _ { infty} ^ {2}) } {2}} – Phi _ {t} – { frac { nabla Phi cdot nabla Phi} {2}}) + 1 right) ^ { frac { gamma} { gamma – 1}} – 1 right] \ приблизительно { frac {2} { gamma M ^ {2}}} left [ left (1 – { frac { gamma -1} {a _ { infty} ^ {2}}} ( phi _ {t} + u _ { infty} phi _ {x}) right) ^ { frac { gamma} { gamma -1}} – 1 right ] \ приблизительно – { frac {2 phi _ {t}} {u _ { infty} ^ {2}}} – { frac {2 phi _ {x}} {u _ { infty} }} end {align}}}

здесь a ∞ { displaystyle a _ { inf ty}}– скорость звука в дальней зоне.

Теория локального поршня

Классическая теория поршня – мощный аэродинамический инструмент. Используя уравнение импульса и предположение об изэнтропических возмущениях, можно получить следующую формулу основной теории поршня для поверхностного давления:

p = p ∞ (1 + γ – 1 2 wa) 2 γ γ – 1 { displaystyle p = p _ { infty} left (1 + { frac { gamma -1} {2}} { frac {w} {a}} right) ^ { frac {2 gamma} { гамма -1}}}

здесь w { displaystyle w}– скорость промывки вниз, а a { displaystyle a}– скорость звука.

С п знак равно п – п ∞ γ 2 п ∞ M 2 = 2 γ M 2 [(1 + γ – 1 2 wa) 2 γ γ – 1-1] { displaystyle { begin {align} C_ { p} = { frac {p-p _ { infty}} {{ frac { gamma} {2}} p _ { infty} M ^ {2}}} = { frac {2} { gamma M ^ {2}}} left [ left (1 + { frac { gamma -1} {2}} { frac {w} {a}} right) ^ { frac {2 gamma} { gamma -1}} – 1 right] end {align}}}

Поверхность определяется как

F (x, y, z, t) = z – f (x, y, t) = 0 { displaystyle { begin {align} F (x, y, z, t) = zf (x, y, t) = 0 end {align}}}

Граничное условие скорости скольжения приводит к

F | ∇ F | (u ∞ + ϕ x, ϕ y, ϕ z) = V стенка ⋅ ∇ F | ∇ F | = – ∂ F ∂ t 1 | ∇ F | { displaystyle { begin {align} { frac { nabla F} {| nabla F |}} (u _ { infty} + phi _ {x}, phi _ {y}, phi _ { z}) = V _ { text {wall}} cdot { frac { nabla F} {| nabla F |}} = – { frac { partial F} { partial t}} { frac { 1} {| nabla F |}} end {align}}}

Скорость промывки вниз w { displaystyle w}приблизительно равна

w = ∂ f ∂ t + U ∞ ∂ е ∂ Икс { Displaystyle { begin {align} w = { frac { partial f} { partial t}} + u _ { infty} { frac { partial f} { partial x }} end {align}}}

Распределение давления

Аэродинамический профиль при заданном угле атаки будет иметь то, что называется распределением давления. Это распределение давления – это просто давление во всех точках вокруг профиля. Обычно графики этих распределений строятся так, чтобы отрицательные числа располагались выше на графике, поскольку C p { displaystyle C_ {p}}для верхней поверхности профиля обычно будет дальше ниже нуля и, следовательно, будет верхней линией на графике.

Связь с аэродинамическими коэффициентами

Все три аэродинамических коэффициента являются интегралами кривой коэффициента давления вдоль хорды. Коэффициент подъемной силы для двумерного сечения профиля с строго горизонтальными поверхностями может быть вычислен из коэффициента распределения давления путем интегрирования или вычисления площади между линиями распределения. Это выражение не подходит для прямого численного интегрирования с использованием панельного метода аппроксимации подъемной силы, так как оно не учитывает направление подъемной силы, вызванной давлением. Это уравнение верно только для нулевого угла атаки.

C l = 1 x TE – x LE ∫ x LE x TE (C pl (x) – C pu (x)) dx { displaystyle C_ {l} = { frac {1} {x_ {TE} -x_ {LE}}} int limits _ {x_ {LE}} ^ {x_ {TE}} left (C_ {p_ {l}} (x) -C_ {p_ {u}} (x) справа) dx}

где:

C pl { displaystyle C_ {p_ {l}}}– коэффициент давления на нижней поверхности

C pu { displaystyle C_ {p_ { u}}}– коэффициент давления на верхней поверхности.

x LE { displaystyle x_ {LE}}– местоположение переднего края

x TE { displaystyle x_ {TE}}– это положение задней кромки

Когда нижняя поверхность C p { displaystyle C_ {p}}выше (более отрицательно) в распределении это считается отрицательной областью, поскольку она будет создавать прижимную силу, а не подъемную силу.

См. Также

• Коэффициент подъемной силы
• Коэффициент лобового сопротивления
• Коэффициент продольного момента

Литература

• Abbott, I.H. и фон Денхофф, А.Е. (1959) Теория сечения крыльев, Dover Publications, Inc., Нью-Йорк, Стандартная книга № 486-60586-8
• Андерсон, Джон Д. (2001) Основы аэродинамики, 3-е издание, McGraw -Хилл. ISBN 0-07-237335-0

Коэффициент давления Калькулятор

Search
Дом	физика ↺
физика	Аэродинамика ↺
Аэродинамика	Невязкий, несжимаемый поток ↺
Невязкий, несжимаемый поток	Основы Inviscid Несжимаемый поток ↺
Основы Inviscid Несжимаемый поток	Давление ↺

Коэффициент давления Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Поверхностное давление в точке: 61670 паскаль –> 61670 паскаль Конверсия не требуется
Давление свободного потока: 18 паскаль –> 18 паскаль Конверсия не требуется
Динамическое давление свободного потока: 5343 паскаль –> 5343 паскаль Конверсия не требуется

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

11.5388358600037 –> Конверсия не требуется

13 Давление Калькуляторы

Коэффициент давления формула

Коэффициент давления = (Поверхностное давление в точке–Давление свободного потока)/(Динамическое давление свободного потока)

C_p = (P–p_∞)/(q_∞)

Как изменяется коэффициент давления в потоке несжимаемой жидкости?

Коэффициент давления в потоке несжимаемой жидкости зависит только от расположения на поверхности тела, формы и ориентации тела. Коэффициент давления не будет изменяться с изменением давления и плотности набегающего потока, пока поток несжимаемый.

Лабораторная
работа №38

ОПРЕДЕЛЕНИЕ
ТЕРМИЧЕСКОГО КОЭФФИЦИЕНТА ДАВЛЕНИЯ
ВОЗДУХА.

Принадлежности:
установка
(газовый термометр), водоподогреватель
«Термекс».

Цель
работы:

1.
Познакомиться с работой газового
термометра.

2.
Экспериментально определить термический
коэффициент давления воздуха.

Введение.
Некоторое
количество газа характеризуется пятью
величинами: массой m,объемом
V,
давлением Р, температурой Т и молекулярным
весом µ.

Эти
величины закономерно связаны друг с
другом. Связь между ними называется
уравнением состояния. В случае идеальных
газов уравнение состояния, называемое
уравнением Клапейрона-Менделеева, имеет
вид

V=

(1)

Где
R-универсальная
газовая постоянная.

Уравнение
(1) характеризует любое состояние газа,
например, первое состояние

₁V₁=₁

(2)

Для
той же массы газа во втором состоянии

₂V₂=₂

(3)

Разделив
(2) на (3), получаем формулу, которую часто
называют объединенным газовым законом:

Известные
экспериментальные газовые законы
Бойля-Мариотта, Гей-Люссака и Шарля
могут рассматриваться как следствия
уравнения Клапейрона-Менделеева, когда
газ переходит из одного состояния в
другое так, таким образом, что один из
его параметров не меняется.

Рассмотрим
изохорический процесс, процесс при
котором газ переходит из первого
состояния во второе и объем его при этом
не меняется V₁=V₂=
соnst.
Кроме того, начальную температуру газа
возьмем Т₁=Т₀=273⁰К.
Для первого состояния уравнение (1)
запишется так

₀V₁=₀,

(4)

Где
Р₀–
давление, соответствующее температуре
273⁰К.

Пусть
температура этого газа меняется от Т₀до
Т, тогда давление будет меняться от Р₀
до Р. Объем газа остается неизменным(
по условию). Для второго состояния этого
газа уравнение Клапейрона-Менделеева
будет иметь вид

V₁=,

(5)

Разделив
(4) на (5), получим

Введем
обозначение

Тогда
Р=Р₀
α∙Т
(6)

Уравнение
(6) называется законом Шарля.

Величину
α называют термическим коэффициентом
давления газа

.

Коэффициент
термического давления есть число,
которое показывает на какую часть
меняется первоначальное давление газа,
взятого при нуле градусов Цельсия, при
изменении температуры на один градус,
если объем газа не меняется.

Формула
закона Шарля (3) будет иметь другой вид,
если температуру отсчитывать не по
шкале Кельвина, а по шкале Цельсия.
Действительно, подставив (6) Т= t+273⁰получаем

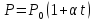
(7)

Как
показывает опыт, все реальные газы, в
состоянии далеком от насыщения, почти
полностью подчиняются законам для
идеальных газов. В данной работе ставится
задача – определить экспериментально
термический коэффициент давления
воздуха α при помощи газового термометра.

Практически
коэффициент α можно определить путем
измерения двух любых температур t₁
и t₂
и соответствующих им давлений газа Р₁
и Р₂
при неизменном объеме. Из закона Шарля

1
cостояние

2
состояние

Получим

.

(8)

Формула
(8) является расчетной для нашего опыта.

Описание
прибора. Общий
вид экспериментальной установки избражен
на рис .1. Установка (рис.2. и рис.3.) состоит
из стеклянного баллона 1, заполненного
воздухом, водяного манометра 15, измерителя
температур 4 и водоподогревателя (на
рисунке не изображен). Стеклянный баллон
с воздухом 1 помещен в металлический
сосуд-термостат 3. Термостат заполняется
циркулирующей через него водой от
водоподогревателя при помощи насоса.
Двухканальный измеритель температур
4 ТРМ-200, подключенный к двум хромель-копелевым
термопарам 2, предназначен для измерения
температуры воздуха в баллоне с воздухом
и температуры воздуха в комнате. Водяной
манометр предназначен для измерения
давления нагретого газа в баллоне.
Давление нагретого газа равно сумме
атмосферного давления, которое
отсчитывается по лабораторному барометру,
и давления, отсчитываемого по водяному
манометру установки. Отсчет уровней
водяного манометра производится по
положению менисков относительно
миллиметровой шкалы 7. При необходимости
выравнивание давления внутри баллона
до атмосферного давления производится
открытием крана 5 трубки.

Измерения.

Внимание!
Перед
выполнением работы тщательно ознакомьтесь
с порядком работы. Заранее подготовьте
таблицу. Конструктивные особенности
лабораторной установки не позволяют
быстро охладить воздух в баллоне.
ИЗМЕРЕНИЯ МОЖНО ПРОВЕСТИ ТОЛЬКО ОДИН
РАЗ ЗА ЗАНЯТИЕ!

1. Включить
   тумблером 8 питание установки.

2. Включить
   тумблером 9 насос водоподогревателя.
   В течении 5 минут термостат наполнится
   циркулирующей через него водой.

3. Включить
   измеритель температур 4 тумблером 1.
   Температура внутри баллона с воздухом
   отображается индикатором с красными
   цифрами, комнатная температура –
   индикатором с зелеными цифрами. Измерение
   комнатной температуры в данной работе
   не используется. Записать в таблицу
   температуру воздуха Т
   (всегда
   записывать красные цифры).

4. Тщательно
   по нижним точкам менисков уровня
   жидкости отсчитать величины положения
   уровней жидкости
   
   в
   правом колене манометра и Һ₂
   – в
   левом
   колене (уровни жидкости должны быть на
   одинаковой отметке шкалы 7). Если уровни
   жидкости находятся на разных отметках
   шкалы, то необходимо повернуть ручку
   крана 5 в положение «ОТКРЫТО». При этом
   уровни
   
   в
   правом и Һ₂
   в левом колене манометра должны
   сравняться.

5. По
   лабораторному барометру определить и
   записать над таблицей 1 атмосферное
   давление Р_атм
   (в Паскалях)._.

6. Повернуть
   ручку крана 5 в положение «ЗАКРЫТО».

7. Тумблером
   10 включить питание водоподогревателя.
   ПОСЛЕ ВКЛЮЧЕНИЯ ПИТАНИЯ ОСТАНОВКА ИЛИ
   ПОВТОРНОЕ ПРОВЕДЕНИЕ ЭКСПЕРИМЕНТА
   НЕВОЗМОЖНЫ В ТЕЧЕНИЕ НЕСКОЛЬКИХ ЧАСОВ!
   На передней панели водоподогревателя
   расположен регулятор режимов. Повернуть
   ручку регулятора на «девятую» точку.
   Не следует изменять режимы нагрева!
   После включения питания водоподогревателя
   вода, циркулирующая в сосуде-термостате,
   будет нагреваться, и температура воздуха
   в баллоне будет медленно увеличиваться.

8. Производить
   измерения уровней воды в манометре
   
   и Һ₂
   
   при увеличении температуры на каждые
   0,5 градуса, до максимально возможного
   значения разности уровней (
   не
   ниже 12 см,
   Һ₂
   не выше 25 см). Результаты измерений
   записывать в таблицу 1.

9. По
   окончании работы открыть кран 5, выключить
   измеритель температур, отключить насос
   водоподогревателя 9, отключить питание
   установки.

Обработка
результатов измерений

1. Для
   каждой температуры T
   рассчитать перепад давлений ΔР=ρg(h₂-h₁),
   где ρ= 1000 кг/м³
   – плотность воды в манометре, g=9,81
   м/с²
   – ускорение свободного падения, h₂
   и h₁
   измеряются в метрах.

2. Далее
   рассчитать давление нагретого воздуха
   в баллоне по формуле Р=Р_атм+ΔР.

3. Построить
   график зависимости давления
   нагретого
   газа
   Р
   (в Паскалях) от
   температуры T
   (в градусах Цельсия) в виде прямой линии.
   На миллиметровой бумаге
   в выбранном масштабе по горизонтальной
   оси температура, а по вертикальной –
   давление газа. Экспериментальные точки
   на графике могут иметь некоторый разброс
   из-за погрешности измерений. Линия
   графика проводится так, чтобы точки
   располагались выше и ниже проводимого
   графика примерно в равном количестве.
   Некоторые точки могут оказаться на
   самой линии.

4. Пользуясь
   полученным графиком, находят два
   значения давления Р₁
   и Р₂,
   соответствующие двум выбранным значениям
   температуры T₁
   и T₂.
   Данные записать в таблицу 2. Вычислить
   термический коэффициент давления
   воздуха α.
   Сравнить с табличным значением α=0,00366
   

Таблица
1

Р_атм=

№	T0,С	h1,мм	h2,мм	h2–h1, м	ΔР, Па	Р, Па

Таблица
2

1 точка на графике	2 точка на графике			Разность	Разность	Температурный коэффициент
T1=	T2=
Р1=	Р2=

Контрольные
вопросы

1. Перечислите
   все изопроцессы. Сформулируйте газовые
   законы для всех изопроцессов и запишите
   соответствующие уравнения.

2. Какой
   процесс наблюдается в данной работе?

3. Дайте
   определение термического коэффициента
   давления.

4. Что
   называют идеальным газом? Запишите
   уравнение состояния идеального газа.

5. Что
   называют давлением газа? Единицы
   измерения давления газа. Давление Р=560
   мм рт.ст. Чему равно Р в паскалях,
   физических атмосферах, барах?

6. Дайте
   определение температуры. Дайте
   определение температурных шкал Кельвина
   и Цельсия.

7. Какие
   типы термометров применяются для
   измерения температуры? Назовите
   преимущества газового термометра.

Список
рекомендуемой литературы

1.
Сивухин Д.В. Общий курс физики. Т 2.
Термодинамика и молекулярная физика.
М.: Физматлит, 2006.

2.
Савельев И.В. Курс общей физики. Т.1.
Механика и молекулярная физика. СПб.:
Лань, 2005.

3.
Трофимова Т.И. Курс физики. М.: Академия,
2006.

Какие
факторы влияют на точность результата,
получаемого в данной работе?

7

Соседние файлы в папке Методички (мол)

• #
• #
• #
• #
• #
• #

коэффициент давления