Как найти коэффициент деления

коэффициент деления

Смотреть что такое «коэффициент деления» в других словарях:

коэффициент деления — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN scaling ratio … Справочник технического переводчика

коэффициент деления частоты интегральной микросхемы — коэффициент деления частоты Отношение частоты входного сигнала интегральной микросхемы к частоте выходного сигнала. Обозначение Kделf [ГОСТ 19480 89] Тематики микросхемы Синонимы коэффициент деления частоты … Справочник технического переводчика

коэффициент деления частоты преобразовательного модуля СВЧ — коэффициент деления Кдел Отношение частоты входного сигнала к частоте основной составляющей спектра выходного сигнала преобразовательного модуля СВЧ. [ГОСТ 23221 78] Тематики компоненты техники связи Обобщающие термины модули СВЧ, блоки СВЧ… … Справочник технического переводчика

коэффициент деления напряжения на выходе — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN output ratiooutput voltage ratio … Справочник технического переводчика

коэффициент деления напряжения потенциометра — Отношение выходного напряжения потенциометра при данном положении его подвижной системы к выходному напряжению [ГОСТ 21414 75] Тематики резисторы EN output ratio DE Spannungsteilungsverhältnis FR rapport de sortie … Справочник технического переводчика

коэффициент деления на быстрых нейтронах — sparčiojo dalijimosi faktorius statusas T sritis Standartizacija ir metrologija apibrėžtis Begalinėje terpėje vidutinio skaičiaus neutronų, atsirandančių dalijimosi, kurį sukelia visų energijų neutronai, metu, ir vidutinio skaičiaus neutronų,… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

Коэффициент деления напряжения потенциометра — 59. Коэффициент деления напряжения потенциометра D. Spannungsteilungsverhältnis E. Output ratio F. Rapport de sortie Отношение выходного напряжения потенциометра при данном положении его подвижной системы к выходному напряжению Источник: ГОСТ… … Словарь-справочник терминов нормативно-технической документации

Коэффициент деления частоты преобразовательного модуля СВЧ — 22. Коэффициент деления частоты преобразовательного модуля СВЧ Источник: ГОСТ 23221 78: Модули СВЧ, блоки СВЧ. Термины, определения и буквенные обозначения оригинал документа … Словарь-справочник терминов нормативно-технической документации

Коэффициент размножения нейтронов — k отношение числа нейтронов последующего поколения к числу нейтронов в предшествующем поколении во всём объеме размножающей нейтронной среды (активной зоны ядерного реактора). В общем случае, этот коэффициент может быть найден с помощью… … Википедия

Коэффициент размножения на быстрых нейтронах — μ показатель, учитывающий влияние деления ядер 238U быстрыми нейтронами на ход цепной реакции в реакторе на тепловых нейтронах. Содержание 1 Размножение на быстрых нейтронах 1.1 Гомогенная среда … Википедия

КОЭФФИЦИЕНТ УВЛАЖНЕНИЯ — индекс континентальности, отношение количества атмосферных осадков к потенциальной величине испарения с поверхности почвы в данной экосистеме. Определяется с помощью специальных приборов испарителей. Вычисляется путем деления годовой суммы… … Экологический словарь

Источник

Большая Энциклопедия Нефти и Газа

Коэффициент деления / гдел выбирается так, чтобы напряжение, снимаемое с делителя, было меньше номинального предела потенциометра и чтобы отсчет на потенциометре производился не менее как на четырех декадах. [2]

Коэффициент деления равен тту и на входе сравнивающего устройства будет напряжение 0 8 в. [3]

Коэффициент деления изменяется путем подачи дополнительных импульсов на вход делителя при уменьшении К. [4]

Коэффициент деления может быть постоянным либо регулируемым. Изменение коэффициента деления достигается путем изменения числа Витков обмоток или их частей, причем в зависимости от места переключения витков ( входной или выходной обмотки) получают схемы о постоянным выходным или входным сопротивлением. Особенностью индуктивного делителя является наличие между витками обмоток тесной индуктивной связи, в идеальном случае в предположении того, что все витки обмоток имеют одинаковое потокосцепление, в потоки рассеяния отсутствуют. [5]

Коэффициент деления может принимать одно и. [9]

Коэффициент деления может принимать одно из значений в соответствии с приведенной ниже таблицей. [10]

Коэффициент деления равен ZN. Счетчики такого вида часто называют счетчиками Джонсона. Большинство счетчиков-делителей серии К176 выполнены по рассмотренной схеме. [12]

Коэффициент деления может быть постоянным либо регулируемым. [13]

Коэффициент деления набор резисторов определяется как отношение выходного напряжения к напряжению на его входе. [14]

Источник

Делители напряжения и тока

В электротехнике очень часто применяются делители напряжения, работу которых можно рассмотреть, применяя правило распределения напряжений. На рисунке показаны схемы делителей напряжения, служащих для уменьшения заданного напряжения источника питания (например, 4, 6, 12 или 220 В) до напряжения любого меньшего значения.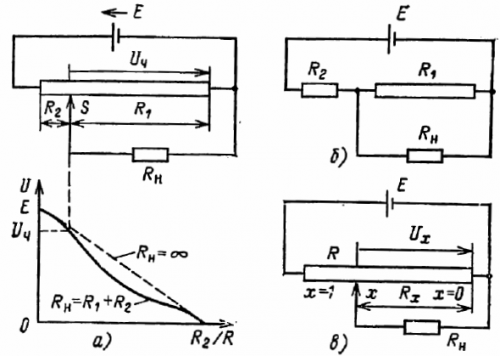

Рис. 1. Схемы делителей напряжения

В электрических электрических приборах, а также при проведении измерений иногда необходимо получить несколько напряжений определенного значения от одного источника. Делители напряжения часто (и прежде всего в слаботочной технике) называют потенциометрами.

Изменяемое частичное напряжение получается при перемещении скользящего контакта реостата или другого типа резистора. Постоянное по значению частичное напряжение может быть получено посредством отпайки от резистора или же может сниматься с точки соединения двух отдельных резисторов.

При помощи скользящего контакта можно плавно изменять необходимое для приемника с сопротивлением (сопротивление нагрузки) частичное напряжение, при этом скользящий контакт обеспечивает параллельное соединение сопротивлений, с которого снимается частичное напряжение.

В составе делителя напряжения для получения фиксированного значения напряжения используют резисторы. В этом случае выходное напряжение U вых связано с входным U вх (без учета возможного сопротивления нагрузки) следующим соотношением:

U вых = U вх х (R2 / R1 + R2)

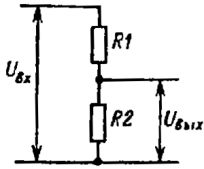
Рис. 2. Делитель напряжения

Пример. С помощью резисторного делителя нужно получить на нагрузке сопротивлением 100 кОм напряжение 1 В от источника постоянного напряжения 5 В. Требуемый коэффициент деления напряжения 1/5 = 0,2. Используем делитель, схема которого приведена на рис. 2.

Сопротивление резисторов R1 и R2 должно быть значительно меньше 100 кОм. В этом случае при расчете делителя сопротивление нагрузки можно не учитывать.

Следовательно, R2 / (R1 +R2) R2 = 0,2

Следует помнить, что сам делитель потребляет ток от первичного источника (в данном случае 1 мА) и этот ток будет возрастать с уменьшением сопротивлений резисторов делителя.

Для получения заданного значения напряжения следует применять высокоточные резисторы.

Недостатком простого резисторного делителя напряжения является то, что с изменением сопротивления нагрузки выходное напряжение ( U вых) делителя изменяется. Ддя уменьшения влияния нагрузки на U выхнеобходимо выбирать соротивление R2 по крайней мере в 10 раз меньше минимального сопротивления нагрузки.

Важно помнить о том, что с уменьшением сопротивлений резисторов R 1 и R2 растет ток, потребляемый от источника входного напряжения. Обычно этот ток не должен превышать 1—10 мА.

Резисторы используются также для того, чтобы заданную долю общего тока направить в соответствующее плечо делителя. Например, в схеме на рис. 3 ток I составляет часть общего тока I вх, определяемую сопротивлениями резисторов R1 и R2, т.е. можно записать, что I вых = I вх х (R1 / R2 + R1)

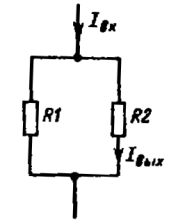
Рис. 3. Делитель тока

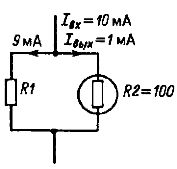
Коэффициент деления тока определяется соотношением:

Требуемое сопротивление резистора R1 можно получить путем последовательного соединения двух стандартных резисторов сопротивлением 9,1 и 2 Ом, выполненных на основе толстопленочной технологии с точностью ±2% (0,25 Вт). Заметим еще раз, что на рис. 3 сопротивление R2 — это внутреннее сопротивление измерительного прибора.

Для обеспечения хорошей точности деления токов следует использовать высокоточные (± 1 %) резисторы.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

коэффициент деления

Тематики

Смотреть что такое «коэффициент деления» в других словарях:

коэффициент деления частоты интегральной микросхемы — коэффициент деления частоты Отношение частоты входного сигнала интегральной микросхемы к частоте выходного сигнала. Обозначение Kделf [ГОСТ 19480 89] Тематики микросхемы Синонимы коэффициент деления частоты … Справочник технического переводчика

коэффициент деления частоты преобразовательного модуля СВЧ — коэффициент деления Кдел Отношение частоты входного сигнала к частоте основной составляющей спектра выходного сигнала преобразовательного модуля СВЧ. [ГОСТ 23221 78] Тематики компоненты техники связи Обобщающие термины модули СВЧ, блоки СВЧ… … Справочник технического переводчика

коэффициент деления напряжения на выходе — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN output ratiooutput voltage ratio … Справочник технического переводчика

коэффициент деления напряжения потенциометра — Отношение выходного напряжения потенциометра при данном положении его подвижной системы к выходному напряжению [ГОСТ 21414 75] Тематики резисторы EN output ratio DE Spannungsteilungsverhältnis FR rapport de sortie … Справочник технического переводчика

коэффициент деления на быстрых нейтронах — sparčiojo dalijimosi faktorius statusas T sritis Standartizacija ir metrologija apibrėžtis Begalinėje terpėje vidutinio skaičiaus neutronų, atsirandančių dalijimosi, kurį sukelia visų energijų neutronai, metu, ir vidutinio skaičiaus neutronų,… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

Коэффициент деления напряжения потенциометра — 59. Коэффициент деления напряжения потенциометра D. Spannungsteilungsverhältnis E. Output ratio F. Rapport de sortie Отношение выходного напряжения потенциометра при данном положении его подвижной системы к выходному напряжению Источник: ГОСТ… … Словарь-справочник терминов нормативно-технической документации

Коэффициент деления частоты преобразовательного модуля СВЧ — 22. Коэффициент деления частоты преобразовательного модуля СВЧ Источник: ГОСТ 23221 78: Модули СВЧ, блоки СВЧ. Термины, определения и буквенные обозначения оригинал документа … Словарь-справочник терминов нормативно-технической документации

Коэффициент размножения нейтронов — k отношение числа нейтронов последующего поколения к числу нейтронов в предшествующем поколении во всём объеме размножающей нейтронной среды (активной зоны ядерного реактора). В общем случае, этот коэффициент может быть найден с помощью… … Википедия

Коэффициент размножения на быстрых нейтронах — μ показатель, учитывающий влияние деления ядер 238U быстрыми нейтронами на ход цепной реакции в реакторе на тепловых нейтронах. Содержание 1 Размножение на быстрых нейтронах 1.1 Гомогенная среда … Википедия

КОЭФФИЦИЕНТ УВЛАЖНЕНИЯ — индекс континентальности, отношение количества атмосферных осадков к потенциальной величине испарения с поверхности почвы в данной экосистеме. Определяется с помощью специальных приборов испарителей. Вычисляется путем деления годовой суммы… … Экологический словарь

Источник

Как определить коэффициент деления счетчика

Поиск по сайту

Счётчики

Соединив последовательно несколько триггерных схем — делителей частоты на два, получим простейший многоразрядный двоичный делитель. Более общее название для делителей частоты — счетчики. Коэффициент деления счетчика, состоящего из n-триггеров типа Т, составляет 2_n; здесь n — число двоичных разрядов счетчика. В настоящее время используется много вариантов счетных схем: асинхронные и синхронные; двоичные и десятичные; однонаправленные, только с увеличением счета, и двунаправленные, счет в которых может увеличиваться или уменьшаться (такие счетчики называют реверсивными). Коэффициент деления счетчика может быть либо постоянным, либо переключаемым.

Основой любой из этих схем служит линейка из нескольких триггеров. Рассмотренные варианты счетчиков различаются схемой управления этими триггерами. Между триггерами добавляются логические связи, назначение которых — запретить прохождение в цикле счета лишним импульсам, К примеру, четырехтриггерный счетчик может делить исходную частоту на 16, так как 2 4 = 16. Получим минимальный выходной код 0000, а максимальный 1111. Чтобы построить счетчик-делитель на 10, трех триггеров недостаточно (10 2 3 ), поэтому десятичный счетчик содержит в своей основе четыре триггера, но имеет обратные связи, останавливающие счет при коде 9 = 1001.

Таким обазом, удобно выпускать четырехтриггерные счетчики в двух вариантах: двоичном и десятичном. Примеры таких микросхем — пары: ИЕ6 и ИЕ7, ИЕ16 и ИЕ17. Расширять функции счетчиков можно; видоизменяя их цепи управления. Первоначально счетчики были асинхронными. В асинхронном режиме предыдущий триггер вырабатывает для последующего тактовые импульсы. Такие счетчики иногда называют счетчиками пульсаций.

В синхронном счетчике все триггеры получают тактовый импульс одновременно, поскольку тактовые входы их соединяются параллельно. Поэтому Триггеры переключатся практически одновременно. В счетчике пульсаций каждый триггер, вносит в процесс счета определенную задержку, поэтому младшие разряды результирующего кода появляются на выходах триггеров неодновременно, т. е. несинхронно с соответствующим тактовым импульсом. Например, для четырехразрядного счетчика пульсаций выходной параллельный код 1111 появится на выходах триггеров уже после того, как поступит шестнадцатый тактовый импульс, кроме того, эти четыре единицы сформируются неодновременно.

Синхронная схема значительно сложнее асинхронной. На ее выходах данные от каждого разряда появляются одновременно и строго синхронно с последним входным импульсом. В синхронный счетчик разрешается синхронная (с тактовым импульсом) параллельная (в каждый триггер) загрузка начальных данных. Триггерная линейка синхронного счетчика снабжается специальным шифратором, который называется схемой ускоренного переноса (СУП).

Внутренние логические элементы управления, которыми часто снабжаются счетчики, позволяют сделать процесс счета реверсивным. Согласно команде, подаваемой на вход управления счетом больше/ меньше , можно либо, увеличивать либо уменьшать на единицу содержимое счетчика при каждом очередном тактовом импульсе. У некоторых счетчиков тактовые входы на увеличение и на уменьшение отдельные.

Сброс данных счетчика, чтобы на всех выходах установился нулевой код, у одних схем асинхронный R, у других синхронный SR, происходит одновременно е приходом тактового импульса. Имеются счетчики с переменным коэффициентом деления. Устанавливаемый коэффициент деления зависит от кода, набранного на входах управления.

Рассмотрим микросхемы КМОП среднего уровня интеграции, необходимых для счета импульсов и деления частот. Счетчики-делители составляют несколько групп. Например, счетчики ИЕ3 ИЕ5 предназначены для построения схем электронных секундомеров, часов, таймеров. Их можно использовать, например, для обслуживания индикаторов цифровых мультиметров, термометров. Счетчики ИЕ8 и ИЕ9 имеют дешифрованные выходы (10 и 8 соответственно). Счетчики ИЕ11 и ИЕ14 однотипные четырехразрядные, реверсивные. Разнообразные возможности деления частот открывает применение счетчиков выполненых на микросхемах КМОП: ИЕ2, ИЕ10, ИЕ16 и ИЕ19. Имеются счетчики асинхронные, синхронные, разрядные и даже 14-разрядный — ИЕ16.

Источник

Счетчики

Счетчиком называется устройство для подсчета числа входных импульсов. С поступлением каждого импульса на вход С состояние счетчика изменяется на единицу. Счетчик можно реализовать на нескольких триггерах, при этом состоя­ние счетчика будет определяться, состоянием его триггеров. В суммирующих счетчиках каждый входной импульс увеличивает число на его выходе на едини­цу, в вычитающих счетчиках каждый входной импульс уменьшает это число на единицу. Наиболее простые счетчики — двоичные. На рис. 5.4 представлен сум­мирующий двоичный счетчик.

При построении счетчика триггеры соединяют последовательно. Выход каж­дого триггера непосредственно действует на тактовый вход следующего. Для того чтобы реализовать суммирующий счетчик, необходимо счетный вход очередного триггера подключать к инверсному выходу предыдущего. Для того чтобы изме­нить направление счета (реализовать вычитающий счетчик), можно предложить следующие способы:

— считывание выходных сигналов счетчика не с прямых, а с инверсных выхо­дов триггеров;

— изменение структуры связей в счетчике путем подачи на счетный вход триг­гера сигнала не с инверсного, а с прямого выхода предыдущего устройства.

Счетчики характеризуются числом состояний в течение одного периода счета (цикла). Число состояний определяется количеством триггеров k в структуре счетчика. Так, при k = 3 число состояний равно N=2 3 =8 (от 000 до 111).

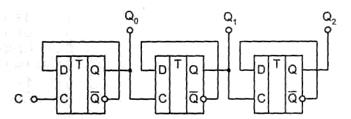
Рисунок 5.4 — Двоичный суммирующий счетчик

Число состояний счетчика принято называть коэффициентом пересчета К_счЭтот коэффициент равен отношению числа импульсов N_вхна входе к числу им­пульсов N_вых на выходе старшего разряда счетчика за период счета:

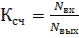(5.9)

Если на вход счетчика подавать периодическую последовательность импуль­сов с частотой 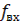, то частота 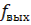на выходе старшего разряда счетчика будет меньше в К_сч раз:

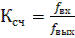(5.10)

Поэтому счетчики можно использовать в качестве делителей частоты, величи­на К_сч в этом случае будет коэффициентом деления. Для увеличения величины К_сч приходится увеличивать число триггеров в цепочке. Каждый дополнитель­ный триггер удваивает число состояний счетчика и число К_сч. Для уменьшения коэффициента К_сч можно в качестве выхода счетчика рассматривать выходы триггеров промежуточных каскадов. Например, для счетчика на трех триггерах К_сч =8, если взять выход 2-го триггера, то К_сч =4. При этом К_сч всегда будет являться целой степенью числа 2, а именно: 2, 4, 8, 16 и т. д.

Можно реализовать счетчик, для которого К_сч окажется любым целым чис­лом. Например, для счетчика на трех триггерах реализуется К_сч в пределах от 2 до 7, но при этом один или два триггера могут оказаться лишними. При использова­нии всех трех триггеров можно получить К_сч = 5. 7, то есть 2 2 3 . Счетчик с К_сч =5 должен иметь 5 состояний, которые в простейшем случае образуют последовательность: <0, 1, 2, 3, 4>. Циклическое повторение этой последовательно­сти означает, что коэффициент деления счетчика равен 5.

Для построения суммирующего счетчика с К_сч =5 надо, чтобы после форми­рования последнего числа из последовательности <0,1,2,3,4>счетчик переходил не к числу 5, а к числу 0. В двоичном коде это означает, что от числа 100 нужно перейти к числу 000, а не 101. Изменение естественного порядка счета возможно при введении дополнительных связей между триггерами счетчика. Можно вос­пользоваться следующим способом: как только счетчик попадает в нерабочее со­стояние (в данном случае 101), этот факт должен быть опознан и повлечь после­дующую выработку сигнала, который перевел бы счетчик в состояние 000.

Факт попадания счетчика в нерабочее состояние описывается логическим уравнением:

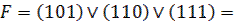
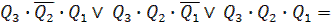
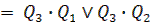(5.11)

Состояния 110 и 111 также являются нерабочими и поэтому учтены при со­ставлении уравнения. Если на выходе эквивалентной логической схемы F = 0, значит, счетчик находится в одном из рабочих состояний: v l v 2 v 3 v 4. Как только он попадает в одно из нерабочих состояний 5 v 6 v 7, формируется сигнал F= 1. Появление сигнала F= 1 должно переводить счетчик в начальное состояние 000, следовательно, этот сигнал нужно использовать для воздействия на устано­вочные входы триггеров счетчика, которые осуществляли бы сброс счетчика в состояние 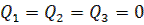. Один из вариантов построения счетчика с К_сч =5 представлен на рисунке 5.5.

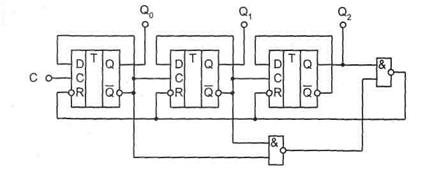
Рисунок 5.5 — Схема счетчика с коэффициентом пересчета 5

Источник

Счетчики с заданным коэффициентом деления

Такой счетчик используется если требуется требуемый коэффициент пересчета.

Коэффициент пересчета (деления) – кол-во различных состояний, в которых может находиться система. Для счетчиков – это число возможных комбинаций, которые счетчик может выдать на выходе. Например если счетчик имеет 4 выхода, то на них могут присутствовать значения от 0000 до 1111 т.е. всего 16 различных состояний, значит коэф. пересчета равен 16! Коэффициент определяется по формуле: N=2 n ,n-число выходов счетчика.

Если же требуется счетчик который должен считать например от 0000 (десятичное 0) до 1011 (десятичное 11), то требуется коэффициент пересчета равный 12! Для этого и применяется счетчик с заданным коэффициентом пересчета. От обычного он отличается тем, что имеет один логический элемент 4И с 4-мью входами (На его выходе появиться 1 ТОЛЬКО если на ВСЕХ входах будут 1!)

Все 4 триггера помимо входа для тактирующих импульсов (С), прямого и инверсных выходов имеют входы сброса (R). Если во время подсчета импульсов счетчика на эти входы подать 1, то произойдет сброс ВСЕХ триггеров в нулевое значение, это означает, что счетчик будет считать ЗАНОВО (от 0000). Для того, чтобы обеспечить сброс триггеров на входы элемента 4И должны быть поданы четыре единицы =) Т.о. в зависимости от требуемого коэффициента пересчета счетчика мы подключаем входы 4И к прямым или инверсным входам триггеров. На рис представлена схема, которая обеспечивает коэффициент пересчета равный 10. Первый вход 4И на прямой выход триггера, второй – на инверсный, третий на инверсный, четвертый на прямой. Т.е. если на выходах 1,2,4,8 счетчика появляется число 1001 (дес. 9), то на входах 4И действует 4 единицы (на 2,4 выходах счетчика сигналы снимаются с инверсных выходов триггеров), что приводит к подаче сигнала сброса на все триггеры и счетчик начинает считать заново.

1.Конденсаторные керамические материалы Конденсаторные керамические материалы отличаются от обычных керамических материалов значительно большей величиной диэлектрической проницаемости (е). Кроме того, большинство конденсаторных керамических материалов обладает малым температурным коэффициентом диэлектрической проницаемости (ТКе). Вследствие этого в электрических установках с керамическими конденсаторами повышение температуры не вызывает заметного изменения емкости в установке.Основным компонентом большинства исходных керамических масс для конденсаторной керамики является двуокись титана (TiOг) или двуокись олова (БпО2), представляющие собой порошки белого цвета. После обжига при температуре 1300—1350° С двуокись титана или двуокись олова приобретает плотную кристаллическую структуру.Конденсаторные керамические материалы па основе двуокиси титана с небольшими добавками глинистых веществ и некоторых других компонентов известны под марками М-70; Т-80. Цифры при буквах показывают величину диэлектрической проницаемости этих материалов. Из них изготовляют керамические конденсаторы на высокие напряжения, так как эти материалы обладают относительно малыми значениями тангенса угла диэлектрических потерь Чтобы получить материалы с еще большими значениями диэлектрической проницаемости и с малыми величинами температурного коэффициента диэлектрической проницаемости, прибегают к соединениям двуокиси титана с окислами других металлов: кальция (СаО), магния (MgO), цинка (ZnO) и др.В процессе обжига смеси этих окислов, взятых в определенном соотношении, образуются титанаты соответствующих металлов: титанат кальция (СаТiО3), титанат магния (MgTiО3), титанат цинка (ZnTiО3) и др. Все титанаты отличаются большими значениями диэлектрической проницаемости (е = 20-250), что объясняется интенсивно развивающимися в них процессами ионной и электронной поляризации при наличии в этих материалах внутреннего электрического поля, усиливающего эти процессы. Внутреннее электрическое поле в титанатах различных металлов вызвано особенностью их кристаллической структуры.Замечено, что у титанатов, имеющих большую величину диэлектрической проницаемости, наблюдается и большая величина температурного коэффициента диэлектрической проницаемости (ТКк).К материалам, идущим для изготовления термостабильных керамических конденсаторов, относятся термоконды (Т-20 и Т-40). Из этих материалов изготовляют термостабильные конденсаторы низкого напряжения, емкость которых в очень малой степени зависит от температуры.В производстве термостабильных керамических конденсаторов высокого и низкого напряжения находят большое применение материалы, получаемые на основе соединений двуокиси олова (SnC2) с другими металлами (СаО; MgO и др.). Такого рода диэлектрики называются станнатами, например станнат кальция (CaSn03), станнат магния (MgSn03) и др.Эти керамические материалы обладают весьма малыми положительными значениями температурного коэффициента диэлектрической проницаемости ТКе=(20-30) -10-6 1/°С.Из станнатной керамики изготовляют высокостабильные керамические конденсаторы высокого и низкого напряжения. Станнатная керамика более устойчива к длительному воздействию постоянного электрического поля высокого напряжения по сравнению с материалами на основе титанатов.У керамических материалов на основе титанатов постоянное электрическое поле вызывает процесс электрохимического старения материала при повышенных температурах (200—300° С). В результате этого необратимого процесса электроизоляционные свойства титанатовой керамики ухудшаются и при высоких напряжениях это приводит к пробою конденсаторов.Керамические конденсаторы (см. рис. 131) изготовляют различными методами: прессованием в стальных пресс-формах из исходных порошкообразных масс (дисковые конденсаторы), протяжкой с помощью вакуум-пресса из пластичных керамических масс, методом литья жидкой керамической массы в гипсовые формы. Последний способ применяют для изготовления керамических конденсаторов на высокие напряжения, например горшковых конденсаторов (см. рис. 131, г). Конденсаторы, полученные одним из трех описанных способов, подвергают термической обработке — обжигу в печах. В результате обжига получают неувлажняемые изделия из плотных керамических материалов. Керамические конденсаторы не нуждаются в герметизации (металлических или пластмассовых кожухах), которая необходима для защиты от влаги бумажных и слюдяных конденсаторов.Металлические электроды наносят па поверхность керамических конденсаторов методом вжигания серебра. Для этого на поверхность уже готовых керамических конденсаторов наносят слой краски, в которой имеются окислы серебра. Затем конденсаторы ставят в печь, где при температуре 750—800° С происходит термическая обработка нанесенного слоя краски. При этом окислы серебра восстанавливаются до металлического серебра, которое прочно сцепляется с поверхностью неглазурованной керамики, образуя слой толщиной 8—12 мкм. К этому слою серебра припаивают медные проводники, а затем весь конденсатор покрывают слоем органической электроизоляционной эмали. Последняя необходима для защиты электродных слоев серебра от коррозии и для предотвращения замыкания электродов частицами влаги в случае применения конденсаторов во влажной атмосфере.Основные характеристики наиболее широко применяемых керамических конденсаторных материалов приведены в табл. 47.

СЕГНЕТОЭЛЕКТРИКИ — кристаллич. диэлектрики (полупроводники), обладающие в определённом диапазоне темп-р спонтанной поляризацией, к-рая существенно изменяется под влиянием внеш. воздействий. Структуру С. можно представить как результат фазового перехода кристалла с искажением структуры (понижением симметрии) из неполярной структуры (параэлектрич. фазы) в полярную (сегнетоэлектрич. фазу). В большинстве случаев это искажение структуры такое же, как и при воздействии электрич. поля на кристалл в неполярной (параэлектрич.) фазе. Такие С. наз. собственными, а искажение неполярной структуры связано с появлением спонтанной электрич. поляризации. В ряде С. поляризация возникает как вторичный эффект, сопровождающий перестройку структуры, к-рая не связана непосредственно с поляризацией и не может быть вызвана электрич. полем. Такие С. наз. несобственными.

Как правило, наблюдается фазовый переход непосредственно между сегнето- и параэлектрической (более симметричной) фазами. Однако есть кристаллы, в к-рых между этими фазами осуществляется промежуточная фаза с особыми свойствами — т. н. несоразмерная фаза (см. ниже).

Особенностью всех С. является относит. близость структур пара- и сегнетоэлектрич. фаз. Изменения ср. положений ионов при возникновении спонтанной поляризации обычно гораздо меньше, чем межионные расстояния. Поэтому спонтанная поляризация С. легко изменяется под влиянием внеш. воздействий — электрич. полей, упругих напряжений, изменений темп-ры и др. С этим связаны весьма высокие (по сравнению с обычными диэлектриками) значения диэлектрич. проницаемости, пьезоэлектрических (см. Пъезоэлектрики)и пироэлектрических (см. Пароэлектрики)постоянных. Сегнетоэлектрич. свойства были впервые обнаружены у кристаллов сегнетовой соли KNaC₄H₄O₆*4H₂O (1921), а затем у дигидрофосфата калия КН₂РО₄ (1935). Интенсивные исследования С. начались в 1945, когда были обнаружены сегнетоэлектрич. свойства керамики ВаТiO₃ — родоначальника обширного семейства С. кислородно-октаэдрич. типа. В 60-х гг. начались исследования несобств. С., в сер. 70-х гг.- С. с несоразмерной фазой. К 1990 известно неск. сотен С.; характеристики нек-рых из них приведены в табл.

Характеристики некоторых сегнетоэлектриков (С — собственный, Н-несобственный, НС-с несоразмерной фазой)

Пьезокерамика — искусственный материал, обладающий пьезоэлектрическими и сегнетоэлектрическими свойствами, имеющий поликристаллическую структуру.

Пьезокерамика не принадлежит к классическим видам керамики, поскольку в ее состав не входит глинистое вещество. Пьезокерамические материалы синтезируются из окислов металлов. Однако применение характерного для керамической технологии приема — обжига при высокой температуре — оправдывает отнесение пьезокерамических материалов к семейству керамики. Пьезо (от греческого «пиезо» — давить) указывает на то, что этому виду керамики присуще особое свойство — пьезоэлектрический эффект.

Размеры кристаллитов обычно от 2 до 100 мкм. Каждый кристаллит представляет собой сегнетоэлектрический кристалл.
В исходном состоянии поляризация пьезокерамических (ПК) элементов равна нулю, поскольку каждый кристаллит разбит на домены и имеет случайное направлениекристаллографической оси. При приложении внешнего электрического поля превышающего определённую величину, называемую коэрцитивным полем, направления поляризации кристаллитов выстраиваются в направлении максимально близком к направлению поляризующего поля. Поляризованная пьезокерамика обладает ярко выраженными пьезоэлектрическими свойствами.

Величина пьезомодуля d33 достигает нескольких сотен пКл/Н. Также для ПК характеризуется высокими значениями относительной диэлектрической проницаемости.

ПК обладают всеми свойствами, присущими кристаллическим сегнетоэлектрикам.
Впервые ПК материал был синтезирован в 1944 г. советским ученым Б. М. Вулом, обнаружившим сегнетоэлектрические свойства титаната бария ВаТiO₃. Практически одновременно эти свойства титаната бария были обнаружены американскими и японскими исследователями.

Дата публикования: 2015-02-03 ; Прочитано: 1056 | Нарушение авторского права страницы

Источник

Если коэффициент деления двух чисел является многозначным числом, то оно делится в столбик. Это также известно как угловое деление.

Получить целое число при делении

В этой статье мы рассмотрим разделение полноты без баланса. Мы будем обсуждать деление чисел целостности только в тех случаях, когда абсолютные числа делятся поровну (см. Деление чисел целостности без равновесия). В отдельной статье мы обсудим деление целых чисел, которые уравновешивают друг друга.

Сначала представлены термины и символы, используемые для описания деления интегралов. Далее вводится понятие расщепления чисел целостности. Это помогает извлечь правила для разбиения положительной полноты, отрицательных целых чисел и целых чисел с разными знаками. В этом разделе также рассматривается пример применения правил разбиения к целым числам. Наконец, мы показываем, как контролируются результаты расщепления последовательности.

Термины и обозначения

Для описания деления целых чисел мы используем те же термины и символы, что и при описании деления натуральных чисел (см. разделение, разделы, части и деления). Позвольте нам напомнить вам.

Делимое целое число называется делителем. Делимое целое число называется делителем. Результат деления целого числа называется делителем.

Деление обозначается символом: между дивидендом и дивидендом (иногда встречается символ, указывающий на деление). Деление целого числа a на целое число a можно записать символом: a:b. Если целое число a приводит к числу C, исключая целое число B, то удобно записать этот факт в виде равенства: выражение b = C вида a:b также называется квантором, как и значение выражения.

Смысл деления целых чисел

Мы знаем о существовании связи между умножением и делением натуральных чисел. Из этой связи мы делаем вывод, что деление — это нахождение неизвестного множителя, когда второй множитель и произведение известны. Давайте придадим такое же значение разделению последовательности. Другими словами, деление последовательности — это одно целое число определенного произведения и другой целочисленный множитель.

Исходя из понятия последовательного деления, можно сказать, что если произведение двух целых чисел a и b равно c, то при делении c на a получается b, а при делении c на b — b. Пример. Допустим, мы знаем, что произведение двух целых чисел 5 и -7 равно -35, мы можем сказать, что коэффициент (-35) : 5 равен -7, а коэффициент (-35) : (-7) равен 5.

Обратите внимание, что коэффициент деления целого числа a на целое число b является целым числом (если A делится на B без остатка).

Результат этого действия считается бесконечно большим и бесконечно равным. Смысл этого выражения заключается в том, что коэффициент бесконечно возрастает (по модулю), если делитель приближается к нулю, а делимое остается равным или близким к A.

Содержание

Целочисленное кольцо не замкнуто на деление. Проще говоря, это означает, что результат деления целого числа на другое целое число может быть нецелым. Однако если результатом является целое число, то говорят, что это деление без остатка.

Деление чисел долгое время считалось самой сложной арифметической операцией. В Средние века мало кто знал «секрет» деления. Это было связано с тем, что существовавшие алгоритмы деления были очень громоздкими и сложными для выполнения и запоминания (например, деление в виде лодочек). С появлением колонного деления ситуация радикально изменилась. Деление, наряду с другими арифметическими действиями, теперь входит в программу по математике для первого класса школы. Однако, как и в случае с умножением (см. Быстрое умножение), недавно был открыт более эффективный алгоритм для вычислительных целей (см. en: Деление (цифровое)).

Существуют правила, позволяющие быстро определить, делится ли число на определенный делитель без остатка (точка деления). Наиболее известными делителями являются 2, 3, 4, 5, 8, 9, 11, 25 и их производные, а также делители 7, 13, 1001 и других чисел.

Целое число, которое одновременно делится на много чисел без остатка, называется наибольшим общим делителем.

Определение количества делителей натурального числа приводит к двум важным понятиям: комплексные числа и простые числа. Простое число имеет два различных делителя: единицу и само число. Комплексные числа имеют три или более различных делителей. 1 не является ни комплексным, ни простым числом.

Если натуральное число не делится на другое число без остатка, его иногда называют делением с остатком. Изучение остатков, их сравнение и стандартизация в выводе привели к созданию целой науки — теории чисел.

На остатки обычно накладываются следующие ограничения (чтобы они были правильно определены, т.е. уникальны).

где — делитель, а — остаток.

Деление целых чисел

Деление на любое целое число по сути ничем не отличается от деления на натуральные числа. При условии, что единицы измерения разделены и учтена конвенция знаков.

Однако деление целых чисел с остатком определяется неоднозначно. В одном случае, (так же как и без остатка) рассматривают сначала модули и в результате остаток приобретает тот же знак, что делитель или делимое (например,

Деление рациональных чисел

Замыкание множества целых чисел действием деления расширяет множество логических чисел. Это приводит к тому, что результат деления целого числа на другое целое число всегда является рациональным числом. Более того, полученные числа (рациональные числа) уже полностью поддерживают акт деления (они замкнуты на него).

Правила деления логических дробей: = frac = frac «ширина =» «» высота = «» />

Если известно количество учеников в классе и количество яблок, взятых каждым из них, то общее количество яблок можно вычислить, умножив количество учеников на количество яблок, взятых каждым из них. Другими словами, количество учеников — это первый фактор, количество яблок — второй фактор, а количество розданных яблок — произведение.

Конкретный смысл действия деление. Название чисел при делении

Минус сказал, что он посетил ГД. Там они кормили голодных кошек и распределяли пойманную рыбу поровну между ними. Таким же образом они ели соседских детей, а также груши. Они решали различные задачи на деление и объясняли, когда нужно делить с минусом.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам из комплекта, необходимо приобрести его в каталоге и добавить в личный кабинет.

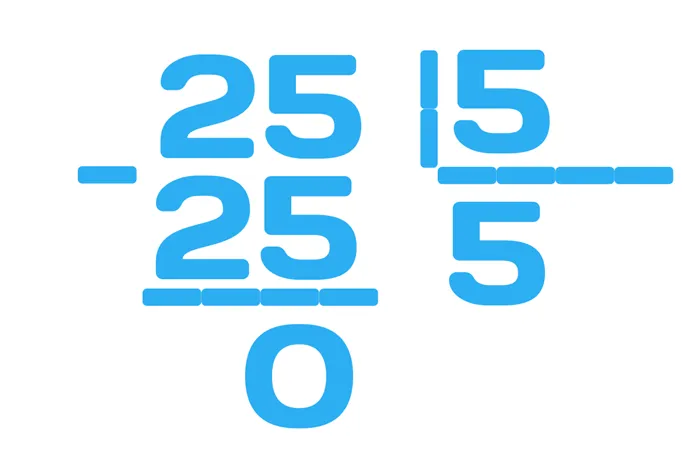
Конспект урока «Конкретный смысл действия деление. Название чисел при делении»

Добрый вечер!!! Я скучал по вам, ребята. Я поехал в отпуск к родственникам. А Плюс был здесь совсем один. Но теперь пришло время отдохнуть. О, все будет хорошо. r

И сегодня я представляю вам новое поведение — ядерное деление. Именно так зовут моего родственника — Ядерное Деление. Он очень добрый. Мы вместе сделали много хорошего. Недалеко от жизни, которую мы разделяем, живет бездомная кошка. Поэтому каждый день мы ловили рыбу и приносили еду. В первый день мы поймали восемь рыб и пошли кормить кота. Кошки подбежали к нам, и мы дали им две рыбки. Как вы думаете, сколько кошек мы накормили в первый день?

Посмотрите, как это произошло. Первый кот побежал и взял две рыбы, затем следующий кот. Он поймал еще две рыбы, затем еще одна кошка поймала две рыбы. И последняя кошка, к которой он подошел, была маленькая рыжая, и он тоже поймал две рыбы. А наше ведро было пустым.

Все котята взяли по две рыбки. Сколько раз ты дал каждому из них по две рыбки? Один, два, три и четыре. Поэтому мы подарили им четырех кошек.

На следующий день мы поймали четырнадцать рыб. Мы накормили кошек и рыбу и подумывали о том, чтобы съесть оставшуюся рыбу. Но на этот раз у нас было больше кошек. Поэтому мы стали кормить двух рыбок равными порциями каждую, пока ведро снова не освободилось. Сколько кошек мы накормили в этот раз?

Поэтому, используя цифры и математические символы, мы записывали, как мы кормили кошек.

Да, это хорошо. Семь раз происходит акт удаления. Другими словами, семь котят ели рыбу.

Но на третий день мы пошли на рыбалку рано утром, и мы поймали котенка, и это был хороший котенок, и это был хороший котенок, и мы поймали его. И мы поймали, вы не поверите — 48 рыб. Но на этот раз пришло целое стадо кошек и все съело. Хотите посчитать, сколько кошек бегает?

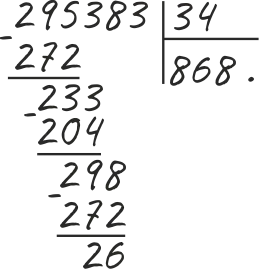
Ну, мы боимся смотреть на снимки. Конечно, мы измерили 24 кошки. Но это очень позорный рекорд. И здесь мне на помощь пришел сектор, который является моим родственником. Если все удаления на самом деле одинаковы, т.е. если что-то распределено поровну и ответ равен нулю, то это действие можно заменить делением. Результат — количество абстрактных факторов.

Посмотрите, как кормили кошку в первый день:.

Затем мы измерили, сколько раз кошке давали рыбу, т.е. два числа. Вместо того чтобы входить в систему таким образом, вы можете делать более короткие записи. Сначала мы пишем число, обозначающее общее количество рыб. Мы пропускаем ячейку и пишем число, указывающее, сколько рыб получил каждый кот. А между ними мы помещаем символ разделения:.

Видите, это мое относительное разделение, а это символ разделения — две точки.

А теперь читаем запись: восемь делится на два получается 4. Поэтому я поставил четырех кошек.

А как вы поделили 14 рыб между кошками:.

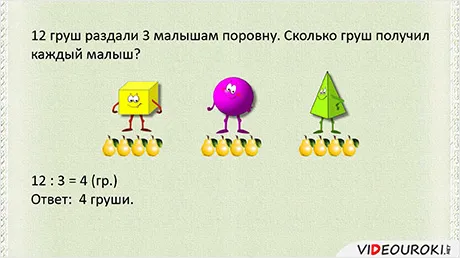
Рядом с адресом живут три малыша — Кубик, Шарик и Пирамидка. При делении они часто превращаются в плоды. А вчера, пока я не пришла домой, мы купили 12 груш и раздали всем поровну. Вы думаете, каждый человек получил его?

Давайте посмотрим, как распределились груши. Вот 12 груш. Сначала каждому ребенку давали по одному, потом еще и еще. Груши готовы. Мы распределяем 12 груш поровну между тремя детьми.

Разделения могут контролироваться подразделениями, если действие разделения не приводит к равновесию. Действительно, если делитель является произведением делимого и делителя, нам нужно взять второй коэффициент, делитель, разделив делимое на делитель (один из коэффициентов).

Деление 3 класс

Дети в третьем классе только начинают проходить через разделение. Поэтому студенты третьего курса решают самые простые задачи.

Задача 1. Работник фабрики обещает положить 56 пирожных в 8 упаковок. Сколько пирожных должно быть в каждой упаковке, чтобы положить в каждую упаковку одинаковое количество пирожных?

Вопрос 2: В канун Нового года классу из 15 детей в школе раздают 75 конфет. Сколько сладостей должен получить каждый ребенок?

Вопрос 3. Роман, Саша и Миса выбрали 27 яблок с одной яблони. Сколько яблок получит каждый, если им придется делиться поровну?

Вопрос 4. Четыре друга купили 58 печений. Но потом они поняли, что не могут разделить их поровну. Сколько еще печенья нужно, чтобы каждый друг получил 15 печений?

Деление 4 класс

Деление на четвертый класс более серьезное, чем на третий. Все расчеты производятся путем разбиения на столбцы, и число, входящее в разбиение, немаленькое. Что такое разделение колонок? Ответ вы найдете ниже:.

Деление в столбик

Найди ответ на свой вопрос Что такое деление в столбик? Это способ поиска ответов для деления больших чисел. Если вы можете разделить такое простое число, как 16 или 4, то ответ очевиден — 4. Тогда 512:8 в детском сознании не так-то просто. Наша задача — рассказать о методах решения таких примеров.

Шаг 1. Напишите делитель и делимое следующим образом.

В итоге части записываются под делителем, а вычисление — под делимым.

Шаг 2. Начните делить слева направо. Во-первых, возьмите число 5.

Шаг 3. Пятая цифра меньше восьмой и поэтому не может быть разделена. Таким образом, получается еще одна цифра делителя.

51 теперь больше 8. Это неполный коэффициент.

Шаг 4. Поставьте точку под разделителем.

Шаг 5. За 51 следует 2, поэтому ответом будет другое число. Другими словами, коэффициент — это двузначное число. Поставьте вторую точку:.

Шаг 6. Запустите режим разделения. Максимальное число делителей от 8 до 51 без остатка равно 48; деление 48 на 8 дает 6. Напишите 6 вместо первой точки под делителем.

Шаг 7. Затем напишите число чуть ниже 51 и добавьте знак ‘-‘.

Шаг 8. Затем вычтите 48 из 51, чтобы получить ответ 3.

Шаг 9*. Вычтите число 2 и запишите его рядом с числом 3.

Шаг 10 Разделите полученное число 32 на 8, чтобы получить вторую цифру ответа — 4.

Ответ — 64, что не является сбалансированным. При делении на 513 остаток равен 1.

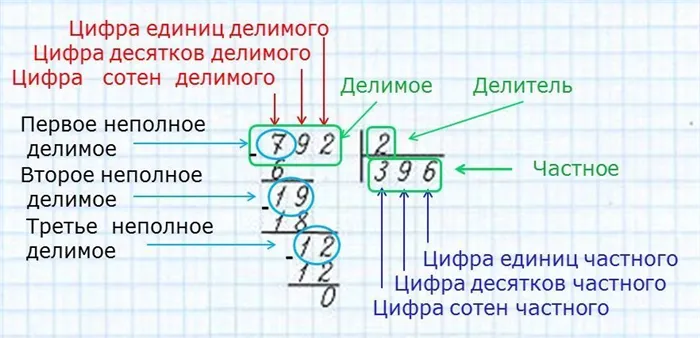
Деление трехзначных

Деление трехзначных чисел выполняется методом деления столбиком, описанным в примере выше. Это пример трехзначного числа.

Деление дробей

Деление не так сложно, как может показаться на первый взгляд. Например, (2/3): (1/4). Метод деления прост. 2/3 — делитель, а 1/4 — делимое. Знак деления (:) может быть заменен знаком умножения (), но для этого позиции числителя и знаменателя делителя меняются местами. Таким образом, мы имеем (2/3) (4/1), (2/3) * 4, что равно 8/3 или 2 целых числа и 2/3. Вот еще один пример с диаграммой для лучшего понимания. Изучение дробей (4/7):( 2/5):.

Как и в предыдущем примере, делитель 2/5 инвертируется для получения 5/2, а делитель заменяется умножением. Таким образом, получаем (4/7)*(5/2). Вычтите и ответьте: 10/7, затем вычтите целую часть: 1 целое число и 3/7.

Деление числа на классы

Введите число 148951784296 и разделите на 3 цифры: 148 951 784296. Таким образом, справа налево: 296 — класс единиц, 784 — класс тысяч, 951 — класс миллионов, 148 — класс миллионов. миллиарды. Аналогично, каждый класс имеет три разряда со своим разрядным классом. Справа налево: первая цифра — единицы, вторая цифра — десятки, третья цифра — сотни. Например, порядок единиц — 296, 6 — единицы, 9 — десятки и 2 — сотни.

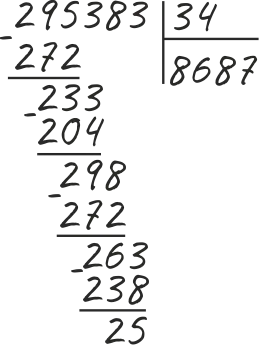
Вопрос 2: В канун Нового года классу из 15 детей в школе раздают 75 конфет. Сколько сладостей должен получить каждый ребенок?

Рассмотрим пример: 6:2 = 3, умножаем на 2σ3= 6, чтобы проверить, правильно ли вы разделили. Примечание 3:0 является неконтролируемым, так как любое число, умноженное на ноль, будет равно нулю. Поэтому примечание 3:0 не имеет смысла. Правило деления: нельзя делить на ноль.

0: 3 = 0 Это письмо имеет смысл. Если ничто разделить на три, то не будет ничего. 0: a = 0 Правило деления: если 0 делится на натуральное число, не равное нулю, то результат всегда равен нулю.

3: 3 = 1 a: a = 1 Правило деления: при делении любого числа, не равного нулю, на само себя результат всегда равен 1.

Вопрос по дивизиону:.

С помощью символики a: b = c, каков здесь коэффициент? Ответ: a: b и c.

Каков здесь коэффициент? ОТВЕТ: Коэффициент показывает, во сколько раз делимое больше делителя.

Что символизирует 0⋅m= 5? Ответ: При умножении на ноль ответ всегда равен нулю. Записи бессмысленны.

Существует ли n такое, что 0⋅n= 0? Ответ: Да, запись имеет смысл. Если умножить любое число на ноль, то оно станет нулем. Следовательно, n — произвольное число.

Пример №1: Найти значение выражения: а) 0:41 б) 41:41 в) 41:1 Ответ: а) 0:41 = 0 б) 41:41 = 1 в) 41:1 = 41

Пример 2: Исходя из значений переменных, применимо следующее уравнение: a) x: 6 = 8 b) 54: x = 9

(a) В данном примере x — это линия раздела. Чтобы найти дивиденд, умножьте делимое на делитель. x — неизвестный делитель, 6 — делимое и 8 — делитель. x = 8⋅6x = 48

(b) 54 — делитель, x — делимое и 9 — делитель. Чтобы найти неизвестный делитель, разделите делимое на делитель. x = 54: 9 x = 6

Задача 1: У Саши 15 марок, а у Мисс — 45. На сколько марок больше у Мисс, чем у Саши? Решение: проблема может быть решена двумя способами. Первый способ: 15+15+15 = 45 Чтобы получить 45, нужно 3 числа 15. Таким образом, масса имеет в 3 раза больше марок, чем Саша. Второй метод: 45:15 = 3

ОТВЕТ: у массы в три раза больше марок, чем у Саши.

You may also like:

Десятичные дроби. Разряды и классы десятичных дробей.

Нужен репетитор по математике (алгебре) или геометрии?

Сравнение неправильных дробей правила и примеры.

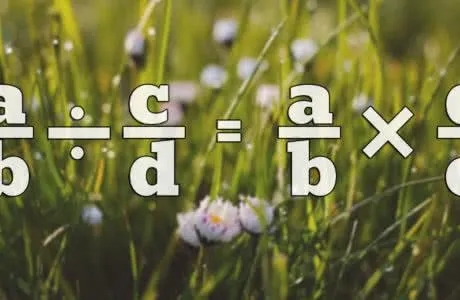
Коэффициент – деление

Cтраница 1

Коэффициент деления / гдел выбирается так, чтобы напряжение, снимаемое с делителя, было меньше номинального предела потенциометра и чтобы отсчет на потенциометре производился не менее как на четырех декадах.
 [2]

Коэффициент деления равен тту и на входе сравнивающего устройства будет напряжение 0 8 в.
 [3]

Коэффициент деления изменяется путем подачи дополнительных импульсов на вход делителя при уменьшении К.
 [4]

Коэффициент деления может быть постоянным либо регулируемым. Изменение коэффициента деления достигается путем изменения числа Витков обмоток или их частей, причем в зависимости от места переключения витков ( входной или выходной обмотки) получают схемы о постоянным выходным или входным сопротивлением. Особенностью индуктивного делителя является наличие между витками обмоток тесной индуктивной связи, в идеальном случае в предположении того, что все витки обмоток имеют одинаковое потокосцепление, в потоки рассеяния отсутствуют.
 [5]

Коэффициент деления постоянен в широкой полосе частот, что при исследовании импульсов особенно важно. На низких частотах правильность деления определяется соотношением сопротивлений делителя, а на высоких – соотношением емкостей делителя с учетом паразитных емкостей. Величина переходного конденсатора С такова, что он почти не оказывает влияния на проходящий сигнал.
 [7]

Коэффициент деления проверяется при подаче на вход прямоугольного импульса длительностью 50 мксек. Рассматривается форма импульса при чувствительности 3 мв / мм и величине изображения 25 – 35 мм. Затем амплитуда на входе увеличивается в 3 раза, и чувствительность устанавливаегся 9 мв / мм.
 [8]

Коэффициент деления может принимать одно и.
 [9]

Коэффициент деления может принимать одно из значений в соответствии с приведенной ниже таблицей.
 [10]

Коэффициент деления равен ZN. Счетчики такого вида часто называют счетчиками Джонсона. Большинство счетчиков-делителей серии К176 выполнены по рассмотренной схеме.
 [12]

Коэффициент деления может быть постоянным либо регулируемым.
 [13]

Коэффициент деления набор резисторов определяется как отношение выходного напряжения к напряжению на его входе.
 [14]

Страницы:  

   1

   2

   3

   4

   5

Делители напряжения и тока

В электротехнике очень часто применяются делители напряжения, работу которых можно рассмотреть, применяя правило распределения напряжений. На рисунке показаны схемы делителей напряжения, служащих для уменьшения заданного напряжения источника питания (например, 4, 6, 12 или 220 В) до напряжения любого меньшего значения.

Рис. 1. Схемы делителей напряжения

В электрических электрических приборах, а также при проведении измерений иногда необходимо получить несколько напряжений определенного значения от одного источника. Делители напряжения часто (и прежде всего в слаботочной технике) называют потенциометрами.

Изменяемое частичное напряжение получается при перемещении скользящего контакта реостата или другого типа резистора. Постоянное по значению частичное напряжение может быть получено посредством отпайки от резистора или же может сниматься с точки соединения двух отдельных резисторов.

При помощи скользящего контакта можно плавно изменять необходимое для приемника с сопротивлением (сопротивление нагрузки) частичное напряжение, при этом скользящий контакт обеспечивает параллельное соединение сопротивлений, с которого снимается частичное напряжение.

В составе делителя напряжения для получения фиксированного значения напряжения используют резисторы. В этом случае выходное напряжение U вых связано с входным U вх (без учета возможного сопротивления нагрузки) следующим соотношением:

Рис. 2. Делитель напряжения

Пример. С помощью резисторного делителя нужно получить на нагрузке сопротивлением 100 кОм напряжение 1 В от источника постоянного напряжения 5 В. Требуемый коэффициент деления напряжения 1/5 = 0,2. Используем делитель, схема которого приведена на рис. 2.

Сопротивление резисторов R1 и R2 должно быть значительно меньше 100 кОм. В этом случае при расчете делителя сопротивление нагрузки можно не учитывать.

Следовательно, R2 / (R1 +R2) R2 = 0,2

Поэтому можно выбрать R2 = 1 кОм, R1 — 4 кОм. Сопротивление R 1 получим путем последовательного соединения стандартных резисторов 1,8 и 2,2 кОм, выполненных на основе металлической пленки с точностью ±1% (мощностью 0,25 Вт).

Следует помнить, что сам делитель потребляет ток от первичного источника (в данном случае 1 мА) и этот ток будет возрастать с уменьшением сопротивлений резисторов делителя.

Для получения заданного значения напряжения следует применять высокоточные резисторы.

Недостатком простого резисторного делителя напряжения является то, что с изменением сопротивления нагрузки выходное напряжение ( U вых) делителя изменяется. Ддя уменьшения влияния нагрузки на U выхнеобходимо выбирать соротивление R2 по крайней мере в 10 раз меньше минимального сопротивления нагрузки.

Важно помнить о том, что с уменьшением сопротивлений резисторов R 1 и R2 растет ток, потребляемый от источника входного напряжения. Обычно этот ток не должен превышать 1—10 мА.

Резисторы используются также для того, чтобы заданную долю общего тока направить в соответствующее плечо делителя. Например, в схеме на рис. 3 ток I составляет часть общего тока I вх, определяемую сопротивлениями резисторов R1 и R2, т.е. можно записать, что I вых = I вх х (R1 / R2 + R1)

Пример. Стрелка измерительного прибора отклоняется на всю шкалу в том случае, если постоянный ток в подвижной катушке равен 1 мА. Активное сопротивление обмотки катушки составляет 100 Ом. Рассчитайте сопротивление измерительного шунта так, чтобы стрелка прибора максимально отклонялась при входном токе 10 мА ( см. рис. 4) .

Коэффициент деления тока определяется соотношением:

I вых / I вх = 1/10 = 0,1 = R1 / R2 + R1 , R2 = 100 Ом.

Требуемое сопротивление резистора R1 можно получить путем последовательного соединения двух стандартных резисторов сопротивлением 9,1 и 2 Ом, выполненных на основе толстопленочной технологии с точностью ±2% (0,25 Вт). Заметим еще раз, что на рис. 3 сопротивление R2 — это внутреннее сопротивление измерительного прибора.

Для обеспечения хорошей точности деления токов следует использовать высокоточные (± 1 %) резисторы.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Делитель напряжения

Делитель напряжения — это это цепь, состоящая из двух и более пассивных радиоэлементов, которые соединены последовательно.

Делитель напряжения на резисторах

Давайте разберем самый простой делитель напряжения, состоящий из двух резисторов. Эти два резистора соединим последовательно и подадим на них напряжение. Напряжение может быть как постоянное, так и переменное.

Подавая напряжение на эту цепь, состоящую из двух резисторов, у нас получается, что цепь становится замкнутой, и в цепи начинает течь электрический ток с какой-то определенной силой тока, которая зависит от номиналов резисторов.

Итак, мы знаем, что при последовательном соединении сила тока в цепи одинакова. То есть какая сила тока протекает через резистор R1, такая же сила тока течет и через резистор R2. Как же вычислить эту силу тока? Оказывается, достаточно просто, используя закон Ома: I=U/R.

Так как наши резисторы соединены последовательно, то и их общее сопротивление будет выражаться формулой

То есть в нашем случае мы можем записать, что

Как найти напряжение, которое падает на резисторе R2?

Так как ток для обоих резисторов общий, то согласно закону Ома

Подставляем вместо I формулу

Для другого резистора ситуация аналогичная. На нем падает напряжение

Для него формула запишется

Давайте докажем, что сумма падений напряжений на резисторах равняется напряжению питания, то есть нам надо доказать, что U=U_R1 +U_R2 . Подставляем значения и смотрим.

что и требовалось доказать.

Эта формула также работает и для большого количества резисторов.

На схеме выше мы видим резисторы, которые соединены последовательно. Чему будет равняться U_общ ? Так как резисторы соединены последовательно, следовательно, на каждом резисторе падает какое-то напряжение. Сумма падений напряжения на всех резисторах будет равняться U_общ . В нашем случае формула запишется как

Как работает делитель напряжения на практике

Итак у нас имеются вот такие два резистора и наш любимый мультиметр:

Замеряем сопротивление маленького резистора, R1=109,7 Ом.

Замеряем сопротивление большого резистора R2=52,8 Ом.

Выставляем на блоке питания ровно 10 Вольт. Замер напряжения производим с помощью мультиметра.

Цепляемся блоком питания за эти два резистора, запаянные последовательно. Напомню, что на блоке ровно 10 Вольт. Показания амперметра на блоке питания тоже немного неточны. Силу тока мы будем замерять в дальнейшем также с помощью мультиметра.

Замеряем падение напряжения на большом резисторе, который обладает номиналом в 52,8 Ом. Мультиметр намерял 3,21 Вольта.

Замеряем напряжение на маленьком резисторе номиналом в 109,7 Ом. На нем падает напряжение 6,77 Вольт.

Ну что, с математикой, думаю, у всех в порядке. Складываем эти два значения напряжения. 3,21+6,77 = 9,98 Вольт. А куда делись еще 0,02 Вольта? Спишем на погрешность щупов и средств измерений. Вот наглядный пример того, что мы смогли разделить напряжение на два разных напряжения. Мы еще раз убедились, что сумма падений напряжений на каждом резистора равняется напряжению питания, которое подается на эту цепь.

Сила тока в цепи при последовательном соединении резисторов

Давайте убедимся, что сила тока при последовательном соединении резисторов везде одинакова. Как измерить силу тока постоянного напряжения, я писал здесь. Как видим, мультиметр показал значение 0,04 А или 40 мА в начале цепи, в середине цепи и даже в конце цепи. Где бы мы не обрывали нашу цепь, везде одно и то же значение силы тока.

Переменный резистор в роли делителя напряжения

Для того, чтобы плавно регулировать выходное напряжение, у нас есть переменный резистор в роли делителя напряжения. Его еще также называют потенциометром.

Его обозначение на схеме выглядит вот так:

Принцип работы такой: между двумя крайними контактами постоянное сопротивление. Сопротивление относительно среднего контакта по отношению к крайним может меняться в зависимости от того, куда мы будем крутить крутилку этого переменного резистора. Этот резистор рассчитан на мощность 1Вт и имеет полное сопротивление 330 Ом. Давайте посмотрим, как он будет делить напряжение.

Так как мощность небольшая, всего 1 Вт, то мы не будем нагружать его большим напряжением. Мощность, выделяемая на каком-либо резисторе рассчитывается по формуле P=I 2 R. Значит, этот переменный резистор может делить только маленькое напряжение при маленьком сопротивлении нагрузки и наоборот. Главное, чтобы значение мощности этого резистора не вышло за грани. Поэтому я буду делить напряжение в 1 Вольт.

Для этого выставляем на блоке напряжение в 1 Вольт и цепляемся к нашему резистору по двум крайним контактам.

Крутим крутилку в каком-нибудь произвольном направлении и останавливаем ее. Замеряем напряжение между левым и средним контактом и получаем 0,34 Вольта.

Замеряем напряжение между средним и правым контактом и получаем 0,64 Вольта

Суммируем напряжение и получаем 0,34+0,64=0,98 Вольт. 0,02 Вольта опять где-то затерялись. Скорее всего на щупах, так как они тоже обладают сопротивлением. Как вы видите, простой переменный резистор мы можем использовать в роли простейшего делителя напряжения.

Похожие статьи по теме «делитель напряжения»

Источник