Как найти коэффициент детерминации через коэффициент корреляции

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 22 апреля 2022 года; проверки требуют 2 правки.

Коэффициент детерминации ( — R-квадрат) — это доля дисперсии зависимой переменной, объясняемая рассматриваемой моделью зависимости, то есть объясняющими переменными. Более точно — это единица минус доля необъяснённой дисперсии (дисперсии случайной ошибки модели, или условной по факторам дисперсии зависимой переменной) в дисперсии зависимой переменной. Его рассматривают как универсальную меру зависимости одной случайной величины от множества других. В частном случае линейной зависимости R^2 является квадратом так называемого множественного коэффициента корреляции между зависимой переменной и объясняющими переменными. В частности, для модели парной линейной регрессии коэффициент детерминации равен квадрату обычного коэффициента корреляции между y и x.

Определение и формула[править | править код]

Истинный коэффициент детерминации модели зависимости случайной величины y от факторов x определяется следующим образом:

${displaystyle R^{2}=1-{frac {D[y|x]}{D[y]}}=1-{frac {sigma ^{2}}{sigma _{y}^{2}}},}$

где ${displaystyle D[y]=sigma _{y}^{2}}$ — дисперсия случайной величины y, а ${displaystyle D[y|x]=sigma ^{2}}$ — условная (по факторам x) дисперсия зависимой переменной (дисперсия ошибки модели).

В данном определении используются истинные параметры, характеризующие распределение случайных величин. Если использовать выборочную оценку значений соответствующих дисперсий, то получим формулу для выборочного коэффициента детерминации (который обычно и подразумевается под коэффициентом детерминации):

${displaystyle R^{2}=1-{frac {{hat {sigma }}^{2}}{{hat {sigma }}_{y}^{2}}}=1-{frac {SS_{res}/n}{SS_{tot}/n}}=1-{frac {SS_{res}}{SS_{tot}}},}$

где ${displaystyle SS_{res}=sum _{i=1}^{n}e_{i}^{2}=sum _{i=1}^{n}(y_{i}-{hat {y}}_{i})^{2}}$ — сумма квадратов остатков регрессии, $y_{i},{hat y}_{i}$ — фактические и расчётные значения объясняемой переменной.

${displaystyle SS_{tot}=sum _{i=1}^{n}(y_{i}-{overline {y}})^{2}=n{hat {sigma }}_{y}^{2}}$ — общая сумма квадратов.

${bar {y}}={frac {1}{n}}sum _{{i=1}}^{n}y_{i}$

В случае линейной регрессии с константой ${displaystyle SS_{tot}=SS_{reg}+SS_{res}}$ , где ${displaystyle SS_{reg}=sum _{i=1}^{n}({hat {y}}_{i}-{overline {y}})^{2}}$ — объяснённая сумма квадратов, поэтому получаем более простое определение в этом случае — коэффициент детерминации — это доля объяснённой суммы квадратов в общей:

${displaystyle R^{2}={frac {SS_{reg}}{SS_{tot}}}}$

Необходимо подчеркнуть, что эта формула справедлива только для модели с константой, в общем случае необходимо использовать предыдущую формулу^{[источник не указан 393 дня]}.

Интерпретация[править | править код]

Коэффициент детерминации для модели с константой принимает значения от 0 до 1. Чем ближе значение коэффициента к 1, тем сильнее зависимость. При оценке регрессионных моделей это интерпретируется как соответствие модели данным. Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 50 % (в этом случае коэффициент множественной корреляции превышает по модулю 70 %). Модели с коэффициентом детерминации выше 80 % можно признать достаточно хорошими (коэффициент корреляции превышает 90 %). Значение коэффициента детерминации 1 означает функциональную зависимость между переменными.
При отсутствии статистической связи между объясняемой переменной и факторами, статистика $nR^{2}$ для линейной регрессии имеет асимптотическое распределение $chi ^{2}(k-1)$ , где — количество факторов модели (см. тест множителей Лагранжа). В случае линейной регрессии с нормально распределёнными случайными ошибками статистика $F={frac {R^{2}/(k-1)}{(1-R^{2})/(n-k)}}$ имеет точное (для выборок любого объёма) распределение Фишера (см. F-тест). Информация о распределении этих величин позволяет проверить статистическую значимость регрессионной модели исходя из значения коэффициента детерминации. Фактически в этих тестах проверяется гипотеза о равенстве истинного коэффициента детерминации нулю.
Коэффициент детерминации не может быть отрицательным, данный вывод исходит из свойств коэффициента детерминации. Однако скорректированный коэффициент детерминации вполне может принимать отрицательные значения.

Недостаток R² и альтернативные показатели[править | править код]

Основная проблема применения (выборочного) R^2 заключается в том, что его значение увеличивается (не уменьшается) от добавления в модель новых переменных, даже если эти переменные никакого отношения к объясняемой переменной не имеют. Поэтому сравнение моделей с разным количеством факторов с помощью коэффициента детерминации, вообще говоря, некорректно. Для этих целей можно использовать альтернативные показатели.

Скорректированный (adjusted) R²[править | править код]

Для того, чтобы была возможность сравнивать модели с разным числом факторов так, чтобы число регрессоров (факторов) не влияло на статистику R^2 обычно используется скорректированный коэффициент детерминации, в котором используются несмещённые оценки дисперсий:

${displaystyle {bar {R}}^{2}=R_{adj}^{2}=1-{frac {s^{2}}{s_{y}^{2}}}=1-{frac {SS_{res}/(n-k)}{SS_{tot}/(n-1)}}=1-(1-R^{2}){(n-1) over (n-k)}leqslant R^{2}}$

который даёт штраф за дополнительно включённые факторы, где n — количество наблюдений, а k — количество параметров.

Данный показатель всегда меньше единицы, но теоретически может быть и меньше нуля (только при очень маленьком значении обычного коэффициента детерминации и большом количестве факторов). Поэтому теряется интерпретация показателя как «доли». Тем не менее, применение показателя в сравнении вполне обоснованно.

Для моделей с одинаковой зависимой переменной и одинаковым объёмом выборки сравнение моделей с помощью скорректированного коэффициента детерминации эквивалентно их сравнению с помощью остаточной дисперсии ${displaystyle s^{2}=SS_{res}/(n-k)}$ или стандартной ошибки модели . Разница только в том, что последние критерии чем меньше, тем лучше.

Информационные критерии[править | править код]

AIC — информационный критерий Акаике — применяется исключительно для сравнения моделей. Чем меньше значение, тем лучше. Часто используется для сравнения моделей временных рядов с разным количеством лагов.
${displaystyle AIC={2k over n}+ln {SS_{res} over n}}$ , где k— количество параметров модели.

BIC или SC — байесовский информационный критерий Шварца — используется и интерпретируется аналогично AIC.
${displaystyle BIC={kln {n} over n}+ln {SS_{res} over n}}$ . Даёт больший штраф за включение лишних лагов в модель, чем AIC.

R²-обобщённый (extended)[править | править код]

В случае отсутствия в линейной множественной МНК регрессии константы свойства коэффициента детерминации могут нарушаться для конкретной реализации. Поэтому модели регрессии со свободным членом и без него нельзя сравнивать по критерию R^2 . Эта проблема решается с помощью построения обобщённого коэффициента детерминации $R_{{extended}}^{2}$ , который совпадает с исходным для случая МНК регрессии со свободным членом, и для которого выполняются четыре свойства, перечисленные выше. Суть этого метода заключается в рассмотрении проекции единичного вектора на плоскость объясняющих переменных.

Для случая регрессии без свободного члена:

$R_{{extended}}^{2}=1-{Y'*(I-P(X))*Y over Y'*(I-pi (X))*Y}$ ,
где X — матрица nxk значений факторов, $P(X)=X*(X'*X)^{{-1}}*X'$ — проектор на плоскость X, $pi (X)={P(X)*i_{n}*i_{n}'*P(X) over i_{n}'*P(X)*i_{n}}$ , где i_n — единичный вектор nx1.

$R_{{extended}}^{2}$ с условием небольшой модификации, также подходит для сравнения между собой регрессий, построенных с помощью: МНК, обобщённого метода наименьших квадратов (ОМНК), условного метода наименьших квадратов (УМНК), обобщённо-условного метода наименьших квадратов (ОУМНК).

История[править | править код]

Основой коэффициента детерминации является регрессионный анализ и коэффициент корреляции. Британский натуралист сэр Фрэнсис Гальтон (1822—1911) основал регрессионный анализ в 1870-х годах. Он, как и его двоюродный брат Чарльз Дарвин, был внуком Эразма Дарвина. Гальтон был известен своей сильной страстью к сбору данных любого рода. Например, он собрал данные о семенах сладкого горошка чина. Сравнивая диаметры семян, он построил то, что сегодня широко известно как корреляционная диаграмма. Связь, обнаруженную им в этой деятельности, он сначала окрестил «реверсией» (разворотом); однако позже он выбрал название «регрессия». Анализируя семена, он обнаружил явление регрессии к центру, согласно которому — после крайне неудачного изменения, последующее изменение снова приближается к среднему: средний диаметр потомства более крупных семян был меньше среднего диаметра семян родителей (изменения разворачиваются). В своих корреляционных диаграммах он нарисовал линию тренда, для которой он использовал коэффициент корреляции в качестве наклона.^[1]

Термин «дисперсия» был введен статистиком Рональдом Фишером (1890—1962) в его статье 1918 года под названием «Корреляция между родственниками на основе предположения о менделевском наследовании» (The Correlation between Relatives on the Supposition of Mendelian Inheritance)^[2]. Фишер был одним из самых выдающихся статистиков 20-го века и известен своим вкладом в эволюционную теорию. F-критерий, тесно связанный с коэффициентом детерминации, также назван в его честь. Карл Пирсон (1857—1936), основатель биометрики, предоставил формально-математическое обоснование коэффициента корреляции, квадратом которого является коэффициент детерминации.^[3]

Коэффициент детерминации подвергся резкой критике в последующие годы. Это произошло потому, что у него есть свойство, что чем больше количество независимых переменных, тем большим он становится. И это не зависит от того, вносят ли дополнительные «объясняющие переменные» вклад в «объяснительную силу». Чтобы учесть это обстоятельство, эконометрик Анри Тейл (1924—2000) в 1961 году предложил скорректированный коэффициент детерминации^[4] (Adjusted coefficient of determination (англ.)), который учитывает потерю степени свободы, связанную с ростом количества объясняющих переменных. Скорректированный коэффициент детерминации изменяется за счет штрафа, который накладывается на модель при увеличении числа переменных. Однако немецкий учёный Хорст Ринне подверг критике данный подход^[5] за недостаточное штрафование за потерю степени свободы по мере увеличения числа объясняющих переменных.

Замечание[править | править код]

Высокие значения коэффициента детерминации, вообще говоря, не свидетельствуют о наличии причинно-следственной зависимости между переменными (так же как и в случае обычного коэффициента корреляции). Например, если объясняемая переменная и факторы, на самом деле не связанные с объясняемой переменой, имеют возрастающую динамику, то коэффициент детерминации будет достаточно высок. Поэтому логическая и смысловая адекватность модели имеют первостепенную важность. Кроме того, необходимо использовать критерии для всестороннего анализа качества модели.

См. также[править | править код]

Коэффициент корреляции
Корреляция
Мультиколлинеарность
Дисперсия случайной величины
Метод группового учёта аргументов
Регрессионный анализ

Примечания[править | править код]

↑ Franka Miriam Brückler: Geschichte der Mathematik kompakt: Das Wichtigste aus Analysis, Wahrscheinlichkeitstheorie, angewandter Mathematik, Topologie und Mengenlehre. Springer-Verlag, 2017, ISBN 978-3-662-55573-6, S. 116. (нем.)
↑ Ronald Aylmer Fisher: The correlation between relatives on the supposition of Mendelian inheritance. In: Trans. Roy. Soc. Edinb. 52, 1918, S. 399—433. (англ.)
↑ Franka Miriam Brückler: Geschichte der Mathematik kompakt: Das Wichtigste aus Analysis, Wahrscheinlichkeitstheorie, angewandter Mathematik, Topologie und Mengenlehre. Springer-Verlag, 2017, ISBN 978-3-662-55573-6, S. 117. (нем.)
↑ Henri Theil: Economic Forecasts and Policy. Amsterdam 1961, S. 213. (англ.)
↑ Horst Rinne: Ökonometrie: Grundlagen der Makroökonometrie. Vahlen, 2004. (нем.)

Литература[править | править код]

Бахрушин В. Е. Методы оценивания характеристик нелинейных статистических связей // Системные технологии. — 2011. — № 2(73). — С. 9—14.[1]

Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс.. — 6,7,8-е изд., доп. и перераб.. — Москва: Дело. — Т. “”. — 576 с. — ISBN 5-7749-0055-X.

Ершов Э.Б. Распространение коэффициента детерминации на общий случай линейной регрессии, оцениваемой с помощью различных версий метода наименьших квадратов (рус., англ.) // ЦЭМИ РАН Экономика и математические методы. — Москва: ЦЭМИ РАН, 2002. — Т. 38, вып. 3. — С. 107—120.

Айвазян С.А., Мхитарян В.С. Прикладная статистика. Основы эконометрики (в 2-х т.). — ??. — Москва: Юнити-Дана (проект TASIS), 2001. — Т. “1,2”. — 1088 с. — ISBN 5-238-00304-8.

Ершов Э.Б. Выбор регрессии максимизирующий несмещённую оценку коэффициента детерминации (рус., англ.) // Айвазян С.А. Прикладная эконометрика. — Москва: Маркет ДС, 2008. — Т. 12, вып. 4. — С. 71—83.

Ссылки[править | править код]

Глоссарий статистических терминов (недоступная ссылка с 13-05-2013 [3659 дней] — история)

Источник

Содержание

Вычисление коэффициента детерминации
- Способ 1: вычисление коэффициента детерминации при линейной функции
- Способ 2: вычисление коэффициента детерминации в нелинейных функциях
- Способ 3: коэффициент детерминации для линии тренда
Вопросы и ответы

Одним из показателей, описывающих качество построенной модели в статистике, является коэффициент детерминации (R^2), который ещё называют величиной достоверности аппроксимации. С его помощью можно определить уровень точности прогноза. Давайте узнаем, как можно произвести расчет данного показателя с помощью различных инструментов программы Excel.

Вычисление коэффициента детерминации

В зависимости от уровня коэффициента детерминации, принято разделять модели на три группы:

0,8 – 1 — модель хорошего качества;
0,5 – 0,8 — модель приемлемого качества;
0 – 0,5 — модель плохого качества.

В последнем случае качество модели говорит о невозможности её использования для прогноза.

Выбор способа вычисления указанного значения в Excel зависит от того, является ли регрессия линейной или нет. В первом случае можно использовать функцию КВПИРСОН, а во втором придется воспользоваться специальным инструментом из пакета анализа.

Способ 1: вычисление коэффициента детерминации при линейной функции

Прежде всего, выясним, как найти коэффициент детерминации при линейной функции. В этом случае данный показатель будет равняться квадрату коэффициента корреляции. Произведем его расчет с помощью встроенной функции Excel на примере конкретной таблицы, которая приведена ниже.

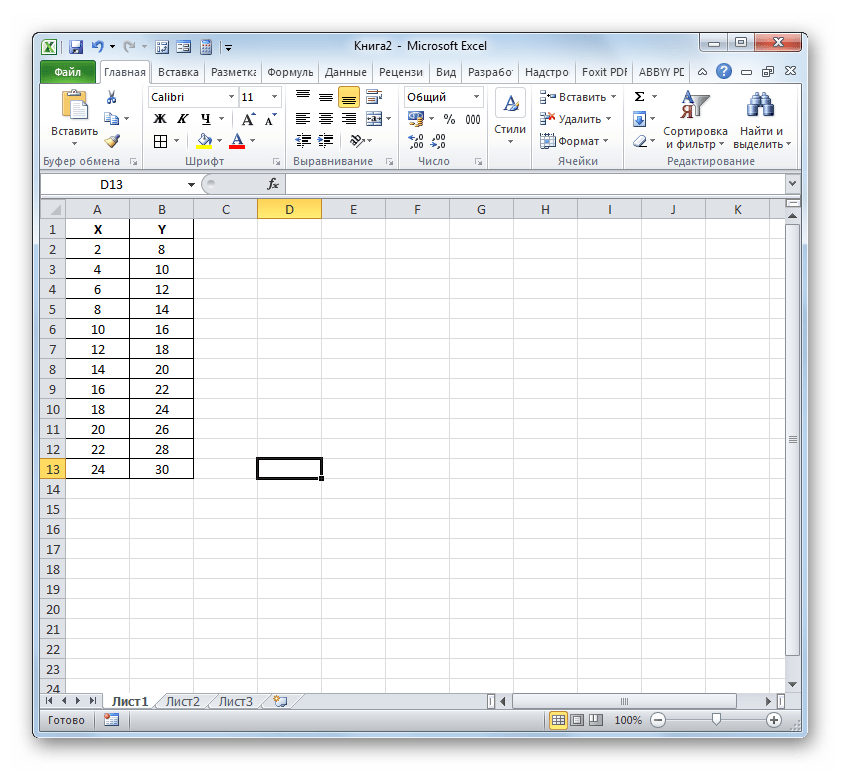
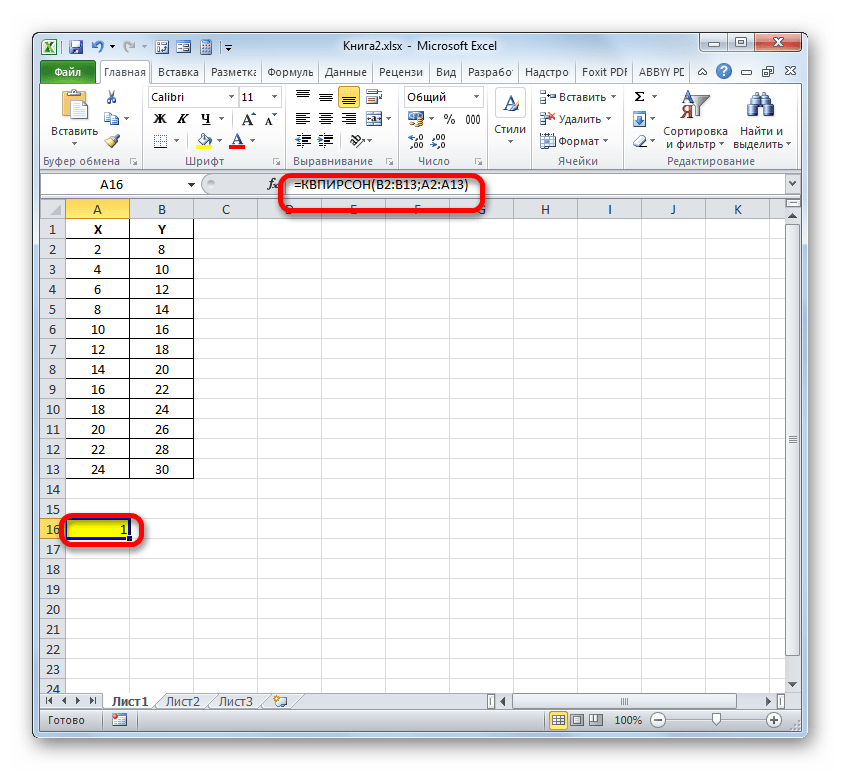
Выделяем ячейку, где будет произведен вывод коэффициента детерминации после его расчета, и щелкаем по пиктограмме «Вставить функцию».

Запускается Мастер функций. Перемещаемся в его категорию «Статистические» и отмечаем наименование «КВПИРСОН». Далее клацаем по кнопке «OK».

Происходит запуск окна аргументов функции КВПИРСОН. Данный оператор из статистической группы предназначен для вычисления квадрата коэффициента корреляции функции Пирсона, то есть, линейной функции. А как мы помним, при линейной функции коэффициент детерминации как раз равен квадрату коэффициента корреляции.
Синтаксис этого оператора такой:

=КВПИРСОН(известные_значения_y;известные_значения_x)

Таким образом, функция имеет два оператора, один из которых представляет собой перечень значений функции, а второй – аргументов. Операторы могут быть представлены, как непосредственно в виде значений, перечисленных через точку с запятой (;), так и в виде ссылок на диапазоны, где они расположены. Именно последний вариант и будет использован нами в данном примере.

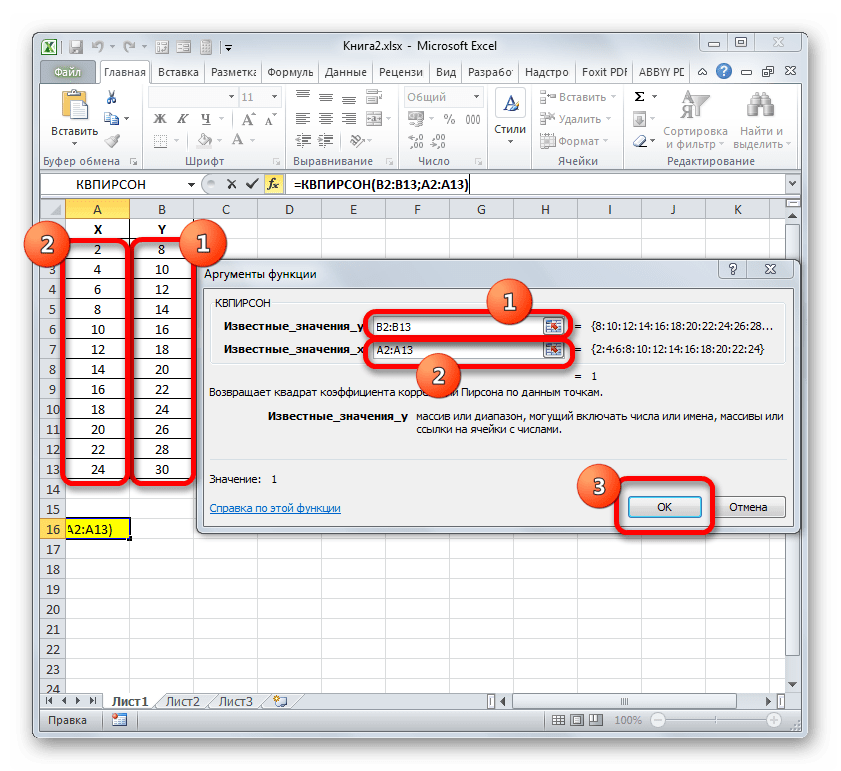
Устанавливаем курсор в поле «Известные значения y». Выполняем зажим левой кнопки мышки и производим выделение содержимого столбца «Y» таблицы. Как видим, адрес указанного массива данных тут же отображается в окне.

Аналогичным образом заполняем поле «Известные значения x». Ставим курсор в данное поле, но на этот раз выделяем значения столбца «X».

После того, как все данные были отображены в окне аргументов КВПИРСОН, клацаем по кнопке «OK», расположенной в самом его низу.

Как видим, вслед за этим программа производит расчет коэффициента детерминации и выдает результат в ту ячейку, которая была выделена ещё перед вызовом Мастера функций. В нашем примере значение вычисляемого показателя получилось равным 1. Это значит, что представленная модель абсолютно достоверная, то есть, исключает погрешность.

Урок: Мастер функций в Microsoft Excel

Способ 2: вычисление коэффициента детерминации в нелинейных функциях

Но указанный выше вариант расчета искомого значения можно применять только к линейным функциям. Что же делать, чтобы произвести его расчет в нелинейной функции? В Экселе имеется и такая возможность. Её можно осуществить с помощью инструмента «Регрессия», который является составной частью пакета «Анализ данных».

Но прежде, чем воспользоваться указанным инструментом, следует активировать сам «Пакет анализа», который по умолчанию в Экселе отключен. Перемещаемся во вкладку «Файл», а затем переходим по пункту «Параметры».

В открывшемся окне производим перемещение в раздел «Надстройки» при помощи навигации по левому вертикальному меню. В нижней части правой области окна располагается поле «Управление». Из списка доступных там подразделов выбираем наименование «Надстройки Excel…», а затем щелкаем по кнопке «Перейти…», расположенной справа от поля.

Производится запуск окна надстроек. В центральной его части расположен список доступных надстроек. Устанавливаем флажок около позиции «Пакет анализа». Вслед за этим требуется щелкнуть по кнопке «OK» в правой части интерфейса окна.

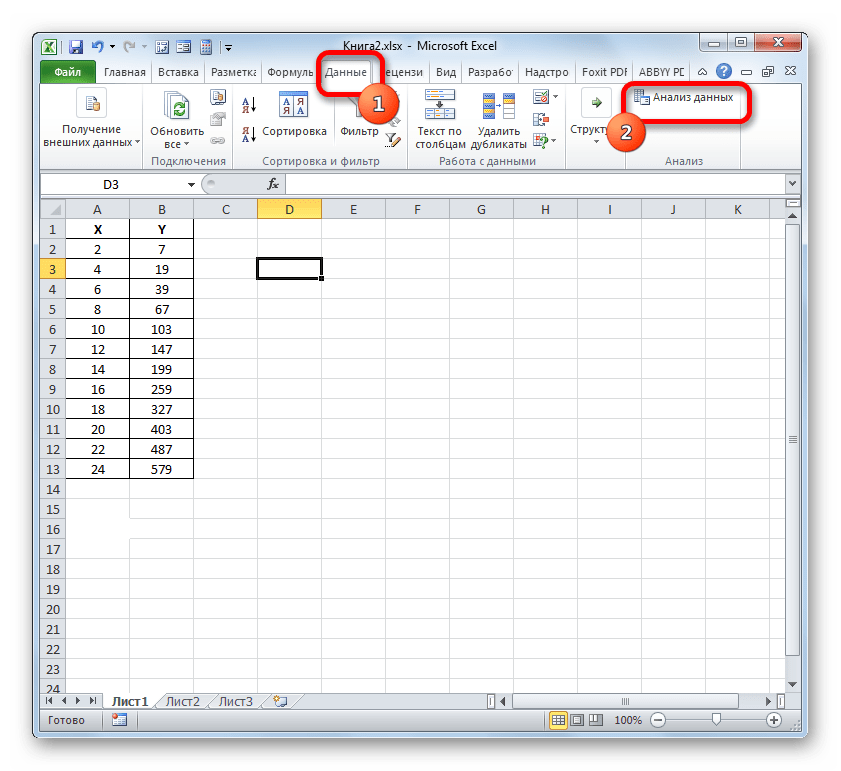
Пакет инструментов «Анализ данных» в текущем экземпляре Excel будет активирован. Доступ к нему располагается на ленте во вкладке «Данные». Перемещаемся в указанную вкладку и клацаем по кнопке «Анализ данных» в группе настроек «Анализ».

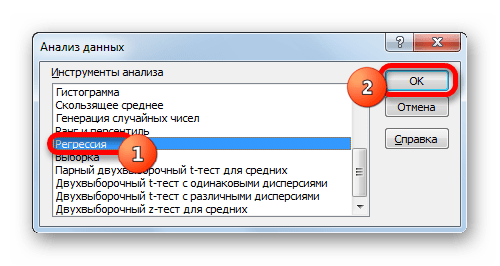
Активируется окошко «Анализ данных» со списком профильных инструментов обработки информации. Выделяем из этого перечня пункт «Регрессия» и клацаем по кнопке «OK».

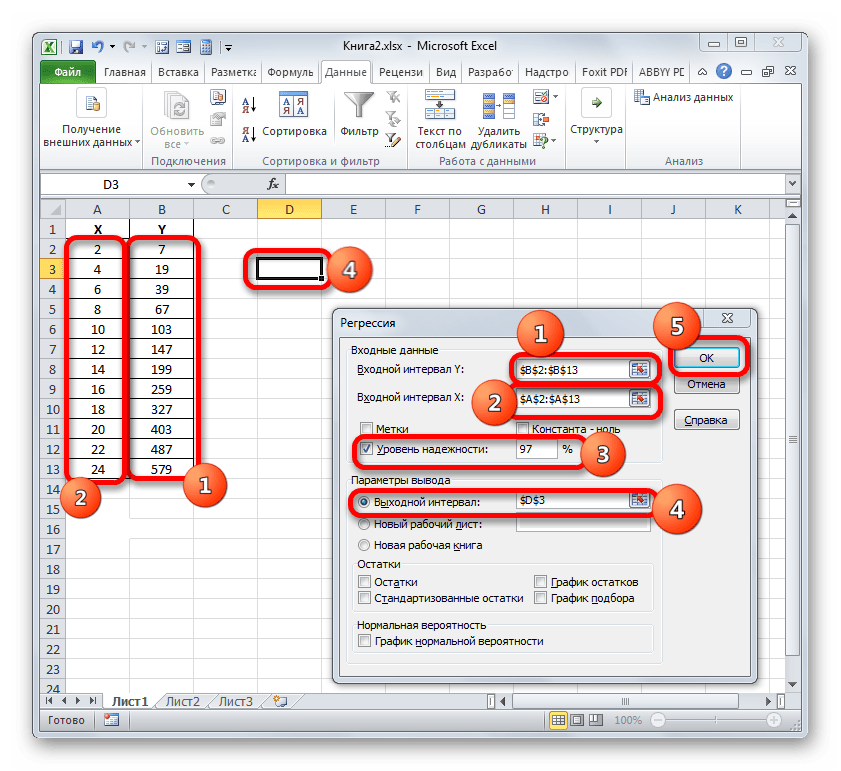
Затем открывается окно инструмента «Регрессия». Первый блок настроек – «Входные данные». Тут в двух полях нужно указать адреса диапазонов, где находятся значения аргумента и функции. Ставим курсор в поле «Входной интервал Y» и выделяем на листе содержимое колонки «Y». После того, как адрес массива отобразился в окне «Регрессия», ставим курсор в поле «Входной интервал Y» и точно таким же образом выделяем ячейки столбца «X».
Около параметров «Метка» и «Константа-ноль» флажки не ставим. Флажок можно установить около параметра «Уровень надежности» и в поле напротив указать желаемую величину соответствующего показателя (по умолчанию 95%).

В группе «Параметры вывода» нужно указать, в какой области будет отображаться результат вычисления. Существует три варианта:
- Область на текущем листе;
- Другой лист;
- Другая книга (новый файл).
Остановим свой выбор на первом варианте, чтобы исходные данные и результат размещались на одном рабочем листе. Ставим переключатель около параметра «Выходной интервал». В поле напротив данного пункта ставим курсор. Щелкаем левой кнопкой мыши по пустому элементу на листе, который призван стать левой верхней ячейкой таблицы вывода итогов расчета. Адрес данного элемента должен высветиться в поле окна «Регрессия».

Группы параметров «Остатки» и «Нормальная вероятность» игнорируем, так как для решения поставленной задачи они не важны. После этого клацаем по кнопке «OK», которая размещена в правом верхнем углу окна «Регрессия».

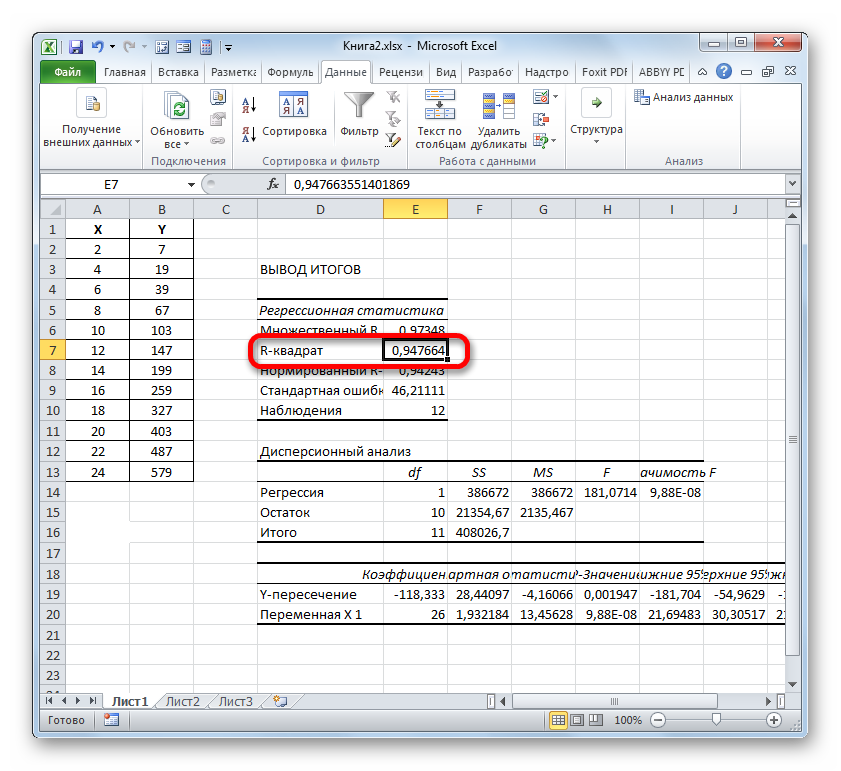
Программа производит расчет на основе ранее введенных данных и выводит результат в указанный диапазон. Как видим, данный инструмент выводит на лист довольно большое количество результатов по различным параметрам. Но в контексте текущего урока нас интересует показатель «R-квадрат». В данном случае он равен 0,947664, что характеризует выбранную модель, как модель хорошего качества.

Способ 3: коэффициент детерминации для линии тренда

Кроме указанных выше вариантов, коэффициент детерминации можно отобразить непосредственно для линии тренда в графике, построенном на листе Excel. Выясним, как это можно сделать на конкретном примере.

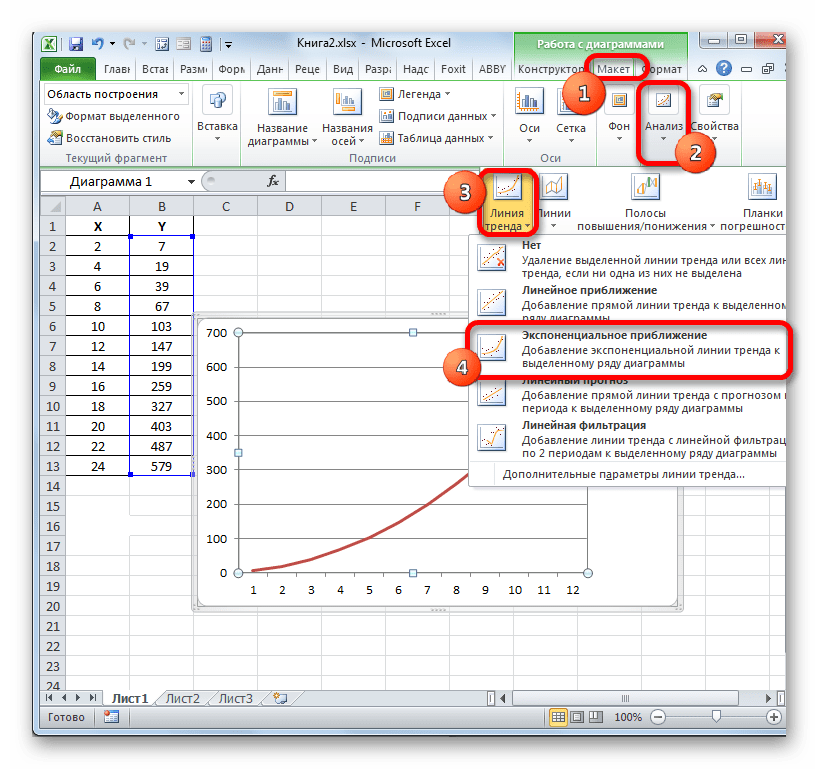
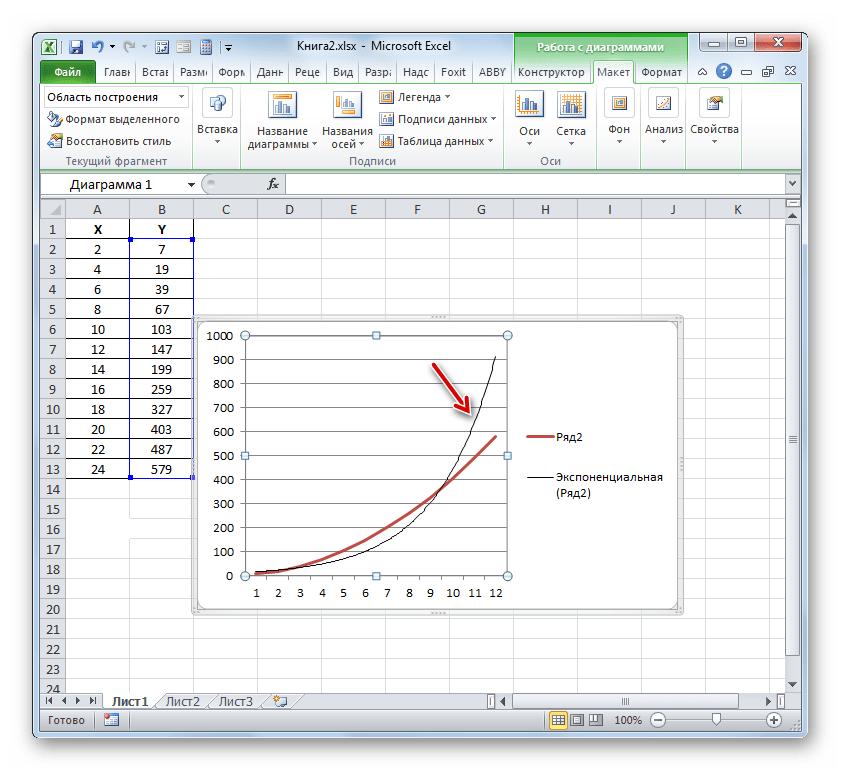
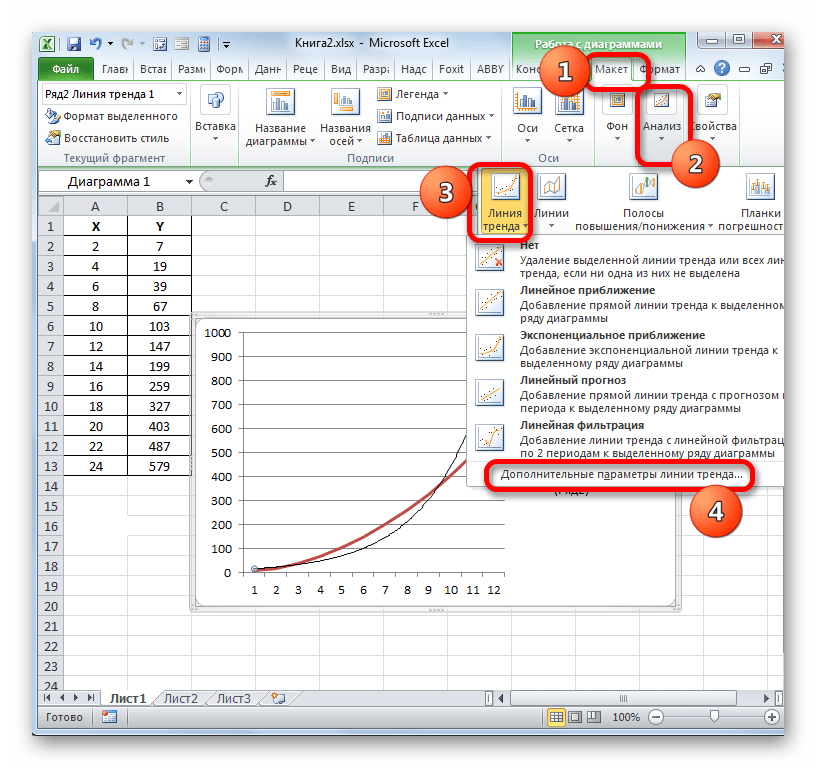
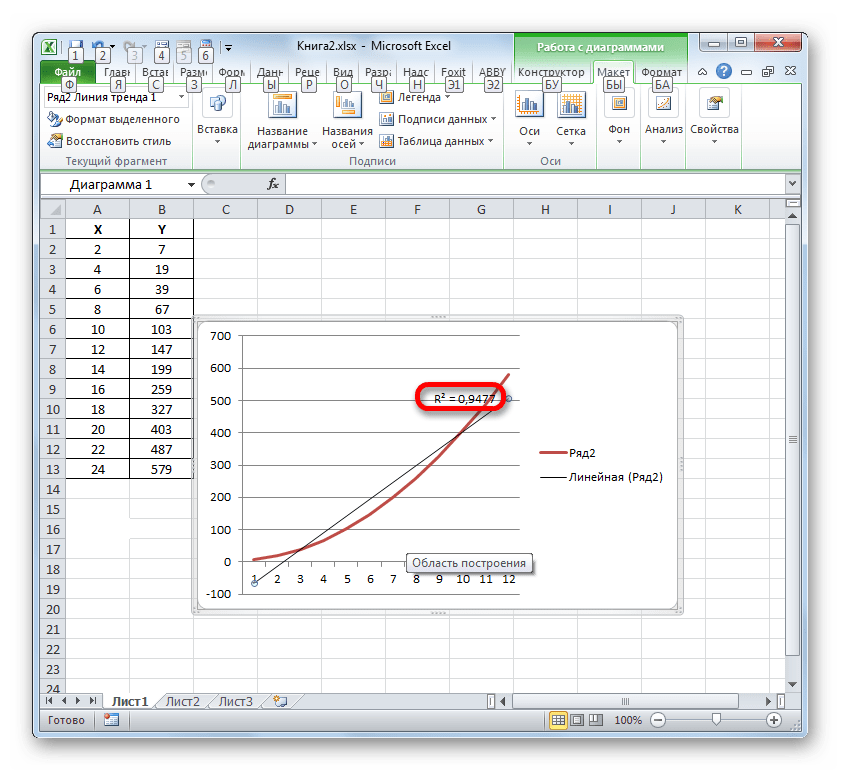
Мы имеем график, построенный на основе таблицы аргументов и значений функции, которая была использована для предыдущего примера. Произведем построение к нему линии тренда. Кликаем по любому месту области построения, на которой размещен график, левой кнопкой мыши. При этом на ленте появляется дополнительный набор вкладок – «Работа с диаграммами». Переходим во вкладку «Макет». Клацаем по кнопке «Линия тренда», которая размещена в блоке инструментов «Анализ». Появляется меню с выбором типа линии тренда. Останавливаем выбор на том типе, который соответствует конкретной задаче. Давайте для нашего примера выберем вариант «Экспоненциальное приближение».

Эксель строит прямо на плоскости построения графика линию тренда в виде дополнительной черной кривой.

Теперь нашей задачей является отобразить собственно коэффициент детерминации. Кликаем правой кнопкой мыши по линии тренда. Активируется контекстное меню. Останавливаем выбор в нем на пункте «Формат линии тренда…».

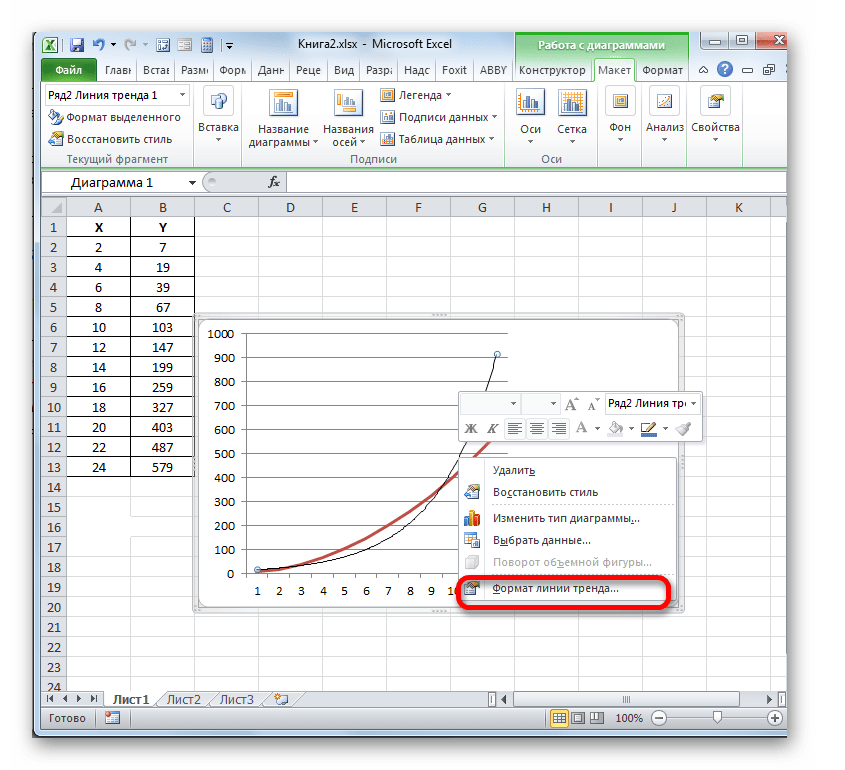
Для выполнения перехода в окно формата линии тренда можно выполнить альтернативное действие. Выделяем линию тренда кликом по ней левой кнопки мыши. Перемещаемся во вкладку «Макет». Клацаем по кнопке «Линия тренда» в блоке «Анализ». В открывшемся списке клацаем по самому последнему пункту перечня действий – «Дополнительные параметры линии тренда…».

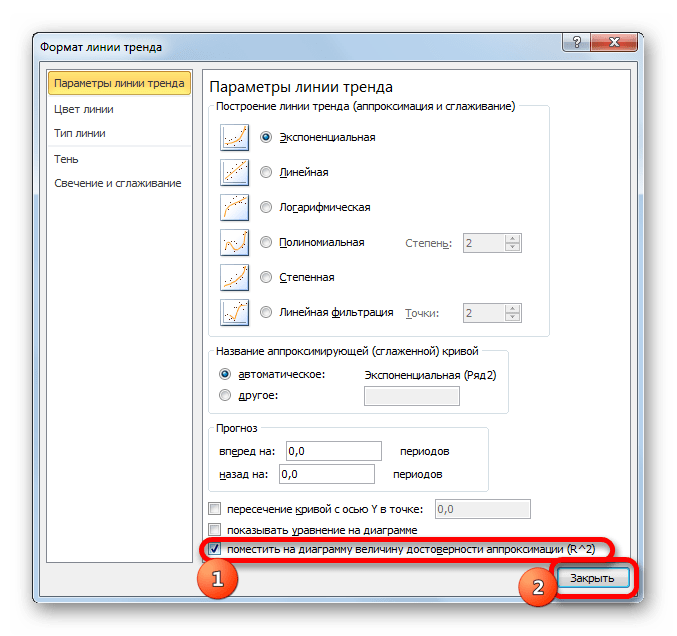
После любого из двух вышеуказанных действий запускается окошко формата, в котором можно произвести дополнительные настройки. В частности, для выполнения нашей задачи необходимо установить флажок напротив пункта «Поместить на диаграмму величину достоверности аппроксимации (R^2)». Он размещен в самом низу окна. То есть, таким образом мы включаем отображение коэффициента детерминации на области построения. Затем не забываем нажать на кнопку «Закрыть» внизу текущего окна.

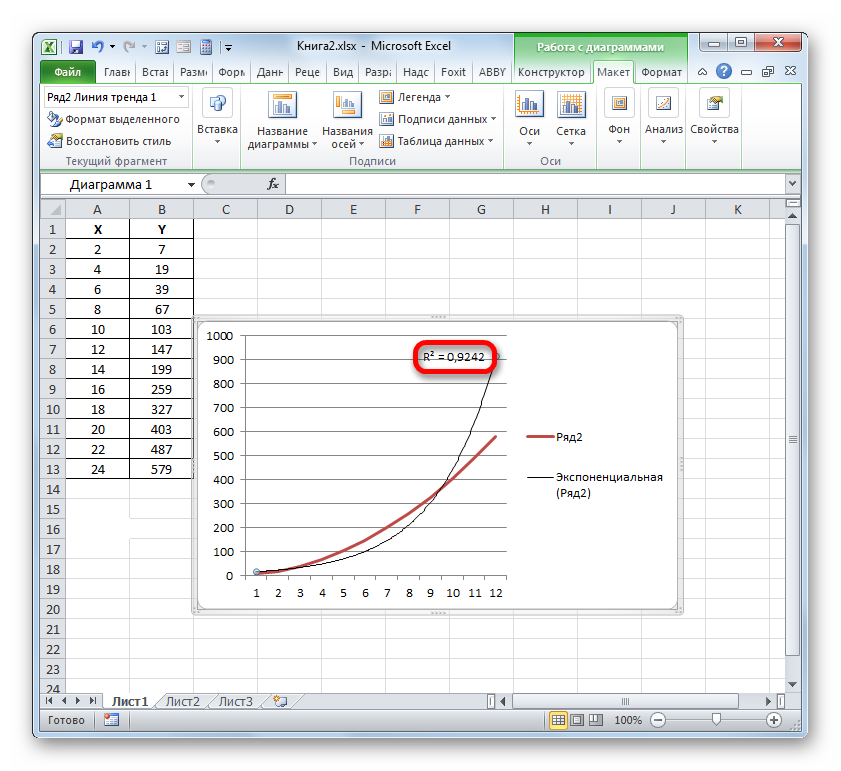
Значение достоверности аппроксимации, то есть, величина коэффициента детерминации, будет отображено на листе в области построения. В данном случае эта величина, как видим, равна 0,9242, что характеризует аппроксимацию, как модель хорошего качества.

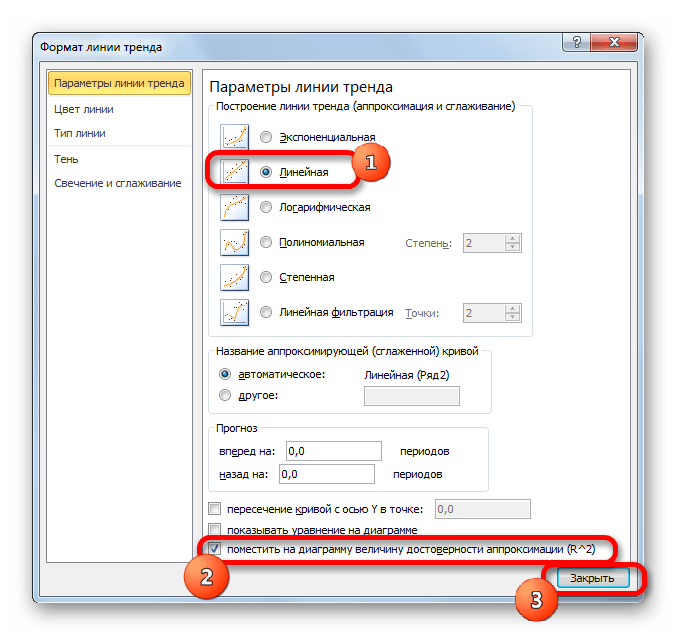
Абсолютно точно таким образом можно устанавливать показ коэффициента детерминации для любого другого типа линии тренда. Можно менять тип линии тренда, произведя переход через кнопку на ленте или контекстное меню в окно её параметров, как было показано выше. Затем уже в самом окне в группе «Построение линии тренда» можно переключиться на другой тип. Не забываем при этом контролировать, чтобы около пункта «Поместить на диаграмму величину достоверности аппроксимации» был установлен флажок. Завершив вышеуказанные действия, щелкаем по кнопке «Закрыть» в нижнем правом углу окна.

При линейном типе линия тренда уже имеет значение достоверности аппроксимации равное 0,9477, что характеризует эту модель, как ещё более достоверную, чем рассматриваемую нами ранее линию тренда экспоненциального типа.

Таким образом, переключаясь между разными типами линии тренда и сравнивая их значения достоверности аппроксимации (коэффициент детерминации), можно найти тот вариант, модель которого наиболее точно описывает представленный график. Вариант с самым высоким показателем коэффициента детерминации будет наиболее достоверным. На его основе можно строить самый точный прогноз.
Например, для нашего случая опытным путем удалось установить, что самый высокий уровень достоверности имеет полиномиальный тип линии тренда второй степени. Коэффициент детерминации в данном случае равен 1. Это говорит о том, что указанная модель абсолютно достоверная, что означает полное исключение погрешностей.

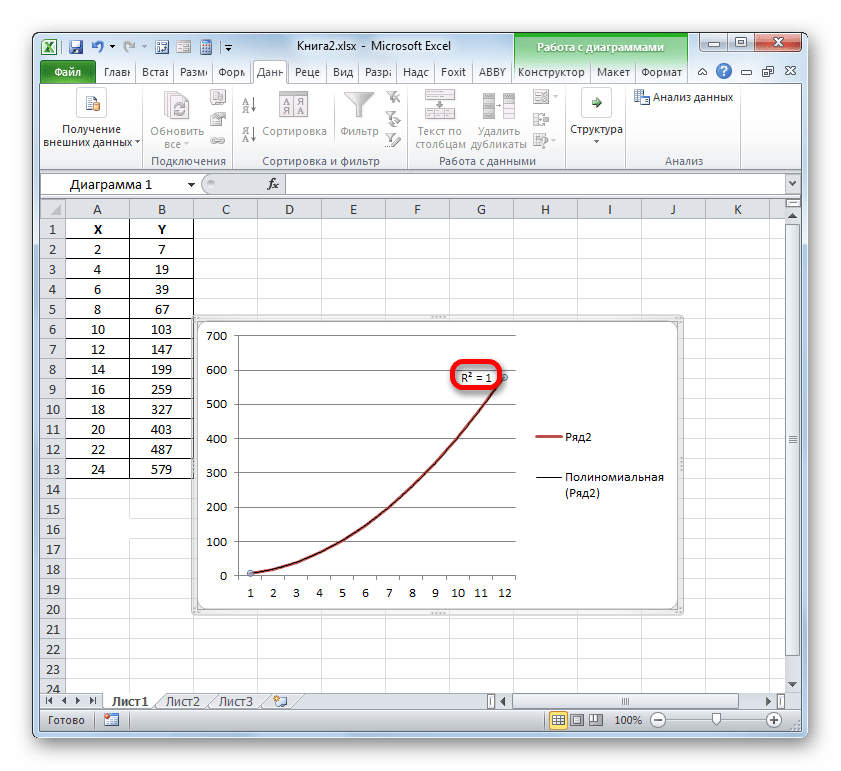
Но, в то же время, это совсем не значит, что для другого графика тоже наиболее достоверным окажется именно этот тип линии тренда. Оптимальный выбор типа линии тренда зависит от типа функции, на основании которой был построен график. Если пользователь не обладает достаточным объемом знаний, чтобы «на глаз» прикинуть наиболее качественный вариант, то единственным выходом определения лучшего прогноза является как раз сравнение коэффициентов детерминации, как было показано на примере выше.

Читайте также:
Построение линии тренда в Excel
Аппроксимация в Excel

В Экселе существуют два основных варианта вычисления коэффициента детерминации: использование оператора КВПИРСОН и применение инструмента «Регрессия» из пакета инструментов «Анализ данных». При этом первый из этих вариантов предназначен для использования только в процессе обработки линейной функции, а другой вариант можно использовать практически во всех ситуациях. Кроме того, существует возможность отображения коэффициента детерминации для линии трендов графиков в качестве величины достоверности аппроксимации. С помощью данного показателя имеется возможность определить тип линии тренда, который располагает самым высоким уровнем достоверности для конкретной функции.

Еще статьи по данной теме:

Помогла ли Вам статья?

Источник

Coefficient of determination is defined as the fraction of variance predicted by the independent variable in the dependent variable. It shows the degree of variation in the data collection offered. It is also known as R² method which is used to examine how differences in one variable may be explained by variations in another. It is used in statistical analysis to predict and explain the future events of a model. It is proportional to the square of the correlation and its value lies between 0 and 1. If its value is zero, the dependent variable cannot be predicted based on the independent variable. If it is 1, the dependent variable may be predicted without mistake from the independent variable. And if it is between 0 and 1, it reflects how well the dependent variable can be predicted. Its value is equal to the square of the correlation coefficient, that is, r².

Formula

$r^2=left[frac{n(sum xy)-(sum x)(sum y)}{sqrt{left [ nsum x^{2}-(sum x)^{2} right ]left [ nsum y^{2}-(sum y)^{2} right ]}}right]^2$

where,

r² is the coefficient of determination,

n is the number of observations of data set,

Σx is the sum of the first variable,

Σy is the sum of the second variable,

Σxy is the sum of the product of first and second variable,

Σx² is the sum of the squares of the first variable,

Σy² is the sum of the squares of the second variable.

If residual sum of squares and total sum of squares of data values are given, the formula for coefficient of determination is given by,

r² = 1 – (R/T)

where,

r² is the coefficient of determination,

R is the residual sum of squares,

T is the total sum of squares.

Sample Problems

Problem 1. Calculate the coefficient of determination for the data:

x	y
1	4
4	8
6	9
8	10

Solution:

The given data set is,

x

y

xy

x²

y²

1

4

4

1

16

4

8

12

16

64

6

9

15

36

81

8

10

18

64

100

Σx = 19

Σy = 31

Σxy = 49

Σx² = 117

Σy² = 261

Using the formula we get,

r² = [ (4 (49) – (19) (31)) / ((4 (117) – 361) (4 (261) – 961)) ]²

= (-393/8881)²

= (-0.044)²

= 0.001936

Problem 2. Calculate the coefficient of determination for the data:

x	y
5	3
2	8
4	1
7	5

The given data set is,

x

y

xy

x²

y²

5

3

15

25

9

2

8

16

4

64

4

1

4

16

1

7

5

35

49

25

Σx = 18

Σy = 17

Σxy = 70

Σx² = 94

Σy² = 99

Using the formula we get,

r² = [ (4 (70) – (18) (17)) / ((4 (94) – 324) (4 (99) – 289)) ]²

= (-26/5564)²

= (-0.046)2

= 0.002116

Problem 3. Calculate the coefficient of determination if correlation coefficient is 0.5.

Solution:

We have,

r = 0.5

Using the formula we get,

Coefficient of determination = r²

= (0.5)²

= 0.25

Problem 4. Calculate the coefficient of determination if correlation coefficient is 0.82.

Solution:

We have,

r = 0.82

Using the formula we get,

Coefficient of determination = r²

= (0.82)²

= 0.67

Problem 5. Calculate the correlation coefficient if the coefficient of determination is 0.54.

Solution:

We have,

r² = 0.54

Using the formula we get,

Coefficient of correlation = √r²

= √0.54

= 0.734

Problem 6. Calculate the correlation coefficient if the coefficient of determination is 0.68.

Solution:

We have,

r² = 0.68

Using the formula we get,

Coefficient of correlation = √r²

= √0.68

= 0.82

Problem 7. Calculate the coefficient of determination if the residual sum of squares is 100 and total sum of squares is 200.

Solution:

We have,

R = 100

T = 200

Using the formula we get,

r² = 1 – (R/T)

= 1 – (100/200)

= 1 – 1/2

= 1/2

= 0.5

Last Updated :
15 May, 2022

Like Article

Save Article

Источник

Для
трактовки линейной связи между двумя
переменными акцентируют внимание на
коэффициенте
корреляции.

Пусть
имеется выборка наблюдений (X_i,
Y_i),
i=1,…,n,
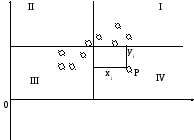
которая представлена на диаграмме
рассеяния, именуемой также полем
корреляции (рис. 2.3).

Рис. 2.3. Диаграмма
рассеяния

Разобьем
диаграмму на четыре квадранта так, что
для любой точки P(X_i, Y_i)
будут определены отклонения

Ясно,
что для всех точек I
квадранта x_iy_i>0;
для всех точек II
квадранта x_iy_i<0;
для всех точек III
квадранта x_iy_i>0;
для всех точек IV
квадранта x_iy_i<0.
Следовательно, величина x_iy_i
может служить мерой зависимости между
переменными X
и Y.
Если большая часть точек лежит в первом
и третьем квадрантах, то x_iy_i>0
и зависимость положительная, если
большая часть точек лежит во втором и
четвертом квадрантах, то x_iy_i<0
и зависимость отрицательная. Наконец,
если точки рассеиваются по всем четырем
квадрантам x_iy_i
близка к нулю и между X
и Y
связи нет.

Указанная
мера зависимости изменяется при выборе
единиц измерения переменных X
и Y.
Выразив x_iy_i
в единицах среднеквадратических
отклонений, получим после усреднения
выборочный
коэффициент
корреляции:

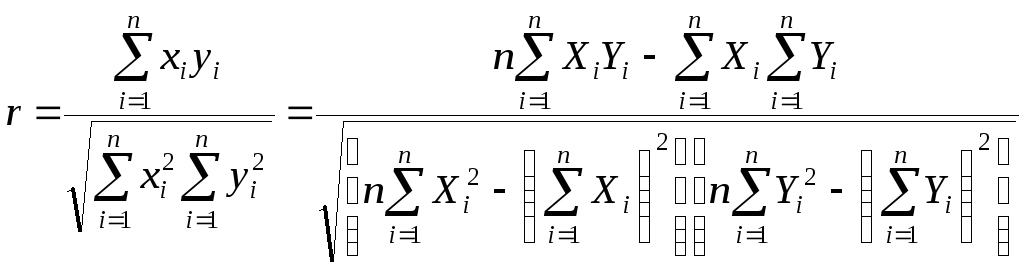(2.9)

Из
последнего выражения можно после
преобразований получить следующую
формулу для квадрата коэффициента
корреляции:

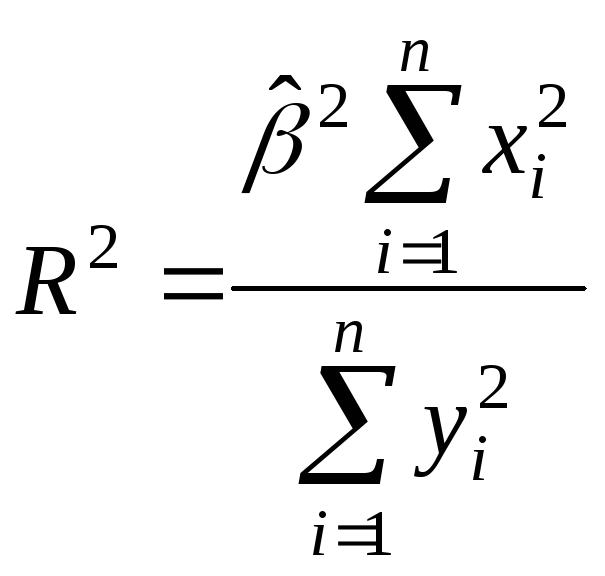или

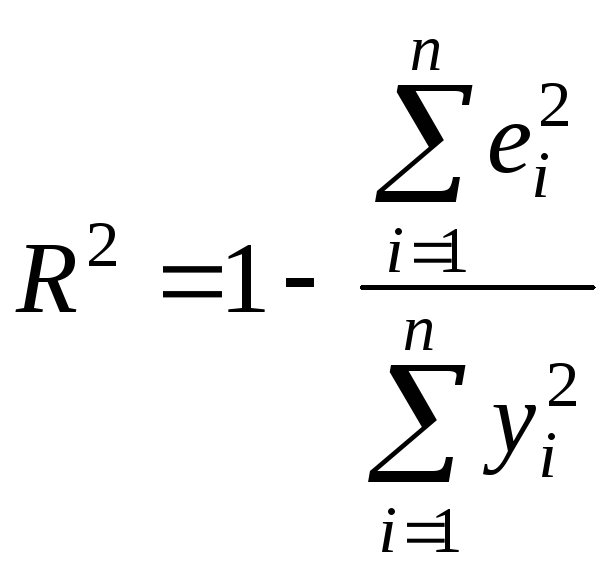(2.10)

Квадрат
коэффициента корреляции называется
коэффициентом
детерминации.
Согласно (2.10) значение коэффициента
детерминации не может быть больше
единицы, причем это максимальное значение
будет достигнуто при
=0,
т.е. когда все точки диаграммы рассеяния
лежат в точности на прямой. Следовательно,
значения коэффициента корреляции лежат
в числовом промежутке от -1 до +1.

Кроме
того, из (2.10) следует, что коэффициент
детерминации равен доле дисперсии Y
(знаменатель формулы), объясненной
линейной зависимостью от X
(числитель формулы). Это обстоятельство
позволяет использовать R²
как обобщенную меру “качества”
статистического подбора модели (2.6). Чем
лучше регрессия соответствует наблюдениям,
тем меньше
и
тем ближеR²
к 1, и наоборот, чем “хуже” подгонка
линии регрессии к данным, тем ближе
значение R²
к 0.

Поскольку
коэффициент корреляции симметричен
относительно X
и Y,
то есть r_XY=r_YX,
то можно говорить о корреляции как о
мере взаимозависимости переменных.
Однако из того, что значения этого
коэффициента близки по модулю к единице,
нельзя сделать ни один из следующих
выводов: Y
является причиной X;
X
является причиной Y;
X
и Y
совместно зависят от какой-то третьей
переменной. Величина r
ничего не говорит о причинно-следственных
связях. Эти вопросы должны решаться,
исходя из содержательного анализа
задачи. Следует избегать и так называемых
ложных корреляций, т.е. нельзя пытаться
связать явления, между которыми
отсутствуют реальные причинно-следственные
связи. Например, корреляция между
успехами местной футбольной команды и
индексом Доу-Джонса. Классическим
является пример ложной корреляции,
приведенный в начале ХХ века известным
российским статистиком А.А. Чупровым:
если в качестве независимой переменной
взять число пожарных команд в городе,
а в качестве зависимой переменной –
сумму убытков от пожаров за год, то между
ними есть прямая корреляционная
зависимость, т.е. чем больше пожарных
команд, тем больше сумма убытков. На
самом деле здесь нет причинно-следственной
связи, а есть лишь следствия общей
причины – величины города.

Проверка
гипотезы о значимости выборочного
коэффициента корреляции эквивалентна
проверке гипотезы о =0
(см. ниже) и, следовательно, равносильна
проверке основной гипотезы об отсутствии
линейной связи между Y
и X.
Вычисляя значение t-статистики

вывод
о значимости r
делается при t>t_,
где t_
– соответствующее табличное значение
t-распределения
с (n-2)
степенями свободы и уровнем значимости
.

Пример.
Вычислим коэффициент корреляции и
проверим его значимость для нашего
примера табл. 2.1.

По
(2.9) r=43145/(4651040068,25)^0,5=0,9994.
R²=0,998.
Значение t-статистики
t=0,9994[10/(1-0,998)]^0,5=70,67.
Поскольку t_0,05;10=2,228,
то t>t_0,05;10
и коэффициент корреляции значим.
Следовательно, можно считать, что
линейная связь между переменными Y
и X
в примере существует. 

Если
между переменными имеет место нелинейная
зависимость, то коэффициент корреляции
теряет смысл как характеристика степени
тесноты связи. В этом случае используется
наряду с расчетом коэффициента
детерминации расчет корреляционного
отношения.

Предположим,
что выборочные данные могут быть
сгруппированы по оси объясняющей
переменной X.
Обозначим s
– число интервалов группирования,
(j=1,…,s)
– число выборочных точек, попавших в
j-й
интервал группирования,
– среднее значение ординат точек, попавших
вj-й
интервал группирования,
– общее среднее по выборке. С учетом
формул для оценок выборочных дисперсий
среднего значенияY
внутри интервалов группирования
и суммарной дисперсии результатов
наблюденияполучим:

.
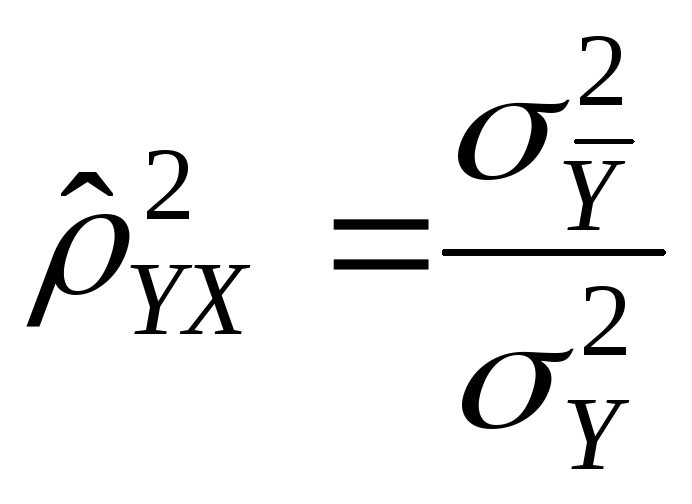(2.11)

Величину
в (2.11) называюткорреляционным
отношением
зависимой переменной Y
по независимой переменной X.
Его вычисление не предполагает каких-либо
допущений о виде функции регрессии.

Величина
по определению неотрицательная и не
превышает единицы, причем=1
свидетельствует о наличии функциональной
связи между переменнымиY
и X.
Если указанные переменные не коррелированны
друг с другом, то
=0.

Можно
показать, что
не может быть меньше величины коэффициента
корреляцииr
(формула (2.9)) и в случае линейной связи
эти величины совпадают.

Это
позволяет использовать величину разности
–R²
в качестве меры
отклонения
регрессионной зависимости от линейного
вида.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Определение и формула[править | править код]

Интерпретация[править | править код]

Недостаток R2 и альтернативные показатели[править | править код]

Скорректированный (adjusted) R2[править | править код]

Информационные критерии[править | править код]

R2-обобщённый (extended)[править | править код]

История[править | править код]

Замечание[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Вычисление коэффициента детерминации

Способ 1: вычисление коэффициента детерминации при линейной функции

Способ 2: вычисление коэффициента детерминации в нелинейных функциях

Способ 3: коэффициент детерминации для линии тренда

Еще статьи по данной теме:

Помогла ли Вам статья?

Sample Problems

Вам также может понравиться

Как составить список фамилий по алфавиту

Как найти человека по имени в смоленске

Как исправить ошибку в игре вышивание крестиком

Добавить комментарий Отменить ответ

Недостаток R² и альтернативные показатели[править | править код]

Скорректированный (adjusted) R²[править | править код]

R²-обобщённый (extended)[править | править код]