Как найти коэффициент детерминации для множественной регрессии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 22 апреля 2022 года; проверки требуют 2 правки.

Коэффициент детерминации ( — R-квадрат) — это доля дисперсии зависимой переменной, объясняемая рассматриваемой моделью зависимости, то есть объясняющими переменными. Более точно — это единица минус доля необъяснённой дисперсии (дисперсии случайной ошибки модели, или условной по факторам дисперсии зависимой переменной) в дисперсии зависимой переменной. Его рассматривают как универсальную меру зависимости одной случайной величины от множества других. В частном случае линейной зависимости R^2 является квадратом так называемого множественного коэффициента корреляции между зависимой переменной и объясняющими переменными. В частности, для модели парной линейной регрессии коэффициент детерминации равен квадрату обычного коэффициента корреляции между y и x.

Определение и формула[править | править код]

Истинный коэффициент детерминации модели зависимости случайной величины y от факторов x определяется следующим образом:

${displaystyle R^{2}=1-{frac {D[y|x]}{D[y]}}=1-{frac {sigma ^{2}}{sigma _{y}^{2}}},}$

где ${displaystyle D[y]=sigma _{y}^{2}}$ — дисперсия случайной величины y, а ${displaystyle D[y|x]=sigma ^{2}}$ — условная (по факторам x) дисперсия зависимой переменной (дисперсия ошибки модели).

В данном определении используются истинные параметры, характеризующие распределение случайных величин. Если использовать выборочную оценку значений соответствующих дисперсий, то получим формулу для выборочного коэффициента детерминации (который обычно и подразумевается под коэффициентом детерминации):

${displaystyle R^{2}=1-{frac {{hat {sigma }}^{2}}{{hat {sigma }}_{y}^{2}}}=1-{frac {SS_{res}/n}{SS_{tot}/n}}=1-{frac {SS_{res}}{SS_{tot}}},}$

где ${displaystyle SS_{res}=sum _{i=1}^{n}e_{i}^{2}=sum _{i=1}^{n}(y_{i}-{hat {y}}_{i})^{2}}$ — сумма квадратов остатков регрессии, $y_{i},{hat y}_{i}$ — фактические и расчётные значения объясняемой переменной.

${displaystyle SS_{tot}=sum _{i=1}^{n}(y_{i}-{overline {y}})^{2}=n{hat {sigma }}_{y}^{2}}$ — общая сумма квадратов.

${bar {y}}={frac {1}{n}}sum _{{i=1}}^{n}y_{i}$

В случае линейной регрессии с константой ${displaystyle SS_{tot}=SS_{reg}+SS_{res}}$ , где ${displaystyle SS_{reg}=sum _{i=1}^{n}({hat {y}}_{i}-{overline {y}})^{2}}$ — объяснённая сумма квадратов, поэтому получаем более простое определение в этом случае — коэффициент детерминации — это доля объяснённой суммы квадратов в общей:

${displaystyle R^{2}={frac {SS_{reg}}{SS_{tot}}}}$

Необходимо подчеркнуть, что эта формула справедлива только для модели с константой, в общем случае необходимо использовать предыдущую формулу^{[источник не указан 390 дней]}.

Интерпретация[править | править код]

Коэффициент детерминации для модели с константой принимает значения от 0 до 1. Чем ближе значение коэффициента к 1, тем сильнее зависимость. При оценке регрессионных моделей это интерпретируется как соответствие модели данным. Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 50 % (в этом случае коэффициент множественной корреляции превышает по модулю 70 %). Модели с коэффициентом детерминации выше 80 % можно признать достаточно хорошими (коэффициент корреляции превышает 90 %). Значение коэффициента детерминации 1 означает функциональную зависимость между переменными.
При отсутствии статистической связи между объясняемой переменной и факторами, статистика $nR^{2}$ для линейной регрессии имеет асимптотическое распределение $chi ^{2}(k-1)$ , где — количество факторов модели (см. тест множителей Лагранжа). В случае линейной регрессии с нормально распределёнными случайными ошибками статистика $F={frac {R^{2}/(k-1)}{(1-R^{2})/(n-k)}}$ имеет точное (для выборок любого объёма) распределение Фишера (см. F-тест). Информация о распределении этих величин позволяет проверить статистическую значимость регрессионной модели исходя из значения коэффициента детерминации. Фактически в этих тестах проверяется гипотеза о равенстве истинного коэффициента детерминации нулю.
Коэффициент детерминации не может быть отрицательным, данный вывод исходит из свойств коэффициента детерминации. Однако скорректированный коэффициент детерминации вполне может принимать отрицательные значения.

Недостаток R² и альтернативные показатели[править | править код]

Основная проблема применения (выборочного) R^2 заключается в том, что его значение увеличивается (не уменьшается) от добавления в модель новых переменных, даже если эти переменные никакого отношения к объясняемой переменной не имеют. Поэтому сравнение моделей с разным количеством факторов с помощью коэффициента детерминации, вообще говоря, некорректно. Для этих целей можно использовать альтернативные показатели.

Скорректированный (adjusted) R²[править | править код]

Для того, чтобы была возможность сравнивать модели с разным числом факторов так, чтобы число регрессоров (факторов) не влияло на статистику R^2 обычно используется скорректированный коэффициент детерминации, в котором используются несмещённые оценки дисперсий:

${displaystyle {bar {R}}^{2}=R_{adj}^{2}=1-{frac {s^{2}}{s_{y}^{2}}}=1-{frac {SS_{res}/(n-k)}{SS_{tot}/(n-1)}}=1-(1-R^{2}){(n-1) over (n-k)}leqslant R^{2}}$

который даёт штраф за дополнительно включённые факторы, где n — количество наблюдений, а k — количество параметров.

Данный показатель всегда меньше единицы, но теоретически может быть и меньше нуля (только при очень маленьком значении обычного коэффициента детерминации и большом количестве факторов). Поэтому теряется интерпретация показателя как «доли». Тем не менее, применение показателя в сравнении вполне обоснованно.

Для моделей с одинаковой зависимой переменной и одинаковым объёмом выборки сравнение моделей с помощью скорректированного коэффициента детерминации эквивалентно их сравнению с помощью остаточной дисперсии ${displaystyle s^{2}=SS_{res}/(n-k)}$ или стандартной ошибки модели . Разница только в том, что последние критерии чем меньше, тем лучше.

Информационные критерии[править | править код]

AIC — информационный критерий Акаике — применяется исключительно для сравнения моделей. Чем меньше значение, тем лучше. Часто используется для сравнения моделей временных рядов с разным количеством лагов.
${displaystyle AIC={2k over n}+ln {SS_{res} over n}}$ , где k— количество параметров модели.

BIC или SC — байесовский информационный критерий Шварца — используется и интерпретируется аналогично AIC.
${displaystyle BIC={kln {n} over n}+ln {SS_{res} over n}}$ . Даёт больший штраф за включение лишних лагов в модель, чем AIC.

R²-обобщённый (extended)[править | править код]

В случае отсутствия в линейной множественной МНК регрессии константы свойства коэффициента детерминации могут нарушаться для конкретной реализации. Поэтому модели регрессии со свободным членом и без него нельзя сравнивать по критерию R^2 . Эта проблема решается с помощью построения обобщённого коэффициента детерминации $R_{{extended}}^{2}$ , который совпадает с исходным для случая МНК регрессии со свободным членом, и для которого выполняются четыре свойства, перечисленные выше. Суть этого метода заключается в рассмотрении проекции единичного вектора на плоскость объясняющих переменных.

Для случая регрессии без свободного члена:

$R_{{extended}}^{2}=1-{Y'*(I-P(X))*Y over Y'*(I-pi (X))*Y}$ ,
где X — матрица nxk значений факторов, $P(X)=X*(X'*X)^{{-1}}*X'$ — проектор на плоскость X, $pi (X)={P(X)*i_{n}*i_{n}'*P(X) over i_{n}'*P(X)*i_{n}}$ , где i_n — единичный вектор nx1.

$R_{{extended}}^{2}$ с условием небольшой модификации, также подходит для сравнения между собой регрессий, построенных с помощью: МНК, обобщённого метода наименьших квадратов (ОМНК), условного метода наименьших квадратов (УМНК), обобщённо-условного метода наименьших квадратов (ОУМНК).

История[править | править код]

Основой коэффициента детерминации является регрессионный анализ и коэффициент корреляции. Британский натуралист сэр Фрэнсис Гальтон (1822—1911) основал регрессионный анализ в 1870-х годах. Он, как и его двоюродный брат Чарльз Дарвин, был внуком Эразма Дарвина. Гальтон был известен своей сильной страстью к сбору данных любого рода. Например, он собрал данные о семенах сладкого горошка чина. Сравнивая диаметры семян, он построил то, что сегодня широко известно как корреляционная диаграмма. Связь, обнаруженную им в этой деятельности, он сначала окрестил «реверсией» (разворотом); однако позже он выбрал название «регрессия». Анализируя семена, он обнаружил явление регрессии к центру, согласно которому — после крайне неудачного изменения, последующее изменение снова приближается к среднему: средний диаметр потомства более крупных семян был меньше среднего диаметра семян родителей (изменения разворачиваются). В своих корреляционных диаграммах он нарисовал линию тренда, для которой он использовал коэффициент корреляции в качестве наклона.^[1]

Термин «дисперсия» был введен статистиком Рональдом Фишером (1890—1962) в его статье 1918 года под названием «Корреляция между родственниками на основе предположения о менделевском наследовании» (The Correlation between Relatives on the Supposition of Mendelian Inheritance)^[2]. Фишер был одним из самых выдающихся статистиков 20-го века и известен своим вкладом в эволюционную теорию. F-критерий, тесно связанный с коэффициентом детерминации, также назван в его честь. Карл Пирсон (1857—1936), основатель биометрики, предоставил формально-математическое обоснование коэффициента корреляции, квадратом которого является коэффициент детерминации.^[3]

Коэффициент детерминации подвергся резкой критике в последующие годы. Это произошло потому, что у него есть свойство, что чем больше количество независимых переменных, тем большим он становится. И это не зависит от того, вносят ли дополнительные «объясняющие переменные» вклад в «объяснительную силу». Чтобы учесть это обстоятельство, эконометрик Анри Тейл (1924—2000) в 1961 году предложил скорректированный коэффициент детерминации^[4] (Adjusted coefficient of determination (англ.)), который учитывает потерю степени свободы, связанную с ростом количества объясняющих переменных. Скорректированный коэффициент детерминации изменяется за счет штрафа, который накладывается на модель при увеличении числа переменных. Однако немецкий учёный Хорст Ринне подверг критике данный подход^[5] за недостаточное штрафование за потерю степени свободы по мере увеличения числа объясняющих переменных.

Замечание[править | править код]

Высокие значения коэффициента детерминации, вообще говоря, не свидетельствуют о наличии причинно-следственной зависимости между переменными (так же как и в случае обычного коэффициента корреляции). Например, если объясняемая переменная и факторы, на самом деле не связанные с объясняемой переменой, имеют возрастающую динамику, то коэффициент детерминации будет достаточно высок. Поэтому логическая и смысловая адекватность модели имеют первостепенную важность. Кроме того, необходимо использовать критерии для всестороннего анализа качества модели.

См. также[править | править код]

Коэффициент корреляции
Корреляция
Мультиколлинеарность
Дисперсия случайной величины
Метод группового учёта аргументов
Регрессионный анализ

Примечания[править | править код]

↑ Franka Miriam Brückler: Geschichte der Mathematik kompakt: Das Wichtigste aus Analysis, Wahrscheinlichkeitstheorie, angewandter Mathematik, Topologie und Mengenlehre. Springer-Verlag, 2017, ISBN 978-3-662-55573-6, S. 116. (нем.)
↑ Ronald Aylmer Fisher: The correlation between relatives on the supposition of Mendelian inheritance. In: Trans. Roy. Soc. Edinb. 52, 1918, S. 399—433. (англ.)
↑ Franka Miriam Brückler: Geschichte der Mathematik kompakt: Das Wichtigste aus Analysis, Wahrscheinlichkeitstheorie, angewandter Mathematik, Topologie und Mengenlehre. Springer-Verlag, 2017, ISBN 978-3-662-55573-6, S. 117. (нем.)
↑ Henri Theil: Economic Forecasts and Policy. Amsterdam 1961, S. 213. (англ.)
↑ Horst Rinne: Ökonometrie: Grundlagen der Makroökonometrie. Vahlen, 2004. (нем.)

Литература[править | править код]

Бахрушин В. Е. Методы оценивания характеристик нелинейных статистических связей // Системные технологии. — 2011. — № 2(73). — С. 9—14.[1]

Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс.. — 6,7,8-е изд., доп. и перераб.. — Москва: Дело. — Т. “”. — 576 с. — ISBN 5-7749-0055-X.

Ершов Э.Б. Распространение коэффициента детерминации на общий случай линейной регрессии, оцениваемой с помощью различных версий метода наименьших квадратов (рус., англ.) // ЦЭМИ РАН Экономика и математические методы. — Москва: ЦЭМИ РАН, 2002. — Т. 38, вып. 3. — С. 107—120.

Айвазян С.А., Мхитарян В.С. Прикладная статистика. Основы эконометрики (в 2-х т.). — ??. — Москва: Юнити-Дана (проект TASIS), 2001. — Т. “1,2”. — 1088 с. — ISBN 5-238-00304-8.

Ершов Э.Б. Выбор регрессии максимизирующий несмещённую оценку коэффициента детерминации (рус., англ.) // Айвазян С.А. Прикладная эконометрика. — Москва: Маркет ДС, 2008. — Т. 12, вып. 4. — С. 71—83.

Ссылки[править | править код]

Глоссарий статистических терминов (недоступная ссылка с 13-05-2013 [3656 дней] — история)

Источник

Задача

По 20
предприятиям региона изучается зависимость выработки продукции на одного
работника

(тыс.руб.) от ввода в действие новых основных
фондов

(% от стоимости фондов на
конец года) и от удельного веса рабочих высокой квалификации в общей
численности рабочих

(смотри таблицу своего варианта).

Требуется:

Построить линейную модель множественной регрессии. Записать стандартизированное
уравнение множественной регрессии. На основе стандартизированных коэффициентов
регрессии и средних коэффициентов эластичности ранжировать факторы по степени
их влияния на результат.
Найти
коэффициенты парной, частной и множественной корреляции. Проанализировать их.
Найти
скорректированный коэффициент множественной детерминации. Сравнить его с
нескорректированным (общим) коэффициентов детерминации.
С
помощью

–критерия Фишера оценить статистическую
надежность уравнения регрессии и коэффициента детерминации

С
помощью частных

–критериев Фишера оценить целесообразность
включения в уравнение множественной регрессии фактора

после

и фактора

после

Составить уравнение линейной парной регрессии, оставив лишь один значащий фактор.

Решение

Для
удобства проведения расчетов поместим результаты промежуточных расчетов в
таблицу:

Найдем
средние квадратические отклонения признаков:

Расчет
парных коэффициентов корреляции и параметров линейного уравнения множественной
регрессии

1) Для
нахождения параметров линейного уравнения множественной регрессии:

необходимо
решить следующую систему линейных уравнений относительно неизвестных параметров

Решать систему уравнений
методом Крамера,
методом обратной матрицы или
методом Гаусса достаточно трудоемко, поэтому
воспользуемся готовыми формулами:

Рассчитаем
сначала парные коэффициенты корреляции:

Находим:

Таким
образом, получили следующее уравнение множественной регрессии:

Коэффициенты
стандартизированного уравнения регрессии

Коэффициенты

стандартизированного уравнения регрессии

находятся по формулам:

То есть
уравнение будет выглядеть следующим образом:

Так как
стандартизованные коэффициенты регрессии можно сравнивать между собой, то можно
сказать, что ввод в действие новых основных фондов оказывает большее влияние на
выработку продукции, чем удельный вес рабочих высокой квалификации.

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Коэффициенты
эластичности

Сравнивать
влияние факторов на результат можно также при помощи средних коэффициентов
эластичности:

Вычисляем:

Т.е.
увеличение только основных фондов (от своего среднего значения) или только
удельного веса рабочих высокой квалификации на 1% увеличивает в среднем
выработку продукции на 0,635% или 0,142% соответственно. Таким образом,
подтверждается большее влияние на результат

фактора

, чем фактора

Частные
и парные коэффициенты корреляции

2) Коэффициенты парной корреляции мы уже нашли:

Они
указывают на весьма сильную связь каждого фактора с результатом, а также
высокую межфакторную зависимость (факторы

явно коллинеарны, так как

). При такой сильной
межфакторной зависимости рекомендуется один из факторов исключить из
рассмотрения.

Частные
коэффициенты корреляции характеризуют тесноту связи между результатом и
соответствующим факторов при элиминировании (устранении влияния) других
факторов, включенных в уравнение регрессии.

При двух
факторах частные коэффициенты корреляции рассчитываются следующим образом:

Если
сравнить коэффициенты парной и частной корреляции, то можно увидеть, что из-за
высокой межфакторной зависимости коэффициенты парной корреляции дают завышенные
оценки тесноты связи. Именно по этой причине рекомендуется при наличии сильной
коллинеарности (взаимосвязи) факторов исключать из исследования тот фактор, у
которого теснота парной зависимости меньше, чем теснота межфакторной связи.

Коэффициенты
множественной корреляции и детерминации

Коэффициент
множественной корреляции определить по формуле:

Коэффициент
множественной корреляции показывает на весьма сильную связь всего набора
факторов с результатом.

3)
Нескорректированный коэффициент множественной детерминации

оценивает долю вариации результата за счет
представленных в уравнении факторов в общей вариации результата. Здесь эта доля
составляет 98,4% и указывает на высокую степень обусловленности вариации
результата вариацией факторов, иными словами – на весьма тесную связь факторов
с результатом.

Скорректированный
коэффициент множественной корреляции:

определяет
тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает
такую оценку тесноты связи, которая не зависит от числа факторов и поэтому
может сравниваться по разным моделям с разным числом факторов. Оба коэффициента
указывают на высокую (более 98%) детерминированность результата

в модели факторами

Надежность
уравнения регрессии. Критерий Фишера

4) Оценку
надежности уравнения регрессии в целом и показателя тесноты связи

дает

–критерий Фишера:

В нашем
случае фактическое значение

–критерия Фишера:

Получили,
что

(при

)
(по таблице F-распределения Фишера-Снедекора, при уровне значимости α=0,05 и числе степеней свободы k₁=2 и k₂=20-2=18), то есть вероятность
случайно получить такое значение

– критерия не превышает допустимый уровень
значимости 5%. Следовательно, полученное значение не случайно, оно
сформировалось под влиянием существенных факторов, то есть подтверждается
статистическая значимость всего уравнения и показателя тесноты связи

5) С
помощью частных

–критериев Фишера оценим целесообразность
включения в уравнение множественной регрессии фактора

после

и фактора

после

при помощи формул:

Найдем

Получили,
что

. Следовательно, включение
в модель фактора

после того, как в модель включен фактор

статистически нецелесообразно: прирост
факторной дисперсии за счет дополнительного признака

оказывается незначительным, несущественным;
фактор

включать в уравнение после фактора

не следует.

Если
поменять первоначальный порядок включения факторов в модель и рассмотреть
вариант включения

после

, то результат расчета
частного

–критерия для

будет иным.

, то есть вероятность его
случайного формирования меньше принятого стандарта

. Следовательно, значение
частного

–критерия для дополнительно включенного
фактора

не случайно, является статистически значимым,
надежным, достоверным: прирост факторной дисперсии за счет дополнительного
фактора

является существенным.
Фактор

должен присутствовать в уравнении, в том числе
в варианте, когда он дополнительно включается после фактора

6) Общий
вывод состоит в том, что множественная модель с факторами

содержит неинформативный фактор

. Если исключить фактор

, то можно ограничится
уравнением парной регрессии:

Источник

Все курсы > Оптимизация > Занятие 4 (часть 2)

В первой части мы рассмотрели теорию линейной регрессии. Теперь перейдем к практике.

Откроем ноутбук к этому занятию⧉

Сквозной пример

Данные и постановка задачи

Обратимся к хорошо знакомому нам датасету недвижимости в Бостоне.

boston = pd.read_csv(‘/content/boston.csv’)

При этом нам нужно будет решить две основные задачи:

Задача 1. Научиться оценивать качество модели не только с точки зрения метрики, но и исходя из рассмотренных ранее допущений модели. Эту задачу мы решим в три этапа.

Этап 1. Построим базовую (baseline) модель линейной регрессии с помощью класса LinearRegression библиотеки sklearn и оценим, насколько выполняются рассмотренные выше допущения.
Этап 2. Попробуем изменить данные таким образом, чтобы модель в большей степени соответствовала этим критериям.
Этап 3. Обучим еще одну модель и посмотрим, как изменится результат.

Задача 2. С нуля построить модель множественной линейной регрессии и сравнить прогноз с результатом, полученным при решении первой задачи. При этом обучение модели мы реализуем двумя способами, а именно, через:

Метод наименьших квадратов
Метод градиентного спуска

Разделение выборки

Мы уже не раз говорили про важность разделения выборки на обучаущую и тестовую части. Сегодня же, с учетом того, что нам предстоит изучить много нового материала, мы опустим этот этап и будем обучать и тестировать модель на одних и тех же данных.

Исследовательский анализ данных

Теперь давайте более внимательно посмотрим на имеющиеся у нас данные. Как вы вероятно заметили, все признаки в этом датасете количественные, за исключением переменной CHAS.

RangeIndex: 506 entries, 0 to 505

Data columns (total 14 columns):

# Column Non-Null Count Dtype

— —— ————– —–

0 CRIM 506 non-null float64

1 ZN 506 non-null float64

2 INDUS 506 non-null float64

3 CHAS 506 non-null float64

4 NOX 506 non-null float64

5 RM 506 non-null float64

6 AGE 506 non-null float64

7 DIS 506 non-null float64

8 RAD 506 non-null float64

9 TAX 506 non-null float64

10 PTRATIO 506 non-null float64

11 B 506 non-null float64

12 LSTAT 506 non-null float64

13 MEDV 506 non-null float64

dtypes: float64(14)

memory usage: 55.5 KB

# мы видим, что переменная CHAS категориальная

boston.CHAS.value_counts()

0.0 471

1.0 35

Name: CHAS, dtype: int64

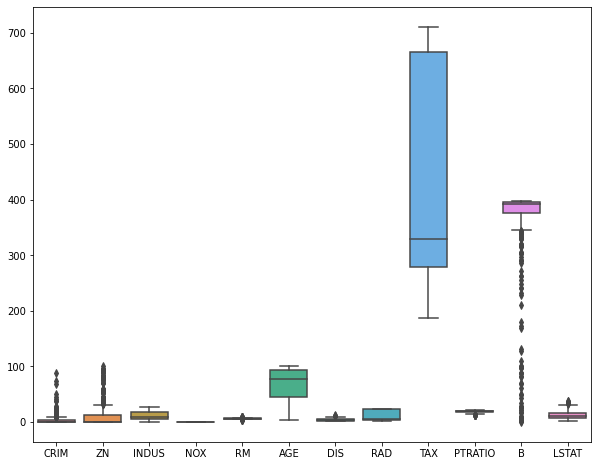
Посмотрим на распределение признаков с помощью boxplots.

plt.figure(figsize = (10, 8))

sns.boxplot(data = boston.drop(columns = [‘CHAS’, ‘MEDV’]))

plt.show()

Посмотрим на распределение целевой переменной.

def box_density(x):

# создадим два подграфика

f, (ax_box, ax_kde) = plt.subplots(nrows = 2, # из двух строк

ncols = 1, # и одного столбца

sharex = True, # оставим только нижние подписи к оси x

gridspec_kw = {‘height_ratios’: (.15, .85)}, # зададим разную высоту строк

figsize = (10,8)) # зададим размер графика

# в первом подграфике построим boxplot

sns.boxplot(x = x, ax = ax_box)

ax_box.set(xlabel = None)

# во втором – график плотности распределения

sns.kdeplot(x, fill = True)

# зададим заголовок и подписи к осям

ax_box.set_title(‘Распределение переменной’, fontsize = 17)

ax_kde.set_xlabel(‘Переменная’, fontsize = 15)

ax_kde.set_ylabel(‘Плотность распределения’, fontsize = 15)

plt.show()

box_density(boston.iloc[:, –1])

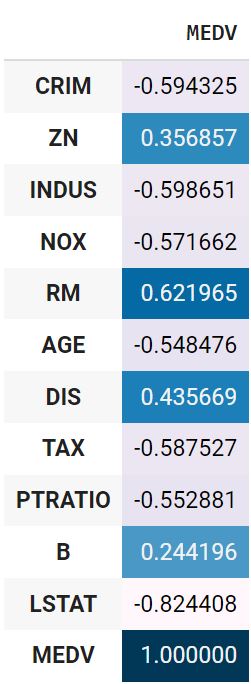
Посмотрим на корреляцию количественных признаков с целевой переменной.

boston.drop(columns = ‘CHAS’).corr().MEDV.to_frame().style.background_gradient()

Используем точечно-бисериальную корреляцию для оценки взамосвязи переменной CHAS и целевой переменной.

def pbc(continuous, binary):

# преобразуем количественную переменную в массив Numpy

continuous_values = np.array(continuous)

# классы качественной переменной превратим в нули и единицы

binary_values = np.unique(binary, return_inverse = True)[1]

# создадим две подгруппы количественных наблюдений

# в зависимости от класса дихотомической переменной

group0 = continuous_values[np.argwhere(binary_values == 0).flatten()]

group1 = continuous_values[np.argwhere(binary_values == 1).flatten()]

# найдем средние групп,

mean0, mean1 = np.mean(group0), np.mean(group1)

# а также длины групп и всего датасета

n0, n1, n = len(group0), len(group1), len(continuous_values)

# рассчитаем СКО количественной переменной

std = continuous_values.std()

# подставим значения в формулу

return (mean1 – mean0) / std * np.sqrt( (n1 * n0) / (n * (n–1)) )

pbc(boston.MEDV, boston.CHAS)

Обработка данных

Пропущенные значения

Посмотрим, есть ли пропущенные значения.

CRIM 0

ZN 0

INDUS 0

CHAS 0

NOX 0

RM 0

AGE 0

DIS 0

RAD 0

TAX 0

PTRATIO 0

B 0

LSTAT 0

MEDV 0

dtype: int64

Выбросы

Удалим выбросы.

from sklearn.ensemble import IsolationForest

clf = IsolationForest(max_samples = 100, random_state = 42)

clf.fit(boston)

boston[‘anomaly’] = clf.predict(boston)

boston = boston[boston.anomaly == 1]

boston = boston.drop(columns = ‘anomaly’)

boston.shape

При удалении выбросов важно помнить, что полное отсутствие вариантивности в данных не позволит выявить взаимосвязи.

Масштабирование признаков

Приведем признаки к одному масштабу (целевую переменную трогать не будем).

boston.iloc[:, :–1] = (boston.iloc[:, :–1] – boston.iloc[:, :–1].mean()) / boston.iloc[:, :–1].std()

Замечу, что метод наименьших квадратов не требует масштабирования признаков, градиентному спуску же напротив необходимо, чтобы все значения находились в одном диапазоне (подробнее в дополнительных материалах).

Кодирование категориальных переменных

После стандартизации переменная CHAS также сохранила только два значения.

boston.CHAS.value_counts()

-0.182581 389

5.463391 13

Name: CHAS, dtype: int64

Ее можно не трогать.

Построение модели

Создадим первую пробную (baseline) модель с помощью библиотеки sklearn.

baseline-модель

X = boston.drop(‘MEDV’, axis = 1)

y = boston[‘MEDV’]

from sklearn.linear_model import LinearRegression

model = LinearRegression()

y_pred = model.fit(X, y).predict(X)

Оценка качества

Диагностика модели, метрики качества и функции потерь

Вероятно, вы заметили, что мы использовали MSE и для обучения модели, и для оценки ее качества. Возникает вопрос, есть ли отличие между функцией потерь и метрикой качества модели.

Функция потерь и метрика качества могут совпадать, а могут и не совпадать. Важно понимать, что у них разное назначение.

Функция потерь — это часть алгоритма, нам важно, чтобы эта функция была дифференцируема (у нее была производная)
Производная метрики качества нас не интересует. Метрика качества должна быть адекватна решаемой задаче.

MSE, RMSE, MAE, MAPE

MSE и RMSE

Для оценки качества RMSE предпочтительнее, чем MSE, потому что показывает насколько ошибается модель в тех же единицах измерения, что и целевая переменная. Например, если диапазон целевой переменной от 80 до 100, а RMSE 20, то в среднем модель ошибается на 20-25 процентов.

В качестве практики напишем собственную функцию.

# параметр squared = True возвращает MSE

# параметр squared = False возвращает RMSE

def mse(y, y_pred, squared = True):

mse = ((y – y_pred) ** 2).sum() / len(y)

if squared == True:

return mse

else:

return np.sqrt(mse)

mse(y, y_pred), mse(y, y_pred, squared = False)

(9.980044349414223, 3.1591208190593507)

Сравним с sklearn.

from sklearn.metrics import mean_squared_error

# squared = False дает RMSE

mean_squared_error(y, y_pred, squared = False)

MAE

Приведем формулу.

$$ MAE = frac{sum |y-hat{y}|}{n} $$

Средняя абсолютная ошибка представляет собой среднее арифметическое абсолютной ошибки $varepsilon = |y-hat{y}| $ и использует те же единицы измерения, что и целевая переменная.

def mae(y, y_pred):

return np.abs(y – y_pred).sum() / len(y)

from sklearn.metrics import mean_absolute_error

mean_absolute_error(y, y_pred)

MAE часто используется при оценке качества моделей временных рядов.

MAPE

Средняя абсолютная ошибка в процентах (mean absolute percentage error) по сути выражает MAE в процентах, а не в абсолютных величинах, представляя отклонение как долю от истинных ответов.

$$ MAPE = frac{1}{n} sum vert frac{y-hat{y}}{y} vert $$

Это позволяет сравнивать модели с разными единицами измерения между собой.

def mape(y, y_pred):

return 1/len(y) * np.abs((y – y_pred) / y).sum()

from sklearn.metrics import mean_absolute_percentage_error

mean_absolute_percentage_error(y, y_pred)

Коэффициент детерминации

В рамках вводного курса в ответах на вопросы к занятию по регрессии мы подробно рассмотрели коэффициент детерминации ($R^2$), его связь с RMSE, а также зачем нужен скорректированный $R^2$. Как мы знаем, если использовать, например, класс LinearRegression, то эта метрика содержится в методе .score().

Также можно использовать функцию r2_score() модуля metrics.

from sklearn.metrics import r2_score

r2_score(y, y_pred)

Для скорректированного $R^2$ напишем собственную функцию.

def r_squared(x, y, y_pred):

r2 = 1 – ((y – y_pred)** 2).sum()/((y – y.mean()) ** 2).sum()

n, k = x.shape

r2_adj = 1 – ((y – y_pred)** 2).sum()/((y – y.mean()) ** 2).sum()

return r2, r2_adj

(0.7965234359550825, 0.7965234359550825)

Диагностика модели

Теперь проведем диагностику модели в соответствии со сделанными ранее допущениями.

Анализ остатков и прогнозных значений

Напишем диагностическую функцию, которая сразу выведет несколько интересующих нас графиков и метрик, касающихся остатков и прогнозных значений.

from scipy.stats import probplot

from statsmodels.graphics.tsaplots import plot_acf

from statsmodels.stats.stattools import durbin_watson

def diagnostics(y, y_pred):

residuals = y – y_pred

residuals_mean = np.round(np.mean(y – y_pred), 3)

f, ((ax_rkde, ax_prob), (ax_ry, ax_auto), (ax_yy, ax_ykde)) = plt.subplots(nrows = 3,

ncols = 2,

figsize = (12, 18))

# в первом подграфике построим график плотности остатков

sns.kdeplot(residuals, fill = True, ax = ax_rkde)

ax_rkde.set_title(‘Residuals distribution’, fontsize = 14)

ax_rkde.set(xlabel = f‘Residuals, mean: {residuals_mean}’)

ax_rkde.set(ylabel = ‘Density’)

# во втором – график нормальной вероятности остатков

probplot(residuals, dist = ‘norm’, plot = ax_prob)

ax_prob.set_title(‘Residuals probability plot’, fontsize = 14)

# в третьем – график остатков относительно прогноза

ax_ry.scatter(y_pred, residuals)

ax_ry.set_title(‘Predicted vs. Residuals’, fontsize = 14)

ax_ry.set(xlabel = ‘y_pred’)

ax_ry.set(ylabel = ‘Residuals’)

# в четвертом – автокорреляцию остатков

plot_acf(residuals, lags = 30, ax = ax_auto)

ax_auto.set_title(‘Residuals Autocorrelation’, fontsize = 14)

ax_auto.set(xlabel = f‘Lags ndurbin_watson: {durbin_watson(residuals).round(2)}’)

ax_auto.set(ylabel = ‘Autocorrelation’)

# в пятом – сравним прогнозные и фактические значения

ax_yy.scatter(y, y_pred)

ax_yy.plot([y.min(), y.max()], [y.min(), y.max()], “k–“, lw = 1)

ax_yy.set_title(‘Actual vs. Predicted’, fontsize = 14)

ax_yy.set(xlabel = ‘y_true’)

ax_yy.set(ylabel = ‘y_pred’)

# в шестом – сравним распределение истинной и прогнозной целевой переменных

sns.kdeplot(y, fill = True, ax = ax_ykde, label = ‘y_true’)

sns.kdeplot(y_pred, fill = True, ax = ax_ykde, label = ‘y_pred’)

ax_ykde.set_title(‘Actual vs. Predicted Distribution’, fontsize = 14)

ax_ykde.set(xlabel = ‘y_true and y_pred’)

ax_ykde.set(ylabel = ‘Density’)

ax_ykde.legend(loc = ‘upper right’, prop = {‘size’: 12})

plt.tight_layout()

plt.show()

Разберем полученную информацию.

В целом остатки модели распределены нормально с нулевым средним значением
Явной гетероскедастичности нет, хотя мы видим, что дисперсия не всегда равномерна
Присутствует умеренная отрицательная корреляция
График y_true vs. y_pred показывает насколько сильно прогнозные значения отклоняются от фактических. В идеальной модели (без шума, т.е. без случайных колебаний) точки должны были би стремиться находиться на диагонали, в более реалистичной модели нам бы хотелось видеть, что точки плотно сосредоточены вокруг диагонали.
Распределение прогнозных значений в целом повторяет распределение фактических.

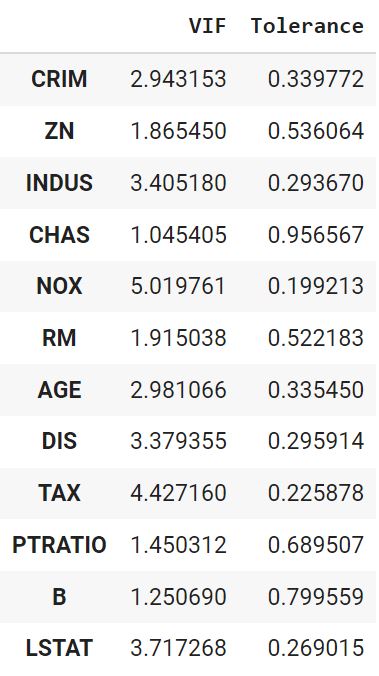
Мультиколлинеарность

Отдельно проведем анализ на мультиколлинеарность. Напишем соответствующую функцию.

def vif(df, features):

vif, tolerance = {}, {}

# пройдемся по интересующим нас признакам

for feature in features:

# составим список остальных признаков, которые будем использовать

# для построения регрессии

X = [f for f in features if f != feature]

# поместим текущие признаки и таргет в X и y

X, y = df[X], df[feature]

# найдем коэффициент детерминации

r2 = LinearRegression().fit(X, y).score(X, y)

# посчитаем tolerance

tolerance[feature] = 1 – r2

# найдем VIF

vif[feature] = 1 / (tolerance[feature])

# выведем результат в виде датафрейма

return pd.DataFrame({‘VIF’: vif, ‘Tolerance’: tolerance})

vif(df = X.drop(‘CHAS’, axis = 1), features = X.drop(‘CHAS’, axis = 1).columns)

Дополнительная обработка данных

Попробуем дополнительно улучшить некоторые из диагностических показателей.

VIF

Уберем признак с наибольшим VIF (RAD) и посмотрим, что получится.

vif(df = X, features = [‘CRIM’,

‘ZN’,

‘INDUS’,

‘CHAS’,

‘NOX’,

‘RM’,

‘AGE’,

‘DIS’,

‘TAX’,

‘PTRATIO’,

‘B’,

‘LSTAT’])

Показатели пришли в норму. Окончательно удалим RAD.

boston.drop(columns = ‘RAD’, inplace = True)

Преобразование данных

Применим преобразование Йео-Джонсона.

from sklearn.preprocessing import PowerTransformer

pt = PowerTransformer()

boston = pd.DataFrame(pt.fit_transform(boston),

columns = boston.columns)

Отбор признаков

Посмотрим на линейную корреляцию Пирсона количественных признаков и целевой переменной.

boston_t.drop(columns = ‘CHAS’).corr().MEDV.to_frame().style.background_gradient()

Также рассчитаем точечно-бисериальную корреляцию.

pbc(boston_t.MEDV, boston_t.CHAS)

Удалим признаки с наименьшей корреляцией, а именно ZN, CHAS, DIS и B.

boston.drop(columns = [‘ZN’, ‘CHAS’, ‘DIS’, ‘B’], inplace = True)

Повторное моделирование и диагностика

Повторное моделирование

Выполним повторное моделирование.

X = boston_t.drop(columns = [‘ZN’, ‘CHAS’, ‘DIS’, ‘B’, ‘MEDV’])

y = boston_t.MEDV

from sklearn.linear_model import LinearRegression

model = LinearRegression()

y_pred = model.fit(X, y).predict(X)

Оценка качества и диагностика

Оценим качество. Так как мы преобразовали целевую переменную, показатель RMSE не будет репрезентативен. Воспользуемся MAPE и $R^2$.

(0.7546883769637166, 0.7546883769637166)

Отклонение прогнозного значения от истинного снизилось. $R^2$ немного уменьшился, чтобы бывает, когда мы пытаемся привести модель к соответствию допущениям. Проведем диагностику.

Распределение остатков немного улучшилось, при этом незначительно усилилась их отрицательная автокорреляция. Распределение целевой переменной стало менее островершинным.

Данные можно было бы продолжить анализировать и улучшать, однако в рамках текущего занятия перейдем к механике обучения модели.

Коэффициенты

Выведем коэффициенты для того, чтобы сравнивать их с результатами построенных с нуля моделей.

model.intercept_, model.coef_

(9.574055157844797e-16,

array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128,

-0.16878987, -0.18057055, -0.49319274]))

Обучение модели

Теперь когда мы поближе познакомились с понятием регрессии, разобрали функции потерь и изучили допущения, при которых модель может быть удачной аппроксимацией данных, пора перейти к непосредственному созданию алгоритмов.

Векторизация уравнения

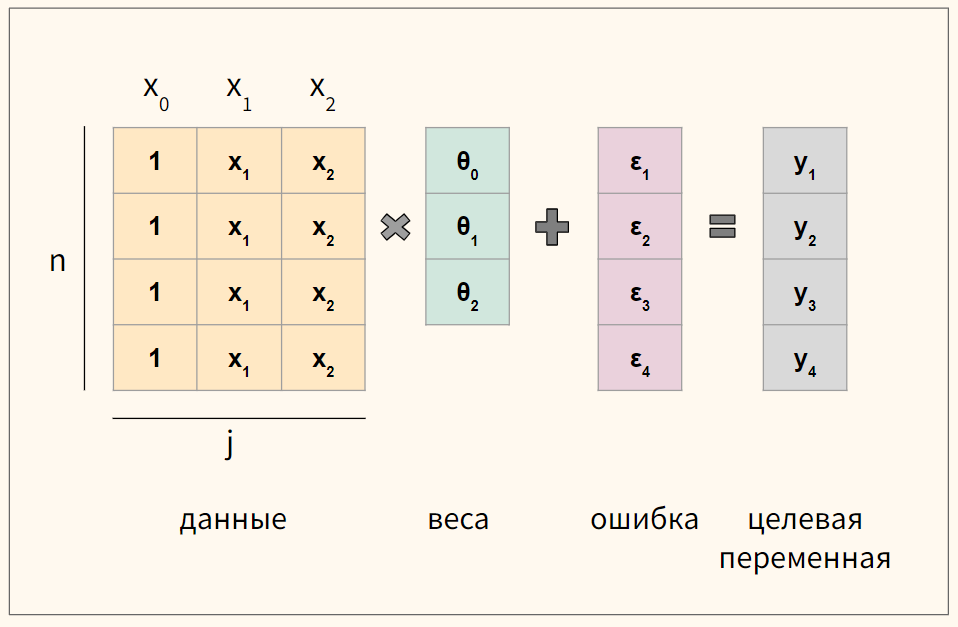
Для удобства векторизуем приведенное выше уравнение множественной линейной регрессии

$$ y = begin{bmatrix} y_1 \ y_2 \ vdots \ y_n end{bmatrix} X = begin{bmatrix} x_0 & x_1 & ldots & x_j \ x_0 & x_1 & ldots & x_j \ vdots & vdots & vdots & vdots \ x_{0} & x_{1} & ldots & x_{n,j} end{bmatrix}, theta = begin{bmatrix} theta_0 \ theta_1 \ vdots \ theta_n end{bmatrix}, varepsilon = begin{bmatrix} varepsilon_1 \ varepsilon_2 \ vdots \ varepsilon_n end{bmatrix} $$

где n — количество наблюдений, а j — количество признаков.

Обратите внимание, что мы создали еще один столбец данных $ x_0 $, который будем умножать на сдвиг $ theta_0 $. Его мы заполним единицами.

В результате такого несложного преобразования значение сдвига не изменится, но мы сможем записать уравнение через умножение матрицы на вектор.

$$ y = Xtheta + varepsilon $$

Кроме того, как мы увидим ниже, так нам не придется искать отдельную производную для коэффициента $ theta_0 $.

Схематично для модели с четырьмя наблюдениями (n = 4) и двумя признаками (j = 2) получаются вот такие матрицы.

Функция потерь

Как мы уже говорили, чтобы подобрать оптимальные коэффициенты $theta$, нам нужен критерий или функция потерь. Логично измерять отклонение прогнозного значения от истинного.

$$ varepsilon = Xtheta-y $$

При этом опять же просто складывать отклонения или ошибки мы не можем. Положительные и отрицательные значения будут взаимоудаляться. Для решения этой проблемы можно, например, использовать модуль и это приводит нас к абсолютной ошибке или L1 loss.

Абсолютная ошибка, L1 loss

При усреднении на количество наблюдений мы получаем среднюю абсолютную ошибку (mean absolute error, MAE).

$$ MAE = frac{sum{|y-Xtheta|}}{n} = frac{sum{|varepsilon|}}{n} $$

Приведем пример такой функции на Питоне.

def L1(y_true, y_pred):

return np.sum(np.abs(y_true – y_pred)) / y_true.size

Помимо модуля ошибку можно возводить в квадрат.

Квадрат ошибки, L2 loss

В этом случай говорят про сумму квадратов ошибок (sum of squared errors, SSE) или сумму квадратов остатков (sum of squared residuals, SSR или residual sum of squares, RSS).

$$ SSE = sum (y-Xtheta)^2 $$

Как мы уже знаем, на практике вместо SSE часто используется MSE, или вернее half MSE для удобства нахождения производной.

$$ MSE = frac{1}{2n} sum (y-theta X)^2 $$

Ниже код на Питоне.

def L2(y_true, y_pred):

return np.sum((y_true – y_pred) ** 2) / y_true.size

На практике у обеих функций есть сильные и слабые стороны. Рассмотрим L1 loss (MAE) и L2 loss (MSE) на графике.

# для построения графиков мы используем x вместо y_true, y_pred

# в качестве входящего значения

def mse(x):

return x ** 2

def mae(x):

return np.abs(x)

plt.figure(figsize = (10, 8))

x_vals = np.arange(–3, 3, 0.01)

plt.plot(x_vals, mae(x_vals), label = ‘MAE’)

plt.plot(x_vals, mse(x_vals), label = ‘MSE’)

plt.legend(loc = ‘upper center’, prop = {‘size’: 14})

plt.grid()

plt.show()

Очевидно, при отклонении от точки минимума из-за возведения в квадрат L2 значительно быстрее увеличивает ошибку, поэтому если в данных есть выбросы при суммированнии они очень сильно влияют на этот показатель, хотя де-факто большая часть значений такого уровня потерь не дали бы.

Функция L1 не дает такой большой ошибки на выбросах, однако ее сложно дифференцировать, в точке минимума ее производная не определена.

Функция Хьюбера

Рассмотрим функцию Хьюбера (Huber loss), которая объединяет сильные стороны вышеупомянутых функций и при этом лишена их недостатков. Посмотрим на формулу.

$$ L_{delta}= left{begin{matrix} frac{1}{2}(y-hat{y})^{2} & if | y-hat{y} | < delta\ delta (|y-hat{y}|-frac1 2 delta) & otherwise end{matrix}right. $$

Представим ее на графике.

plt.figure(figsize = (10, 8))

def huber(x, delta = 1.):

huber_mse = 0.5 * np.square(x)

huber_mae = delta * (np.abs(x) – 0.5 * delta)

return np.where(np.abs(x) <= delta, huber_mse, huber_mae)

x_vals = np.arange(–3, 3, 0.01)

plt.plot(x_vals, mae(x_vals), label = ‘MAE’)

plt.plot(x_vals, mse(x_vals), label = ‘MSE’)

plt.plot(x_vals, huber(x_vals, delta = 2), label = ‘Huber’)

plt.legend(loc = ‘upper center’, prop = {‘size’: 14})

plt.grid()

plt.show()

Также приведем код этой функции.

def huber(y_pred, y_true, delta = 1.0):

# пропишем обе части функции потерь

huber_mse = 0.5 * (y_true – y_pred) ** 2

huber_mae = delta * (np.abs(y_true – y_pred) – 0.5 * delta)

# выберем одну из них в зависимости от дельта

return np.where(np.abs(y_true – y_pred) <= delta, huber_mse, huber_mae)

На сегодняшнем занятии мы, как и раньше, в качестве функции потерь используем MSE.

Метод наименьших квадратов

Нормальные уравнения

Для множественной линейной регрессии коэффициенты находятся по следующей формуле

$$ theta = (X^TX)^{-1}X^Ty $$

Разберем эту формулу подробнее. Сумму квадратов остатков (SSE) можно переписать как произведение вектора $ hat{varepsilon} $ на самого себя, то есть $ SSE = varepsilon^{T} varepsilon$. Помня, что $varepsilon = y-Xtheta $ получаем (не забывая транспонировать)

$$ (y-Xtheta)^T(y-Xtheta) $$

Раскрываем скобки

$$ y^Ty-y^T(Xtheta)-(Xtheta)^Ty+(Xtheta)^T(Xtheta) $$

Заметим, что $A^TB = B^TA$, тогда

$$ y^Ty-(Xtheta)^Ty-(Xtheta)^Ty+(Xtheta)^T(Xtheta)$$

$$ y^Ty-2(Xtheta)^Ty+(Xtheta)^T(Xtheta) $$

Вспомним, что $(AB)^T = A^TB^T$, тогда

$$ y^Ty-2theta^TX^Ty+theta^TX^TXtheta $$

Теперь нужно найти градиент этой функции

$$ nabla_{J(theta)} left( y^Ty-2theta^TX^Ty+theta^TX^TXtheta right) $$

После дифференцирования относительно $theta$ мы получаем следующий результат

$$ nabla_{J(theta)} = -2X^Ty+2X^TXtheta $$

Как мы помним, оптимум функции находится там, где производная равна нулю.

$$ -2X^Ty+2X^TXtheta = 0 $$

$$ -X^Ty+X^TXtheta = 0 $$

$$ X^TXtheta = X^Ty $$

Выражение выше называется нормальным уравнением (normal equation). Решив его для $theta$ мы найдем аналитическое решение минимизации суммы квадратов отклонений.

$$ theta = (X^TX)^{-1}X^Ty $$

По теореме Гаусса-Маркова, оценка через МНК является наиболее оптимальной (обладающей наименьшей дисперсией) среди всех методов построения модели.

Код на Питоне

Перейдем к созданию класса линейной регрессии наподобие LinearRegression библиотеки sklearn. Вначале напишем функцию гипотезы (т.е. функцию самой модели), снабдив ее еще одной функцией, которая добавляет столбец из единиц к признакам.

$$ h_{theta}(x) = theta X $$

def add_ones(x):

# важно! метод .insert() изменяет исходный датафрейм

return x.insert(0,‘x0’, np.ones(x.shape[0]))

def h(x, theta):

x = x.copy()

add_ones(x)

return np.dot(x, theta)

Перейдем к функции, отвечающей за обучение модели.

$$ theta = (X^TX)^{-1}X^Ty $$

# строчную `x` используем внутри функций и методов класса

# заглавную `X` вне функций и методов

def fit(x, y):

x = x.copy()

add_ones(x)

xT = x.transpose()

inversed = np.linalg.inv(np.dot(xT, x))

thetas = inversed.dot(xT).dot(y)

return thetas

Обучим модель и выведем коэффициенты.

thetas = fit(X, y)

thetas[0], thetas[1:]

(9.3718435789647e-16,

array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128,

-0.16878987, -0.18057055, -0.49319274]))

Примечание. Замечу, что не все матрицы обратимы. В этом случае можно найти псевдообратную матрицу (pseudoinverse). Для этого в Numpy есть функция np.linalg.pinv().

Сделаем прогноз.

y_pred = h(X, thetas)

y_pred[:5]

array([1.24414666, 0.55999778, 1.48103299, 1.49481605, 1.21342788])

Создание класса

Объединим код в класс.

class ols():

def __init__(self):

self.thetas = None

def add_ones(self, x):

return x.insert(0,‘x0’, np.ones(x.shape[0]))

def fit(self, x, y):

x = x.copy()

self.add_ones(x)

xT = x.T

inversed = np.linalg.inv(np.dot(xT, x))

self.thetas = inversed.dot(xT).dot(y)

def predict(self, x):

x = x.copy()

self.add_ones(x)

return np.dot(x, self.thetas)

Создадим объект класса и обучим модель.

model = ols()

model.fit(X, y)

Выведем коэффициенты.

model.thetas[0], model.thetas[1:]

(9.3718435789647e-16,

array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128,

-0.16878987, -0.18057055, -0.49319274]))

Сделаем прогноз.

y_pred = model.predict(X)

y_pred[:5]

array([1.24414666, 0.55999778, 1.48103299, 1.49481605, 1.21342788])

Оценка качества

Оценим качество через MAPE и $R^2$.

(0.7546883769637167, 0.7546883769637167)

Мы видим, что результаты аналогичны.

Метод градиентного спуска

В целом с этим методом мы уже хорошо знакомы. В качестве упражнения давайте реализуем этот алгоритм на Питоне для многомерных данных.

Нахождение градиента

Покажем расчет градиента на схеме.

В данном случае мы берем датасет из четырех наблюдений и двух признаков ($x_1$ и $x_2$) и соответственно используем три коэффициента ($theta_0, theta_1, theta_2$).

Пошаговое построение модели

Начнем с функции гипотезы.

$$ h_{theta}(x) = theta X $$

def h(x, thetas):

return np.dot(x, thetas)

Объявим функцию потерь.

$$ J({theta_j}) = frac{1}{2n} sum (y-theta X)^2 $$

def objective(x, y, thetas, n):

return np.sum((y – h(x, thetas)) ** 2) / (2 * n)

Объявим функцию для расчета градиента.

$$ frac{partial}{partial theta_j} J(theta) = -x_j(y — Xtheta) times frac{1}{n} $$

где j — индекс признака.

def gradient(x, y, thetas, n):

return np.dot(–x.T, (y – h(x, thetas))) / n

Напишем функцию для обучения модели.

$$ theta_j := theta_j-alpha frac{partial}{partial theta_j} J(theta) $$

Символ := означает, что левая часть равенства определяется правой. По сути, с каждой итерацией мы обновляем веса, умножая коэффициент скорости обучения на градиент.

def fit(x, y, iter = 20000, learning_rate = 0.05):

x, y = x.copy(), y.copy()

# функцию add_ones() мы объявили выше

add_ones(x)

thetas, n = np.zeros(x.shape[1]), x.shape[0]

loss_history = []

for i in range(iter):

loss_history.append(objective(x, y, thetas, n))

grad = gradient(x, y, thetas, n)

thetas -= learning_rate * grad

return thetas, loss_history

Обучим модель, выведем коэффициенты и достигнутый (минимальный) уровень ошибки.

thetas, loss_history = fit(X, y, iter = 50000, learning_rate = 0.05)

thetas[0], thetas[1:], loss_history[–1]

(9.493787734953824e-16,

array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128,

-0.16878987, -0.18057055, -0.49319274]),

0.1226558115181417)

Полученный результат очень близок к тому, что было найдено методом наименьших квадратов.

Прогноз

Сделаем прогноз.

def predict(x, thetas):

x = x.copy()

add_ones(x)

return np.dot(x, thetas)

y_pred = predict(X, thetas)

y_pred[:5]

array([1.24414666, 0.55999778, 1.48103299, 1.49481605, 1.21342788])

Создание класса

Объединим написанные функции в класс.

class gd():

def __init__(self):

self.thetas = None

self.loss_history = []

def add_ones(self, x):

return x.insert(0,‘x0’, np.ones(x.shape[0]))

def objective(self, x, y, thetas, n):

return np.sum((y – self.h(x, thetas)) ** 2) / (2 * n)

def h(self, x, thetas):

return np.dot(x, thetas)

def gradient(self, x, y, thetas, n):

return np.dot(–x.T, (y – self.h(x, thetas))) / n

def fit(self, x, y, iter = 20000, learning_rate = 0.05):

x, y = x.copy(), y.copy()

self.add_ones(x)

thetas, n = np.zeros(x.shape[1]), x.shape[0]

# объявляем переменную loss_history (отличается от self.loss_history)

loss_history = []

for i in range(iter):

loss_history.append(self.objective(x, y, thetas, n))

grad = self.gradient(x, y, thetas, n)

thetas -= learning_rate * grad

# записываем обратно во внутренние атрибуты, чтобы передать методу .predict()

self.thetas = thetas

self.loss_history = loss_history

def predict(self, x):

x = x.copy()

self.add_ones(x)

return np.dot(x, self.thetas)

Создадим объект класса, обучим модель, выведем коэффициенты и сделаем прогноз.

model = gd()

model.fit(X, y, iter = 50000, learning_rate = 0.05)

model.thetas[0], model.thetas[1:], model.loss_history[–1]

(9.493787734953824e-16,

array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128,

-0.16878987, -0.18057055, -0.49319274]),

0.1226558115181417)

y_pred = model.predict(X)

y_pred[:5]

array([1.24414666, 0.55999778, 1.48103299, 1.49481605, 1.21342788])

Оценка качества

(0.7546883769637167, 0.7546883769637167)

Теперь рассмотрим несколько дополнительных соображений, касающихся построения модели линейной регрессии.

Диагностика алгоритма

Работу алгоритма можно проверить с помощью кривой обучения (learning curve).

Ошибка постоянно снижается
Алгоритм остановится, после истечения заданного количества итераций
Можно задать пороговое значение, после которого он остановится (например, $10^{-1}$)

Построим кривую обучения.

plt.plot(loss_history)

plt.show()

plt.plot(loss_history[:100])

plt.show()

Она также позволяет выбрать адекватный коэффициент скорости обучения.

Подведем итог

Сегодня мы подробно рассмотрели модель множественной линейной регрессиии. В частности, мы поговорили про построение гипотезы, основные функции потерь, допущения модели линейной регрессии, метрики качества и диагностику модели.

Кроме того, мы узнали как изнутри устроены метод наименьших квадратов и метод градиентного спуска и построили соответствующие модели на Питоне.

Отдельно замечу, что, изучив скорректированный коэффициент детерминации, мы начали постепенно обсуждать способы усовершенствования базовых алгоритмов и метрик. На последующих занятиях мы продолжим этот путь в двух направлениях: познакомимся со способами регуляризации функции потерь и начнем создавать более сложные алгоритмы оптимизации.

Но прежде предлагаю в деталях изучить уже знакомый нам алгоритм логистической регрессии.

Дополнительные материалы к занятию.

Источник

Определение и формула[править | править код]

Интерпретация[править | править код]

Недостаток R2 и альтернативные показатели[править | править код]

Скорректированный (adjusted) R2[править | править код]

Информационные критерии[править | править код]

R2-обобщённый (extended)[править | править код]

История[править | править код]

Замечание[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Задача

Расчет парных коэффициентов корреляции и параметров линейного уравнения множественной регрессии

Коэффициенты стандартизированного уравнения регрессии

Коэффициенты эластичности

Частные и парные коэффициенты корреляции

Коэффициенты множественной корреляции и детерминации

Надежность уравнения регрессии. Критерий Фишера

Сквозной пример

Данные и постановка задачи

Разделение выборки

Исследовательский анализ данных

Обработка данных

Пропущенные значения

Выбросы

Масштабирование признаков

Кодирование категориальных переменных

Построение модели

baseline-модель

Оценка качества

Диагностика модели, метрики качества и функции потерь

MSE, RMSE, MAE, MAPE

MSE и RMSE

MAE

MAPE

Коэффициент детерминации

Диагностика модели

Анализ остатков и прогнозных значений

Мультиколлинеарность

Дополнительная обработка данных

VIF

Преобразование данных

Отбор признаков

Повторное моделирование и диагностика

Повторное моделирование

Оценка качества и диагностика

Коэффициенты

Обучение модели

Векторизация уравнения

Функция потерь

Абсолютная ошибка, L1 loss

Квадрат ошибки, L2 loss

Функция Хьюбера

Метод наименьших квадратов

Нормальные уравнения

Код на Питоне

Создание класса

Оценка качества

Метод градиентного спуска

Нахождение градиента

Пошаговое построение модели

Прогноз

Создание класса

Оценка качества

Диагностика алгоритма

Подведем итог

Вам также может понравиться

Как найти человека по телефону в беларуси

Как найти в скайриме ферму

Как найти папку на карте андроид

Добавить комментарий Отменить ответ

Недостаток R² и альтернативные показатели[править | править код]

Скорректированный (adjusted) R²[править | править код]

R²-обобщённый (extended)[править | править код]

Расчет
парных коэффициентов корреляции и параметров линейного уравнения множественной
регрессии

Коэффициенты
стандартизированного уравнения регрессии

Коэффициенты
эластичности

Частные
и парные коэффициенты корреляции

Коэффициенты
множественной корреляции и детерминации

Надежность
уравнения регрессии. Критерий Фишера