Как найти коэффициент динамичности - Сайт, где вы сможете решить свои вопросы

Коэффициентом динамичности в теории колебаний называют безразмерную скалярную физическую величину, определяемую следующим выражением:

${displaystyle beta ={frac {A}{A_{0}}}={frac {1}{sqrt {(1-{frac {omega ^{2}}{p^{2}}})^{2}+{frac {4n^{2}omega ^{2}}{p^{4}}}}}}qquad qquad (1)}$

где

А — амплитуда
А₀ — равновесная амплитуда, представляющая собой статическую деформацию упругой связи под действием максимальной силы P₀
ω — частота возмущения
p — собственная частота колебаний
n — коэффициент, характеризующий силы вязкого трения

Коэффициент динамичности применяется для оценки влияния частоты возмущающей силы.
Так же он показывает во сколько раз амплитуда вынужденных колебаний больше статического отклонения.

Непосредственное определение коэффициента n затруднительно. Поэтому в формулу (1) целесообразно вместо n ввести коэффициент поглощения ψ. Тогда

${displaystyle beta ={frac {1}{sqrt {(1-{frac {omega ^{2}}{p^{2}}})^{2}+{frac {psi ^{2}}{4pi ^{2}}}}}}qquad qquad (2)}$

Преимуществом формулы (2) является то, что коэффициент динамичности поставлен в зависимость от энергетической характеристики трения ψ, что позволяет использовать эту формулу не только для вязкого трения, но и для других законов трения.

Можно также ввести в формулу для коэффициента динамичности логарифмический декремент δ. Воспользовавшись приближенной зависимостью

${displaystyle delta approx {frac {1}{2psi _{omega =p}}}}$

получим

${displaystyle beta ={frac {1}{sqrt {(1-{frac {omega ^{2}}{p^{2}}})^{2}+({frac {delta }{pi }})^{2}({frac {omega }{p}})^{2}}}}qquad qquad (3)}$

Из анализа приведённых выше зависимостей следует, что при приближении частоты возмущения ω к частоте собственных колебаний p коэффициент динамичности возрастает. Максимум амплитуды колебаний достигается при ω/p=1; при этом

${displaystyle beta _{max}={frac {2pi }{Psi _{(omega =p)}}}approx {frac {pi }{delta }}qquad qquad (4)}$

где

δ — логарифмический декремент колебаний
ω — частота возмущения
p — собственная частота колебаний

По аналогии с электрическими системами эта величина называется добротностью механической системы.

Литература[править | править код]

В. Л. Бидерман. Теория механических колебаний. — Высшая школа, 1980. — 408 с. — 10 000 экз. (недоступная ссылка)

См. также[править | править код]

Добротность

Источник

Рис.12

Итак, уравнение движения точки принимает вид

x = 2		h	sin(	p −k	t) cos pt.
k 2	− p2
	2

Движение, соответствующее этому уравнению, представляет собой колебания, происходящие с частотой возмущающей силы р. Период этих коле-

баний равен τ =	2π	, амплитуда колебаний, равная 2		h		sin(	p −k	t) , ме-
k	2	2

			р			− p			2
няется по периодическому закону, частота изменения амплитуды равна
	p −k	, а период ее изменения TА =	4π	. Таким образом, для	р ≈ k период
2	p −k

изменения амплитуды ТА значительно превышает период колебаний τ. Такое движение называется биениями, график этого движения показан на рис. 12.

3.2. Вынужденные колебания: коэффициент динамичности

Подробно исследуем вынужденные колебания, описываемые уравнени-

ем (28):

x2 = k 2 −h p2 sin pt.

Амплитуда вынужденных колебаний	A =				h	зависит от частоты
	k	2	− p	2

возмущающей силы р и частоты собственных колебаний k. Обозначим z = p/k, величина z называется коэффициентом расстройки.

Исследуем зависимость амплитуды вынужденных колебаний от коэффициента расстройки z = p/k.

Преобразуем выражение, полученное для амплитуды:

A =

xст

− p

−

− z

где xст = H / c – величина статического отклонения точки под действием

постоянной силы Н.

Определим отношение амплитуды вынужденных колебаний к величине статического отклонения точки, называемое μ

коэффициентом динамичности:

μ =	A	=	1
		1 − z 2
	xст
Коэффициент динамичности показыва-	1
ет, во сколько раз амплитуда вынужденных
колебаний превышает статическое отклоне-
ние точки. Построим график зависимости ко-	0
1	z
эффициента динамичности от коэффициента		Рис. 13
расстройки z=p/k.	Из графика (рис.13) сле-

дует, что при p→ k коэффициент динамич-

ности резко возрастает, следовательно, возрастает амплитуда колебаний. При р<<k амплитуда незначительно отличается от хст , при р>>k амплитуда становится очень малой.

3.3. Резонанс

Рассмотрим движение точки в том случае, когда частота возмущающей силы равна частоте собственных колебаний, т.е. при p = k.

Явление совпадения частот возмущающей силы и собственных колебаний называется резонансом.

Дифференциальное уравнение (21) движения точки под действием восстанавливающей и возмущающей сил имеет вид

&&	+k	2	x = hsin pt	(21)
x

Частное решение этого уравнения при резонансе (k = p) следует искать в виде:

x2 = At sin( pt +γ) .

Для определения постоянных А и γ вычислим сначала вторую производную &x&2 .

&	= Asin( pt +γ) + Atpcos( pt +γ) ,
x2
&&	= 2Apcos( pt +γ) − Atp	2	sin( pt +γ) .
x2
Подставим значения х	&&
и x в уравнение (3.21):
2 Ap cos( pt +γ ) − Atp 2 sin( pt +γ ) + Atk 2 sin( pt +γ ) = h sin pt .
Здесь p = k, значит
2 Ap cos( pt +γ) = h sin pt ,	х

или				ht
			x= 2 p

2 Ap cos pt cosγ −2 Ap sin pt sin γ = hsin pt .
Это равенство удовлетворяется то-	О	t

ждественно, если равны коэффициенты,			ht
стоящие перед одинаковыми тригоно-
метрическими функциями в левой и			x= – 2 p
правой его частях:

−2 Ap sin γ = h, 2 Ap cosγ = 0 .			Рис.14
Отсюда, принимая, что А > 0, получаем	A =	h	γ = – π⁄2.
2 p

Окончательно уравнение вынужденных колебаний при резонансе принимает вид

x2 = 2hp t sin( pt −π2 ) = −2hp t cos pt .

Как следует из этого уравнения амплитуда вынужденных колебаний, с течением времени неограниченно возрастает, причем рост амплитуды пропорционален времени (рис.14). Частота и период вынужденных колебаний при резонансе равны частоте периода свободных гармонических колебаний, а фаза колебаний по отношению к фазе возмущающей силы отстает на π/2.

3.4. Вынужденные колебания с учетом силы сопротивления

Рассмотрим прямолинейное движение материальной точки, на которую действуют три силы: восстанавливающая сила, сила сопротивления, проек-

ции которых на ось х равны Fx = −cx , Rx = −μVx = −μ dxdt , и возмущающая

сила, изменяющаяся по гармоническому закону Рх = H sin pt . Дифференциальное уравнение движения точки имеет вид

d 2 x

= −cx

− μ

+ H sin pt

d 2 x

dt 2

Заменим

2n =

, k

h =

, получим

= x,

= x , обозначим

x = hsin pt ,

(33)

+2nx +k

Уравнение (33) является неоднородным линейным уравнением, его решение дается формулой х = х1 + х2 , в которой х1 – общее решение од-

&&	&	2	x = 0 ,	х2 – частное
нородного дифференциального уравнения x + 2nx + k
решение уравнения (33).
При k > n общее решение однородного уравнения
x1 = e−nt (C1 cos k 2 −n2 t +C2 sin	k 2 −n2 t)	(34)

представляет собой уравнение затухающих колебаний.

Частное решение уравнения (33) находим в форме правой части:
x2 = Asin( pt +γ)	(35)

Уравнение (35) является уравнением вынужденных колебаний материальной точки, происходящих с частотой возмущающей силы р. Определим амплитуду А и начальную фазу γ вынужденных колебаний, для чего найдем первую и вторую производные от х2 по времени и подставим их значения в уравнение (33):

&	= pAcos( pt +γ) ,	&&	= −p	2	Asin( pt +γ) .
x2	x2
− p2 Asin(pt +γ) +2n pAcos(pt +γ) +k 2 Asin(pt +γ) = hsin pt .	(36)

Положим pt +γ =ϕ , тогда pt =ϕ −γ , следовательно,

sin pt = sin(ϕ −γ ) = sin ϕ cos γ − cos ϕ sin γ .

Подставим новые переменные в уравнение (36):

− p2 Asinϕ +2n pAcosϕ +k 2 Asinϕ = hsinϕсosγ −hcosϕsinγ

или

A(k 2 − p2 )sinϕ +2n pAcosϕ = hsinϕсosγ −hcosϕsinγ .

Приравняем коэффициенты, стоящие в левой и правой частях уравнения (36), при одинаковых тригонометрических функциях:

A(k 2 − p2 ) = h cosγ ,

2Anp = −h sin γ .

Возведем в квадрат каждое из этих уравнений и сложим их:

A2 (k 2 − p2 )2 +4A2 p2 n2 = h .

Отсюда

A =		h	.	(37)

	(k 2 − p2 )2 −4n2 p2
Разделив второе уравнение на первое, получим
	tgγ	=	2np		.	(38)
	k 2 − p 2
Тогда			h
х2	=			sin( pt +γ)	(39)
− p2 )2 +
	(k 2	4n2 p2

Теперь общее решение х =х1+х2 дифференциального уравнения (3.33) можно записать в виде

x =	e−nt (C cos	k 2 −n2 t +C	sin k 2	−n2 t) +	h	sin( pt +γ) .
2
	1		(k 2	− p2 )2 +4n2 p2

(40)

Таким образом, движение материальной точки, как следует из уравнения

(40), складывается из затухающих колебаний с частотой kC = k 2 −n2 и

вынужденных колебаний с частотой возмущающей силы p. Первое движение со временем затухает, и основным движением остаются вынужденные колебания с частотой р и начальной фазой γ.

Установим зависимость амплитуды вынужденных колебаний от коэффициента расстройки z = kp . Разделим на k2 числитель и знаменатель формулы (3.37), определяющей значение амплитуды:

A =

k 2

p2 .

(41)

(1 −

) +

k 2

h =

, k 2

тогда числитель выражения (41) приводится к виду:

H m

= xст .

m k

m c

Заменим

= z

= хст ,

= β , тогда

A =

xст

(1 − z 2 ) +4β2 z 2

Определим отношение амплитуды вынужденных колебаний к величине статического перемещения, которое называется динамическим коэффици-

ентом μ:

μ =

(1 − z 2 )2 + 4β2 z 2 .

(42)

xст

(1 −

)

+ 4

k 2

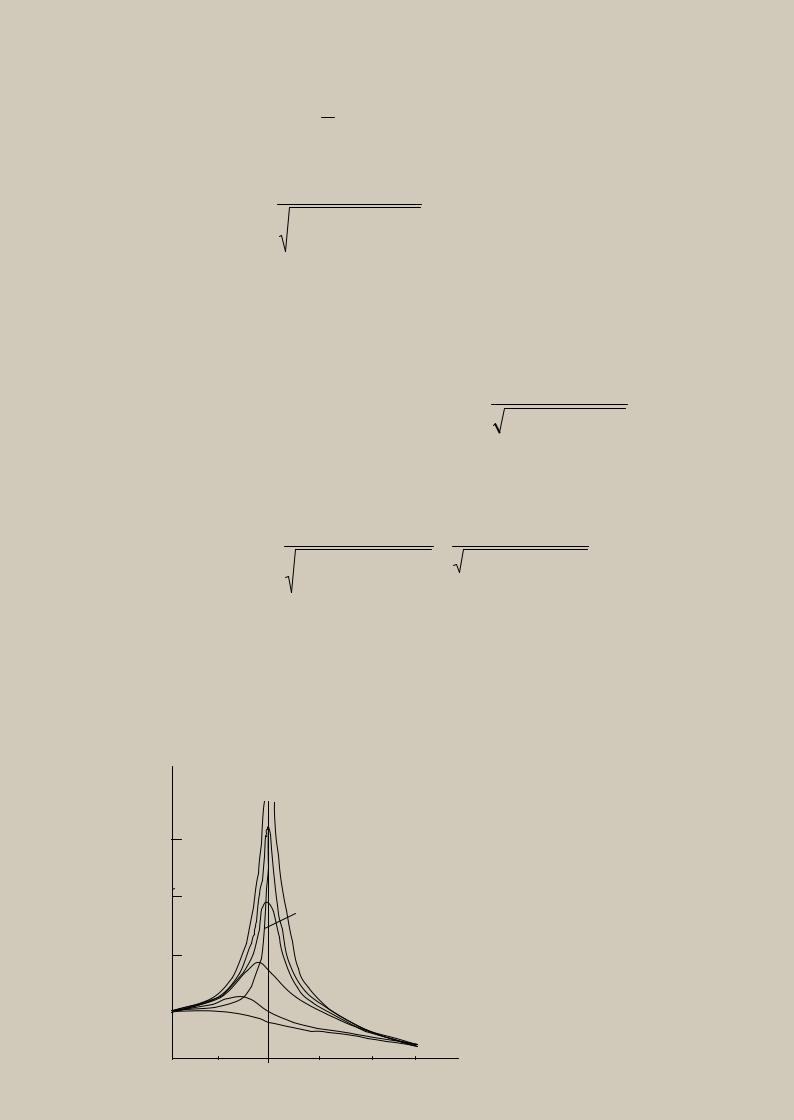
Исследуем характер изменения μ

в зависимости от z при конкретном

значении β, и построим

соответствующие графики (рис.15). Как следует из

графика при малых значениях

z ( p>> k) величина μ =1, и амплитуда вынуж-

денных колебаний практически равна статическому отклонению

А= хст.

При z = 1 (p = k) величина μ имеет максимум, при этом чем меньше сопротивление, тем сильнее возрастает амплитуда.

Линия максимумов

Рис. 15

Итак, движение материальной точки, на которую действуют восстанавливающая сила, сила сопротивления, пропорциональная скорости, и возмущающая сила, представляет собой наложение вынужденных колебаний на затухающие. Затухающие колебания с течением времени прекращаются. При установившемся режиме через достаточно большой промежуток времени останутся только

вынужденные колебания, определяемые уравнением

х2	=	h	sin( pt +γ) .
− p2 )2
	(k 2	+4n2 p2

Уравнение показывает, что вынужденные колебания материальной точки при наличии силы сопротивления, пропорциональной скорости, являются гармоническими, так как амплитуда их с течением времени не изменяется, т.е. вынужденные колебания не затухают. Этим вынужденные колебания существенно отличаются от свободных колебаний, которые затухают даже при незначительном сопротивлении. Частота и период вынужденных колебаний при наличии сопротивления равны частоте и периоду изменения возмущающей силы, т.е. сила сопротивления не влияет на частоту и период вынужденных колебаний.

Контрольные вопросы по теме «Колебания материальной точки»

1.Какая сила называется восстанавливающей?

2.Записать дифференциальное уравнение движение точки под действием восстанавливающей силы.

3.Какое движение совершает точка под действием восстанавливающей силы?

4.Записать уравнение свободных гармонических колебаний.

5.Начертить график свободных гармонических колебаний.

6.Что называется амплитудой свободных гармонических колебаний?

7.Что называется начальной фазой гармонических колебаний?

8.Чему равна частота гармонических колебаний?

9.Что называется периодом гармонических колебаний?

10.Какие из перечисленных величин зависят от начальных условий: амплитуда, начальная фаза, частота, период гармонических колебаний?

11.Под действием каких сил точка совершает затухающие колебания? 12.Начертите график затухающих колебаний.

13.Записать дифференциальное уравнение затухающих колебаний.

14.Записать уравнение движения точки при затухающих колебаниях.

15.Что называется амплитудой затухающих колебаний?

16.Чему равен период затухающих колебаний?

17.Сравните период гармонических колебаний с периодом затухающих колебаний.

18.Что называется декрементом колебаний?

19.Как движется точка под действием восстанавливающей силы в случае большого сопротивления?

20.Какое движение называется апериодическим?

21.Под действием каких сил точка совершает вынужденные колебания? 22.Что называется восстанавливающей силой?

23.Записать дифференциальные уравнения вынужденных колебаний без учета сил сопротивления.

24. Записать уравнение вынужденных колебаний.

25.С какой частотой происходят вынужденные колебания точки?

26.Что называется резонансом?

27.Начертите график изменения амплитуды для вынужденных колебаний при отсутствии сил сопротивления.

28.Как влияет на резонанс сила сопротивления?

29.Что называется биениями?

30.Под действием каких сил и при каких начальных условиях возникают биения?

31. Нарисуйте график биений.

Соседние файлы в папке Термех

#
08.06.201578 б18Desktop.ini
#
#
#
#
#
#
#
#

Источник

А. А. КОМАРОВ, д-р техн. наук, профессор кафедры комплексной безопасности в строительстве, Национальный исследовательский Московский государственный строительный университет (Россия, 129337, г. Москва, Ярославское шоссе, 26; e-mail: ICA_kbs@mgsu.ru) Д. А. КОРОЛЬЧЕНКО, канд. техн. наук, доцент, директор Института комплексной безопасности в строительстве, Национальный исследовательский Московский государственный строительный университет (Россия, 129337, г. Москва, Ярославское шоссе, 26; e-mail: ICA_kbs@mgsu.ru)

ФАН ТУАН АНЬ, аспирант кафедры гидравлики и водных ресурсов, Национальный исследовательский Московский государственный строительный университет (Россия, 129337, г. Москва, Ярославское шоссе, 26; e-mail: ptuananh26789@gmail.com)

УДК 614.834

ОСОБЕННОСТИ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ДИНАМИЧНОСТИ ПРИ ИМПУЛЬСНЫХ НАГРУЗКАХ

Рассмотрена методология оценки коэффициента динамичности при ударных нагрузках, сопровождающих, например, взрывы, падение массивных тел, гидроудары. Отмечены особенности, связанные с определением коэффициента динамичности при импульсных нагрузках, свойственных многим чрезвычайным ситуациям. Выявлены недостатки метода по определению коэффициента динамичности при импульсных нагрузках. Проведено интегрирование уравнения для нескольких видов нагрузок и различных соотношений между длительностью нагрузки и периодом собственных колебаний конструкции. Определены значения коэффициента динамичности для различных соотношений между длительностью нагрузки и периодом собственных колебаний конструкции при нагрузках пяти видов. Приведены критерии, при которых коэффициент динамичности определяется только импульсом ударной нагрузки и не зависит от ее формы. Установлены соотношения для определения коэффициента динамичности при ударных нагрузках, сопровождающих чрезвычайные ситуации.

Ключевые слова: статическая нагрузка; динамическая нагрузка; коэффициент динамичности; расчет строительных конструкций; типовые нагрузки; период собственных колебаний конструкции.

ЭО!: 10.18322/РУВ.2018.27.02-03.37-43

Введение

В практике строительного проектирования принято приводить нестационарные нагрузки к эквивалентным статическим нагрузкам [1-4]. При расчетах последствий динамического воздействия на строительные конструкции используется следующая методология. Динамическая нагрузка заменяется эквивалентной ей по действию статической нагрузкой Рэ, которая определяется по формуле [5-10]:

Р = P K

1 э 1 макс ^д;

(1)

где рм

максимальная динамическая нагрузка;

Кд — коэффициент динамичности, равный максимальному значению функции динамичности описывающей движение (перемещение сечений) конструкции во времени. Как следует из выражения (1), для замены динамической нагрузки эквивалентной ей статической необходимо определить коэффициент динамичности Кд. Величину Кд при нагрузке треугольной фор-

мы проектировщики часто определяют по графикам (рис. 1), приведенным во многих справочниках по прочностному расчету сооружений, где круговая частота основного тона собственных колебаний конструкций юк определяется методами строительной механики.

Из графика рис. 1 следует, что если величина 0] стремится к нулю (при нагрузке пилообразной формы), то численное значение коэффициента динамичности приближается к двум. Исходя из этих соображений проектировщики любую нагрузку пилообразной формы при проведении статических расчетов удваивают. Однако этот подход неправомерен для кратковременных (импульсных) нагрузок. Именно этот вопрос и рассматривается в настоящей статье.

При чрезвычайных ситуациях (ЧС) достаточно часто возникают кратковременные нагрузки [11-14]. При взрывах зарядов взрывчатых веществ (ВВ), при аварийном падении массивных тел (например, транспортных контейнеров в бассейны выдержки на АЭС),

Схематизация взрывной нагрузки Schematization of blast load

Рис. 1. Графики для определения коэффициента динамичности Кд: 1 — 0/0! = 2; 2 — 0/01 = 6; 3 — 0/01 = 10; 4 — 0/01 = 20; 5 — 0/01 = 50; 6 — 0/01 = 100; 7 — 0^>200;0и01 —время соответственно действия динамической нагрузки и ее нарастания до максимальной величины; АР — взрывная нагрузка Fig. 1. Graphs for determining of dynamic amplification factors

Kdyn: 1 — 0/0j =2; 2 — 0/01 = 6; 3 — I

10; 4 — 0/0J

20; 5 — 0/01 = 50; 6 — 0/01 = 100; 7 — 0/01 > 200; 0 и 01 — time respectively of the action of the dynamic load and its increase to the maximum value; АР — blast load

при гидроударах и т. д. формируются нагрузки, длительность которых исчисляется миллисекундами при очень высоких давлениях [15-20].

Цель нашей работы заключается в выявлении некоторых особенностей, связанных с расчетом коэффициента динамичности при импульсных нагрузках, свойственных многим чрезвычайным ситуациям. В связи с этим необходимо установить критерии, при которых коэффициент динамичности определяется только импульсом ударной нагрузки, а также привести соотношения для определения коэффициента динамичности при ударных нагрузках, сопровождающих взрывы, падение массивных тел, гидроудары и т. д.

Теоретические расчеты

Рассмотрим методологию оценки коэффициента динамичности при подобных нагрузках. В своих рассуждениях будем придерживаться принятых в динамике сооружений подходов.

Известно, что движение конструкции в стадии упругих деформаций описывается уравнением

d 2т

+ ю2Т = ю2 f(t),

d t2

(2)

S(t) — смещение конструкции при статическом

воздействии на нее нагрузки Р;

SMaKC — смещение конструкции при статическом

воздействии на нее нагрузки Рмакс;

юк — круговая частота собственных колебаний

конструкции;

f (t) — функция, описывающая изменение безразмерной динамической нагрузки во времени; f(t)= Рф/Рмакс-

Решение уравнения (2) при нулевых начальных условиях имеет вид:

T(t) = ю| f(u) • sin (ю(t – u))du =

sin ю- t J f(u) • cos(rou )du – (3)

t Л

cos ю- tJf(u) • sin(rou)du ,

= ю

где и — модуль упругости конструкции.

Численное интегрирование выражения (3) дает функцию перемещения конструкции под действием силы/(?) во времени. Максимальное значение функции перемещения Г(?) есть коэффициент динамичности Кд.

Для определения коэффициента динамичности необходимо знать частоту основного тона собственных колебаний конструкций юк, которая определяется по формуле [4]:

(4)

где T(t) — относительное перемещение конструкции или функция динамичности; T(t) = S^VS^^;

где а — коэффициент, определяемый по справочной литературе (например, [4]); Ь — длина пролета конструкции; В — изгибная жесткость; В = Е1; Е — динамический модуль упругости; I — осевой момент инерции сечения; Мк — погонная масса конструкции; Мк = q/g; д — погонная нагрузка от взрыва плюс нагрузка от собственного веса конструкции; g — ускорение свободного падения. Решение уравнения (2) можно получить, численно разрешив систему дифференциальных уравнений первого порядка:

<1и 2_ 2 п ¿Г тт — = -ю2Г +ю2 /(г); — = и, (5) а г а г

где и — энергия упругой деформации.

К недостаткам описанного метода следует отнести следующее обстоятельство. В расчетах предполагается, что колебательный процесс каждого элемента происходит на определенной частоте (как правило, на частоте основного тона), хотя в действительности колебания происходят во всем спектре

юк =

собственных частот упругого элемента. Кроме того, в данном методе произвольные граничные условия можно задавать с определенными приближениями. Тем не менее при расчетах строительных конструкций на прочность при ЧС, когда в качестве исходных данных принимаются максимально возможные нагрузки, которые маловероятны, данный подход в определении Кд в некоторой степени оправдан.

На рис. 2 приведены значения коэффициента динамичности для различных соотношений между длительностью действия нагрузки Тнагр и периодом собственных колебаний конструкции Т0 при нагрузках пяти типов.

Из рис. 2 видно, что временной характер нагрузки влияет на коэффициент динамичности только при соотношении между длительностью действия нагрузки и периодом собственных колебаний конструкции, превышающем 0,5Т0. Этот факт, собственно, и отражает рис. 1, который построен применительно к достаточно продолжительным (по отношению к периоду собственных колебаний конструкций), а не импульсным нагрузкам.

На рис. 3 приведены значения коэффициента динамичности для различных соотношений между

^/■^макс /-^/^тах

О 0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 t/T0

К,

dyn 1,5

1,0

0,5

0 0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 Гнагр/Г0

TloadAo

Рис. 2. Коэффициенты динамичности при нагрузках пяти типов: 1 — K = 0,10; 2 — K = 0,25; 3 — K =0,50; 4 — K =0,75; 5 — K = 0,90; K = Г1/Гнагр; T1 — длительность нарастания нагрузки; Тнагр — длительность действия нагрузки Fig. 2. Dynamic amplification factors under loads of five types: 1 — K = 0,10; 2 — K = 0,25; 3 — K = 0,50; 4 — K =0,75; 5 — K = 0,90; K = T1/rload; T1 — load rise duration; Tload — load action duration

длительностью действия нагрузки и периодом собственных колебаний конструкции, при нагрузке ударного вида К = 0 и нагрузке, имеющей только фазу нарастания, К =1. Условно их можно считать “крайними” формами нагрузок — ударной и плавной.

^/^маке /^/^тах

0 0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 t/T0

К,

dyn 1,5

1,0

0,5

0 0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 Гнагр/Г0

TioadAo

Рис. 3. Коэффициенты динамичности при нагрузках двух “крайних” типов — K =0; K =6

Fig. 3. Dynamic amplification factors under loads of two “extreme” types— K =0; K =6

^/^маке /^V^max

‘натр ^load

-0,2

0 0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 t/T0

K„

dyn 1,5

1,0

0,5

0 0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 Гнагр/Г0

rloadAo

Рис. 4. Коэффициенты динамичности для Гнагр jT0 < 0,5 при нагрузках прямоугольного (1) и треугольного (2) типов Fig. 4. Dynamic amplification factors for ratios of Tload/T0 < 0,5 under rectangular (1) or triangular (2) type of loads

Для соотношений Тнагр/ Т0 < 0,5, как указывалось ранее (см. рис. 2), форма нагрузки не влияет на численные значения коэффициента динамичности. Основное влияние на него оказывает импульс давления I = | Р (г )-г. Это видно из рис. 4, где приведены значения коэффициента динамичности при нагрузках треугольной (I = 0,5РмаксТнагр) и прямоугольной (1 = РМаксТнагр) формы.

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

В результате проведенных расчетов было получено, что коэффициент динамичности при кратковременных нагрузках (Тнагр/ Т0 < 0,5) приближенно можно определить по следующей формуле:

Kд =

2Р,

2 -1,5

1 -■

P Т

макс натр

(6)

Тотда имеем: • для натрузки треутольной формы (I =0 5P Т ):

V-1 макс^натр/’

27L™

Кд = 1,25

(7)

для натрузки прямоутольной формы

(I = P

Т ):

макс натр

Кд = 2,0

271

(8)

Выводы

Отмечены особенности, связанные с определением коэффициента динамичности при импульсных нагрузках, свойственных многим чрезвычайным ситуациям. Было проведено интегрирование уравнения (2) для различных соотношений между длительностью нагрузки Тнагр и периодом собственных колебаний конструкции Т0 при нагрузках нескольких типов. Приведены критерии, при которых коэффициент динамичности определяется только импульсом ударной нагрузки и не зависит от ее формы. Установлены соотношения для определения коэффициента динамичности при ударных нагрузках, сопровождающих чрезвычайные ситуации (взрывы ВВ, падение массивных тел, гидроудары и т. д.).

СПИСОК ЛИТЕРАТУРЫ

1. Назаров В. П., Коротовских Я. В. Компьютерные технологии прогнозирования пожаровзрыво-опасности производственных объектов // Технолотии техносферной безопасности. — 2010. — №5.— С. 21-26.

2. Ефремов К. В., ЛисановМ. В., СофьинА. С., СамусеваЕ. А., Сумской С. И., Кириенко А. П. Расчет зон разрушения зданий и сооружений при взрывах топливно-воздушных смесей на опасных производственных объектах // Безопасность труда в промышленности. — 2011. — №9. — С. 70-77.

3. Yan S., WangJ.-H., WangD., ZhangL. Mechanism analysis on progressive collapse ofRC frame structure under blast effect // Gongcheng Lixue / Engineering Mechanics. — 2009. —No. 26 (suppl. 1). — P. 119-123, 129.

4. ChenH. L.,XiaZ. C., Zhou J. N., FanH. L., JinF. N. Dynamic responses of underground arch structures subjected to conventional blast loads: Curvature effects // Archives of Civil and Mechanical Engineering. — 2013. — Vol. 13, Issue 3. — P. 322-333. DOI: 10.1016/j.acme.2013.04.004.

5. Попов Н. Н., Расторгуев Б. С. Динамический расчет железобетонных конструкций. — М. : Стройиздат, 1974. — 207 с.

6. Расторгуев Б. С. Методические указания по проектированию новых и обследованию существующих строительных конструкций зданий взрывоопасных производств. — М. : Изд-во Ассоциации строительных вузов, 1996. — 227 c.

7. СНиП 2.01.07-85. Натрузки и воздействия (с изм. № 1, 2). URL: http://docs.cntd.ru/document/ 5200280 (дата обращения: 15.01.2018).

8. Динамический расчет сооружений на специальные воздействия. Справочник проектировщика / Под ред. Б. Г. Коренева, И. М. Рабиновича. — М. : Стройиздат, 1981. — 218 с.

9. Polandov Iu., Korolchenko D. The consideration of the turbulence influence on the gas explosion expansion in non-closed areas // MATEC Web of Conferences. — 2017. — Vol. 106, Art. 01040. — 8 p. DOI: 10.1051 /matecconf/201710601040.

10. Korolchenko D., Pizhurin A. Simulating operational control of production in lumber house building businesses // MATEC Web of Conferences. — 2017. — Vol. 117, Art. 00084. — 7 p. DOI: 10.1051/matecconf/201711700084.

11. Korolchenko D. A., Sharovarnikov A. F., ByakovA. K.The analysis of oil suppression by aqueous film forming foam through a gas-salt layer of water // Advanced Materials Research. — 2014. — Vol. 1073-1076. — P. 2353-2357. DOI: 10.4028/www.scientific.net/amr.1073-1076.2353.

12. KomarovA., BazhinaE., Bobrov Yu. Relationship between gas-dynamic flows and impacts of emergency explosions indoors // MATEC Web of Conferences. — 2016. — Vol. 86, Art. 04048. — 5 p. DOI: 10.1051/matecconf/20168604048.

13. Сулименко В. А., Комаров А. А., ВасюковГ. В., ЗагуменниковР. А. Особенности расчета параметров процесса возникновения взрывоопасных смесей при аварийных ситуациях // Технологии техносферной безопасности. — 2015. — № 4(62) — С. 109-116.

14. Kabantsev O., Perelmuter A. Modeling transition in design model when analyzing specific behaviors of structures // Procedia Engineering. —2013. — Vol. 57.—P. 479-488. DOI: 10.1016/j.proeng.2013.04.062.

15. Fialko S. Yu. Iterative methods for solving large-scale problems of structural mechanics using multi-core computers // Archives ofCivil and Mechanical Engineering.—2014.—Vol. 14,Issue 1.—P. 190-203. DOI: 10.1016/j.acme.2013.05.009.

16. Fialko S. Parallel finite element solver for multi-core computers // Federated Conference on Computer Science and Information Systems (September 9-12,2012, Wroclaw, Poland). — 2012. —Art. 6354298. — P. 525-532.

17. ЮдаковА. А., Бойков В. /.Численные методы интегрирования уравнений движения многокомпонентных механических систем, основанные на методах прямого интегрирования уравнений динамики метода конечных элементов // Вестник Удмуртского университета. Математика. Механика. Компьютерные науки. — 2013. — Вып. 1. — С. 131-144.

18. Котляревский В. А. Коррекция динамических испытаний конструкций на моделях при наличии масштабных эффектов // Строительная механика и расчет сооружений. — 2014. —№ 1(252). — С. 43-48.

19. Котляревский В. А. Особенности вибрационной диагностики в строительстве // Наука и безопасность. — 2013. — Вып. 4(9). — С. 2-10.

20. КашевароваГ. Г., ПепеляевА. А. Моделирование и ретроспективный анализ взрыва бытового газа в кирпичном здании // Строительная механика и расчет сооружений. — 2010. — №2. — C. 31-36.

Материал поступил в редакцию 25 января 2018 г.

Для цитирования: Комаров А. А., Корольченко Д. А., Фан ТуанАнъ. Особенности определения

коэффициента динамичности при импульсных нагрузках // Пожаровзрывобезопасность / Fire and

Explosion Safety.—2018. — Т. 27, №2-3. — С. 37-43. DOI: 10.18322/PVB.2018.27.02-03.37-43.

= English

FEATURES OF DETERMINATION OF THE DYNAMIC AMPLIFICATION FACTOR UNDER IMPULSE LOADS

KOMAROV A. A., Doctor of Technical Sciences, Professor of Department of Integrated Safety in Civil Engineering, National Research Moscow State University of Civil Engineering (Yaroslavskoye Shosse, 26, Moscow, 129337, Russian Federation; e-mail: ICA_kbs@mgsu.ru)

KOROLCHENKO D. A., Candidate of Technical Sciences, Docent, Head of Institute of Integrated Safety in Construction, National Research Moscow State University of Civil Engineering (Yaroslavskoye Shosse, 26, Moscow, 129337, Russian Federation; e-mail: ikbs@mgsu.ru)

PHAN TUAN ANH, Postgraduate Student of Hydraulics and Water Resources Department, National Research Moscow State University of Civil Engineering (Yaroslavskoye Shosse, 26, Moscow, 129337, Russian Federation; e-mail: ptuananh26789@gmail.com)

ABSTRACT

It is accepted to lead non-stationary loads to equivalent static loads in practice of construction design. Different methodologies are used to calculate the effects of dynamic impact on building structures. This article describes evaluation methodology of dynamic amplification factor under impact loads, arising in case of explosions, falling of massive bodies, hydraulic impact. To calculate the dynamic amplification factor it was determined frequency of fundamental tone of natural oscillation. A shortcoming of described evaluation method of dynamic amplification factor under impact loads is the assumption that oscillation process of each element happens at a certain frequency (usually at the fundamental tone frequency); though in fact oscillations happen in all range of natural frequencies of elastic element. Besides, any boundary conditions for this methodology can be set with certain approximations. Nevertheless structural analysis of building constructions in conditions of emergency situation, when the maximum possible loadings have been taken as initial data, such approach in determination

of Kdyn is justified in a certain degree. The integrating equations for different types of loads and various ratios between load duration and natural oscillation period has allowed to determine values of dynamic amplification factor for such ratios at five types of loads. It have been shown that temporality of loading influences dynamic amplification factor only at certain ratios between load duration and natural oscillation period. This fact can be attributed to a sufficiently long (in ratio to the natural oscillation period), but not to impulse loads. Values of dynamic amplification factor for various ratios between load duration and natural oscillation period under the impact forces and under the growth phase load were given. The type of load have not affect numerical values of dynamic amplification factor for the presented ratios. The main influence on dynamic amplification factor is the pressure pulse.

Keywords: static load; dynamic load; dynamic amplification factor; structural analysis; typical loads; natural oscillation period.

REFERENCES

1. Nazarov V. P., Korotovskikh Ya. V. Computer technology prediction fire and explosion hazard of production objects. Tekhnologii tekhnosfernoy bezopasnosti / Technology of Technosphere Safety, 2010, no. 5, pp. 21-26 (in Russian).

2. Efremov K. V., Lisanov M. V., Sofin A. S., Samuseva E. A., Sumskoy S. I., Kirienko A. P. Calculation of buildings and structures destruction zones resulted from explosions of fuel-air mixtures at hazardous production facilities. Bezopasnost truda v promyshlennosti / Occupational Safety in Industry, 2011, no. 9, pp. 70-77 (in Russian).

3. Yan S., Wang J.-H., Wang D., Zhang L. Mechanism analysis on progressive collapse ofRC frame structure under blast effect. Gongcheng Lixue / Engineering Mechanics, 2009, no. 26 (suppl. 1), pp. 119-123, 129.

4. ChenH. L.,XiaZ. C., Zhou J. N., FanH. L., Jin F.N. Dynamic responses of underground arch structures subjected to conventional blast loads: Curvature effects. Archives of Civil and Mechanical Engineering, 2013, vol. 13, issue 3, pp. 322-333. DOI: 10.1016/j.acme.2013.04.004.

5. Popov N. N., Rastorguev B. S. Dinamicheskiy raschet zhelezobetonnykh konstruktsiy [Dynamic calculation of reinforced concrete structures]. Moscow, Stroyizdat Publ., 1974. 207 p. (in Russian).

6. Rastorguev B. S. Metodicheskiye ukazaniyapoproyektirovaniyu novykh i obsledovaniyu sushchestvu-yushchikh stroitelnykh konstruktsiy zdaniy vzryvoopasnykhproizvodstv [Methodology on design the new buildings and on inspection the explosive production premises]. Moscow, Association of Higher Construction Institutions Publ., 1996. 227 p. (in Russian).

7. Construction norms and rules 2.01.07-85. Loads and impacts (with changes No. 1, 2) (in Russian). Available at: http://docs.cntd.ru/document/5200280 (Accessed 15 January 2018).

8. Korenev B. G., Rabinovich I. M. (eds.). Dinamicheskiy raschet sooruzheniy na spetsialnyye vozdey-stviya. Spravochnikproyektirovshchika [Dynamic calculation of structures for special impacts. Reference book of the designer]. Moscow, Stroyizdat Publ., 1981. 218 p. (in Russian).

9. Polandov Iu., Korolchenko D. The consideration of the turbulence influence on the gas explosion expansion in non-closed areas. MATEC Web of Conferences, 2017, vol. 106, art. 01040. 8 p. DOI: 10.1051 /matecconf/201710601040.

10. Korolchenko D., Pizhurin A. Simulating operational control of production in lumber house building businesses. MATEC Web of Conferences, 2017, vol. 117, art. 00084. 7 p. DOI: 10.1051/matecconf/ 201711700084.

11. Korolchenko D. A., Sharovarnikov A. F., Byakov A. V. The analysis of oil suppression by aqueous film forming foam through a gas-salt layer of water. Advanced Materials Research, 2014, vol. 1073-1076, pp. 2353-2357. DOI: 10.4028/www.scientific.net/amr.1073-1076.2353.

12. Komarov A., Bazhina E., Bobrov Yu. Relationship between gas-dynamic flows and impacts of emergency explosions indoors. MATEC Web of Conferences, 2016, vol. 86, art. 04048. 5 p. DOI: 10.1051/matecconf/20168604048.

13. Sulimenko V. A., Komarov A. A., Vasjukov G. V., Zagumennikov R. A. Features of calculation of parameters the occurrence of explosive mixtures at emergency. Tekhnologii tekhnosfernoy bezopasnosti / Technology of Technosphere Safety, 2015, no. 4(62), pp. 109-116 (in Russian).

14. Kabantsev O., Perelmuter A. Modeling transition in design model when analyzing specific behaviors of structures. Procedia Engineering, 2013, vol. 57, pp. 479-488. DOI: 10.1016/j.proeng.2013.04.062.

15. Fialko S. Yu. Iterative methods for solving large-scale problems of structural mechanics using multi-core computers. Archives of Civil and Mechanical Engineering, 2014, vol. 14, issue 1, pp. 190-203. DOI: 10.1016/j.acme.2013.05.009.

16. Fialko S. Parallel finite element solver for multi-core computers. In: Federated Conference on Computer Science and Information Systems (September 9-12, 2012, Wroclaw, Poland), 2012, art. 6354298, pp. 525-532.

17. Yudakov A. A., Boikov V. G. Numerical methods ofmultibody mechanical system’s dynamic equations integration, based on methods of direct integration of finite element method’s dynamic equations. Vestnik Udmurtskogo universiteta. Matematika. Mekhanika. Komp’yuternye nauki / The Bulletin of Udmurt University. Mathematics. Mechanics. Computer Science, 2013, issue 1, pp. 131-144 (in Russian).

18. Kotlyarevsky V. A. Correction of structures dynamic tests on models under influence of scale effects. Stroitelnaya mekhanika i raschet sooruzheniy / Structural Mechanics and Analysis of Constructions, 2014, no. 1(252), pp. 43-48 (in Russian).

19. Kotlyarevsky V. A. Features of vibration diagnostics in construction. Nauka i bezopasnost / Science and Safety, 2013, issue 4(9), pp. 2-10 (in Russian).

20. Kashevarova G. G., Pepelyaev A. A. Modeling and retrospective analysis for the domestic gas explosion in brick building. Stroitelnaya mekhanika i raschet sooruzheniy / Structural Mechanics and Analysis of Constructions, 2010, no. 2, pp. 31-36 (in Russian).

For citation: Komarov A. A., Korolchenko D. A., Phan Tuan Anh. Features of determination of

the dynamic amplification factor under impulse loads. Pozharovzryvobezopasnost / Fire andExplo-

sion Safety, 2018, vol. 27,no. 2-3, pp. 37-43 (in Russian). DOI: 10.18322/PVB.2018.27.02-03.37-43.

121352, г. Москва, а/я 43; тел./факс: (495) 228-09-03; e-mail: info@fire-smi.ru

Источник

При проектировании согласно действующим ГОСТ и СП для зданий и сооружений класса КС-3, а также класса КС-2 с массовым нахождением людей необходимо рассчитывать конструкции на аварийные и особые воздействия, ведущие к прогрессирующему обрушению. Расчеты на прогрессирующее обрушение ведутся с учетом динамического коэффициента. В зависимости от методики расчета коэффициент может приниматься равным константе, либо вычисляться по эмпирическим формулам. Существуют несколько различных способов вычисления коэффициента динамичности как в зарубежном, так и в отечественном проектировании.

Ключевые слова:

прогрессирующее обрушение, коэффициент динамичности, линейно-статический расчет, нелинейно-статический расчет, динамический нелинейный расчет.

Расчет зданий и сооружений на непропорциональное обрушение нормируется российской и зарубежной обязательной строительной документацией. Непропорциональное обрушение это характеристика величины разрушения. Механизм разрушения может быть различным, например прогрессирующее (лавинообразное) разрушение [1]. Прогрессирующее разрушение возникает вследствие воздействия аварийных нагрузок [2], которые необходимо учитывать на стадии проектирования. Однако, учесть все факторы в ходе такого разрушения достаточно затруднительно, несмотря на возможности современных расчетно-вычислительных комплексов.

Наиболее распространенным методом расчета здания на прогрессирующее обрушение является описанный в нормах США [3] метод Альтернативных путей. Он позволяет не учитывать причину возникновения разрушения, в отличии от Косвенного метода, который подразумевает либо защиту конструкции от конкретных чрезвычайных ситуаций за счёт превентивных мер, либо создание избыточных связей для повышения статической неопределимости. Кроме того, метод Альтернативных путей включает три различных методики расчета:

— Линейный статический расчет (LSP);

— Нелинейный статический расчет (NSP);

— Нелинейный динамический расчет (NDP).

Основная идея расчета по методу Альтернативных путей заключается в том, что здание при аварийном воздействии и выключении из работы одного или нескольких несущих элементов, разрушалось до заданного состояния, например, с сохранением эксплуатационных качеств сразу после разрушения или после восстановления.

Для статических расчетов предусмотрено использование коэффициента динамичности для учета динамического фактора, что упрощает расчет, одновременно приближая его результаты к наиболее точному нелинейному динамическому расчету.

Величина динамического коэффициента в статических расчетах — это ключевое значение. Одна из самых ранних работ по определению коэффициентов динамичности при прогрессирующем обрушении — статья группы ученых Ruth P., Marchand K. и Williamson E [4]. В ней было были проанализировано влияние увеличения нагрузки на параметры, характеризующие пластические деформации при нелинейном статическом и нелинейном динамическом расчетах. В результате было определено, что пластичность имеет наибольшее влияние на коэффициент. Данный вывод в следующем исследовании, публикация Stevens D., Crowder B., Hall B. и Marchand K. [5], позволил определить характер зависимости динамического коэффициента от параметра пластических деформаций. На основе данных исследований в 2009 году McKay A. представил формулы по расчету динамического коэффициента, вошедшие в нормы США.

В настоящее время в нормах США [3] величина динамического коэффициента учитывается в зависимости от некоторых факторов:

— Назначение, тип и материал рассчитываемого элемента конструкции — первичный или вторичный элемент;

— Способ нагружения здания после удаления несущего элемента — pulldown и pushdown.

Для различных методик приведены следующие коэффициенты динамичности:

Для линейного статического расчета:

— при расчете параметров НДС по деформациям;

— при расчете параметров НДС по усилиям.

В общем случае данные коэффициенты обозначаются как LIF (LoadIncreaseFactor).

Для нелинейного статического расчета:

— DIF (DynamicIncreaseFactor).

Существует иной подход к расчету коэффициента динамичности, основанный не только на пластических деформациях, но и на существующих запасах поврежденной конструкции. Такой подход рассмотрен в исследовании Liu M [6]. Если здание рассчитано на восприятие значительных кратковременных нагрузок, то при удалении колонны его конструкции могут не достигнуть пластики, следовательно расчеты по формулам, учитывающим пластические деформации будут некорректны, так как в случае упругих деформаций динамический коэффициент условно равняется 2.

Однако запасы конструкций можно учесть, анализируя пластичность конструкции, полученную после приложения увеличенных на коэффициент динамичности нагрузок.

Стоит заметить, что на основе исследования влияния запасов конструкции авторами Saffari H. и Mashhadi J. [7] были выведены формулы коэффициентов DIF для pulldown-анализа железобетонных рам. Формулы зависят от параметра max(Mu/My), который характеризует степень нагруженности конструкции весовыми нагрузками GLA (Gravity Load Amplifier).

где

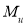
— момент, в балке после удаления колонны без учета нагрузок с коэффициентом динамичности;

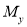
— предельный момент, в балке, соответствующий образованию пластических шарниров.

В линейных статических расчетах также существует альтернативный подход на основе частичного pulldown анализа, не входящий в нормативную базу, разработанный Mahmoudi M., Teimoori T. и Kozani H [8]. Подход заключается в том, что в месте удаления колонны верхнему узлу сообщается вынужденное перемещение

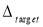
, вычисляемое как перемещение данного узла в первоначальной системе

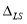
, умноженное на коэффициент динамичности по перемещению

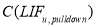
Динамический коэффициент определяется по нижеприведенным формулам.

Для внутренней колонны:

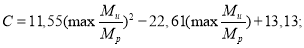
Для внешней колонны:

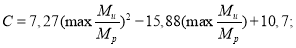
где

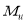
— полученные в линейном статическом расчете поврежденной конструкции моменты в балках, примыкающих к узлу над удаляемой колонной;

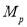
— предельные моменты в балках, примыкающих к узлу над удаляемой колонной, соответствующие реализации пластических шарниров.

Если

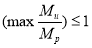
, то конструкция работает в упругой стадии. Следовательно, коэффициент динамичности равен 2.

Данный метод также учитывает не только пластичность элементов, но и весовые нагрузки GLA (Gravity Load Amplifier).

В отечественных исследованиях динамический коэффициент часто выражается формулой [9]:

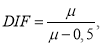
где

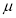
— коэффициент пластичности, равный отношению полного прогиба ригеля к предельному упругому (для железобетонных конструкций).

Для расчетов в упругой стадии

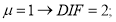
Для расчетов в пластике

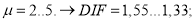
Однако Расторгуев Б. С., выводя эту формулу в своих работах принимал, что все ригели над удаляемой колонной в расчетной схеме имеют одинаковую деформируемость. Позже, чтобы учесть, разность наступления пластических деформаций в ригелях в каркасах высотой более 10 этажей Као Зуй Кхой было предложено уточнение [10]:

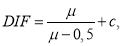
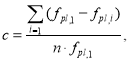
где

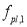
— максимальный пластический прогиб ригеля 1-го этажа;

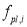
— пластический прогиб ригеля i-го этажа перед разрушением ригеля первого этажа;

n

— общее число этажей каркаса,

i

= 1…

n

.

Данное уточнение позволяет учитывать неодинаковость работы ригелей при расчете методом pulldown не только в пластической, но и в упругой стадии вне зависимости от количества этажей.

Литература:

1. Грачев В. Ю., Вершинина Т. А., Пузаткин А. А., Непропорциональное разрушение. Сравнение методов расчета. Екатеринбург, Издательство «Ажур», 2010,

2. СП 296.1325800.2017 Здания и сооружения. Особые воздействия. М.: ЦНИИСК им. В. А. Кучеренко при участии АО МНИИТЭП, ФГБУ «ГГО им. А. И. Воейкова», 2017.

3. UFC 3–340–02 Structures To Resist The Effects Of Accidental Explosions, With Change 2, 2008.

4. Ruth P., Marchand Kirk A., Williamson Eric B., «Static Equivalency in Progressive Collapse Alternate Path Analysis: Reducing Conservatism while Retaining Structural Integrity». Journal of Performance of Constructed Facilities Vol. 20, Issue 4 (November 2006). https://doi.org/10.1061/(ASCE)0887–3828(2006)20:4(349)

5. Stevens D., Crowder B., Hall B., Marchand K. «Unified progressive collapse design requirements for DoD and GSA», Structures Congress 2008, Vancouver, Canada, April 24–26, 2008.

6. Liu M. «A new dynamic increase factor for nonlinear static alternate path analysis of building frames against progressive collapse», Engineering Structures, 2013, Vol. 48, pp. 666–673.

7. Saffari H., Javad Mashhadi J. «Effects of damping ratio on dynamic increase factor in progressive collapse», Steel and Composite Structures 22(3):677–690 · October 2016, DOI: 10.12989/scs.2016.22.3.677

8. Mahmoudi M., Teimoori T., Kozani H. «Presenting displacement-based nonlinear static analysis method to calculate structural response against progressive collapse». International Journal of Civil Engineering, Vol. 13, No. 4A, Transaction A: Civil Engineering, December, 2015

9. Алмазов В. О., Плотников В. О., Расторгуев Б. С. «Проблемы сопротивления здания прогрессирующему разрушению». 2/2011, ВЕСТНИК МГСУ.

10. Као Зуй Кхой. Динамика прогрессирующего разрушения монолитных многоэтажных каркасов. Автореферат на соискание степени к. т.н., МГСУ, Москва, 2010.

Основные термины (генерируются автоматически): динамический коэффициент, коэффициент динамичности, прогрессирующее обрушение, DIF, GLA, линейный статический расчет, норма США, расчет, удаляемая колонна, упругая стадия.

Источник

6.1 Нормирование и оценка коэффициента динамичности

6.1.1 При движении транспортных средств касательные и вертикальные воздействия от их колес на дорожную конструкцию имеют динамический характер и переменны по величине, направлению и статистическим показателям.

Динамическое воздействие автомобиля на дорожную конструкцию становится значимым при движении по неровной поверхности дорожного покрытия, сопровождающемся ударами и колебаниями колес и кузова.

6.1.2 Коэффициент динамичности K_д рекомендуется находить по формуле

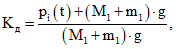(11)

где p_i(t) – динамическая составляющая нагрузки i-й оси;

M_i, m_i – соответственно подрессоренная и неподрессоренная массы транспортного средства;

g – ускорение свободного падения.

6.1.3 Динамическая составляющая нагрузки определяется произведением вертикального ускорения на массу транспортного средства, распределенную на i-ю ось.

6.1.4 Нормативные межремонтные сроки службы дорожных покрытий устанавливают по моменту достижения ими предельно допускаемого эксплуатационного состояния, оцениваемого их ровностью. Эти значения связывают с безопасностью движения и проектным уровнем надежности дорожной конструкции в целом. Например, при уровне надежности 0,95 (автомобильная дорога I категории) накопленные неровности на дорожном покрытии, измеренные толчкомером ТХК-2 на автомобиле УАЗ, не должны быть больше 80 – 100 см/км, а при надежности 0,9 – не более 170 см/км (автомобильная дорога III категории). При превышении этих показателей дорожное покрытие подлежит ремонту.

6.1.5 На рисунке 8 показана типовая расчетная схема амплитудно-временной характеристики K_д для определения силы динамического воздействия колеса на поверхность дорожного покрытия при наличии на нем одной из часто встречаемых неровностей в виде впадины, выбоины или ямы.

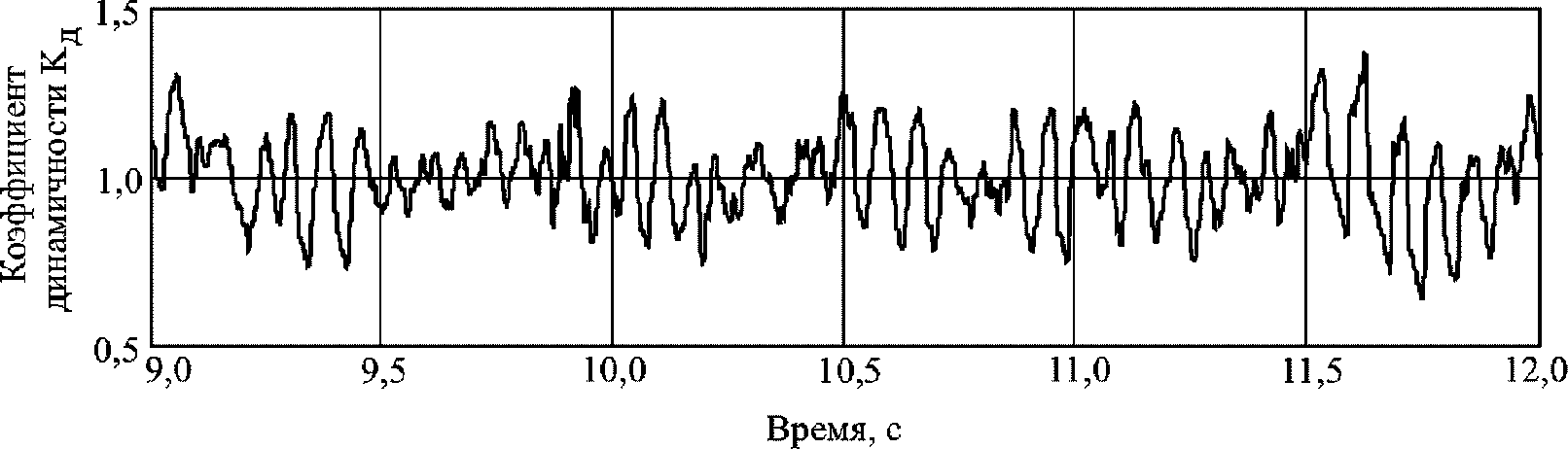
Рисунок 8 – Амплитудно-временная характеристика

коэффициента динамичности

6.1.6 На дорожных покрытиях могут быть неровности глубиной от 6 до 10 мм (в среднем 8 мм). Согласно СП 78.13330.2012 количество их допускается не более 10%. Грузовое транспортное средство при весе заднего моста с колесами около 2% – 3% от общего веса с грузом при движении со скоростью 60 км/ч по этой неровности (шириной или диаметром 0,5 м) воздействует на покрытие с максимальной динамической силой, превосходящей статическую нагрузку на эти колеса примерно в 1,5 раза (K_д = 1,45).

6.1.7 При неровностях большей глубины или высоты динамические нагрузки возрастают еще значительнее. Например, при движении автомобиля по ровному покрытию K_д не выходит за пределы 1,15. На неровной проезжей части при повышении скорости движения до 80 км/ч этот коэффициент возрастает до 3,0.

6.1.8 Коэффициент динамичности зависит от загруженности транспортного средства: для грузового автомобиля при полной (номинальной) загрузке он составляет от 1,4 до 1,8; для ненагруженного – от 2,0 до 2,4. Увеличение скорости движения сопровождается вначале быстрым ростом K_д, затем замедленным. Для высоких скоростей его значение практически не изменяется.

6.1.9 Коэффициент динамичности зависит от геометрии неровностей дорожного покрытия, квадрата скорости движения, механических свойств транспортного средства. В общем случае это функция времени K_д(t).

6.1.10 С учетом результатов работ проф. Е.В. Угловой рекомендуется следующий порядок статистического анализа коэффициента динамичности [10].

1 При обработке числовых экспериментальных рядов исследуется непротиворечие закону нормального распределения

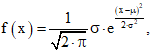(12)

где x – значение случайной величины;

– среднее значение случайной величины x;

– дисперсия величины x;

e = 2,81 – логарифмическая постоянная.

2 Для оценки достоверности этой гипотезы используются разные критерии и оценки, например, связанные с анализом симметрии. Коэффициент асимметрии A рассчитывается по формуле

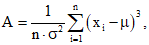(13)

где n – количество результатов измерений.

3 Оценивается отклонение формы экспериментальной кривой от нормальной, т.е. вычисляется коэффициент эксцесса A’

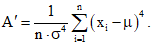(14)

4 Рекомендуется проводить анализ гистограмм распределения K_д по критериям “толстые и укороченные хвосты распределений” и “тонкие и длинные хвосты распределений”.

Такой анализ можно провести на типовом примере гистограммы распределения коэффициента динамичности, полученной Е.В. Угловой (рисунок 9) [10].

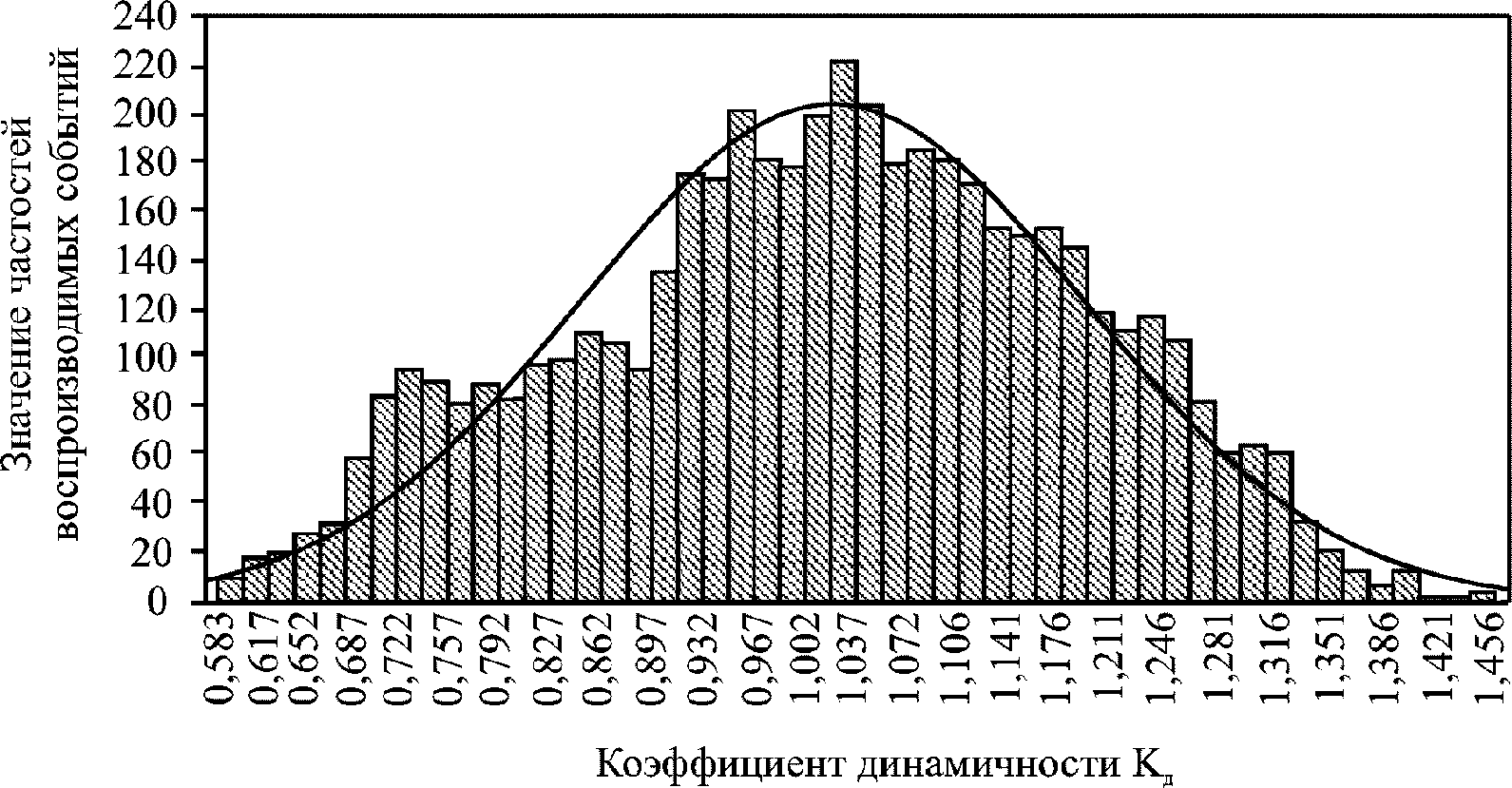
Рисунок 9 – Гистограмма распределения коэффициента

динамичности на участке автомобильной дороги

Азов – Староминская (км 45) при движении автомобиля

ВАЗ-21213 со скоростью 100 км/ч

5 На основе функции K_д(t) определяются характеристики коэффициента динамичности на участке автомобильной дороги. Так, максимальный коэффициент динамичности вычисляется по формуле

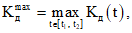(15)

где t₁, t₂ – время соответственно начала и конца прохождения участка.

Этот показатель характеризует максимальное воздействие транспортного средства на автомобильную дорогу. В предположении о постоянстве скорости движения он может свидетельствовать о степени локальной неровности или поврежденности дорожного покрытия. Время, соответствующее значению , является временем достижения показателей этой неровности.

Средний коэффициент динамичности рекомендуется определять следующим образом. Пусть – совокупность интервалов на отрезке [t₁, t₂], на которых коэффициент динамичности больше единицы. Тогда величина

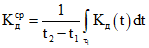(16)

может быть принята за оценку среднего коэффициента динамичности на участке автомобильной дороги.

Продолжительность динамических перегрузок рекомендуется определять с учетом того, что в отечественных нормативных документах в качестве предельного коэффициента динамичности принято значение 1,3. Пусть – совокупность интервалов на отрезке [t₁, t₂], на которых K_д > 1,3. Тогда за меру динамической перегрузки T_перегр можно принять

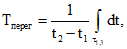(17)

т.е. это доля времени, когда воздействие на автомобильную дорогу больше нормативного.

Средний коэффициент динамических перегрузок находится по формуле

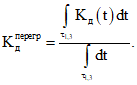(18)

Степень изменчивости динамического воздействия на дорожное покрытие транспортного средства при его движении по отношению к статическому воздействию выражается соответственно минимальным и максимальным коэффициентами динамичности

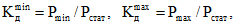(19)

где P_min, P_max – соответственно минимальное и максимальное значение нагрузки колеса транспортного средства на дорожное покрытие при его движении;

P_стат – статическая нагрузка колеса на покрытие.

6 Для оценки динамического воздействия используются различные критерии. Наиболее распространенные из них можно разделить на две группы.

Первая группа коэффициентов (коэффициент динамической нагрузки DLC, динамический коэффициент транспортного средства (оси), совокупный коэффициент силы DAFC) определяет отношение динамических усилий, возникающих при движении автомобиля к его статическому весу.

7 Ко второй группе коэффициентов (дорожный коэффициент напряжения F, совокупный критерий силы, коэффициент усталостного повреждения ESAL) можно отнести критерии, позволяющие оценить динамические перегрузки посредством определения размеров различных видов дорожных повреждений, вызванных приложением нагрузок. При этом в качестве характеристики динамических нагрузок на колесо автомобиля за рубежом используется показатель DLC, представляющий собой отношение

DLC = M/N, (20)

где M – среднее квадратичное отклонение;

N – статическое значение нагрузки на колесо транспортного средства.

Показатель DLC отражает физический смысл коэффициента вариации.

8 При эксплуатации автомобильных дорог динамическое воздействие транспортных средств выражено коэффициентом динамичности, значение которого больше нормативного, равного 1,3, и рассматривается как динамические перегрузки.

9 При проектировании жестких дорожных одежд в соответствии с рекомендациями [1] K_д допускается принимать в зависимости от осевой массы автомобиля (таблица 3).

Таблица 3

Коэффициенты динамичности для расчета жестких дорожных одежд

Осевая масса автомобиля, т	2	4	6	8	10	12
K_д	1,6	1,3	1,15	1,08	1,06	1,04

10 Исследования, проведенные А.В. Смирновым [11], позволили рекомендовать следующие коэффициенты динамичности для ровных вновь устраиваемых дорожных покрытий (таблица 4).

Таблица 4

Коэффициенты динамичности для ровных вновь устраиваемых

дорожных покрытий

Скорость движения автомобиля, км/ч	20	40	50	60	70	80	100	120
	1,1	1,3	1,4	1,55	1,62	1,7	1,75	1,8
	0,9	0,7	0,6	0,45	0,37	0,3	0,25	0,2

11 При расчете дорожных одежд Б.С. Радовский [12] предлагает учитывать K_д колесной нагрузки, имеющий величины, приведенные в таблице 5.

Таблица 5

Коэффициент динамичности колесной нагрузки

Скорость движения автомобиля, км/ч	10	20	30	40	50	60	80	100
K_д	1,12	1,21	1,28	1,34	1,38	1,41	1,45	1,47

Анализ таблиц 4 и 5 показывает, что при скорости движения автомобиля более 40 км/ч рекомендуется использовать значение коэффициента динамичности свыше 1,3.

6.2 Определение вероятности появления неровностей на дорожном покрытии по причине роста коэффициента динамичности (метод В.В. Столярова)

Скачать документ целиком в формате PDF

Источник

Литература[править | править код]

См. также[править | править код]

3.2. Вынужденные колебания: коэффициент динамичности

3.3. Резонанс

Вам также может понравиться

Как найти медиану математического ряда

Как найти скорость движения с отставанием

Как правильно составить план местности

Добавить комментарий Отменить ответ