Сторонников использования ROI (Return on Investment) достаточно много, как и его противников. Первые утверждают, что коэффициент рентабельности позволяет хотя бы примерно оценить полезность тех или иных инвестиций. Противники же уверяют, что использовать ROI нет смысла, так как этот показатель не может быть объективным, а человек, занимающийся составлением отчета, на первый план будет стараться выставить свою полезность, а не общий показатель доходности капиталовложений.
Что такое ROI
ROI – это коэффициент рентабельности инвестиций. Данный показатель измеряется в процентах и позволяет оценить убыточность или прибыльность той или иной инвестиции. Для расчета данного показателя нужно знать только 2 вещи: размер инвестиций и доход от вложений.
ROMI – то же, что и ROI, но только для оценки эффективности маркетинговых вложений. Показатель ROMI учитывает только маркетинговые расходы, не принимая в расчет остальные затраты, например расходы на производство товара.
Если говорить простыми словами, то ROI (Return on Investment) – это показатель, который демонстрирует то, насколько невыгодной или выгодной является инвестиция. Под инвестициями подразумеваются капиталовложения непосредственно в бизнес, то есть: расходы на аренду помещения, оплату налогов, зарплаты сотрудникам, закупку сырья, маркетинг, оборудование для работы и т. д.
Зачем считать ROI
Расчет ROI необходимо делать тогда, когда нужно узнать, в каком объеме возвращаются средства, вложенные в проект, команду или рекламную кампанию. Также РОИ нужен для того, чтобы не допустить ошибок в процессе распределения бюджетных средств, которые могут привести к пустой трате средств.
Коэффициент рентабельности позволяет принять верное управленческое решение: прекратить участие в проекте или закрыть его, оставить канал продвижения или убрать его, продолжить покупать сырье для производства продукта и т. п. В основном, ROI используется инвесторами, однако и маркетологи используют этот показатель для оценки эффективности рекламных кампаний, называя его ROMI (формула расчет при этом идентична).
ROI используется:
-
при капиталовложениях в новое дело, покупке акций и прочих инвестициях;
-
для анализа рекламных вложений, чтобы оценить, какой процент прибыли получен за тот или иной рекламный проект;
-
при инвестировании в свою компанию – к примеру, при обновлении ПО используемого оборудования, улучшении качества обслуживания и т. д.
Показатель ROI показывает эффективность вложений, а значит – указывает, что на полученный результат нужно обращать внимание.
ROI формула расчета
Рентабельность проекта формула расчета:

Первая часть формулы — это чистый доход (выручка, которую получила компания за определенный период). Затраты – это все издержки и расходы.
Формула окупаемости учитывает весь доход и все затраты на один проект, а результаты расчетов выражаются в процентах. Для инвесторов формула максимально понятна. Из общего дохода вычитается сумма инвестиций. Получая конечную прибыль, делим результат на сумму инвестиций. Умножаем на 100, чтобы получить результат в процентных выражениях. Важно заметить, что результат вложений может быть как положительным, так и отрицательным.
Какой ROI считается хорошим
Пример возможных результатов расчета ROI:
-
ROI < 100% – вложения не окупились, а потраченные средства превысили полученный чистый доход. Нужно пересмотреть эффективность инвестиций, но для начала следует проверить остальные показатели эффективности.
-
ROI > 100% – вложения полностью окупились, доля рекламных расходов не превышает доход, проект приносит прибыль. Никаких действий проводить не нужно, рентабельность инвестиций высокая.
-
ROI = 100% – вложения полностью окупились (есть возврат инвестиций), но проект так и не начал приносить доход от капиталовложений. Рекомендуется полностью проверить продукт, затраты и устранить ошибки.
Однако важно заметить, что для валютных и фондовых рынков, показатель ROI может считаться хорошим как при положительных, так и при отрицательных значениях. Все дело в том, что многие инвесторы вкладывают деньги в недооцененные активы (металлы, ценные бумаги и т. п.), которые со временем резко изменяются в цене. В данном случае рост и падение стоимости активов может наблюдаться всего за пару часов, поэтому ROI будет необъективным в качестве показателя эффективности капиталовложений.
Как рассчитать ROI: в Excel или онлайн?
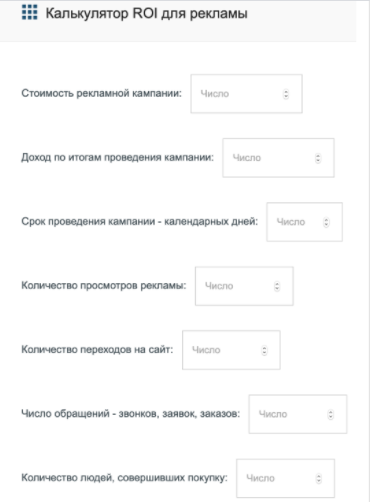
Считая показатель ROI есть большая вероятность допустить ошибку, не учтя важные показатели. Именно поэтому нужно знать, как считать ROI правильно. Так, чтобы потратить на расчет минимум времени, не допустив ошибок в процессе указания данных, можно использовать несколько автоматических способов для расчета ROI: специальный сервис для расчета или таблицы Excel.
Ciox – удобный калькулятор, который имеет все необходимые переменные.
Checkroi – сервис, позволяющий рассчитать ROI и еще ряд других маркетинговых показателей.
Также для расчета можно воспользоваться таблицей в Excel и там же хранить все полученные данные.
Отличие ROI от ДРР
ДРР – это доля рекламных расходов. Данный показатель особенно популярен в российском e-commerce. ДРР показывает отношение затрат на рекламу и полученную с неё прибыль. С помощью специальной формулы удается произвести точный расчет, чтобы определить, сколько % от полученного дохода составляют затраты на продвижение рекламной кампании.
Реальный доход – формула расчета ДРР:

Показатель ДРР не должен быть выше 100%, а иначе рекламная кампания будет считаться убыточной. Чем ниже показатель ДРР, тем выше эффективность рекламной кампании.
В каких случаях ROI не работает
ROI – это не универсальный инструмент. Существует достаточно много ситуаций, в которых опираться на данный показать абсолютно бессмысленно. Так, ROI не работает в случаях, когда клиент принимает решение об инвестиции спустя определенное время. К примеру, когда на продажу выставлена квартира, предприятие или другая дорогая вещь. В таком случае, клиент совершит покупку не сразу, а только после того, как взвесит все за и против. В результате этого показатель ROI будет не актуальным и утратит свою ценность.
Как правильно посчитать окупаемость: примеры
Пример расчета ROI для рекламной кампании в Google Ads.
В месяц мы тратим на рекламную кампанию 40 тысяч рублей. Покупатели купили товаров на 120 тысяч рублей. Себестоимость составила 90 тысяч рублей.
Валовая прибыль – 120 000 – 90 000 = 30 000 рублей.
ROI = (30 000 — 40 000) / 40 000 х 100 = -25%.
Исходя из приведенного примера мы получаем, что на каждый инвестируемый рубль мы потеряли 0,25 копеек. В этом случае рекомендуется запустить другой вид рекламы или внимательно пересмотреть канал продвижения.
Пример расчета ROI для ценных бумаг:
Инвестор вкладывает деньги в акции. В апреле их стоимость составляла 8 долларов (за 1 шт.). Каждый месяц инвестор получает с акций дивиденды – 0,5 доллара. В августе стоимость акций возросла до 20 долларов. Инвестор решил их продать и получил прибыль:
Дивиденды + Чистый доход = (20 — 8) + (0,5 х 5) = 14,5 доллара.
(0,5 x 5) — это дивиденды за 5 месяцев: с апреля по август.
ROI = 14,5 / 8 х 100% = 181,25%.
В этом случае показатель ROI высокий. Это говорит о том, что инвестиция была удачна, а за каждый вложенный доллар мы получили 1,8 доллара чистой прибыли.
Заключение
ROI – это показатель, отражающий убыточность или прибыльность совершенных инвестиций. Однако несмотря на явные преимущества, данный инструмент имеет два недостатка, которые важно учитывать:
-
оценка ROI малоинформативная, а показатель будет работать только в совокупности с другими данными;
-
показатель не статичен и никак не привязан к экономическим факторам и курсам валют.
Обобщая все вышеперечисленное, нужно понимать, что ROI – это действительно полезный и удобный инструмент, однако нужно знать, как и в каких ситуациях им следует пользоваться.
Открыть эту статью в PDF
Определение PI
Индекс доходности (profitability index, PI) — показатель отношения дисконтированных денежных потоков от инвестиций к сумме инвестиций. Его также называют индекс рентабельности или прибыльности. Формула PI имеет следующий вид:
где:
CFt — денежные потоки за период t
d — ставка дисконтирования
I — начальные инвестиции
В этом варианте записи формулы предполагается, что денежные потоки CF не включают начальные инвестиции. Можно записать формулу PI и в другой форме:
В данном случае NPV —текущая приведенная стоимость всех денежных потоков проекта или иной инвестиции, включая и начальные вложения I.
Инвестиционный проект считается привлекательным, если PI ≥ 1.
Пример расчета PI
Предположим, что инвестиционный проект требует начальных вложений в размере 1000 руб., и после этого в течение четырех лет приносит чистый денежный поток по 400 руб. в год. Ставка дисконтирования для него установлена на уровне 10%.
Расчет индекса доходности будет выглядеть следующим образом:

Из этого расчета видно, что проект является привлекательным и вложение средств в этот проект увеличит их стоимость в 1,27 раза.
Сравнение PI и NPV
Показатели PI и NPV выполняют похожую роль в оценке инвестиционных проектов. Оба этих показателя сравнивают начальные инвестиции с дисконтированными будущими денежными потоками.
Из второго варианта записи формулы PI можно легко увидеть, что PI будет больше 1 только тогда, когда NPV > 0, то есть во всех проектах, которые могут быть признаны привлекательными на основании значения NPV (которое должно быть больше или равно нулю) значение PI будет больше 1, что также будет означать привлекательность проекта.
Однако у показателей NPV и PI есть два важных отличия:
- NPV показывает абсолютную величину экономической прибыли. Если мы знаем, что проект имеет NPV=268, значит он обеспечил требуемую доходность вложений и сверх того зарабатывает 268 рублей. Но насколько это много? Если инвестиции составили 100 000, то сумма избыточного дохода ничтожно мала, если 1000, то прирост заметный. А вот PI показывает доход по отношению к исходным инвестициям, что может быть полезнее для принятия решения.
- NPV дисконтирует все денежные потоки проекта без попытки разделить их на инвестиции и текущие потоки, в то время как PI предполагает, что начальные инвестиции существуют у нас отдельно, одной суммой, в начале проекта. Но это не всегда так. Инвестиции могут быть растянуты на несколько лет, они могут пересекаться с текущей деятельностью, а иногда просто сложно сказать, относить ли какую-то выплату к инвестициям или к текущим затратам. Такие факторы создают неопределенность в формуле PI, и с этой точки зрения NPV намного удобнее.
Сравнение PI и IRR
Показатель IRR демонстрирует доходность инвестиционного проекта в виде процентов, вычисляемых на вложенные средства. В этом смысле он похож на PI, но дальше в них обнаруживаются серьезные различия:
- PI учитывает требуемую доходность капитала, отраженную в ставке дисконтирования, и только после этого рассчитывает дополнительный прирост стоимости. IRR содержит полную доходность инвестиций.
- В приросте стоимости, рассчитанном на основе PI, фактор времени учтен только в части применения дисконтирования. Если PI одного проекта равен 1,2, а другого — 1,3, мы не можем сказать, какой из них прибыльнее. Если окажется, что первый проект длится 2 года, а второй — 6 лет, то наиболее прибыльным окажется проект, у которого PI меньше. IRR показывает доходность в виде годовых процентов.
Такие статьи мы публикуем регулярно. Чтобы получать информацию о новых материалах, а также быть в курсе учебных программ, вы можете подписаться на новостную рассылку.
Если вам необходимо отработать определенные навыки в области инвестиционного или финансового анализа и планирования, посмотрите программы наших семинаров.
Спасибо, Вы зарегистрированы
на семинар «Альт-Инвест»!
Наш менеджер свяжется с Вами в ближайшее время.
Спасибо, Ваша заявка принята!
Мы отправили Вам письмо для проверки контактной информации на адрес info@alt-invest.ru.
Подтвердите, пожалуйста, свой адрес, и заявка будет направлена консультанту. После этого мы свяжемся с Вами для уточнения наиболее удобного времени и формата презентации.
Спасибо, Вы почти подписаны на новостную рассылку «Альт-Инвест»!
Мы отправили Вам письмо для подтверждения вашего e-mail на адрес info@alt-invest.ru.
Теперь проверьте почту.
Спасибо за интерес к нашим программам!
Мы отправили Вам письмо, где сказано как получить демо-версию, на адрес info@alt-invest.ru.
Теперь проверьте свою почту.
Название показателя
Правильное название показателя — Accounting Rate of Return (ARR), в переводе на русский язык — учетная норма прибыли.
Параллельно используется множество синонимов:
- рентабельность проекта;
- коэффициент эффективности инвестиций;
- средневзвешенная ставка рентабельности;
- учетная доходность;
- средняя норма прибыли и другие.
Несмотря на обилие названий, сущность показателя остается неизменной: он определяет, сколько рублей может получить вкладчик за каждый рубль, инвестированный в конкретный проект.
Формула расчета
Есть три варианта расчета учетной нормы прибыли.
Вариант 1. Расчет по средней стоимости вложений
Применяется, если по ходу осуществления проекта все инвестиции будут списаны на расходы без остатка.
ARR = (чистая среднегодовая прибыль / ½ * общая сумма инвестиций) * 100%
Например. Предприятие планирует купить новое оборудование за 3 000 000 рублей. Срок его эксплуатации составляет три года. Ожидаемые расходы составят 1 500 000 рублей в первый год, а дальше будут возрастать на 4% ежегодно. Амортизация будет начисляться линейным способом, то есть каждый год на расходы будет списываться по 1 000 000 рублей. Налог на прибыль — 20%. Прогнозируемая сумма выручки по годам представлена в таблице.
Исходные данные для расчетов:
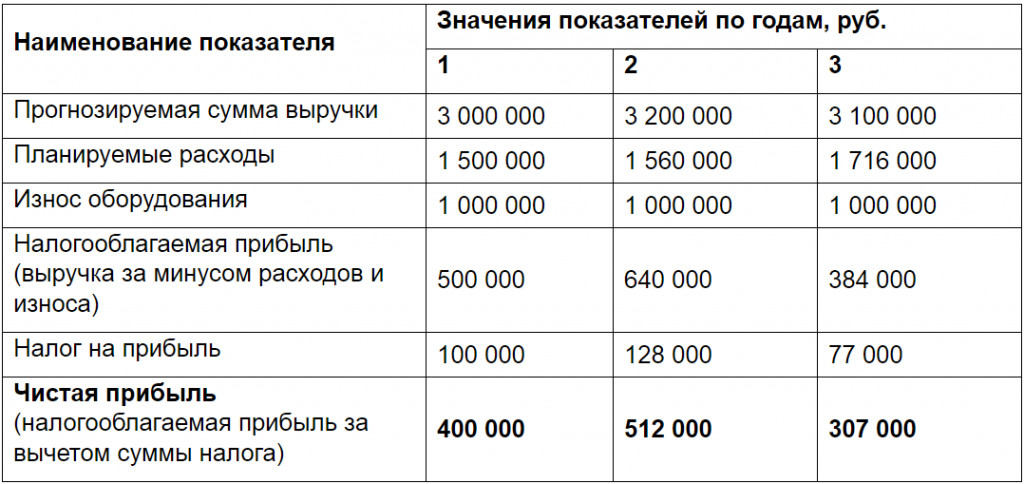
Таким образом, среднегодовая чистая прибыль = (400 000 + 512 000 + 307 000) / 3 = 406 000 рублей.
ARR = (406 000 / ½ * 3 000 000) * 100% = 27%
Вариант 2. Расчет с учетом остаточной стоимости имущества
Применяется, если нужно учесть остаточную стоимость актива. То есть разницу между его первоначальной стоимостью и суммой износа, начисленной за весь срок его использования.
ARR = (чистая среднегодовая прибыль / ½ * (первоначальные инвестиции — остаточная стоимость)) * 100%
Например. Предприниматель планирует купить производственную линию за 5 200 000 рублей. Износ будет начисляться линейным способом на протяжении пяти лет, то есть каждый год на расходы будет списываться по 1 000 000 рублей. Остаточная стоимость оборудования по истечении срока его эксплуатации составит 200 000 рублей. Прогнозируемая среднегодовая прибыль — 400 000 рублей.
ARR = (400 000 / ½ * (5 200 000 — 200 000)) * 100% = 16%
Вариант 3. Расчет по размеру первоначальных инвестиций
Применяется для оценки проектов, которые обеспечивают равномерный объем доходов на очень длительный или неопределенный срок. К таким проектам относится, например, покупка недвижимости, которую можно сдавать в аренду в течение многих лет.
ARR = (чистая среднегодовая прибыль / сумма инвестиций) * 100%
Например, компания планирует купить недвижимость и сдавать ее в аренду коммерческим предприятиям. Стоимость объекта нежилого фонда — 100 миллионов рублей. Ожидаемая среднегодовая сумма прибыли — 30 миллионов рублей. Подсчитаем рентабельность проекта.
ARR = 30 / 100 * 100% = 30%
Значение показателя в бизнес-планировании
Итак, рентабельность проекта отражает прибыльность объекта инвестирования. Чем она выше, тем больше прибыли получит вкладчик.
Величина показателя сравнивается:
- во-первых, с показателем рентабельности собственного капитала самого предприятия: учетная норма прибыли проекта должна быть выше;
- во-вторых, со среднеотраслевыми значениями рентабельности капитала (показателями конкурентов).
Например, рентабельность собственного капитала компании составляет 30%. То есть на 1 рубль, вложенный в свой бизнес, предприятие получает 30 копеек чистой прибыли. Руководству предложили поучаствовать в новом проекте, норма прибыли которого оценивается в 20%. Стоит ли компании принять предложение? Если других выгод вроде выхода на новые рынки или улучшения деловой репутации сделка не принесет, то не стоит. Ведь доходов от этого проекта будет меньше, чем может получить фирма от своей обычной деятельности.
Универсального значения учетной нормы прибыли не существует. Она зависит от отрасли, в которой планируется реализовать проект. Например, для сельского хозяйства норма прибыли в 15% — очень хороший показатель, он выше среднеотраслевой рентабельности капитала. А для строительства и 50% будет недостаточно.
Величина показателя должна соответствовать степени риска. Если инвестируется стабильное предприятие, давно и плотно занявшее свою нишу на рынке, норма прибыли на уровне среднеотраслевых значений считается хорошей. Но если вкладчику предстоит инвестировать новый инновационный проект, когда существует риск потери дохода или всех вложенных денег, норма рентабельности должна быть на порядок выше.
Если вкладчик выбирает самый доходный проект из нескольких, нужно рассчитать и сравнить нормы прибыли по каждому из них.
Преимущества и недостатки
Основное достоинство учетной нормы прибыли — простота расчета. С другой стороны, она не учитывает такие факторы:
Стоимость денег во времени
В данном случае деньги, поступающие на n-ый год реализации проекта, оцениваются по тому же уровню рентабельности, что и поступления в первый год. Один рубль сегодня стоит больше, чем через год. Деньги можно пустить в оборот и на конец года получить реальный доход. Если же инвестор сможет вернуть вложения только через несколько лет (проект с длительным сроком реализации), то он потеряет возможность получения такого дохода. Кроме того, деньги ежегодно дешевеют из-за инфляции.
Распределение прибыли по годам
Например, инвестор рассматривает два взаимоисключающих проекта. Базовые данные в обоих случаях идентичны: стоимость 20 миллионов рублей, ожидаемая среднегодовая прибыль — 6 миллионов рублей. На первый взгляд проекты выглядят равнозначными, поскольку учетная норма прибыли одинакова:
ARR = (6 / ½ * 20) * 100% = 60%
Однако прогнозируемые объемы прибыли по годам заметно отличаются. В таблице приведены ожидаемые показатели за пять лет реализации проекта.

Из таблицы видно, что второй проект привлекательней для инвестора, поскольку прибыль в первые два года здесь значительно выше.
Разницу в продолжительности срока жизни активов
Если оценивать несколько проектов равной стоимости с приблизительно равной суммой ежегодной прибыли, но разным сроком эксплуатации актива, то результат расчетов будет очень схож. Однако если срок службы активов заметно отличается, то инвестору выгоднее вложить деньги в тот проект, который просуществует дольше.
Сложность прогнозирования будущей прибыли
Если речь идет о новом бизнесе, то прогнозирование прибыли может вызывать затруднения. А в условиях отечественной экономики разброс между ожидаемым и реальным результатом может быть значительным.
Использование различных методов амортизации
Например, амортизация на предприятии начисляется не линейным, а иным способом, то есть сумма варьируется из года в год и спрогнозировать ее нереально. В таком случае расчет по приведенному алгоритму теряет смысл.
Вывод: учетная норма прибыли — удобный и простой инструмент, но область его применения ограничена. Он хорошо подходит для прогнозирования прибыли от внедрения краткосрочных проектов при условии равномерного поступления доходов.
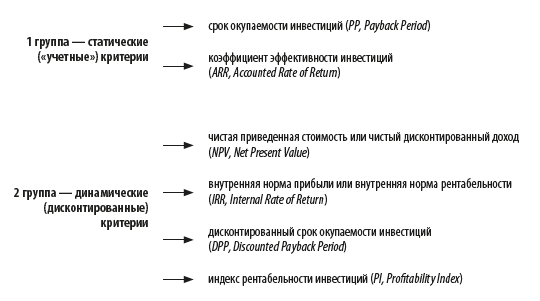
Общий подход к оценке эффективности инвестиционных проектов
Срок окупаемости инвестиций
Коэффициент эффективности инвестиций
Чистая приведенная стоимость
Внутренняя норма прибыли
Дисконтированный срок окупаемости инвестиций
Индекс рентабельности инвестиций
В условиях снижения инвестиционных возможностей бизнеса важен точный анализ эффективности инвестиций. Чтобы уменьшить инвестиционные риски, обусловленных большим числом допущений, используется комплекс показателей инвестиционного анализа, каждый из которых имеет свои плюсы и минусы. В статье рассмотрим проблемы и способы повышения качества оценки инвестиционных проектов, а также алгоритм проведения инвестиционного анализа на примере.
Общий подход к оценке эффективности инвестиционных проектов
В основе принятия решений инвестиционного характера лежит оценка экономической эффективности инвестиций. Она зависит от совокупности следующих факторов:
• способность инвестиционного проекта приносит доходы, т. е. положительные денежные потоки в будущем в течение всего срока функционирования проекта;
• размер единовременных и будущих расходов, требующихся для реализации проекта;
• размер и соотношение собственных и заемных источников финансирования проекта;
• стоимость собственного и заемного капитала;
• фактор времени (учитывается разная стоимость будущих денежных потоков).
При прогнозном анализе этих факторов могут возникнуть сложности:
• инвестиционные расходы могут осуществляться как единовременно, так и на протяжении длительного периода времени;
• помимо капитальных затрат могут быть необходимы финансовые расходы на пополнение оборотных средств для реализации проекта;
• расчет результатов реализации инвестиционного проекта проводится в пределах прогнозного периода, в то время как срок полного функционирования проекта в большинстве случаев превышает время прогнозного периода;
• длительный период инвестиционного проекта приводит к росту неопределенности при оценке всех аспектов инвестиций, т. е. к росту инвестиционного риска.
Поэтому для оценки эффективности инвестиционного проекта используется система показателей, так или иначе отражающих соотношение полученных результатов и понесенных затрат в зависимости от интересов всех участников инвестиционного проекта или конкретного участника в отдельности.
Итак, комплексный инвестиционный анализ предполагает расчет и последующую оценку следующих показателей:
Рассмотрим подробно методику расчета данных показателей, а также сложности и проблемы их практического использования.
Срок окупаемости инвестиций (PP, Payback period)
Срок окупаемости инвестиций — это период времени с момента начала реализации инвестпроекта до момента, когда доходы от инвестиций становятся равными первоначальным инвестиционным затратам, понесенным в виде капитальных вложений, и инвестиционным расходам на пополнение оборотных средств. Экономический смысл показателя заключается в определении срока, за который инвестор может вернуть вложенный инвестированный капитал.
Алгоритм расчета срока окупаемости зависит от равномерности распределения прогнозируемых доходов от инвестиций:
• если доход распределен по годам равномерно, то срок окупаемости рассчитывается делением общих инвестиционных затрат на величину годового дохода, обусловленного ими. При получении дробного числа оно округляется в сторону увеличения до ближайшего целого.
• если доходы распределены неравномерно, а в большинстве случаев так оно и есть, то срок окупаемости рассчитывается прямым подсчетом числа лет, в течение которых инвестиции будут покрыты кумулятивным чистым доходом, т. е. доходом, рассчитанным нарастающим итогом.
Общая формула расчета показателя срока окупаемости инвестиций:
РР = n, при котором Рn > IC, (1)
где n — число временных периодов (календарных лет, месяцев);
Рn — кумулятивный чистый доход от реализации инвестпроекта;
IC — инвестированный капитал.
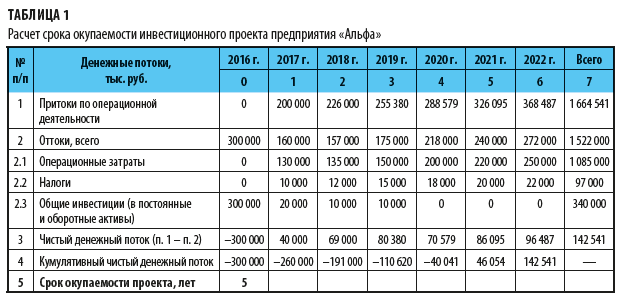
Рассмотрим пример расчета срока окупаемости инвестиций предприятия «Альфа». Данные о денежных потоках и определенный срок окупаемости проекта представлены в табл. 1.
Период первоначальных инвестиционных затрат, в котором еще нет притоков от операционной деятельности, принимается за нулевой.
Показатель чистого денежного потока (№ 3) определяется как разность между притоками по операционной деятельности (№ 1) и всеми оттоками (№ 2) по каждому периоду в отдельности. Показатель кумулятивного чистого денежного потока представляет собой сумму всех чистых денежных потоков, рассчитанных нарастающим итогом за весь период проекта.
Таким образом, срок окупаемости инвестиций наступает в тот момент, когда кумулятивный чистый денежный поток становится положительным. В рассмотренном примере он равен 5 годам.
Как видим, показатель срока окупаемости инвестиций очень прост в расчете и понимании. Однако он имеет ряд недостатков, которые необходимо учитывать при проведении инвестиционного анализа.
Ключевой недостаток этого показателя заключается в том, что он не учитывает разность стоимости денежных средств во времени, т. е. не делает различия между инвестиционными проектами с одинаковым общим размером положительных денежных потоков (доходов), но с разным распределением их по времени.
Еще один важный недостаток этого показателя — он не учитывает фактор влияния доходов, полученных в периоды после срока окупаемости, на общую эффективность инвестиций.
В связи с этим показатель срока окупаемости инвестиций дает лишь первичную (общую) оценку инвестиционного проекта и не может служить основой для принятия инвестиционных решений.
Коэффициент эффективности инвестиций (ARR, Accounted Rate of Return)
Коэффициент эффективности инвестиций показывает общую рентабельность проекта и используется для предварительной оценки привлекательности инвестиций.
У этого показателя есть две особенности:
• во-первых, как и срок окупаемости инвестиций (РР), он не предполагает расчет дисконтированных денежных потоков;
• во-вторых, за показатель чистых положительных потоков принимается бухгалтерская прибыль (за вычетом фискальных платежей), которая применяется в среднегодовом исчислении.
Рассчитывается показатель эффективности инвестиции (ARR) так: среднегодовая чистая прибыль за весь период инвестиционного проекта сопоставляется со средней величиной инвестиционных затрат. Далее возможны два варианта расчета:
1) если предполагается, что по истечении срока реализации инвестпроекта все капитальные вложения будут списаны, то средняя величина инвестиционных затрат рассчитывается как среднее арифметическое первоначальных и итоговых инвестиций;
2) если проект предполагает наличие остаточной (ликвидационной) стоимости активов, то ее стоимость исключается из величины итоговых инвестиций. В этом случае показатель эффективности инвестиции (ARR, %) рассчитывается по формуле:
ARR = Pav / (1/2 × (IC0 + (ICn – RV))) × 100 %, (2)
где Pav — среднегодовая чистая прибыль, рассчитанная за весь срок инвестпроекта;
IC0 — первоначальная величина инвестированного капитала;
ICn — общая величина инвестированного капитала;
RV — остаточная (ликвидационная) стоимость инвестпроекта.
Рассмотрим на примере порядок расчета показателя эффективности инвестиций (ARR).
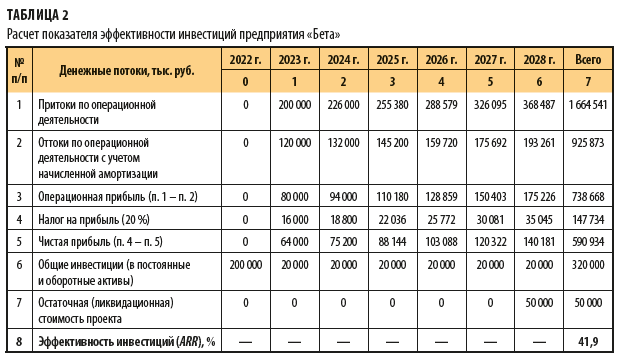
Данные о денежных потоках, инвестированном капитале, остаточной (ликвидационной) стоимости инвестпроекта и рассчитанном показателе ARR представлены в табл. 2.
Используя данные табл. 2 и формулу 2, рассчитаем показатель эффективности инвестиций (ARR):
1) сначала рассчитаем среднегодовую чистую прибыль весь срок инвестпроекта (Pav):
(64 000 тыс. руб. + 75 200 тыс. руб. + 88 144 тыс. руб. + 103 088 тыс. руб. + 120 322 тыс. руб. + 140 181 тыс. руб.) / 6 лет = 98 489 тыс. руб.;
2) далее рассчитаем показатель эффективности инвестиций (ARR):
98 489 тыс. руб. / (1/2 × (200 000 тыс. руб. + (320 000 тыс. руб. – 50 000 тыс. руб.))) × 100 % = 41,9 %.
Показатель эффективности инвестиций (ARR) используется, как правило, для оценки привлекательности инвестпроекта — он сравнивается с показателями рентабельности инвестированного и (или) собственного капитала.
Материал публикуется частично. Полностью его можно прочитать в журнале «Справочник экономиста» № 4, 2022.
Практически всегда действует правило: чем выше возможная доходность, тем выше риски.
Но вот в обратную сторону правило работает не всегда, и это обидно: потенциальная доходность по активу так себе, а риск этого актива довольно высокий. Получается, для относительно невысокой доходности приходится рисковать так, будто вкладываешься в высокодоходный актив. В этом случае на помощь инвестору может прийти расчет соотношения «риск-доходность».
В статье я рассмотрю показатели, по которым можно оценить, насколько адекватно у определенного актива соотношение его риска и доходности. Вот какие показатели буду рассматривать:
- Коэффициент вариации — coefficient of variation.
- Коэффициент Шарпа — Sharpe ratio.
- Коэффициент информации — information ratio.
- Коэффициент Сортино — Sortino ratio.
- Коэффициент Трейнора — Treynor ratio.
Но прежде чем разбираться с показателями риска-доходности, нужно разобраться и с основой — с тем, как считаются сами доходность и риск.
Как считается доходность
Доходность — это показатель, характеризующий финансовый результат от инвестирования. Простыми словами, это процент от стоимости актива, который инвестор заработал «сверху». В общем виде доходность от вложения в финансовый актив считается так:
(Pt + 1 − Pt + CF) / Pt,
где Pt + 1 — цена актива сейчас или на момент продажи,
Pt — цена актива на момент покупки,
CF — промежуточный денежный поток, который принес актив за время владения им, — например, выплаченные дивиденды.
Бытовой пример: инвестор купил акцию за 100 $ и продал за 150 $, а за время владения получил 3 $ дивидендов. Доходность по формуле выше будет считаться так:
(150 − 100 + 3) / 100 = 0,53, или 53%
Для упрощения расчетов из формулы иногда убирают CF — промежуточные денежные потоки в виде дивидендов.
В зависимости от того, за какой период мы рассчитываем доходность, она может быть дневной, месячной, квартальной, годовой или общей.
Например, акции Apple 31 декабря 2016 стоили 27,4 $, а 30 сентября 2020 — 115,6 $. Посчитаем общую доходность за этот период:
(115,6 − 27,4) / 27,4 = 3,22, или 322%
Но доходность за все время владения инструментом не так показательна, если мы хотим сравнить активы, которыми владели в течение разных периодов. Например, один актив принес вам 11% за полгода, а второй — 30% за полтора года. Чтобы сравнить эффективность этих инструментов, их доходности нужно привести к общему знаменателю — годовой доходности. Годовая доходность показывает, сколько в среднем приносил актив за год владения им.
Для расчета годовой доходности можно использовать три подхода — в зависимости от того, какими данными владеет инвестор. Если есть сразу все данные, можно использовать любой из способов — результат будет одинаковый.
Если есть информация о доходности за каждый год владения активом, то доходность рассчитывается по следующей формуле:
((1 + r1) × (1 + r2) × (1 + r3) × (1 + rn))1/n − 1,
где rn — доходность за каждый анализируемый период,
n — количество периодов (лет).
Например, инвестор купил акцию компании за 100 $ и владел ею 3 года. За первый год стоимость акции выросла на 20%, во второй год — упала на 10% по отношению к прошлому периоду, а за третий год акции прибавили в цене 30%. Общая годовая доходность за эти три года будет считаться так:
((1 + 20%) × (1 − 10%) × (1 + 30%))1/3 − 1 = 11,98%
Кажется, что формула слишком сложная и что можно было бы просто взять доходность за каждый год, сложить и поделить на три — то есть посчитать среднее арифметическое. Но корректнее считать не среднее арифметическое, а среднее геометрическое — что и делает наша формула. И этому есть причина.
Для примера выше среднее арифметическое составило бы 13,33%:
(20% − 10% + 30%) / 3
Наше значение, полученное через среднее геометрическое, на 1,35 процентного пункта меньше. Геометрический показатель учитывает, что доходность неравномерна и меняется от года к году, — то есть такая доходность уже учитывает в себе некоторую волатильность.
Другими словами, чем выше волатильность актива, тем ниже будет значение среднего геометрического доходности к среднему арифметическому.
Для примера возьмем акции A и B и предположим, что за 4 года после покупки акции показали одинаковую итоговую доходность. Но на протяжении этих четырех лет вели себя по-разному: акции A росли более плавно, а акции B сильнее проседали и сильнее росли, то есть были более волатильными.
Котировки акций A и B за 4 года
| Покупка | Первый год | Второй год | Третий год | Четвертый год | |
|---|---|---|---|---|---|
| Акция A | 100 $ | 140 $ (+40%) | 150 $ (+7%) | 125 $ (−17%) | 180 $ (+44%) |
| Акция B | 100 $ | 70 $ (−30%) | 120 $ (+71%) | 100 $ (−17%) | 180 $ (+80%) |
Четвертый год
180 $ (+44%)
Четвертый год
180 $ (+80%)
Посчитаем данные для обоих активов: среднее арифметическое и среднее геометрическое, то есть годовую доходность.
Актив A:
Среднее арифметическое: (40% + 7% − 17% + 44%) / 4 = 18,5%.
Среднее геометрическое (годовая доходность): (1 + 40%) × (1 + 7%) × (1 − 17%) × (1 + 44%)1/4 = 15,8%.
Актив B:
Среднее арифметическое: (−30% + 71% − 17% + 80%) = 26%.
Среднее геометрическое (годовая доходность): (1 − 30%) × (1 + 71%) × (1 − 17%) × (1 + 80%)1/4 = 15,8%.
Среднее арифметическое актива А больше, чем актива В, — и если бы мы посчитали только среднее арифметическое, то сделали бы ложный вывод, что акции актива B выгоднее. Но ведь мы знаем, что это не так: в результате акции принесли одинаковую прибыль.
Годовая доходность по обеим акциям одинаковая — 15,8%. Но у акций B больше волатильность — и это выражается в разнице между средним арифметическим и средним геометрическим: чем она больше, тем больше волатильность.
В случае с акцией A разница между двумя арифметическим и геометрическим равна 2,8 процентных пункта. А у акции B эта разница составляет 10,4 процентных пункта — при равных доходностях по этой разнице можно сделать вывод, что акции B более волатильны.
Если известна совокупная доходность за весь срок владения, то формула для расчета годовой доходности будет выглядеть так:
(1 + Общая доходность)(365 / Количество дней владения активом) − 1
Например, инвестор купил акцию компании за 100 $, держал ее 714 дней, а на 715-й день продал и получил доходность 74% за весь период владения. Общая годовая доходность за рассматриваемый период будет считаться так:
(1 + 74%)(365 / 715) − 1 = 32,68%
Таким образом, на инвестициях в компанию инвестор заработал 32,68% годовых за рассматриваемый период.
Если известна начальная и конечная стоимость инвестиций, то общую годовую доходность можно вычислить по следующей формуле:
(Конечная стоимость актива / Начальная стоимость актива)(1 / Количество периодов) − 1
Например, инвестор купил 20 акций по 200 $ и решил удерживать их 2 года. За этот период компания каждый год выплачивала 1 $ дивидендов на акцию. На момент продажи цена акции составила 270 $. В этом случае общая годовая доходность будет такой:
((270 × 20 + 2 × 20) / 200 × 20)(1/2) − 1 = 16,62%
Совокупная доходность в данном кейсе составила 36%, а общая годовая доходность — 16,62%.
Как считается риск
Риск — это вероятность частичной или полной потери вложенного капитала. В классической портфельной теории риск вложения определяется как стандартное отклонение его доходности — то есть возможный разброс его фактической доходности вокруг средней доходности.
Предположим, в среднем акция растет на 10% в год, но при этом возможны отклонения на 5% в каждую сторону — то есть она может вырасти как на 15% в год, так и на 5%. Вот эти возможные отклонения нам и нужно рассчитать. Рассчитывается стандартное отклонение по следующей формуле:
где rn — доходность за n-й период, обычно годовая,
r̄ — среднее арифметическое доходности актива за все время владения,
n — количество периодов: если считаем по годовой доходности, то количество лет.
Например, инвестор владел активом 4 года — он знает доходность за каждый год и теперь хочет рассчитать стандартное отклонение доходности этого актива.
Доходность актива
| Период | Доходность |
|---|---|
| Первый год | −11,5% |
| Второй год | 15,9% |
| Третий год | 10% |
| Четвертый год | 7,2% |
Чтобы посчитать стандартное отклонение доходности, в первую очередь посчитаем — среднее арифметическое доходности:
(−11,5% + 15,9% + 10% + 7,2%) / 4 = 5,4%
Теперь можем подставить данные в формулу выше:
Стандартное отклонение составило 11,8%. Если допустить, что доходность акции нормально распределена, то по правилу трех сигм инвестор вправе ожидать, что с вероятностью 68,3% (одно стандартное отклонение — 68,3% вероятности) доходность акции в следующем году будет находиться в диапазоне от −6,4% до 17,2% — то есть от (5,4% − 11,8%) до (5,4% + 11,8%).
Чем сильнее значения фактической доходности отклоняются от ее среднего значения, тем больше стандартное отклонение, а значит, больше риск. Низкое значение стандартного отклонения означает, что годовые доходности лежат вблизи среднего значения и риск от вложения в актив невелик.
Формулу выше используют в случаях, если берутся котировки по акции не за весь период ее существования, а, предположим, за 2—3 года из возможных 10 лет, прошедших с момента первичного размещения акции на фондовом рынке. А если берутся котировки за весь период существования акции, то для расчета стандартного отклонения используется следующая формула — она отличается только знаменателем — берется полное количество периодов:
Анализируем на примере портфеля Баффетта
Итак, в общем виде мы рассмотрели понятия доходности и риска. Теперь я построю диаграмму «риск-доходность», чтобы проанализировать, какие активы показывают оптимальное отношение риска к доходности. Простыми словами, по диаграмме можно понять, какой актив дает максимальную доходность на единицу риска.
Для примера возьмем портфель Уоррена Баффетта: я взял те активы, по которым есть данные котировок за период с 2012 по 2020 год. По отчетным данным на 30 сентября 2020 года в портфель Баффетта входило 49 компаний, но лишь по 6 компаниям, составляющим существенную долю портфеля, были данные за нужный период.
6 крупнейших по весу компаний в портфеле Berkshire Hathaway на 30.09.2020
| Компания | Тикер | Вес актива в портфеле |
|---|---|---|
| Apple | AAPL | 47,78% |
| Bank of America | BAC | 10,63% |
| Coca-Cola | KO | 8,63% |
| American Express | AXP | 6,64% |
| Moody’s | MCO | 3,12% |
| US Bancorp | USB | 2,07% |
Вес актива в портфеле
47,78%
Вес актива в портфеле
10,63%
Вес актива в портфеле
8,63%
Вес актива в портфеле
6,64%
Вес актива в портфеле
3,12%
Вес актива в портфеле
2,07%
В расчетах для повышения точности я опираюсь на ежедневные котировки акций с 2012 по 2020 год — данные и расчеты представлены в гугл-таблице.
Еще для расчетов нам понадобится бенчмарк и безрисковая ставка. Бенчмарк — это портфель, с которым мы будем сравнивать эффективность наших активов. Обычно в качестве бенчмарка берут индекс на широкий рынок США — я взял ETF SPDR S&P 500.
Безрисковая ставка нужна для расчета показателей эффективности инвестиций: в ряде этих показателей она используется как доходность от вложения в безрисковый актив, то есть актив, риск наступления дефолта по которому стремится к нулю. Конечно, абсолютно безрисковых активов не существует, поэтому в качестве безрисковой ставки часто используют процентную ставку по государственным облигациям или определяют ее равной нулю. В качестве безрисковой ставки (RFR, risk-free rate) я взял 10-летние казначейские облигации США — 10-Year Treasury Constant Maturity Rate.
Шаги будут такие:
- Берем дневные доходности активов.
- Рассчитываем по ним среднюю годовую доходность и стандартное отклонение — как делали в разделе с расчетом риска.
- Строим карту «риск-доходность».
Показатели доходности и риска
| Компания | Тикер | Среднегодовая доходность | Стандартное отклонение |
|---|---|---|---|
| Apple | AAPL | 30,2% | 28,6% |
| Bank of America | BAC | 18,4% | 31,1% |
| Coca-Cola | KO | 10,0% | 18,3% |
| American Express | AXP | 15,0% | 29,3% |
| Moody’s | MCO | 27,1% | 27,7% |
| US Bancorp | USB | 10,8% | 26,1% |
| ETF S&P 500 | SPY | 15,5% | 16,8% |
| 10-Y Treasury Bonds | DGS10 | 2,1% | 0,0% |
Среднегодовая доходность
30,2%
Стандартное отклонение
28,6%
Среднегодовая доходность
18,4%
Стандартное отклонение
31,1%
Среднегодовая доходность
10,0%
Стандартное отклонение
18,3%
Среднегодовая доходность
15,0%
Стандартное отклонение
29,3%
Среднегодовая доходность
27,1%
Стандартное отклонение
27,7%
Среднегодовая доходность
10,8%
Стандартное отклонение
26,1%
Среднегодовая доходность
15,5%
Стандартное отклонение
16,8%
Среднегодовая доходность
2,1%
Стандартное отклонение
0,0%
Теперь строим карту по данным из таблицы: данные по среднегодовой доходности откладываем по вертикали, а по стандартному отклонению (риску) — по горизонтали.
Из диаграммы выше можно сделать ряд выводов относительно соотношения доходности и риска активов, определить наиболее предпочтительные и исключить наиболее убыточные из них: например, можно сделать вывод, что акции AAPL дают большую доходность, чем BAC и AXP, но при этом риск инвестирования в AAPL ниже.
Но зачастую неочевидно, какой из активов лучше, — в таком случае на помощь приходят показатели оценки соотношения риска и доходности.
Считаем индикаторы привлекательности активов
Индикаторы привлекательности активов приводят данные из таблицы выше к одному знаменателю: мы можем посчитать конкретные показатели для каждой бумаги и сравнить их. Разберем основные показатели.
Коэффициент вариации показывает величину риска, приходящуюся на единицу доходности. Он рассчитывается по следующей формуле:
CV = σ / r̄,
где σ — стандартное отклонение доходности актива,
r̄ — среднее арифметическое доходности актива.
Коэффициент вариации применяется для сравнения активов с разными доходностями и стандартными отклонениями. Применение показателя позволяет ранжировать активы по степени их рискованности. Чем больше значение показателя, тем выше риск инвестиций.
Коэффициент вариации для рассматриваемых акций
| Тикер | Среднегодовая доходность | Стандартное отклонение | Коэффициент вариации |
|---|---|---|---|
| AAPL | 30,2% | 28,6% | 0,95 |
| MCO | 27,1% | 27,7% | 1,03 |
| SPY | 15,5% | 16,8% | 1,09 |
| BAC | 18,4% | 31,1% | 1,70 |
| KO | 10,0% | 18,3% | 1,82 |
| AXP | 15,0% | 29,3% | 1,95 |
| USB | 10,8% | 26,1% | 2,40 |
Среднегодовая доходность
30,2%
Стандартное отклонение
28,6%
Коэффициент вариации
0,95
Среднегодовая доходность
27,1%
Стандартное отклонение
27,7%
Коэффициент вариации
1,03
Среднегодовая доходность
15,5%
Стандартное отклонение
16,8%
Коэффициент вариации
1,09
Среднегодовая доходность
18,4%
Стандартное отклонение
31,1%
Коэффициент вариации
1,70
Среднегодовая доходность
10,0%
Стандартное отклонение
18,3%
Коэффициент вариации
1,82
Среднегодовая доходность
15,0%
Стандартное отклонение
29,3%
Коэффициент вариации
1,95
Среднегодовая доходность
10,8%
Стандартное отклонение
26,1%
Коэффициент вариации
2,40
Можно сделать вывод относительно того, какой из активов несет больше или меньше риска. Теперь мы видим, что инвестиции в AAPL выгоднее не только инвестиций в BAC и AXP, но и вообще в любой из рассматриваемых активов: на единицу риска тут приходится наибольшая доходность. Самый рискованный актив — USB: на 1% доходности приходится 2,4% стандартного отклонения.
Коэффициент Шарпа показывает, во сколько раз избыточная доходность от инвестирования в портфель по сравнению с безрисковым активом выше уровня риска инвестиций. Избыточная доходность показывает, насколько доходность инвестиционного портфеля выше доходности безрискового актива, в роли которого чаще всего выступают государственные облигации.
Коэффициент Шарпа определяется по следующей формуле:
R̄x − R̄f / σx,
где R̄x — средняя доходность актива (среднемесячная, среднегодовая и так далее),
R̄f — средняя доходность безрискового актива за сопоставимый период,
σx — стандартное отклонение доходности актива за сопоставимый период.
Рассмотрим пример. Предположим, что средняя доходность по акции составляет 30% годовых при 20% стандартного отклонения, а средняя доходность по государственным облигациям США (безрисковый актив) равна 3% годовых. Тогда коэффициент Шарпа для нашей акции будет считаться так:
(30% − 3%) / 20% = 1,35
Это значение показателя говорит о высокой инвестиционной привлекательности нашей акции: доходность по ней выше доходности безрискового актива и превышает уровень риска.
Из формулы видно, что коэффициент Шарпа измеряет вознаграждение в виде средней избыточной доходности на единицу риска. Также следует отметить, что коэффициент был создан для анализа портфелей, а не отдельных инструментов, но все же его следует учитывать при отборе активов в портфель: он позволяет сделать вывод об эффективности вложения.
Критерии эффективности инвестиций на основе коэффициента Шарпа
| Критерий | Вывод по активу |
|---|---|
| Коэффициент Шарпа > 1 | Доходность инвестиций выше доходности безрискового актива и превышает уровень риска |
| 1 > коэффициент Шарпа > 0 | Риск инвестирования выше, чем доходность от инвестирования, — необходимо пересмотреть инвестиционное решение относительно этого актива или группы активов. Инвестирование в актив не приносит достаточной доходности |
| Коэффициент Шарпа < 0 | Доходность от инвестирования ниже доходности безрискового актива. Вероятно, лучше инвестировать в безрисковый актив |
Коэффициент Шарпа > 1
Доходность инвестиций выше доходности безрискового актива и превышает уровень риска
1 > коэффициент Шарпа > 0
Риск инвестирования выше, чем доходность от инвестирования, — необходимо пересмотреть инвестиционное решение относительно этого актива или группы активов. Инвестирование в актив не приносит достаточной доходности
Коэффициент Шарпа < 0
Доходность от инвестирования ниже доходности безрискового актива. Вероятно, лучше инвестировать в безрисковый актив
Рассмотрим результаты расчетов по коэффициенту Шарпа для акций в нашем примере.
Коэффициент Шарпа у акций из портфеля Баффетта
| AAPL | 0,98 |
| MCO | 0,90 |
| SPY | 0,79 |
| BAC | 0,52 |
| AXP | 0,44 |
| KO | 0,43 |
| USB | 0,33 |
Коэффициент информации характеризует соотношение риска-доходности актива или портфеля по сравнению с бенчмарком. Коэффициент расчетами напоминает коэффициент Шарпа, только вместо безрисковой ставки используется определенный эталон — бенчмарк. Бенчмарком могут выступать широкие рыночные индексы — MSCI, S&P 500, отраслевые индексы — DJA, собственноручно разработанные бенчмарки и так далее.
Иными словами, коэффициент информации — это отношение сверхдоходности к стандартному отклонению этой сверхдоходности у актива и бенчмарка. Коэффициент помогает понять, выгодно ли инвестировать в актив или набор активов — или проще и безопасней инвестировать в актив, выбранный бенчмарком. В нашем случае в качестве бенчмарка мы взяли ETF на S&P 500.
Формула выглядит так:
R̄x − R̄m / σx − m,
где R̄x — средняя доходность актива (среднемесячная, среднегодовая и так далее),
R̄m — средняя доходность бенчмарка за сопоставимый период,
σx − m — стандартное отклонение разности доходности актива и бенчмарка за сопоставимый период.
На примере AAPL и S&P 500 все будет выглядеть так:
В числителе: считаем разницу между средней доходностью акции AAPL (30,2% годовых) и средней доходностью индекса S&P 500 (15,5% годовых).
В знаменателе: сначала считаем разницу между дневными доходностями акции AAPL и индекса S&P 500, а потом по полученной совокупности дневных сверхдоходностей определяем стандартное отклонение и приводим дневное значение стандартного отклонения к годовому, перемножив дневное стандартное отклонение на корень из 252. Перемножаем на 252, так как в году 252 торговых дня. В нашей таблице этот расчет произведен на листе «Дневная доходность».
Итого получается:
(30,2% − 15,5%) / 21,28% = 0,69. Значение показателя выше 0,5 говорит о хорошей инвестиционной привлекательности акции.
Следует отметить, что этот коэффициент показывает эффективность активного управления, — при пассивном управлении, если мы просто покупаем индексный фонд и держим его, коэффициент будет равен нулю.
Чем больше значение коэффициента, тем выше избыточная «отдача» от инвестирования в определенный актив или портфель по сравнению с бенчмарком. Значение коэффициента информации в диапазоне от 0,5 до 0,74 считается хорошим, значение от 0,75 до 0,99 считается очень хорошим, а значение свыше 0,99 считается отличным. Ниже представлены результаты расчетов коэффициента информации для рассматриваемых акций.
Коэффициент информации у рассматриваемых акций
| AAPL | 0,69 |
| MCO | 0,63 |
| BAC | 0,13 |
| SPY | 0 |
| AXP | −0,02 |
| KO | −0,36 |
| USB | −0,26 |
Можно заметить, что для SPY (ETF на S&P 500) коэффициент информации равен нулю, так как он отражает движение рынка и не подразумевает сверхдоходности за активное управление. Напротив, хорошее значение коэффициента имеют акции AAPL и MCO, у которых на 1% стандартного отклонения сверхдоходности приходится 0,69 и 0,63% сверхдоходности соответственно. В случае с KO, AXP и USB отрицательные значения коэффициента связаны с отрицательными избыточными доходностями относительно бенчмарка.
Коэффициент Сортино — показатель, напоминающий коэффициент Шарпа, он отличается лишь расчетом риска. В коэффициенте Сортино для расчета риска учитываются только доходности актива ниже определенного уровня — чаще всего этот уровень определяется как доходность безрискового актива за сопоставимый период либо нулевая ставка.
Предполагается, что положительные отклонения доходностей — выше доходности безрискового актива — не несут риск, так как повышают доходность актива, — соответственно, учитывать их при расчете риска не нужно. Таким образом, для расчета стандартного отклонения необходимо выбрать только те дневные доходности, значение которых будет ниже доходности безрискового актива за этот же день. В нашей таблице все посчитано на листе «Кф. Сортино». Вот по какой формуле этот коэффициент рассчитывается:
R̄x − R̄f / σxd,
где R̄x — средняя доходность актива (среднемесячная, среднегодовая и так далее),
R̄f — средняя доходность безрискового актива за сопоставимый период,
σxd — стандартное отклонение доходности актива ниже заданного уровня.
Для примера рассмотрим логику, по которой фильтруются доходности для расчета риска по коэффициенту Сортино.
Месячные доходности акции и безрискового актива
| Период | Доходность акции | Доходность безрискового актива | Отфильтрованная доходность |
|---|---|---|---|
| 1 месяц | 0,16% | 0,18% | 0,16% |
| 2 месяц | −2,54% | 0,18% | −2,54% |
| 3 месяц | 0,29% | 0,18% | 0,00% |
| 4 месяц | 0,00% | 0,18% | 0,00% |
| 5 месяц | 2,24% | 0,18% | 0,00% |
| 6 месяц | −11,80% | 0,18% | −11,80% |
| 7 месяц | 14,10% | 0,18% | 0,00% |
| 8 месяц | 8,36% | 0,18% | 0,00% |
| 9 месяц | −2,14% | 0,18% | −2,14% |
| 10 месяц | 9,67% | 0,18% | 0,00% |
| 11 месяц | 7,00% | 0,18% | 0,00% |
| 12 месяц | 0,90% | 0,18% | 0,00% |
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,16%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
−2,54%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
−11,80%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
−2,14%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
В последней колонке оказались лишь те значения доходности акции, которые были ниже доходности безрискового актива за соответствующий период. Затем с помощью формулы стандартного отклонения рассчитываем риск по отфильтрованной доходности — он составит 3,54%. Среднемесячная доходность по акции — 2,19%, а среднемесячная доходность по безрисковому активу — 0,18%. Таким образом, коэффициент Сортино для акции из примера считается так:
(2,19% − 0,18%) / 3,54% = 0,57. Значение показателя ниже единицы указывает на то, что актив не обеспечивает должного уровня доходности на единицу нисходящего риска.
Чем больше значение коэффициента, тем выше вероятность безубыточности вложения и тем большей инвестиционной привлекательностью обладает рассматриваемый актив. Минимально допустимое значение показателя, определяющее инвестиционную привлекательность актива, — 1. Таким образом, на примере портфеля Баффетта допустимая и большая привлекательность у AAPL, MCO и SPY, а остальные же активы по коэффициенту Сортино непривлекательны, потому что не обеспечивают должного уровня доходности на единицу нисходящего риска.
Коэффициент Сортино у рассматриваемых акций
| AAPL | 1,59 |
| MCO | 1,40 |
| SPY | 1,19 |
| BAC | 0,86 |
| AXP | 0,73 |
| KO | 0,66 |
| USB | 0,53 |
Коэффициент Трейнора — еще один показатель, напоминающий коэффициент Шарпа и отличающийся только расчетом риска. В качестве риска берется коэффициент бета акции — он отражает волатильность актива по отношению к рынку. Коэффициент Трейнора показывает отношение сверхдоходности к рыночному риску.
Для расчета коэффициента бета акции используется следующая формула — рассчитанную бета акции можно найти на Yahoo Finance в разделе Summary на странице акции:
где σxm — ковариация между доходностью актива (портфеля) и доходностью рынка,
σm2 — дисперсия доходности рынка.
Методика расчета коэффициента бета акции раскрыта на листе «Дневная доходность» нашей таблицы, в столбце «Рыночный риск».
Коэффициент бета, находящийся в диапазоне от 0 до 1, свидетельствует о том, что акция движется в целом в одном направлении с рынком: если фондовый индекс растет, то растет и акция. Но значение коэффициента меньше 1 говорит о том, что актив менее чувствителен к движению рынка.
Коэффициент бета, равный 1, говорит о том, что движение актива полностью повторяет движение фондового индекса. Можно заметить, что значение 1 наблюдается у SPY, то есть у рыночного индекса.
Коэффициент бета больше 1 говорит о том, что динамика акции коррелирует с движением индекса, но при этом акция более чувствительно реагирует на любое движение рыночного индекса.
Коэффициент бета у рассматриваемых акций
| BAC | 1,38 |
| MCO | 1,26 |
| AXP | 1,26 |
| AAPL | 1,14 |
| SPY | 1,00 |
| USB | 1,15 |
| KO | 0,69 |
Зная коэффициент бета, доходность актива и доходность безрискового актива, мы можем рассчитать коэффициент Трейнора по следующей формуле:
R̄x − R̄f / βx,
где R̄x — средняя доходность актива (среднемесячная, среднегодовая и так далее),
R̄f — средняя доходность безрискового актива за сопоставимый период,
βx — коэффициент бета актива.
Допустим, необходимо рассчитать коэффициент Трейнора для акции USB — US Bancorp. Переходим на страницу компании на Yahoo Finance и находим Beta — 1,14 на момент написания статьи. Далее для расчета коэффициента Трейнора достаточно найти разницу между среднегодовой доходностью акции — 10,8% и среднегодовой доходностью безрискового актива — 2,1% и поделить полученное значение на бета акции.
Для акции USB:
(10,8% − 2,1%) / 1,14 = 0,076
Значение показателя выше нуля указывает на то, что инвестирование в актив более привлекательно, чем в рыночный индекс. Если коэффициент ниже нуля, то целесообразнее вкладывать в рыночный индекс, так как актив проигрывает рынку по соотношению риска и доходности. Таким образом, все акции портфеля инвестиционно привлекательны по этому показателю.
Коэффициент Трейнора у рассматриваемых акций
| AAPL | 0,24 |
| MCO | 0,20 |
| SPY | 0,13 |
| BAC | 0,12 |
| KO | 0,11 |
| AXP | 0,10 |
| USB | 0,08 |
Выводы
Теперь мы можем собрать сводную таблицу и оценить инвестиционную привлекательность активов на примере акций из портфеля Баффетта.
По данным из таблицы можно сделать вывод, что из рассмотренных активов наиболее привлекательны для инвестора Apple (AAPL), Moody’s (MCO) и SPDR S&P 500 (SPY).
Но важно помнить: кроме расчета индикаторов нужно оценивать перспективы отрасли и самой компании — и только когда картина собрана целиком, можно решать, инвестировать ли в компанию.