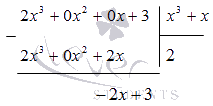Как найти коэффициент дроби

Решение уравнений с дробями

О чем эта статья:

5 класс, 6 класс, 7 класс

Понятие дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:

• обыкновенный вид — ½ или a/b,
• десятичный вид — 0,5.

Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.

Дроби бывают двух видов:

1. Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
2. Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.

Основные свойства дробей

Дробь не имеет значения, если делитель равен нулю.

Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

Дроби a/b и c/d называют равными, если a × d = b × c.

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:

• Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
• Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все его корни или убедиться, что корней нет.

Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.

Линейное уравнение выглядит так	ах + b = 0, где a и b — действительные числа. Что поможет в решении: если а не равно нулю, то у уравнения единственный корень: х = −b : а; если а равно нулю, а b не равно нулю — у уравнения нет корней; если а и b равны нулю, то корень уравнения — любое число.
Квадратное уравнение выглядит так:	ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Понятие дробного уравнения

Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:

Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.

Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:

На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.

Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.

Как решать уравнения с дробями

1. Метод пропорции

Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.

Итак, у нас есть линейное уравнение с дробями:

В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.

После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.

2. Метод избавления от дробей

Возьмем то же самое уравнение, но попробуем решить его по-другому.

В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:

• подобрать число, которое можно разделить на каждый из знаменателей без остатка;
• умножить на это число каждый член уравнения.

Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!

Вот так просто мы получили тот же ответ, что и в прошлый раз.

Что еще важно учитывать при решении

• если значение переменной обращает знаменатель в 0, значит это неверное значение;
• делить и умножать уравнение на 0 нельзя.

Универсальный алгоритм решения

Определить область допустимых значений.

Найти общий знаменатель.

Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.

Раскрыть скобки, если нужно и привести подобные слагаемые.

Решить полученное уравнение.

Сравнить полученные корни с областью допустимых значений.

Записать ответ, который прошел проверку.

Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.

Примеры решения дробных уравнений

Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.

Пример 1. Решить дробное уравнение: 1/x + 2 = 5.

1. Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
2. Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
3. Избавимся от знаменателя. Умножим каждый член уравнения на х.

Решим обычное уравнение.

Пример 2. Найти корень уравнения

1. Область допустимых значений: х ≠ −2.
2. Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
3. Избавимся от знаменателя. Умножим каждый член уравнения на х.

Переведем новый множитель в числитель..

Сократим левую часть на (х+2), а правую на 2.

Пример 3. Решить дробное уравнение:

Найти общий знаменатель:

Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:

Выполним возможные преобразования. Получилось квадратное уравнение:

Решим полученное квадратное уравнение:

Получили два возможных корня:

Если x = −3, то знаменатель равен нулю:

Если x = 3 — знаменатель тоже равен нулю.

Вывод: числа −3 и 3 не являются корнями уравнения, значит у данного уравнения нет решения.

Рациональные уравнения онлайн калькулятор

Наш калькулятор поможет вам решить рациональное уравнение или неравенство. Искусственный интеллект, который лежит в основе калькулятора, даст ответ с подробным решением и пояснениями.

Калькулятор полезен старшеклассникам при подготовке к контрольным работам и экзаменам, для проверки знаний перед ЕГЭ, родителям школьников с целью контроля решения многих задач по математике и алгебре.

Добро пожаловать на сайт Pocket Teacher

Наш искусственный интеллект решает сложные математические задания за секунды

Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!

начать

Рациональные уравнения

В рациональных уравнениях обе части уравнения представляют собой рациональные выражения вида: s(x) = 0 или расширено: s(x) = b(x), где s(x), b(x) – рациональные выражения.

Рациональное выражение является алгебраическим выражением, которое состоит из рациональных чисел и переменной величины, соединенных с помощью сложения, вычитания, умножения, деления и возведения в степень с натуральным показателем. Таким образом, это целые и дробные выражения без радикалов.

Действия с рациональными числами обладают свойствами действий с целыми числами.

К примеру, при умножении рациональных чисел есть дополнительное свойство – умножение взаимно обратных чисел. Для того чтобы умножить два рациональных числа, необходимо умножить модули этих чисел, а перед ответом поставить «плюс», если у множителей одинаковые знаки и «минус», если знаки разные.

Умножение рационального числа на ноль. Когда в рациональном уравнении хоть один множитель – ноль, то и произведение будет равняться нолю.

Умножение рациональных чисел с разными знаками. При умножении нескольких чисел с разными знаками, необходимо умножить модули каждого из этих чисел. Если количество множителей с отрицательными знаками – четное, то произведение всегда будет со знаком «плюс», если количество множителей с отрицательными знаками – нечетное, то и произведение будет со знаком «минус».

Делить на ноль в рациональных уравнениях, как и в обычных нельзя.

Чтобы решить рациональное уравнение, необходимо определить тип этого уравнения и применить некоторые математические хитрости, созданные для этого типа. Если Вы не помните этих хитростей, то можете воспользоваться калькулятором для решения рациональных уравнений, который быстро подберёт все корни данного уравнений.

Решением рационального уравнения будут являться корень – конкретное число, при постановке которого в уравнение даст верное равенство. Корней рационального уравнения может быть много и важно в решении не упустить ни один корень.

Бесплатный онлайн калькулятор

Наш бесплатный решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в калькуляторе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей группе ВКонтакте: pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

Наш искусственный интеллект решает сложные математические задания за секунды.

Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!

Разложение дроби на простейшие

Для закрепления материала будут рассмотрены несколько примеров и рассмотрена теория по разложению дробей на простейшие. Подробно рассмотрим метод неопределенных коэффициентов и метод частных значений, изучим всевозможные комбинации.

Простые дроби имеют название элементарных дробей.

Типы дробей

1. A x — a ;
2. A ( x — a ) n ;
3. M x + N x 2 + p x + q ;
4. M x + N ( x 2 + p x + q ) n .

A , M , N , a , p , q из которых являются числами, а дискриминант дробей 3 и 4 меньше нуля, то есть корней не имеет выражение.

При упрощении выражения быстрее выполняются вычислительные функции. Представление дробно-рациональной дроби как суммы простейших дробей аналогично. Для этого применяют ряды Лорана для того, чтобы разложить в степенные ряды или для поиска интегралов.

Например, если необходимо брать интеграл от дробно-рациональной функции вида ∫ 2 x 3 + 3 x 3 + x d x . После чего необходимо произвести разложение подынтегральной функции на простейшие дроби. Все это к формированию простых интегралов. Получаем, что

∫ 2 x 3 + 3 x 3 + x d x = ∫ 2 + 2 x — 3 x + 2 x 2 + 1 d x = = ∫ 2 d x + ∫ 3 x d x — ∫ 3 x + 2 x 2 + 1 d x = = 2 x + 3 ln x — 3 2 ∫ d ( x 2 + 1 ) x 2 + 1 — 2 ∫ d x x 2 + 1 = = 2 x + 3 ln x — 3 2 ln x 2 + 1 — 2 a r c tan ( x ) + C

Произвести разложение дроби вида — 2 x + 3 x 3 + x .

Когда степень числителя многочлена меньше степени многочлена в знаменателе, имеет место разложение на простейшие дроби. Иначе применяется деление для выделения целой части, после чего производят разложение дробно-рациональной функции.

Применим деление углом. Получаем, что

Отсюда следует, что дробь примет вид

2 x 3 + 3 x 3 + x = 2 + — 2 x + 3 x 3 + x

Значит, такое разложение приведет к тому, что результат будет равен — 2 x + 3 x 3 + x .

Алгоритм метода неопределенных коэффициентов

Для того, чтобы правильно произвести разложение, необходимо придерживаться нескольких пунктов:

• Произвести разложение на множители. можно применять вынесение за скобки, формулы сокращенного умножения, подбор корня. Имеющийся пример x 3 + x = x x 2 + 1 для упрощения выносят х за скобки.
• Разложение дроби на простейшие дроби с неопределенными коэффициентами.

Рассмотрим на нескольких примерах:

Когда в знаменателе имеется выражение вида ( x — a ) ( x — b ) ( x — c ) ( x — d ) , количество множителей не имеет значения, дробь можно представить в виде дроби первого типа A x — a + B x — b + C x — c + D x — d , где a , b , c и d являются числами, A , B , C и D – неопределенными коэффициентами.

Когда знаменатель имеет выражение ( x — a ) 2 ( x — b ) 4 ( x — c ) 3 , количество множителей также не имеет значения, причем саму дробь необходимо привести ко второму или первому типу вида:

A 2 x — a 2 + A 1 x — a + B 4 x — b 4 + B 3 x — b 3 + B 2 x — b 2 + B 1 x — b + + C 3 x — c 3 + C 2 x — c 2 + C 1 x — c

где имеющиеся a , b , c являются числами, а A 1 , A 2 , B 1 , B 2 , B 3 , B 4 , C 1 , C 2 , C 3 — неопределенными коэффициентами. Какова степень многочлена, такое количество слагаемых имеем.

Когда знаменатель имеет вид типа x 2 + p x + q x 2 + r x + s , тогда количество квадратичных функций значения не имеет, а дробь принимает вид третьего типа P x + Q x 2 + p x + q + R x + S x 2 + r x + s ,где имеющиеся p , q , r и s являются числами, а P , Q , R и S – определенными коэффициентами.

Когда знаменатель имеет вид x 2 + p x + q 4 x 2 + r x + s 2 , количество множителей значения не имеет также , как и их степени, дробь представляется в виде третьего и четверного типов вида

P 4 x + Q 4 ( x 2 + p x + q ) 4 + P 3 x + Q 3 ( x 2 + p x + q ) 3 + P 2 x + Q 2 ( x 2 + p x + q ) 2 + P 1 x + Q 1 x 2 + p x + q + + R 2 x + S 2 ( x 2 + r x + s ) 2 + R 1 x + S 1 x 2 + r x + s

где имеющиеся p , q , r и s являются числами, а P 1 , P 2 , P 3 , P 4 , R 1 , R 2 , S 1 , S 2 — неопределенными коэффициентами.

Когда имеется знаменатель вида ( x — a ) ( x — b ) 3 ( x 2 + p x + q ) ( x 2 + r x + s ) 2 , тогда дробь необходимо представить в виде четвертого типа

A x — a + B 3 x — b 3 + В 2 x — b 2 + В 1 x — b + + P x + Q x 2 + p x + q + R 2 x + S 2 x 2 + r x + s 2 + R 1 x + S 1 x 2 + r x + s

Рассмотрим на примере дроби. Когда дробь раскладывается в сумму третьим типом вида 2 x — 3 x 3 + x = 2 x — 3 x ( x 2 + 1 ) = A x + B x + C x 2 + 1 , где A , B и C являются неопределенными коэффициентами.

Приведение полученной суммы простейших дробей при наличии неопределенного коэффициента к общему знаменателю, применяем метода группировки при одинаковых степенях х и получаем, что

2 x — 3 x 3 + x = 2 x — 3 x ( x 2 + 1 ) = A x + B x + C x 2 + 1 = = A ( x 2 + 1 ) + ( B x + C ) x x ( x 2 + 1 ) = A x 2 + A + B x 2 + C x x ( x 2 + 1 ) = = x 2 ( A + B ) + x C + A x ( x 2 + 1 )

Когда х отличен от 0 , тогда решение сводится к приравниванию двух многочленов. Получаем 2 x — 3 = x 2 ( A + B ) + x C + A . Многочлены считаются равными тогда, когда совпадают коэффициенты при одинаковых степенях.

• Приравнивание коэффициентов с одинаковыми степенями х. Получим, что система линейных уравнений при наличии определенных коэффициентов:
  A + B = 0 C = 2 A = — 3
• Решение полученной системы при помощи любого способа для нахождения неопределенных коэффициентов: A + B = 0 C = 2 A = — 3 ⇔ A = — 3 B = 3 C = 2
• Производим запись ответа:
  2 x 3 + 3 x 3 + x = 2 — 2 x — 3 x 3 + x = 2 — 2 x — 3 x ( x 2 + 1 ) = = 2 — A x + B x + C x 2 + 1 = 2 — — 3 x + 3 x + 2 x 2 + 1 = 2 + 3 x — 3 x + 2 x 2 + 1

Необходимо постоянно выполнять проверки. Это способствует тому, что приведение к общему знаменателю получит вид

2 + 3 x — 3 x + 2 x 2 + 1 = 2 x ( x 2 + 1 ) — ( 3 x + 2 ) x x ( x 2 + 1 ) = 2 x 3 + 3 x 3 + x

Методом неопределенных коэффициентов считают метод разложения дроби на другие простейшие.

Использование метода частных значений способствует представлению линейных множителей таким образом:

x — a x — b x — c x — d .

Произвести разложение дроби 2 x 2 — x — 7 x 3 — 5 x 2 + 6 x .

По условию имеем, что степень многочлена числителя меньше степени многочлена знаменателя, тогда деление выполнять не нужно. Необходимо перейти к разложению на множители. для начала необходимо выполнить вынесение х за скобки. Получим, что

x 3 — 5 x 2 + 6 x = x ( x 2 — 5 x + 6 )

Квадратный трехчлен x 2 — 5 x + 6 имеет корни, которые находим не по дискриминанту, а по теореме Виета. Получим:

x 1 + x 2 = 5 x 1 · x 2 = 6 ⇔ x 1 = 3 x 2 = 2

Запись трехчлена может быть в виде x 2 — 5 x + 6 = ( x — 3 ) ( x — 2 ) .

Тогда изменится знаменатель: x 2 — 5 x 2 + 6 x = x ( x 2 — 5 x + 6 ) = x ( x — 3 ) ( x — 2 )

Имея такой знаменатель, дробь раскладываем на простейшие дроби с неопределенными коэффициентами. Выражение примет вид:

2 x 2 — x — 7 x 3 — 5 x 2 + 6 x = 2 x 2 — x — 7 x ( x — 3 ) ( x — 2 ) = A x + B x — 3 + C x — 2

Полученный результат необходимо приводить к общему знаменателю. Тогда получаем:

2 x 2 — x — 7 x 3 — 5 x 2 + 6 x = 2 x 2 — x — 7 x ( x — 3 ) ( x — 2 ) = A x + B x — 3 + C x — 2 = = A ( x — 3 ) ( x — 2 ) + B x ( x — 2 ) + C x ( x — 3 ) x ( x — 3 ) ( x — 2 )

После упрощения придем к неравенству вида

2 x 2 — x — 7 x ( x — 3 ) ( x — 2 ) = A ( x — 3 ) ( x — 2 ) + B x ( x — 2 ) + C x ( x — 3 ) x ( x — 3 ) ( x — 2 ) ⇒ ⇒ 2 x 2 — x — 7 = A ( x — 3 ) ( x — 2 ) + B x ( x — 2 ) + C x ( x — 3 )

Теперь переходим к нахождению неопределенных коэффициентов. Нужно подставлять полученные значения в равенство для того, чтобы знаменатель обратился в ноль, то есть значения х = 0 , х = 2 и х = 3 .

Если х = 0 , получим:

2 · 0 2 — 0 — 7 = A ( 0 — 3 ) ( 0 — 2 ) + B · 0 · ( 0 — 2 ) + C · 0 · ( 0 — 3 ) — 7 = 6 A ⇒ A = — 7 6

Если x = 2 , тогда

2 · 2 2 — 2 — 7 = A ( 2 — 3 ) ( 2 — 2 ) + B · 2 · ( 2 — 2 ) + C · 2 · ( 2 — 3 ) — 1 = — 2 C ⇒ C = 1 2

Если x = 3 , тогда

2 · 3 2 — 3 — 7 = A ( 3 — 3 ) ( 3 — 2 ) + B · 3 · ( 3 — 2 ) + C · 3 · ( 3 — 3 ) 8 = 3 B ⇒ B = 8 3

Ответ: 2 x 2 — x — 7 x 3 — 5 x 2 + 6 x = A x + B x — 3 + C x — 2 = — 7 6 · 1 x + 8 3 · 1 x — 3 + 1 2 · 1 x — 2

Метод коэффициентов и метод частных значений отличаются только способом нахождения неизвестных. Данные методы могут быть совмещены для быстрого упрощения выражения.

Произвести разложение выражения x 4 + 3 x 3 + 2 x — 11 ( x — 1 ) ( x + 1 ) ( x — 3 ) 3 на простейшие дроби.

По условию имеем, что степень числителя многочлена меньше знаменателя, значит зазложение примет вид

x 4 + 3 x 3 + 2 x — 11 ( x — 1 ) ( x + 1 ) ( x — 3 ) 3 = A x — 1 + B x + 1 + C ( x — 3 ) 3 + C ( x — 3 ) 2 + C x — 3

Производим приведение к общему знаменателю. Имеем, что

x 4 + 3 x 3 + 2 x — 11 ( x — 1 ) ( x + 1 ) ( x — 3 ) 3 = A x — 1 + B x + 1 + C ( x — 3 ) 3 + C ( x — 3 ) 2 + C x — 3 = = A ( x + 1 ) ( x — 3 ) 3 + B ( x — 1 ) ( x — 3 ) 3 ( x — 1 ) ( x + 1 ) ( x — 3 ) 3 + + C 3 ( x — 1 ) ( x + 1 ) + C 2 ( x — 1 ) ( x + 1 ) ( x — 3 ) + C 1 ( x — 1 ) ( x + 1 ) ( x — 3 ) 2 ( x — 1 ) ( x + 1 ) ( x — 3 ) 3

Приравняем числители и получим, что

x 4 + 3 x 3 + 2 x + 11 = = A ( x + 1 ) ( x — 3 ) 3 + B ( x — 1 ) ( x — 3 ) 3 + + C 3 ( x — 1 ) ( x + 1 ) + C 2 ( x — 1 ) ( x + 1 ) ( x — 3 ) + C 1 ( x — 1 ) ( x + 1 ) ( x — 3 ) 2

Из выше написанного понятно, что нули знаменателя – это х = 1 , х = — 1 и х = 3 . Тогда применим метод частных решений. Для этого подставим значения х. получим, что если х=1:

— 5 = — 16 A ⇒ A = 5 16

— 15 = 128 B ⇒ B = — 15 128

157 = 8 C 3 ⇒ C 3 = 157 8

Отсюда следует, что нужно найти значения C 1 и C 3 .

Поэтому подставим полученный значения в числитель, тогда

x 4 + 3 x 3 + 2 x — 11 = = 5 16 ( x + 1 ) ( x — 3 ) 3 — 15 128 ( x — 1 ) ( x — 3 ) 3 + 157 8 ( x — 1 ) ( x + 1 ) + + C 2 ( x — 1 ) ( x + 1 ) ( x — 3 ) + C 1 ( x — 1 ) ( x + 1 ) ( x — 3 ) 2

Раскроем скобки для того, чтобы привести подобные слагаемые с одинаковыми степенями. Придем к выражению вида

x 4 + 3 x 3 + 2 x — 11 = x 4 25 128 + C 1 + x 3 — 85 64 + C 2 — 6 C 1 + + x 2 673 32 — 3 C 2 + 8 C 1 + x 405 64 — C 2 + 6 C 1 + 3 C 2 — 9 C 1 — 3997 128

Необходимо приравнять соответствующие коэффициенты с одинаковыми степенями, тогда сможем найти искомое значение C 1 и C 3 . Теперь необходимо решить систему:

25 128 + C 1 = 1 — 85 64 + C 2 — 6 C 1 = 3 673 32 — 3 C 2 + 8 C 1 = 0 405 64 — C 2 + 6 C 1 = 2 3 C 2 — 9 C 1 — 3997 128 = 11

Первое уравнение дает возможность найти C 1 = 103 128 , а второе C 2 = 3 + 85 64 + 6 C 1 = 3 + 85 64 + 6 · 103 128 = 293 32 .

Итог решения – это искомое разложение дроби на простейшие вида:

x 4 + 3 x 3 + 2 x — 11 ( x — 1 ) ( x + 1 ) ( x — 3 ) 3 = A x — 1 + B x + 1 + C 3 x — 3 3 + C 2 x — 3 2 + C 1 x — 3 = = 5 16 1 x — 1 — 15 128 1 x + 1 + 157 8 · 1 x — 3 3 + 293 32 1 x — 3 2 + 103 128 1 x — 3

При непосредственном применении метода неопределенных коэффициентов необходимо было бы решать все пять линейных уравнений, объединенных в систему. Такой метод упрощает поиск значения переменных и дальнейшее решение в совокупности. Иногда применяется несколько методов. Это необходимо для быстрого упрощения всего выражения и поиска результата.

Для закрепления материала будут рассмотрены несколько примеров и рассмотрена теория по разложению дробей на простейшие. Подробно  рассмотрим метод неопределенных коэффициентов и метод частных значений, изучим всевозможные комбинации.

Простые дроби имеют название  элементарных дробей.

Типы дробей

Дроби различают:

1.  Ax-a;
2. A(x-a)n;
3. Mx+Nx2+px+q;
4. Mx+N(x2+px+q)n.

A, M, N, a, p, q из которых являются числами, а дискриминант дробей 3 и 4 меньше нуля, то есть корней не имеет выражение.

При упрощении выражения быстрее выполняются вычислительные функции. Представление дробно-рациональной дроби как суммы простейших дробей аналогично. Для этого применяют ряды Лорана для того, чтобы разложить в степенные ряды или для поиска интегралов.

Например, если необходимо брать интеграл от дробно-рациональной функции вида ∫2×3+3×3+xdx.  После чего необходимо произвести разложение подынтегральной функции на простейшие дроби. Все это к формированию простых интегралов. Получаем, что

∫2×3+3×3+xdx=∫2+2x-3x+2×2+1dx==∫2dx+∫3xdx-∫3x+2×2+1dx==2x+3lnx-32∫d(x2+1)x2+1-2∫dxx2+1==2x+3lnx-32lnx2+1-2arctan(x)+C

Алгоритм метода неопределенных коэффициентов

Для того, чтобы правильно произвести разложение, необходимо придерживаться нескольких пунктов:

• Произвести разложение на множители. можно применять вынесение за скобки, формулы сокращенного умножения, подбор корня. Имеющийся пример x3+x=xx2+1 для упрощения выносят х за скобки.
• Разложение дроби на простейшие дроби с неопределенными коэффициентами.

Рассмотрим на нескольких примерах:

Когда в знаменателе имеется  выражение вида (x-a)(x-b)(x-c)(x-d), количество множителей не имеет значения, дробь можно представить в виде дроби первого типа Ax-a+Bx-b+Cx-c+Dx-d, где a, b, c и d являются числами, A, B, C и D – неопределенными коэффициентами.

Когда знаменатель имеет вид типа x2+px+qx2+rx+s, тогда количество квадратичных функций значения не имеет,  а дробь принимает вид третьего типа Px+Qx2+px+q+Rx+Sx2+rx+s,где имеющиеся p, q, r и s являются числами, а P, Q, R и S – определенными коэффициентами.

Рассмотрим на примере дроби. Когда дробь раскладывается  в сумму третьим типом вида 2x-3×3+x=2x-3x(x2+1)=Ax+Bx+Cx2+1, где A, B и C являются неопределенными коэффициентами.

Приведение полученной суммы простейших дробей при наличии неопределенного коэффициента к общему знаменателю, применяем метода группировки при одинаковых степенях х и получаем, что

2x-3×3+x=2x-3x(x2+1)=Ax+Bx+Cx2+1==A(x2+1)+(Bx+C)xx(x2+1)=Ax2+A+Bx2+Cxx(x2+1)==x2(A+B)+xC+Ax(x2+1)

Когда х отличен от 0, тогда решение сводится к приравниванию двух многочленов. Получаем 2x-3=x2(A+B)+xC+A. Многочлены считаются равными тогда, когда совпадают коэффициенты при одинаковых степенях.

• Приравнивание коэффициентов с одинаковыми степенями х. Получим, что система линейных уравнений при наличии определенных коэффициентов:
  A+B=0C=2A=-3
• Решение полученной системы при помощи любого способа для нахождения неопределенных коэффициентов: A+B=0C=2A=-3⇔A=-3B=3C=2
• Производим запись ответа:
  2×3+3×3+x=2-2x-3×3+x=2-2x-3x(x2+1)==2-Ax+Bx+Cx2+1=2–3x+3x+2×2+1=2+3x-3x+2×2+1

Необходимо постоянно выполнять проверки. Это способствует тому, что приведение к общему знаменателю получит вид

2+3x-3x+2×2+1=2x(x2+1)-(3x+2)xx(x2+1)=2×3+3×3+x

Методом неопределенных коэффициентов считают метод разложения дроби на другие простейшие.

Использование метода частных значений способствует представлению линейных множителей таким образом:

x-ax-bx-cx-d.

Метод коэффициентов и метод частных значений  отличаются только способом нахождения неизвестных. Данные методы могут быть совмещены для быстрого упрощения выражения.

Простейшие дроби

Среди огромного разнообразия алгебраических дробей можно выделить те, что «попроще», например $frac{1}{x}$ или $frac{3}{x-4}$. У данных дробей знаменатель можно записать в виде (x-a); в первом случае a = 0, во втором a = 4.

Также, не слишком «сложными» кажутся дроби $frac{5}{(x-3)}^2$ или $frac{7}{(x+5)}^6$ . У этих дробей знаменатель вида $(x-a)^n$.

Если рассматривать знаменатели в виде квадратного трёхчлена $x^2+px+q$, то их либо можно разложить на множители, либо нельзя. Например:

$x^2+7x-30 = (x+10)(x-3)$ – на множители раскладывается.

$x^2+7x+30$ – не раскладывается.

Обобщая, получаем следующее определение:

Примеры простейших дробей:

$$ frac{2}{x+4}, frac{3}{(x-15)^2}, frac{2x+7}{x^2+3x+5}, frac{4x-1}{(x^2+4)^2} $$

Оказывается, что:

Любая рациональная алгебраическая дробь может быть разложена на сумму простейших дробей, и притом единственным способом.

Алгоритм разложения дроби на сумму простейших дробей

Из определения получается, что дробь $frac{4x+1}{x^2+7x-30} = frac{4x+1}{(x+10)(x-3)}$ – не является простейшей.

Попробуем её разложить на две простейшие дроби следующим образом:

$$ frac{4x+1}{(x+10)(x-3)} = frac{A}{x+10} + frac{B}{x-3} $$

$$ frac{4x+1}{(x+10)(x-3)} = frac{A(x-3)+B(x+10)}{(x+10)(x-3)} $$

Дроби равны, знаменатели равны, значит, должны быть равны и числители:

4x+ 1 = A(x-3)+B(x+10) = (A+B)x+ (-3A+10B)

Теперь используем важнейшее свойство многочленов:

У равных многочленов коэффициенты при соответствующих степенях переменной равны.

Собираем коэффициенты:

$$ x^1 | 4 = A+B $$

$$x^0 | 1 = -3A+10B $$

Это система двух линейных уравнений с двумя неизвестными (см. §43 справочника для 7 класса)

$$ {left{ begin{array}{c} A+B = 4 | times 3 \ -3A+10B = 1 end{array} right.} Rightarrow {left{ begin{array}{c} 3A+3B = 12 \ -3A+10B = 1 end{array} right.} Rightarrow {left{ begin{array}{c} A = 4-B \ 13B = 13 end{array} right.} Rightarrow {left{ begin{array}{c} A = 3 \ B = 1 end{array} right.} $$

Получаем представление дроби в виде суммы простейших дробей:

$$ frac{4x+1}{x^2+7x-30} = frac{3}{x+10}+ frac{1}{x-3}$$

Этот способ разложения был предложен в 17 веке Декартом и получил название «метода неопределённых коэффициентов».

Алгоритм метода неопределённых коэффициентов

Примеры

Пример 1. Разложите на простейшие дроби:

а) $$ frac{2x-7}{x^2+5x+6} $$

Раскладываем знаменатель на множители:$ x^2+5x+6 = (x+2)(x+3)$

Записываем разложение с неопределенными коэффициентами:

$$ frac{2x-7}{x^2+5x+6} = frac{A}{x+2} + frac{B}{x+3}$$

$$ frac{2x-7}{x^2+5x+6} = frac{A(x+3)+B(x+2)}{(x+2)(x+3)} $$

$$ 2x-7 = (A+B)x+(3A+2B) $$

Приравниваем коэффициенты при одинаковых степенях x:

$$ {left{ begin{array}{c} A+B = 2 |times 2 \ 3A+2B = -7 end{array} right.} Rightarrow {left{ begin{array}{c} 2A+2B = 4 \ 3A+2B = -7 end{array} right.} Rightarrow {left{ begin{array}{c} A = -11 \ B = 2-A = 13 end{array} right.} $$

Получаем:

$$ frac{2x-7}{x^2+5x+6} = -frac{11}{x+2} + frac{13}{x+3} $$

б) $$ frac{4x+3}{x^2-1} $$

Раскладываем знаменатель на множители: $x^2-1 = (x-1)(x+1)$

Записываем разложение с неопределенными коэффициентами:

$$ frac{4x+3}{x^2-1} = frac{A}{x-1} + frac{B}{x+1} $$

4x+3 = A(x+1)+B(x-1)

4x+3 = (A+B)x+(A-B)

$$ {left{ begin{array}{c} A+B = 4 \ A-B = 3 end{array} right.} Rightarrow {left{ begin{array}{c} 2A = 7 \ 2B = 1 end{array} right.} Rightarrow {left{ begin{array}{c} A = 3 \ B = 0,5 end{array} right.} $$

Получаем:

$$ frac{4x+3}{x^2-1} = frac{3,5}{x-1} + frac{0,5}{x+1} $$

в) $$ frac{x+15}{x^2-25} $$

Раскладываем знаменатель на множители: $x^2-25 = (x-5)(x+5)$

Записываем разложение с неопределенными коэффициентами:

$$ frac{x+15}{x^2-25} = frac{A}{x-5} + frac{B}{x+5} $$

x+15 = A(x+5)+B(x-5)

x+15 = (A+B)x+(5A-5B)

$$ {left{ begin{array}{c} A+B = 1 | times 5 \ 5A+5B = 5 end{array} right.} Rightarrow {left{ begin{array}{c} 5A+5B = 5 \ 5A-5B = 5end{array} right.} Rightarrow {left{ begin{array}{c} 10A = 20 \ B = 1-A end{array} right.} Rightarrow {left{ begin{array}{c} A = 2 \ B = -1 end{array} right.} $$

Получаем:

$$ frac{x+15}{x^2-25} = frac{2}{x-5} – frac{1}{x+5} $$

г) $$ frac{3x+8}{9x^2-4} $$

Раскладываем знаменатель на множители:$ 9x^2-4 = (3x-2)(3x+2)$

Записываем разложение с неопределенными коэффициентами:

$$ frac{3x+8}{9x^2-4} = frac{A}{3x-2} + frac{B}{3x+2} $$

3x+8 = A(3x+2)+B(3x-2)

3x+8 = (3A+3B)x+(2A-2B)

$$ {left{ begin{array}{c} 3A+3B = 3 \ 2A-2B = 8 end{array} right.} Rightarrow {left{ begin{array}{c} A+B = 1 \ A-B = 4 end{array} right.} Rightarrow {left{ begin{array}{c} 2A = 5 \ 2B = -3 end{array} right.} Rightarrow {left{ begin{array}{c} A = 2,5 \ B = -1,5 end{array} right.} $$

Получаем:

$$ frac{3x+8}{9x^2-4} = frac{2,5}{3x-2} – frac{1,5}{3x+2} $$

Пример 2*. Разложите на простейшие дроби:

а) $ frac{7x+18}{x^3+6x^2+9x}$

$$ frac{7x+18}{x^3+6x^2+9x} = frac{7x+18}{x(x^2+6x+9)} = frac{7x+18}{x(x+3)^2} = frac{A^{/×2(x+3)}}{x} + frac{B^{/×x(x+3)}}{x+3} + frac{C^{/×x}}{(x+3)^2} $$

$$ 7x-11 = A(x+3)^2+Bx(x+3)+Cx = $$

$$ = A(x^2+6x+9)+B(x^2+3x)+Cx = (A+B) x^2+(6A+3B+C)x+9A $$

$$ {left{ begin{array}{c} A+B = 0 \ 6A+3B+C = 7 \ 9A = 18 end{array} right.} Rightarrow {left{ begin{array}{c} A = 2 \ B = -2 \ C = 7-6A-3B = 7-12+6 = 1 end{array} right.} $$

Получаем:

$$ frac{7x+18}{x^3+6x^2+9x} = frac{2}{x} – frac{2}{x+3} + frac{1}{(x+3)^2} $$

б) $ frac{8x^3+3x^2-4}{x^4-16}$

$$ frac{8x^3+3x^2-4}{x^4-16} = frac{8x^3+3x^2-4}{(x^2-4)(x^2+4)} = frac{8x^3+3x^2-4}{(x-2)(x+2)(x^2+4)} = $$

$$ = frac{A^{/×(x+2)(x^2+4)}}{x-2} + frac{B^{/×(x-2)(x^2+4)}}{x+2} + frac{Cx+D^{/×(x^2-4)}}{x^2+4} $$

$$ 8x^3+3x^2-4 = A(x+2)(x^2+4)+B(x-2)(x^2+4)+(Cx+D)(x^2-4) = $$

$$ = A(x^3+2x^2+4x+8)+B(x^3+2x^2+4x-8)+C(x^3-4x)+D(x^2-4) = $$

$$ = (A+B+C) x^3+(2A+2B+D) x^2+(4A+4B-4C)x+(8A-8B-4D) $$

$$ {left{ begin{array}{c} A+B+C = 8 \ 2A+2B+D = 3 \ 4A+4B-4C = 0 \ 8A-8B-4D = -4 end{array} right.} Rightarrow {left{ begin{array}{c} A+B+C = 8 \ 2A+2B+D = 3 \ A+B-C = 0 \ 2A-2B-D = -1 end{array} right.} Rightarrow {left{ begin{array}{c} 2(A+B) = 8 \ 2C = 8 \ 4A = 2 \ 4B+2D = 4 end{array} right.} Rightarrow $$

$$ Rightarrow {left{ begin{array}{c} A = 0,5 \ B = 4-A = 3,5 \ C = 4 \ D = 2-2B = -5 end{array} right.} $$

Получаем:

$$ frac{8x^3+3x^2-4}{x^4-16} = frac{0,5}{x-2} + frac{3,5}{x+2} + frac{4x-5}{x^2+4} $$

Разложение рациональной дроби на простейшие ― представление рациональной дроби в виде суммы многочлена и простейших дробей. Разложение на простейшие используется во многих задачах, например для интегрирования^[1], разложения в ряд Лорана^[2], расчёта обратного преобразования Лапласа рациональных функций^[3].

Определение[править | править код]

Рациональная дробь называется простейшей если её знаменатель представляет собой степень некоторого неприводимого многочлена и степень её числителя меньше степени этого неприводимого многочлена.^[4]

Представление дроби в виде , где ― многочлен, а дроби ― простейшие, называется разложением дроби на простейшие.

Такое представление существует для любой рациональной дроби над полем и единственно с точностью до перестановки слагаемых.

Способы разложения[править | править код]

Выделение целой части[править | править код]

Любую рациональную дробь над полем можно единственным образом представить в виде суммы многочлена (называемого целой частью дроби) и правильной дроби (называемой дробной частью).^[5] В свою очередь любая правильная дробь раскладывается в сумму одних только простейших дробей без слагаемого многочлена. Таким образом, задача разложения дроби на простейшие может быть решена в два этапа: сначала разложить в сумму целой и дробной части (эта процедура называется выделением целой части), а зачем разложить дробную часть в сумму простейших.

Выделение целой части происходит с помощью деления многочлена в числителе на многочлен в знаменателе в столбик. Полученное в результате неполное частное ― это целая часть, а остаток делённый на делимое ― дробная.

Алгоритм деления в столбик на каждой итерации получает новое значение остатка и частного. Перед началом положим значение остатка равным делимому, а значение частного равным 0.

1. Если степень остатка меньше степени делителя, то алгоритм завершается.
2. Пусть ― член остатка со старшей степенью, ― член делителя со старшей степенью. Тогда к частному прибавляем , а из остатка вычитаем и переходим к шагу 1.^[6]

Таким образом в конце мы получим неполное частное и остаток . В итоге , где ― правильная дробь, раскладывающаяся в сумму простейших дробей. Задача свелась к разложению в сумму простейших правильной дроби.

Несмотря на то, что большинство методов разложения правильной дроби на простейшие могут быть применены и к неправильной, все эти методы существенно сложнее деления многочленов в столбик. Предварительное нахождение коэффициентов целой части делением в столбик уменьшает количество коэффициентов, которые придётся искать «сложными» методами, тем самым упрощая вычисления.

Метод неопределённых коэффициентов[править | править код]

Метод неопределённых коэффициентов состоит в том, чтобы записать разложение на простейшие с неизвестными коэффициентами, составить систему уравнений на эти коэффициенты и решить ее. Пусть ― правильная дробь в несократимой записи, ― разложение знаменателя на неприводимые множители. Тогда разложение на простейшие имеет вид .
Умножим обе части равенства на . Получим равенство многочленов .
Многочлены равны тогда, когда их коэффициенты при одинаковых степенях равны. Приравняв их получим систему линейных алгебраических уравнений над с уравнениями и неизвестными. Решив её, получим искомые значения .^[7]

Получающиеся таким способом уравнения часто довольно громоздки. Поэтому на практике подстановкой стараются получить более простые уравнения. Общая схема этого приёма такова: равенство умножают на некоторый многочлен, а затем подставляют в него вместо x какое-то определённое значение.
Чаще всего умножают на и подставляют его корень. Таким образом, почти все слагаемые зануляются и получается довольно простое уравнение, позволяющее почти сразу вычислить один из коэффициентов. Этот приём позволяет находить коэффициенты при старших степенях линейных множителей.^[8]
В качестве подставляемого корня можно даже использовать корень не принадлежащий основному полю. Например, в действительных числах часто используют подстановку комплексного корня, а затем приравнивают действительную и мнимую часть уравнения. Аналогично можно сделать и над произвольным полем. Впрочем, это приравнивание не обязательно, недостающие уравнения можно получить и другими способами.
Также иногда используют подстановку бесконечности: умножают на один из линейных многочленов, входящих в разложение , и подставляют бесконечность (тут правильность дроби становится существенна). Данный приём позволяет просто находить коэффициенты при первой степени линейных множителей.^[9]
В общем преобразование уравнения и последующая подстановка может быть какой угодно, важно лишь то, чтобы эта подстановка имела смысл и не превращала слагаемые в бесконечности. Например при подстановке корня знаменателя нужно предварительно умножить уравнение на многочлен, избавляющий от деления на 0, а при подстановке бесконечности смотреть, чтобы нигде не получилось целое слагаемое, содержащее .

Решение системы линейных алгебраических уравнений довольно трудоёмкий процесс, из-за чего на практике используют менее универсальные, но более простые методы.

Метод прикрытия Хевисайда[править | править код]

Метод Хевисайда состоит в прямом вычислении коэффициентов с помощью следующей формулы. Пусть в разложении на неприводимые множители есть линейный множитель , ― его кратность. В разложении на простейшие содержатся слагаемые вида , где . Тогда

― формула Хевисайда^[10]

Формула Хевисайда позволяет без каких-либо затруднений сразу же получить большую часть коэффициентов, из-за чего она очень широко применяется на практике. В случае если знаменатель дроби раскладывается на линейные множители, методом Хэвисайда можно получить всё разложение сразу. Если же нет, то вычисление оставшихся коэффициентов требует использования иных методов, например метода неопределённых коэффициентов.

Метод Лагранжа[править | править код]

Метод Лагранжа предлагает другую формулу для вычисления коэффициентов. Пусть ― корень знаменателя кратности 1. Тогда коэффициент при равен

― формула Лагранжа. ^[11]

Аналогично методу Хевисайда метод Лагранжа позволяет сразу найти разложение на простейшие в случае если знаменатель раскладывается на линейные множители.

Обобщение формулы Лагранжа[править | править код]

Формулу Лагранжа можно обобщить для корня кратности :

, где ― коэффициент при .^[12]

Таким образом, любой коэффициент, который может быть найден с помощью этой формулы, может быть найден с помощью формулы Хевисайда, и наоборот.

Вынесение повторяющихся множителей[править | править код]

Один из способов нахождения остальных коэффициентов без применения метода неопределённых коэффициентов ― вынесение повторяющихся множителей.^[13] Рассмотрим его на примере.

Пусть нужно разложить дробь . Вынесем повторяющиеся множители.
. Правый множитель состоит только из линейных множителей, а значит, его можно разложить по методу Хэвисайда или Лагранжа. Разложим.
. Раскроем скобки.
. Разложение правой дроби на простейшие мы уже знаем.
― искомое разложение.

Рекурсивный метод[править | править код]

Метод заключается в том, чтобы найти все старшие простейшие слагаемые со старшей степенью при помощи метода Хевисайда (или обобщённого Лагранжа), затем вычесть из первоначальной дроби и повторить эту процедуру для получившейся дроби.^[14]

Пусть нужно разложить дробь . Найдём старшие простейшие слагаемые:
. Вычтем их из первоначальной дроби.
. Полученная дробь это сумма оставшихся простейших дробей, а значит эти оставшиеся дроби есть ни что иное как разложение полученной дроби на простейшие. Вновь находим старшие простейшие слагаемые.
. Вычитаем.
. Получилась правильная дробь, а значит все слагаемые разложения найдены.
.

Наибольшую сложность в этом методе представляет вычитание дробей с последующим её сокращением. Для упрощения этого шага выполняют следующий приём.

Пусть нужно найти .
Знаменатель дроби нам и так известен: это , поделенный на произведение (без учёта кратности). Поэтому задача состоит в том, чтобы найти . Для этого умножим всё равенство на . Получим, что равен сумме дробей. Но, так как сумма правильных дробей вновь правильная дробь, сумма дробных частей этих дробей будет равна 0, а сам многочлен будет равен сумме целых частей. Таким образом, достаточно найти лишь неполное частное от деления этих дробей, а на остатки не обращать внимания. С данной модификацией этот метод называется методом отбрасывания остатков.^[15]

Рассмотрим на примере сверху.
. Умножим на
. Первое слагаемое правильное, значит его можно отбросить. Считаем целую часть второго слагаемого. Поделим на в столбик. Получим . Аналогично целая часть последнего слагаемого ― −1. Складываем их и получаем искомый многочлен ― .

Простые преобразования[править | править код]

Иногда разложение на простейшие можно получить просто преобразовывая выражения.^[16]

Метод вычетов[править | править код]

Формула Хевисайда может быть обобщена для произвольного коэффициента.

Пусть в разложении на неприводимые множители есть линейный множитель , ― его кратность. В разложении на простейшие содержатся слагаемые вида , где . Тогда:

^[12]

Для множителей высокой кратности данная формула требует подсчёта производной рациональной дроби высокого порядка, что является достаточно трудоёмкой операцией.

Коэффициенты у многочленов старших степеней[править | править код]

Если в знаменателе простейшей дроби стоит неприводимый многочлен выше первой степени, то для нахождения её числителя из всех перечисленных методов можно использовать только метод неопределённых коэффициентов. Однако этой проблемы можно избежать, если найти разложение на простейшие в алгебраическом замыкании поля (или, точнее, в любом расширении, содержащим поле разложения знаменателя), а затем сложить слагаемые с сопряжёнными знаменателями. Такой способ очень часто используется для нахождения разложения на простейшие над полем действительных чисел.^[17]

Рассмотрим пример. Пусть нужно найти разложение
. Перейдём в поле комплексных чисел и разложим знаменатель на линейные множители.
. Воспользуемся методом Хэвисайда.
. Теперь сложим дроби с сопряжёнными знаменателями.
― искомое разложение.

Комбинации методов[править | править код]

Приведённые методы дают способы вычисления отдельных коэффициентов, однако они не требуют вычисления остальных именно этим методом. Таким образом, можно как угодно комбинировать эти методы: один коэффициент посчитать методом Хевисайда, другой методом Лагранжа, а оставшиеся методом неопределённых коэффициентов, который уже будет значительно проще, чем если бы все коэффициенты были неизвестны. Использование в нужных случаях подходящих методов даст возможность просто и эффективно находить разложение.

Вариации и обобщения[править | править код]

В евклидовом кольце[править | править код]

Понятие простейшей дроби можно очевидным образом обобщить для поля частных евклидова кольца. Назовём правильной дробью дробь, если евклидова норма её числителя меньше евклидовой нормы её знаменателя. Правильную дробь назовём простейшей, если в её знаменателе стоит неприводимый элемент в некоторой степени. Тогда разложение дроби на простейшие определяется как представление в виде суммы некоторого элемента из евклидова кольца и простейших дробей.

Для любой дроби из поля частных евклидова кольца существует разложение на простейшие, однако не для любого евклидова кольца оно всегда будет единственным.^[18] Например над целыми числами с дроби могут иметь несколько разложений: (здесь евклидова норма ― модуль целого числа, ― простейшая дробь, поэтому она является разложением на простейшие самой себя, но при этом мы смогли получить ещё одно разложение).

Разложение на простейшие единственно для всех элементов поля частных евклидова кольца тогда и только тогда, когда это кольцо либо поле, либо изоморфно кольцу многочленов над полем (при этом евклидова норма эквивалентна степени многочлена).^[19].

В целых числах[править | править код]

Для целых чисел можно рассмотреть альтернативное определение разложения на простейшие. Потребуем, чтобы все простейшие слагаемые были положительными. Тогда для любого рационального числа существует и единственно разложение на простейшие.^[20]

Например, ― единственное разложение на простейшие с положительными простейшими слагаемыми. Если разрешить отрицательные простейшие слагаемые, то, как уже было показано выше, разложение перестанет быть единственным.

См. также[править | править код]

• Разложение дробей при интегрировании
• Метод неопределённых коэффициентов
• Ряд Лорана

Примечания[править | править код]

Литература[править | править код]

• Зорич В. А. Математический анализ. Часть 1. — 10-е изд. — М.: МЦНМО, 2019. — 564 p.
• Краснов М. Л., Киселёв А. И., Макаренко Г. И. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. — М.: Наука, 1971. — 256 p.
• Фаддеев Д. К. Лекции по алгебре. — М.: Наука, 1984. — 416 p.
• Bauldry W.C. Partial Fractions via Calculus (англ.) // Daniel Alpay Problems, Resources, and Issues in Mathematics Undergraduate Studies : журнал. — 2018. — 9 May (vol. 28, iss. 5). — P. 425–437. — ISSN 1051-1970. — doi:10.1080/10511970.2017.1388312.
• Gustafson G. B. Heviside’s Method (англ.) (pdf). Grant B. Gustafson at math.utah.edu (2008). Дата обращения: июль 2021.
• Brazier R. A., Boman E. C. How to Compute the Partial Fraction Decomposition Without Really Trying (англ.) // AMATYC Review : журнал. — 2007. — Vol. 21, no. 1. — P. 20–29. — ISSN 0740-8404.
• Hazra M. Decomposition of Partial Fractions Using Lagrange Method (англ.) // Research Journal Of Pure Science : журнал. — 2016. — Vol. 5, no. 2. — P. 27–32. — ISSN 2348-5361.
• Yiu-Kwong Man. An improved Heaviside approach to partial fraction expansion and its applications (англ.) // International Journal of MathematicalEducation in Science and Technology : журнал. — 2009. — 4 August (vol. 40, iss. 6). — P. 808–814. — doi:10.1080/00207390902825310.
• Bradley W. T., Cook W. J. Two Proofs of the Existence and Uniqueness of the Partial Fraction Decomposition (англ.) // International Mathematical Forum : журнал. — 2012. — Vol. 7, no. 31. — P. 1517–1535.
• Кудрявцев Л. Д. Курс математического анализа. В 3-х томах. Том 1. Дифференциальное и интегральное исчисления функций многих переменных. — М.: Дрофа, 2003. — 704 p.