
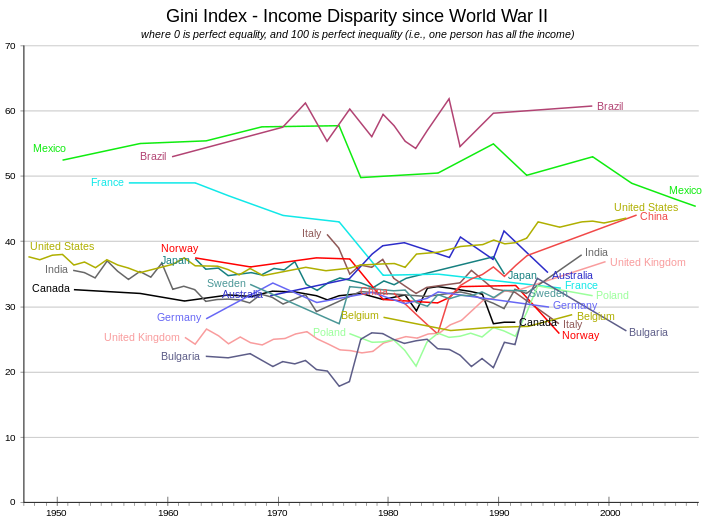
Индекс Джини по распределению национального дохода стран мира в 2018 году, согласно данным Всемирного банка[1]
Коэффициент Джини — статистический показатель степени расслоения общества данной страны или региона по какому-либо изучаемому признаку. Используется для оценки экономического неравенства.
Коэффициент Джини изменяется от 0 до 1. Чем больше его значение отклоняется от нуля и приближается к единице, тем в большей степени доходы сконцентрированы в руках отдельных групп населения.
Индекс Джини — процентное представление этого коэффициента.
Наиболее часто в современных экономических расчётах в качестве изучаемого признака берётся уровень годового дохода. Коэффициент Джини можно определить как макроэкономический показатель, характеризующий дифференциацию денежных доходов населения в виде степени отклонения фактического распределения доходов от абсолютно равного их распределения между жителями страны[2].
Иногда коэффициент Джини (как и кривую Лоренца) используют также и для выявления уровня неравенства по накопленному богатству, однако в таком случае необходимым условием становится неотрицательность чистых активов домохозяйства.
Также коэффициент Джини применяется в машинном обучении для предсказания непрерывных величин. Смысл его — погрешность должна быть настолько равномерной, насколько возможно[источник не указан 1640 дней].
История вопроса[править | править код]
Эта статистическая модель была предложена и разработана итальянским статистиком и демографом Коррадо Джини и опубликована в 1912 году в его труде «Вариативность и изменчивость признака» («Изменчивость и непостоянство»).
Расчёт[править | править код]
Рассчитать коэффициент можно как отношение площади фигуры, образованной кривой Лоренца и прямой равенства, к площади треугольника, образованного прямой равенства и осями. Иначе говоря, следует найти площадь первой фигуры и поделить её на площадь второй. В случае полного равенства коэффициент будет равен 0; в случае полного неравенства он будет равен 1.
Коэффициент Джини можно рассчитать по формуле Брауна:

или по формуле Джини:

где 






Преимущества коэффициента Джини[править | править код]
- Позволяет сравнивать распределение признака в совокупностях с различным числом единиц (например, регионы с разной численностью населения).
- Дополняет данные о ВВП и среднедушевом доходе. Служит своеобразной поправкой этих показателей.
- Может быть использован для сравнения распределения признака (дохода) между различными совокупностями (например, разными странами). При этом нет зависимости от масштаба экономики сравниваемых стран.
- Может быть использован для сравнения распределения признака (дохода) по разным группам населения (например, коэффициент Джини для сельского населения и коэффициент Джини для городского населения).
- Позволяет отслеживать динамику неравномерности распределения признака (дохода) в совокупности на разных этапах.
- Анонимность — одно из главных преимуществ коэффициента Джини. Нет необходимости знать, кто имеет какие доходы персонально.
Недостатки коэффициента Джини[править | править код]
- Довольно часто коэффициент Джини приводится без описания группировки совокупности, то есть часто отсутствует информация о том, на какие же именно квантили поделена совокупность. Так, чем на большее количество групп поделена одна и та же совокупность (больше квантилей), тем выше для неё значение коэффициента Джини.
- Коэффициент Джини не учитывает источник дохода, то есть для определённой географической единицы (страны, региона и т. п.) коэффициент Джини может быть довольно низким, но при этом какая-то часть населения свой доход обеспечивает за счёт труда, а другая — за счёт собственности. Так в Швеции значение коэффициента Джини довольно низко, но при этом только 5 % домохозяйств владеют 77 % акций от общего количества акций, которым владеют все домохозяйства. Это обеспечивает этим 5 % доход, который остальное население получает за счёт труда.
- Метод кривой Лоренца и коэффициента Джини в деле исследования неравномерности распределения доходов среди населения имеет дело только с денежными доходами, меж тем некоторым работникам заработную плату выдают в виде продуктов питания и т. п.; также широкое распространение получает практика выдачи заработной платы работникам в виде опционов на покупку акций компании-работодателя (последнее соображение несущественно, опцион сам по себе не является доходом, это только возможность получить доход, продав, например, акции, а когда акции проданы и продавец получил деньги, этот доход уже учитывается при расчёте коэффициента Джини).
- Различия в методах сбора статистических данных для вычисления коэффициента Джини приводят к затруднениям (или даже невозможности) в сопоставлении полученных коэффициентов.
- Коэффициент Джини отчасти неадекватен для плановых экономик, где распределение ресурсов зависит не только от доходов, но и от лояльности к государству (партии). Кроме того, так как частное предпринимательство запрещено в плановой экономике, выходит ситуация когда получаемые доходы фиксируются не у предпринимателей, а у государства. Из-за этого, формально выходит что доходы концентрируют предприниматели, в отличие от плановой экономики, где доходы принадлежат государству. Коэффициент Джини учитывает разницу доходов граждан, а не государства. Это приводит к значительно более положительным показателям коэффициента Джини в плановых экономиках.
Пример расчёта коэффициента Джини[править | править код]
По данным Росстата коэффициент Джини в России составлял в разные годы[4]:
| Год | 1992 | 1994 | 1996 | 1998 | 2000 | 2002 | 2004 | 2006 | 2008 | 2010 | 2012 | 2014 | 2016 | 2018 | 2019 | 2020 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Коэффициент Джини |
0,289 | 0,409 | 0,387 | 0,394 | 0,395 | 0,397 | 0,409 | 0,415 | 0,421 | 0,421 | 0,42 | 0,416 | 0,414 | 0,411 | 0,411 | 0,406[5] |
Составленный банком Credit Suisse отчёт Global Wealth Report оценивает индекс Джини в России в 2012 году в 84 % (0,84; по богатству, а не по доходам), что по мнению банка является максимальным значением среди всех крупных стран мира[6]. По мнению российских экономистов и аналитиков, опрошенных журналом «Эксперт», выводы Credit Suisse не соответствуют действительности, а «по имущественному неравенству Россия примерно соответствует таким странам как США, Япония, Индия и Китай». Приводятся и другие фактические ошибки в отчёте: «стоимость одного только жилья в России в несколько раз выше, чем цифра, которая в Global Wealth Report указана в качестве стоимости всего имущества жителей России»[7].
Согласно собственной статистике Китая в этой стране коэффициент Джини в 2012 году составил 0,474, за прошедшие 10 лет коэффициент достиг локального максимума в 2008 году, когда составлял 0,491[8]. В 2000 году этот же показатель в Китае составлял 0,41, в 1990 году — 0,33, в 1980 году — 0,31[9]. Проф. Ху Аньган в 2004 году, когда коэффициент Джини в Китае по оценке Всемирного банка составлял 0,437, в интервью отмечал: «Если учесть ещё неофициальные доходы, уклонение от налогообложения, коррупцию, то коэффициент Джини будет 0,51 и выше. Судя по официальным номинальным доходам, разрыв уже достаточно велик. За время реформ, то есть за одно поколение, Китай прошёл путь от коэффициента 0,2 до 0,5. Переход от справедливого к подчеркнуто несправедливому обществу очень заметен. Тем более что на начальном этапе реформ число бедных в большом масштабе снижалось, а со второй половины 1990-х годов эти пропорции менялись очень мало»[10].
См. также[править | править код]
- Список стран по показателям неравенства доходов
- Индекс человеческого развития
- Индекс Аткинсона
- Индекс Тейла
Примечания[править | править код]
- ↑ GINI index (World Bank estimate) | Data. data.worldbank.org. Дата обращения: 23 июля 2020. Архивировано 29 июля 2020 года.
- ↑ Гальперин В. В., Гальперин В. М. 50 лекций по микроэкономике Архивная копия от 6 апреля 2009 на Wayback Machine. — 2004. (Лекция 44 «Перераспределение дохода»)
- ↑ Под ред. С. Д. Ильенковой: Микроэкономическая статистика : Учебник . — М.: Финансы и статистика, 2004, с 544.
- ↑ Госкомстат. РАСПРЕДЕЛЕНИЕ ОБЩЕГО ОБЪЕМА ДЕНЕЖНЫХ ДОХОДОВ И ХАРАКТЕРИСТИКИ ДИФФЕРЕНЦИАЦИИ ДЕНЕЖНЫХ ДОХОДОВ НАСЕЛЕНИЯ Архивная копия от 15 ноября 2019 на Wayback Machine Примечание: оценка на основании данных выборочных обследований домашних хозяйств и макроэкономического показателя денежных доходов населения.
- ↑ Минэкономразвития России, Федеральная служба государственной статистики (РОССТАТ). Социально-экономическое положение России, 2020 год. Дата обращения: 14 февраля 2021. Архивировано 10 февраля 2021 года.
- ↑ Сергей Гуриев, Олег Цывинский. Россия – лидер по неравенству распределения богатства, Ведомости (6 ноября 2012). Архивировано 4 сентября 2014 года. Дата обращения: 23 августа 2017.
- ↑ Рейтинг со многими неизвестными. Дата обращения: 23 августа 2017. Архивировано 23 августа 2017 года.
- ↑ Рассекречены первые за 12 лет данные о социальном неравенстве КНР. Дата обращения: 26 января 2013. Архивировано 7 февраля 2013 года.
- ↑ http://www.tiger.edu.pl/publikacje/TWPNo117.pdf Архивная копия от 31 мая 2015 на Wayback Machine страница 27
- ↑ Встреча Архивировано 23 октября 2013 года.
Литература[править | править код]
- Джини коэффициент / В. Г. Минашкин // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
Экономика07 марта 2019 в 08:00126 266
Коэффициент Джини: все ли равны?
Разбираемся с показателем экономического неравенства
Индекс неравенства
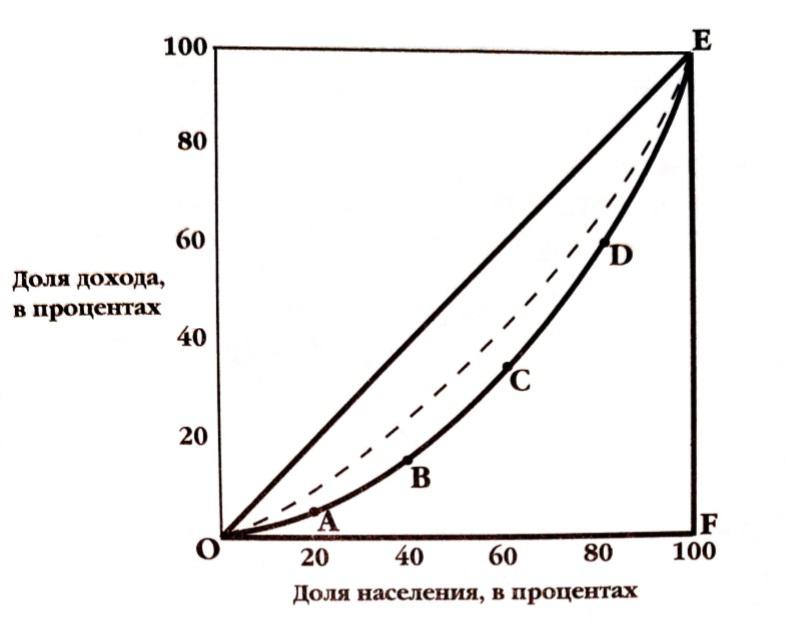
Рис 1. Кривая Лоренца
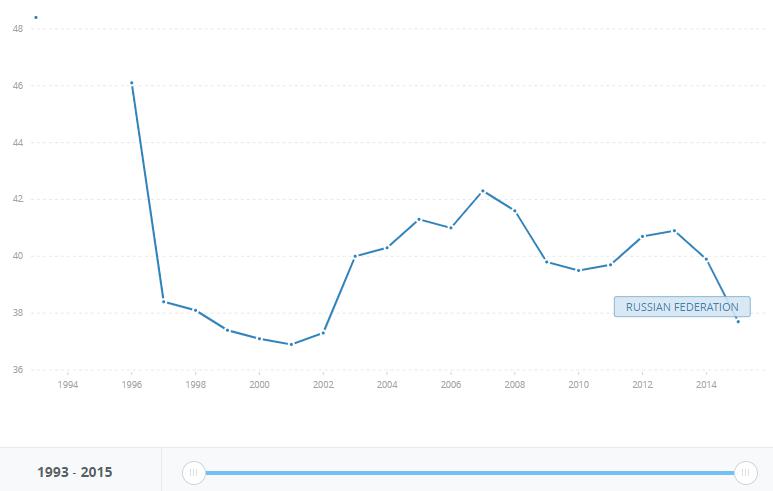
Рис. 2. Динамика коэффициента Джини, 1996-2015 года. Источник: https://data.worldbank.org/indicator/SI.POV.GINI?end=2015&locations=RU&start=1993&view=chart
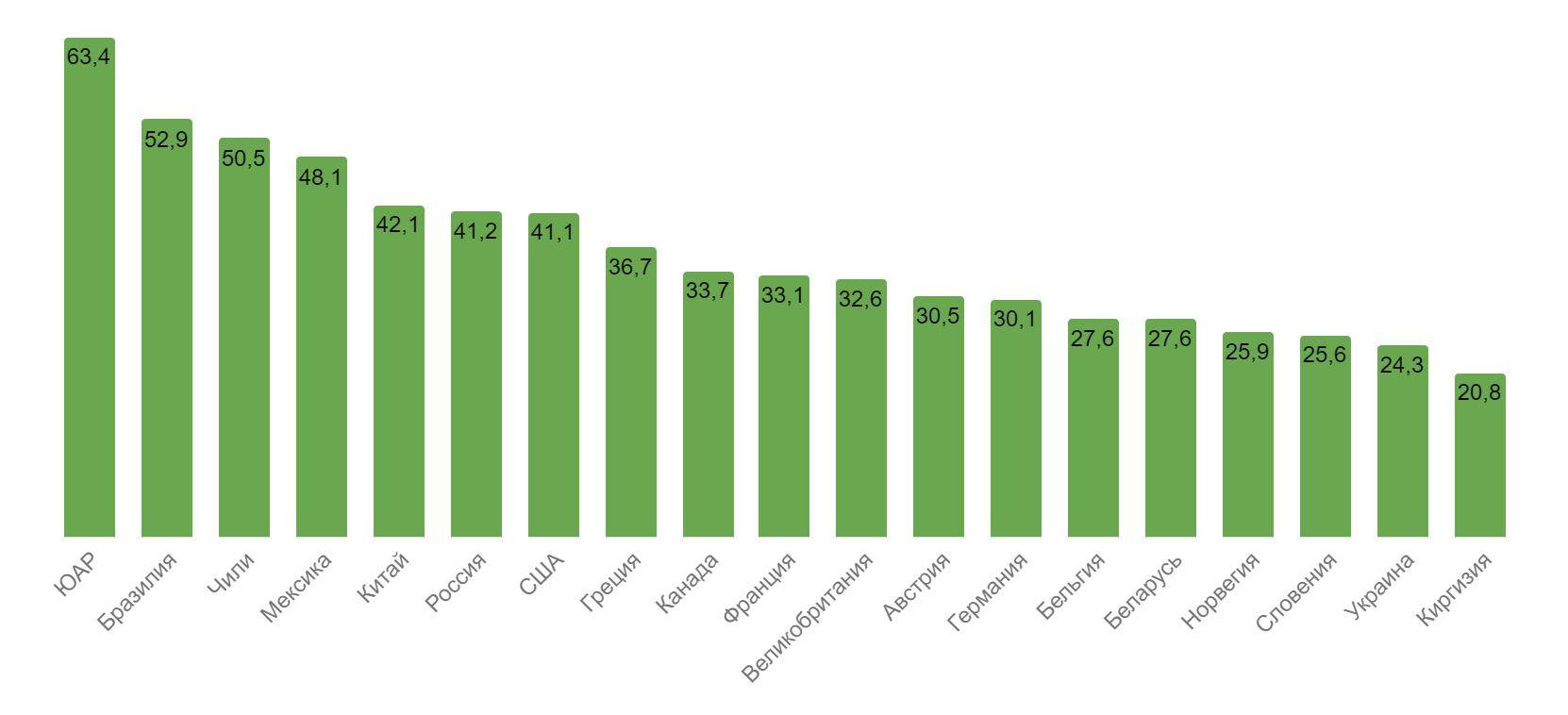
Рис. 3. Индекс Джини в странах мира (данные на 2016 год).
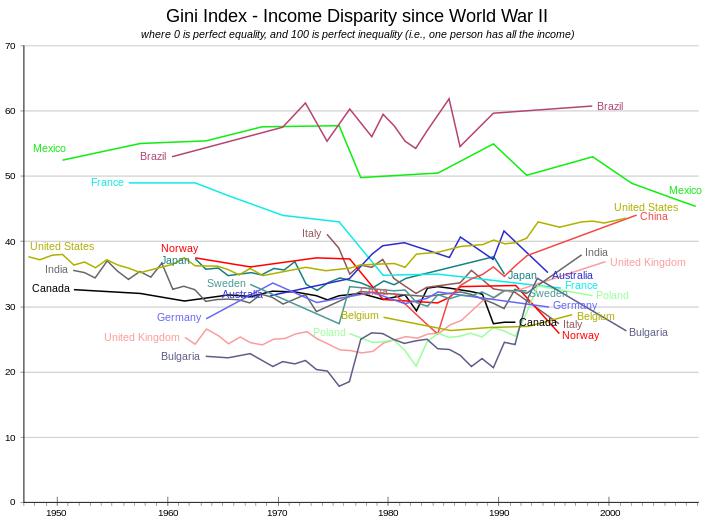
Рис. 4. Динамика индекса Джини. Источник: https://www.people.iup.edu/rhoch/ClassPages/Global_Cities/Spring17/Notes/RGPL103_ForExam1.pdf
Богатство и бедность
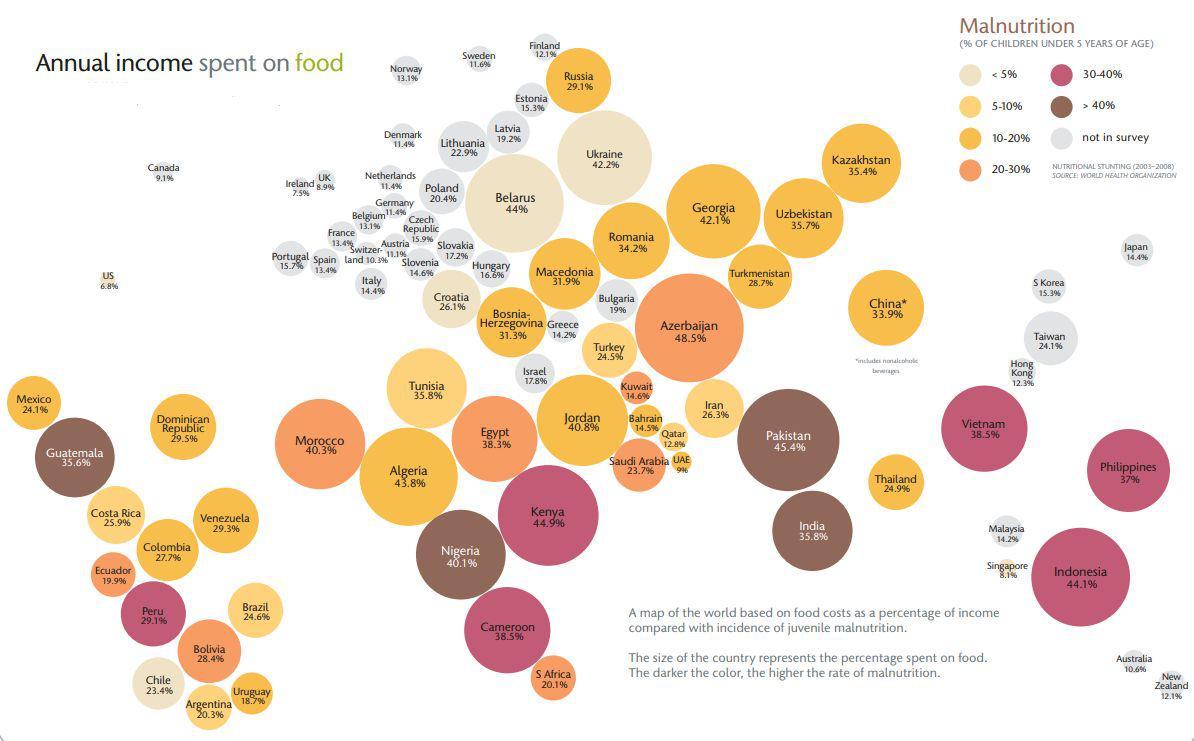
Рис. 5. Доля трат на продукты по странам мира. Источник: http://wsm.wsu.edu/researcher/WSMaug11_billions.pdf
Могу ли я изменить личную ситуацию?

Рис. 6. Количество миллиардеров по странам мира. Источник: https://howmuch.net/articles/world-map-of-billionaires-2018
Подведем итоги
Больше интересных материалов
Что такое кривая Лоренца, коэффициент Джини (индекс Джини) и как их рисовать и считать?
Начнем с кривой Лоренца.
Кривая Лоренца
Кривая Лоренца — это график, демонстрирующий степень неравенства в распределении дохода или богатства в обществе. Ее придумал в 1905 году американский статистик Макс Лоренц.
Собственно говоря, эта кривая может отражать неравенство в распределении самых разных величин, но вначале она предназначалась именно для отражения экономического неравенства в обществе.
Кривая выглядит следующим образом:
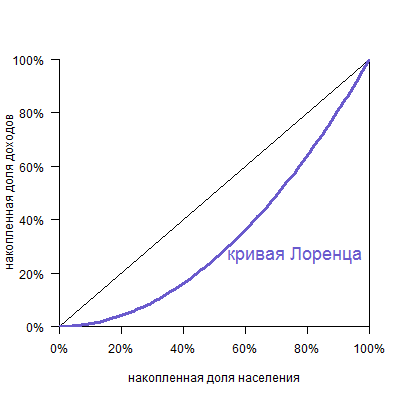
По горизонтальной оси указана накопленная доля населения (причем население отсортировано от беднейших, то есть получающих наименьший доход, до богатейших), а по вертикальной — доля получаемого дохода.
Это лучше понять на примере:
Предположим, мы разбили все население страны на 4 группы, в каждой из которых по 25% населения. При этом первая, «бедная» группа получает 10% общего дохода страны, вторая, «ниже среднего» — 20%, третья, «выше среднего» — 30% и четвертая, «богатая» — 40%.
| Группа | Доля населения | Доля от общего дохода |
| бедная | 25% | 10% |
| ниже среднего | 25% | 20% |
| выше среднего | 25% | 30% |
| богатая | 25% | 40% |
Теперь переведем это в накопленные доли: 25% населения будут получать 10%, 50% населения (это «бедная» и «ниже среднего» группы) суммарно получают 10%+20%=30%, 75% населения («бедная», «ниже среднего» и «выше среднего» группы) получат 10%+20%+30%=60% всего дохода, и, разумеется, 100% населения получат 100% дохода.
| Накопленная доля населения | Накопленная доля общего дохода |
| 25% | 10% |
| 50% | 30% |
| 75% | 60% |
| 100% | 100% |
Теперь можно построить график.
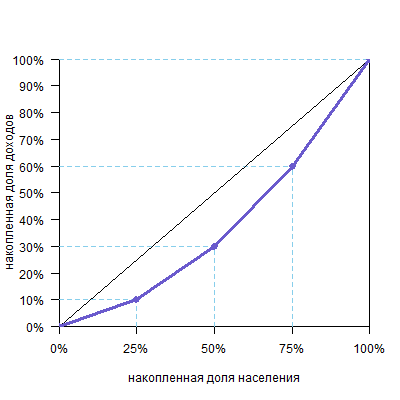
Обратите внимание, что кривая всегда исходит из точки (0%;0%) и приходит в точку (100%;100%), так как ясно, что 0% населения получают 0% дохода, а 100% населения получают 100% дохода.
Необязательно, чтобы группы были равными. Например, возьмем такие данные:
| Доля населения | Доля от общего дохода | Накопленная доля населения | Накопленная доля общего дохода |
| 20% | 10% | 20% | 10% |
| 40% | 30% | 60% | 40% |
| 30% | 30% | 90% | 70% |
| 10% | 30% | 100% | 100% |
Обратите внимание, что группы нужно распределить от бедных к богатым. Если группы одинаковые, то они сортируются просто по столбцу «Доля от общего дохода» — от маленьких значений к большим (см. прошлый пример). Но у нас группы разного размера, поэтому нужно учитывать отношение второго столбца к первому (доли дохода к доле населения). Например, у нас вторая и третья группы получают одинаковую долю дохода. Но во второй группе населения больше, а значит, в расчете на одного человека они беднее. То же с третьей и четвертой группой. Вообще говоря, случай с разными группами редкий и встречается только в условных задачах. Но если будут такие условия, то нужно делить долю дохода на долю населения. Для наших групп получим:
10%/20%=1/2
30%/40%=3/4
30%/30%=1
30%/10%=3
Это значит, что в третьей группе население получает именно средний по стране доход на человека. В первой группе доход в два раза ниже среднего, во второй — 75% от среднего, а в четвертой — три средних дохода на человека. Вот в таком порядке их и нужно расположить для построения кривой Лоренца.
Получим такой график:
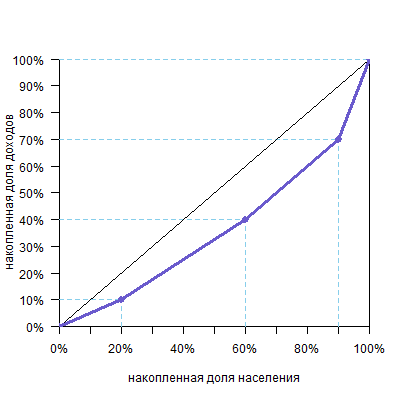
И, конечно, количество групп может быть любым. Желательно, чтобы их было побольше, тогда кривая будет построена по большему числу точек, станет более гладкой и точной.
Можно представить себе кривую абсолютно равного распределения: это будет просто диагональ, так как любые N% населения получают N% дохода:
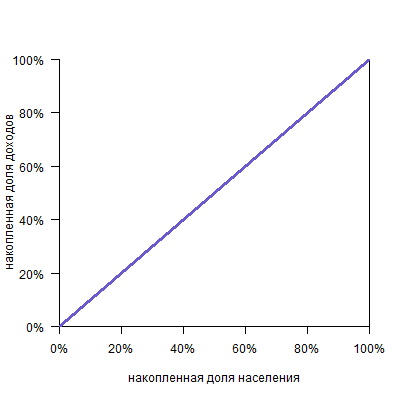
И кривую абсолютного неравенства, когда все работают бесплатно, а один-единственный человек получает весь доход:
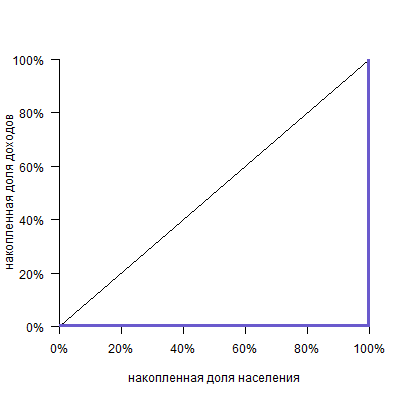
(Не думайте, что это совершенно умозрительная кривая: например, если у единственного человека в стране есть, скажем, говорящий еж, то кривая распределения говорящих ежей будет именно такой!)
А теперь:
Коэффициент Джини
К 1912 году итальянский статистик Коррадо Джини разработал алгебраическую интерпретацию кривой Лоренца: коэффициент, призванный указывать, насколько неравным является экономическое распределение.
Все очень просто. Коэффициент этот равен отношению площади фигуры между диагональю и кривой Лоренца:
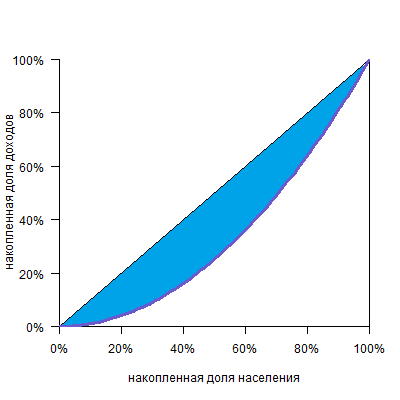
К площади треугольника под диагональю (а она всегда равна 0,5):
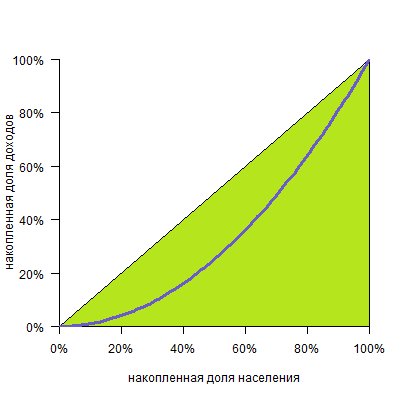
Таким образом, при полном равенстве площадь первой фигуры равна нулю, и коэффициент тоже равен нулю. При полном неравенстве эта фигура займет весь треугольник и коэффициент будет равен единице.
Чем ниже коэффициент, тем более равным является распределение.
Как его считать?
Считать коэффициент Джини можно графическим или алгебраическим способом. Посмотрим, как это можно сделать.
Графический способ
Вертикальными линиями можно разделить фигуру над кривой Лоренца на два треугольника и несколько трапеций.
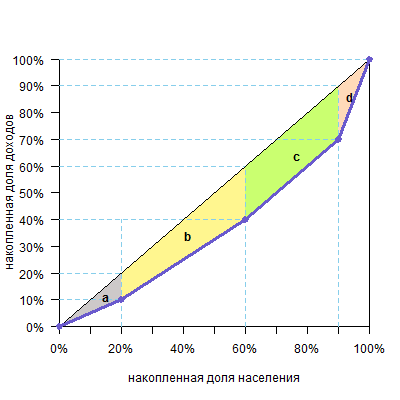
Площадь треугольника — половина основания на высоту, а трапеции — полусумма оснований на высоту (поверните голову на 90º, высоты расположены горизонтально, а основания — вертикально). Высоты равны размерам групп, а основания легко посчитать. В нашем случае площадь фигуры будет такой:
| фигура | расчет площади | площадь |
| треугольник a | 10%*20%/2=0,1*0,2/2 | 0,01 |
| трапеция b | (10%+20%)/2*40%=0,3/2*0,4 | 0,06 |
| трапеция c | (20%+20%)/2*30%=0,4/2*0,3 | 0,06 |
| треугольник d | 20%*10%/2=0,2*0,1/2 | 0,01 |
| Всего площадь фигуры (a+b+c+d) | 0,14 |
Теперь разделим ее на площадь треугольника под диагональю (а он, напоминаю, всегда равен 0,5) и получим: 0,14/0,5=0,28
Таким образом, 0,28 или 28% и есть значение коэффициента Джини.
Другой графический способ: посчитать площадь фигур под кривой Лоренца, а затем вычесть их из площади треугольника под диагональю (0,5) и получить площадь над кривой. И ее уже разделить на 0,5.
Этот случай удобнее, когда цифры не такие круглые и ширина оснований трапеций над кривой неочевидна.
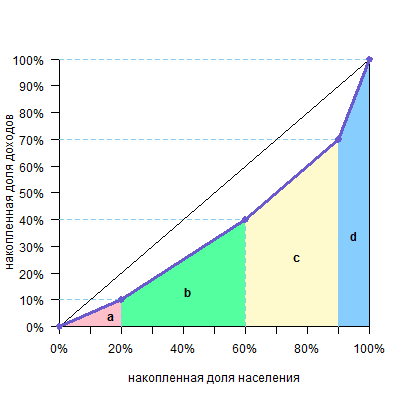
В нашем случае
| фигура | расчет площади | площадь |
| треугольник a | 10%*20%/2=0,1*0,2/2 | 0,01 |
| трапеция b | (10%+40%)/2*40%=0,5/2*0,4 | 0,1 |
| трапеция c | (40%+70%)/2*30%=1,1/2*0,3 | 0,165 |
| трапеция d | (70%+100)%/2*10%=1,7/2*0,1 | 0,085 |
| Всего площадь фигуры (a+b+c+d) | 0,36 |
Отнимаем 0,36 от 0,5 и получаем 0,14 — площадь фигуры над кривой
Далее, как и в первом способе, делим эту площадь на 0,5 (площадь треугольника под диагональю) и получаем: 0,14/0,5=0,28
Алгебраический способ
Наиболее проста в употреблении формула:[latexpage]
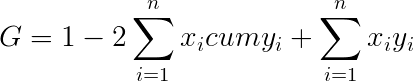
где:
$x{_{i}}$-доля i-ой группы в составе населения
$y{_{i}}$-доля i-ой группы в объеме доходов
$cum y{_{i}}$-кумулированная (накопленная) доля i-ой группы в составе населения
Составим таблицу на основе данных предыдущего примера:
| Доля населения ($x{_{i}}$) |
Доля от общего дохода ($y{_{i}}$) |
Накопленная доля общего дохода ($cum y{_{i}}$) |
$x{_{i}}y{_{i}}$ | $x{_{i}}cum y{_{i}}$ |
| 20% | 10% | 10% | 0,02 | 0,02 |
| 40% | 30% | 40% | 0,12 | 0,16 |
| 30% | 30% | 70% | 0,09 | 0,21 |
| 10% | 30% | 100% | 0,03 | 0,1 |
| Итого | 0,26 | 0,49 |
Если вы не понимаете, как построена эта таблица, откройте спойлер:
Первый и второй столбцы — это исходные данные, они такие же, как и в разделе «Графический способ».
Третий столбец получается из второго путем накопления значений из второго столбца: берем значение из ячейки слева и всех ячеек выше нее и складываем.
Четвертый столбец — произведение первого и второго.Чтобы не запутаться в процентах, переведите их в доли, например для первой строки: 20%10%=0,20,1=0,02.
Пятый столбец — произведение первого и третьего.
Далее подсчитываем суммы по четвертому и пятому столбцу.
Теперь можно подставить полученные суммы в формулу, которая приведена выше:
$G=1-2*0,49+0,26=1-0,98+0,26=0,28$
Мы получили ответ 0,28 — такой же, как и графическим методом.
Это самая простая в применении формула. Советую ее запомнить. А если вдруг хочется понять, как она выведена, откройте этот спойлер (объяснение довольно длинное!):
В основе этой формулы лежит уже известная вам идея: чтобы посчитать площадь фигуры над кривой Лоренца:
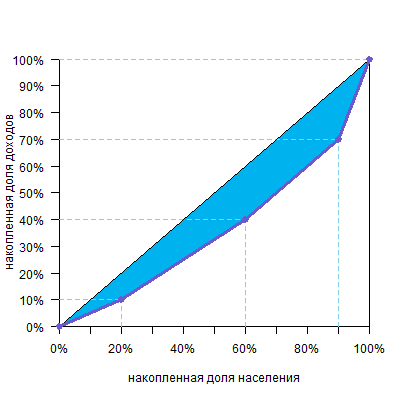
можно сперва посчитать площадь фигуры под кривой Лоренца
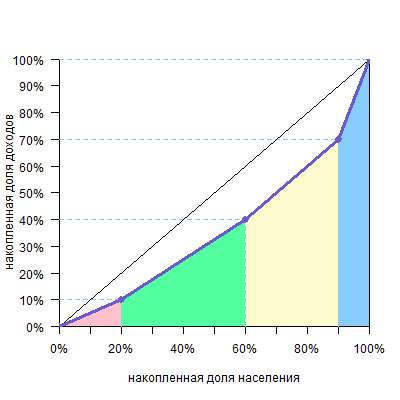
а потом вычесть ее из площади диагонального треугольника, которая равна 0,5, и получим искомое. Саму же площадь под кривой будем считать по группам. Можно видеть, что над каждой группой образуется треугольник или четырехугольник — они выделены разными цветами.
Рассмотрим, например, вторую группу (зеленый четырехугольник).
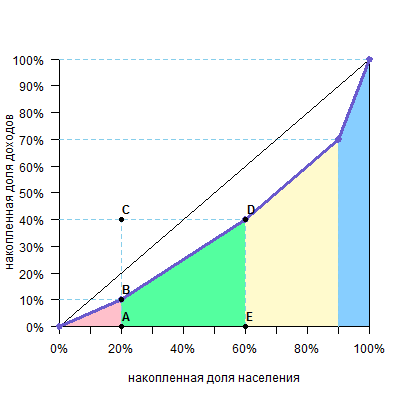
Площадь четырехугольника ABDE равна площади прямоугольника ACDE минус площадь прямоугольного треугольника BCD. При этом площадь прямоугольника ACDE равна AEDE, а площадь прямоугольного треугольника BCD равна CDBC/2. Таким образом, площадь ABDE равна
AEDE-CDBC/2
При этом можно увидеть на графике, что ВС — доля дохода по группе (y), DE — накопленная доля дохода по группе (cum y), а AE или CD — доля группы в численности населения (x). Тогда формула принимает вид
хcum y — xy/2
Можно видеть, что такая формула (прямоугольник минус прямоугольный треугольник) пригодна для всех цветных фигур, включая и левый розовый треугольник.
Тогда сумма всех фигур под кривой Лоренца будет равна
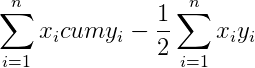
Эту сумму, как вы помните, нужно вычесть из 0,5, чтобы получить площадь фигуры над кривой
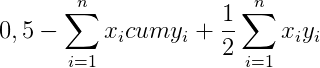
И наконец, разделив все это на площадь диагонального треугольника (то есть опять же на 0,5), получим формулу коэффициента Джини:
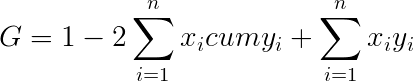
Есть и другие формулы, расчет по одной из них приведен, например, вот тут. Мне кажется, что в ней проще запутаться, а получается ровно то же самое.
Чтобы проверить себя, решите задачу. Ответ и решение под спойлерами:
Задача
Предположим, что в некоторой стране N проживают три группы населения: бедные, средний класс и богатые. Группы равны по численности жителей, но различаются по уровню дохода: средний класс зарабатывает в два раза больше, чем бедные, а богатые зарабатывают в два раза больше, чем средний класс. Внутри групп доходы распределены равномерно. Нарисуйте график кривой Лоренца и рассчитайте коэффициент Джини.
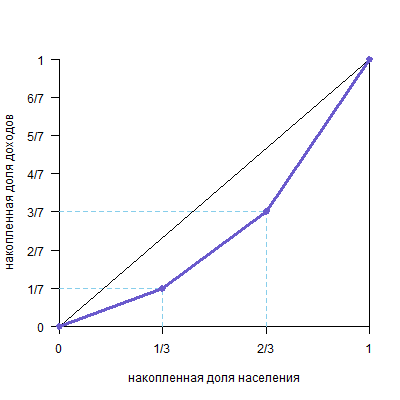
G≈0,286
Удобней считать площадь под кривой, так как цифры в натуральных дробях.
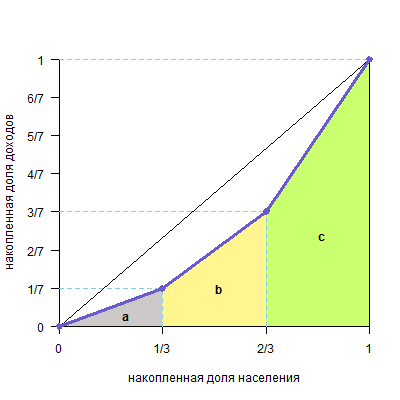
Площадь треугольника a равна (1/7*1/3)/2=1/42
Площадь трапеции b равна (1/7+3/7)/21/3=2/71/3=2/21
Площадь трапеции c равна (3/7+1)/21/3=5/71/3=5/21
Общая сумма фигур 1/42+2/21+10/21=1/42+4/42+10/42=15/42
Чтобы получить фигуру над кривой Лоренца, нужно эту сумму вычесть из 0,5
0,5-15/42=21/42-15/42=6/42=3/21
Для того, чтобы получить значение коэффициента Джини, делим это число на 0,5
3/21 / 0,5 = 6/21 ≈0,286
Поскольку средний класс зарабатывает в два раза больше, чем бедные, а богатые — в два раза больше среднего класса, то всего они зарабатывают семь долей бедного класса, то есть, соответственно, 1/7, 2/7 и 4/7, что примерно равно 0,143, 0,286 и 0,571
| Доля населения(x) | Доля от общего дохода (y) |
Накопленная доля общего дохода (cum y) |
x*y | x*cum y |
| 0,333 | 0,143 | 0,143 | 0,048 | 0,048 |
| 0,333 | 0,286 | 0,429 | 0,095 | 0,143 |
| 0,333 | 0,571 | 1,000 | 0,190 | 0,333 |
| Итого: | 0,333 | 0,524 |
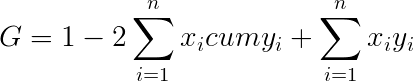
G=1-2*0,524+0.333≈0,286
На чтение 10 мин Просмотров 33.7к.
Изучая проблемы неравенства, экономисты рассчитывают коэффициент Джини. Этот показатель дает ответ на вопрос о том, как распределяются доходы среди населения.
Содержание
- Коэффициент Джини (индекс концентрации доходов, индекс неравенства)
- Как построить кривую Лоренца
- Коэффициент Джини и кривая Лоренца простыми словами
- Как рассчитать коэффициент Джини (формула)
- Индекс Джини в России
- Пример по годам
- Коэффициент Джини по странам
- Богатство и бедность
- Причины неравенства
- Уровень бедности
- Возможно ли из бедного превратится в богатого
- Преимущества коэффициента Джини
- Недостатки коэффициента Джини
- Пример расчета коэффициента Джини
Коэффициент Джини (индекс концентрации доходов, индекс неравенства)
Свое название данный коэффициент получил по инициалам демографа и статиста Корадо Джини, предложившего эту статистическую модель. Работая над трудом «Вариативность и изменчивость признака», Корадо впервые использовал этот множитель для характеристики неравенства доходов в обществе. Его труд был опубликован в 1912 г.
Таким образом, Коэффициент Джини (Gini coefficient) – это статистический показатель, который используют для оценки неравенства. Он отображает степень размежевания общества конкретной страны (либо региона) по исследуемому признаку. При расчетах в качестве такого признака принимают уровень дохода за год. Кроме этого коэффициент позволяет выяснить при определенном условии уровень неравенства по еще одному признаку – накопленному богатству.
Зачастую его рассчитывают как макроэкономический показатель, позволяющий выяснить различие в денежных доходах граждан. Здесь он показывает отклонения между фактическим и равным разделением доходов между гражданами. Его значение варьируется от 0 до 7. Принято считать, что чем ближе его значение к единице, тем более сконцентрированы доходы у отдельных групп граждан. Значение = 0 означает, что доходы сосредоточены у одного лица.
Важно! Индекс Джини – это коэффициент, выраженный в процентах. Его также называют индексом концентрации доходов либо неравенства.
Как построить кривую Лоренца
Чтобы измерить Gini coefficient, показать его функцию распределения, используют графический метод, который назевается кривой Лоренца (Lorenz curve). В экономике ее, как показатель неравенства доходов граждан, впервые ввел американец Макс Отто Лоренц (1905 г.). Чтобы ее построить, нужно выполнить действия по следующему образцу:
- Поделить данные о населении соответствующего региона (либо страны) по 20%, например, на 5 частей.
- Ось Х: обозначить поделенные 5 частей.
- Ось Y: обозначить долю дохода на каждый квинтиль (в %).
Если значение Gini coefficient = 0, тогда графическое изображение коэффициента будет построено в виде биссектрисы (ровной линии под углом 45 гр). Это – линия абсолютного равенства, которая показывает, что доходы между гражданами распределены равномерно.
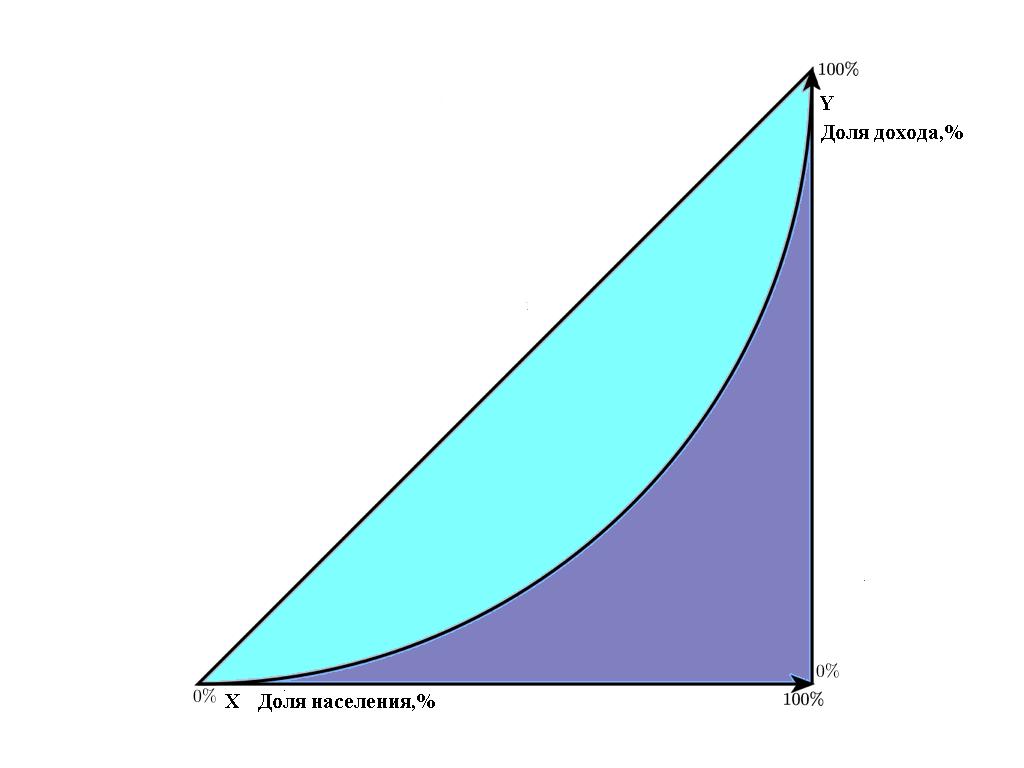
В реальности равномерное распределение доходов среди граждан невозможно. Всегда есть те, кто богаче, и те, кто беднее. Если, предположим, на 5% населения приходится около 50% доходов и больше, то кривая отклонится в сторону оси Х. Чем больше выражено неравенство, тем более дугообразной будет кривая. Государство с целью «сглаживания» неравенства разрабатывает специальные спецпрограммы и устанавливает лояльные ставки НДФЛ.
Коэффициент Джини и кривая Лоренца простыми словами
Уровень доходов у граждан отличается и это обусловлено разными факторами, например, разницей между:
- способностями, деловой активностью;
- имущественным положением;
- заработком, соцвыплатами и др.
Граждане могут получать доход от предпринимательской деятельности, собственности, ЛПХ и иных источников. Эти и иные объективные различия и приводят к тому, что доходы распределяются среди граждан неравномерно. Коэффициент Джини (Gini coefficient) и кривая Лоренца (Lorenz curve) – это показатели, при помощи которых экономисты оценивают данное распределение, дифференциацию доходов граждан.
Кривая Лоренца позволяет отобразить, передать данную функцию разделения в графическом изображении. Т. е. ее используют для того, чтобы показать в виде изображения распределение:
- доходов граждан;
- долей рынка (для компаний, применительно к отраслям);
- имуществ домашних хозяйств;
- компонентов природной среды (по государствам).
Gini coefficient характеризует распределение (концентрацию) доходов граждан. С его участием изучают степень расслоения общества конкретной страны либо региона, как правило, по уровню годового дохода. Принято считать за оптимальную норму значение, которое не больше 0,3 – 0,4. Дальнейшее повышение значения говорит о росте неравенства.
Как рассчитать коэффициент Джини (формула)
Расчет коэффициента проще всего разобрать на примере графического изображения, представленного выше. Формула для расчета геометрическим способом будет следующей: Gini coefficient = А / (А+ Б ) (1). По приведенной формуле видно, что коэффициент – соразмерная интерпретация кривой Лоренца. Рассмотрим особенности расчета по этой формуле. На рисунке 1 показаны:
- Фигура А (образована линией абсолютного равенства и кривой Лоренца).
- Фигура Б (образована той же линией равенства и осями Х, Y)
Для того, чтобы рассчитать значение Gini coefficient, нужно последовательно:
- Выяснить площадь каждой фигуры (А и Б).
- Узнать площадь всего треугольника (А + Б).
- Поделить площадь фигуры А на площадь треугольника (А + Б).
Полученный результат и есть Gini coefficient. Второй способ калькуляции, аналитический, предполагает расчет коэффициента по формуле Брауна: Gini coefficient =
Сокращения: n – число домохозяйств, Хk – кумулятивная доля населения, Yk – доля, которую получает Хk в совокупности/
Индекс Джини в России
В РФ Gini coefficient тоже рассчитывают, а результаты публикуют на сайте Росстата. На протяжении 1991 – 1999 гг. значение коэффициента варьировалось в пределах 0,26 – 0,409. Учитывая то, что определенная часть доходов не декларировалась, можно предположить, что на самом деле его значение было несколько выше. После 2000 г. его значение стало расти и ниже отметки 0,395 не опускалось. Для части населения с низким уровнем жизни это не совсем оптимистичная динамика показателя.
Пример по годам
По данным Росстата, которые представлены вплоть до 2018 г., последние значения Джини за 5 лет были следующими.
| Год | 2014 | 2015 | 2016 | 2017 | 2018 |
| Данные Росстата | 0,416 | 0,413 | 0.412 | 0,410 | 0,417 |
Коэффициент Джини по странам
Сопоставление коэффициента по данным за 2016 г. показывает, что на тот момент самое большое значение Джини было в ЮАР, Бразилии, Чили, Мексике. В пятерку стран с низким Gini coefficient входили: Киргизия, Украина, Словения, Норвегия, Беларусь. По данным Федеральной службы государственной статистики РФ в 2016 г. Gini coefficient по странам был следующим.
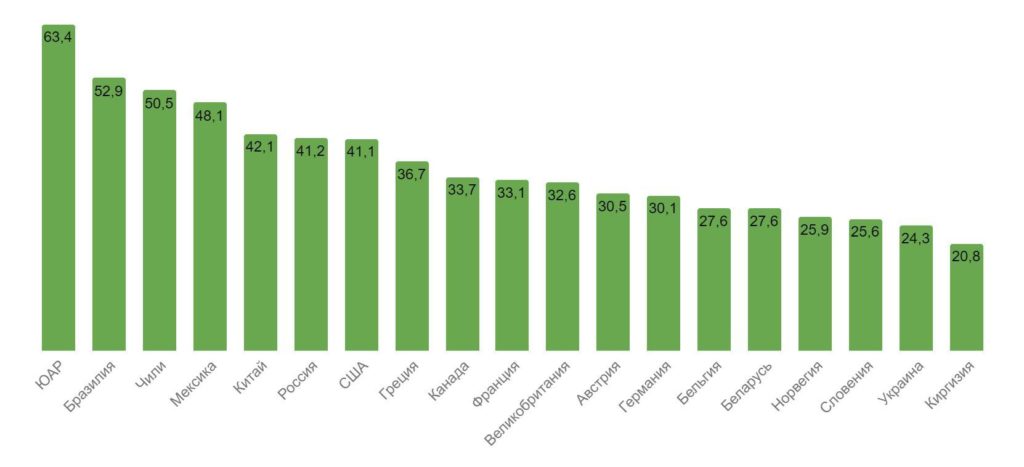
Что примечательно: малое значение Джини (на примере Киргизии) говорит о том, что доходы распределены в стране равномерно, но богатых мало, а почти 40% граждан находятся за чертой бедности.
Богатство и бедность
Это относительные понятия, которые, тем не менее, сосуществуют с общественными отношениями. Они характеризуют социальное неравенство, неравномерность распределения между слоями населения таких ограниченных ресурсов, как деньги, образование, власть и т. д.
Причины неравенства
Многие видят причину этого явления в разном уровне личностных качеств, способностей, условий труда. Как показывают медиа опросы, в бедности граждане винят:
- Экономическую систему (свыше 80% респондентов).
- Безделье, лень, пьянство (свыше 70% респондентов).
- Отсутствие равных возможностей (свыше 60% респондентов).
- Пассивность, бездействие, отсутствие инициатив (свыше 40% респондентов).
- Отсутствие выдающихся способностей, таланта (свыше 30% респондентов).
Опрошенные респонденты считают, что для решения проблемы, нужно:
- предоставить возможности для хорошего заработка;
- вместе с ростом цен периодически повышать доходы;
- «заморозить», не увеличивать цены на продукцию первой необходимости;
- предусматривать больше господдержки для малообеспеченных граждан.
Следует заметить, что аспекты неравенства в обществе (в т. ч. экономического) – актуальный объект исследований. Подходы к интерпретации данного явления разные.
Уровень бедности
К бедным относят тех граждан, у которых доход меньше либо равен прожиточному минимуму (ПМ). ПМ – минимально допустимая материальная обеспеченность (на человека) в стране (регионе). ПМ привязывается к минимальному набору продовольственных, непродовольственных товаров, услуг. По РФ: в 2018 г. ПМ = 8 726 тыс. руб., в 2019 г. – 8 846тыс. руб., а в 2020 г. – 9 311 руб. По данным Росстата на 2019 г. уровень бедности составил 19%.
Оценка уровня жизни производится также по потребительским тратам, а также по тратам на продукты питания. На бедные семьи затраты по питанию составляют около 30% всего дохода. Между тем состоятельные граждане тратят больше на питание, чем бедные, раз в пять. Но чем меньше денег идет на питание, тем больше остается денег на остальные нужды, на образование, открытие бизнеса и др.
По данным Росстата потребительские траты богатых выше в 3 раза, чем у средних слоев населения. А у бедных – в 5 раз меньше, чем у средних. Естественно, из расчета на одного человека. Далее, если рассматривать эти общие расходы по-отдельности, то получится следующее. Богатые, по сравнению с бедными, тратят больше в 5 раз на питание, в 12 раз – на одежду, 20 раз – на медицину. Т. е. их траты значительно выше, но при этом их сбережения выше на 18 раз.
Возможно ли из бедного превратится в богатого
Если исходить из статистики, то можно заметить некоторые неутешительные тенденции. Бедные становятся еще беднее, им труднее зарабатывать и приумножать свой капитал, чем богатым. Между тем количество миллиардеров растет и это тоже факт. У богатых денег больше, соответственно, и возможностей больше. Они увеличивают свое состояние быстрее. Поэтому даже при равных условиях в более выгодном положении остается тот, у кого средств оказалось больше.
Но, как говорится, нет ничего не возможного. Если абстрагироваться от размера капитала, и исходить из реальности, то оптимальной позицией будет следующая. Самостоятельность в действиях, анализ доходов и трат, четкий план действий, а также грамотное распределение денег, накопление, откладывание, инвестиции – необходимый минимум на пути к благосостоянию.
Подытоживая, следует заметить, что, безусловно, есть много людей, которые считают, что со временем ситуация ухудшится и число бедных будет только расти. Но если все время придерживаться этой позиции и ничего совсем не делать, то лучше от этого точно не станет. Все в руках человека. Т.. е. от того, как он способен действовать в своей ситуации, накопить и приумножить свой капитал зависит и его благосостояние.
Преимущества коэффициента Джини
Gini coefficient позволяет:
- Провести сопоставления по распределению исследуемого признака в совокупностях, разных по числу единиц, и между разными совокупностями. К примеру, в регионах с различной численностью либо между странами.
- Скорректировать данные по ВВП и среднедушевому доходу.
- Проследить динамику неравномерного рассредоточения изучаемого признака.
- Сопоставить также разделение рассматриваемого признака по разнородным группам населения (к примеру, для сельчан и горожан).
Одним из несомненных достоинств Gini coefficient признается его анонимность. О чьих доходах идет речь, остается неизвестным, т. к. в этом, по сути, нет необходимости.
Недостатки коэффициента Джини
Как и все статистические показатели, Gini coefficient не может дать полноценную (объективную) оценку картины неравенства доходов. Коэффициент имеет следующие минусы:
- Распределение совокупностей по группам производится без описания этих группировок. Неизвестно, на какие именно составляющие, значения поделена совокупность. Коэффициент «подается» без этих описаний. И чем больше таких групп, тем выше его значение.
- Gini coefficien «опускает» источник доходов для страны (региона и т. д.). По факту его значение может быть низким. В то же время часть граждан зарабатывает деньги тяжелым «каторжным» трудом, а часть – получает доход от собственности. Подобную ситуацию экономисты набюдали в Швеции, где значение Gini coefficien низкое, и при этом лишь 5% домохозяйств (household) обладают 77% акций от совокупного числа акций. Таким образом они получают 5-процентный доход, которые большинство граждан зарабатывают своим трудом.
- Для расчета Gini coefficien требуются определенные данные по статистике. Но методы, применяемые для их сбора, различны. Это значительно усложняет процесс сопоставления коэффициентов, а подчас делает это невозможным.
- Несоответствия при применении Gini coefficien в плановой экономике, где материальные ресурсы принадлежат государству (обществу), распределяются централизованно. Поскольку Джини принимает к учету лишь разницу доходов населения, а не государства (общества), то именно в плановой экономике его значение может быть некорректным, более положительным.
- Gini coefficien и кривая Лоренца применяются только в отношении доходов граждан, выраженных в денежной форме. Между тем многим работникам заработок выдают в натуральной форме. Например, продукцией (продуктами питания) собственного производства либо закупленными в др. организации.
Важно! Выдача заработка опционами на акции имеет особенности при его учете для расчета Джини. Опцион, не являясь доходом, дает возможность заработать на акциях. Вырученные за продажу акций деньги учитывают при расчете коэффициента.
Пример расчета коэффициента Джини
Задача: определить Gini coefficien для трех групп населения по данным из таблицы, применив аналитический способ расчета.
|
Группа населения |
Доля населения |
Доход в общем объеме |
Кумулятивная доля дохода |
Кумулят. доля дохода * 0,333 | Доля населения * Доход в общем объеме |
| 1 | 0,1429 | 0,1429 | 0,0475724 | 0,0475724 | |
| 2 |
0,333 |
0,2857 | 0,4286 (0,1429 + 0,2857) | 0,1427138 | 0,0951414 |
| 3 | 0,5714 | 1.0 (0,4286 + 0,5714) | 0,333 | 0,1902862 |
Исходя из имеющихся данных, можно сказать, что самая состоятельная группа (3) обладает 57,14% доходов. На бедную часть населения (группа 1) приходится 14,29%.тКалькуляция Джини производится с применением формулы:
Отсюда следует, Gini coefficient = 1 — 2 * (0,0475724 + 0,1427138 + 0,333) + (0,0475724 + 0,0951414 + 0,1902862) = 0,286.
Если рассчитать коэффициент вторым, геометрическим способом, результат будет тот же: Gini coefficient = 0,286. Его значение находится в пределах нормы, что свидетельствует о равномерном распределении доходов.
Чтобы фиксировать уровень расслоения в обществе разных стран, социологами был разработан индекс Джини – показатель, отражающий разницу между слоями населения государств. Индекс применяется в разных сферах, в том числе и в финансовой отрасли. Благодаря индексу Джини социологи могут вывести процентное соотношение расслоения в доходах жителей каждой страны.
Индекс показывает, насколько велик разрыв между уровнями заработной платы разных слоев общества страны. Если значение близко к 100%, разрыв является огромным, почти все деньги страны находятся в руках одной группы населения. Если же процентное соотношение близко к нулю, то доходы у всех жителей государства находятся почти на одном уровне. В абсолютном значении индекса 0% будет в стране, где каждый человек имеет одинаковый доход (что, конечно, утопия).
Где применяется индекс Джини
Показатель часто помогает людям, которые планируют перебраться на ПМЖ в другое государство. Человек может ознакомиться с индексом, к примеру, в Нидерландах, и узнать, насколько местные состоятельные граждане зарабатывают больше, чем среднестатистические.
На показатель, отражающий неравенство доходов, влияют многие факторы. В странах, где население стареет или на 20-30% состоит из детей, используется другой вариант индекса. Всего показатель насчитывает свыше 10 вариаций, которые применяются в отдельных случаях.
Коэффициент позволяет также определить процент роста или падения ВВП, темпы роста долгов граждан перед банками, возрастание поляризации в политике или уровня нищеты.
Ошибочные выводы на фоне применения индекса
На достоверность расчетов с применением коэффициента Джини влияет множество нюансов и факторов, на которые следует обратить внимание, чтобы не сделать неправильный вывод. Индекс не учитывает доходы от продажи услуг или продуктов собственного производства или выращивания, а также источники прибыли. Половина населения может получать заработную плату, находясь на официальной должности, а другая часть – от сданного жилья в аренду, процентов со счетов в банке и прочего.
Индекс Джини не применяется для анализа государств, где действует плановая экономика, поскольку уровень дохода в таких странах априори не имеет большого разрыва между трудящимися, так как регулируется государством.
Также этот коэффициент не является мерилом уровнем экономического развития и богатства страны. Наоборот, беднейшие страны планеты могут иметь самый высокий индекс Джини! Иногда и бедные, и богатые страны могут иметь одинаковый показатель. В каждой стране, которая попала под исследование, индекс выведен в разные годы: к примеру, в Китае расчет проводился в 2016 году, а в России – в 2012.
Удобство расчетов
Если применять коэффициент, соблюдая все правила, можно определить реальный уровень неравенства в доходах и других экономических показателях разных государств мира. Правильно выведенный индекс Джини позволит изучить средние доходы гражданина выбранной страны, узнать подробную информацию об уровне ВВП, посмотреть динамику изменения уровня неравенства за каждый год.
В каких странах самый большой уровень неравенства
В десятку стран с самым большим неравенством дохода среди населения регулярно входят государства, расположенные на территории Африки, однако есть и страны из Латинской Америки.
- Первой с конца является Южно-Африканская Республика – коэффициент Джини здесь достиг 63%.
- Почти 60% зафиксировано на территории Намибии – ей достается второе место в списке.
- Тройку «лидеров» замыкает Суринам – небольшое государство в Южной Америке. Коэффициент Джини здесь равен 58%.
- В Замбии, занимающей 4 место, показатель равен 57%.
- Пятое место в рейтинге досталось маленькому островному государству с названием Сан-Томе и Принсипи. Здесь индекс Джини достиг 56?5%.
Самый низкий индекс Джини в мире
Рейтинг лидеров возглавляют европейские государства:
- Золотая медаль достается Словении, где индекс Джини в 2017 году составил всего 24.2%.
- На второй строчке расположилась Чешская Республика. Здесь коэффициент приблизился к 25%. Этот же показатель достался и Словакии.
- Беларусь находится на 3-4 строчках рейтинга: в соседнем государстве индекс Джини равен 25,3%.
- Пятерка лидеров замыкается Молдавией – здесь показатель находится на уровне 25.5%.
Европа является регионом, где наблюдается очень низкий уровень неравенства в принципе. В Соединенных Штатах, к примеру, индекс Джини равен 41%. 7 лет назад проводилось исследование, в ходе которого установили, что 1% населения США имеет доход, в 40 раз превышающий уровень зарплаты самых бедных жителей страны. В России этот показатель также приближается к 40%, но результатов за последние 4 года в общем доступе нет.
ПОДПИСЫВАЙТЕСЬ на мой YouTube канал!
Ставьте ПАЛЕЦ ВВЕРХ и ПОДПИСЫВАЙТЕСЬ на Дзен канал.
Читайте также:
✅ Запретит ли Евросоюз россиянам въезд в Шенгенскую зону
✅ Как отечественная «Черноголовка» будет вымещать «Пепси» и «Кока-Колу» с рынка
✅ Русские начали массово скупать недвижимость в Турции. Сравниваем цены
