
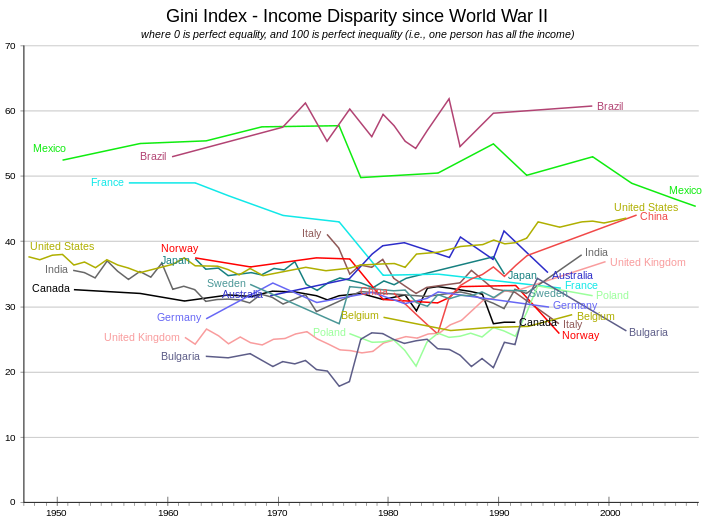
Индекс Джини по распределению национального дохода стран мира в 2018 году, согласно данным Всемирного банка[1]
Коэффициент Джини — статистический показатель степени расслоения общества данной страны или региона по какому-либо изучаемому признаку. Используется для оценки экономического неравенства.
Коэффициент Джини изменяется от 0 до 1. Чем больше его значение отклоняется от нуля и приближается к единице, тем в большей степени доходы сконцентрированы в руках отдельных групп населения.
Индекс Джини — процентное представление этого коэффициента.
Наиболее часто в современных экономических расчётах в качестве изучаемого признака берётся уровень годового дохода. Коэффициент Джини можно определить как макроэкономический показатель, характеризующий дифференциацию денежных доходов населения в виде степени отклонения фактического распределения доходов от абсолютно равного их распределения между жителями страны[2].
Иногда коэффициент Джини (как и кривую Лоренца) используют также и для выявления уровня неравенства по накопленному богатству, однако в таком случае необходимым условием становится неотрицательность чистых активов домохозяйства.
Также коэффициент Джини применяется в машинном обучении для предсказания непрерывных величин. Смысл его — погрешность должна быть настолько равномерной, насколько возможно[источник не указан 1640 дней].
История вопроса[править | править код]
Эта статистическая модель была предложена и разработана итальянским статистиком и демографом Коррадо Джини и опубликована в 1912 году в его труде «Вариативность и изменчивость признака» («Изменчивость и непостоянство»).
Расчёт[править | править код]
Рассчитать коэффициент можно как отношение площади фигуры, образованной кривой Лоренца и прямой равенства, к площади треугольника, образованного прямой равенства и осями. Иначе говоря, следует найти площадь первой фигуры и поделить её на площадь второй. В случае полного равенства коэффициент будет равен 0; в случае полного неравенства он будет равен 1.
Коэффициент Джини можно рассчитать по формуле Брауна:

или по формуле Джини:

где 






Преимущества коэффициента Джини[править | править код]
- Позволяет сравнивать распределение признака в совокупностях с различным числом единиц (например, регионы с разной численностью населения).
- Дополняет данные о ВВП и среднедушевом доходе. Служит своеобразной поправкой этих показателей.
- Может быть использован для сравнения распределения признака (дохода) между различными совокупностями (например, разными странами). При этом нет зависимости от масштаба экономики сравниваемых стран.
- Может быть использован для сравнения распределения признака (дохода) по разным группам населения (например, коэффициент Джини для сельского населения и коэффициент Джини для городского населения).
- Позволяет отслеживать динамику неравномерности распределения признака (дохода) в совокупности на разных этапах.
- Анонимность — одно из главных преимуществ коэффициента Джини. Нет необходимости знать, кто имеет какие доходы персонально.
Недостатки коэффициента Джини[править | править код]
- Довольно часто коэффициент Джини приводится без описания группировки совокупности, то есть часто отсутствует информация о том, на какие же именно квантили поделена совокупность. Так, чем на большее количество групп поделена одна и та же совокупность (больше квантилей), тем выше для неё значение коэффициента Джини.
- Коэффициент Джини не учитывает источник дохода, то есть для определённой географической единицы (страны, региона и т. п.) коэффициент Джини может быть довольно низким, но при этом какая-то часть населения свой доход обеспечивает за счёт труда, а другая — за счёт собственности. Так в Швеции значение коэффициента Джини довольно низко, но при этом только 5 % домохозяйств владеют 77 % акций от общего количества акций, которым владеют все домохозяйства. Это обеспечивает этим 5 % доход, который остальное население получает за счёт труда.
- Метод кривой Лоренца и коэффициента Джини в деле исследования неравномерности распределения доходов среди населения имеет дело только с денежными доходами, меж тем некоторым работникам заработную плату выдают в виде продуктов питания и т. п.; также широкое распространение получает практика выдачи заработной платы работникам в виде опционов на покупку акций компании-работодателя (последнее соображение несущественно, опцион сам по себе не является доходом, это только возможность получить доход, продав, например, акции, а когда акции проданы и продавец получил деньги, этот доход уже учитывается при расчёте коэффициента Джини).
- Различия в методах сбора статистических данных для вычисления коэффициента Джини приводят к затруднениям (или даже невозможности) в сопоставлении полученных коэффициентов.
- Коэффициент Джини отчасти неадекватен для плановых экономик, где распределение ресурсов зависит не только от доходов, но и от лояльности к государству (партии). Кроме того, так как частное предпринимательство запрещено в плановой экономике, выходит ситуация когда получаемые доходы фиксируются не у предпринимателей, а у государства. Из-за этого, формально выходит что доходы концентрируют предприниматели, в отличие от плановой экономики, где доходы принадлежат государству. Коэффициент Джини учитывает разницу доходов граждан, а не государства. Это приводит к значительно более положительным показателям коэффициента Джини в плановых экономиках.
Пример расчёта коэффициента Джини[править | править код]
По данным Росстата коэффициент Джини в России составлял в разные годы[4]:
| Год | 1992 | 1994 | 1996 | 1998 | 2000 | 2002 | 2004 | 2006 | 2008 | 2010 | 2012 | 2014 | 2016 | 2018 | 2019 | 2020 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Коэффициент Джини |
0,289 | 0,409 | 0,387 | 0,394 | 0,395 | 0,397 | 0,409 | 0,415 | 0,421 | 0,421 | 0,42 | 0,416 | 0,414 | 0,411 | 0,411 | 0,406[5] |
Составленный банком Credit Suisse отчёт Global Wealth Report оценивает индекс Джини в России в 2012 году в 84 % (0,84; по богатству, а не по доходам), что по мнению банка является максимальным значением среди всех крупных стран мира[6]. По мнению российских экономистов и аналитиков, опрошенных журналом «Эксперт», выводы Credit Suisse не соответствуют действительности, а «по имущественному неравенству Россия примерно соответствует таким странам как США, Япония, Индия и Китай». Приводятся и другие фактические ошибки в отчёте: «стоимость одного только жилья в России в несколько раз выше, чем цифра, которая в Global Wealth Report указана в качестве стоимости всего имущества жителей России»[7].
Согласно собственной статистике Китая в этой стране коэффициент Джини в 2012 году составил 0,474, за прошедшие 10 лет коэффициент достиг локального максимума в 2008 году, когда составлял 0,491[8]. В 2000 году этот же показатель в Китае составлял 0,41, в 1990 году — 0,33, в 1980 году — 0,31[9]. Проф. Ху Аньган в 2004 году, когда коэффициент Джини в Китае по оценке Всемирного банка составлял 0,437, в интервью отмечал: «Если учесть ещё неофициальные доходы, уклонение от налогообложения, коррупцию, то коэффициент Джини будет 0,51 и выше. Судя по официальным номинальным доходам, разрыв уже достаточно велик. За время реформ, то есть за одно поколение, Китай прошёл путь от коэффициента 0,2 до 0,5. Переход от справедливого к подчеркнуто несправедливому обществу очень заметен. Тем более что на начальном этапе реформ число бедных в большом масштабе снижалось, а со второй половины 1990-х годов эти пропорции менялись очень мало»[10].
См. также[править | править код]
- Список стран по показателям неравенства доходов
- Индекс человеческого развития
- Индекс Аткинсона
- Индекс Тейла
Примечания[править | править код]
- ↑ GINI index (World Bank estimate) | Data. data.worldbank.org. Дата обращения: 23 июля 2020. Архивировано 29 июля 2020 года.
- ↑ Гальперин В. В., Гальперин В. М. 50 лекций по микроэкономике Архивная копия от 6 апреля 2009 на Wayback Machine. — 2004. (Лекция 44 «Перераспределение дохода»)
- ↑ Под ред. С. Д. Ильенковой: Микроэкономическая статистика : Учебник . — М.: Финансы и статистика, 2004, с 544.
- ↑ Госкомстат. РАСПРЕДЕЛЕНИЕ ОБЩЕГО ОБЪЕМА ДЕНЕЖНЫХ ДОХОДОВ И ХАРАКТЕРИСТИКИ ДИФФЕРЕНЦИАЦИИ ДЕНЕЖНЫХ ДОХОДОВ НАСЕЛЕНИЯ Архивная копия от 15 ноября 2019 на Wayback Machine Примечание: оценка на основании данных выборочных обследований домашних хозяйств и макроэкономического показателя денежных доходов населения.
- ↑ Минэкономразвития России, Федеральная служба государственной статистики (РОССТАТ). Социально-экономическое положение России, 2020 год. Дата обращения: 14 февраля 2021. Архивировано 10 февраля 2021 года.
- ↑ Сергей Гуриев, Олег Цывинский. Россия – лидер по неравенству распределения богатства, Ведомости (6 ноября 2012). Архивировано 4 сентября 2014 года. Дата обращения: 23 августа 2017.
- ↑ Рейтинг со многими неизвестными. Дата обращения: 23 августа 2017. Архивировано 23 августа 2017 года.
- ↑ Рассекречены первые за 12 лет данные о социальном неравенстве КНР. Дата обращения: 26 января 2013. Архивировано 7 февраля 2013 года.
- ↑ http://www.tiger.edu.pl/publikacje/TWPNo117.pdf Архивная копия от 31 мая 2015 на Wayback Machine страница 27
- ↑ Встреча Архивировано 23 октября 2013 года.
Литература[править | править код]
- Джини коэффициент / В. Г. Минашкин // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
Экономика07 марта 2019 в 08:00126 276
Коэффициент Джини: все ли равны?
Разбираемся с показателем экономического неравенства
Индекс неравенства
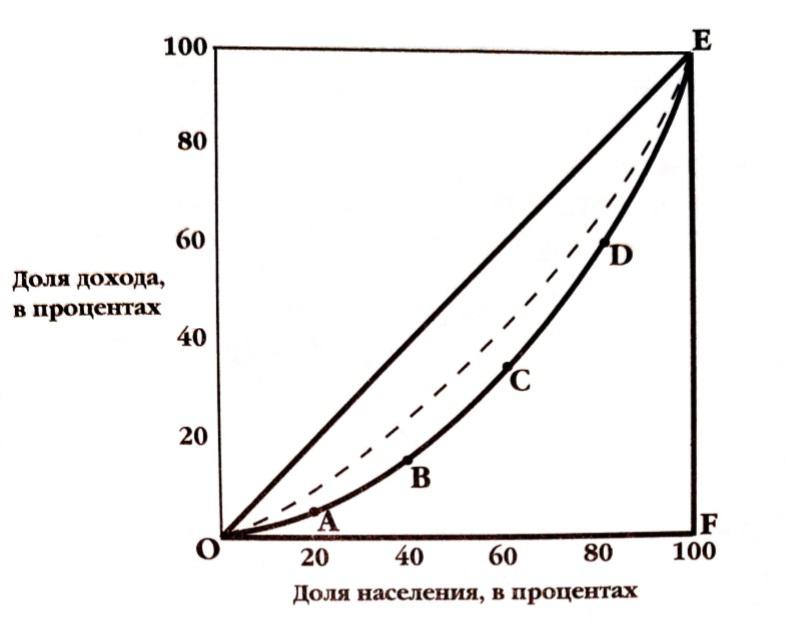
Рис 1. Кривая Лоренца
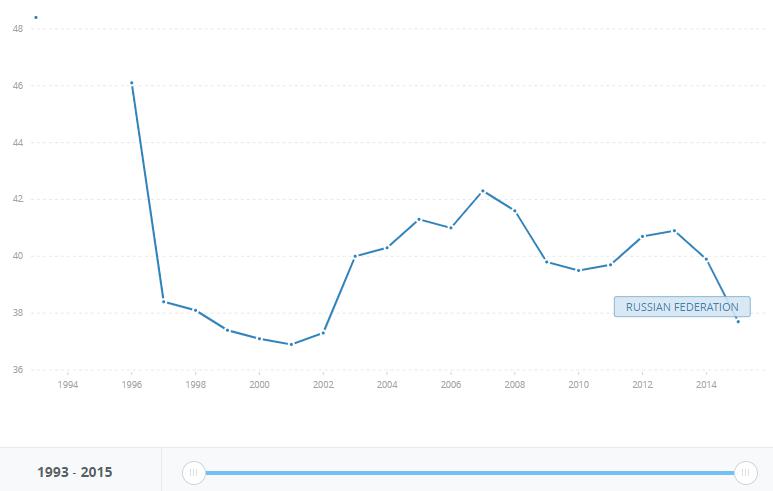
Рис. 2. Динамика коэффициента Джини, 1996-2015 года. Источник: https://data.worldbank.org/indicator/SI.POV.GINI?end=2015&locations=RU&start=1993&view=chart
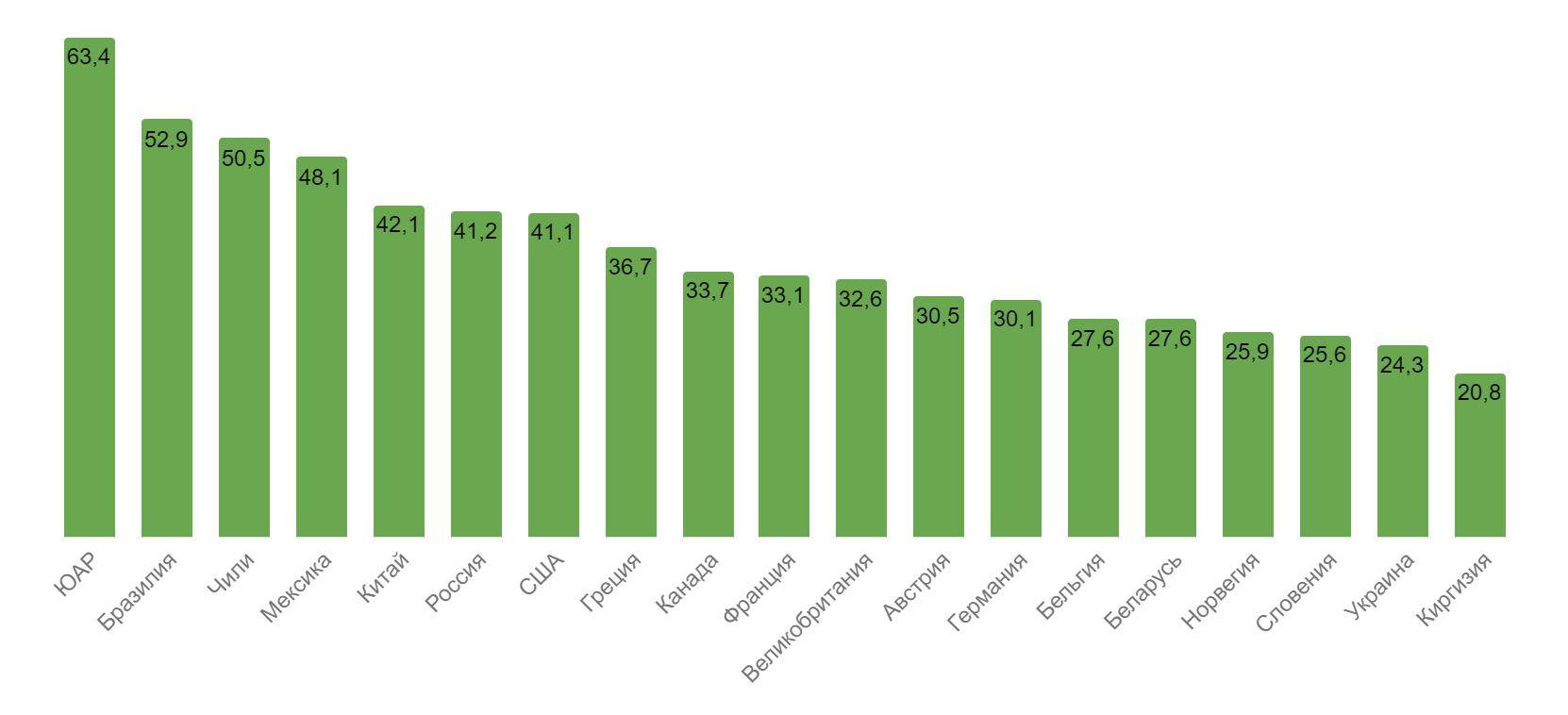
Рис. 3. Индекс Джини в странах мира (данные на 2016 год).
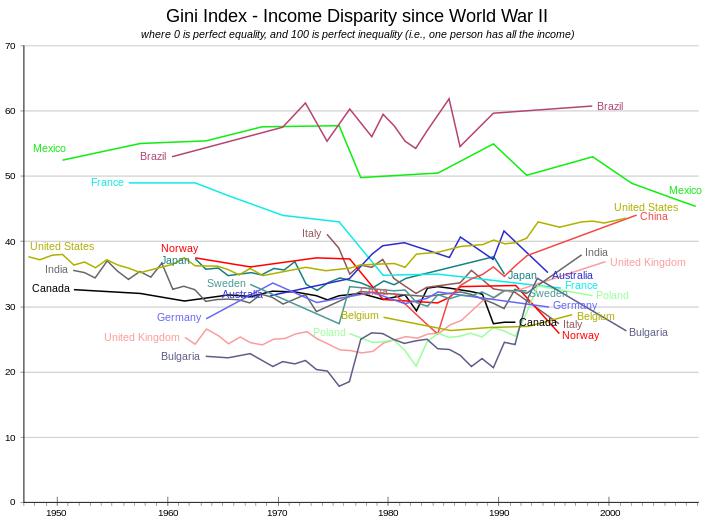
Рис. 4. Динамика индекса Джини. Источник: https://www.people.iup.edu/rhoch/ClassPages/Global_Cities/Spring17/Notes/RGPL103_ForExam1.pdf
Богатство и бедность
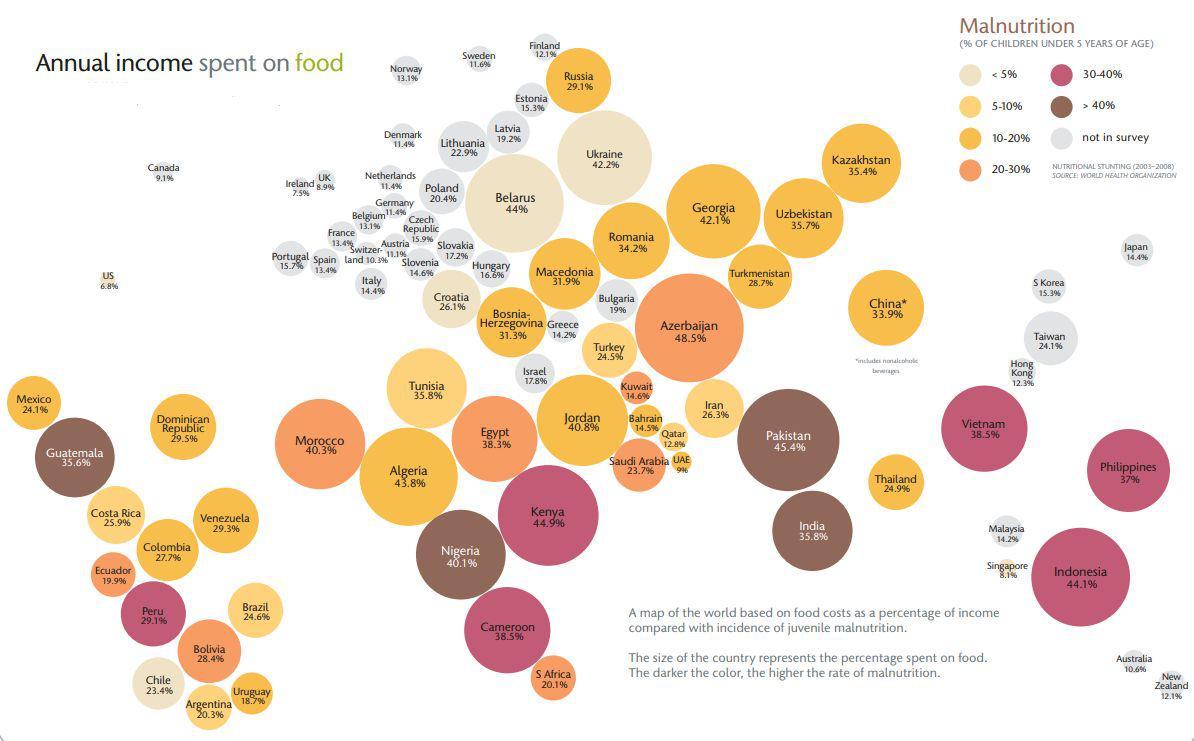
Рис. 5. Доля трат на продукты по странам мира. Источник: http://wsm.wsu.edu/researcher/WSMaug11_billions.pdf
Могу ли я изменить личную ситуацию?

Рис. 6. Количество миллиардеров по странам мира. Источник: https://howmuch.net/articles/world-map-of-billionaires-2018
Подведем итоги
Больше интересных материалов
Что такое кривая Лоренца, коэффициент Джини (индекс Джини) и как их рисовать и считать?
Начнем с кривой Лоренца.
Кривая Лоренца
Кривая Лоренца — это график, демонстрирующий степень неравенства в распределении дохода или богатства в обществе. Ее придумал в 1905 году американский статистик Макс Лоренц.
Собственно говоря, эта кривая может отражать неравенство в распределении самых разных величин, но вначале она предназначалась именно для отражения экономического неравенства в обществе.
Кривая выглядит следующим образом:
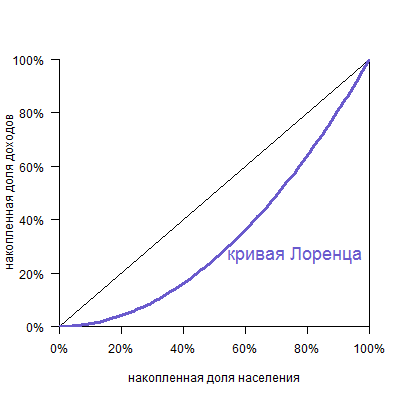
По горизонтальной оси указана накопленная доля населения (причем население отсортировано от беднейших, то есть получающих наименьший доход, до богатейших), а по вертикальной — доля получаемого дохода.
Это лучше понять на примере:
Предположим, мы разбили все население страны на 4 группы, в каждой из которых по 25% населения. При этом первая, «бедная» группа получает 10% общего дохода страны, вторая, «ниже среднего» — 20%, третья, «выше среднего» — 30% и четвертая, «богатая» — 40%.
| Группа | Доля населения | Доля от общего дохода |
| бедная | 25% | 10% |
| ниже среднего | 25% | 20% |
| выше среднего | 25% | 30% |
| богатая | 25% | 40% |
Теперь переведем это в накопленные доли: 25% населения будут получать 10%, 50% населения (это «бедная» и «ниже среднего» группы) суммарно получают 10%+20%=30%, 75% населения («бедная», «ниже среднего» и «выше среднего» группы) получат 10%+20%+30%=60% всего дохода, и, разумеется, 100% населения получат 100% дохода.
| Накопленная доля населения | Накопленная доля общего дохода |
| 25% | 10% |
| 50% | 30% |
| 75% | 60% |
| 100% | 100% |
Теперь можно построить график.
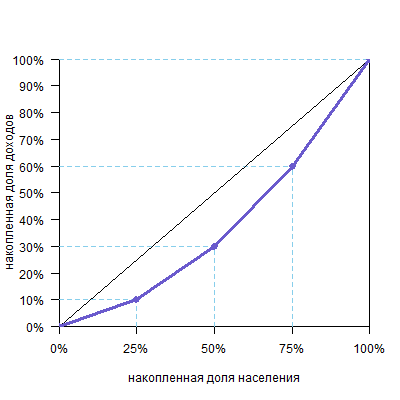
Обратите внимание, что кривая всегда исходит из точки (0%;0%) и приходит в точку (100%;100%), так как ясно, что 0% населения получают 0% дохода, а 100% населения получают 100% дохода.
Необязательно, чтобы группы были равными. Например, возьмем такие данные:
| Доля населения | Доля от общего дохода | Накопленная доля населения | Накопленная доля общего дохода |
| 20% | 10% | 20% | 10% |
| 40% | 30% | 60% | 40% |
| 30% | 30% | 90% | 70% |
| 10% | 30% | 100% | 100% |
Обратите внимание, что группы нужно распределить от бедных к богатым. Если группы одинаковые, то они сортируются просто по столбцу «Доля от общего дохода» — от маленьких значений к большим (см. прошлый пример). Но у нас группы разного размера, поэтому нужно учитывать отношение второго столбца к первому (доли дохода к доле населения). Например, у нас вторая и третья группы получают одинаковую долю дохода. Но во второй группе населения больше, а значит, в расчете на одного человека они беднее. То же с третьей и четвертой группой. Вообще говоря, случай с разными группами редкий и встречается только в условных задачах. Но если будут такие условия, то нужно делить долю дохода на долю населения. Для наших групп получим:
10%/20%=1/2
30%/40%=3/4
30%/30%=1
30%/10%=3
Это значит, что в третьей группе население получает именно средний по стране доход на человека. В первой группе доход в два раза ниже среднего, во второй — 75% от среднего, а в четвертой — три средних дохода на человека. Вот в таком порядке их и нужно расположить для построения кривой Лоренца.
Получим такой график:
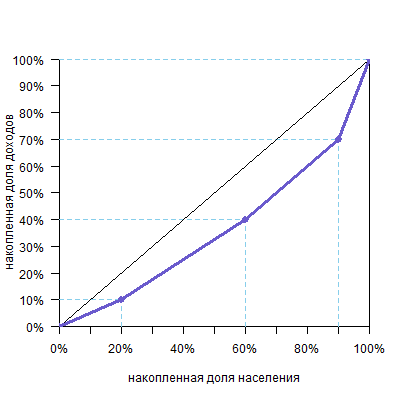
И, конечно, количество групп может быть любым. Желательно, чтобы их было побольше, тогда кривая будет построена по большему числу точек, станет более гладкой и точной.
Можно представить себе кривую абсолютно равного распределения: это будет просто диагональ, так как любые N% населения получают N% дохода:
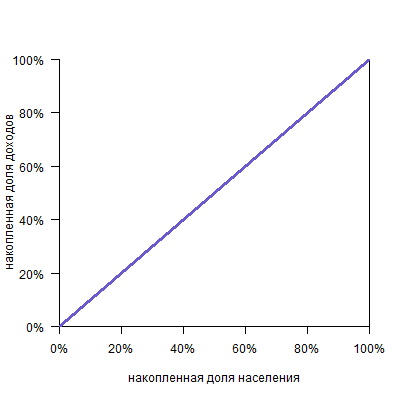
И кривую абсолютного неравенства, когда все работают бесплатно, а один-единственный человек получает весь доход:
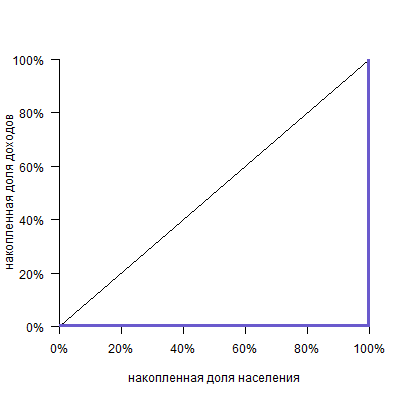
(Не думайте, что это совершенно умозрительная кривая: например, если у единственного человека в стране есть, скажем, говорящий еж, то кривая распределения говорящих ежей будет именно такой!)
А теперь:
Коэффициент Джини
К 1912 году итальянский статистик Коррадо Джини разработал алгебраическую интерпретацию кривой Лоренца: коэффициент, призванный указывать, насколько неравным является экономическое распределение.
Все очень просто. Коэффициент этот равен отношению площади фигуры между диагональю и кривой Лоренца:
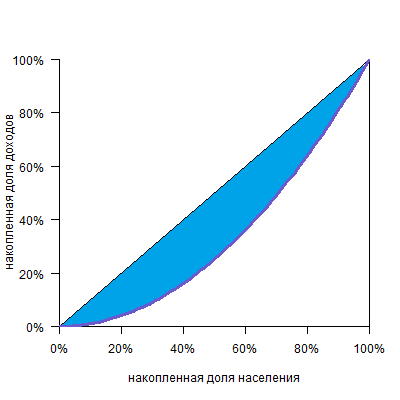
К площади треугольника под диагональю (а она всегда равна 0,5):
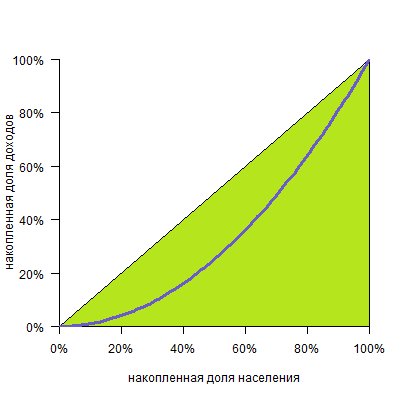
Таким образом, при полном равенстве площадь первой фигуры равна нулю, и коэффициент тоже равен нулю. При полном неравенстве эта фигура займет весь треугольник и коэффициент будет равен единице.
Чем ниже коэффициент, тем более равным является распределение.
Как его считать?
Считать коэффициент Джини можно графическим или алгебраическим способом. Посмотрим, как это можно сделать.
Графический способ
Вертикальными линиями можно разделить фигуру над кривой Лоренца на два треугольника и несколько трапеций.
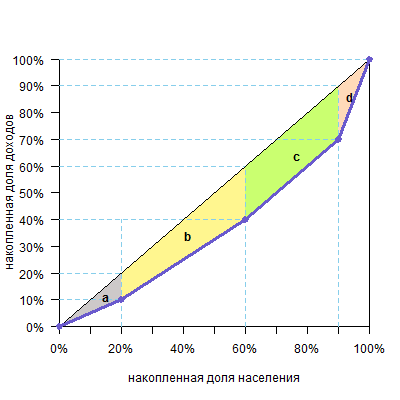
Площадь треугольника — половина основания на высоту, а трапеции — полусумма оснований на высоту (поверните голову на 90º, высоты расположены горизонтально, а основания — вертикально). Высоты равны размерам групп, а основания легко посчитать. В нашем случае площадь фигуры будет такой:
| фигура | расчет площади | площадь |
| треугольник a | 10%*20%/2=0,1*0,2/2 | 0,01 |
| трапеция b | (10%+20%)/2*40%=0,3/2*0,4 | 0,06 |
| трапеция c | (20%+20%)/2*30%=0,4/2*0,3 | 0,06 |
| треугольник d | 20%*10%/2=0,2*0,1/2 | 0,01 |
| Всего площадь фигуры (a+b+c+d) | 0,14 |
Теперь разделим ее на площадь треугольника под диагональю (а он, напоминаю, всегда равен 0,5) и получим: 0,14/0,5=0,28
Таким образом, 0,28 или 28% и есть значение коэффициента Джини.
Другой графический способ: посчитать площадь фигур под кривой Лоренца, а затем вычесть их из площади треугольника под диагональю (0,5) и получить площадь над кривой. И ее уже разделить на 0,5.
Этот случай удобнее, когда цифры не такие круглые и ширина оснований трапеций над кривой неочевидна.
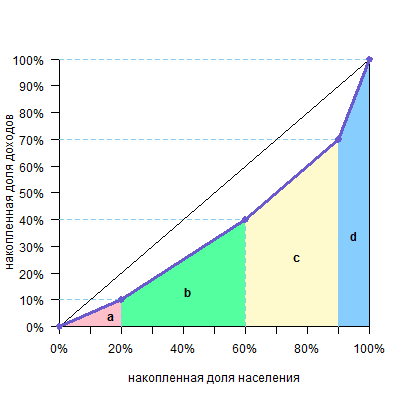
В нашем случае
| фигура | расчет площади | площадь |
| треугольник a | 10%*20%/2=0,1*0,2/2 | 0,01 |
| трапеция b | (10%+40%)/2*40%=0,5/2*0,4 | 0,1 |
| трапеция c | (40%+70%)/2*30%=1,1/2*0,3 | 0,165 |
| трапеция d | (70%+100)%/2*10%=1,7/2*0,1 | 0,085 |
| Всего площадь фигуры (a+b+c+d) | 0,36 |
Отнимаем 0,36 от 0,5 и получаем 0,14 — площадь фигуры над кривой
Далее, как и в первом способе, делим эту площадь на 0,5 (площадь треугольника под диагональю) и получаем: 0,14/0,5=0,28
Алгебраический способ
Наиболее проста в употреблении формула:[latexpage]
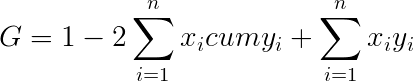
где:
$x{_{i}}$-доля i-ой группы в составе населения
$y{_{i}}$-доля i-ой группы в объеме доходов
$cum y{_{i}}$-кумулированная (накопленная) доля i-ой группы в составе населения
Составим таблицу на основе данных предыдущего примера:
| Доля населения ($x{_{i}}$) |
Доля от общего дохода ($y{_{i}}$) |
Накопленная доля общего дохода ($cum y{_{i}}$) |
$x{_{i}}y{_{i}}$ | $x{_{i}}cum y{_{i}}$ |
| 20% | 10% | 10% | 0,02 | 0,02 |
| 40% | 30% | 40% | 0,12 | 0,16 |
| 30% | 30% | 70% | 0,09 | 0,21 |
| 10% | 30% | 100% | 0,03 | 0,1 |
| Итого | 0,26 | 0,49 |
Если вы не понимаете, как построена эта таблица, откройте спойлер:
Первый и второй столбцы — это исходные данные, они такие же, как и в разделе «Графический способ».
Третий столбец получается из второго путем накопления значений из второго столбца: берем значение из ячейки слева и всех ячеек выше нее и складываем.
Четвертый столбец — произведение первого и второго.Чтобы не запутаться в процентах, переведите их в доли, например для первой строки: 20%10%=0,20,1=0,02.
Пятый столбец — произведение первого и третьего.
Далее подсчитываем суммы по четвертому и пятому столбцу.
Теперь можно подставить полученные суммы в формулу, которая приведена выше:
$G=1-2*0,49+0,26=1-0,98+0,26=0,28$
Мы получили ответ 0,28 — такой же, как и графическим методом.
Это самая простая в применении формула. Советую ее запомнить. А если вдруг хочется понять, как она выведена, откройте этот спойлер (объяснение довольно длинное!):
В основе этой формулы лежит уже известная вам идея: чтобы посчитать площадь фигуры над кривой Лоренца:
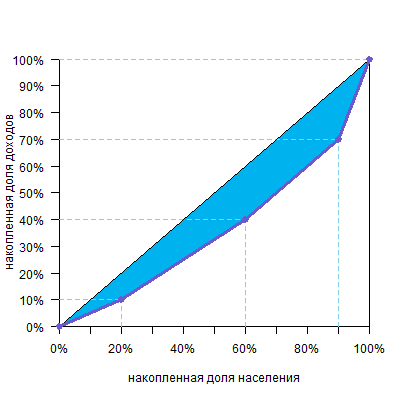
можно сперва посчитать площадь фигуры под кривой Лоренца
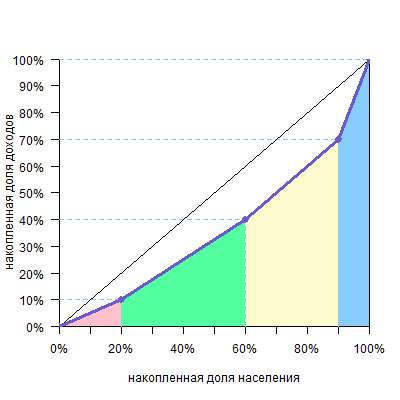
а потом вычесть ее из площади диагонального треугольника, которая равна 0,5, и получим искомое. Саму же площадь под кривой будем считать по группам. Можно видеть, что над каждой группой образуется треугольник или четырехугольник — они выделены разными цветами.
Рассмотрим, например, вторую группу (зеленый четырехугольник).
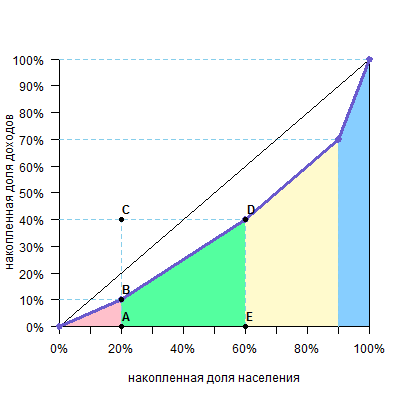
Площадь четырехугольника ABDE равна площади прямоугольника ACDE минус площадь прямоугольного треугольника BCD. При этом площадь прямоугольника ACDE равна AEDE, а площадь прямоугольного треугольника BCD равна CDBC/2. Таким образом, площадь ABDE равна
AEDE-CDBC/2
При этом можно увидеть на графике, что ВС — доля дохода по группе (y), DE — накопленная доля дохода по группе (cum y), а AE или CD — доля группы в численности населения (x). Тогда формула принимает вид
хcum y — xy/2
Можно видеть, что такая формула (прямоугольник минус прямоугольный треугольник) пригодна для всех цветных фигур, включая и левый розовый треугольник.
Тогда сумма всех фигур под кривой Лоренца будет равна
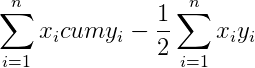
Эту сумму, как вы помните, нужно вычесть из 0,5, чтобы получить площадь фигуры над кривой
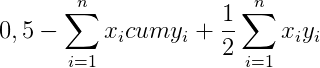
И наконец, разделив все это на площадь диагонального треугольника (то есть опять же на 0,5), получим формулу коэффициента Джини:
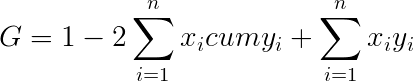
Есть и другие формулы, расчет по одной из них приведен, например, вот тут. Мне кажется, что в ней проще запутаться, а получается ровно то же самое.
Чтобы проверить себя, решите задачу. Ответ и решение под спойлерами:
Задача
Предположим, что в некоторой стране N проживают три группы населения: бедные, средний класс и богатые. Группы равны по численности жителей, но различаются по уровню дохода: средний класс зарабатывает в два раза больше, чем бедные, а богатые зарабатывают в два раза больше, чем средний класс. Внутри групп доходы распределены равномерно. Нарисуйте график кривой Лоренца и рассчитайте коэффициент Джини.
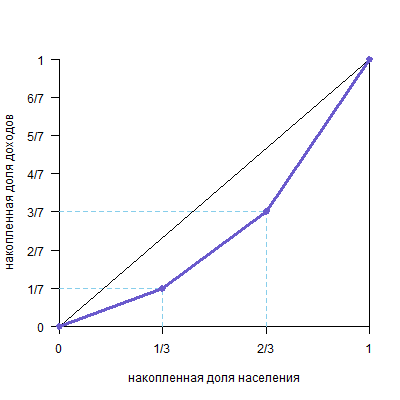
G≈0,286
Удобней считать площадь под кривой, так как цифры в натуральных дробях.
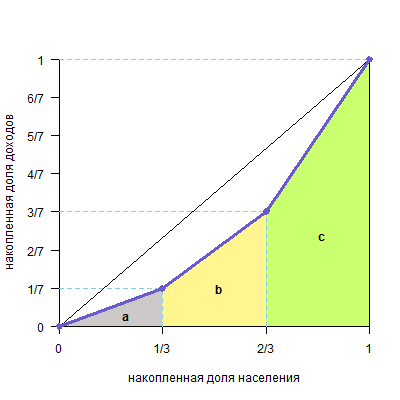
Площадь треугольника a равна (1/7*1/3)/2=1/42
Площадь трапеции b равна (1/7+3/7)/21/3=2/71/3=2/21
Площадь трапеции c равна (3/7+1)/21/3=5/71/3=5/21
Общая сумма фигур 1/42+2/21+10/21=1/42+4/42+10/42=15/42
Чтобы получить фигуру над кривой Лоренца, нужно эту сумму вычесть из 0,5
0,5-15/42=21/42-15/42=6/42=3/21
Для того, чтобы получить значение коэффициента Джини, делим это число на 0,5
3/21 / 0,5 = 6/21 ≈0,286
Поскольку средний класс зарабатывает в два раза больше, чем бедные, а богатые — в два раза больше среднего класса, то всего они зарабатывают семь долей бедного класса, то есть, соответственно, 1/7, 2/7 и 4/7, что примерно равно 0,143, 0,286 и 0,571
| Доля населения(x) | Доля от общего дохода (y) |
Накопленная доля общего дохода (cum y) |
x*y | x*cum y |
| 0,333 | 0,143 | 0,143 | 0,048 | 0,048 |
| 0,333 | 0,286 | 0,429 | 0,095 | 0,143 |
| 0,333 | 0,571 | 1,000 | 0,190 | 0,333 |
| Итого: | 0,333 | 0,524 |
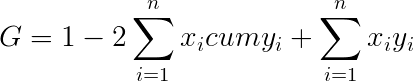
G=1-2*0,524+0.333≈0,286
17 авг. 2022 г.
читать 2 мин
Названный в честь итальянского статистика Коррадо Джини , коэффициент Джини — это способ измерения распределения доходов населения.
Значение коэффициента Джини варьируется от 0 до 1, где более высокие значения представляют большее неравенство в доходах и где:
- 0 представляет идеальное равенство доходов (все имеют одинаковый доход)
- 1 представляет собой идеальное неравенство доходов (все доходы принадлежат одному человеку).
Список коэффициентов Джини по странам можно найти здесь .
В следующем пошаговом примере показано, как рассчитать коэффициент Джини в Excel.
Шаг 1: введите данные
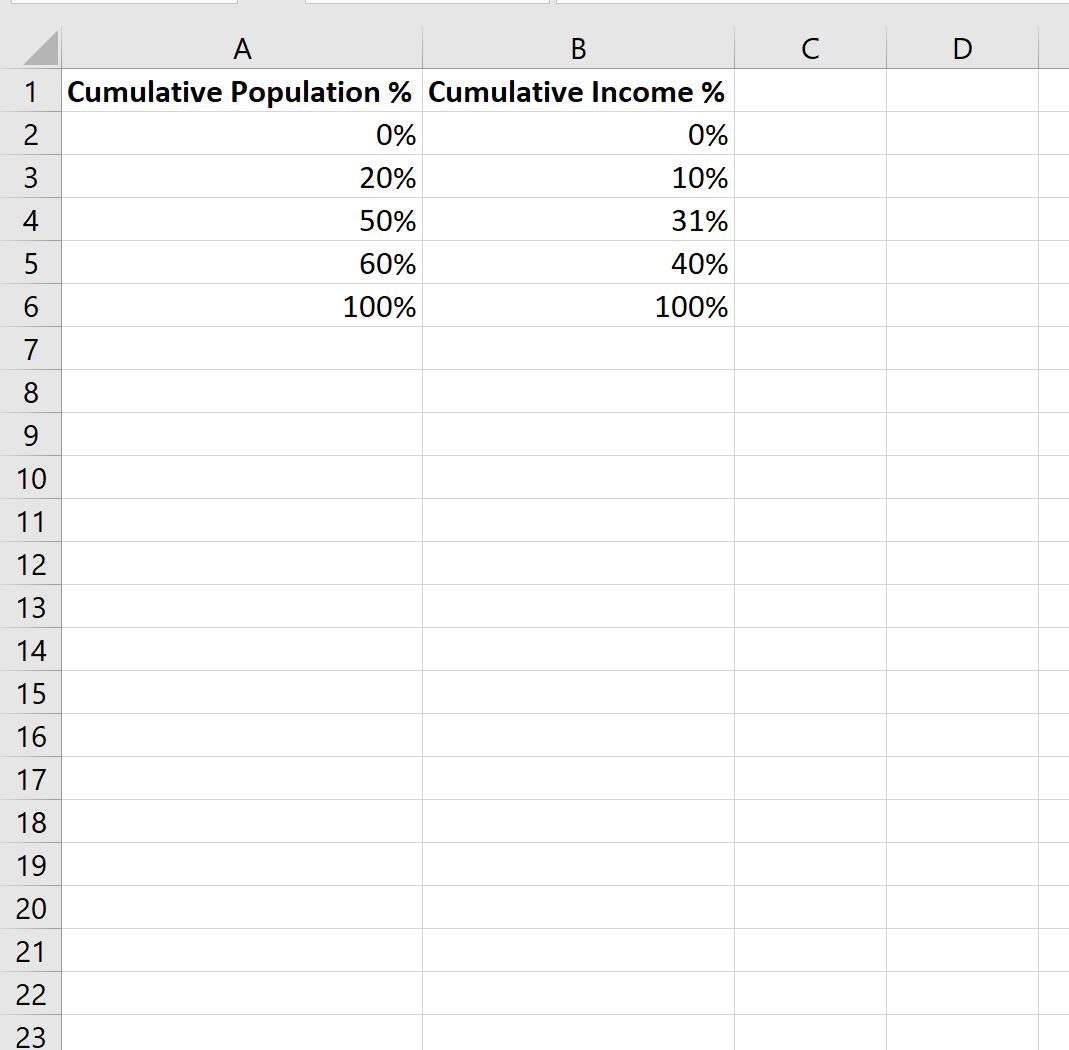
Во-первых, мы должны ввести значения для двух столбцов: % совокупного населения и % совокупного дохода отдельных лиц в определенной стране:
Вот как интерпретировать значения:
- Нижние 20% людей в этой стране составляют 10% от общего дохода.
- Нижние 50% людей в этой стране составляют 31% от общего дохода.
- Нижние 60% людей в этой стране составляют 40% от общего дохода.
- На 100% физических лиц в этой стране приходится 100% общего дохода.
Шаг 2: Рассчитайте площади под кривой Лоренца
Затем нам нужно рассчитать отдельные площади под кривой Лоренца , которую мы используем для визуализации распределения доходов в стране.
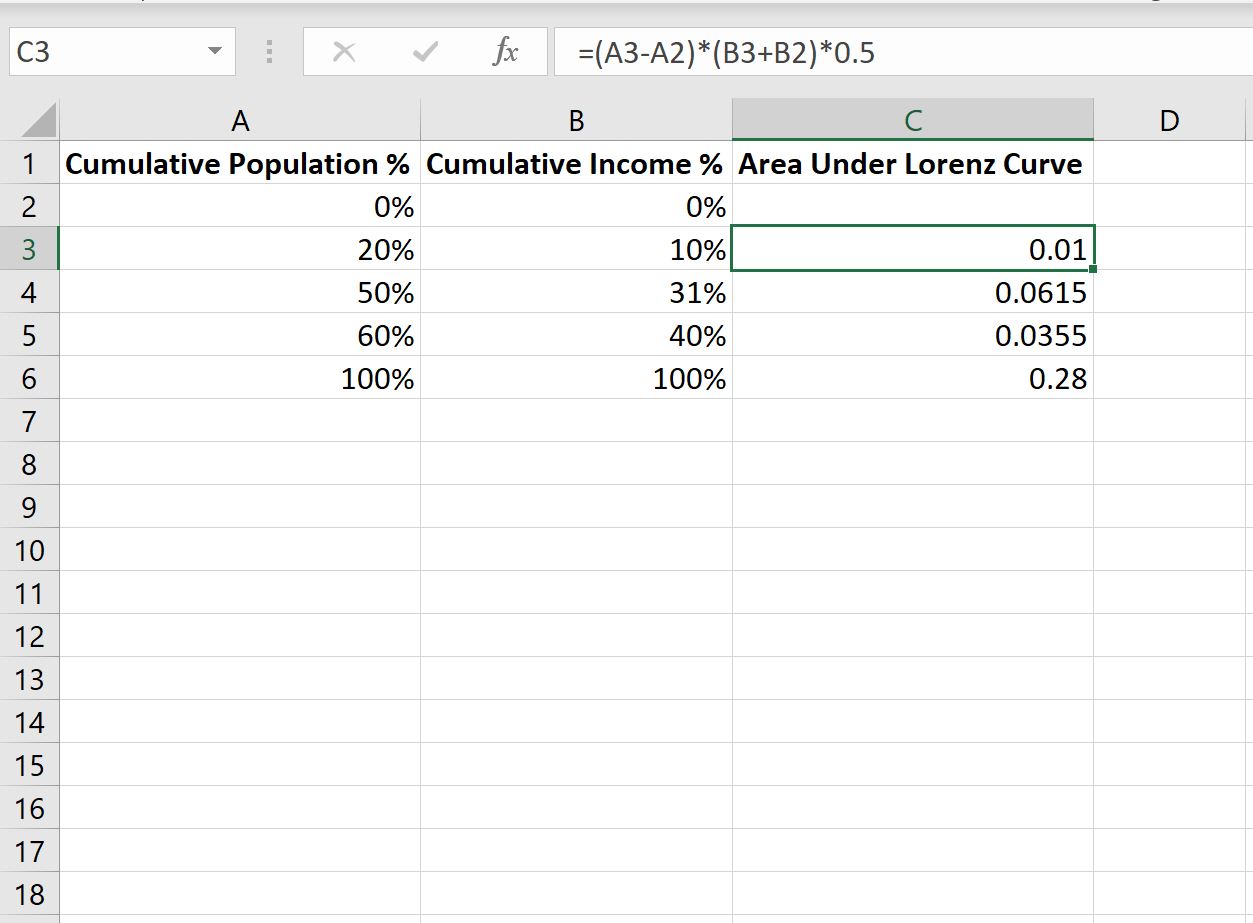
В нашем примере мы введем следующую формулу в ячейку C3 :
=( A3 - A2 )*( B3 + B2 )*0.5
Затем мы скопируем и вставим эту формулу в каждую оставшуюся ячейку в столбце C:
Шаг 3: Рассчитайте коэффициент Джини
Наконец, мы можем ввести следующую формулу в ячейку D2 , чтобы рассчитать коэффициент Джини для этой совокупности:
=1-2*SUM( C3:C6 )
На следующем снимке экрана показано, как использовать эту формулу на практике:
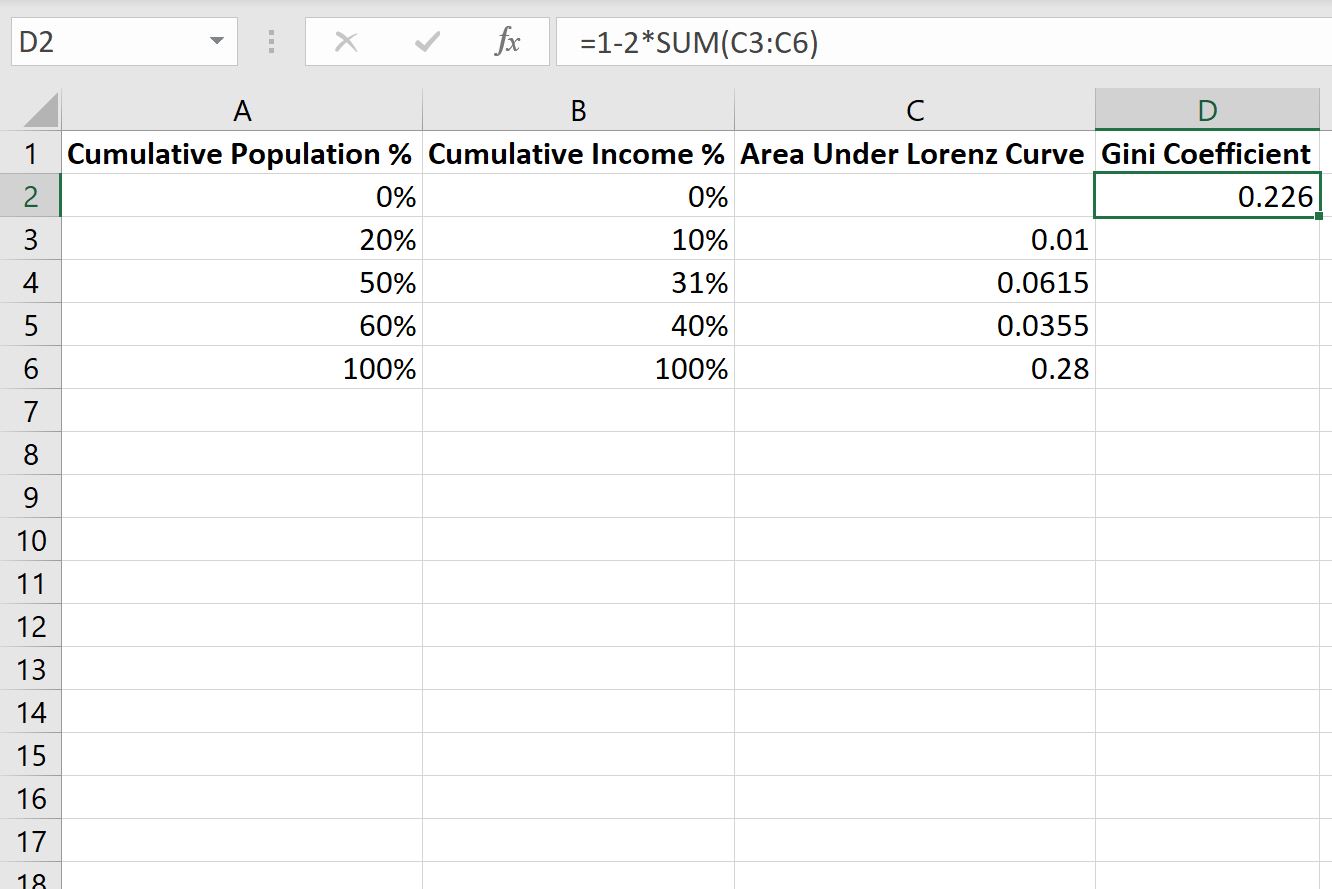
Коэффициент Джини для этой совокупности оказывается равным 0,226 .
Это чрезвычайно простой пример того, как рассчитать коэффициент Джини, но вы можете использовать те же самые формулы для расчета коэффициента Джини для гораздо большего набора данных.
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Предположим, что в некоторой стране N проживают три группы населения: бедные, средний класс и богатые. Группы равны по численности жителей, но различаются по уровню дохода: средний класс зарабатывает в два раза больше, чем бедные, а богатые зарабатывают в два раза больше, чем средний класс. Внутри групп доходы распределены равномерно. Совокупный доход всех жителей страны равен Y. Нарисуйте график кривой Лоренца и рассчитайте индекс Джини.
Решение:
Третья часть населения, по условию задачи, бедные. Их доходы обозначим через х.
Тогда 2х – величина доходов среднего класса,
4х – величина доходов богатых.
Следовательно, совокупный доход всех жителей страны Y состоит из 7 одинаковых частей.
1/7 – доля доходов бедных,
2/7 – доля доходов среднего класса,
4/7 – доля доходов богатых.
Представим условие задачи в табличной форме:
| Социальная группа населения | Доля населения, xi | Доля в общем объёме денежных доходов, уi | Расчётные величины
|
||
|---|---|---|---|---|---|
| Кумулятивная доля дохода, cum yi | xi cum yi | xi уi | |||
| Бедные | 0,333 | 0,1429 | 0,1429 | 0,0475724 | 0,0475724 |
| Средний класс |
0,333 | 0,2857 | 0,4286 | 0,1427138 | 0,0951414 |
| Богатые | 0,333 | 0,5714 | 1,0000 | 0,333 | 0,1902862 |
| Итого | 1,000 | 1,0000 | – | 0,5232862 | 0,333 |
Построим кривую Лоренца:
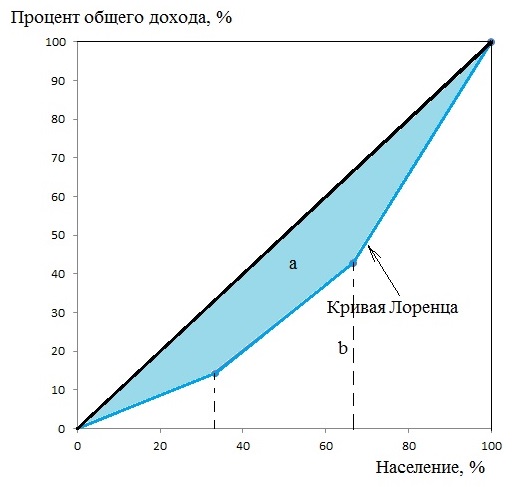
Индекс Джини рассчитаем двумя способами.
1) Способ аналитический. Коэффициент Джини рассчитывается по формуле:
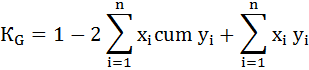
где
xi – доля населения, принадлежащая к i-й социальной группе в общей численности населения;
уi – доля доходов, сосредоточенная у i-й социальной группы населения;
n – число социальных групп;
cum yi – кумулятивная доля дохода.
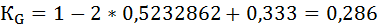
2) Способ геометрический. Коэффициент Джини определяется как отношение площади фигуры, образуемой кривой Лоренца и линией равномерного распределения (Sa), к площади треугольника ниже линии равномерного распределения (Sa+b):
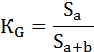
Площадь фигуры, образуемой кривой Лоренца и линией равномерного распределения (Sa) легко найти вычитанием из площади треугольника (Sa+b) площадь фигуры, лежащей ниже кривой Лоренца.
Площадь фигуры b, лежащей ниже кривой Лоренца можно разбить на треугольник и две трапеции:
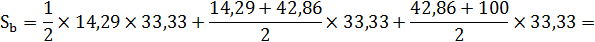
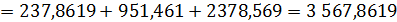
Площадь фигуры a будет равна:
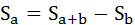
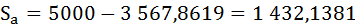
Индекс Джини будет равен:
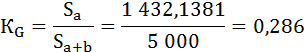
Оба способа дали одинаковый результат.
Как видно из таблицы, наиболее обеспеченная группа населения сконцентрировала 57,14% доходов, а доля наименее обеспеченной группы в общем доходе составила 14,29%.
