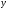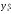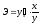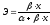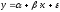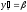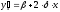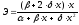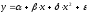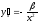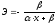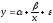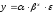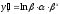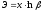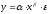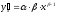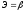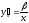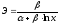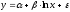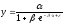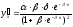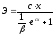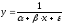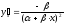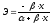Как найти коэффициент эластичности функции

Содержание:

1. Эластичность функции
2. Определение и свойства эластичности функций
3. Свойства эластичности функции
4. Эластичность спроса относительно цены
5. Эластичность предложения относительно цены

Эластичность функции

В экономических исследованиях приросты тех или иных показателей, характеризующих экономические процессы, чаще всего выражают в процентах к базовым значениям. Поэтому и изменение величин, которые связаны с ними функциональной зависимостью, также выражают в процентах. Для этого используют понятие эластичности функции, которое выражается через производную функции.

Определение и свойства эластичности функций

Пусть задана функция y = f (x). Если аргумент x получил приращение Δx и при этом функция y получила приращение Δy, то  называют относительным приращением аргумента, а — относительным приращением функции.

Определение. Предел отношения относительного приращения функции к относительному приращению аргумента при условии, что приращение аргумента стремится к нулю, если существует, называется эластичностью функции.

Обозначают эластичность функции y = f (x) относительно переменной x   E_x(y). То есть,

Итак, если в точке x функция имеет производную, то эластичность определяется формулой  
Эластичность выражает приближенный процент приращения функции, который соответствует 1 % приращения аргумента.

Пример. Найти эластичность функции  y = x² – 4 x +7  и вычислить ее при x = 1,  x = 2,  x = 5.

Решение.

Итак, если x  вырастет на 1 % с 1 до 1,01, то y снизится на 0,5 %. Если x вырастет на 1 % с 2 до 2,02, то значение переменной y практически не изменится. Если x вырастет на 1 % с 5 до 5,05, то y вырастет на 2,5 %.

Свойства эластичности функции

ТЕОРЕМА 1. Эластичность произведения двух функций равна сумме эластичности сомножителей:
E_x (U ⋅ V) = E_x (U) + E_x (V).

Доказательство. По определению эластичности

ТЕОРЕМА 2. Эластичность частного двух функций равна разности показателей эластичности делимого и делителя:

Доказательство. По определению эластичности

Эластичность спроса относительно цены

В анализе и прогнозах ценовой политики применяется понятие эластичности спроса и предложения.

Пусть p цена одного изделия, а Q — количество изделий, произведенных и проданных через некоторое время, что определяет спрос. Величина Q зависит от цены, т. е. Q является функцией от p: Q = f (p).

Пусть приращение цены Δp вызывает приращение ΔQ. тогда относительные приращения цены и спроса будут соответственно     и   
Отношение   показывает относительное изменение спроса, если цена изделия возросла на 1 %.

Эластичностью спроса относительно цены называется предел отношения относительного приращения спроса к относительному приращению цены при условии, что приращение цены стремится к нулю.

Эластичность спроса относительно цены приближенно определяет, как меняется спрос на данное изделие, если его цена возрастает на 1 %.

Так, например, если рост цены на 5 % вызывает падение спроса на 8 %, то эластичность будет  
Если эластичность спроса η = –0,5, то 10 % роста стоимости товара вызывает падение спроса на (–0,5) 10% = –5%.

Определение. Если процент изменения спроса больше процента изменения цены (η < 1), то спрос называют эластичным, если процент изменения спроса меньше процента изменения цены (-1 < η < 0), то спрос называют не эластичным, а если процент изменения спроса равен проценту изменения цены (η = 1), то спрос называют нейтральным.

Пример. Установлено, что количество произведенных и проданных изделий Q по цене p определяется по формуле Q = 10000 – 500p (0 < p < 20). Определить, при какой цене спрос эластичный, нейтральный, не эластичный.

Решение. Эластичность спроса относительно цены

Спрос будет эластичным, если η < –1,  Отсюда, учитывая, что 20 – p > 0, имеем      p > 20 – p;   2 p > 20;   p > 10.   Итак, спрос эластичен при цене  10 < p < 20 (руб.).

Спрос нейтральный при цене p = 10 (руб.). Спрос будет не эластичный, когда -1 < η < 0.

Итак, спрос не эластичный при цене меньшей 10 руб. за изделие.

Пример 2. Установить связь между доходом предприятия и эластичностью спроса от цены.

Решение. Доход определяется как произведение стоимости каждого изделия на количество произведенных и проданных изделий Q :   D (Q) = p⋅ Q.

Найдем маржинальный доход, учитывая, что Q есть функция от p.

Если η ≤ –1, то 1 + η < 0, а   И поэтому доход падает при росте p, когда спрос эластичен.
Если –1 < η < 0, то 1 + η > 0,   а    
То есть функция D (Q) дохода растет с ростом цены p,  когда спрос не эластичный.

Эластичность предложения относительно цены

Понятие эластичности можно применять и к другим функциям экономического содержания.

Рассмотрим понятие эластичности предложения S в зависимости от цены товара p. Под предложением понимают количество некоторого товара, который предлагается на продажу за единицу времени. Как правило, предложение какого-либо товара является возрастающей функцией цены. Но бывают случаи, когда предложение повышается со снижением цены. Величина S является функцией от цены товара. То есть, S = S (p).

Пусть Δp — приращение цены, а ΔS — соответствующее приращение предложения. Тогда относительные приращения цены и предложения будут соответственно   и  .
Эластичностью предложения относительно цены называется предел отношения относительного приращения предложения к относительному приращению цены при условии, что приращение цены стремится к нулю.

Эластичность предложения относительно цены приближенно определяет процент приращения предложения на 1 % приращения цены.

Пример 3. Функция предложения некоторого товара   . Определить эластичность предложения при цене p = 2.

Коэффициент эластичности

Как и в экономической теории и ряде других дисциплинах в эконометрике есть понятие среднего коэффициента эластичности Э – который показывает, на сколько процентов в среднем изменится показатель у от своего среднего значения при изменении фактора х на 1% от своей средней величины:

Для более подробного изучения вопроса об эластичности советуем посмотреть это видео

Коэффициент эластичности для степенной модели

В эконометрических исследованиях и экономической теории при изучении эластичности спроса от цен широко используется степенная функция

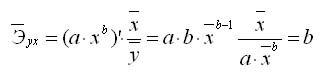
Коэффициент эластичности, можно определить и при наличии других форм связи, но только для степенной функции он представляет постоянную величину, равную параметру b. В других функциях коэффициент зависит от значений фактора х, поэтому интерпретировать модель сразу для прочих моделей невозможно, требуются дополнительные расчеты

Коэффициент эластичности для линейной модели

В силу того что k-эластичности для линейной регрессии не является постоянной, а зависит от соответствующего значения Х, то рассчитывается средний показатель эластичности по формуле

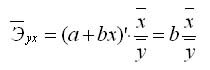
k-эластичности гиперболической модели:

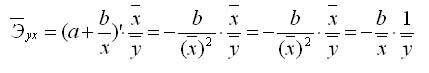
k-эластичности для экспоненциальной модели:

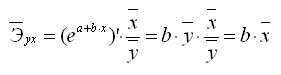
k-эластичности для обратной модели:

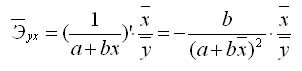
Несмотря на обширное использование в эконометрике коэффициентов эластичности, иногда бывает, когда их расчет не имеет экономического смысла. Это происходит в тех случаях, когда для рассматриваемых признаков бессмысленно определение изменения значений в процентах. Например, вряд ли стоит определять, на сколько процентов может измениться заработная плата с ростом стажа работы на 1 %. В таких случаях степенная функция, даже если она оказывается оптимальной по формальным соображениям (исходя из минимального значения остаточной вариации), не может быть экономически интерпретирована.

Например, изучая соотношение ставок межбанковского кредита у (в % годовых) и срока его предоставления (в днях) было получено степенное уравнение регрессии с очень высоким коэффициентом корреляции (0,98). k-эластичности 0,4% лишен смысла, так как срок предоставления кредита не измеряется в процентах.

В множественной регрессии k-эластичности показывает, на сколько процентов изменяется в среднем результат с изменением соответствующего фактора на 1 % при неизменности действия других факторов. Степенные модели множественной регрессии получили широкое распространение в производственных функциях, при анализе спроса и потребления.

Таблица коэффициентов эластичности

Коэффициент эластичности

формула расчета
коэффициента эластичности:

,

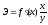где f'(x) – первая
производная, характеризующая соотношение
приростов результата и фактора для
соответствующей формы связи.

Для степенной
функции она составит:
.
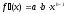Соответственно, коэффициент эластичности
окажется равным:

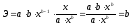
Коэффициент
эластичности только для степенной
функции он представляет собой постоянную
величину, равную параметру b. В других
функциях коэффициент эластичности
зависит от значений фактора x. Так,
для линейной регрессии

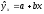
производная функции и эластичность
следующие:

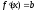
и
.

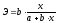В силу того, что
коэффициент эластичности для линейной
функции не является величиной постоянной,
а зависит от соответствующего значения
x, то обычно рассчитывается средний
показатель эластичности по формуле:

.

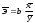Для оценки параметров
степенной функции

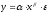
применяется МНК к линеаризованному
уравнению
,
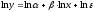т.е. решается система нормальных
уравнений:

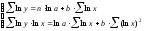
Параметр b
определяется непосредственно из системы,
а параметр a – косвенным путем после
потенцирования величины ln a. Так,
решая систему нормальных уравнений для
зависимости спроса от цен, было получено
уравнение:
.
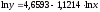Если потенцировать его, получим:

.

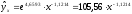Поскольку параметр
a экономически не интерпретируется,
то нередко зависимость записывается в
виде логарифмически-линейной, т.е.
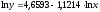.В
виде степенной функции изучается не
только эластичность спроса, но и
предложения. При этом обычно эластичность
спроса характеризуется параметром b<0,
а эластичность предложения – b>0.

Поскольку
коэффициенты эластичности представляют
экономический интерес, а виды моделей
не ограничиваются только степенной
функцией, приведем формулы расчета
коэффициентов эластичности для наиболее
распространенных типов уравнений
регрессии.

Таблица 2.5.

Коэффициенты
эластичности для ряда математических
функций.

Вид функции,	Первая производная,	Коэффициент эластичности,
линейная
парабола
гипербола
показательная
степенная
полулогарифмическая
логистическая
обратная

Несмотря на широкое
использование в эконометрике коэффициентов
эластичности, возможны случаи, когда
их расчет экономического смысла не
имеет. Это происходит тогда, когда для
рассматриваемых признаков бессмысленно
определение изменения значений в
процентах. Например, вряд ли кто будет
определять, на сколько процентов может
измениться заработная плата с ростом
стажа работы на 1%. Или, например, на
сколько процентов изменится урожайность
пшеницы, если качество почвы, измеряемое
в баллах, изменится на 1%. В такой ситуации
степенная функция, даже если она
оказывается наилучшей по формальным
соображениям (исходя из наименьшего
значения остаточной вариации) не может
быть экономически интерпретирована.
Например, изучая соотношение ставок
межбанковского кредита y (в процентах
годовых) и срока их предоставления x
(в днях), было получено уравнение
регрессии:

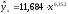
с очень высоким показателем корреляции
(0,9895). Коэффициент эластичности 0,352%
лишен смысла, ибо срок предоставления
кредита не измеряется в процентах.
Значительно больший интерес для этой
зависимости может представить линейная
функция
,
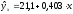имеющая более низкий показатель
корреляции 0,85. Коэффициент регрессии
0,403 показывает в процентных пунктах
изменение ставок кредита с увеличением
срока их предоставления на 1 день.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Возьмем некоторую функцию $y=f(x)$. Возьмем некоторый произвольный $x_1$ из области определения данной функции, ему будет соответствовать единственный $y_1=f(x_1)$. Теперь вместо $x_1$ подставим в имеющуюся функцию $x_2$ (также принадлежащий её области определения). Получим $y_2=f(x_2)$. В зависимости от вида данной функции $y=f(x)$ можем получить, что $y_2=y_1$ или же, что $y_2neq y_1$. Функция реагирует на изменение её аргумента. $y_2$ может отличаться от $y_1$ на большую величину $Delta y$, а может и на маленькую. Эластичность функции как раз и показывает степень её реакции а изменение аргумента.

Коэффициент эластичности показывает, на сколько процентов изменяется значение функции при увеличении аргумента на один процент.

$E_x^y=dfrac {Delta F(x) (проценты) }{Delta x (проценты) }=dfrac {Delta y / y }{Delta x / x}=dfrac{Delta y}{Delta x} cdot dfrac{x}{y}$

В данной формуле $x$ традиционно был принят за независимую переменную.

Если нам нужно посчитать эластичность функции в какой-либо точке (когда изменение аргумента стремится к 0), то можно воспользоваться следующей формулой точечной эластичности:

$E=limlimits_{Delta x to 0} dfrac {Delta y}{Delta x} cdot dfrac{x}{y}=y'(x) cdot dfrac{x}{y}$

Пример 1
Функция спроса имеет вид $Q(P)=100-P$, посчитать эластичность в точке $Q=50$.

$Q=50$, значит и $P=50$

$Q'(P)=-1$

$E=-1 cdot dfrac{50}{50}= -1$

Формулой точечной эластичности можно также пользоваться, когда нужно узнать эластичность в окрестностях какой-либо точки – при малых изменениях функции и аргумента (до 10%):

$E=dfrac{Delta y}{Delta x} cdot dfrac{x}{y}=dfrac{y_2-y_1}{x_2-x_1} cdot dfrac{x_1}{y_1}$

Пример 2
При увеличении цены с 50 до 51 д.ед количество покупаемого товара снизилось с 200 до 195 шт. Найти точечную эластичность

$E=dfrac{195-200}{51-50} cdot {50}{200}=-1{,}25$

При больших приращениях функции и аргумента (более 10%) мы ищем чувствительность функции к изменению аргумента на некотором отрезке измерения. Тогда воспользуемся формулой дуговой эластичности, которая поможет избежать проблемы, возникшей бы, если бы мы пользовались формулой для расчета точечной эластичности – при использовании формулы точечной эластичности для подсчета эластичности на отрезке на конечный результат влияет то, какую точку мы считаем $x_1$, а какую $x_2$:

Пример 3
Имеется линейная функция $Q=100-P$, взята точка $A$ c координатами $(25;75)$ и точка $B$ с координатами $(75;25)$ (на первом месте стоит цена). Необходимо посчитать эластичность на отрезке $AB$

Посчитаем по формуле точечной эластичности. Пусть $P_1=x_1=25$, $P_2=x_2=75$. Тогда:

$E=dfrac{25-75}{75-25} cdot dfrac{25}{75}=-dfrac{1}{3}$

Теперь пусть $x_1=75$, $x_2=25$

$E=dfrac{75-25}{25-75} cdot {75}{25}=-3$

Показатели эластичности на отрезке $AB$ различаются в зависимости от того, какую точку $A$ или $B$ принять за начало отрезка. поэтому для расчета эластичности функции при больших изменениях аргумента и зависимой переменной используется формула дуговой эластичности:

$E=dfrac{y_2-y_1}{x_2-x_1} cdot dfrac { dfrac{x_2+x_1}{2}}{dfrac{y_2-y_1}{2}}=dfrac{y_2-y_1}{x_2-x_1} cdot {x_2+x_1}{y_2+y_1}$

В данной формуле для расчета эластичности вторым множителем выступает не координата начальной точки, а координата точки, располагающейся в середине отрезка $AB$. Теперь значение эластичности не зависит от выбора направления движения.

Посчитаем эластичность по новой формуле. $x_1=25$, $x_2=75$

$E=dfrac{25-75}{75-25} cdot dfrac{75+25}{25+75}=-1$

Теперь $x_1=75$, $x_2=25$

$E=dfrac{75-25}{25-75} cdot dfrac{25+75}{75+25}=-1$

Считать эластичность по формуле дуговой эластичности можно и при малых (до 10%) изменениях аргумента и функции. Значение дуговой и точечной эластичности тогда будут близки. Точечная эластичность показывает реакцию функции на изменение аргумента в точке или в её окрестности, дуговая же показывает чувствительность функции к изменению аргумента на некотором отрезке.

Если эластичность функции в какой-любо точке/ на каком-либо отрезке равна 0, то данная функция в этом месте является совершенно неэластичной, если $0< E< 1$, то это неэластичный фрагмент, если $E=1$, то это фрагмент с единичной эластичностью, если $1< E< infty$, то фрагмент функции эластичен, если $E=infty$, то он совершенно эластичен.

Коэффициенты эластичности

Коэффициенты эластичности наряду с индексами корреляции и детерминации для нелинейных форм связи применяются для характеристики зависимости между результативной переменной и факторными переменными. С помощью коэффициентов эластичности можно оценить степень зависимости между переменными х и у.

Коэффициент эластичности показывает, на сколько процентов изменится величина результативной переменной у, если величина факторной переменной изменится на 1 %.

В общем случае коэффициент эластичности рассчитывается по формуле:

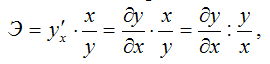
y’_x – первая производная результативной переменной у по факторной переменной x.

Коэффициенты эластичности могут быть рассчитаны как средние и точечные коэффициенты.

Средний коэффициент эластичности характеризует, на сколько процентов изменится результативная переменная у относительно своего среднего уровня y если факторная переменная х изменится на 1 % относительного своего среднего уровня x Общая формула для расчёта коэффициента эластичности для среднего значения x факторной переменной х:

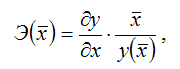
где y( x ) – значение функции у при среднем значении факторной переменной х.

Для каждой из разновидностей нелинейных функций средние коэффициенты эластичности рассчитываются по индивидуальным формулам.

Для линейной функции вида:

средний коэффициент эластичности определяется по формуле:

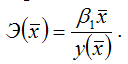
Для полиномиальной функции второго порядка (параболической функции) вида:

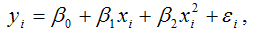
средний коэффициент эластичности определяется по формуле:

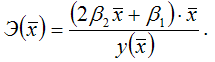
Для показательной функции вида:

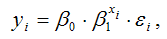
средний коэффициент эластичности определяется по формуле:

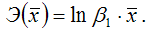
Для степенной функции вида:

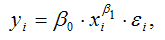
средний коэффициент эластичности определяется по формуле:

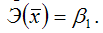
Это единственная нелинейная функция, для которой средний коэффициент эластичности

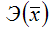
равен коэффициенту регрессии β₁.

Точечные коэффициенты эластичности характеризуются тем, что эластичность функции зависит от заданного значения факторной переменной х₁.

Точечный коэффициент эластичности характеризует, на сколько процентов изменится результативная переменная у относительно своего значения в точке х₁, если факторная переменная изменится на 1 % относительно заданного уровня х₁.

Общая формула для расчёта коэффициента эластичности для заданного значения х₁ факторной переменной х:

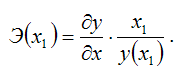
Для каждой из разновидностей нелинейных функций средние коэффициенты эластичности рассчитываются по индивидуальным формулам.

Для линейной функции вида:

точечный коэффициент эластичности определяется по формуле:

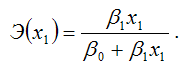
В знаменателе данного показателя стоит значение линейной функции в точке х₁.

Для полиномиальной функции второго порядка (параболической функции) вида:

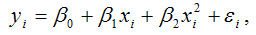
точечный коэффициент эластичности определяется по формуле:

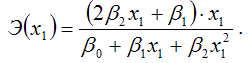
В знаменателе данного показателя стоит значение параболической функции в точке х₁.

Для показательной функции вида:

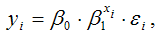
точечный коэффициент эластичности определяется по формуле:

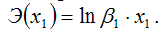
Для степенной функции вида:

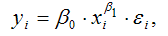
точечный коэффициент эластичности определяется по формуле:

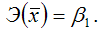
Докажем данное утверждение.

Запишем точечный коэффициент эластичности для степенной функции вида

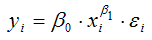
через первую производную результативной переменной по заданной факторной переменной x₁:

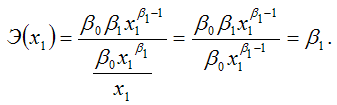
Следовательно, Э(x₁) = β₁, что и требовалось доказать.

Чаще всего коэффициенты эластичности применяются в анализе производственных функций. Однако их расчёт не всегда имеет смысл, потому что в некоторых случаях интерпретация факторных переменных в процентном отношении невозможна или бессмысленна.

Раздел 1. Исходные основы микроэкономики

Практическая работа 2

Целью данного практикума является усвоение методики расчета коэффициентов эластичности и их применения на практике.

Задачами практикума являются:

• во-первых, приобретение навыков расчетов коэффициентов эластичности;
• во-вторых, использование коэффициентов эластичности для определения ценовой и производственной политики фирмы.

Оглавление

Задачи на расчет коэффициентов эластичности

Задача 1

Постановка задачи: Рассмотрите рисунок. Определите коэффициент ценовой эластичности на отрезке АВ кривой спроса d₁. О каком товаре идет речь?

Технология решения задачи: Для решения задачи необходимо вспомнить, как определяется дуговой коэффициент ценовой эластичности. Коэффициент эластичности обозначим Е_d/p, тогда

Поставив в формулу значения, получим:

Этот коэффициент характеризует эластичный товар.

Ответ: коэффициент эластичности равен –2,3. Товар эластичен.

Задача 2

Постановка задачи: Даны три товара. Изменения объемов спроса в зависимости от изменения цены приведены в таблице. Определите коэффициенты ценовой эластичности по каждому товару.

Товар А

Товар В

Товар С

Цена

Количество

Цена

Количество

Цена

Количество

Технология решения задачи: необходимо определить коэффициенты дуговой эластичности спроса по цене по каждому товару. Коэффициент эластичности товара А (Е_{d/p A}) определяется по формуле

Поставив в формулу значения, получим:

Этот коэффициент характеризует эластичный товар.

Аналогично рассчитаем коэффициент эластичности по товару В:

Задача 3

Постановка задачи: В результате роста цены с 4 до 7 долл., объем спроса на товар Х упал с 1000 до 800 штук. Определите коэффициент эластичности спроса по цене.

Технология решения задачи: Коэффициент эластичности обозначим Еd/р, тогда

Поставив в формулу значения, получим:

Этот коэффициент характеризует малоэластичный товар.

Ответ: коэффициент эластичности равен –0,4; это малоэластичный товар.

Задача 4

Постановка задачи: Цена на товар А выросла со 100 до 200 ден. ед. Спрос на этот товар упал с 3000 до 1000 штук. Спрос на товар В вырос с 500 до 1000. Определите коэффициенты эластичности товара А и В. О каких коэффициентах идет речь?

Технология решения задачи: Так как цена товара А выросла, а спрос на этот товар упал, то можно определить коэффициент ценовой эластичности товара А:

Поставив в формулу значения, получим:

Реакцию спроса товара В на изменение цены товара А показывает коэффициент перекрестной эластичности, который определяется по формуле

Подставим значения и получим:

Поскольку коэффициент положительный, то речь идет о товарах, взаимозаменяющих друг друга.

Ответ: коэффициент ценовой эластичности товара А составляет (–1,5), коэффициент перекрестной эластичности +1.

Задача 5

Постановка задачи: Цена на товар А выросла со 10 до 15 ден. ед. Спрос на товар В вырос с 1000 до 2000 штук, на товар С упал с 50 до 40 кг. Определите коэффициенты перекрестной эластичности.

Технология решения задачи:

Сначала рассчитываем коэффициент перекрестной эластичности товара В по формуле

Подставим значения и получим:

Поскольку коэффициент положительный, то речь идет о товарах, взаимозаменяющих друг друга.

Затем определяем коэффициент перекрестной эластичности товара С по такой же формуле:

Подставим значения и получим:

Поскольку коэффициент отрицательный, то речь идет о товарах, взаимодополняющих друг друга.

Задача 6

Постановка задачи: Цена на товар А выросла со 1 до 4 ден. ед. Спрос на товар В упал с 3000 до 1000 штук. Спрос на товар С вырос с 500 до 1000, на товар Д не изменился. Определите коэффициенты перекрестной эластичности.

Технология решения задачи:

Сначала рассчитываем коэффициент перекрестной эластичности товара С по формуле

Подставим значения и получим:

Поскольку коэффициент положительный, то речь идет о товарах, взаимозаменяющих друг друга.

Затем определяем коэффициент перекрестной эластичности товара В по такой же формуле:

Подставим значения и получим:

Поскольку коэффициент отрицательный, то речь идет о товарах, взаимодополняющих друг друга.

Поскольку спрос на товар Д не изменился, коэффициент перекрестной эластичности равен 0, т. е. товары являются нейтральными.

Задача 7

Постановка задачи: На рынке товара А объем спроса определяется формулой . Определите эластичность спроса в точке, соответствующей Q = 10.

Технология решения задачи: Для решения задачи необходимо применить формулу расчета коэффициента точечной эластичности:

, где B – коэффициент, показывающий угол наклона кривой спроса. Сначала надо найти цену: , следовательно, Р = 4. Отсюда .

Ответ: коэффициент эластичности равен 0,8.

Задача 8

Постановка задачи: Спрос на товар Х определяется формулой . Определите коэффициент эластичности при цене, равной 30 у. е.

Технология решения задачи: Для решения задачи необходимо применить формулу расчета коэффициента точечной эластичности:

, где B – коэффициент, показывающий угол наклона кривой спроса. Найдем объем спроса при заданной цене:

30 = 60 – 2 Qd, отсюда Qd = 15. Подставив значения в формулу, получим:

Задача 9

Постановка задачи: На рынке товара две группы потребителей, функции спроса которых записываются следующими формулами: , . Определите, какой будет эластичность спроса по цене в точке, соответствующей Qd, равной 12.

Технология решения задачи: Сначала определяется формула рыночного спроса на товар: Q_d1 + Q_d2 = 12 – Р + 12 – 3Р = 24 – 4Р. Находим цену товара при объеме спроса на рынке, равном 12 единиц: 12 = 24 – 4Р; Р = 3. Затем, применяя формулу точечной эластичности, находим коэффициент эластичности:

, где B – коэффициент, показывающий угол наклона кривой спроса.

Задача 10

Постановка задачи: Функция спроса на товар имеет вид Qd = 50 – 2Р. Определите дуговую эластичность спроса по цене при снижении цены с 10 до 9 евро.

Технология решения задачи: Определяем объем спроса при цене 10 евро: , а затем при цене 9 евро:

. После этого рассчитываем коэффициент эластичности:

Задачи на использование коэффициентов эластичности

Задача 11

Постановка задачи: Ценовая эластичность спроса населения на товар составляет (–0,8), а эластичность спроса по доходу 1,3. Если цена на товар снизится на 2 %, а доход увеличится на 5 %, что произойдет со спросом на данный товар?

Технология решения задачи: Объем спроса увеличится под воздействием снижения цены товара и увеличения дохода с учетом коэффициентов эластичности. Это рассчитывается следующим образом:

, где Inc – доход потребителя. Подставив значения, получим:

Ответ: Объем спроса увеличится на 8,1 %.

Задача 12

Постановка задачи: Коэффициент перекрестной эластичности Еx/y = (–2). Цена товара Y равна 100 у. е. Определите спрос на товар Х, если цена товара Y увеличится на 10 %, а первоначальный спрос на товар Х равен 80 т.

Технология решения задачи: Для решения задачи необходимо воспользоваться формулой расчета коэффициента перекрестной эластичности товара Х по формуле

Следовательно, изменение объема спроса товара Х определяется путем перемножения коэффициента перекрестной эластичности на изменение цены товара У: . Следовательно, объем спроса будет равен: Qdх = 80 * 0,95 = 76 т.

Задача 13

Постановка задачи: При цене 10 у. е. объем спроса на товар А равен 1000 штук. Предприниматель решает изменить цену. Он определил, что при росте цены на 10 % эластичность товара становится равной (–1,2), при снижении цены на 10 % коэффициент эластичности равен (–0,8). На какой цене остановится предприниматель?

Технология решения задачи: Для решения задачи надо определить, каким станет спрос при новой цене, а затем рассчитать выручку от продажи товара. При цене 10 у. е. предприниматель получает 10 000 у.е. Если цена снизится на 10 %, она станет равна 9 у. е., спрос на товар вырастет на , т. е. станет 1000 * 1,08 = 1080 штук. Предприниматель получит от продажи этих товаров:

у. е. Выручка сократилась на 10 000 – 9720 = 280 у. е., следовательно, снижать цену нельзя.

Если цена увеличится на 10 %, т. е. станет 11 у. е., спрос на товар упадет на 12 % (1,2 * 10 %), т. е. станет равен . Продавая их по 11 у. е., предприниматель выручит 9680 у. е. Выручка снова сократилась, значит, увеличивать цену на 10 % тоже нельзя. Поэтому предпринимателю следует сохранить старую цену.

Частные коэффициенты эластичности

Пример . 1. Оценка уравнения регрессии. Определим вектор оценок коэффициентов регрессии. Согласно методу наименьших квадратов, вектор получается из выражения:
s = (X T X) -1 X T Y
Матрица X

Можно также посмотреть, как было найдено решение аналогичного примера.
Видеоинструкция
Матрица Y
Матрица X T

Умножаем матрицы, (X T X)

24	4459.4	1907.7	214.2	417.47
4459.4	907391.96	353017.36	40134.04	87383.93
1907.7	353017.36	152366.77	17041.58	33412.82
214.2	40134.04	17041.58	1921.32	3807
417.47	87383.93	33412.82	3807	8907.78

В матрице, (X T X) число 24, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы X T и 1-го столбца матрицы X
Умножаем матрицы, (X T Y)

2743.3

557558.59

218286.47

24740.08

54488.32

Находим определитель det(X T X) T = 871494173124.25
Находим обратную матрицу (X T X) -1

67.5762	-0.0883	-0.4341	-3.3069	0.7404
-0.0883	0.0002	0.0006	0.0037	-0.0012
-0.4341	0.0006	0.0036	0.0134	-0.0047
-3.3069	0.0037	0.0134	0.2444	-0.0358
0.7404	-0.0012	-0.0047	-0.0358	0.01

Вектор оценок коэффициентов регрессии равен
s = (X T X) -1 X T Y =

-55.01

0.43

0.86

-1.14

0.95

Уравнение регрессии (оценка уравнения регрессии)
Y = -55.0117 + 0.4315X 1 + 0.8571X 2 -1.1392X 3 + 0.9481X 4
2. Матрица парных коэффициентов корреляции.
Число наблюдений n = 24. Число независимых переменных в модели ровно 4, а число регрессоров с учетом единичного вектора равно числу неизвестных коэффициентов. С учетом признака Y, размерность матрицы становится равным 6. Матрица, независимых переменных Х имеет размерность (24 х 6). Матрица Х T Х определяется непосредственным умножением или по следующим предварительно вычисленным суммам.
Матрица составленная из Y и X
Транспонированная матрица.
Матрица A T A.

24	2743.3	4459.4	1907.7	214.2	417.47
2743.3	344649.05	557558.59	218286.47	24740.08	54488.32
4459.4	557558.59	907391.96	353017.36	40134.04	87383.93
1907.7	218286.47	353017.36	152366.77	17041.58	33412.82
214.2	24740.08	40134.04	17041.58	1921.32	3807
417.47	54488.32	87383.93	33412.82	3807	8907.78

Полученная матрица имеет следующее соответствие:

∑n	∑y	∑x1	∑x2	∑x3	∑x4
∑y	∑y 2	∑x1·y	∑x2·y	∑x3·y	∑x4·y
∑x1	∑x1·y	∑x1 2	∑x2·x1	∑x3·x1	∑x4·x1
∑x2	∑x2·y	∑x2·x1	∑x2 2	∑x3·x2	∑x4·x2
∑x3	∑x3·y	∑x3·x1	∑x3·x2	∑x3 2	∑x3·x4
∑x4	∑x4·y	∑x4·x1	∑x4·x2	∑x4·x3	∑x4 2

Найдем парные коэффициенты корреляции.
Для y и x 1
Уравнение имеет вид y = ax + b
Средние значения

Для y и x 2
Уравнение имеет вид y = ax + b
Средние значения

Для y и x 3
Уравнение имеет вид y = ax + b
Средние значения

Для y и x 4
Уравнение имеет вид y = ax + b
Средние значения

Для x 1 и x 2
Уравнение имеет вид y = ax + b
Средние значения

Для x 1 и x 3
Уравнение имеет вид y = ax + b
Средние значения

Для x 1 и x 4
Уравнение имеет вид y = ax + b
Средние значения

Для x 2 и x 3
Уравнение имеет вид y = ax + b
Средние значения

Для x 2 и x 4
Уравнение имеет вид y = ax + b
Средние значения

Для x 3 и x 4
Уравнение имеет вид y = ax + b
Средние значения

Матрица парных коэффициентов корреляции.

–	y	x 1	x 2	x 3	x 4
y	1	0.97	0.05	0.47	0.95
x 1	0.97	1	-0.19	0.38	0.86
x 2	0.05	-0.19	1	0.18	0.21
x 3	0.47	0.38	0.18	1	0.65
x 4	0.95	0.86	0.21	0.65	1

Анализ первой строки этой матрицы позволяет произвести отбор факторных признаков, которые могут быть включены в модель множественной корреляционной зависимости. Факторные признаки, у которых r yxi j y) > r(x k x j ) ; r(x k y) > r(x k x j ).
Если одно из неравенств не соблюдается, то исключается тот параметр x k или x j , связь которого с результативным показателем Y оказывается наименее тесной.
3. Анализ параметров уравнения регрессии.
Перейдем к статистическому анализу полученного уравнения регрессии: проверке значимости уравнения и его коэффициентов, исследованию абсолютных и относительных ошибок аппроксимации
Для несмещенной оценки дисперсии проделаем следующие вычисления:
Несмещенная ошибка e = Y – X*s (абсолютная ошибка аппроксимации)

10.93
9.67
9.31
9.91
9.05
7.65
7.11
8.68
12.84
12.97
15.56
22.48
13.97
14.04
15.95
12.88
15.87
15.08
16.81
19.89
22.34
24.13
24.08
21.31

s e 2 = (Y – X*s) T (Y – X*s)
Несмещенная оценка дисперсии равна

Оценка среднеквадратичного отклонения равна

Найдем оценку ковариационной матрицы вектора k = σ*(X T X) -1

1183.8	-1.55	-7.6	-57.93	12.97
-1.55	0	0.01	0.06	-0.02
-7.6	0.01	0.06	0.23	-0.08
-57.93	0.06	0.23	4.28	-0.63
12.97	-0.02	-0.08	-0.63	0.17

Дисперсии параметров модели определяются соотношением S 2 i = K ii , т.е. это элементы, лежащие на главной диагонали
С целью расширения возможностей содержательного анализа модели регрессии используются частные коэффициенты эластичности, которые определяются по формуле

Частные коэффициент эластичности E 1 2 3 4 2 = 0.9 2 = 0.81
т.е. в 81.2384 % случаев изменения х приводят к изменению y. Другими словами – точность подбора уравнения регрессии – высокая
Значимость коэффициента корреляции

По таблице Стьюдента находим Tтабл
T табл (n-m-1;a) = (19;0.05) = 1.729
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически – значим.

4. Оценка значения результативного признака при заданных значениях факторов.
Y(0.0,0.0,0.0,0.0,) = -55.01 + 0.4315 * 0.0 + 0.8571 * 0.0-1.1392 * 0.0 + 0.9481 * 0.0 = -55.01
Доверительные интервалы с вероятностью 0.95 для индивидуального значения результативного признака.
S 2 = X 0 T (X T X) -1 X 0
где
X 0 T = [ 1 0.0 0.0 0.0 0.0]
(X T X) -1

67.5762	-0.0883	-0.4341	-3.3069	0.7404
-0.0883	0.0002	0.0006	0.0037	-0.0012
-0.4341	0.0006	0.0036	0.0134	-0.0047
-3.3069	0.0037	0.0134	0.2444	-0.0358
0.7404	-0.0012	-0.0047	-0.0358	0.01

X 0

S 2 = 67.58

(Y – t*S Y ; Y + t*S Y )
(-55.01 – 1.729*144.01 ; -55.01 + 1.729*144.01)
(-304;193.98)
Доверительные интервалы с вероятностью 0.95 для среднего значения результативного признака.

(-55.01 – 1.729*145.07 ; -55.01 + 1.729*145.07)
(-305.84;195.82)
5. Проверка гипотез относительно коэффициентов уравнения регрессии (проверка значимости параметров множественного уравнения регрессии).
1) t-статистика

Статистическая значимость коэффициента регрессии b 0 не подтверждается

Статистическая значимость коэффициента регрессии b 1 подтверждается

Статистическая значимость коэффициента регрессии b 2 подтверждается

Статистическая значимость коэффициента регрессии b 3 не подтверждается

Статистическая значимость коэффициента регрессии b 4 подтверждается
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(b i – t i S i ; b i + t i S i )
b 0 : (-114.5003;4.477)
b 1 : (0.3419;0.521)
b 2 : (0.4234;1.2908)
b 3 : (-4.7171;2.4386)
b 4 : (0.2255;1.6707)
2) F-статистика. Критерий Фишера

Fkp = 2.74
Поскольку F > Fkp, то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно
6. Проверка на наличие гетероскедастичности методом графического анализа остатков.
В этом случае по оси абсцисс откладываются значения объясняющей переменной X i , а по оси ординат квадраты отклонения e i 2 .

[spoiler title=”источники:”]

http://eos.ibi.spb.ru/umk/2_6/15/15_P2_R1_T2.html

http://math.semestr.ru/regress/regres2.php

[/spoiler]