2.4.3. Функция ПЛОТНОСТИ распределения вероятностей
или дифференциальная функция распределения. Она представляет собой производную функции распределения: ![]() .
.
Примечание: для дискретной случайной величины такой функции не существует
В нашем примере:
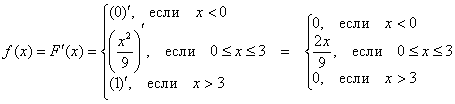
то есть, всё очень просто – берём производную от каждого куска, и порядок.
Но настоящий порядок состоит в том, что несобственный интеграл от ![]() с пределами интегрирования от «минус» до «плюс» бесконечности:
с пределами интегрирования от «минус» до «плюс» бесконечности:
![]() – равен единице, и строго единице. В противном случае перед нами не функция плотности, и если эта функция была найдена как производная, то
– равен единице, и строго единице. В противном случае перед нами не функция плотности, и если эта функция была найдена как производная, то ![]() – не является функцией распределения (несмотря на какие бы то ни было другие признаки).
– не является функцией распределения (несмотря на какие бы то ни было другие признаки).
Проверим «подлинность» наших функций. Если случайная величина ![]() принимает значения из конечного промежутка, то всё дело сводится к вычислению определённого интеграла. В силу свойства аддитивности, делим интеграл на 3 части:
принимает значения из конечного промежутка, то всё дело сводится к вычислению определённого интеграла. В силу свойства аддитивности, делим интеграл на 3 части:

Совершенно понятно, что левый и правый интегралы равны нулю и нам осталось вычислить средний интеграл:
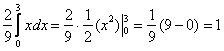 , что и требовалось проверить.
, что и требовалось проверить.
С вероятностной точки зрения это означает, что случайная величина ![]() достоверно примет одно из значений отрезка
достоверно примет одно из значений отрезка ![]() . Геометрически же это значит, что площадь между осью
. Геометрически же это значит, что площадь между осью ![]() и графиком
и графиком ![]() равна единице, и в данном случае речь идёт о площади треугольника
равна единице, и в данном случае речь идёт о площади треугольника ![]() . Сторона
. Сторона ![]() является фрагментом прямой
является фрагментом прямой ![]() и для её построения достаточно найти точку
и для её построения достаточно найти точку ![]() :
:
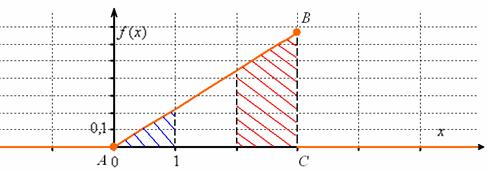
Ну вот, теперь всё наглядно – где бОльшая площадь, там и сконцентрированы более вероятные значения.
Так как функция плотности «собирает под собой» вероятности, то она неотрицательна ![]() и её график не может располагаться ниже оси
и её график не может располагаться ниже оси ![]() . В общем случае функция разрывна (смотрим, где «жирные» оранжевые точки!).
. В общем случае функция разрывна (смотрим, где «жирные» оранжевые точки!).
Теперь разберём весьма любопытный факт: поскольку действительных чисел несчётно много, то вероятность того, что случайная величина ![]() примет какое-то конкретное значение стремится к нулю. И поэтому вероятности рассчитывают не для отдельно взятых точек, а для целых промежутков (пусть даже очень малых). Как вы правильно догадываетесь:
примет какое-то конкретное значение стремится к нулю. И поэтому вероятности рассчитывают не для отдельно взятых точек, а для целых промежутков (пусть даже очень малых). Как вы правильно догадываетесь:
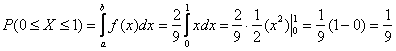 (синяя площадь на чертеже) – вероятность того, что случайная величина примет значение из отрезка
(синяя площадь на чертеже) – вероятность того, что случайная величина примет значение из отрезка ![]() ;
;
![]() (красная площадь) – вероятность того, что случайная величина примет значение из отрезка
(красная площадь) – вероятность того, что случайная величина примет значение из отрезка ![]() .
.
По той причине, что отдельно взятые значения можно не принимать во внимание, с помощью этих же интегралов рассчитываются и вероятности по интервалам и полуинтервалам, в частности:
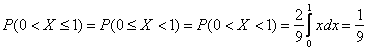
Этим же объяснятся аналогичная «вольность» с функцией ![]() .
.
Возможно, кто-то спросит: а зачем считать интегралы, если есть функция ![]() ?
?
А дело в том, что во многих задачах непрерывная случайная величина ИЗНАЧАЛЬНО задана функцией ![]() плотности распределения, которая ТОЖЕ однозначно определяет случайную величину. Но, как вариант, можно сначала найти функцию
плотности распределения, которая ТОЖЕ однозначно определяет случайную величину. Но, как вариант, можно сначала найти функцию ![]() (с помощью тех же интегралов), после чего использовать «лёгкий способ» бросить курить отыскания вероятностей. Впрочем, об этом чуть позже:
(с помощью тех же интегралов), после чего использовать «лёгкий способ» бросить курить отыскания вероятностей. Впрочем, об этом чуть позже:
Задача 105
Непрерывная случайная величина ![]() задана своей функцией распределения:
задана своей функцией распределения:
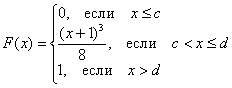
Найти значения ![]() и функцию
и функцию ![]() . Проверить, что
. Проверить, что ![]() действительно является функцией плотности распределения. Вычислить вероятности
действительно является функцией плотности распределения. Вычислить вероятности ![]() . Построить графики
. Построить графики ![]() .
.
Тренируемся самостоятельно! Если возникнут затруднения, то внимательно перечитайте вышеизложенный материал. Краткое решение и ответ в конце книги.
Вообще, типовые задачи на непрерывную случайную величину можно разделить на 2 большие группы:
1) когда дана функция ![]() , 2) когда дана функция
, 2) когда дана функция ![]() .
.
В первом случае не составляет особых трудностей отыскать функцию плотности распределения – почти всегда производные не то что простЫ, а примитивны (в чём мы только что убедились). Но вот когда НСВ задана функцией ![]() , то нахождение функции распределения – есть более кропотливый процесс:
, то нахождение функции распределения – есть более кропотливый процесс:
Задача 106
Непрерывная случайная величина ![]() задана функцией плотности распределения:
задана функцией плотности распределения:
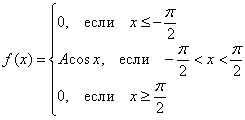
Найти значение ![]() и составить функцию распределения вероятностей
и составить функцию распределения вероятностей ![]() . Вычислить
. Вычислить ![]() .
.
Построить графики ![]() .
.
Решение: найдём константу ![]() . Это классика (в подавляющем большинстве задач вам не предложат готовую функцию плотности). Используем свойство
. Это классика (в подавляющем большинстве задач вам не предложат готовую функцию плотности). Используем свойство ![]() .
.
В данном случае:

На практике нулевые интегралы можно опускать, а константу сразу выносить за знак интеграла:
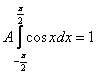 (*)
(*)
Пользуясь чётностью подынтегральной функции, вычислим интеграл:
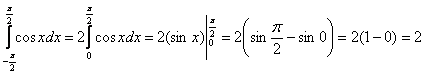 и подставим результат в уравнение (*):
и подставим результат в уравнение (*):
![]() , откуда выразим
, откуда выразим ![]()
Таким образом, функция плотности распределения:
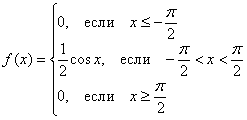
Выполним проверку, а именно, вычислим тот же самый интеграл, но уже с известной константой. Для разнообразия я не буду пользоваться чётностью:
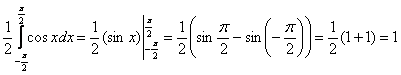 , отлично.
, отлично.
Обратите внимание, что только при ![]() и только при этом значении предложенная в условии функция является функцией плотности распределения. Ну и тут не лишним будет проконтролировать, что на интервале
и только при этом значении предложенная в условии функция является функцией плотности распределения. Ну и тут не лишним будет проконтролировать, что на интервале ![]() , т.е. условие неотрицательности действительно выполнено. Доверяй условию, да проверяй 😉 Не раз и не два мне встречались функции, которые в принципе не могли быть плотностью, что говорило об опечатках или о невнимательности авторов задач.
, т.е. условие неотрицательности действительно выполнено. Доверяй условию, да проверяй 😉 Не раз и не два мне встречались функции, которые в принципе не могли быть плотностью, что говорило об опечатках или о невнимательности авторов задач.
Теперь начинается самое интересное. Функции распределения вероятностей – есть интеграл:
![]()
Так как ![]() состоит из трёх кусков, то решение разобьётся на 3 шага:
состоит из трёх кусков, то решение разобьётся на 3 шага:
1) На промежутке ![]() , поэтому:
, поэтому: ![]()
2) На интервале ![]() , и мы прицепляем следующий вагончик:
, и мы прицепляем следующий вагончик:
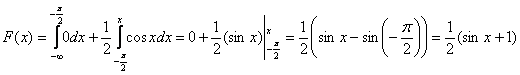
При подстановке верхнего предела интегрирования можно считать, что вместо «икс» мы подставляем «икс». Если же возник вопрос с пределом нижним, то вспоминаем график синуса либо его нечётность: ![]() .
.
3) И, наконец, на ![]() , и детский паровозик отправляется в путь:
, и детский паровозик отправляется в путь:

Внимание! А вот в этом задании нулевые интегралы пропускать НЕ НАДО. Чтобы показать своё понимание функции распределения 😉 К тому же, они могут оказаться вовсе не нулевыми, и тогда придётся иметь дело с интегралами несобственными. И такой пример я обязательно разберу ниже.
Записываем наши достижения под единую скобку:
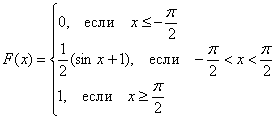
С высокой вероятностью всё правильно, но, тем не менее, устно возьмём производную: 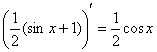 , а также «прозвоним» точки «стыка»:
, а также «прозвоним» точки «стыка»:
![]()
Правильность решения можно проконтролировать и в ходе построения графика, но, во-первых, он не всегда требуется, а во-вторых, до сего момента можно успеть «наломать дров». Ибо вероятности попадания чаще находят с помощью функции распределения:
![]()
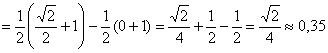 – вероятность того, что случайная величина
– вероятность того, что случайная величина ![]() примет значение из промежутка
примет значение из промежутка ![]()
Второй способ состоит в вычислении интеграла:
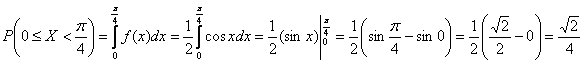 что, кстати, не труднее. И проверочка заодно получилась.
что, кстати, не труднее. И проверочка заодно получилась.
Выполним чертежи. График ![]() представляет собой
представляет собой косинусоиду, сжатую вдоль ординат в 2 раза. Тот редкий случай, когда функция плотности непрерывна:
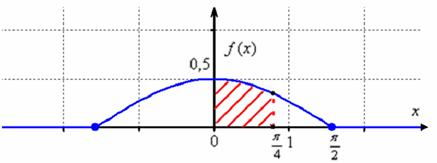
Значение ![]() численно равно заштрихованной площади – это я специально нарисовал, чтобы напомнить вероятностный смысл плотности функции распределения. И вся площадь под «дугой» равна единице, то есть, достоверным является тот факт, что случайная величина примет значение из интервала
численно равно заштрихованной площади – это я специально нарисовал, чтобы напомнить вероятностный смысл плотности функции распределения. И вся площадь под «дугой» равна единице, то есть, достоверным является тот факт, что случайная величина примет значение из интервала ![]() . Заметьте, что значения
. Заметьте, что значения ![]() по условию, невозможны.
по условию, невозможны.
Осталось изобразить функцию распределения. График ![]() представляет собой синусоиду, сжатую в 2 раза вдоль оси ординат и сдвинутую на
представляет собой синусоиду, сжатую в 2 раза вдоль оси ординат и сдвинутую на ![]() вверх:
вверх:
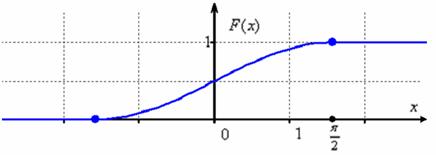
В принципе, тут можно было не заморачиваться преобразованием графиков, а найти несколько опорных точек и догадаться, как выглядит кривая (тригонометрическая таблица в помощь). Но «любительский» подход чреват тем, что график получится принципиально не точным. Так, в нашем примере в точке ![]() существует перегиб графика функции
существует перегиб графика функции ![]() , и велик риск неверно отобразить его выпуклость / вогнутость.
, и велик риск неверно отобразить его выпуклость / вогнутость.
Чертежи желательно расположить так, чтобы оси ординат (вертикальные оси) лежали ровненько одна под другой. Это будет хорошим тоном.
И я так чувствую, вам уже не терпится проверить свои силы. Как водится, пример попроще:
Задача 107
Задана плотность распределения вероятностей непрерывной случайной величины ![]() :
:
![]()
Требуется:
1) определить коэффициент ![]() ;
;
2) найти функцию распределения ![]() ;
;
3) построить графики ![]() ;
;
4) найти вероятность того, что ![]() примет значение из промежутка
примет значение из промежутка ![]()
и задачка поинтереснее:
Задача 108
Непрерывная случайная величина ![]() задана плотностью распределения вероятностей:
задана плотностью распределения вероятностей:
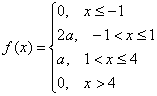
Найти значение ![]() и построить график плотности распределения. Найти функцию распределения вероятностей
и построить график плотности распределения. Найти функцию распределения вероятностей ![]() и построить её график. Вычислить вероятность
и построить её график. Вычислить вероятность ![]() .
.
Дерзайте! Свериться с решением можно внизу книги.
Следует отметить, что все эти задачи реально предлагают студентам-заочникам, и поэтому я не предлагаю вам ничего необычного.
И в заключение параграфа обещанные случаи с несобственными интегралами:
Задача 109
Непрерывная случайная величина ![]() задана своей плотностью распределения:
задана своей плотностью распределения:
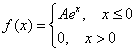
Найти коэффициент ![]() и функцию распределения
и функцию распределения ![]() . Построить графики.
. Построить графики.
Решение: по свойству функции плотности распределения:
![]()
В данной задаче ![]() состоит из 2 частей, поэтому:
состоит из 2 частей, поэтому:
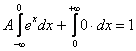
Правый интеграл равен нулю, а вот левый – есть «живой» несобственный интеграл с бесконечным нижним пределом:
![]()
Таким образом, наше уравнение превратилось в готовый результат:
![]()
и функция плотности:
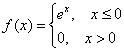
Функция ![]() , как нетрудно понять, отыскивается в 2 шага:
, как нетрудно понять, отыскивается в 2 шага:
1) На промежутке ![]() , следовательно:
, следовательно:
![]() – вот такая вот у нас замечательная экспонента. Как птица Феникс.
– вот такая вот у нас замечательная экспонента. Как птица Феникс.
2) На интервале ![]() и:
и:
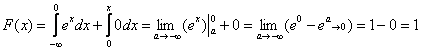 , что и должно получиться.
, что и должно получиться.
Для построения графиков найдём пару опорных точек: ![]() и аккуратно прочертим кусочки экспонент с причитающимися дополнениями:
и аккуратно прочертим кусочки экспонент с причитающимися дополнениями:

Заметьте, что теоретически случайная величина ![]() может принять сколь угодно большое по модулю отрицательное значение, и ось абсцисс является горизонтальной асимптотой для обоих графиков при
может принять сколь угодно большое по модулю отрицательное значение, и ось абсцисс является горизонтальной асимптотой для обоих графиков при ![]() .
.
В соответствующей статье сайта я рассмотрел ещё более интересный пример с функцией ![]() , где случайная величина теоретически принимает вообще ВСЕ действительные значения. Но это уже несколько повышенный уровень сложности.
, где случайная величина теоретически принимает вообще ВСЕ действительные значения. Но это уже несколько повышенный уровень сложности.
 2.4.4. Как вычислить математическое ожидание и дисперсию НСВ?
2.4.4. Как вычислить математическое ожидание и дисперсию НСВ?
 2.4.2. Вероятность попадания в промежуток
2.4.2. Вероятность попадания в промежуток
| Оглавление |
Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Непрерывная случайная величина
Ранее мы представили примеры решений задач о дискретной случайной величине, теперь переходим к непрерывной. Формально в задачах требуется найти тоже самое: вычислить числовые характеристики, начертить графики, определить неизвестные параметры, найти вероятности событий.
Но формулы-то совсем другие (в силу непрерывности СВ), поэтому стоит разобраться в них хорошенько. Надеемся, наши примеры вам помогут (а если нет времени, закажите решение).
Ниже вы найдете примеры решений на самые разные законы распределений непрерывных случайных величин: законы $arcsin$ и $arctan$, тригонометрические и логарифмические функции, показательный, равномерный закон распределения, законы Коши, Симпсона, Лапласа и т.д.
Примеры для других НСВ: Нормальный закон, Равномерный закон, Показательный закон.
Полезная страница? Сохрани или расскажи друзьям
Примеры решений
Задача 1. Случайная величина X задана дифференциальной функцией распределения
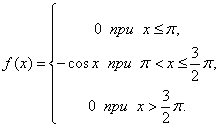
1) Определить вероятность попадания случайной величины X в интервал $[pi, 5/4 pi]$.
2) Найти математическое ожидание и дисперсию случайной величины X.
Задача 2. Случайная величина X задана плотностью вероятности:
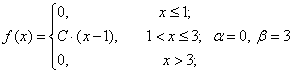
Требуется:
а) найти коэффициент C;
б) найти функцию распределения F(x);
в) найти M(X), D(X), σ(X)
г) найти вероятность P(α < X < β);
д) построить графики f(x) и F(x).
Задача 3. Случайная величина Х задана функцией распределения F(x).
А) является ли случайная величина Х непрерывной?
Б) имеет ли случайная величина Х плотность вероятности f(X)? Если имеет, найти ее.
В) постройте схематично графики f(X) и F(X).
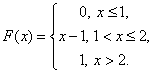
Задача 4. Дана функция распределения F(x) непрерывной случайной величины X.
1. Найти значения параметров a,b
2. Построить график функции распределения F(x)
3. Найти вероятность P(α < X < β)
4. Найти плотность распределения p(x) и построить ее график.
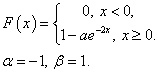
Задача 5. Время в годах безотказной работы прибора подчинено показательному закону, т.е. плотность распределения этой случайной величины такова: f(t)=2e-2t при t ≥ 0 и f(t)=0 при t<0.
1) Найти формулу функции распределения этой случайной величины.
2) Определить вероятность того, что прибор проработает не более года.
3) Определить вероятность того, что прибор безотказно проработает 3 года.
4) Определить среднее ожидаемое время безотказной работы прибора.
Задача 6. Функция распределения вероятностей случайной величины $X$ имеет вид:
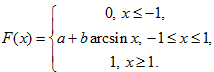
А) найти $a$ и $b$;
Б) найти плотность $f(x)$;
В) нарисовать график $F(x)$;
Г) нарисовать график $f(x)$;
Д) найти $M[X]$;
Е) найти $D[X]$.
Задача 7. Функция распределения вероятностей случайной величины $X$ имеет вид:
$$F(x)=A+B arctan (x/2), -infty lt x lt infty $$ (закон Коши).
А) определить постоянные $A$ и $B$;
Б) найти плотность распределения вероятностей
В) найти $P(-1 lt X lt 1)$;
Г) нарисовать график $F(x)$;
Д) нарисовать график $f(x)$.
Задача 8. Случайная величина $X$ имеет распределение Парето с плотностью вероятности $f(x)=4/23(23/x)^5$
при $23 le x$ и $f(x)=0$ при $x lt 23$.
Найдите $M(X)$ и $P(23lt X lt 27)$.
Задача 9. Непрерывная случайная величина задана интегральной функцией (функцией распределения) $F(x)$. Найти:
А) вероятность попадания случайной величины $X$ в интервал $(a;b)$.
Б) дифференциальную функцию (функцию плотности вероятностей) $f(x)$.
В) математическое ожидание, дисперсию и среднее квадратическое отклонение величины $X$.
Г) построить графики функций $F(x)$ и $f(x)$.
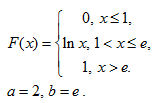
Задача 10. Случайная величина $X$ подчинена закону Лапласа $p(x)=acdot e^{-lambda |x|}$, $lambda gt 0.$ Найти $a$, $M(x)$, $D(x)$ и $F(x)$. Построить графики $p(x)$ и $F(x)$.
Задача 11. Случайная величина $X$ задана функцией распределения $F(x)$. Найти:
5) дифференциальную функцию $f(x)$ (плотность распределения),
6) математическое ожидание $M(X)$, дисперсию $D(X)$, среднее квадратическое отклонение $sigma(X)$.
7) Моду $Mo$ и медиану $Me$,
8) $P(1/2 lt X lt 2).$
Построить графики функции и плотности распределения.
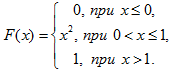
Задача 12. Случайная величина $Х$ подчинена закону Симпсона (закону равнобедренного треугольника) на участке от $-a$ до $+a$.
а) Написать выражение для плотности распределения.
б) Построить график функции распределения.
в) Определить числовые характеристики случайной величины Х.
Мы отлично умеем решать задачи по теории вероятностей
Решебник по теории вероятности онлайн
Больше 11000 решенных и оформленных задач по теории вероятности:
Функция
распределения полностью характеризует
случайную величину, однако, имеет один
недостаток. По функции распределения
трудно судить о характере распределения
случайной величины в небольшой окрестности
той или иной точки числовой оси.
Определение. Плотностью
распределения вероятностей
непрерывной случайной величины Х
называется функция f(x) –
первая производная от функции
распределения F(x).
Плотность
распределения также называют дифференциальной
функцией.
Для описания дискретной случайной
величины плотность распределения
неприемлема.
Смысл
плотности распределения состоит в том,
что она показывает как часто появляется
случайная величина Х в некоторой
окрестности точки х при
повторении опытов.
После
введения функций распределения и
плотности распределения можно дать
следующее определение непрерывной
случайной величины.
Определение. Случайная
величина Х называется непрерывной,
если ее функция распределенияF(x)
непрерывна на всей оси ОХ, а плотность
распределения f(x)
существует везде, за исключением( может
быть, конечного числа точек.
Зная
плотность распределения, можно вычислить
вероятность того, что некоторая случайная
величина Х примет значение, принадлежащее
заданному интервалу.
Теорема. Вероятность
того, что непрерывная случайная величина
Х примет значение, принадлежащее
интервалу (a, b),
равна определенному интегралу от
плотности распределения, взятому в
пределах от a до b.
Доказательство
этой теоремы основано на определении
плотности распределения и третьем
свойстве функции распределения,
записанном выше.
Геометрически
это означает, что вероятность того, что
непрерывная случайная величина примет
значение, принадлежащее интервалу
(a, b),
равна площади криволинейной трапеции,
ограниченной осью ОХ, кривой
распределения f(x)
и прямыми x=a и x=b.
№31. Равномерное
распределение НСВ: ф-я распр-я, плотность
расп-я, график, мат ожидание, дисперсия
Понятие НСВ,
функция ее распределения
Случайной
непрерывной величиной является
величина,
которая может принять любое из значений
некоторого промежутка.
Здесь нельзя
отделить одно возможное значение от
другого промежутком, не содержащим
возможных значений случайной величины.
Случайной
непрерывной величиной является
величина,
функция распределения F(x)
которой, непрерывна на всей числовой
оси.
Функция распределения
HСВ
F(x)
есть кусочно-дифференцируемая функция
с непрерывной производной.
Вероятность того,
что случайная величина примет значение,
заключенное в некотором интервале (а,
b),
равна приращению функции распределения
на этом интервале;P(a
≤ X
≤b)
= F
(b)
– F
(а).
При рассмотрении
функции распределения, числовой
промежуток записывается так же в виде
[x1;
x2],
тогда вероятность того, что случайная
величина примет значение, заключенное
в этом интервале равна:
p(x1≤
x
≤ x2)
= F
(x2)
– F
(x1).-
что более понятно и привычно.
Вероятность того,
что случайная непрерывная величина X
примет одно определенное значение,
равна нулю.
Понятие
плотности распределения, функция
плотности НСВ
Плотностью
распределения вероятностей
непрерывной случайной величины X
называют
функцию f
(х) –
первую производную от функции распределения
F
(х): f
(х)= F'(х)
Из этого определения
следует, что функция распределения
F(х)
является
первообразной для плотности распределения
f
(х):
F(х)=
f
(х).
Функцию f
(х) можно
называть
дифференциальной функцией
Таким образом, зная
интегральную функцию (функцию
распределения) можно найти дифференциальную
функцию(функцию плотности) и наоборот
по формулам:f
(х)= F'(х)
F(х)=
f
(х).

Математическим
ожиданием непрерывной случайной
величины Х, возможные значения которой
принадлежат отрезку [a,b], называется
определенный интеграл
![]()
Если
возможные значения случайной величины
рассматриваются на всей числовой оси,
то математическое ожидание находится
по формуле:
При этом, конечно,
предполагается, что несобственный
интеграл сходится.
Свойства
математического ожидания НСВ аналогичны
свойствам математического ожидания
ДСВ.
Дисперсией
непрерывной случайной величины называется
математическое ожидание квадрата ее
отклонения.
![]()
По
аналогии с дисперсией дискретной
случайной величины, для практического
вычисления дисперсии используется
формула:
![]()
№32 Нормальное
расп-е
Это такое расп-е
случ.велечины Х, плотность Р которого
опис. Формулой f(x)=(1/(x)*2)*exp(-(x–M(x)2 )/(22(x),
где (х)-
сред.квадрат.отклонение, М(х)-матем.ожидание
№33
Нормальное расп-е: 1)вероятность попадания
в заданный интервал, вероятность заданого
отклонения
1)Если случайная
величина Х задана плотностью распределения
f(x), то вероятность того, что Х примет
значение, принадлежащее заданному
интервалу, вычисляется по формуле .
Подставив в формулу значение плотности
распределения из для нормального
распределения N(a, s) и сделав ряд
преобразований, вероятность того, что
Х примет значение, принадлежащее
заданному интервалу [x1,
x2],
будет равна:
|
|
Где а-мат.ожидание |
2)
|
P |
№34 Показательное
расп-е НСВ: график, ф-я расп-я, плотность
расп-я, матем ожидание, дисперсия
№35 Показательное
расп-е: ф-я надежности, показательный
закон надежности, характеристичесткое
свойство этого закона
Функция надежности
Будем называть
элементом
некоторое
устройство независимо от того, “простое”
оно или “сложное”.
Пусть элемент
начинает работать в момент времени
t0=0,
а по истечении времени длительностью
t
происходит отказ. Обозначим через Т
непрерывную
случайную величину – длительность
времени безотказной работы элемента.
Если элемент проработал безотказно (до
наступления отказа) время, меньшее t
то, следовательно, за время длительностью
t
наступит
отказ.
Таким образом,
функция распределения F
(t)=P(T<t)
определяет
вероятность отказа за время длительностью
t.
Следовательно,
вероятность безотказной работы за это
же время длительностью t,
т. е. вероятность
противоположного события Т
> t,
равна
![]()
Функцией надежности
R
(t)
называют
функцию, определяющую надежность работы
элемента за время длительностью t:
Показательный
закон надежности
Часто длительность
времени безотказной работы элемента
имеет показательное распределение,
функция распределения которого![]()
Следовательно,
функция надежности в случае показательного
распределения времени безотказной
работы элемента имеет вид![]()
Показательным
законом надежности называют
функцию надежности, определяемую
равенством![]()
где
интенсивность отказов
Как следует из
определения функции надежности, эта
формула позволяет найти вероятность
безотказной работы элемента на
интервале времени длительностью tt
если время
безотказной работы имеет, показательное
распределение.
Характеристическое
свойство показательного закона
надежности.
Показательный
закон надежности весьма прост и удобен
для решения задач, возникающих на
практике. Очень многие формулы теории
надежности значительно упрощаются.
Объясняется это тем, что этот закон
обладает следующим важным свойством:
“Вероятность безотказной работы
элемента на интервале времени
длительностью t
не зависит от времени предшествующей
работы до начала рассматриваемого
интервала, а зависит только от длительности
времени t
(при заданной интенсивности отказов
)”.
Итак, в случае
показательного закона надежности
безотказная работа элемента “в
прошлом” не сказывается на величине
вероятности его безотказной работы “в
ближайшем будущем”.
Замечание.
Можно доказать, что рассматриваемым
свойством обладает только показательное
распределение. Поэтому если на практике
изучаемая случайная величина этим
свойством обладает, то она распределена
по показательному закону. Например, при
допущении, что метеориты распределены
равномерно в пространстве и во времени,
вероятность попадания метеорита в
космический корабль не зависит от того,
попадали или не попадали метеориты в
корабль до начала рассматриваемого
интервала времени. Следовательно,
случайные моменты времени попадания
метеоритов в космический корабль
распределены по показательному закону.
№36 Ф-я одного
случ аргумента, матем ожидание
Если каждому
возможному значению случайной величины
Х
соответствует одно возможное значение
случайной величины Y,
то Y
называют
функцией
случайного аргу-мента Х:
Y
=
φ(X).
Выясним, как найти закон распределения
функции по известному закону распределения
аргумента.
1) Пусть аргумент
Х
– дискретная случайная величина, причем
различным значениям Х
соот-ветствуют различные значения Y.
Тогда вероятности соответствующих
значений Х
и Y
равны.
2) Если разным
значениям Х
могут соответствовать одинаковые
значения Y,
то вероятности значений аргумента, при
которых функция принимает одно и то же
значение, складываются.
3) Если Х
– непрерывная случайная величина, Y
= φ(X),
φ(x)
– монотонная и дифференцируемая функция,
а ψ(у)
– функция, обратная к
φ(х),
то плотность распределения g(y)
случайно функции Y
равна:
![]()
Математическое
ожидание функции одного случайного
аргумента.
Пусть Y
= φ(X)
– функция случайного аргумента Х,
и требуется найти ее математическое
ожидание, зная закон распределения Х.
1)
Если Х
– дискретная случайная величина, то
![]()
Пример 3. Найдем
M(Y)
для примера 1: M(Y)
= 47·0,1 + 69·0,2 + 95·0,3 + 125·0,4 = 97.
2)
Если Х
– непрерывная случайная величина, то
M(Y)
можно искать по-разному. Если известна
плотность распределения g(y),
то
![]()
Если же g(y)
найти сложно, то можно использовать
известную плотность распределения
f(x):
![]()
В частности, если
все значения Х
принадлежат промежутку (а,
b),
то
№37 Ф-я двух случ
аргументов, закон расп-я![]()
Если каждой паре
возможных значений случайных величин
Х
и Y
соответ-ствует одно возможное значение
случайной величины Z,
то Z
называют
функцией двух
случайных аргументов
X
и
Y
: Z
= φ(X,
Y).
Рассмотрим в
качестве такой функции сумму Х
+ Y.
В некоторых случаях можно найти ее закон
распределения, зная законы распределения
слагаемых.
1) Если X
и
Y
– дискретные
независимые
случайные величины, то для определения
закона распределения Z
= Х + Y
нужно найти
все возможные значения Z
и соответствующие
им вероятности.
3)
Если X
и
Y
– непрерывные
независимые
случайные величины, то, если плотность
вероятно-сти хотя бы одного из аргументов
задана на (-∞, ∞) одной формулой, то
плотность суммы g(z)
можно найти по формулам
![]()
где f1(x),
f2(y)
– плотности распределения слагаемых.
Если возможные значения аргументов
неотрицательны, то
![]()
Замечание.
Плотность
распределения суммы двух независимых
случайных величин называют композицией.
№38 Закон больших
чисел: неравенство Чебышева
Вероятность того,
что отклонение случайной величины X
от ее математического ожидания по
абсолютной величине меньше положительного
числа не меньше чем :
p(
| X — M(X)|
< ε ) ≥ D(X)
/ ε².
Доказательство.
Пусть Х
задается рядом распределения
|
х1 |
х2 |
… |
хп |
||||||||||
|
р |
р1 |
р2 |
… |
рп |
Так как события |X
— M(X)|
< ε и |X —
M(X)|
≥ ε противоположны, то р
( |X — M(X)|
< ε ) + + р
( |X — M(X)|
≥ ε ) = 1, следовательно, р
( |X — M(X)|
< ε ) = 1 – р
( |X — M(X)|
≥ ε ). Найдем р
( |X — M(X)|
≥ ε ).
D(X)
= (x1
— M(X))²p1
+ (x2
— M(X))²p2
+ … + (xn
— M(X))²pn
. Исключим
из этой суммы те слагаемые, для которых
|X — M(X)|
< ε. При этом сумма может только
уменьшиться, так как все входящие в нее
слагаемые неотрицательны. Для
определенности будем считать, что
отброшены первые k
слагаемых.
Тогда
D(X)
≥ (xk+1
— M(X))²pk+1
+ (xk+2
— M(X))²pk+2
+ … + (xn
— M(X))²pn
≥ ε² (pk+1
+ pk+2
+ … + pn).
Отметим, что pk+1
+ pk+2
+ … + pn
есть вероятность того, что |X
— M(X)|
≥ ε, так как это сумма вероятностей всех
возможных значений Х,
для которых это неравенство справедливо.
Следовательно, D(X)
≥ ε² р(|X
— M(X)|
≥ ε), или р
(|X — M(X)|
≥ ε) ≤ D(X)
/ ε². Тогда вероятность противоположного
события p(
| X — M(X)|
< ε ) ≥ D(X)
/ ε², что и требо-валось доказать.
№39 Теоремы
Чебышева и Бернули
Теоремы Чебышева
и Бернулли.
Рассмотрим
последовательность случайных величин![]()
(2).
Введем среднее
арифметическое:
![]()
Запишем математическое
ожидание:
![]()
Обозначим
![]()
Def: говорят, что для
последовательности выполняется закон
больших чисел, если для любого![]()
справедливо равенство:
![]()
О равенстве (3) также
говорят, что среднее арифметическое
случайных величин в вероятностном
смысле (по вероятности) сходится к
среднему арифметическому их математических
ожиданий.
Если последовательность
случайных величин (2) удовлетворяет
закону больших чисел, то, как видно из
равенства (3), среднее арифметическое
ведет себя фактически как величина
неслучайная, поскольку ее значение в
вероятностном смысле как угодно мало
отличается от числа (среднего
арифметического математического
ожидания случайной величины ).
Теорема Чебышева:
пусть случайные величины последовательности
(2) таковы, что:
1) Они попарно
независимы.
2) Имеют конечное
математическое ожидание.
![]()
3) Имеют равномерно
ограниченные дисперсии
Тогда к
последовательности применим закон
больших чисел.
Доказательство.
Оценим дисперсию:
![]()
Применим неравенство
(1):
![]()
Левую часть выразим
через вероятность противоположного
события:
![]()
Умножим обе части
на (-1):
![]()
![]()
С другой стороны:
![]()
На основании двух
предыдущих формул получаем формулу (3)
Теорема Бернулли:
относительная частота события “А” в
вероятностном смысле сходится к
вероятности этого события:
(4)
![]()
Доказательство.
С каждым испытанием
свяжем случайную величину![]()
.
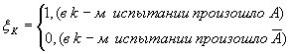
Тогда число
наступлений события “А” в “n” независимых
испытаний будет равно:
![]()
Покажем, что к этой
последовательности применим закон
больших чисел (равенство 3). Проверим
выполнение условий теоремы Чебышева:
1)
![]()
– попарно независимы.
2)
![]()
3)
![]()
Таким образом в
силу теоремы Чебышева к последовательности
случайных величин {
}
применим закон больших чисел, выражаемый
равенством (3). В данном случае среднее
арифметическое:
![]()
– относительная частота.
![]()
В
силу (3) получаем равенство (4).
№40 Оценка
отклонения распределения НСВ от
нормального коэффициента ассиметрии
и эксцесса
Коэффициент
асимметрии задает
степень асимметричности плотности
вероятности относительно оси, проходящий
через ее центр тяжести. Коэффициент
асимметрии определяется третьим
центральным моментом распределения. В
любом симметричном распределении с
нулевым математическиможиданием,
например, нормальным, все нечетные
моменты, в том числе итретий, равны нулю,
поэтому коэффициент асимметрии тоже
равен нулю.
Степень сглаженности
плотности вероятности в окрестности
главного максимума задается еще одной
величиной – коэффициентом
эксцесса. Он
показывает, насколько острую вершину
имеет плотность вероятности по сравнению
с нормальным распределением. Если
коэффициент эксцесса большенуля, то
распределение имеет более острую
вершину, чем распределениеГаусса, если
меньше нуля, то более плоскую.
Для
расчета коэффициентов асимметрии и
эксцесса в MathCAD имеютсядве встроенные
функции.
– kurt (x) – коэффициент эксцесса
(kurtosis) выборки
случайных данных х;
– skew(x) – коэффициент
асимметрии (skewness)
выборки
случайных данных X .
№41 Распределение
«хи-квадрат»
Пусть х1,х2,…,хn-независ.
Норм.расп-е случ.величины с нулевым
матем.ожиданием и сред.квадрат.отклонением=1,тогда
закон расп-я суммы кварт.величин(Х-квадрат)
х2=х1
2+х22+…+хn2
назв. Законом Х-квадрат с nстепенями
свободы. Плотность расп-я этого закона
опред:
0, при х<0
f(x)
(e–x/2*xn/2-1)/2n/2+Г’(n/2)x
≥0
№42 распределение
Стьюдента
Пусть х0,х1,…,хn-независ.
Норм.расп-е случ.величины с нулевым
матем.ожиданием и сред.квадрат.отклонением=1,
тогда величина опред по ф-ле:Т=(
х0/mn=1*x2/n)
назв. Величиной имеющей расп-е Стьюдента
с n-степенями
свободы
Плотность имеет
вид f(x)=
bn(1+
x2/2)-((n+1)/n)
bn=Г((n+1)/2)/Гn/2*n
№43 Распределение
Фишера-Снедекора
Пусть х1,х2,…,хn
,у1,у2,…,уn
независ. Норм.расп-е случ.величины с
нулевым матем.ожиданием и
сред.квадрат.отклонением=1, тогда случ
величина ,заданная ф-лой Fnm=((xi
2/n)/
yj
2/m)
назв. Случ величиной, имеющей расп-е
Фишера-Снедекора с n
и m
степенями свободы, плотность расп-я
имеет вид
F(x)=
0,при x0
C0
*(x(n-2)/2/(n+n
x(+2)/2),для
х>0
C0=Г(((n+m)/2)*nn/2
*m
m/2
))Г
n/2Г
m/2
№44 Система двух
случайных величин. Закон расп-я.Ф-я
расп-я. Свойства функции расп-я
Законом расп-я
назв перечень возможных значений двумерн
величины , т.е А(xi,уi)
и их соотв. Вероятностей Р(xi,уi).
Обычно закон задают таблицей с двойным
ходом.1строка-все возможн.значения.
составляющие х.1 столбец- все
возможн.значения. составляющие у клетки
на их пересечении (xi,уi)
заполняют соответств. Вероятность ,
причем кол-вл знач-й х,у могут быть
различными, т.к событие х=уi
и у=уi
образуют полную группу , то сумма
вероятностей помещенных во всех клетках
=1.
Ф-я расп-я:
Пусть х,у пара
действительных чисел, вероятность
события состоит в том, что составляющая
х примет знач-е меньше х; составляющая
у примет знач-е меньше у. X<x;
Y<y.
обозначение Р(X<x;
Y<y)=F(x;y)
– ф-я расп-я
Свойства функции
расп-я
1.Значения ф-и расп-я
удовлетв. Неравенству 0< F(x;y)<1
2. Ф-я F(x;y)
явл. Неубывающей ф-ей.
3. Имеют место след
соотношения:1)F(-∞;
y)=0
2) F(x;-∞)=0
3) F(-∞;-∞)=0
4) F(+∞;+∞)=1
4. При у=∞, ф-я расп-я
с-мы становиться ф-ей расп-я составляющей
х. При х=∞, ф-я расп-я с-мы становиться
ф-ей расп-я составляющей у
№45 Система двух
случайных величин: плотность совместного
расп-я вероятностей, нахождение ф-и
расп-я по плотности расп-я, свойства
двумерной плотности расп-я
Плотность совм.расп-я
вероятностей назв частную производную
второго порядка, смешанная по переменным
х, у
нахождение ф-и
расп-я по плотности расп-я
F(x,y)=sinx*siny
0x/2;
0y/2
Решение:
Fх(x,y)=cosx*siny
;Fxy=
cosx cosy. Зная
плотность расп-я можно найти ф-ю расп-я
F(x,y)=-∞∞
-∞∞f(x,y)
dx
dy
свойства двумерной
плотности расп-я:
1.плотность
вероятности не отрицательна f(x,y)≥0
2. -∞∞
-∞∞f(x,y)
dx
dy=1
3. можно найти
плотность расп-я для каждой составляющей
46.
Определение. Плотностью
совместного распределения вероятностей
двумерной случайной величины (X, Y)
называется вторая смешанная частная
производная от функции распределения.
Условные
законы распределения составляющих
системы дискретных случайных величин.

Рассмотрим
дискретную двумерную случайную величину
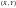
,
пусть возможные значения составляющих
таковы:

Предположим,
что в результате испытания случайная
величина Y
приняла значение

,
тогда X
может принять одно из своих возможных
значений. Обозначим условную вероятность
того, что X
примет значение

через
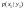
Условным
распределением случайной величины X
при условии, что Y
приняла значение
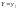
называют совокупность условных
вероятностей
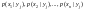
Зная
закон распределения двумерной дискретной
случайной величины можно вычислить
условные законы распределения
составляющих:

Условные
законы распределения составляющих
системы непрерывных случайных величин
Условной
дифференциальной функцией

составляющей X
при условии, что

,
называют отношение дифференциальной
функции системы к дифференциальной
функции составляющей Y.
47.
Условное математическое ожидание
Условным
математическим ожиданием
случайной величины Y
при
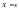
называют сумму произведений возможных
значений Y
на их условные вероятности.

Для
непрерывных величин:

48.
Зависимые и независимые случайные
величины
Теорема.
Для
того чтобы случайные величины X
и Y
были независимы, необходимо и достаточно,
чтобы интегральная функция системы

была равна произведению интегральных
функций случайных величин X
и Y.

Следствие.
Для того чтобы случайные величины X
и Y
были независимы, необходимо и достаточно,
чтобы дифференциальная функция системы
была равна произведению дифференциальных
функций случайных величин X
и Y.

КОРРЕЛЯЦИОННЫЙ
МОМЕНТ Корреляционным моментом двух случайных
величин X и Y называют математическое
ожидание произведения
отклонений этих
величин: xy = M{[X – M(X)][Y – M(Y)]}.
Корреляционный момент служит
для характеристики связи между
величинами X и Y.
Корреляционный момент двух независимых случайных
величин X и Y равен
нулю. Если корреляционный момент не
равен нулю, то X и Y – зависимые случайные
величины. Из определения корреляционного
момента следует, что он имеет размерность,
равную произведению размерностей
величин X и Y.
Другими словами, корреляционный момент
зависит от единиц измеренияслучайных
величин. Безразмерной
числовой характеристикой связи
двух случайных величин является коэффициент
корреляции.
коэффициент
корреляции.
Он рассчитывается следующим образом:
Есть
массив из n точек
{x1,i, x2,i}
Рассчитываются
средние значения для каждого параметра: ![]()
И
коэффициент корреляции: 
r изменяется
в пределах от -1 до 1. В данном случае это
линейный коэффициент корреляции, он
показывает линейную взаимосвязь
между x1 и x2: r равен
1 (или -1), если связь линейна.
Коэффициент r является
случайной величиной, поскольку вычисляется
из случайных величин. Для него можно
выдвигать и проверять следующие гипотезы:
Содержание:
Непрерывные случайные величины: функция распределения случайной величины:
Если вычислить вероятность появления непрерывной случайной величины не составляет особого труда, то решение основной задачи теории вероятностей для непрерывной случайной величины несёт большие трудности. Поэтому в материалах сегодняшней лекции мы рассмотрим методы определения вероятности попадания непрерывной случайной величины на интервал с помощью функции распределения.
Функция распределения непрерывной случайной величины
Зная функцию распределения непрерывной случайной величины, задача определения вероятности её попадания на интервал (а; b) может быть решена следующим образом.
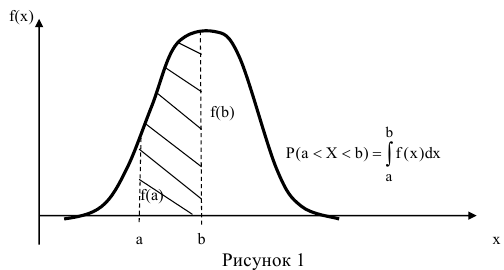
По известной функции распределения вероятность попадания непрерывной случайной величины на интервал (а; b) равна приращению функции распределения на этом участке (рис. 1).
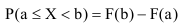
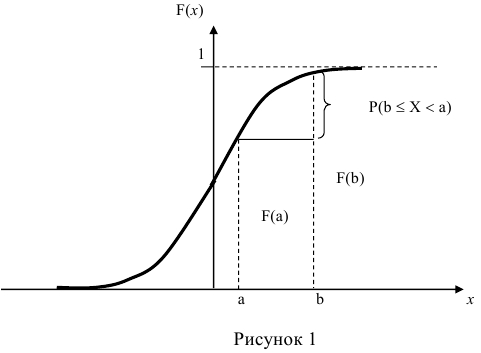
Во всех рассмотренных выше случаях случайная величина определялась путём задания значений самой величины и вероятностей этих значений.
Однако такой метод применим далеко не всегда. Например, в случае непрерывной случайной величины, её значения могут заполнять некоторый произвольный интервал. Очевидно, что в этом случае задать все значения случайной величины просто нереально.
Даже в случае, когда это сделать можно, зачастую задача решается чрезвычайно сложно. Рассмотренный только что пример даже при относительно простом условии (приборов только четыре) приводит к достаточно неудобным вычислениям, а если в задаче будет несколько сотен приборов?
Поэтому встает задача по возможности отказаться от индивидуального подхода к каждой задаче и найти по возможности наиболее общий способ задания любых типов случайных величин.
Пусть х – действительное число. Вероятность события, состоящего в том, что X примет значение, меньшее х, т.е. X
Определение. Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина X в результате испытания примет значение, меньшее х.
F(x) = Р(Х < х)
Функцию распределения также называют интегральной функцией. Функция распределения существует как для непрерывных, так и для дискретных случайных величин. Она полностью характеризует случайную величину и является одной из форм закона распределения.
Для дискретной случайной величины функция распределения имеет
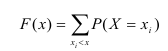
Знак неравенства под знаком суммы показывает, что суммирование распространяется на те возможные значения случайной величины, которые меньше аргумента х.
Функция распределения дискретной случайной величины X разрывна и возрастает скачками при переходе через каждое значение 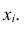
Так для примера, который мы будем рассматривать на следующем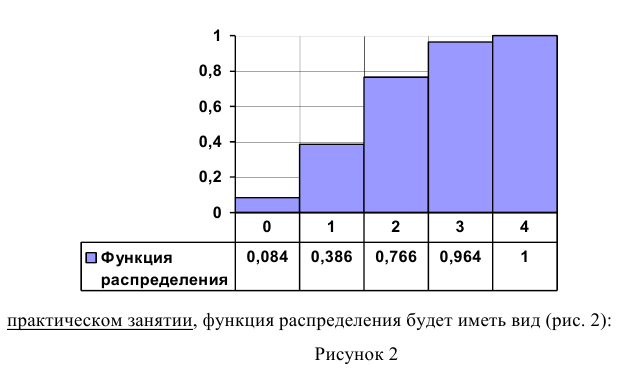
Свойства функции распределения
1) значения функции распределения принадлежат отрезку [0, 1].
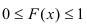
2) F(x) – неубывающая функция.
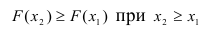
3) Вероятность того, что случайная величина примет значение, заключенное в интервале (а, b) , равна приращению функции распределения на этом интервале.
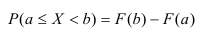
4) На минус бесконечности функция распределения равна нулю, на плюс бесконечности функция распределения равна единице.
5) Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна нулю.
Таким образом, не имеет смысла говорить о каком – либо конкретном значении случайной величины. Интерес представляет только вероятность попадания случайной величины в какой – либо интервал, что соответствует большинству практических задач.
Заключение по лекции:
В лекции мы рассмотрели методы решения основной задачи теории вероятностей – определения вероятности попадания непрерывной случайной величины на интервал с помощью функции распределения.
Плотность вероятности. Числовые характеристики. Моменты случайных величин
Если вычислить вероятность появления непрерывной случайной величины не составляет особого труда, то решение основной задачи теории вероятностей для непрерывной случайной величины несёт большие трудности. Поэтому в материалах сегодняшней лекции мы рассмотрим методы определения вероятности попадания непрерывной случайной величины на интервал с помощью плотности
распределения.
Плотность распределения
Функция распределения полностью характеризует случайную величину, однако, имеет один недостаток. По функции распределения трудно судить о характере распределения случайной величины в небольшой окрестности той или иной точки числовой оси.
Определение. Плотностью распределения вероятностей непрерывной случайной величины X называется функция f(x) – первая производная от функции распределения F(x).
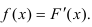
Плотность распределения также называют дифференциальной функцией. Для описания дискретной случайной величины плотность распределения неприемлема.
Смысл плотности распределения состоит в том, что она показывает как часто появляется случайная величина X в некоторой окрестности точки х при повторении опытов.
После введения функций распределения и плотности распределения можно дать следующее определение непрерывной случайной величины.
Определение. Случайная величина X называется непрерывной, если её функция распределения F(x) непрерывна на всей оси ОХ, а плотность распределения f(x) существует везде, за исключением (может быть, конечного числа точек).
Зная плотность распределения, можно вычислить вероятность того, что некоторая случайная величина X примет значение, принадлежащее заданному интервалу.
Теорема. Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (а, b), равна определенному интегралу от плотности распределения, взятому в пределах от а до b.
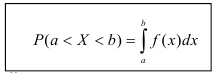
Доказательство этой теоремы основано на определении плотности распределения и третьем свойстве функции распределения (см. лекцию тема № 10).
Геометрически это означает, что вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (а, b), равна площади криволинейной трапеции, ограниченной осью ОХ, кривой распределения f(x) и прямыми х=а и х=b.
Геометрически вероятность Р(а < X < b) представляется в виде заштрихованной области, ограниченной кривой распределения и осью Ох на интервале(а; b) (рис 1).
Функция распределения может быть легко найдена, если известна плотность распределения, по формуле:
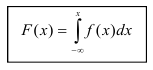
Свойства плотности распределения
1) Плотность распределения – неотрицательная функция.
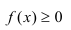
2) Несобственный интеграл от плотности распределения в пределах от –
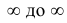 равен единице.
равен единице.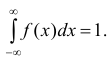
Плотность распределения 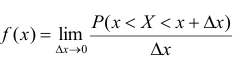
можно представить как:
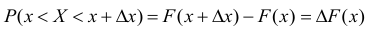
тогда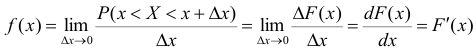
Поэтому иногда функцию плотности распределения f(x) называют также дифференциальной функцией распределения или дифференциальным законом распределения величины X, а функцию распределения F(x) -интегральной функцией распределения или интегральным законом распределения.
Следует заметить, что интеграл 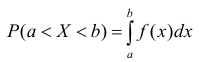 возможно трактовать как сумму бесконечно большого числа несовместных элементарных событий, каждое из которых заключается в попадании случайной величины в бесконечно малый участок (х, х + dx) и имеет вероятность:
возможно трактовать как сумму бесконечно большого числа несовместных элементарных событий, каждое из которых заключается в попадании случайной величины в бесконечно малый участок (х, х + dx) и имеет вероятность:
Р(х < X < х + dx) = dF(x) = f(x)dx
Величину f(x)dx называют элементом вероятности.
По своему содержанию элемент вероятности есть вероятность попадания случайной величины X на элементарный участок dx, прилежащий к точке X.
Функция распределения случайной величины X по известной плотности распределения может быть найдена, как интеграл от плотности распределения в интервале от 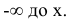
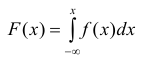
В схеме непрерывных случайных величин можно вывести аналогии формулы полной вероятности и формулы Бейеса, рассмотренные при изучении темы 4.
Обозначим Р(А /х) условную вероятность события А при условии Х= х. Заменяя в формуле полной вероятности вероятность гипотезы элементом вероятности f(x)dx, а сумму – интегралом, получим полную вероятность события А.
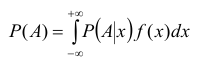
Данная формула называется интегральной формулой полной вероятности.
Соответствующий аналог в схеме непрерывных случайных величин имеет и формула Бейеса. Обозначив условную плотность распределения случайной величины X при условии, что в результате опыта появилось событие A через 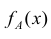 , получим:
, получим:
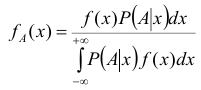
Данная формула называется интегральной формулой Бейеса.
Числовые характеристики непрерывных случайных величин
Пусть непрерывная случайная величина X задана функцией распределения f(x). Допустим, что все возможные значения случайной величины принадлежат отрезку [а,b].
Математическое ожидание
Определение. Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а,b], называется определенный интеграл
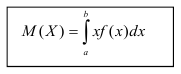
Если возможные значения случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле:
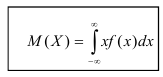
При этом, конечно, предполагается, что несобственный интеграл сходится.
Дисперсия
Определение. Дисперсией непрерывной случайной величины называется математическое ожидание квадрата её отклонения.
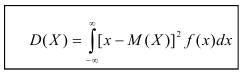
По аналогии с дисперсией дискретной случайной величины, для практического вычисления дисперсии используется формула:
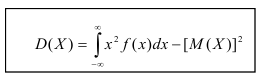
Среднеквадратичное отклонение
Определение. Средним квадратичным отклонением называется квадратный корень из дисперсии.
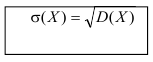
Мода
Определение. Модой 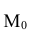 дискретной случайной величины называется её наиболее вероятное значение. Для непрерывной случайной величины мода – такое значение случайной величины, при которой плотность распределения имеет максимум.
дискретной случайной величины называется её наиболее вероятное значение. Для непрерывной случайной величины мода – такое значение случайной величины, при которой плотность распределения имеет максимум.
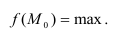
Если многоугольник распределения для дискретной случайной величины или кривая распределения для непрерывной случайной величины имеет два или несколько максимумов, то такое распределение называется двухмодальным или многомодальным.
Если распределение имеет минимум, но не имеет максимума, то оно
называется антимодальным.
Медиана
Определение. Медианой 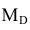 случайной величины X называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины.
случайной величины X называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины.
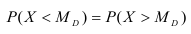
Геометрически медиана – абсцисса точки, в которой площадь, ограниченная кривой распределения делится пополам.
Отметим, что если распределение одномодальное, то мода и медиана совпадают с математическим ожиданием.
Начальный момент
Определение. Начальным моментом порядка k случайной величины X называется математическое ожидание величины 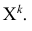
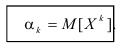
Для дискретной случайной величины: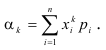
Для непрерывной случайной величины: 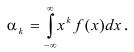
Начальный момент первого порядка равен математическому ожиданию.
Центральный момент
Определение. Центральным моментом порядка k случайной величины X называется математическое ожидание величины 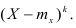
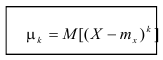
Для дискретной случайной величины: 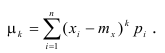
Для непрерывной случайной величины: 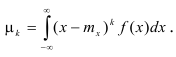
Центральный момент первого порядка всегда равен нулю, а центральный момент второго порядка равен дисперсии. Центральный момент третьего порядка характеризует асимметрию распределения.
Коэффициент асимметрии
Определение. Отношение центрального момента третьего порядка к среднеквадратическому отклонению в третьей степени называется коэффициентом асимметрии.
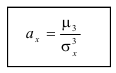
Эксцесс
Определение. Для характеристики островершинности и плосковершинности распределения используется величина, называемая эксцессом.
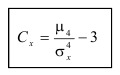
Кроме рассмотренных величин используются также так называемые абсолютные моменты:
Абсолютный начальный момент: 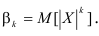
Абсолютный центральный момент: 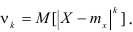
Абсолютный центральный момент первого порядка называется средним арифметическим отклонением.
Заключение по лекции:
В лекции мы рассмотрели методы решения основной задачи теории вероятностей – определения вероятности попадания непрерывной случайной величины на интервал с помощью плотности распределения.
Законы распределения непрерывных величин: нормальное, равномерное, показательное
В материалах сегодняшней лекции мы рассмотрим законы распределения непрерывных величин.
Равномерное распределение
Определение. Непрерывная случайная величина имеет равномерное распределение на отрезке [а,b], если на этом отрезке плотность
распределения случайной величины постоянна, а вне его равна нулю.
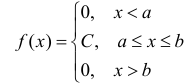
Постоянная величина С может быть определена из условия равенства единице площади, ограниченной кривой распределения, представленной на рис. 1
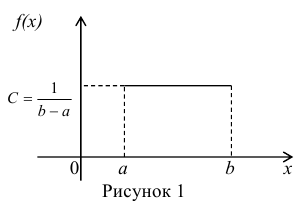
Получаем 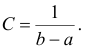 .
.
Найдём функцию распределения F(x) на отрезке [а,b] (рис. 2).
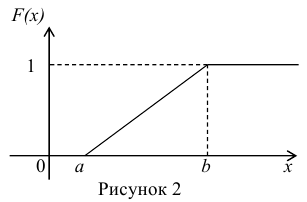
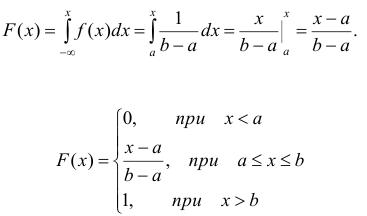
Для того, чтобы случайная величина подчинялась закону равномерного распределения необходимо, чтобы её значения лежали внутри некоторого определенного интервала, и внутри этого интервала значения этой случайной величины были бы равновероятны.
Определим математическое ожидание и дисперсию случайной величины, подчиненной равномерному закону распределения.
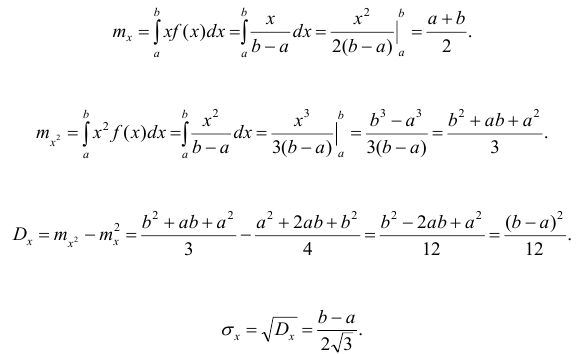
Вероятность попадания случайной величины в заданный интервал:
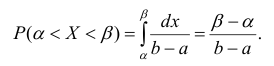
Показательное распределение
Определение. Показательным (экспоненциальным) называется распределение вероятностей непрерывной случайной величины X, которое описывается плотностью
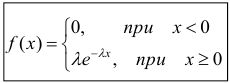
где 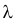 – положительное число.
– положительное число.
Найдём закон распределения.
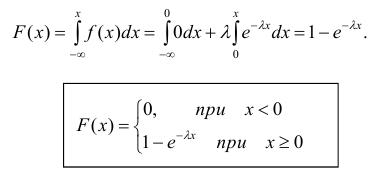
Графики функции распределения и плотности распределения представлены на рис. 3, 4.
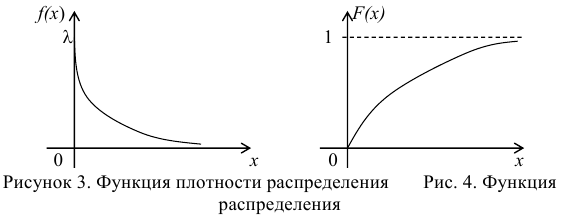
Найдём математическое ожидание случайной величины, подчинённой показательному распределению.
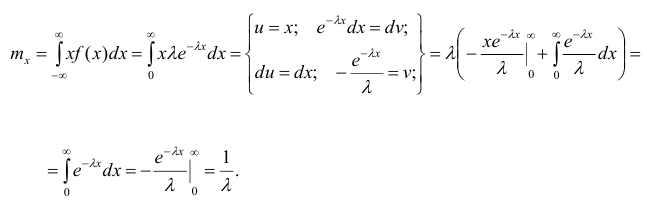
Результат получен с использованием того факта, что

Для нахождения дисперсии найдём величину 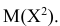
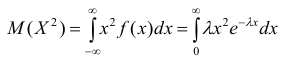
Дважды интегрируя по частям, аналогично рассмотренному случаю, получим:
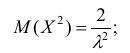
Тогда 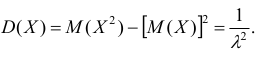
Итого: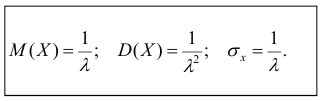
Видно, что в случае показательного распределения математическое ожидание и среднеквадратическое отклонение равны.
Также легко определить и вероятность попадания случайной величины, подчиненной показательному закону распределения, в заданный интервал.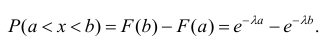
Показательное распределение широко используется в теории надёжности.
Допустим, некоторое устройство начинает работать в момент времени to=0, а через какое- то время t происходит отказ устройства.
Обозначим Т непрерывную случайную величину – длительность безотказной работы устройства.
Таким образом, функция распределения F(t) = P(T
Вероятность противоположного события (безотказная работа в течение времени t) равна R(t) = P(T>t) – l – F(t).
Функция надежности
Определение. Функцией надёжности R(t) называют функцию, определяющую вероятность безотказной работы устройства в течение времени t.
Часто на практике длительность безотказной работы подчиняется показательному закону распределению.
Вообще говоря, если рассматривать новое устройство, то вероятность отказа в начале его функционирования будет больше, затем количество отказов снизится и будет некоторое время иметь практически одно и то же значение. Затем (когда устройство выработает свой ресурс) количество отказов будет возрастать.
Другими словами, можно сказать, что функционирование устройства на протяжении всего существования (в смысле количества отказов) можно описать комбинацией двух показательных законов (в начале и конце функционирования) и равномерного закона распределения.
Функция надёжности для какого- либо устройства при показательном законе распределения равна:
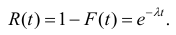
Данное соотношение называют показательным законом надежности.
Важным свойством, позволяющим значительно упростить решение задач теории надежности, является то, что вероятность безотказной работы устройства на интервале времени t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности времени t.
Таким образом, безотказная работа устройства зависит только от интенсивности отказов 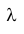 и не зависит от безотказной работы устройства в
и не зависит от безотказной работы устройства в
прошлом.
Так как подобным свойством обладает только показательный закон распределения, то этот факт позволяет определить, является ли закон распределения случайной величины показательным или нет.
Нормальный закон распределения
Определение. Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности

Нормальный закон распределения также называется законом Гаусса.
Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.
Можно легко показать, что параметры 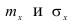 входящие в плотность распределения являются соответственно математическим ожиданием и среднеквадратическим отклонением случайной величины X.
входящие в плотность распределения являются соответственно математическим ожиданием и среднеквадратическим отклонением случайной величины X.
Найдём функцию распределения F(x).
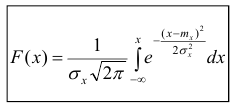
График плотности нормального распределения называется нормальной кривой или кривой Гаусса.
Нормальная кривая обладает следующими свойствами:
1) Функция определена на всей числовой оси.
2) При всех х функция распределения принимает только положительные значения.
3) Ось ОХ является горизонтальной асимптотой графика плотности вероятности, т.к. при неограниченном возрастании по абсолютной величине аргумента л значение функции стремится к нулю.
4) Найдём экстремум функции.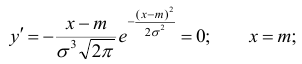
Т.к. при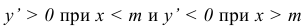 , то в точке х = m функция имеет максимум, равный
, то в точке х = m функция имеет максимум, равный 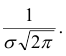
5) Функция является симметричной относительно прямой x = а, т.к. разность
(х – а) входит в функцию плотности распределения в квадрате.
6) Для нахождения точек перегиба графика найдем вторую производную функции плотности.
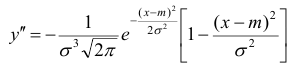
При 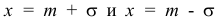 вторая производная равна нулю, а при переходе через эти точки меняет знак, т.е. в этих точках функция имеет перегиб.
вторая производная равна нулю, а при переходе через эти точки меняет знак, т.е. в этих точках функция имеет перегиб.
В этих точках значение функции равно 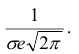
Построим график функции плотности распределения (рис. 5).
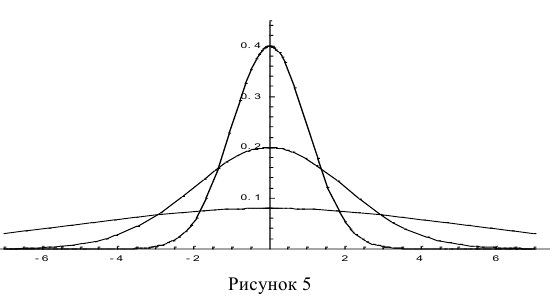
Построены графики при м =0 и трёх возможных значениях среднеквадратичного отклонения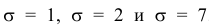 . Как видно, при увеличении значения среднего квадратичного отклонения график становится более пологим, а максимальное значение уменьшается.
. Как видно, при увеличении значения среднего квадратичного отклонения график становится более пологим, а максимальное значение уменьшается.
Если а > 0, то график сместится в положительном направлении, если а < 0 – в отрицательном.
При а = 0 и 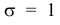 кривая называется нормированной. Уравнение нормированной кривой:
кривая называется нормированной. Уравнение нормированной кривой:
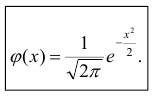
Функция Лапласа
Найдём вероятность попадания случайной величины, распределенной по нормальному закону, в заданный интервал.
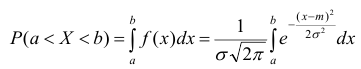
Обозначим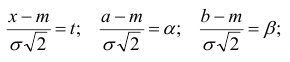
Тогда 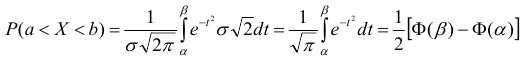
Т.к. интеграл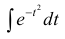 не выражается через элементарные функции, то вводится в рассмотрение функция
не выражается через элементарные функции, то вводится в рассмотрение функция
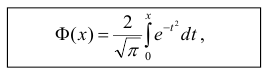
которая называется функцией Лапласа или интегралом вероятностей.
Значения этой функции при различных значениях х посчитаны и приводятся в специальных таблицах.
На рис. 6 показан график функции Лапласа.
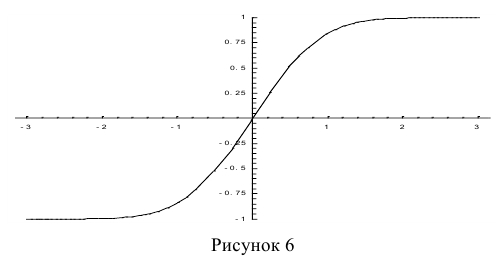
Функция Лапласа обладает следующими свойствами:
- 1) Ф(0) = 0;
- 2) Ф(-х) = – Ф(х);
- 3)
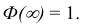
Функцию Лапласа также называют функцией ошибок и обозначают
erf х.
Ещё используется нормированная функция Лапласа, которая связана с функцией Лапласа соотношением:
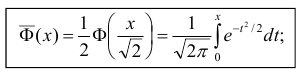
На рис. 7 показан график нормированной функции Лапласа.
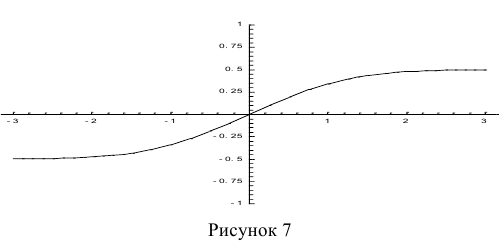
Правило трёх сигм
При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм.
Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины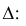
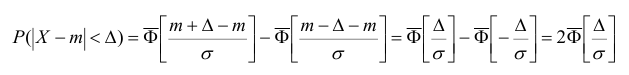
Если принять 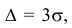 , то получаем с использованием таблиц значений функции Лапласа:
, то получаем с использованием таблиц значений функции Лапласа:
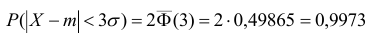
Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую, чем утроенное среднее квадратичное отклонение, практически равна нулю.
Это правило называется правилом трех сигм.
Не практике считается, что если для какой-либо случайной величины выполняется правило трёх сигм, то эта случайная величина имеет нормальное распределение.
Пример:
Случайная величина Х задана плотностью распределения вероятностей:
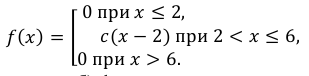
Найти: а) значение с; б) функцию распределения F(х) и построить ее график; в)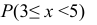
Решение:
а) Значение с найдем из условия нормировки: 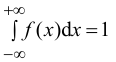
Следовательно,
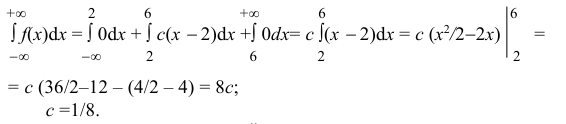
б) Известно, что 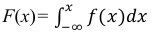
Поэтому, если 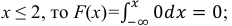
если 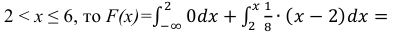
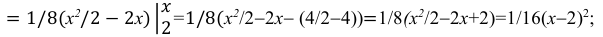
если 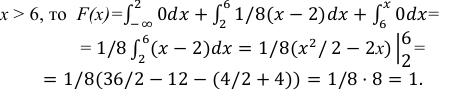
Таким образом,
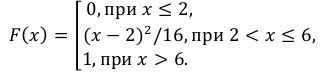
График функции F(х) изображен на рис. 5. 3.
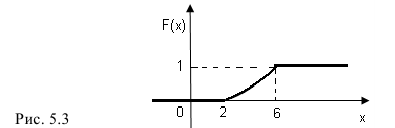
в) 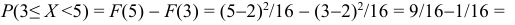
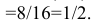
Пример:
Случайная величина Х задана функцией распределения:
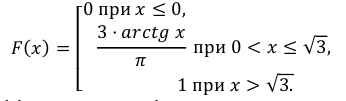
Найти дифференциальную функцию распределения 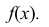
Решение:
Так как 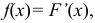 то
то
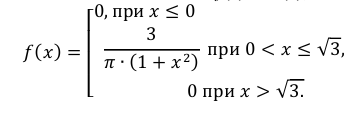
Пример:
Случайная величина Х задана дифференциальной функцией 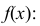
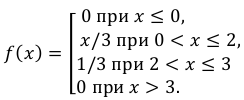
Найти 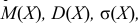 а также
а также 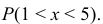
Решение:
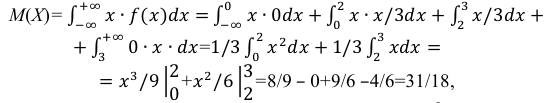
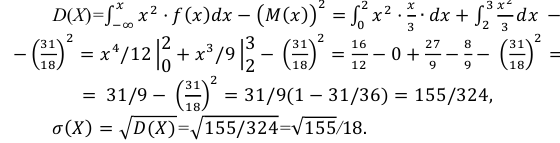
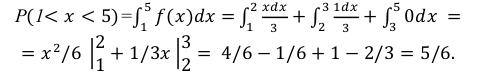
Некоторые законы распределения непрерывной случайной величины
Пример:
Случайная величина Х равномерно распределена на отрезке [3;7]. Найти:
а) плотность распределения вероятностей 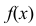 и построить ее график;
и построить ее график;
б) функцию распределения 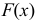 и построить ее график;
и построить ее график;
в) 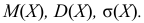
Решение: Воспользовавшись формулами, рассмотренными выше, при а = 3, b = 7, находим:
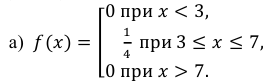
Построим ее график (рис. 6.3):
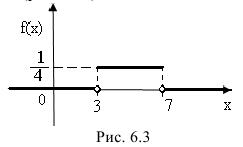
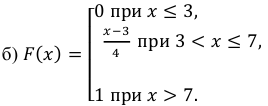
Построим ее график (рис. 6.4):
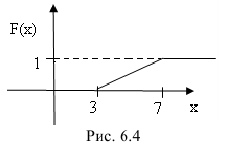
Пример:
Среднее время безотказной работы прибора равно 100 ч.
Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти:
а) плотность распределения вероятностей;
б) функцию распределения;
в) вероятность того, что время безотказной работы прибора превысит 120 ч.
Решение.
По условию математическое ожидание 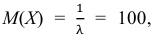
откуда 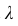 = 1/100 = 0,01.
= 1/100 = 0,01.
Следовательно,
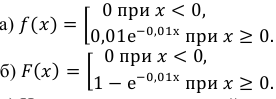
в) Искомую вероятность найдем, используя функцию распределения:
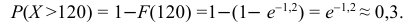
Пример:
Случайная величина Х распределена нормально с математическим ожиданием 32 и дисперсией 16. Найти: а) плотность распределения вероятностей 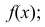 б) вероятность того, что в результате испытания Х примет значение из интервала (28;38).
б) вероятность того, что в результате испытания Х примет значение из интервала (28;38).
Решение:
По условию m = 32, σ2 = 16, следовательно, σ = 4, тогда
а) 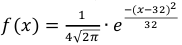
б) Воспользуемся формулой:
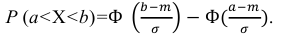
Подставив a = 28, b = 38, m = 32, σ = 4, получим
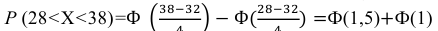
По таблице значений функции Ф(х) находим Ф(1,5) = 0,4332, Ф(1) = 0,3413.
Итак, искомая вероятность:
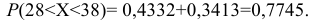
Заключение по лекции:
В лекции мы рассмотрели законы распределения непрерывных величин.
- Закон больших чисел
- Генеральная и выборочная совокупности
- Интервальные оценки параметров распределения
- Алгебра событий – определение и вычисление
- Правило «трех сигм» в теории вероятности
- Производящие функции
- Теоремы теории вероятностей
- Основные законы распределения дискретных случайных величин
