Согласно
уравнению конвективной теплоотдачи,
называемому также законом Ньютона-Рихмана,
тепловой поток прямо пропорционален
разности температур стенки и жидкости
и площади поверхности теплообмена.
Коэффициент пропорциональности
![]()
в этом уравнении называют средним
коэффициентом конвективной теплоотдачи:
![]() ,
,
(1)
или
![]() ,
,
(2)
или
![]() ,
,
(3)
где
Q – тепловой поток, Вт; q = Q/F – поверхностная
плотность теплового потока, Вт/м2;
![]() – средний коэффициент конвективной
– средний коэффициент конвективной
теплоотдачи, Вт/(м2∙К);
![]() –
–
температурный напор теплоотдачи,оС;
![]() –
–
температура поверхности теплообмена
(стенки),оС;
![]() – температура жидкости вдали от стенки,оС;
– температура жидкости вдали от стенки,оС;
F – площадь поверхности теплообмена
(стенки), м2.
Независимо
от направления теплового потока (от
стенки к жидкости или наоборот) будем
считать его положительным, то есть будем
использовать модуль разности температур.
Величина
коэффициента теплоотдачи зависит от
большого числа различных факторов: а)
физических свойств жидкости ; б) скорости
движения жидкости ; в) формы, размеров
и ориентации в пространстве поверхности
теплообмена; г) величины температурного
напора, направления теплообмена и т.п.
Поэтому его теоретическое определение
в большинстве случаев невозможно.
Выражения
(1)-(3) позволяют опытным путем определить
средний коэффициент теплоотдачи
посредством измерения величин Q, F,
![]() и
и![]() :
:
![]() ,
,
(4)
то
есть средний коэффициент теплоотдачи
численно равен тепловому потоку,
передаваемому через единицу поверхности
теплообмена при единичном температурном
напоре (1 оС
или 1 К).
3. Локальный (местный) коэффициент конвективной теплоотдачи
Средний
коэффициент теплоотдачи является
важной, но не всегда достаточной
характеристикой процессов теплообмена.
Во многих случаях требуются значения
коэффициентов теплоотдачи в отдельных
точках поверхности теплообмена, то есть
локальные (местные) значения. Локальные
коэффициенты характеризуют теплоотдачу
в окрестности заданной точки (x)
и входят в состав локального уравнения
теплоотдачи:
![]() ,
,
(5)
или
![]() ,
,
(6)
где
dF
– элементарная (бесконечно малая)
поверхность теплообмена в окрестности
точки x,
м2;
![]() – элементарный тепловой поток, Вт ;
– элементарный тепловой поток, Вт ;![]() –
–
локальная плотность теплового потока,
Вт/м2;
![]() – локальный коэффициент конвективной
– локальный коэффициент конвективной
теплоотдачи, Вт/(м2∙К);
![]() – локальный температурный напор,оС;
– локальный температурный напор,оС;
![]() –
–
локальная температура поверхности
(стенки),оС;
![]() –
–
температура жидкости вдали от стенки
(полагаем, что она постоянна вдоль всей
поверхности теплообмена),оС.
Из
выражений (5) и (6) следует, что локальные
коэффициенты теплоотдачи в принципе
могут быть найдены опытным путем
посредством измерения величин
![]() ,dF,
,dF,
![]() и
и![]() ,
,
относящихся к соответствующему бесконечно
малому участку:
![]() .
.
(7)
На
практике вдоль поверхности выделяют
необходимое количество конечных, но
достаточно малых участков и производят
измерения для каждого i-го участка
поверхности:
![]() ,
,
(8)
где
![]() –
–
среднее для i-го участка значение
коэффициента теплоотдачи, Вт/(м2∙К);
![]() –
–
площадь поверхности i-го участка, м2;
![]() –
–
тепловой поток в пределах i-го участка,
Вт;![]() –
–
среднее для i-го участка значение
температуры поверхности;![]() –
–
средняя плотность теплового потока в
пределах i-го участка, Вт/м2;
i = 1,2,…,n – номер очередного участка; n
– количество участков.
При
теплоотдаче на вертикальной поверхности
выделяют n
одинаковых по высоте участков (см.
рис.4). Если измерять температуру
поверхности на границах выделенных
участков, начиная с ее нижней кромки
(i=1),
то средняя для i-го участка температура
определится по формуле
![]() . (9)
. (9)
Среднее
для малого i-го участка значение
коэффициента теплоотдачи (8) является
приближенным значением локального
коэффициента теплоотдачи (7). Чем меньше
размеры участка, тем точнее получаемый
результат.
Результаты
большого количества опытов по определению
коэффициентов теплоотдачи (8) обобщают
в виде эмпирических (опытных) критериальных
уравнений (см.разд.5). В дальнейшем
эти уравнения используют в инженерных
расчетах для определения коэффициентов
теплоотдачи.
Содержание:
- Теплоотдача при вынужденном течении жидкости в трубах и каналах
Теплоотдача при ламинарном течении
Теплоотдача в трубах и каналах при турбулентном режиме
Расчет теплоотдачи при вынужденной конвекции - Теплоотдача при свободной конвекции в трубах и каналах
Свободная конвекция в неограниченном пространстве
Свободная конвекция в ограниченном объеме
Расчет теплоотдачи при свободной конвекции
Теплоотдача при вынужденном течении жидкости в трубах и каналах
Теплоотдача в трубах и каналах может происходить при вынужденном или свободном характере конвекционных потоков (возможны также их сочетания в случае существенного влияния гравитационных сил).
При вынужденном течении (вынужденная конвекция) жидкость нагнетается или отводится под действием сил внешнего давления, например, ветра, насоса или вентилятора.
Свободное течение жидкости происходит под действием подъемных (гравитационных) сил за счет изменения ее плотности из-за разницы температуры – слой жидкости с меньшей плотностью стремиться занять верхнее положение относительно холодного слоя (свободная или естественная конвекция).
Интенсивность теплоотдачи, как при вынужденной, так и при свободной конвекции характеризуется коэффициентом теплоотдачи α, имеющим размерность Вт/(м2·град), который определяется по формуле:
![]()
Nu – число Нуссельта; λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);
d – эквивалентный диаметр, равный
![]()
F – площадь сечения канала, м2; П – периметр канала, м.
Для трубы круглого сечения, эквивалентный диаметр равен внутреннему диаметру трубы.
В целом, расчет коэффициента теплоотдачи сводится к определению числа Нуссельта, значение которого задается соответствующими критериальными уравнениями конвективного теплообмена, зависящими от режима течения жидкости и формы канала.
Течение жидкости в трубах определяется значением числа Рейнольдса Re и в зависимости от его величины может быть ламинарным, переходным или турбулентным.
- Ламинарный режим течения жидкости характеризуется величиной числа Re до 2300.
- При значении числа Re от 2300 до 10000 режим течения в трубах является переходным.
- Турбулентный режим течения в трубах наблюдается при числах Re более 10000.
Число (критерий) Рейнольдса представляет собой безразмерный комплекс, связывающий скоростные и вязкостные характеристики жидкости с определяющим размером канала (для трубы – это ее диаметр).
Число Re определяется по формуле:
![]()
w – скорость течения жидкости, м/с; d – эквивалентный диаметр канала, м; ν — кинематическая вязкость жидкости при средней температуре, м2/с.
Теплоотдача в трубах и каналах существенно зависит от режима течения жидкости. При ламинарном режиме интенсивность теплоотдачи значительно меньше, чем при развитом турбулентном.
Теплоотдача при ламинарном течении в трубах и каналах
Ламинарный режим течения жидкости обычно характеризуется низкой скоростью потока. При этом в некоторых случаях влиянием конвекции, обусловленной действием гравитационных сил, пренебрегать нельзя.
Для выбора правильного критериального уравнения теплообмена и оценки влияния естественной конвекции на интенсивность теплопередачи при ламинарном режиме служит критерий Грасгофа Gr.
![]()
g – ускорение свободного падения, м/с2;
β – температурный коэффициент объемного расширения, град-1;
d – эквивалентный диаметр канала, м;
ν — кинематическая вязкость жидкости при средней температуре, м2/с;
Δt – средняя разность температур жидкости и стенки, °С.
Теплоотдача при ламинарном течении в трубах и каналах с учетом естественной конвекции. Если величина комплекса GrPr превышает 8·105, то расчет коэффициента теплоотдачи необходимо проводить с учетом влияния естественной конвекции в потоке жидкости по следующему критериальному уравнению:
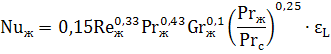
Индекс «ж» означает, что свойства среды, входящие в критерии подобия Re, Pr и Gr берутся при средней температуре жидкости.
Число Прандтля с индексом «с» Prс берется для жидкости при температуре стенки.
εL – коэффициент, учитывающий изменение теплоотдачи по длине трубы или канала. Его можно определить с помощью таблицы:
| L/d | 1 | 2 | 5 | 10 | 15 | 20 | 30 | 40 | 50 |
|---|---|---|---|---|---|---|---|---|---|
| εL | 1,9 | 1,7 | 1,44 | 1,28 | 1,18 | 1,13 | 1,05 | 1,02 | 1 |
Теплоотдача при ламинарном течении в трубах и каналах без учета естественной конвекции. При значении GrPr<8·105, влияние естественной конвекции на теплоотдачу жидкости пренебрежительно мало, и расчет коэффициента теплоотдачи можно проводить по следующему критериальному уравнению:
![]()
d – эквивалентный диаметр канала, м;
L – длина трубы (канала), м.
Представленные критериальные уравнения теплообмена при ламинарном режиме позволяют определить среднее значение числа Нуссельта, по величине которого можно рассчитать средний коэффициент теплоотдачи:
![]()
λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);
d – эквивалентный диаметр, м.
Теплоотдача в трубах и каналах при турбулентном режиме
Теплоотдача в трубах и каналах при турбулентном режиме осуществляется путем передачи тепла при интенсивном перемешивании слоев жидкости. Критериальное уравнение теплообмена для расчета средней теплоотдачи в трубах и каналах в этом случае имеет вид:
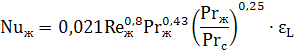
Критерии подобия Re и Pr берутся при средней температуре жидкости. Число Прандтля с индексом «с» Prс берется при температуре стенки.
Представленное критериальное уравнение применяется в диапазоне чисел Re от 1·104 до 5·106 и Pr от 0,6 до 2500.
εL – коэффициент, учитывающий изменение среднего коэффициента теплоотдачи по длине трубы или канала при турбулентном режиме течения. Значения εL приведены в следующей таблице при различных числах Рейнольдса и отношениях длины канала к его эквивалентному диаметру:
| Reж | L/d | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 5 | 10 | 15 | 20 | 30 | 40 | 50 | |
| 1·104 | 1,65 | 1,5 | 1,34 | 1,23 | 1,17 | 1,13 | 1,07 | 1,03 | 1 |
| 2·104 | 1,51 | 1,4 | 1,27 | 1,18 | 1,13 | 1,1 | 1,05 | 1,02 | 1 |
| 5·104 | 1,34 | 1,27 | 1,18 | 1,13 | 1,1 | 1,08 | 1,04 | 1,02 | 1 |
| 1·105 | 1,28 | 1,22 | 1,15 | 1,1 | 1,08 | 1,06 | 1,03 | 1,02 | 1 |
| 1·106 | 1,14 | 1,11 | 1,08 | 1,05 | 1,04 | 1,03 | 1,02 | 1,01 | 1 |
Расчет теплоотдачи в изогнутых трубах и каналах проводится по тому же критериальному уравнению с добавлением множителя — поправки на действие центробежных сил, которая определяется по формуле:
![]()
R — радиус изгиба трубы или канала, м; d – эквивалентный диаметр трубы или канала, м.
Теплоотдача в изогнутых трубах проходит более интенсивно, чем в прямых, за счет большего вихреобразования и лучшего перемешивания жидкости.
Расчет теплоотдачи при вынужденной конвекции
Пример расчета. Рассчитаем средний коэффициент теплоотдачи воды, текущей по трубопроводу длиной 1 м, диаметром d=0,01 м с расходом Q=20 л/мин. Средняя температура воды tж=50°С, температура стенки трубы tс=10°С.
1. Определим физические свойства воды при температуре 50°С:
- Теплопроводность воды λж= 0,648 Вт/(м·град);
- Плотность воды ρж=988 кг/м3;
- Кинематическая вязкость воды νж=0,556·10-6, м2/с;
- Число Прандтля при температуре жидкости Prж=3,54;
- Число Прандтля при температуре стенки Prс=9,52.
2. Рассчитаем среднюю скорость течения воды w по трубе:
![]()
3. Определим число Рейнольдса Re:
![]()
4. Поскольку число Рейнольдса имеет значение больше 1·104, то режим течения является турбулентным и расчет теплоотдачи необходимо проводить по следующему критериальному уравнению:
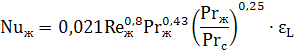
Определим коэффициент εL по соотношению L/d=1/0,01=100. Поскольку L/d>50, то коэффициент εL=1.
Выполним расчет числа Нуссельта по приведенному критериальному уравнению:
![]()
5. Рассчитаем средний коэффициент теплоотдачи от воды к стенке трубы по формуле:
![]()
Выполним расчет:
![]()
Таким образом, средний коэффициент теплоотдачи от воды к стенке трубы составляет 14,65 кВт/(м2·град).
Теплоотдача при свободной конвекции в трубах и каналах
Теплообмен при свободном движении жидкости (или газа) происходит вследствие разности плотностей нагретых и холодных ее слоев. Интенсивность теплоотдачи жидкости в трубах и каналах при свободной конвекции существенно зависит от их положения в пространстве относительно силы тяжести.
Теплоотдача при свободной конвекции имеет различный характер в случаях свободного течения в неограниченном пространстве и теплообмена в ограниченном объеме (в узкой трубе или канале).
Свободная конвекция в неограниченном пространстве
Конвекция в неограниченном пространстве протекает, например при охлаждении трубопровода центрального отопления, расположенного на улице в безветренную погоду, вблизи от которого отсутствуют препятствия для движения воздушных потоков.
Горизонтальный канал или труба. Интенсивность теплоотдачи при свободной конвекции зависит от величины комплекса GrPr. При значении GrPr от 103 до 109 критериальное уравнение, описывающее среднюю теплоотдачу от поверхности горизонтальных труб и каналов, имеет вид:
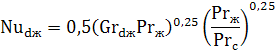
В качестве определяющего размера принимается наружный диаметр d канала или трубы.
Вертикальный канал (труба, пластина). Для вертикальных труб и каналов при значении GrPr от 103 до 109 критериальное уравнение, описывающее среднюю теплоотдачу, имеет вид:
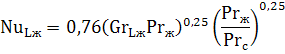
При GrPr>109:
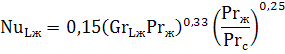
Примечание: В приведенных критериальных уравнениях теплообмена свойства жидкости, входящие в числа Gr и Pr, определяются при температуре окружающей среды. Число Прандтля с индексом «с» Prс берется для жидкости при температуре стенки. В качестве определяющего размера принимается длина L (высота) вертикально стоящей трубы или канала.
Свободная конвекция в ограниченном объеме
Теплообмен жидкости в ограниченном объеме при свободной конвекции характеризуется совместным протеканием процессов нагрева и охлаждения соседних слоев жидкости (или газа). Эти процессы сопровождаются сложным течением нисходящих и восходящих потоков, зависящих от рода жидкости, разницы температуры, формы канала и его геометрических размеров.
Для упрощения расчета таких сложных процессов конвективного теплообмена принято рассматривать их, как явление теплопроводности в щели толщиной δ с учетом понятия эквивалентного коэффициента теплопроводности λэк.
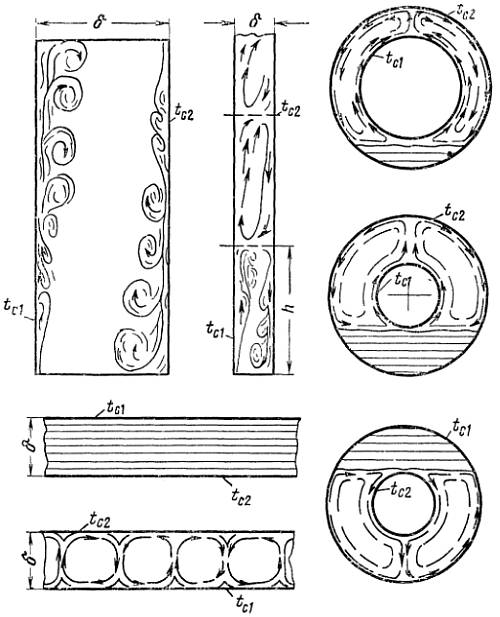
Эквивалентный коэффициент теплопроводности определяется по формуле:
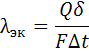
Q — количество переданного тепла, Вт; δ — толщина слоя жидкости (или газа), м; F — площадь теплоотдающей поверхности, м2; Δt=tc1-tc2 — температурный напор между нагретой и холодной стенками, °С.
Отношение эквивалентного коэффициента теплопроводности λэк к величине теплопроводности окружающей жидкости при средней температуре называется коэффициентом конвекции εк, который определяется значением комплекса GrPr.
При малых значениях комплекса GrPr<1000 коэффициент конвекции εк=1, то есть теплоотдача просходит только за счет теплопроводности среды (λэк=λ).
В случае 103<GrPr<106:
![]() При 106<GrPr<1010:
При 106<GrPr<1010:
![]()
Примечание: Числа подобия Gr и Pr рассчитываются при средней температуре жидкости (или газа), равной tж=0,5(tc1+tc2). В качестве определяющего размера принимается δ — толщина слоя жидкости.
Расчет теплоотдачи при свободной конвекции
Пример расчета. Рассчитаем потери тепла естественной конвекцией от горизонтального трубопровода центрального отопления, находящегося на открытом воздухе. Диаметр трубопровода d=0,15 м, длина L=5 м, средняя температура наружной стенки tс=80°С. Температура окружающего воздуха tж=20°С.
1. Определим физические свойства воздуха при температуре 20°С:
- Теплопроводность воздуха λж= 0,0259 Вт/(м·град);
- Кинематическая вязкость воздуха νж=15,06·10-6, м2/с;
- Число Прандтля при температуре жидкости Prж=0,703;
- Число Прандтля при температуре стенки Prс=0,69;
- Коэффициент объемного расширения βж=1/(273+20)=0,00341 град-1.
2. Вычислим число Грасгофа Gr по формуле:
![]()
Получаем:
![]()
3. Определим значение комплекса GrPr:
![]()
Этому значению комплекса соответствует следующее критериальное уравнение теплообмена при свободной конвекции в случае горизонтальной трубы:
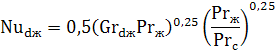
4. Вычислим значение числа Нуссельта Nu:
![]()
5. Рассчитаем коэффициент теплоотдачи от трубы α по формуле:
![]()
Получаем:
![]()
6. Определим потери тепла с боковой поверхности трубопровода по формуле:
![]()
Подставляя численные значения, окончательно получаем потерю тепла:
![]()
Таким образом, только путем естественной (свободной) конвекции рассмотренный трубопровод отопления отдает воздуху 1681 Вт тепла.
Источники:
- Михеев М. А., Михеева И. М. Основы теплопередачи.
- Исаченко В. П., Осипова В. А., Сукомел А. С. Теплопередача. Учебник для вузов — М.: «Энергия», 1975.
Расчет и оценка коэффициента теплоотдачи
Теплоотдача при теплообмене между атмосферным воздухом и дневной поверхностью может быть определена несколькими формулами. Наиболее распространённая из них следующая [1].
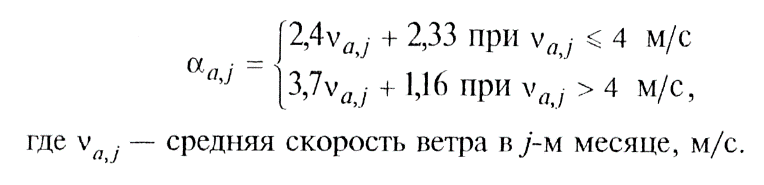
Несмотря на то, что расчёт по данным формулам показывает отличающиеся друг от друга значения, выбор конкретных формулы для моделирования не всегда важен. Дело в том, что если проводить адаптацию параметров теплообмена с окружающей средой, то данной процедурой несколько нивелируются погрешности определения других составляющих теплообмена, в том числе и теплоотдачи.
При моделировании инженерных сооружений, часто бывает необходимым определение коэффициента теплоотдачи от инженерного сооружения к поверхности.
При наличии воздуха, осуществляющего теплоотдачу, расчёт может быть затруднён, так как зачастую достаточно сложно рассчитать или оценить скорость его движения (например, конвекция воздуха в замкнутых полостях). Для проектирования, можно рекомендовать использовать коэффициенты рекомендуемые СП 50.13330.2012 «Тепловая защита зданий. (Актуализированная редакция СНиП 23-02.2003)».
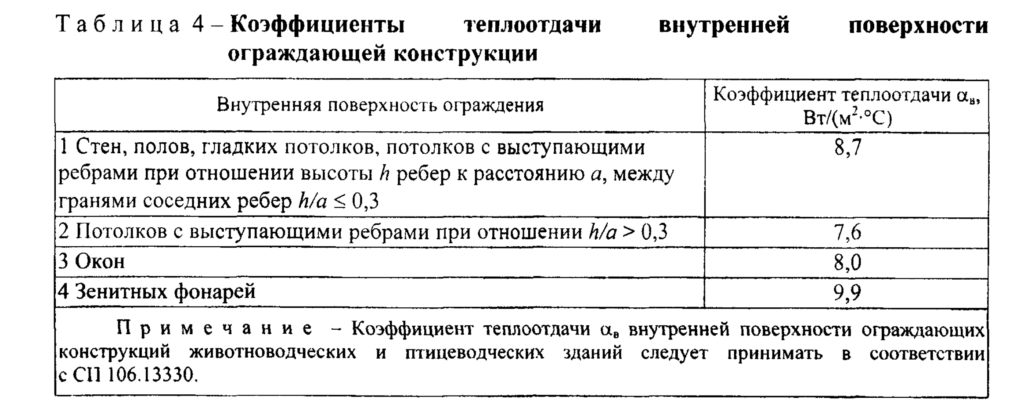
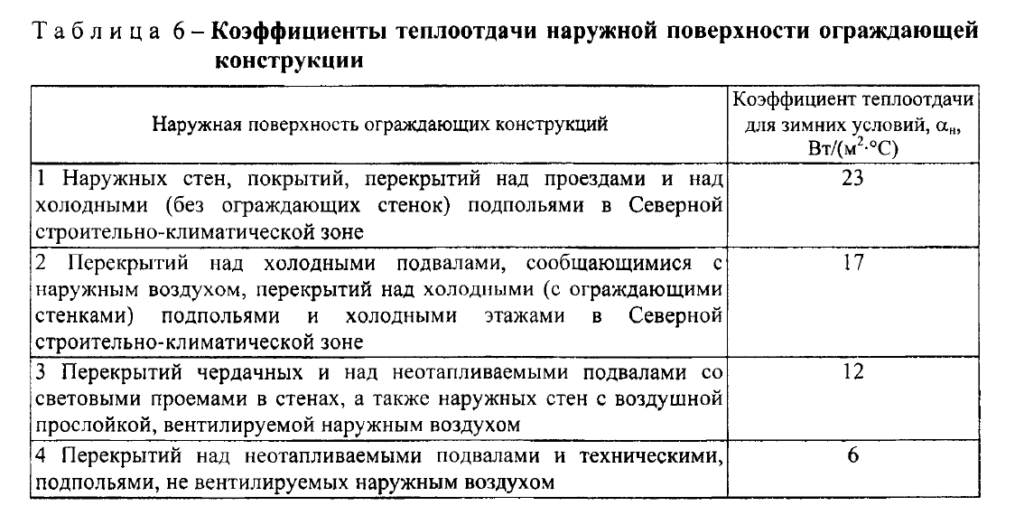
Данные коэффициенты представляются нам несколько завышенными, но для использования при проектировании, они будут обеспечивать некоторый запас надёжности, закладываемый вами в расчёт. Как правило, это то, что нужно.
В случае, когда мы имеем подвижную среду (жидкую или газообразную), т.е. имеющую конвективную составляющую теплообмена, отличного от воздуха вещества или если нам нужно будет более точно определить коэффициент теплоотдачи от воздуха, то следует воспользоваться формулами из теории теплообмена. Теория теплообмена обычно имеет эмпирический закономерности основанные на критериях подобия.
Критерии подобия — это числа, имеющие безразмерную величину и характеризующие различные аспекты подобия моделей и процессов (например, критерий Эйлера характеризует геометрическое подобие, а критерий Рейнольдса гидродинамическое). Таким образом, получив зависимость от критерия подобия на экспериментальных данных с лабораторного стенда, мы можем перенести эту зависимость на другие объекты имеющих имеющие те же значения критериев подобия. Более подробную информацию о критериях подобия и теории теплообмена можно получить различной литературе по теплообмену.
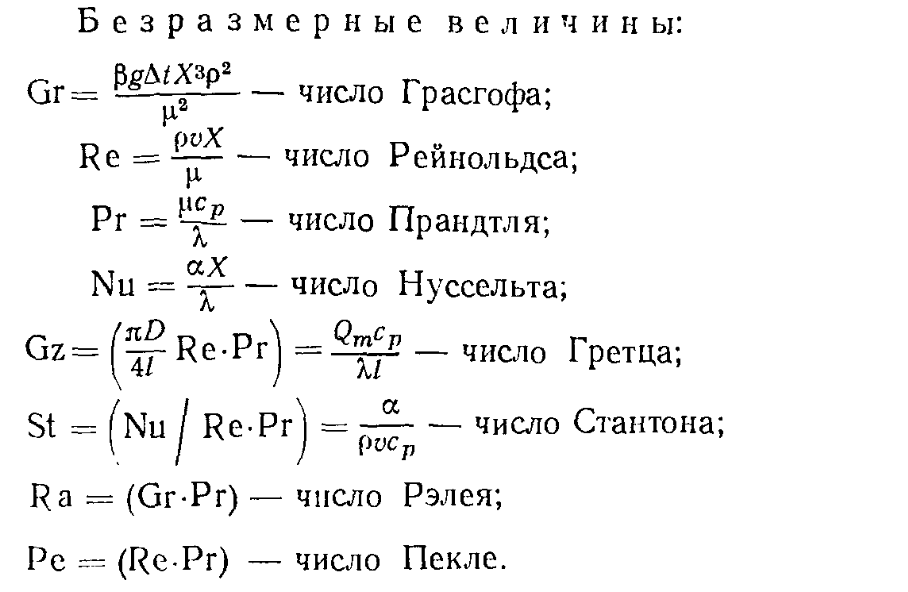
Зависимости для расчёта коэффициента теплоотдачи часто будут иметь следующий вид:
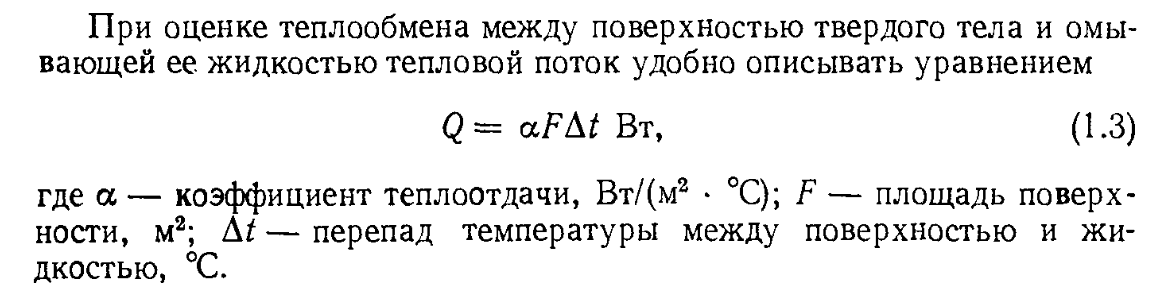
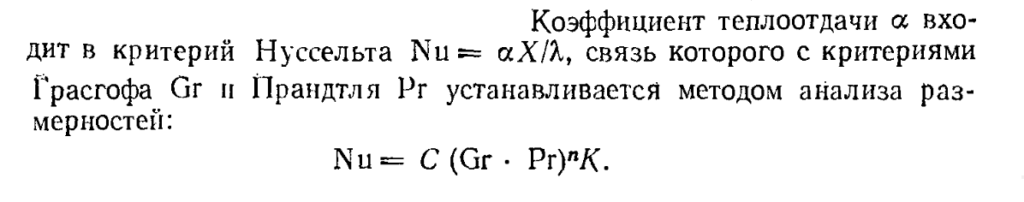
Где C, n и К – значения, которые принимаются по методике или справочнику для конкретного процесса;
Gr — число Графгофа;
Pr — число Прандтля;
Nu — число Нуссельта.
Обычно значение числа Нуссельта Nu находят по критериальной зависимости из теории теплообмена, а теплоотдачу α получают, выражая ее из определения критерия Нуссельта.
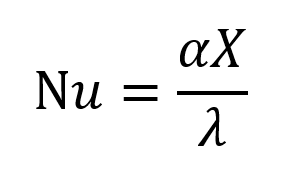
Эмпирические зависимости из теории теплообмена могут иметь достаточно сложную форму. Для строительного проектирования можно рекомендовать справочники по теплообмену [2-6], в которых различные зависимости будут представлены в несколько упрощённом виде.
Часто бывают такие ситуации, что воспользоваться формулами из теории теплообмена не представляется возможным в виду отсутствия исходных данных (например, связанных со скоростями движения воздуха или теплоносителя). В ряде случаев, при проектировании объектов, нужны величины обеспечивающие некоторые запас поступления теплоты в модель. Т.е. в этих случаях определение точных значений теплоотдачи не является необходимым, а достаточно оценки величины теплоотдачи с некоторым запасом.
В заметке для многослойной стенки мы уже рассматривали следующую особенность. Наибольший вклад в значение коэффициента теплопередачи вносит наибольшее термическое сопротивление. Например, учёт термического сопротивления металла при расчёте суммарного коэффициента теплопередачи теплоизолированного трубопровода приводит к изменению коэффициента теплопередачи менее чем на 0,1% (ссылка).
Схожая ситуация имеет место быть с другими инженерными сооружениями. Часто бывает так, что термическое сопротивление грунта (а теплопроводность грунта достаточно небольшая величина), оказывается наибольшим и теплоотдача от многих инженерных сооружений вносит незначительный вклад в суммарной коэффициент теплопередачи.
Для иллюстрации этого факта рассмотрим изменение радиуса промораживания грунта вокруг трубопровода 100 мм за 1 год, при изменении коэффициента теплоотдачи от трубопровода.
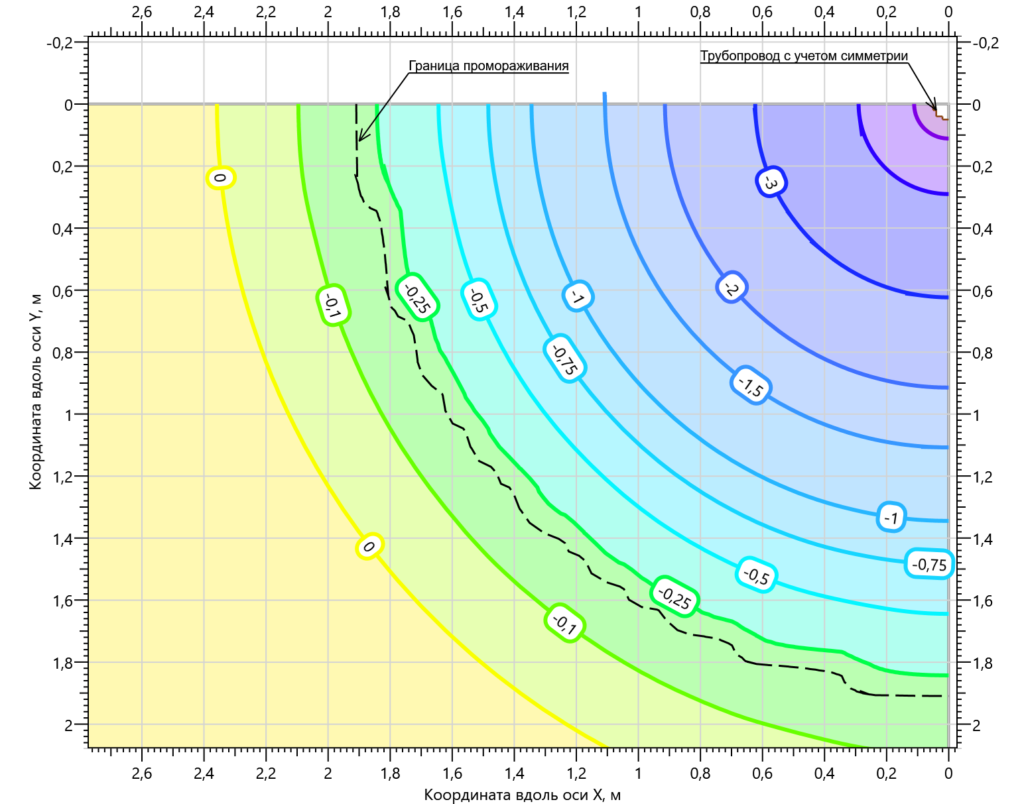
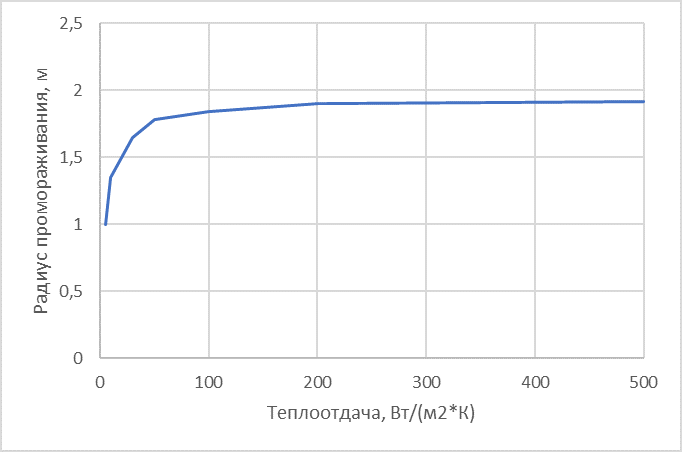
Из представленных результатов мы видим, что начиная с некоторых величин теплоотдачи радиус промораживания грунта перестаёт расти. Дело в том, что в процессе промораживания увеличивается слой мерзлого грунта и с некоторого момента времени данный слой начинает оказывать наибольшее термическое сопротивление. Что в свою очередь приводит к тому, что коэффициент теплоотдачи начинает вносить всё меньший и меньший вклад в теплообмен.
Т.е. для ряда сооружений достаточно оценить коэффициент теплоотдачи с некоторым запасом, а не пользоваться сложными соотношениями и методиками из теории теплообмена. Например, коэффициенты теплоотдачи при транспортировке нефти, газа или воды по трубопроводу, зачастую настолько велики, что их учёт в задачах теплообмена с грунтами не имеет практического смысла. В таком случае температуру на внутренней стенке трубы или на внутренней поверхности теплоизоляции можно принять равной температуре транспортируемой среды.
Для выполнения оценки коэффициента теплоотдачи можно воспользоваться таблицами ориентировочных значений теплоотдачи в различных процессах.
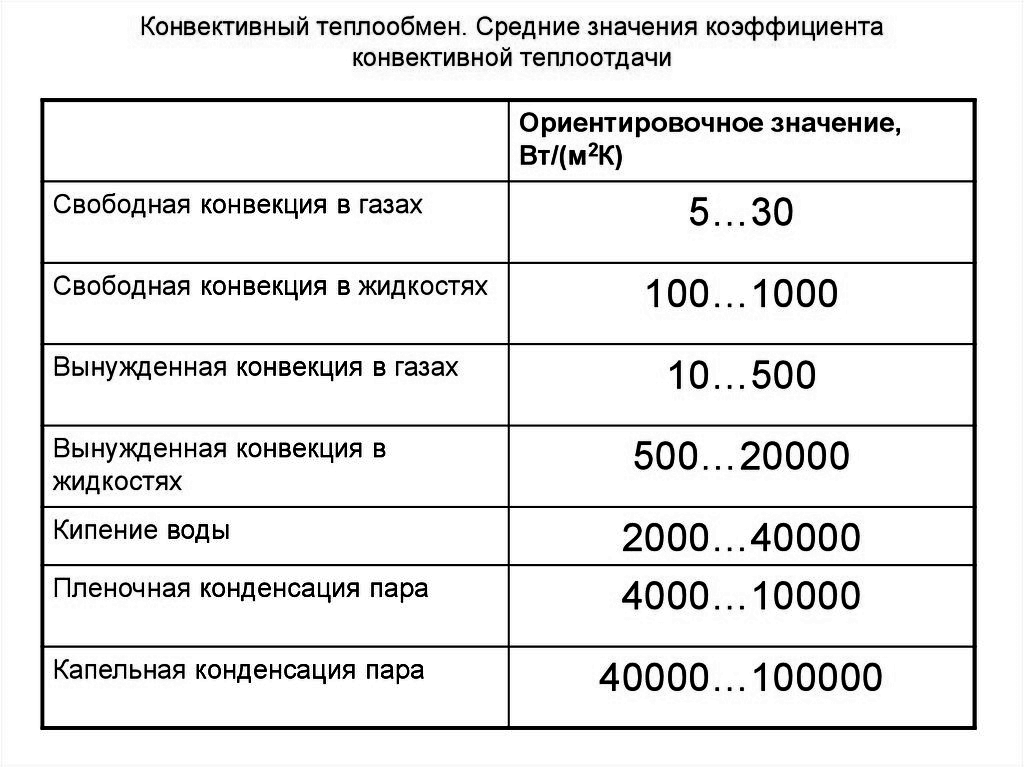

Несмотря на то, что во многих случаях коэффициент теплоотдачи достаточно просто оценить, при проектировании ряда инженерных сооружений простой экспресс оценки коэффициента теплоотдачи недостаточно и нужно прибегать к использованию сложных зависимостей теории теплообмена для точного расчета теплоотдачи.
Список литературы
- Хрусталев Л.Н. Основы геотехники в криолитозоне: Учебник. – М.: Изд-во МГУ, 2005.
- Уонг Х., Основные формулы и данные по теплообмену для инженеров. М.:Атомиздат, 1979г.
- Цветков Ф.Ф., Керимов Р.В., Величко В.И. Задачник по тепломассообмену. Второе издание, исправленное и дополненное. М.: Издательский дом МЭИ, 2008г. — 195с.
- Бажан П.И. и др. Справочник по теплообменным аппаратам. М.:Машиностроение, 1989.-369с.
- Справочник по теплообменникам: В 2-х т. Т. 1 / Пер. с англ. под ред. О. Г. Мартыненко и др.— М.: Энергоатомиздат, 1987.— 560 с: ил.
- Справочник по теплообменникам: В 2-х т. Т. 2 / Пер. с англ. под ред. О. Г. Мартыненко и др.— М.: Энергоатомиздат, 1987.— 352 с: ил.
Коэффициент теплоотдачи поверхность — воздух
Опубликовано 06 Апр 2020
Рубрика: Теплотехника | 29 комментариев
 В статье рассмотрен расчет мощности теплового потока от горизонтальных и вертикальных плоских поверхностей тела, помещенного в «безразмерное» воздушное пространство при принудительной и естественной конвекции с учетом радиационной составляющей теплоотдачи.
В статье рассмотрен расчет мощности теплового потока от горизонтальных и вертикальных плоских поверхностей тела, помещенного в «безразмерное» воздушное пространство при принудительной и естественной конвекции с учетом радиационной составляющей теплоотдачи.
Зная коэффициент теплоотдачи на поверхности (α), разделяющей твердое тело и окружающее это тело воздушное пространство, очень просто определить мощность теплового потока (Q) по известной разности температур (Δt).
Q=α*A*Δt, Вт – мощность теплового потока от или к поверхности тела.
- α=αк+αр, Вт/(м2*К) – суммарный коэффициент теплоотдачи на границе воздух – поверхность тела
- αк=?, Вт/(м2*К) – коэффициент конвективной теплоотдачи
- αр=ε*5,67*10-8*((tп+273,15)4— (tв+273,15)4)/(tп-tв)), Вт/(м2*К) – коэффициент радиационной теплоотдачи (теплоотдачи излучением), ε – степень черноты поверхности
- А, м2 – площадь поверхности
- Δt=|tп-tв|, К – разность температур поверхности и воздушной среды
- tп, °C – температура поверхности
- tв, °C – температура воздуха
Основная сложность расчета заключается в определении коэффициента конвективной теплоотдачи (αк)! Автоматизировать в первую очередь решение этой трудоемкой задачи поможет Excel.
Нестабильность процесса естественной конвекции у поверхностей различной формы и расположения в пространстве породила большое разнообразие эмпирических формул для вычисления коэффициента конвективной теплоотдачи (αк). Неизбежные погрешности экспериментальных данных привели к тому, что результаты вычислений для одних и тех же поверхностей и условий по формулам разных авторов отличаются друг от друга на 20% и более.
После тщательного детального ознакомления с материалами современных западных изданий по теплообмену (список литературы – в конце статьи) были выбраны формулы, рекомендованные к применению большинством авторов, для использования в представленной далее программе в Excel.
Схемы теплообмена:
На представленных ниже рисунках показаны 8 вариантов схем, для которых программа может выполнить вычисления.
Розовый цвет пластин свидетельствует о том, что они горячее окружающего воздуха. Голубой цвет – пластины холоднее воздуха.
На схемах 1а и 1б воздух принудительно движется (вентилятор, ветер) вдоль поверхности пластины независимо от её ориентации в пространстве. На всех остальных схемах окружающий воздух находится в спокойном состоянии (помещение, полный штиль), а положение пластин сориентировано в пространстве.




Расчет в Excel:

Формулы алгоритма программы:
t0=(tв+tп)/2
l0=L – для схем 1а и 1б
l0=(B*L)/(2*(B+L)) – для схем 2а, 2б, 3а, 3б, 4а, 4б
Для определения теплофизических параметров воздуха при определяющей температуре (t0) в диапазоне -70°C … +1200°C использованы формулы из предыдущей статьи на сайте.
Re=w*l0/ν
Gr=g*β*|tп— tв|*l03/ν2
Ra=Gr*Pr

αк=Nu*λ/l0
αр=ε*0,00000005670367*((tп+273,15)4— (tв+273,15)4)/(tп-tв)) – при tв<tп
*)αр=0 – при tв>tп
α=αк+αр
q=α*(tп-tв)
Q=q*B*L
*)Нагрев поверхностей Солнцем или иными источниками теплового излучения программой игнорируется.
Вычисление теплофизических параметров воздуха и числа Нуссельта, как видно из вышеприведенных формул, являются ключевыми и самыми трудоемкими при определении конвективного коэффициента теплоотдачи.
Тестирование программы проводилось на примерах из книг, представленных в конце статьи. Отклонения результатов в основном не выходили за пределы ±5%.
Замечание:
В отечественной теплотехнической литературе для решения рассмотренных задач широко используются формулы второй половины прошлого века М.А. Михеева и В.П. Исаченко, которые в современной западной литературе не упоминаются. Беглый сравнительный анализ результатов расчетов по формулам разных авторов дал противоречивые и неоднозначные ответы. Если при принудительной конвекции результаты фактически идентичны, то при естественной конвекции отличаются порой на 30% и более, но иногда почти совпадают…
Литература:
- John H. Lienhard IV, John H. Lienhard V, A Heat Transfer Textbook (Fifth Edition), 2019.
- Frank Kreith, Raj M. Manglik, Mark S. Bohn, Principles of heat transfer (Seventh Edition), 2011.
- Adrian Bejan, Convection Heat Transfer (Fourth Edition), 2013.
- Michel Favre-Marinet, Sedat Tardu, Convective Heat Transfer, 2009.
- Harlan H. Bengtson, Convection Heat Transfer Coefficient Estimation, 2010.
- Rajendra Karwa, Heat and Mass Transfer, 2017.
- Stuart W. Churchill, Humbert H. S. Chu, Correlating equations for laminar and turbulent free convection from a vertical plate, International Journal of Heat and Mass Transfer, Volume 18, Issue 11, November 1975.
- http://people.csail.mit.edu/jaffer/SimRoof/Convection/
- И. И. Кирвель, М. М. Бражников, Е. Н. Зацепин ЭНЕРГОСБЕРЕЖЕНИЕ В ПРОЦЕССАХ ТЕПЛООБМЕНА, 2007.
Ссылка на скачивание файла: koehfficient-teplootdachi-poverhnost-vozduh (xlsx 225KB).
P. S. (01.11.2020)
Дополнение по естественной конвекции у вертикальной поверхности:
Если построить графики по вышеприведенным формулам Черчилля и Чу для числа Нуссельта при естественной конвекции у вертикальной изотермической поверхности (схемы 2а и 2б), то можно увидеть, что при Ra=109 кривые не совпадают!

По этому поводу авторы формул Черчилль и Чу дают примерно следующее пояснение: «уравнение, основанное на исследованиях Черчилля и Усаги Nu=(0,825+0,387*Ra1/6/(1+(0,492/Pr)9/16)8/27)2 дает хорошие результаты для средней теплопередачи при свободной конвекции у изотермической вертикальной пластины во всем диапазоне значений Ra и Pr от 0 до ∞, даже если оно не работает для обозначения дискретного перехода от ламинарного к турбулентному потоку». Линхарды в [1] отмечают, что рассматриваемое уравнение чуть менее точно для ламинарных условий при Ra<109 и рекомендуют в этом диапазоне использовать первое уравнение тех же авторов Nu=0,68+0,67*Ra¼/(1+(0,492/Pr)9/16)4/9. Хотя, судя по графикам, в диапазоне Ra<107 для воздуха обе функции чрезвычайно близки друг к другу.
Еще один нюанс, который встретился только у Линхардов в [1]: «свойства флюида следует оценивать при t0=(tв+tп)/2 за одним исключением, если флюид – газ, то коэффициент объемного расширения β следует определять при t0=tв». Но сами авторы зависимостей Черчилль и Чу о таком условии ничего не пишут. По этому поводу в их статье [7], говорится, что «для больших температурных перепадов, когда физические свойства существенно различаются, Ид рекомендует оценивать физические свойства как средние значения температуры поверхности и объема, а Уайли дает более подробные теоретические указания для режима ламинарного пограничного слоя».
Максимальная относительная ошибка для Nu=(0,825+0,387*Ra1/6/(1+(0,492/Pr)9/16)8/27)2, если β=1/tв вместо β=2/( tв+tп), составляет в процентах:
ε=(((tв+tп)/(2*tв))1/3-1)*100%, или
ε=((|(tп— tв)|/(2*tв)+1)1/3-1)*100%

Как видно из графика при температуре среды – воздуха tв=20°C=293,15K и при перепаде температур поверхности и воздуха Δt=|tп— tв|<90 °C максимальная погрешность ε не превышает 5%.
При Δt>90 °C расхождение результатов быстро нарастает.
Правы Линхарды или множество других авторов, рассчитывающих все свойства флюидов при одном значении определяющей температуры t0=(tв+tп)/2? Однозначного ответа у меня нет.
(По материалам Обри Джаффера [8].)
Эмпирические уравнения для суммарного коэффициента теплоотдачи:
В инженерных расчетах для быстрого приближенного определения суммарного коэффициента теплоотдачи, учитывающего и конвекцию, и излучение на границе поверхность тела – среда, можно использовать более простые зависимости, приведенные в [9].
При расчете тепловых потерь через наружные поверхности тел, которые находятся в спокойном воздухе закрытых помещений, можно применить нижеприведенные формулы. Результаты вычислений по этим формулам достаточно близки к результатам более точных расчетов.
α=9,74+0,07*(tп-tв), Вт/(м2*°C) при tп<150 °C
α=9,3+0,058*tп, Вт/(м2*°C) при tп=50…350 °C
On-line калькуляторы для расчетов коэффициентов конвективной теплоотдачи от плоских, цилиндрических и сферических поверхностей:
Инструменты представлены Группой исследований теплопередачи (HTRG). Группа была создана в 2014 году преподавателями Лаборатории теплотехники и жидкостей факультета машиностроения инженерной школы Сан-Карлоса (EESC) Университета Сан-Паулу (USP) для проведения передовых, качественных фундаментальных и прикладных исследований по вопросам теплопередачи для многофазных и однофазных систем.
www.heatgroup.eesc.usp.br/tools/
Точность результатов вычислений по on-line калькуляторам детально не проверял.
Другие статьи автора блога
На главную
