Download Article
Calculate correlation by hand, online, or with a graphing calculator
Download Article
- By Hand
- Online Calculators
- Graphing Calculators
- Reviewing the Fundamentals
- Q&A
|
|
|
|
The correlation coefficient, denoted as r or ρ, is the measure of linear correlation (the relationship, in terms of both strength and direction) between two variables. It ranges from -1 to +1, with plus and minus signs used to represent positive and negative correlation. If the correlation coefficient is exactly -1, then the relationship between the two variables is a perfect negative fit; if the correlation coefficient is exactly +1, then the relationship is a perfect positive fit. Otherwise, two variables may have a positive correlation, a negative correlation, or no correlation at all. You can calculate correlation by hand, by using some free correlation calculators available online, or by using the statistical functions of a good graphing calculator.
-

1
Assemble your data. To begin calculating a correlation efficient, first examine your data pairs. It is helpful to put them in a table, either vertically or horizontally. Label each row or column x and y.[1]
- For example, suppose you have four data pairs for x and y. Your table may look like this:
- x || y
- 1 || 1
- 2 || 3
- 4 || 5
- 5 || 7
- For example, suppose you have four data pairs for x and y. Your table may look like this:
-

2
Calculate the mean of x. In order to calculate the mean, you must add all the values of x, then divide by the number of values.[2]
Advertisement
-

3
Find the mean of y. To find the mean of y, follow the same steps, adding all the values of y together, then dividing by the number of values.[3]
-

4
Determine the standard deviation of x. Once you have your means, you can calculate standard deviation. To do so, use the formula:[4]
-

5
Calculate the standard deviation of y. Using the same basic steps, find the standard deviation of y. You will use the same formula, using the y data points.[5]
-

6
Review the basic formula for finding a correlation coefficient. The formula for calculating a correlation coefficient uses means, standard deviations, and the number of pairs in your data set (represented by n). The correlation coefficient itself is represented by the lower-case letter r or the lower-case Greek letter rho, ρ. For this article, you will use the formula known as the Pearson correlation coefficient, shown below:[6]
- You may notice slight variations in the formula, here or in other texts. For example, some will use the Greek notation with rho and sigma, while others will use r and s. Some texts may show slightly different formulas; but they will be mathematically equivalent to this one.
-

7
Find the correlation coefficient. You now have the means and standard deviations for your variables, so you can proceed to use the correlation coefficient formula. Remember that n represents the number of values you have. You have already worked out the other relevant information in the steps above.[7]
-

8
Interpret your result. For this data set, the correlation coefficient is 0.988. This number tells you two things about the data. Look at the sign of the number and the size of the number.[8]
- Because the correlation coefficient is positive, you can say there is a positive correlation between the x-data and the y-data. This means that as the x values increase, you expect the y values to increase also.
- Because the correlation coefficient is very close to +1, the x-data and y-data are very closely connected. If you were to graph these points, you would see that they form a very good approximation of a straight line.
Advertisement
-

1
Search the Internet for correlation calculators. Measuring correlation is a fairly standard calculation for statisticians. The calculation can become very tedious if done by hand for large data sets. As a result, many sources have made correlation calculators available online. Use any search engine and enter the search term “correlation calculator.”
-

2
Enter your data. Carefully review the instructions on the website so you will enter your data properly. It is important that your data pairs are kept in order, or you will generate an incorrect correlation result. Different websites use different formats to enter data.
- For example, at the website http://ncalculators.com/statistics/correlation-coefficient-calculator.htm, you will find one horizontal box for entering x-values and a second horizontal box for entering y-values. You enter your terms, separated only by commas. Thus, the x-data set that was calculated earlier in this article should be entered as 1,2,4,5. The y-data set should be 1,3,5,7.
- At another site, http://www.alcula.com/calculators/statistics/correlation-coefficient/, you can enter data either horizontally or vertically, as long as you keep the data points in order.
-

3
Calculate your results. These calculation sites are popular because, after you enter your data, you generally need only to click on the button that says “Calculate,” and the result will appear automatically.
Advertisement
-

1
Enter your data. Using a handheld graphing calculator, enter your calculator’s statistics function and then select the “Edit” command.[9]
- Each calculator will have slightly different key commands. This article will give the specific instructions for the Texas Instruments TI-86.
- Enter the Stat function by pressing [2nd]-Stat (above the + key), then hit F2-Edit.
-

2
Clear any old stored data. Most calculators will keep statistical data until cleared. To make sure that you do not confuse old data with new data, you should first clear any previously stored information.[10]
- Use the arrow keys to move the cursor to highlight the heading “xStat.” Then press Clear and Enter. This should clear all values in the xStat column.
- Use the arrow keys to highlight the yStat heading. Press Clear and Enter to empty the data from that column as well.
-

3
Enter your data values. Using the arrow keys, move the cursor to the first space under the xStat heading. Type in your first data value and then hit Enter. You should see the space at the bottom of the screen display “xStat(1)=__,” with your value filling the blank space. When you hit Enter, the data will fill the table, the cursor will move to the next line, and the line at the bottom of the screen should now read “xStat(2)=__.”[11]
- Continue entering all the x-data values.
- When you complete the x-data, use the arrow keys to move to the yStat column and enter the y-data values.
- After all the data has been entered, hit Exit to clear the screen and leave the Stat menu.
-

4
Calculate the linear regression statistics. The correlation coefficient is a measure of how well the data approximates a straight line. A statistical graphing calculator can very quickly calculate the best-fit line and the correlation coefficient.[12]
- Enter the Stat function and then hit the Calc button. On the TI-86, this is [2nd][Stat][F1].
- Choose the Linear Regression calculations. On the TI-86, this is [F3], which is labeled “LinR.” The graphic screen should then display the line “LinR _,” with a blinking cursor.
- You now need to enter the names of the two variables that you want to calculate. These are xStat and yStat.
- On the TI-86, select the Names list by hitting [2nd][List][F3].
- The bottom line of your screen should now show the available variables. Choose [xStat] (this is probably button F1 or F2), then enter a comma, then [yStat].
- Hit Enter to calculate the data.
-

5
Advertisement
-

1
Understand the concept of correlation. Correlation refers to the statistical relationship between two quantities. The correlation coefficient is a single number that you can calculate for any two sets of data points. The number will always be something between -1 and +1, and it indicates how closely connected the two data sets tend to be.[14]
- For example, if you were to measure the heights and ages of children up to the age of about 12, you would expect to find a strong positive correlation. As children get older, they tend to get taller.
- An example of negative correlation would be data comparing a person’s time spent practicing golf shots and that person’s golf score. As the practice increases, the score should decrease.
- Finally, you would expect very little correlation, either positive or negative, between a person’s shoe size, for example, and SAT scores.
-

2
Know how to find a mean. The arithmetic mean, or “average,” of a set of data is calculated by adding all of the values of the data together, then dividing by the number of values in the set. When you find the correlation coefficient for your data, you will need to calculate the mean of each set of data.[15]
- The mean of a variable is denoted by the variable with a horizontal line above it. This is often referred to as “x-bar” or “y-bar” for the x and y data sets. Alternatively, the mean may be signified by the lower-case Greek letter mu, μ. To indicate the mean of x-data points, for example, you could write μx or μ(x).
- As an example, if you have a set of x-data points (1,2,5,6,9,10), then the mean of this data is calculated as follows:
-

3
Note the importance of standard deviation. In statistics, standard deviation measures variation, showing how numbers are spread out in relationship to the mean. A group of numbers with a low standard deviation are fairly tightly collected. A group of numbers with a high standard deviation are widely scattered.[16]
- Symbolically, standard deviation is expressed with either the lower-case letter s or the lower-case Greek letter sigma, σ. Thus, the standard deviation of the x-data is written as either sx or σx.
-

4
Recognize summation notation. The summation operator is one of the most common operators in mathematics, indicating a sum of values. It is represented by the upper-case Greek letter, sigma, or ∑.[17]
- As an example, if you have a set of x-data points (1,2,5,6,9,10), then ∑x means:
- 1+2+5+6+9+10 = 33.
- As an example, if you have a set of x-data points (1,2,5,6,9,10), then ∑x means:
Advertisement
Add New Question
-
Question
You are given the following information about two variables x and y: Mean(x)= 315 and Mean(y)=1,103. Variance(x)=59 and Variance(y)=156. Covariance(x,y)= -54. Calculate the coefficient of correlation between X and Y. Calculate your answer to two decimal places.

This question raises a higher level of statistics than is addressed in this article. It is possible to calculate the correlation coefficient from the means, variance and covariance, without actually having the original data points to begin with. The relationship is Correlation Coefficient = Covariance / ((Std. Dev. (x) * (Std. Dev. (y)). The standard deviation is the square root of the variance. So, with your data, this simplifies to Corr.Coeff.=-54/sqrt(59)sqrt(156) = -0.56.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Thanks for submitting a tip for review!
Video
Tips
- In general, a correlation coefficient higher than 0.8 (either positive or negative) represents a strong correlation; a correlation coefficient lower than 0.5 (again, either positive or negative) represents a weak one.
- The correlation coefficient is sometimes called the “Pearson product-moment correlation coefficient” in honor of its developer, Karl Pearson.
Warnings
- Correlation shows that the two sets of data are connected in some way. However, be careful not to interpret this as causation. For example, if you compare people’s shoe sizes and their height, you will probably find a strong positive correlation. Taller people generally have larger feet. However, this does not mean that growing tall causes your feet to grow, or that large feet cause you to grow tall. They just happen together.
References
About This Article
Article SummaryX
To find the correlation coefficient by hand, first put your data pairs into a table with one row labeled “X” and the other “Y.” Then calculate the mean of X by adding all the X values and dividing by the number of values. Calculate the mean for Y in the same way. Next, use the formula for standard deviation to calculate it for both X and Y. Finally, use the means and standard deviations and the number of pairs in your data set as inputs to the correlation coefficient formula, and solve the resulting equation. To learn how to find the correlation coefficient with an online calculator or your own graphing calculator, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 203,884 times.
Did this article help you?
Post Views:
10 503
Корреляционный анализ (КА) — это статистический инструмент, позволяющий установить связь между двумя различными переменными, а также оценить, насколько сильна взаимосвязь между этими переменными. Такой анализ применим исключительно для количественных данных. Исчисляется с помощью коэффициента корреляции, также известного как коэффициент Пирсона.
Коэффициент корреляции Пирсона — это ковариация двух переменных, деленная на произведение их стандартных отклонений. Коэффициент может иметь значение в диапазоне от (+1) до (-1), которое отражает степень взаимосвязи между переменными.
Результаты корреляционного анализа
Если результат корреляционного анализа положительный, то взаимосвязь двух переменных прямо пропорциональная. Это означает, что при увеличении одной переменной, вторая будет также увеличиваться. Как правило, такой результат принято называть “позитивной корреляцией”.
Если результат корреляционного анализа отрицательный, то взаимосвязь двух переменных обратно пропорциональная. Это означает, что при увеличении одной переменной, вторая будет уменьшаться. Такой эффект называется “отрицательной корреляцией”.
Таким образом, чем ближе значение КА к (+1) или (-1), тем сильнее взаимосвязь между двумя переменными. Соответственно, если результат анализа стремится к нулю, то взаимосвязь между двумя переменными отсутствует. Статистически значимыми принято считать значения, результат которых выше 0,5 в обоих направлениях.
Корреляционный анализ следует использовать, когда вы считаете, что есть связь между двумя переменными и вы хотите в этом убедиться. Также, КА можно использовать между несколькими переменными, проводя последовательную оценку, для определения наибольшей взаимосвязи.
Применение корреляционного анализа
Применение КА широко распространено, поскольку он позволяет выявить неожиданные взаимосвязи, которые позволяют делать более глубокий анализ и использовать полученные результаты для извлечения выгоды. Анализ полезен при тестировании гипотез ценообразования и продаж, развития стратегии и продуктового портфеля.
Например, корреляционный анализ поможет ответить на такие вопросы:
- Влияет ли скидка на увеличение продаж?
- Влияет ли уменьшение цены на увеличение продаж?
- Являются ли лояльные клиенты самыми прибыльными?
Самый простой пример: такие факторы, как жаркая погода и продажи мороженного можно подвергнуть корреляционному анализу. Логично сделать заключение, что жаркая погода является причиной того, что люди покупают больше мороженного. При этом, жаркая погода может стать причиной увеличения продаж хлора для бассейнов. Но при этом продажа мороженного никак не коррелируется с продажей хлора.
Более того, корреляционный анализ применяется в рамках концепции Lean SixSigma для поиска коренных причин проблемы и их взаимного влияния друг на друга.
Корреляционный анализ: формула

Порядок расчета коэффициента корреляции:
- Собрать данные исследуемых переменных — “X” и “Y”.
- Сгруппировать данные двух исследуемых переменных в столбцы (см. пример ниже).
- Добавить столбцы “ХХ”, “XY”, “YY”.
- Провести расчеты для столбцов (перемножение данных: Х*Х; Х*У; У*У).
- Просуммировать данные столбцов.
- Внести полученные данные в формул расчета.
Пример расчета коэффициента корреляции
Рассмотрим пример взаимосвязи цены и проданных единиц продукции, потому что самое популярное предположение — чем ниже цена, тем больше количество проданных единиц продукции. Учитывая, важность получаемой выручки, проверим данную гипотезу по формуле, которая указана выше. В таблице представлена условная цена и количество проданных единиц продукции по заданной цене. Рассчитаем последовательно остальные данные необходимые для коэффициента корреляции.


Полученные расчеты используем в формуле и получаем значение корреляции, равное (-0,412). Данный результат будет означать, что взаимосвязь между ценой и количеством проданных единиц товара не существенная.

Корреляционный анализ в MS Excel
Рассчитаем коэффициент корреляции для вышеприведенного примера в MS Excel. Для это необходимо занести два столбца с переменными данными.

Далее, открываем меню “Формулы”, нажимаем кнопку “Вставить функцию” и через мастера функций находим функцию PEARSON.

Выделяем область данных для полей “Массив1” и “Массив 2”, то есть столбец “Х” и столбец “У”. В левом нижнем углу видим результат, равный ( ‑0,412), что полностью соответствует вышеприведенным расчетам.

Содержание:
Корреляционный анализ:
Связи между различными явлениями в природе сложны и многообразны, однако их можно определённым образом классифицировать. В технике и естествознании часто речь идёт о функциональной зависимости между переменными x и у, когда каждому возможному значению х поставлено в однозначное соответствие определённое значение у. Это может быть, например, зависимость между давлением и объёмом газа (закон Бойля—Мариотта).
В реальном мире многие явления природы происходят в обстановке действия многочисленных факторов, влияния каждого из которых ничтожно, а число их велико. В этом случае связь теряет свою однозначность и изучаемая физическая система переходит не в определённое состояние, а в одно из возможных для неё состояний. Здесь речь может идти лишь о так называемой статистической связи. Статистическая связь состоит в том, что одна случайная переменная реагирует на изменение другой изменением своего закона распределения. Следовательно, для изучения статистической зависимости нужно знать аналитический вид двумерного распределения. Однако нахождение аналитического вида двумерного распределения по выборке ограниченного объёма, во-первых, громоздко, во-вторых, может привести к значительным ошибкам. Поэтому на практике при исследовании зависимостей между случайными переменными X и У обычно ограничиваются изучением зависимости между одной из них и условным математическим ожиданием другой, т.е. 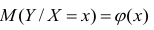
Вопрос о том, что принять за зависимую переменную, а что — за независимую, следует решать применительно к каждому конкретному случаю.
Знание статистической зависимости между случайными переменными имеет большое практическое значение: с её помощью можно прогнозировать значение зависимой случайной переменной в предположении, что независимая переменная примет определенное значение. Однако, поскольку понятие статистической зависимости относится к осредненным условиям, прогнозы не могут быть безошибочными. Применяя некоторые вероятностные методы, как будет показано далее, можно вычислить вероятность того, что ошибка прогноза не выйдет за определенные границы.
Введение в корреляционный анализ
Связь, которая существует между случайными величинами разной природы, например, между величиной X и величиной Y, не обязательно является следствием прямой зависимости одной величины от другой (так называемая функциональная связь).
В некоторых случаях обе величины зависят от целой совокупности разных факторов, общих для обеих величин, в результате чего и формируется связанные друг с другом закономерности. Когда связь между случайными величинами обнаружена с помощью статистики, мы не можем утверждать, что обнаружили причину происходящего изменения параметров, скорее мы лишь увидели два взаимосвязанных следствия.
Например, дети, которые чаще смотрят по телевизору американские боевики, меньше читают. Дети, которые больше читают, лучше учатся. Не так-то просто решить, где тут причины, а где следствия, но это и не является задачей статистики.
Статистика может лишь, выдвинув гипотезу о наличии связи, подкрепить ее цифрами. Если связь действительно имеется, говорят, что между двумя случайными величинами есть корреляция. Если увеличение одной случайной величины связано с увеличением второй случайной величины, корреляция называется прямой.
Например, количество прочитанных страниц за год и средний балл (успеваемость). Если, напротив рост одной величины связано с уменьшением другой, говорят об обратной корреляции. Например, количество боевиков и количество прочитанных страниц. Взаимная связь двух случайных величин называется корреляцией, корреляционный анализ позволяет определить наличие такой связи, оценить, насколько тесна и существенна эта связь. Все это выражается количественно.
Как определить, есть ли корреляция между величинами? В большинстве случаев, это можно увидеть на обычном графике. Например, по каждому ребенку из нашей выборки можно определить величину 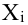 (число страниц) и
(число страниц) и 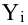 (средний балл годовой оценки), и записать эти данные в виде таблицы. Построить оси X и Y, а затем нанести на график весь ряд точек таким образом, чтобы каждая из них имела определенную пару координат (
(средний балл годовой оценки), и записать эти данные в виде таблицы. Построить оси X и Y, а затем нанести на график весь ряд точек таким образом, чтобы каждая из них имела определенную пару координат (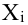 ,
,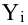 ) из нашей таблицы. Поскольку мы в данном случае затрудняемся определить, что можно считать причиной, а что следствием, не важно, какая ось будет вертикальной, а какая горизонтальной.
) из нашей таблицы. Поскольку мы в данном случае затрудняемся определить, что можно считать причиной, а что следствием, не важно, какая ось будет вертикальной, а какая горизонтальной.
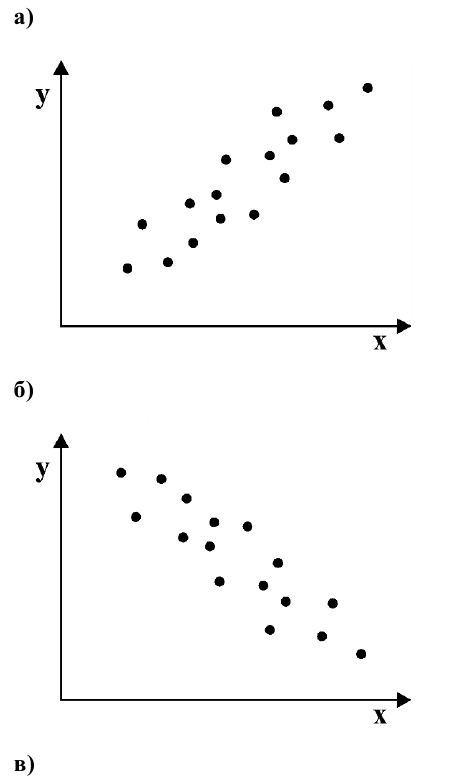
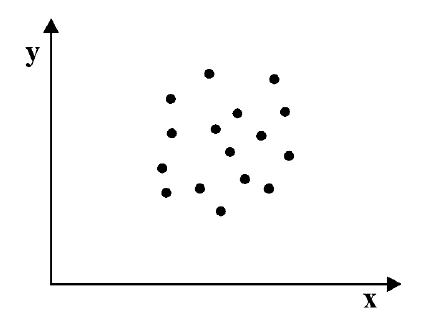
Если график имеет вид а), то это говорит о наличии прямой корреляции, в случае, если он имеет вид б) – корреляция обратная. Отсутствие корреляции тоже можно приблизительно определить по виду графика – это случай в).
С помощью коэффициента корреляции можно посчитать насколько тесная связь существует между величинами.
Пусть, существует корреляция между ценой и спросом на товар. Количество купленных единиц товара в зависимости от цены у разных продавцов показано в таблице:  Видно, что мы имеем дело с обратной корреляцией. Для количественной оценки тесноты связи используют коэффициент корреляции:
Видно, что мы имеем дело с обратной корреляцией. Для количественной оценки тесноты связи используют коэффициент корреляции: 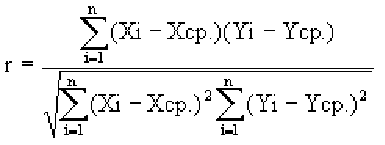
Коэффициент r мы считаем в Excel, с помощью функции 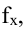 далее статистические функции, функция KOPPEЛ. По подсказке программы вводим мышью в два соответствующих поля два разных массива (X и Y). В нашем случае коэффициент корреляции получился r = -0,988.
далее статистические функции, функция KOPPEЛ. По подсказке программы вводим мышью в два соответствующих поля два разных массива (X и Y). В нашем случае коэффициент корреляции получился r = -0,988.
Надо отметить, что чем ближе к 0 коэффициент корреляции, тем слабее связь между величинами. Наиболее тесная связь при прямой корреляции соответствует коэффициенту r, близкому к +1. В нашем случае, корреляция обратная, но тоже очень тесная, и коэффициент близок к -1.
Что можно сказать о случайных величинах, у которых коэффициент имеет промежуточное значение? Например, если бы мы получили r = 0,65. В этом случае, статистика позволяет сказать, что две случайные величины частично связаны друг с другом. Скажем на 65% влияние на количество покупок оказывала цена, а на 35% – другие обстоятельства. И еще одно важное обстоятельство надо упомянуть.
Поскольку мы говорим о случайных величинах, всегда существует вероятность, что замеченная нами связь – случайное обстоятельство. Причем вероятность найти связь там, где ее нет, особенно велика тогда, когда точек в выборке мало, а при оценке Вы не построили график, а просто посчитали значение коэффициента корреляции на компьютере. Так, если мы оставим всего две разные точки в любой произвольной выборке, коэффициент корреляции будет равен или +1 или -1. Из школьного курса геометрии мы знаем, что через две точки можно всегда провести прямую линию. Для оценки статистической достоверности факта обнаруженной Вами связи полезно использовать так называемую корреляционную поправку: 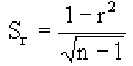
Связь нельзя считать случайной, если: 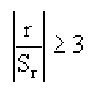
В то время как задача корреляционного анализа – установить, являются ли данные случайные величины взаимосвязанными, цель регрессионного анализа – описать эту связь аналитической зависимостью, т.е. с помощью уравнения. Мы рассмотрим самый несложный случай, когда связь между точками на графике может быть представлена прямой линией. Уравнение этой прямой линии 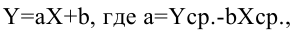
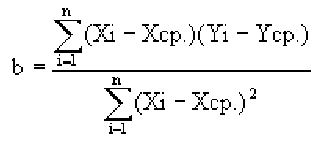
Зная уравнение прямой, мы можем находить значение функции по значению аргумента в тех точках, где значение X известно, a Y – нет. Эти оценки бывают очень нужны, но они должны использоваться осторожно, особенно, если связь между величинами не слишком тесная. Отметим также, что из сопоставления формул для b и r видно, что коэффициент не дает значение наклона прямой, а лишь показывает сам факт наличия связи.
Определение формы связи. Понятие регрессии
Определить форму связи — значит выявить механизм получения зависимой случайной переменной. При изучении статистических зависимостей форму связи можно характеризовать функцией регрессии (линейной, квадратной, показательной и т.д.).
Условное математическое ожидание 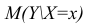 случайной переменной К, рассматриваемое как функция х, т.е.
случайной переменной К, рассматриваемое как функция х, т.е. 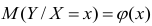 , называется
, называется
функцией регрессии случайной переменной Y относительно X (или функцией регрессии Y по X). Точно так же условное математическое ожидание
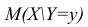 случайной переменной X, т.е.
случайной переменной X, т.е. 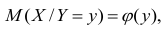 называется функцией регрессии случайной переменной X относительно Y (или функцией регрессии X по Y).
называется функцией регрессии случайной переменной X относительно Y (или функцией регрессии X по Y).
На примере, дискретного распределения найдём функцию регрессии.
Функция регрессии имеет важное значение при статистическом анализе зависимостей между переменными и может быть использована для прогнозирования одной из случайных переменных, если известно значение другой случайной переменной. Точность такого прогноза определяется дисперсией условного распределения.
Несмотря на важность понятия функции регрессии, возможности её практического применения весьма ограничены. Для оценки функции регрессии необходимо знать аналитический вид двумерного распределения (X, Y). Только в этом случае можно точно определить вид функции регрессии, а затем оценить параметры двумерного распределения. Однако для подобной оценки мы чаще всего располагаем лишь выборкой ограниченного объема, по которой нужно найти вид двумерного распределения (X, Y), а затем вид функции регрессии. Это может привести к значительным ошибкам, так как одну и ту же совокупность точек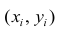 на плоскости можно одинаково успешно описать с помощью различных функций. Именно поэтому возможности практического применения функции регрессии ограничены. Для характеристики формы связи при изучении зависимости используют понятие кривой регрессии.
на плоскости можно одинаково успешно описать с помощью различных функций. Именно поэтому возможности практического применения функции регрессии ограничены. Для характеристики формы связи при изучении зависимости используют понятие кривой регрессии.
Кривой регрессии Y по X (или Y на А) называют условное среднее значение случайной переменной У, рассматриваемое как функция определенного класса, параметры которой находят методом наименьших квадратов по наблюдённым значениям двумерной случайной величины (х, у), т.е.
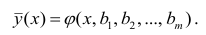
Аналогично определяется кривая регрессии X по Y (X на Y):
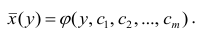
Кривую регрессии называют также эмпирическим уравнением регрессии или просто уравнением регрессии. Уравнение регрессии является оценкой соответствующей функции регрессии.
Возникает вопрос: почему для определения кривой регрессии
используют именно условное среднее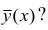 Функция у(х) обладает одним замечательным свойством: она даёт наименьшую среднюю погрешность оценки прогноза. Предположим, что кривая регрессии — произвольная функция. Средняя погрешность прогноза по кривой регрессии определяется математическим ожиданием квадрата разности между измеренной величиной и вычисленной по формуле кривой регрессии, т.е.
Функция у(х) обладает одним замечательным свойством: она даёт наименьшую среднюю погрешность оценки прогноза. Предположим, что кривая регрессии — произвольная функция. Средняя погрешность прогноза по кривой регрессии определяется математическим ожиданием квадрата разности между измеренной величиной и вычисленной по формуле кривой регрессии, т.е. 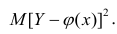 . Естественно потребовать вычисления такой кривой регрессии, средняя погрешность прогноза по которой была бы наименьшей. Таковой является
. Естественно потребовать вычисления такой кривой регрессии, средняя погрешность прогноза по которой была бы наименьшей. Таковой является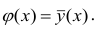 Это следует из свойств минимальности рассеивания около центра распределения
Это следует из свойств минимальности рассеивания около центра распределения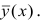
Если рассеивание вычисляется относительно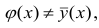 то средний квадрат отклонения увеличивается. Поэтому можно сказать, что кривая регрессии, выражаемая как
то средний квадрат отклонения увеличивается. Поэтому можно сказать, что кривая регрессии, выражаемая как 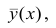 минимизирует среднеквадратическую погрешность прогноза величины Y по X.
минимизирует среднеквадратическую погрешность прогноза величины Y по X.
Основные положения корреляционного анализа
Статистические связи между переменными можно изучать методом корреляционного и регрессионного анализа. С помощью этих методов решают разные задачи; требования, предъявляемые к исследуемым переменным, в каждом методе различны.
Основная задача корреляционного анализа — выявление связи между случайными переменными путём точечной и интервальной оценки парных коэффициентов корреляции, вычисления и проверки значимости множественных коэффициентов корреляции и детерминации, оценки частных коэффициентов корреляции. Корреляционный анализ позволяет также оценить функцию регрессии одной случайной переменной на другую.
Предпосылки корреляционного анализа следующие:
- 1) переменные величины должны быть случайными;
- 2) случайные величины должны иметь совместное нормальное распределение.
Рассмотрим простейший случай корреляционного анализа — двумерную модель. Введём основные понятия и опишем принцип проведения корреляционного анализа. Пусть X и Y — случайные переменные, имеющие совместное нормальное распределение. В этом случае связь между X и Y можно описать коэффициентом корреляции p;. Этот коэффициент определяется как ковариация между X и Y, отнесённая к их среднеквадратическим отклонениям:
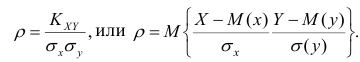 (1.1)
(1.1)
Оценкой коэффициента корреляции является выборочный коэффициент корреляции r. Для его нахождения необходимо знать оценки следующих параметров: 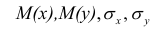 . Наилучшей оценкой
. Наилучшей оценкой
математического ожидания является среднее арифметическое, т.е.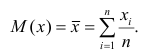
Оценкой дисперсии служит выборочная дисперсия, т.е.
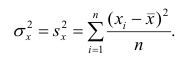
Тогда выборочный коэффициент корреляции
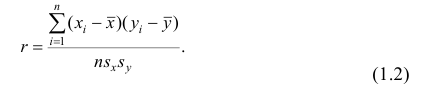
Коэффициент р называют также парным коэффициентом корреляции, а r— выборочным парным коэффициентом корреляции.
При совместном нормальном законе распределения случайных величин X и Y, используя рассмотренные выше параметры распределения и коэффициент корреляции, можно получить выражение для условного математического ожидания, т. е, записать выражение для функции регрессии одной случайной величины на другую. Так, функция регрессии Y на X имеет вид:
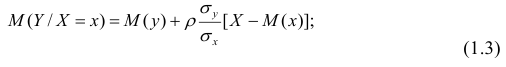
функция регрессии X на Y — следующий вид:
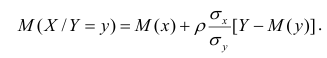
Выражения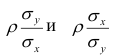 — называют коэффициентами регрессии.
— называют коэффициентами регрессии.
Подставив в (1.3) соответствующие оценки параметров, получим уравнения регрессии, график которых — прямая линия, проходящая через точку 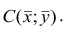 Запишем уравнение регрессии у на х и х на у:
Запишем уравнение регрессии у на х и х на у:
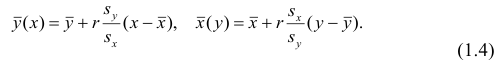
Таким образом, в корреляционном анализе на основе оценок параметров двумерной нормальной совокупности получаем оценки тесноты связи между случайными переменными и можем оценить регрессию одной переменной на другую. Особенностью корреляционного анализа является строго линейная зависимость между переменными. Это обусловливается исходными предпосылками. На практике корреляционный анализ можно применять для обработки наблюдений, сделанных на предприятиях при нормальных условиях работы, если случайные изменения свойства сырья или других факторов вызывают случайные изменения свойств продукции.
Свойства коэффициента корреляции
Коэффициент корреляции является одним из самых распространенных способов измерения связи между случайными переменными. Рассмотрим некоторые свойства этого коэффициента.
Теорема 1. Коэффициент корреляции принимает значения на интервале (-1, +1).
Доказательство. Докажем справедливость утверждения для случая дискретных переменных. Запишем явно неотрицательное выражение:
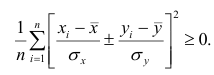
Возведём выражение под знаком суммы в квадрат:
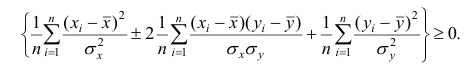
Первое и третье из слагаемых равны единице, поскольку из определения дисперсии следует, что 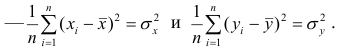
Таким образом, окончательно получаем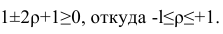
Если коэффициент корреляции положителен, то связь между переменными также положительна и значения переменных увеличиваются или уменьшаются одновременно. Если коэффициент корреляции имеет отрицательное значение, то при увеличении одной переменной уменьшается другая.
Приведём следующее важное свойство коэффициента корреляции: коэффициент корреляции не зависит от выбора начала отсчёта и единицы измерения, т. е. от любых постоянных 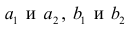 таких, что
таких, что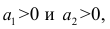 т.е.
т.е.
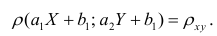
Таким образом, переменные X и У можно уменьшать или увеличивать в а раз, а также вычитать или прибавлять к значениям X и У одно и то же число b. В результате величина коэффициента корреляции не изменится.
Если коэффициент корреляции 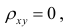 то случайные переменные некоррелированы. Понятие некоррелированности не следует смешивать с понятием независимости, независимые величины всегда некоррелированы. Однако обратное утверждение невероятно: некоррелированные величины могут быть зависимы и даже функционально, однако эта связь не линейная.
то случайные переменные некоррелированы. Понятие некоррелированности не следует смешивать с понятием независимости, независимые величины всегда некоррелированы. Однако обратное утверждение невероятно: некоррелированные величины могут быть зависимы и даже функционально, однако эта связь не линейная.
Выборочный коэффициент корреляции вычисляют по формуле (1.2). Имеется несколько модификаций этой формулы, которые удобно использовать при той или иной форме представления исходной информации. Так, при малом числе наблюдений выборочный коэффициент корреляции удобно вычислять по формуле
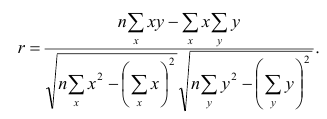
Если информация имеет вид корреляционной таблицы (см. п 1.5), то удобно пользоваться формулой
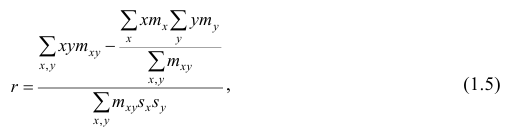
где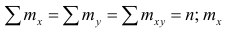 — суммарная частота наблюдаемого значенияпризнака х при всех значениях
— суммарная частота наблюдаемого значенияпризнака х при всех значениях 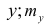 — суммарная частота наблюдаемого значения признака упри всех значениях х;
— суммарная частота наблюдаемого значения признака упри всех значениях х; 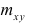 — частота появления пары признаков (x, у).
— частота появления пары признаков (x, у).
Из формулы (1.2) очевидно, что 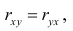 т.е. величина выборочного коэффициента корреляции не зависит от порядка следования переменных, поэтому обычно пишут просто r.
т.е. величина выборочного коэффициента корреляции не зависит от порядка следования переменных, поэтому обычно пишут просто r.
Поле корреляции. Вычисление оценок параметров двумерной модели
На практике для вычисления оценок параметров двумерной модели удобно использовать корреляционную таблицу и поле корреляции. Пусть, например, изучается зависимость между объёмом выполненных работ (у) и накладными расходами (x). Имеем выборку из генеральной совокупности, состоящую из 150 пар переменных 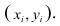 Считаем, что предпосылки корреляционного анализа выполнены.
Считаем, что предпосылки корреляционного анализа выполнены.
Пару случайных чисел 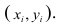 можно изобразить графически в виде точки с координатами
можно изобразить графически в виде точки с координатами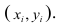 . Аналогично можно изобразить весь набор пар случайных чисел (всю выборку). Однако при большом объёме выборки это затруднительно. Задача упрощается, если выборку упорядочить, т.е. переменные сгруппировать. Сгруппированные ряды могут быть как дискретными, так и интервальными.
. Аналогично можно изобразить весь набор пар случайных чисел (всю выборку). Однако при большом объёме выборки это затруднительно. Задача упрощается, если выборку упорядочить, т.е. переменные сгруппировать. Сгруппированные ряды могут быть как дискретными, так и интервальными.
По осям координат откладывают или дискретные значения переменных, или интервалы их изменения. Для интервального ряда наносят координатную сетку. Каждую пару переменных из данной выборки изображают в виде точки с соответствующими координатами для дискретного ряда или в виде точки в соответствующей клетке для интервального ряда. Такое изображение корреляционной зависимости называют полем корреляции. На рис. 1.1 изображено поле корреляции для выборки, состоящей из 150 пар переменных (ряд интервальный).
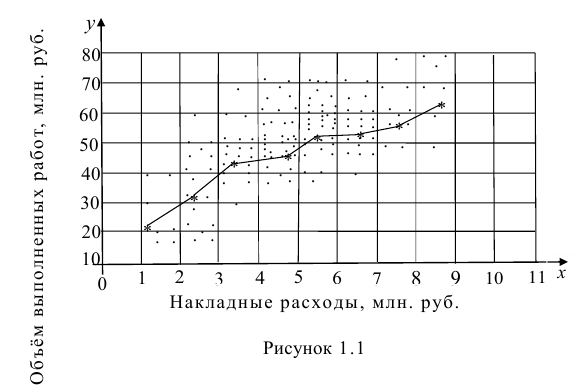
Если вычислить средние значения у в каждом интервале изменения х [обозначим их 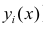 )], нанести эти точки на рис. 1.1 и соединить между собой, то получим ломаную линию, по виду которой можно судить, как в среднем меняются у в зависимости от изменения х. По виду этой линии можно также сделать предположение о форме связи между переменными. В данном случае ломаную линию можно аппроксимировать прямой линией, так как она достаточно хорошо приближается к ней. По выборочным данным можно построить также корреляционную табл. 1.1.
)], нанести эти точки на рис. 1.1 и соединить между собой, то получим ломаную линию, по виду которой можно судить, как в среднем меняются у в зависимости от изменения х. По виду этой линии можно также сделать предположение о форме связи между переменными. В данном случае ломаную линию можно аппроксимировать прямой линией, так как она достаточно хорошо приближается к ней. По выборочным данным можно построить также корреляционную табл. 1.1.
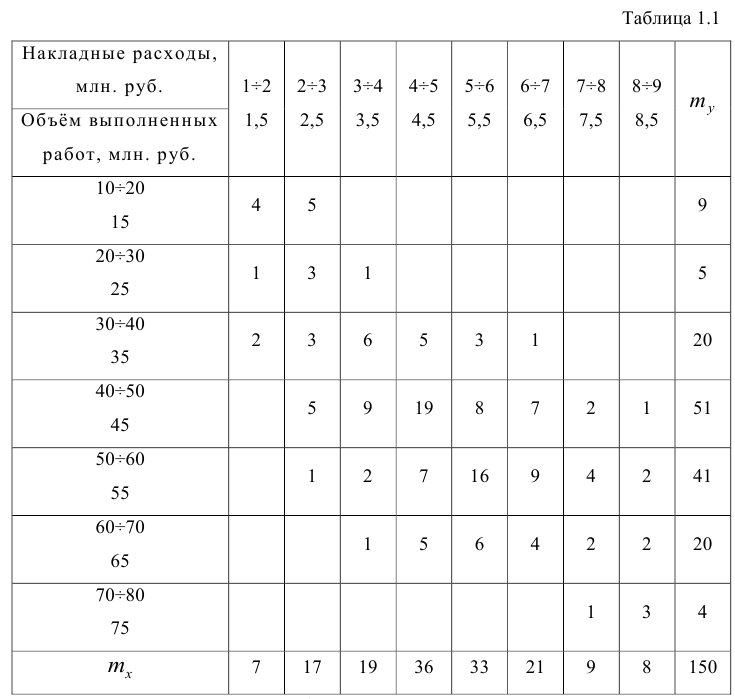
Корреляционную таблицу, как и поле корреляции, строят по
сгруппированному ряду (дискретному или интервальному). Табл. 1.1 построена на основе интервального ряда. В первой строке и первом столбце таблицы помещают интервалы изменения х и у и значения середин интервалов. Так, например, 1,5 — середина интервала изменения *=1-2,15— середина интервала изменения у= 10-20. В ячейки, образованные пересечением строк и столбцов, заносят частоты попадания пар значений (л у) в соответствующие интервалы по х и у. Например, частота 4 означает, что в интервал изменения у от 10 до 20 попало 4 пары наблюдавшихся значений. Эти частоты обозначают 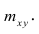 В 9-й строке и 10-м столбце находятся значения
В 9-й строке и 10-м столбце находятся значения 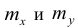 – суммы
– суммы 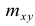 по соответствующим столбцу и строке.
по соответствующим столбцу и строке.
Как будет показано в дальнейшем, корреляционно таблицей удобно пользоваться при вычислении коэффициентов корреляций и параметров уравнений регрессии.
Корреляционная таблица построена на основе интервального ряда, поэтому для оценок параметров воспользуемся формулами гл. 1 для вычисления средней арифметической и дисперсии. Имеем:
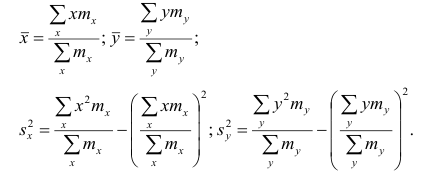 (1.6)
(1.6)
Проверка гипотезы о значимости коэффициента корреляции
На практике коэффициент корреляции р обычно неизвестен. По результатам выборки может быть найдена его точечная оценка — выборочный коэффициент корреляции r.
Равенство нулю выборочного коэффициента корреляции ещё не свидетельствует о равенстве нулю самого коэффициента корреляции, а следовательно, о некоррелированности случайных величин X и Y. Чтобы выяснить, находятся ли случайные величины в корреляционной зависимости, нужно проверить значимость выборочного коэффициента корреляции г, т.е. установить, достаточна ли его величина для обоснованного вывода о наличии корреляционной связи. Для этого проверяют нулевую гипотезу 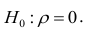 . Предполагается наличие двумерного нормального распределения случайных переменных; объём выборки может быть любым. Вычисляют
. Предполагается наличие двумерного нормального распределения случайных переменных; объём выборки может быть любым. Вычисляют
которая имеет распределение Стьюдента с k=n-2
степенями свободы. Для проверки нулевой гипотезы по уровню значимости а и числу степеней свободы к находят по таблицам распределения Стьюдента (t-распределение; см. табл. 1 приложения) критическое значение 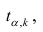 удовлетворяющее условию
удовлетворяющее условию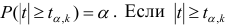 , то нулевую гипотезу об отсутствии корреляционной связи между переменными X и Y следует отвергнуть. Переменные считают зависимыми. При
, то нулевую гипотезу об отсутствии корреляционной связи между переменными X и Y следует отвергнуть. Переменные считают зависимыми. При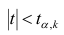 нет оснований отвергать нулевую гипотезу.
нет оснований отвергать нулевую гипотезу.
В случае значимого выборочного коэффициента, корреляции есть смысл построить доверительный интервал для коэффициента корреляций р. Однако для этого нужно знать закон распределения выборочного коэффициента корреляции r.
Плотность вероятности выборочного коэффициента корреляции имеет сложный вид, поэтому прибегают к специально подобранным функциям от выборочного коэффициента корреляции, которые сводятся к хорошо изученным распределениям, например нормальному или Стьюдента. Чаще всего для подбора функции применяют преобразование Фишера. Вычисляют статистику:
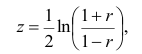
где r=thz — гиперболический тангенс от z.
Распределение статистики z хорошо аппроксимируется нормальным распределением с параметрами
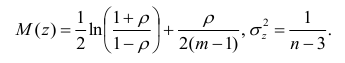
В этом, случае доверительный интервал для римеетвид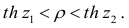 Величины
Величины 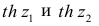 находят по таблицам по следующим значениям:
находят по таблицам по следующим значениям:
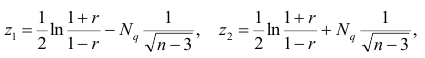
где 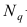 — нормированная функция Лапласа для q % доверительного интервала (см. табл. 2 приложений значение функции
— нормированная функция Лапласа для q % доверительного интервала (см. табл. 2 приложений значение функции 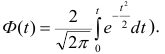
Если коэффициент корреляции значим, то коэффициенты регрессии также значимо отличаются от нуля, а интервальные оценки для них можно получить по следующим формулам:
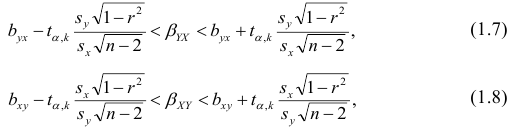
где 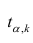 имеет распределение Стьюдента с k=n—2 степенями свободы.
имеет распределение Стьюдента с k=n—2 степенями свободы.
Корреляционное отношение
На практике часто предпосылки корреляционного анализа нарушаются: один из признаков оказывается величиной не случайной, или признаки не имеют совместного нормального распределения. Однако статистическая зависимость между ними существует. Для изучения связи между признаками в этом случае существует общий показатель зависимости признаков, основанный на показателе изменчивости — общей (или полной) дисперсии.
Полной называется дисперсия признака относительно его математического ожидания. Так, для признака Y это 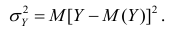 Дисперсию
Дисперсию 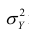 можно разложить на две составляющие, одна из которых характеризует влияние фактора X на Y, другая — влияние прочих факторов.
можно разложить на две составляющие, одна из которых характеризует влияние фактора X на Y, другая — влияние прочих факторов.
Очевидно, чем меньше влияние прочих факторов, тем теснее связь, тем более приближается она к функциональной. Представим 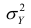 в следующем виде:
в следующем виде:
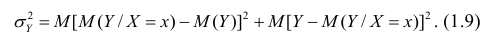
Первое слагаемое обозначим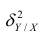 Это дисперсия функции регрессии относительно математического ожидания признака (в данном случае признака У);.она измеряет влияние признака X на Y. Второе слагаемое обозначим
Это дисперсия функции регрессии относительно математического ожидания признака (в данном случае признака У);.она измеряет влияние признака X на Y. Второе слагаемое обозначим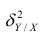 . Это дисперсия признака Y относительно функции регрессии. Её называют также средней из условных дисперсий или остаточной дисперсией
. Это дисперсия признака Y относительно функции регрессии. Её называют также средней из условных дисперсий или остаточной дисперсией 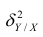 измеряет влияние на Y прочих факторов.
измеряет влияние на Y прочих факторов.
Покажем, что 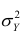 действительно можно разложить на два таких слагаемых:
действительно можно разложить на два таких слагаемых:
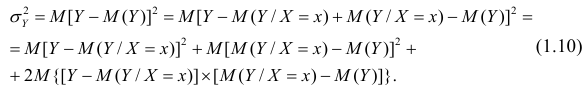
Для простоты полагаем распределение дискретным. Имеем 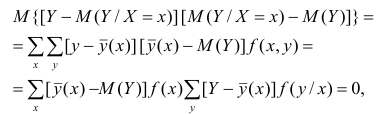
так как при любом х справедливо равенство
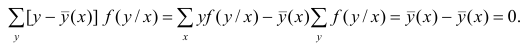
Третье слагаемое в равенстве (1.10) равно нулю, поэтому равенство (1.9) справедливо. Поскольку второе слагаемое в равенстве (1.9) оценивает влияние признака X на Y, то его можно использовать для оценки тесноты связи между X и Y. Тесноту связи удобно оценивать в единицах общей дисперсии 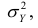 т.е. рассматривать отношение
т.е. рассматривать отношение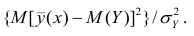 . Эту величину обозначают
. Эту величину обозначают 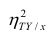 и называют теоретическим корреляционным отношением. Таким образом,
и называют теоретическим корреляционным отношением. Таким образом,
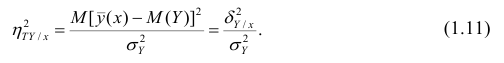
Разделив обе части равенства (1.9) на 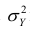 получим
получим
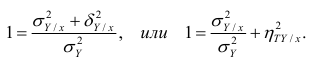
Из последней формулы имеем

Поскольку 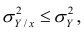 так как
так как 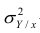 — составная часть
— составная часть 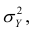 то из равенства (1.12) следует, что значение
то из равенства (1.12) следует, что значение 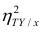 всегда заключено между нулем и единицей.
всегда заключено между нулем и единицей.
Все сделанные выводы справедливы и для 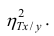 Из равенства (1.12)
Из равенства (1.12)
следует, что 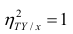 только тогда, когда
только тогда, когда 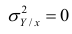 , т.е. отсутствует влияние прочих факторов и всё распределение сконцентрировано на кривой регрессии
, т.е. отсутствует влияние прочих факторов и всё распределение сконцентрировано на кривой регрессии 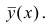 . В этом случае между Y и X существует функциональная зависимость.
. В этом случае между Y и X существует функциональная зависимость.
Далее, из равенства (1.12) следует, что 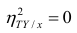 тогда и только тогда, когда
тогда и только тогда, когда
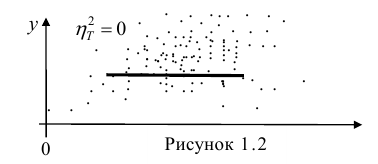
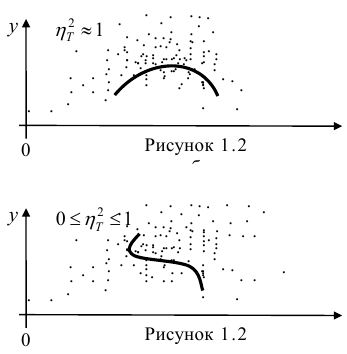
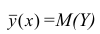 = const, т.е. линия регрессии У по X — горизонтальная прямая, проходящая через центр распределения. В этом случае можно сказать, что переменная У не коррелирована с X (рис. 1.2,а, б, в).
= const, т.е. линия регрессии У по X — горизонтальная прямая, проходящая через центр распределения. В этом случае можно сказать, что переменная У не коррелирована с X (рис. 1.2,а, б, в).
Аналогичными свойствами обладает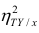 — показатель тесноты связи между X и У.
— показатель тесноты связи между X и У.
Часто используют величину

Считают, что она не может быть отрицательной. Значения величины 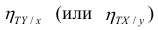 также могут находиться лишь в пределах от нуля до единицы. Это очевидно из формулы (1.13).
также могут находиться лишь в пределах от нуля до единицы. Это очевидно из формулы (1.13).
Значения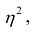 лежащие в интервале
лежащие в интервале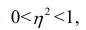 являются показателями тесноты группировки точек около кривой регрессии независимо от её вида (формы связи). Корреляционное отношение
являются показателями тесноты группировки точек около кривой регрессии независимо от её вида (формы связи). Корреляционное отношение 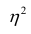 связано
связано 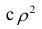 следующим образом:
следующим образом: 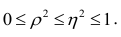 В случае линейной зависимости между переменными
В случае линейной зависимости между переменными 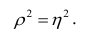
Разность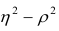 может быть использована как показатель нелинейности связи между переменными.
может быть использована как показатель нелинейности связи между переменными.
При вычислении 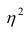 по выборочным данным получаем выборочное корреляционное отношение. Обозначим его
по выборочным данным получаем выборочное корреляционное отношение. Обозначим его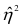 . Вместо дисперсий в этом случае используются их оценки. Тогда формула (1.12) принимает вид
. Вместо дисперсий в этом случае используются их оценки. Тогда формула (1.12) принимает вид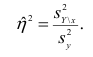
Понятие о многомерном корреляционном анализе
Частный коэффициент корреляции. Основные понятия корреляционного анализа, введенные для двумерной модели, можно распространить на многомерный случай. Задачи и предпосылки корреляционного анализа были сформулированы в п. 1.3. Однако если при изучении взаимосвязи переменных по двумерной модели мы ограничивались рассмотрением парных коэффициентов корреляции, то для многомерной модели этого недостаточно. Многообразие связей между переменными находит отражение в частных и множественных коэффициентах корреляции.
Пусть имеется многомерная нормальная совокупность с m признаками 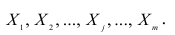 В этом случае взаимозависимость между признаками
В этом случае взаимозависимость между признаками
можно описать корреляционной матрицей. Под корреляционной матрицей будем понимать, матрицу, составленную из парных коэффициентов корреляции (вычисляются по формуле (1,1)):
где 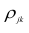 — парные коэффициенты корреляции; m — порядок матрицы.
— парные коэффициенты корреляции; m — порядок матрицы.
Оценкой парного коэффициента корреляции является выборочный парный коэффициент корреляции, определяемый по формуле (1.2), однако для m признаков формула (9.2) принимает вид
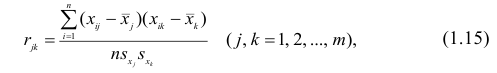
где  — порядковые номера признаков.
— порядковые номера признаков.
Как и в двумерном случае, для оценки коэффициента корреляции необходимо оценить математические ожидания и дисперсии. В многомерном корреляционном анализе имеем т математических ожиданий и m дисперсий, а также m(m—1)/2 парных коэффициентов корреляции. Таким образом, нужно произвести оценку 2m+m(m—1)/2 параметров.
В случае многомерной корреляции зависимости между признаками более многообразны и сложны, чем в двумерном случае. Одной корреляционной матрицей нельзя полностью описать зависимости между признаками. Введём понятие частного коэффициента корреляции l-го порядка.
Пусть исходная совокупность состоит из т признаков. Можно изучать зависимости между двумя из них при фиксированном значении l признаков из m-2 оставшихся. Рассмотрим, например, систему из 5 признаков. Изучим зависимости между  при фиксированном значении признака
при фиксированном значении признака 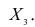 В этом случае имеем частный коэффициент корреляции первого порядка, так как фиксируем только один признак.
В этом случае имеем частный коэффициент корреляции первого порядка, так как фиксируем только один признак.
Рассмотрим более подробно структуру частных коэффициентов корреляции на примере системы из трёх признаков 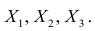 . Эта система позволяет изучить частные коэффициенты корреляции только первого порядка, так как нельзя фиксировать больше одного признака. Частный коэффициент корреляции первого порядка для признаков
. Эта система позволяет изучить частные коэффициенты корреляции только первого порядка, так как нельзя фиксировать больше одного признака. Частный коэффициент корреляции первого порядка для признаков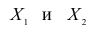 при фиксированном значении
при фиксированном значении 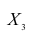 выражается через парные коэффициенты
выражается через парные коэффициенты
корреляции и имеет вид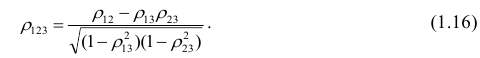
Частный коэффициент корреляции, так же как и парный коэффициент корреляции, изменяется от —1 до +1, В общем виде, когда система состоит из m признаков, частный коэффициент корреляции l-го порядка может быть найден из корреляционной матрицы. Если 1=m—2, то рассматривается матрица порядка m, при — подматрица порядкаl+2, составленная из элементов матрицы
— подматрица порядкаl+2, составленная из элементов матрицы  , которые отвечают индексам коэффициента частной
, которые отвечают индексам коэффициента частной
корреляции. Например, корреляционная матрица системы из пяти признаков имеет вид
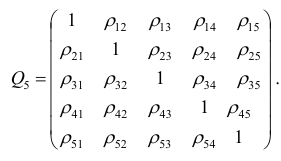
Для определения частного коэффициента корреляции второго порядка, например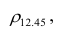 следует использовать подматрицу четвертого порядка,
следует использовать подматрицу четвертого порядка,
вычеркнув из исходной матрицы 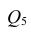 третью строку и третий столбец, так как признак
третью строку и третий столбец, так как признак 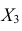 не рассматривают.
не рассматривают.
В общем виде формулу частного коэффициента корреляции l-го порядка (1=m—2) можно записать в виде
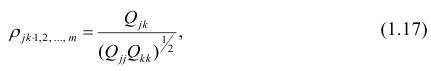
где 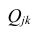 — алгебраические дополнения к элементу
— алгебраические дополнения к элементу 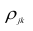 корреляционной
корреляционной
матрицы 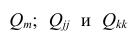 — алгебраические дополнения к элементам
— алгебраические дополнения к элементам 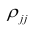 и ркк корреляционной матрицы
и ркк корреляционной матрицы 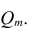
Очевидно, что выражение (1.16) является частым случаем выражения (1.17), в чём легко убедиться, рассмотрев корреляционную матрицу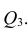
Оценкой частного коэффициента корреляции l-го порядка является выборочный частный коэффициент корреляции l-го порядка. Он вычисляется на основе корреляционной матрицы, составленной из выборочных парных коэффициентов корреляции:
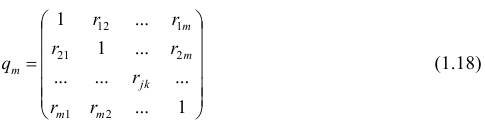
Формула выборочного частного коэффициента корреляции имеет вид

где 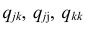 — алгебраические дополнения к соответствующим элементам матрицы (1.18).
— алгебраические дополнения к соответствующим элементам матрицы (1.18).
Частный коэффициент корреляции l-го порядка, вызволенный на основе п наблюдений над признаками, имеет такое же распределение, что и парный коэффициент корреляции, вычисленный 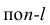 наблюдениям. Поэтому значимость частных коэффициентов корреляции оценивают так же, как и в п. 1.6.
наблюдениям. Поэтому значимость частных коэффициентов корреляции оценивают так же, как и в п. 1.6.
Множественный коэффициент корреляции
Часто представляет интерес оценить связь одного из признаков со всеми остальными. Это можно сделать с помощью множественного, или совокупного, коэффициента корреляции

где 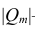 —определитель корреляционной матрицы
—определитель корреляционной матрицы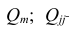 —алгебраическое
—алгебраическое
дополнение к элементу 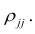
Квадрат коэффициента множественной корреляции 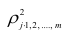 называется
называется
множественным коэффициентом детерминации. Коэффициенты множественной корреляции и детерминации — величины положительные, принимающие значения в интервале Оценками этих
Оценками этих
коэффициентов являются выборочные множественные коэффициенты корреляции и детерминации, которые обозначают соответственно 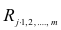 и
и
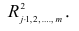 Формула для вычисления выборочного множественного коэффициента корреляции имеет вид
Формула для вычисления выборочного множественного коэффициента корреляции имеет вид

где 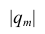 —определитель корреляционной матрицы, составленной из выборочных парных коэффициентов корреляции;
—определитель корреляционной матрицы, составленной из выборочных парных коэффициентов корреляции; 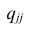 алгебраическое дополнение к элементу
алгебраическое дополнение к элементу 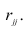
Многомерный корреляционный анализ позволяет получить оценку функции регрессии — уравнение регрессии. Коэффициенты в уравнении регрессии можно найти непосредственно через выборочные парные коэффициенты корреляции или воспользоваться методом многомерной регрессии, который мы рассмотрим в вопросе 2.7. В этом случае все предпосылки регрессионного анализа оказываются выполненными и, кроме того, связь между переменными строго линейна.
Ранговая корреляция
В некоторых случаях встречаются признаки, не поддающиеся количественной оценке (назовём такие признаки объектами). Попытаемся, например, оценить соотношение между математическими и музыкальными способностями группы учащихся. «Уровень способностей» является переменной величиной в том смысле; что он варьирует от одного индивидуума к другому. Его можно измерить, если выставлять каждому индивидууму отметки. Однако этот способ лишен объективности, так как разные экзаменаторы могут выставить одному и тому же учащемуся разные отметки. Элемент субъективизма можно исключить, если учащиеся будут ранжированы. Расположим учащихся по порядку, в соответствии со степенью способностей и присвоим каждому из них порядковый номер, который назовем рангом. Корреляция между рангами более точно отражает соотношение между способностями учащихся, чем корреляция между отметками.
Тесноту связи между рангами измеряют так же, как и между признаками. Рассмотрим уже известную формулу коэффициента корреляции
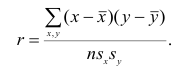
Пусть 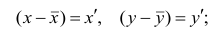 тогда, учитывая,
тогда, учитывая,
что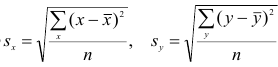 ,можно записать
,можно записать

В зависимости от того, что принять за меру различия между величинами 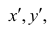 можно получить различные коэффициенты связи между рангами. Обычно используют коэффициент корреляции рангов Кэнделла
можно получить различные коэффициенты связи между рангами. Обычно используют коэффициент корреляции рангов Кэнделла 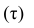 и коэффициент корреляции рангов Спирмэна р.
и коэффициент корреляции рангов Спирмэна р.
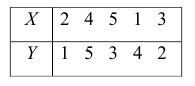
Введём следующую меру различия между объектами: будем считать 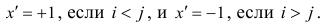 Поясним сказанное на примере. Имеем две последовательности:
Поясним сказанное на примере. Имеем две последовательности:
Рассмотрим отдельно каждую из них. В последовательности X первой паре элементов —2; 4 припишем значение +1, так как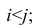 второй паре 2; 5 также припишем значение +1, третьей паре 2; 1 припишем значение —1, поскольку
второй паре 2; 5 также припишем значение +1, третьей паре 2; 1 припишем значение —1, поскольку 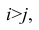 и т.д. Последовательно перебираем все пары, причём каждая пара должна быть учтена один раз. Так, если учтена пара 2; 1, то не следует учитывать пару 1; 2. Аналогичные действия проделаем с последовательностью У, причём порядок перебора пар должен в точности повторять порядок перебора пар в последовательности X. Результаты этих действий представим в виде табл. 1.3.
и т.д. Последовательно перебираем все пары, причём каждая пара должна быть учтена один раз. Так, если учтена пара 2; 1, то не следует учитывать пару 1; 2. Аналогичные действия проделаем с последовательностью У, причём порядок перебора пар должен в точности повторять порядок перебора пар в последовательности X. Результаты этих действий представим в виде табл. 1.3.
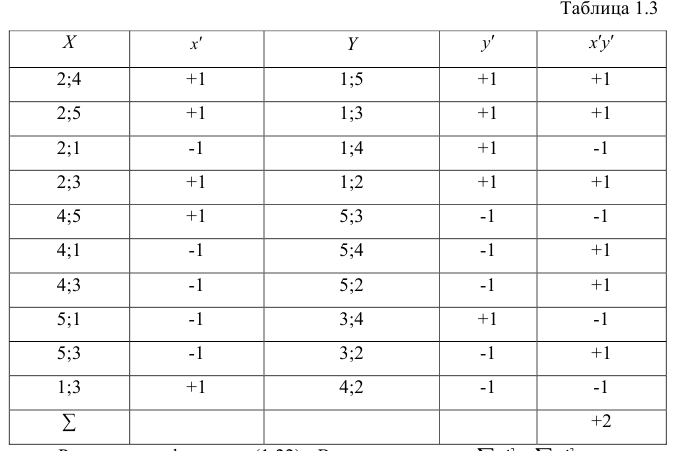
Рассмотрим формулу ( 1 .22). В нашем случае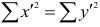 и равна
и равна
количеству пар, участвовавших в переборе. Каждая пара встречается только один раз, поэтому их общее количество равно числу сочетаний из n по 2, т.е.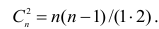 Обозначая
Обозначая 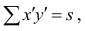 получаем формулу коэффициента корреляции рангов Кэнделла:
получаем формулу коэффициента корреляции рангов Кэнделла:
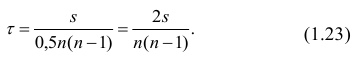
Теперь рассмотрим другую меру различия между объектами. Если обозначить через 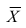 средний ранг последовательности X, через
средний ранг последовательности X, через 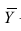 — средний ранг последовательности Т, то
— средний ранг последовательности Т, то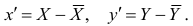 Поскольку ранги последовательности X и Y есть числа натурального ряда, то их сумма равна
Поскольку ранги последовательности X и Y есть числа натурального ряда, то их сумма равна 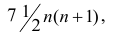 а средний ранг
а средний ранг 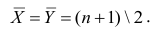
Тогда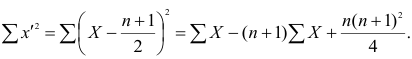 Сумма
Сумма
чисел натурального ряда равна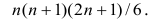
Тогда 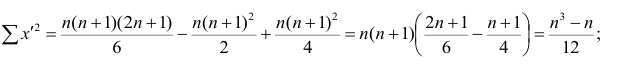
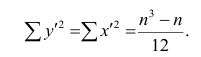
Введём новую величину d, равную разности между рангами: d=X—Y, и определим через неё величину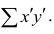 . Имеем:
. Имеем: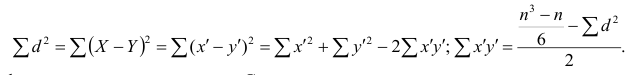
Коэффициент корреляции рангов Спирмэна

У коэффициентов 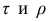 разные масштабы, они отличаются шкалами измерений. Поэтому на практике нельзя ожидать, что они совпадут. Чаще всего, если значения обоих коэффициентов не слишком, близки к 1, p; по абсолютной величине примерно на 50% превышает
разные масштабы, они отличаются шкалами измерений. Поэтому на практике нельзя ожидать, что они совпадут. Чаще всего, если значения обоих коэффициентов не слишком, близки к 1, p; по абсолютной величине примерно на 50% превышает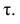 Выведены неравенства, связывающие
Выведены неравенства, связывающие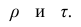 Например, при больших n можно пользоваться следующим приближённым соотношением:
Например, при больших n можно пользоваться следующим приближённым соотношением: 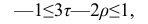 или
или
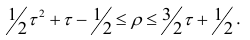 Коэффициент p легче рассчитать, однако с теоретической точки зрения больший интерес представляет коэффициент
Коэффициент p легче рассчитать, однако с теоретической точки зрения больший интерес представляет коэффициент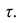
При вычислении коэффициента корреляций рангов Кэнделла для подсчёта s можно использовать следующий приём: одну из последовательностей упорядочивают так, чтобы её элементы были числами натурального ряда; соответственно изменяют и другую последовательность. Тогда сумму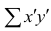 можно подсчитывать лишь по последовательности К, так как все
можно подсчитывать лишь по последовательности К, так как все 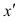 равны +1.
равны +1.
Если нельзя установить ранговое различие нескольких объектов, говорят, что такие объекты являются связанными. В этом случае объектам приписывается средний ранг. Например, если связанными являются объекты 4 и 5, то им приписывают ранг 4.5; если связанными являются объекты 1, 2, 3, 4 и 5, то их средний ранг (1+2+3+4+5)/5=3. Сумма рангов связанных объектов должна быть равна сумме рангов при ранжировании без связей. Формулы коэффициентов корреляции для 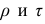 в этом случае также можно вывести из формулы обобщённого коэффициента корреляции, только знаменатель выражения (1.21) в этом случае не равен n(n—1)/2. Если / последовательных членов связаны, то все оценки, относящиеся к любой вобранной из них паре, равны нулю; число таких пар t(t—1), Следовательно,
в этом случае также можно вывести из формулы обобщённого коэффициента корреляции, только знаменатель выражения (1.21) в этом случае не равен n(n—1)/2. Если / последовательных членов связаны, то все оценки, относящиеся к любой вобранной из них паре, равны нулю; число таких пар t(t—1), Следовательно,
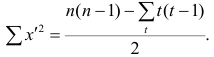 Соответственно для другой последовательности
Соответственно для другой последовательности
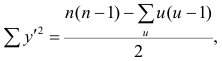
где t и u—число связанных пар в последовательностях.
Обозначая 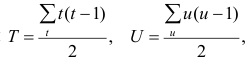 получаем
получаем
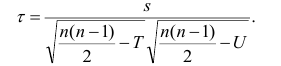
Аналогично находим выражение для р. Только в этом случае
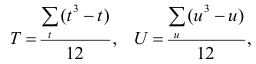 , где е и г – число связанных пар в
, где е и г – число связанных пар в
последовательностях, а
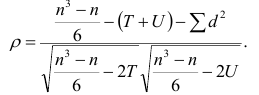
Если имеется несколько последовательностей, то возникает необходимость определить общую меру согласованности между ними. Такой мерой является коэффициент копкордации.
Пусть ь — число последовательностей, т — количество рангов в каждой последовательности. Тогда коэффициент конкордации

где d — фактически встречающееся отклонение от среднего значения суммы рангов одного объекта.
Коэффициент корреляции рангов может быть использован для быстрого оценивания взаимосвязи между признаками, не имеющими нормального распределения, и полезен в тех случаях, когда признаки поддаются ранжированию, но не могут быть точно измерены.
Пример:
Для данных табл. 13 найти выборочный коэффициент корреляции, проверить его значимость на уровне 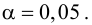
Решение. Для вычислений составим таблицу. Находим суммы
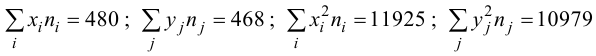 и заносим их в таблицу. Вычислим
и заносим их в таблицу. Вычислим
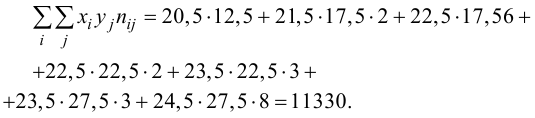
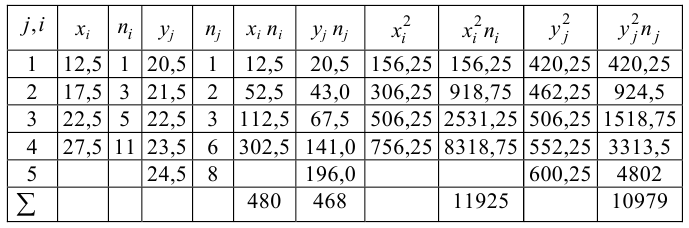
Подставляя полученные значения сумм в (8), найдем выборочный коэффициент корреляции
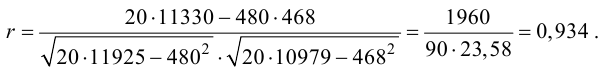
Проверим значимость 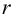 на уровне
на уровне 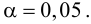 Для этого вычислим статистику
Для этого вычислим статистику
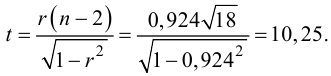
По таблице распределения П6 Стьюдента 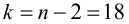 находим критическое значение
находим критическое значение 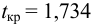 Так как
Так как 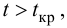 то считаем
то считаем 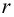 значимым.
значимым.
Пример:
Для данных табл. 13 найти корреляционное отношение 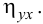
Для вычисления эмпирического корреляционного отношения найдем групповые средние 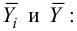
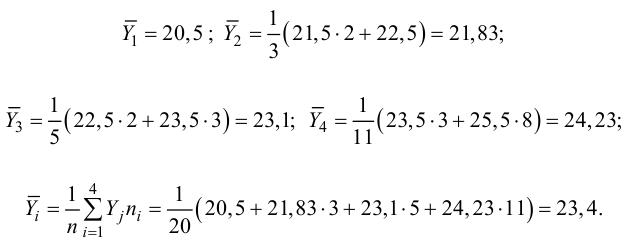
Тогда
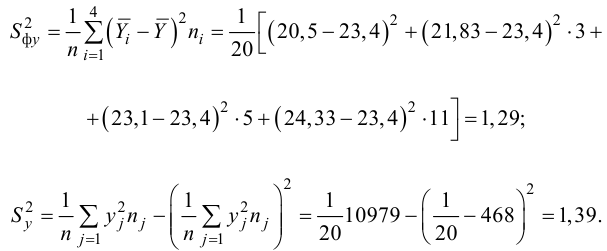
Вычисляем корреляционное отношение
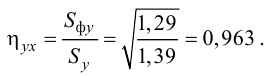
- Статистические решающие функции
- Случайные процессы
- Выборочный метод
- Статистическая проверка гипотез
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии
- Проверка статистических гипотез
- Регрессионный анализ
Как рассчитать коэффициент корреляции Пирсона вручную
17 авг. 2022 г.
читать 2 мин
Коэффициент корреляции Пирсона измеряет линейную связь между двумя переменными.
Он всегда принимает значение от -1 до 1, где:
- -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными
- 0 указывает на отсутствие линейной корреляции между двумя переменными
- 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.
Формула для расчета коэффициента корреляции Пирсона, обозначаемая r , выглядит следующим образом:
Источник: Википедия В этом руководстве представлен пошаговый пример того, как вручную рассчитать коэффициент корреляции Пирсона для следующего набора данных:
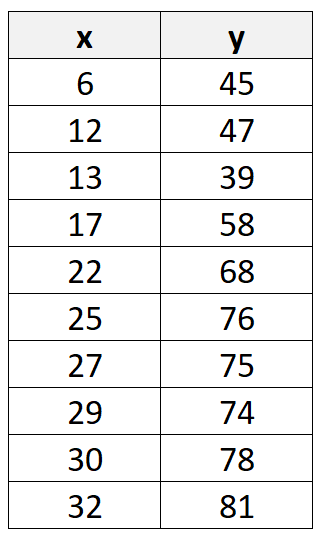
Шаг 1: вычислить среднее значение X и Y
Сначала мы вычислим среднее значение значений X и Y:
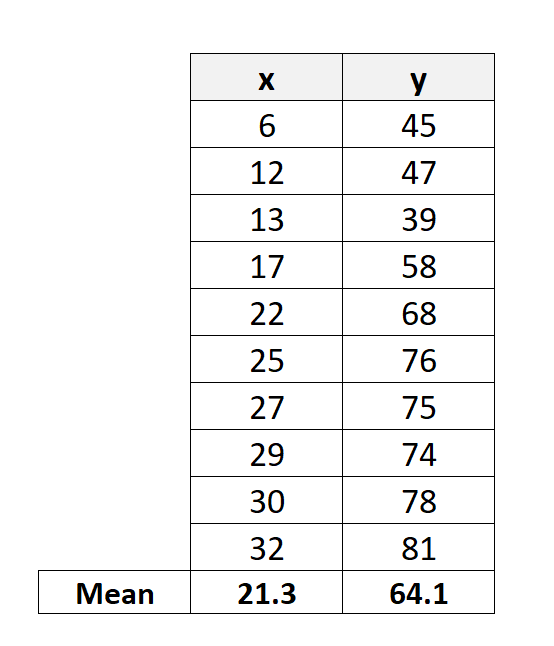
Шаг 2: Рассчитайте разницу между средними значениями
Далее мы рассчитаем разницу между каждым из отдельных значений X и Y и их соответствующими средними значениями:
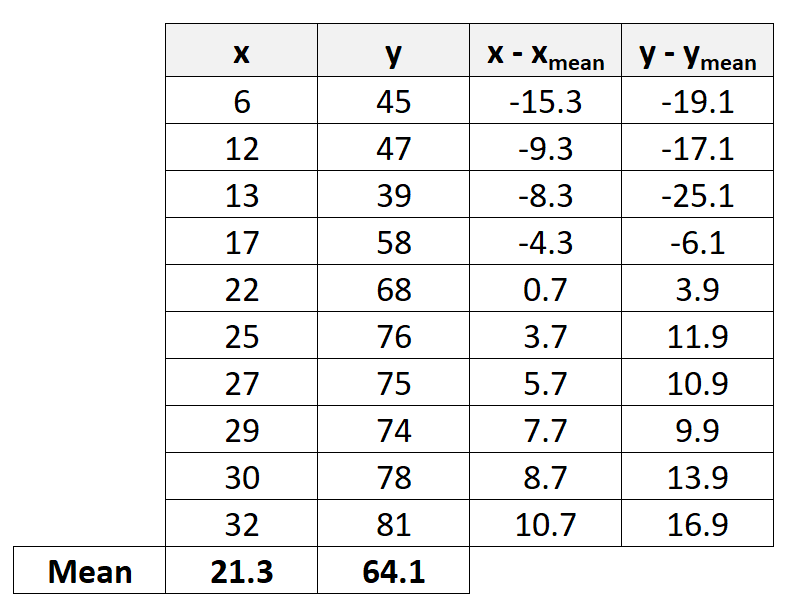
Шаг 3: Рассчитайте оставшиеся значения
Далее мы рассчитаем оставшиеся значения, необходимые для завершения формулы коэффициента корреляции Пирсона:
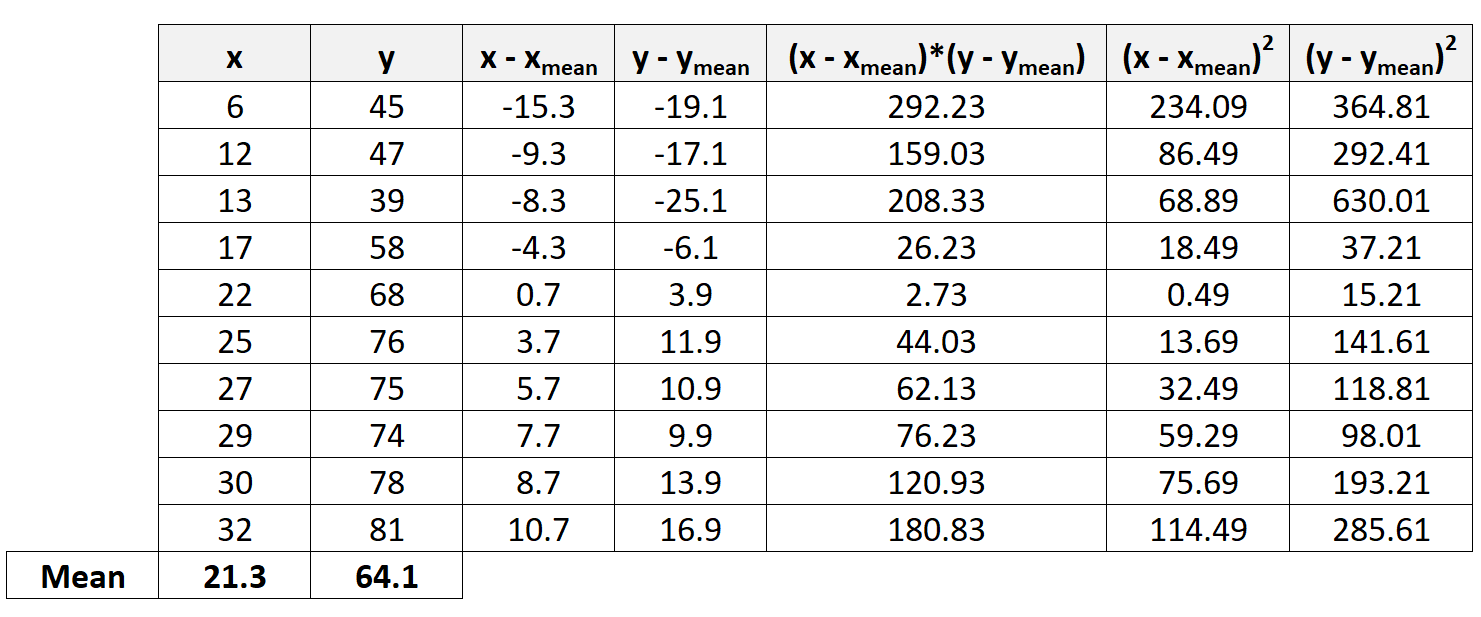
Шаг 4: Рассчитайте суммы
Далее мы вычислим суммы последних трех столбцов:
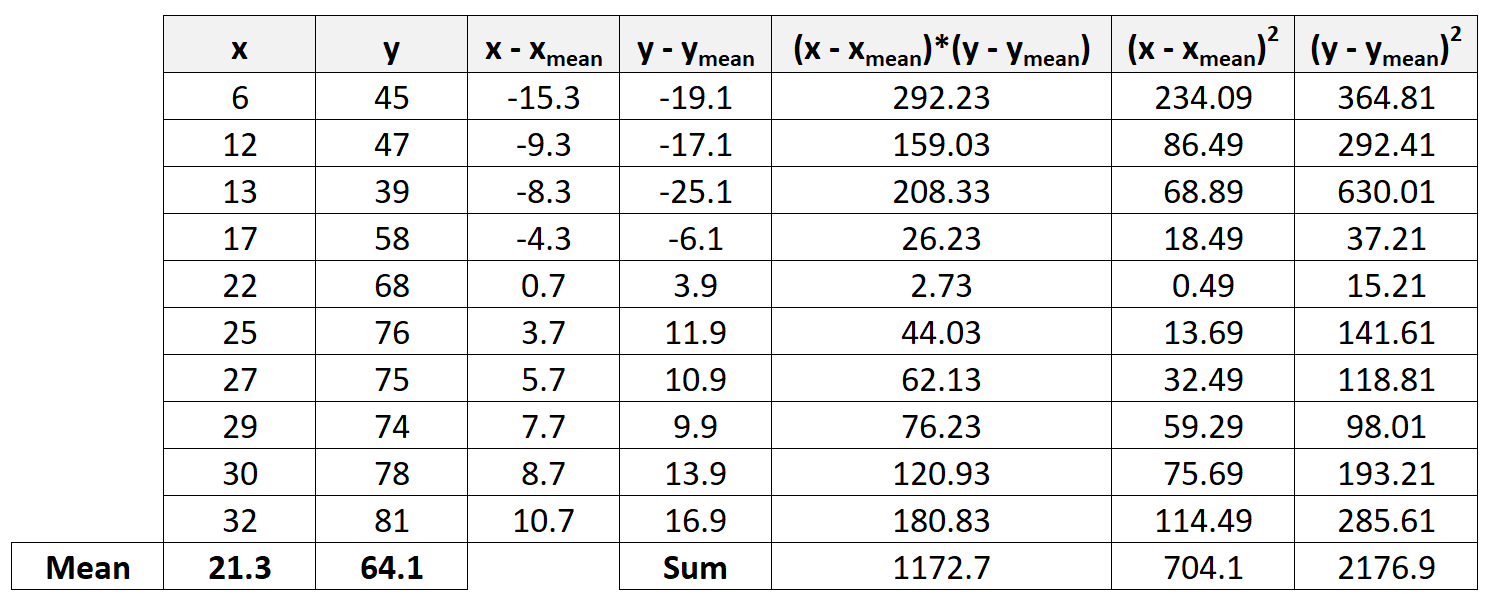
Шаг 5. Рассчитайте коэффициент корреляции Пирсона.
Теперь мы просто подставим суммы из предыдущего шага в формулу коэффициента корреляции Пирсона:
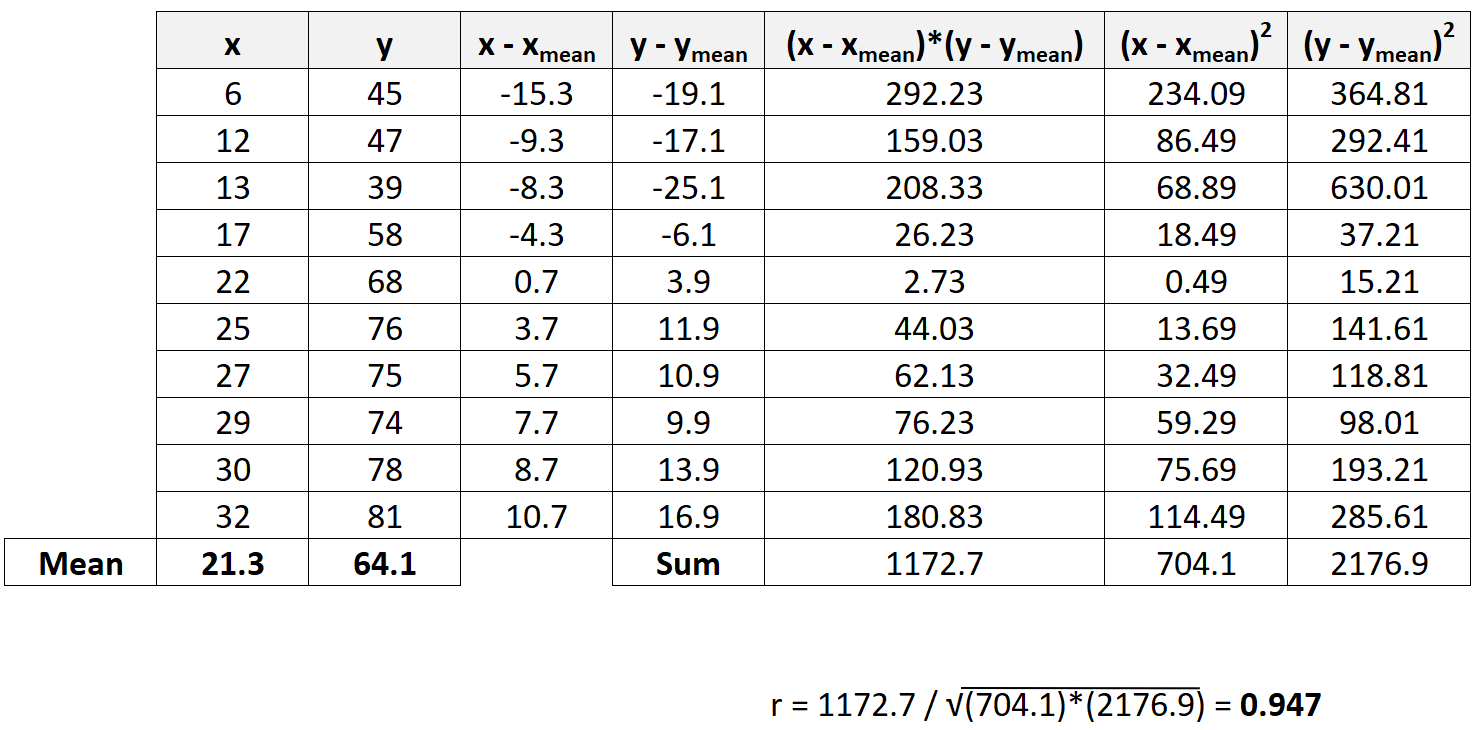
Коэффициент корреляции Пирсона оказывается равным 0,947 .
Поскольку это значение близко к 1, это свидетельствует о сильной положительной корреляции X и Y.
Другими словами, по мере увеличения значения X значение Y также увеличивается весьма предсказуемым образом.
Дополнительные ресурсы
Введение в коэффициент корреляции Пирсона
Как найти доверительный интервал для коэффициента корреляции
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Линейный коэффициент корреляции
Краткая теория
Под теснотой связи между
двумя величинами понимают степень сопряженности между ними, которая
обнаруживается с изменением изучаемых величин. Если каждому заданному
значению
соответствуют
близкие друг другу значения
, то связь считается тесной (сильной); если
же значения
сильно
разбросаны, то связь считается менее тесной.
Рассмотрим наиболее важный
для практики и теории случай линейной зависимости вида:
При тесной корреляционной
связи корреляционное поле представляет собой более или менее сжатый эллипс. Две
корреляционные зависимости переменной
от
приведены на рисунке.
Очевидно, что в случае (а)
зависимость между переменными менее тесная, чем в случае (б), так как точки
корреляционного поля (а) дальше отстоят от линии регрессии, чем точки поля (б).
Перейдем к оценке тесноты
линейной корреляционной зависимости. Для показателя тесноты связи нужная такая
стандартная система единиц измерения, в которой данные по различным
характеристикам оказались бы сравнимы между собой. Статистика знает такую
систему единиц. Эта система использует в качестве единицы измерения переменной
ее среднее квадратическое отклонение
.
Учтем, что
и запишем
уравнение парной линейной зависимости
в эквивалентном виде:
В этой системе величина:
показывает, на сколько
величин
изменится
в среднем
, когда
увеличится
на одно
.
Величина
является
показателем тесноты связи и называется линейным коэффициентом корреляции. Коэффициент
корреляции, определяемый по выборочным данным, называется выборочным коэффициентом корреляции.
Если
, то корреляционная связь между переменными
называется прямой, если
– обратной.
Приведем другие модификации
формулы для расчета линейного коэффициента корреляции:
или
Наиболее часто для расчета
используют формулу, получаемую простыми преобразованиями:
По этой формуле
находится
непосредственно из данных наблюдений и на значении
не
скажутся округления данных, связанных с расчетом средних и дисперсий.
Линейный выборочный
коэффициент корреляции
(при
достаточно большом объеме выборки
) обладает следующими свойствами:
-
Коэффициент корреляции
принимает значения на отрезке
, т.е.
. При этом, чем ближе по модулю
к
единице – тем теснее связь.
При
корреляционная
связь представляет собой линейную функциональную зависимость. При этом все
наблюдаемые значения располагаются на прямой линии.
При
линейная
корреляционная связь отсутствует. При этом линия регрессии параллельна оси
.
Расчет линейного коэффициента корреляции предполагает, что
переменные
и
распределены нормально. В других случаях
(когда распределения
и
отклоняются от нормальных) линейный
коэффициент корреляции не следует рассматривать как строгую меру взаимосвязи
переменных.
Пример решения задачи
Задача
Компания,
занимающаяся продажей радиоаппаратуры, установила на видеомагнитофон
определенной модели цену, дифференцированную по регионам. Следующие данные
показывают цены на видеомагнитофон в 10 различных регионах о соответствующее им
число продаж:
|
Число продаж, шт. |
420 | 380 | 350 | 400 | 440 | 380 | 450 | 425 | 430 | 480 |
| Цена, тыс.руб. | 5.6 | 6.0 | 6.5 | 6.0 | 5.0 | 6.4 | 4.5 | 5.0 | 5.7 | 4.4 |
Рассчитайте
выборочный коэффициент линейной корреляции и проверьте его значимость
при
.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Составим
расчетную таблицу:
Вычислим
линейный коэффициент корреляции:
Вывод
Связь
между числом продаж и ценой очень тесная, обратная – с уменьшением цены
увеличивается объем продаж.
Проверим
значимость коэффициента корреляции:
По таблице критических точек t-критерия Стьюдента (по уровню значимости
и числу степеней свободы
) находим:
– коэффициент корреляции значим.
Кроме этой задачи на другой странице сайта есть еще
задача на расчет коэффициента корреляции, коэффициента детерминации, построение линии линейной регрессии и корреляционного поля.





