Как найти коэффициент кратности пример

Основные теоретические сведения

Опр.
Нониусом
(линейным или круговым) называется
специальная шкала, дополняющая обычный
масштаб и позволяющая повысить точность
измерений в 10-20 раз.

1.
Линейный
нониус
представляет собой небольшую линейку,
скользящую вдоль основной шкалы (рис.1,
а)).

Чтобы понять
принцип действия линейного нониуса,
рассмотрим на 2-х примерах его изготовление
(построение шкалы) и применение.

Пример 1.
Пусть имеется основная шкала с
сантиметровыми
делениями. Выберем следующие значения
основных необходимых для достижения
поставленной цели параметров:

Длина эталона –
10 см,

N=10
– число делений на шкале нониуса,

k=1
– коэффициент кратности (натуральное
число: чаще 1 или 2).

Длина эталона –
это отрезок длины на основном масштабе,
с которым производится сравнение
длины всей шкалы нониуса, равен (k∙N)
см,
т.е. 1∙10=10 см.
Сравнение состоит в следующем: длина
шкалы нониуса берется меньшей на единицу
(у нас единица – это 1 см),
чем длина эталона. В нашем примере длина
всей шкалы нониуса будет равна

10 см
– 1 см
= 9 см.

Следовательно,
далее на отрезке длиной 9 см размечаем
N
делений нониуса, т.е. 10 делений. При этом
цена деления шкалы нониуса будет равна:

(1) – формула для
определения цены деления нониуса.

В формуле (1) цифра
1 означает одно деление основной шкалы.
Тогда величина
измеряется в делениях основной шкалы.
А найти ее величину в единицах длины,
т.е. в сантиметрах или миллиметрах и
пр. можно, умножая полученную по (1)
величину на цену одного деления основной
шкалы.

Имеем в данном
примере:

(делений)


Вывод: одно деление
нониуса меньше одного деления основного
масштаба на 0,1 см 
эта величина и будет (в данном
примере, а не «всегда»)
точностью измерений на полученном
приборе (например, штангенциркуле).

Иначе говоря, по
построению имеем: 10 делений нониуса
меньше 10 делений масштаба на 1 см,
тогда 1 деление нониуса меньше 1 деления
масштаба на 1/10 см.

Применение.
При совмещении нулей обеих шкал
расстояние между рабочими зажимами
шкал равно нулю (рис.1 б)).
При измерении длины образца, например
диаметра болта (рис.1 в)),
он вплотную располагается между
зажимами. При этом нулевая отметка на
нониусе смещается относительно нуля
основной шкалы на искомое
расстояние. По рисунку видно, что в это
расстояние вмещается 1 целое
деление масштаба и еще какая-то его
часть. Для определения длины этой части
ищут номер деления на нониусе, совпавшего
с некоторым делением основной шкалы:
на рисунку это – 9-ое деление, совпадающее
в точности по положению с делением
номер 10 на основной шкале.

Теперь будем
рассуждать, следуя от места совпадения
делений к месту измерения (отсчета
значения диаметра):

9-е деление нониуса
отстоит от 10-го деления шкалы на 0 см
(они совпадают),

8-е деление нониуса
отстоит от 9-го деления шкалы на 0,1 см
(т.к. разница в цене деления, определенная
нами выше составляет 0,1 см),

7-е деление нониуса
отстоит от 8-го деления шкалы на
0,1+0,1=0,2 см,

6-е деление нониуса
отстоит от 7-го деления шкалы на
0,2+0,1=0,3 см,

5-е деление нониуса
отстоит от 6-го деления шкалы на
0,3+0,1=0,4 см,

4-е деление нониуса
отстоит от 5-го деления шкалы на
0,4+0,1=0,5 см,

3-е деление нониуса
отстоит от 4-го деления шкалы на
0,5+0,1=0,6 см,

2-е деление нониуса
отстоит от 3-го деления шкалы на
0,6+0,1=0,7 см,

1-е деление нониуса
отстоит от 2-го деления шкалы на
0,7+0,1=0,8 см,

0-е деление нониуса
отстоит от 1-го деления шкалы на
0,8+0,1=0,9 см – а это и есть длина искомой
части (см. по рисунку 1
в)). Т.е. длина
искомой части равна произведению
порядкового номера совпавшего деления
нониуса, т.е. 9, на величину разницы цен
делений, т.е. на 0,1 см, и равна 0,9 см.

В целом размер
диаметра болта равен одному целому
делению основной шкалы, т.е. 1 см, и плюс
длина части 0,9 см, итого 1,9 см.

Теперь разберем
пример для случая, когда коэффициент
кратности равен 2, при равенстве прочих
условий и величин.

Пример 2.
Пусть имеется основная шкала с
сантиметровыми
делениями. Выберем следующие значения
основных необходимых для достижения
поставленной цели параметров:

Длина эталона 20
см,

N=10
– число делений на шкале нониуса,

k=2
– коэффициент кратности.

Тогда отрезок
длины на основном масштабе (называем
его эталоном),
с которым производится сравнение
длины всей шкалы нониуса равен (k∙N)
см,
т.е. 2∙10=20 см.
Сравнение состоит в следующем: длина
шкалы нониуса берется меньшей на единицу
(у нас единица – это 1 см),
чем длина этого отрезка. В нашем примере
длина всей шкалы нониуса будет равна

20 см
– 1 см
= 19 см.

Следовательно,
далее на отрезке длиной 1,9 см размечаем
N
делений нониуса, т.е. 10 делений. При этом
цена деления шкалы нониуса будет равна
по формуле (1):

делений или 1,9 см

Вывод: одно деление нониуса меньше двух
делений (деление на нониусе сравнивается
с k
делениями на основной шкале) основного
масштаба на 0,1 см 
эта величина и будет точностью измерений
на полученном приборе (например,
штангенциркуле).

Иначе говоря, по
построению имеем: 10 делений нониуса
меньше 20 делений масштаба на 1 см,
тогда 1 деление нониуса меньше 2 делений
масштаба на 1/10 см,
при этом разница распределена в пределах
между 2-мя этими делениями.

Получается, что
проделанные изменения в построении не
сказались на величине точности (все
также 0,1 см).

Но что же изменилось?
Для нахождения ответа изучим рис. 2.

Исходное
положение: при совмещении нулей обеих
шкал расстояние между рабочими зажимами
шкал равно нулю (рис.2а)),
10-е (последнее) деление нониуса совпадает
с 19-м делением основной шкалы.

При помещении
образца, например болта (рис.2 б)),
между зажимами нулевая отметка на
нониусе смещается относительно нуля
основной шкалы на искомое
расстояние. По рисунку видно, что в это
расстояние теперь вмещается 3 целых
деления масштаба и еще какая-то его
часть. Для определения длины этой части
ищем номер деления на нониусе, совпавшего
с некоторым делением основной шкалы:
на рисунку это – 8-ое деление, совпадающее
в точности по положению с делением
номер 19 на основной шкале.

По аналогии с
первым примером мы должны утверждать,
что длина искомой части равна 8∙0,1=0,8
см, а измеряемое расстояние 3+0,8=3,8 см.

Однако заметим
следующее: соседние с совпавшим делением,
а именно 7-е и 9-е деления нониуса отстоят
от ближайших делений основной шкалы
(соответственно 17-м и 21-м) на 0,1 см. Эти
деления – вторые на очереди претендентов
на «совпадение». Чтобы совпало какое-либо
из этих делений, расстояние между
зажимами должно уменьшиться или
увеличиться на 0,1. представим же себе
ситуацию, что оно уменьшилось лишь на
0,05, т.е. на половину от 0,1 см. Какое же
деление нониуса теперь будет совпадающим?

Теперь 8-е деление
нониуса будет левее 19 основной шкалы
на 0,05 см, а 7-е деление нониуса правее
17-го на такую же величину. При этом
истинная длина образца будет 3,75 см, но
на данном приборе мы может с имеющейся
точностью получить его значение как
3,7 см (примем совпадение на 7-м делении
нониуса) или как 3,8 см (если принять
совпадающим 8-е). Тогда в обоих случаях
будет верно: 3,75=3,7 0,1
и 3,75=3,8 0,1.
Полученные значения соответствуют
округлению до десятых долей сантиметра,
но с недостатком или с избытком.

В заключение
подумаем, когда же предпочесть второй
способ построения первому?

Разница между
ними состоит в «укрупнении» делений
шкалы нониуса, по сравнению с делениями
основной шкалы.

Поэтому предпочтение
второму способу будет отдано скорее
всего тогда, когда деления основной
шкалы настолько мелки, что построение
нониуса с еще более мелкими делениями
нецелесообразно из-за возможного
возникновения затруднений при снятии
показаний, т.е. к возрастанию субъективной
погрешности отсчета.

Обобщая проделанное,
получаем следующие результаты:

• (2) – точность
  измерений по шкале с нониусом
  (штангенциркуля).

В обоих разобранных
примерах это была величина
.

Следовательно,
увеличить точность можно за счет
увеличения числа делений на нониусе.
Но, не меняя при этом длину основного
отрезка (эталона), будем получать
одновременное «мельчание» этих делений,
что также на определенном пределе
становится источником дополнительных
трудностей, т.е. не целесообразно.

Таким образом,
при создании шкал с нониусом необходимо
подбирать оптимальное соотношении
основных параметров: длины
эталона
(числа делений на основной шкале,
по сравнению с общей длиной которых
длина шкалы нониуса меньше на одно
такое деление; в примере 1 – 10 делений,
в примере 2 – 20 делений. Иначе, это
эквивалентно выбору размеров шкалы
нониуса), числа
делений шкалы нониуса N
(примеры 1 и 2 – 10 делений) и коэффициента
кратности k
(пример 1: k=1;
пример 2: k=2).

• (3) – длина
  предмета, где m
  – число полных делений основной шкалы
  (масштаба) между нулевыми отметками
  двух шкал, n
  – порядковый номер совпадающего
  деления нониуса.

2.
Круговой нониус представляет
собой дуговую линейку (рис. 3), скользящую
вдоль кругового масштаба (лимба),
предназна­ченного
для измерения углов. Так как длина дуги
s
окружности радиуса
R
и
центральный угол

связаны соотношением

рис.
3

то
измерение углов можно заме­нить
измерением дуг. В принципе круговой
нониус ничем не отли­чается от
линейного и для него справедливы те же
формулы. Так, для случая кругового
нониуса формулу (3) можно записать так:

,
где—
цена деления лимба, m
– число полных делений лимба, n
– порядковый номер совпадающего деления
нониуса.

Штангенциркуль.

Штангенциркуль
служит
для линейных
измерений, не требующих высокой точности.
Отсчетным
приспособлением у всех конструкций
штангенинструментов служат
шкала штанги и линейный нониус. Цена
деления основ­ной
шкалы штанги равна обычно 1 мм.
Нониусы
штангенциркулей изготавливаются
таким образом, что k=1,
2,
5 (см. формулу (1)). Погрешность
нониусов обычно равна 0,1; 0,05 или 0,2 мм.

Н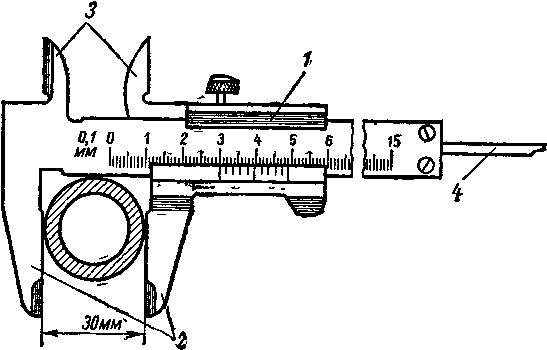ониус
укреплен в подвижной рамке, скользящей
вдоль ос­новной
шкалы штанги. При нулевом показании
инструмента нуль нониуса совпадает с
нулевым штрихом основной шкалы. При
измерении
детали подвижная рамка 1
с
нониусом смещается, и
деталь зажимается губками 2
штангенциркуля.
Существует несколько
видов штангенциркулей. Они отличаются
типом и ко­личеством
измерительных губок, длиной штанги,
типом нониусов или
наличием некоторых вспомогательных
деталей. При наличии у
штангенциркулей верхних 3
и
нижних 2
измерительных
губок, его
можно применить как для внутренних
измерений, так и для внешних.
Часто штангенциркуль снабжается
линейкой 4,
служа­щей
для измерения глубин.

Микрометр.

Для
более точных измерений применяют
микрометрические
инструменты. Они бывают нескольких
типов: микрометр
для наружных измерений, микрометрический
глуби­номер
и микрометрический нутромер.

• М
  

  рис.4

  икрометр для наружных измерений
  (рис. 4) состоит из по­лого
  стержня, жестко соединенного со скобой.
  В полость стержня ввинчен микрометрический
  винт. При измерении предмет зажи­мается
  между неподвижным стержнем 2
  и подвижным
  торцом мик­рометрического
  винта 3.
  Микровинт
  вращают, держась за трещот­ку
  4 (в
  более совершенных микрометрах момент
  соприкосновения мик­рометрического
  винта с измеряемой поверхностью
  фиксируется по шкале чувствительного
  динамометра, укрепленной в скобе);
  вместе с микровинтом вращается корпус
  барабана 1,
  переме­щаясь
  при этом поступательно относительно
  стержня. Отсчет ве­дется
  по горизонтальной шкале, нанесенной
  на полый стержень, и по шкале барабана.
  Отсчетное устройство микрометра
  состоит из
  двух шкал. Горизонтальная шкала стержня
  представляет собой
  двойную шкалу с ценой деления 0,5 мм,
  нанесенную
  по обе стороны
  продольной черты таким образом, что
  верхняя сдвинута относительно
  нижней на половину деления. Цена деления
  шкалы барабана
  может быть установлена следующим
  образом: пусть число
  делений круговой шкалы барабана
  n=50.
  Шаг микровинта h
  =0,5 мм.
  Следовательно,
  одному полному обороту микровинта (и
  барабана) соответствует линейное
  перемещение края барабана на
  0,5 мм.
  Цена
  деления круговой шкалы

Отсчет
производится следующим образом: по
горизонтальной шкале
стержня отсчитывается размер измеряемого
предмета с
точностью до 0,5 мм.
Сотые
доли миллиметра отсчитываются по
круговой
шкале барабана. Полу­ченные
результаты складываются. Число
сотых долей соответствует делению
шкалы, расположенному против
продольной черты на стер­жне.
Порядок отсчета одинаков для
всех типов микрометриче­ских
инструментов. Микрометры изготовляются
с пределами изме­рений
0-25,
50, 75 мм
и
т.д., до
1600 мм.
Увеличение
пределов измерений
достигается увеличе­нием
размера скобы.

Содержание
экспериментальных заданий

Задание 1.
Рассчитайте точность имеющихся в
лаборатории шкал с нониусами (различных
штангенциркулей) и сравните свои расчеты
с отметками на самих приборах.

Задание 2.
Постройте шкалу с нониусом, точность
которой будет 1 мм (0,5 мм, 0,25 мм, 0,05 мм),
считая что основная шкала имеет деления
ценой 1 мм. В каждом случае укажите
выбранные вами значения трех рассмотренных
выше параметров таких шкал.

Задание 3.
Для имеющихся твердых тел измерить
соответствующие линейные размеры.
Вычислить их площади поверхности и
объемы и рассчитать погрешности
полученных результатов как косвенных
измерений.

Часть
Первая

Лабораторная
работа № 1.1.

Определение
плотности тел, имеющих правильную

геометрическую
форму.

Цель
работы:
научиться проводить прямые и косвенные
измерения физических величин (масса,
длина, объем, плотность) и оценивать
погрешность полученных результатов;
познакомиться с некоторыми источниками
погрешностей при измерении плотности
тел в воздухе.

Приборы
и принадлежности:
штангенциркуль, микрометр, технические
весы, разновесы, исследуемые образцы.

Оценка корректирующей способности блокового (n, k) кода

Кодовое (хемминговое) расстояние  — число несовпадающих разрядов двух кодовых комбинаций.

Минимальное кодовое расстояние (d) — минимальное расстояние, взятое по всем парам разрешенных кодовых комбинаций.

Кратность ошибки (r) —  число искаженных символов кодовой комбинации.

Вес кодовой комбинации — число единиц в двоичной кодовой комбинации.

Вектор ошибки — двоичный код, содержащий 1 в искаженных и 0 в остальных разрядах.

Доля обнаруживаемых ошибок  2^k(2ⁿ-2^k)/(2^k2ⁿ) = 1 — 2^k—n

Число кодовых комбинаций: любых 2ⁿ , разрешенных 2^к, запрещенных  2ⁿ — 2^k .

Число вариантов передачи кода  2^к 2ⁿ. Ошибка обнаруживается, если при передаче разрешенной комбинации получена запрещенная комбинация. Число таких вариантов 2^k(2ⁿ-2^k).

Рекомендуемые материалы

Доля исправляемых ошибок среди обнаруживаемых 2^k(2^n—k-1)/2^k(2ⁿ-2^k)=2^—k. Запрещенную кодовую комбинацию заменяют ближайшей разрешенной комбинацией. Ближайшими к разрешенной комбинации являются 2^n-k-1 запрещенных кодовых комбинаций. Ошибка будет исправлена, если принятая запрещенная комбинация окажется «ближайшей» к  переданной разрешенной комбинации. Число таких случаев  2^k(2^n-k-1).

Установим связь кодового расстояния d и кратности обнаруживаемых и исправляемых ошибок. Все возможные кодовые комбинации можно представить точками или векторами в многомерном пространстве.   Точки подмножества запрещенных комбинаций, соответствующих разрешенной комбинации, можно считать расположенными на сферах радиусов 1, 2, и т.д., равных кодовому расстоянию до разрешенной комбинации. Как видно из рисунка, где кодовое расстояние      d =6, можно обнаружить ошибки кратности r =5 и исправить ошибки кратности s =2. В общем случае должны выполняться условия:

Вместе с этой лекцией читают «3.6 Точечные случайные процессы. Формула Ито для считающих процессов. Компенсаторы».

d ³ r + 1   для обнаружения ошибки кратности r,

d ³ 2s + 1 для исправления  ошибки кратности s,

d ³ r + s + 1 (r ³ s) для обнаружения и одновременного исправления ошибок кратности  r и s.

Для исправления ошибки контрольная кодовая комбинация должна указывать место ошибки. Следовательно, число различных контрольных кодовых комбинаций должно быть не менее количества различных ошибок.. Число ошибок кратности r равно числу сочетаний С_n^r .   При  s = 1 (исправление ошибки кратности 1) должно выполняться условие 2^n—k-1 > C_n¹  = n, при  s = 2 — условие  2^n—k-1 > C_n¹+ C_n², в общем случае – условие

Эта оценка Хемминга определяет минимальную избыточность, необходимую для исправления ошибок. Коды с минимальной избыточностью, для которых неравенство превращается в равенство, называются совершенными.

Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется. 

Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.

Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.

Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.

В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:

• запрос повторной передачи (Automatic Repeat reQuest, ARQ): с помощью помехоустойчивого кода выполняется только обнаружение ошибок, при их наличии производится запрос на повторную передачу пакета данных;
• прямое исправление ошибок (Forward Error Correction, FEC): производится декодирование помехоустойчивого кода, т. е. исправление ошибок с его помощью.

Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу. 

Исправление ошибок в помехоустойчивом кодировании

Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность. 

Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.

Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию. 

Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка. 

Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный. 

Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.

Параметры помехоустойчивого кодирования

Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k

• где n – количество символов закодированного сообщения (результата кодирования);
•   m – количество проверочных символов, добавляемых при кодировании;
•   k – количество информационных символов.

Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов,  Рида-Соломона (15, 11) и т.д. 

Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.

Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).

Контроль чётности

Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит. 

Если нечетное количество единиц, добавляем 0.

1 0 1 0 0 1 0 0 | 0

Если четное количество единиц, добавляем 1.

1 1 0 1 0 1 0 0 | 1

Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.

1 1 0 0 0 1 0 0 | 1 

Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1. 

Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности. 

Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:

И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется. 

Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные. 

Рассчитаем скорость кода для: 

• 1 1 0 0 0 1 0 0 | 1 

Здесь R=8/9=0,88

• И для прямоугольного кода:

Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)

Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде. 

Классификация помехоустойчивых кодов

• Непрерывные — процесс кодирования и декодирования носит непрерывный характер. Сверточный код является частным случаем непрерывного кода. На вход кодера поступил один символ, соответственно, появилось несколько на выходе, т.е. на каждый входной символ формируется несколько выходных, так как добавляется избыточность.
• Блочные (Блоковые) — процесс кодирования и декодирования осуществляется по блокам. С точки зрения понимания работы, блочный код проще, разбиваем код на блоки и каждый блок кодируется в отдельности. 

По используемому алфавиту:

• Двоичные. Оперируют битами.
• Не двоичные (код Рида-Соломона). Оперируют более размерными символами. Если изначально информация двоичная, нужно эти биты превратить в символы. Например, есть последовательность 110 110 010 100 и нужно их преобразовать из двоичных символов в не двоичные, берем группы по 3 бита — это будет один символ, 6, 6, 2, 4 — с этими не двоичными символами работают не двоичные помехоустойчивые коды. 

Блочные коды делятся на

• Систематические  — отдельно не измененные информационные символы, отдельно проверочные символы. Если на входе кодера присутствует блок из k символов, и в процессе кодирования сформировали еще какое-то количество проверочных символов и проверочные символы ставим рядом к информационным в конец или в начало. Выходной блок на выходе кодера будет состоять из информационных символов и проверочных. 
• Несистематические — символы исходного сообщения в явном виде не присутствуют. На вход пришел блок k, на выходе получили блок размером n, блок на выходе кодера не будет содержать в себе исходных данных. 

В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе. 

Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.  

Код Хэмминга

Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную. 

Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности. 

Декодирование кода Хэмминга

Декодирование происходит через вычисление синдрома по выражениям:

Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:

Расстояние Хэмминга

Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.

Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость. 

Помехоустойчивые коды

Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)

Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k. 

• n — количество символов на входе. 
• k — количество символов на выходе. 
• t — кратность исправляемых ошибок. 
• Отношение k/n — скорость кода. 
• G (энергетический выигрыш) — величина, показывающая на сколько можно уменьшить отношение сигнал/шум (Eb/No) для обеспечения заданной вероятности ошибки.

Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности. 

Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость. 

Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель. 

Компромиссы при использовании помехоустойчивых кодов

Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи. 

Компромисс:

1. Достоверность vs полоса пропускания.
2. Мощность vs полоса пропускания.
3. Скорость передачи данных vs полоса пропускания

Необходимость чередования (перемежения)

Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.

Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения. 

Пример блочного перемежения:

На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам. 

Коэффициент – кратность

Cтраница 2

Коэффициент кратности представляет собой сумму убывающей геометрической прогрессии, в которой первый член и знаменатель прогрессии равны месячному коэффициенту падения, а число членов равно двенадцати.
 [16]

Коэффициент кратности принимается по тому месяцу, указанному в таблице коэффициентов, календарный номер которого на единицу меньше планируемого числа месяца эксплуатации новых скважин.
 [17]

Коэффициент кратности одинаковым образом определяется н для волновой и для петлевой сложных обмоток.
 [18]

Коэффициент кратности равен числу простых обмоток, составляющих сложную обмотку.
 [19]

Коэффициент кратности равен числу простых обмоток, из которых состоит сложная обмотка.
 [20]

Коэффициенты кратности могут и отсутствовать.
 [21]

Коэффициент кратности указывает, во сколько раз компилятор должен увеличить поле памяти, размер которого устанавливается типом данного и модификатором длины, чтобы получить общее поле объявляемой переменной. Он может быть задан как целым десятичным числом, так и выражением. Если коэффициент кратности задан нулем, то компилятор не резервирует поле памяти, а производит только выравнивание значения счетчика адреса в зависимости от указанного типа данного.
 [22]

Коэффициент кратности магнитных усилителей в значительной степени зависит от материала сердечника.
 [23]

Коэффициентом кратности называется сумма членов убывающей геометрической прогрессии, у которой первый член и знаменатель прогрессии равны месячному коэффициенту падения, а число членов равно двенадцати.
 [24]

Коэффициентом кратности пользуются для ориентировочных ( предварительных) наметок плана добычи по старым и новым скважинам.
 [25]

Коэффициентом кратности пользуются для ориентировочных ( предварительных) наметок плана добычи по старым и новым скважинам. Допустим, что на промысле имеется 30 скважин со средним суточным дебитом в декабре 70 т / сут.
 [26]

Эти коэффициенты кратности даны для двигателей с коротко-замкнутым ротором при прямом их включении на полное напряжение, а для двигателей с фазным ротором – при пуске их с включенным в цепь ротора реостатом.
 [28]

Эти коэффициенты кратности даны для двигателей с коротко-замкнутым ротором при прямом их включении на полное напряжение, а для двигателей с фазным ротором при их пуске с включенным в цепь ротора пусковым реостатом.
 [29]

Задаваясь коэффициентом кратности pN от 1 до 5, определяем наружный диаметр тепловой изоляции и суммарные приведенные затраты на перекачку, подогрев и тепловую изоляцию.
 [30]

Страницы:  

   1

   2

   3

   4

			Понедельник, 15.05.2023, 18:29 Приветствую Вас Гость | RSS
Главная | Регистрация | Вход
ТО и ремонт автомобилей Узнай всё про автомобиль

Из задания на проектирование принимается:

– тип заданного состава;

– среднесписочное количество автомобилей;

– пробег автомобилей с начала эксплуатации;

– среднесуточный пробег автомобилей;

– категория условий эксплуатации;

– природно-климатические условия эксплуатации;

– количество рабочих дней в году;

– режим работы автомобилей на линии.

Нормативы и коэффициенты корректирования принимаются из ОНТП-01-91.

Исходные данные заносим в таблицу 1. 

2.1.1. Определение расчетной периодичности ТО-1 и ТО-2

Расчёт периодичности пробегов автомобилей между первым L₁ и вторым L₂ техническими обслуживаниями, выполняется по следующим формулам:

L₁ = L^Н₁ · К₁ · К₃ км, 

L₂ = L^Н₂ · К₁ · К₃ км, 

Где:       L^Н₁₍₂₎ – нормативная периодичность ТО-1, (ТО-2)

              К₁ – коэффициент корректирования, учитывающий категорию условий эксплуатации

              К₃ – коэффициент корректирования, учитывающий природно-климатические условия

Для удобства составления графика постановки автомобилей на соответствующий вид технического воздействия, расчётные периодичности ТО-1, ТО-2 и пробег до капитального ремонта следует скорректировать с учётом кратности со среднесуточным пробегом Lсс  и между собой.

n_то-1 = L_1 /L_сс 

где n_то-1 величина кратности (округляется до целого числа)

 Скорректированная по кратности величина периодичности ТО-1 принимает вид

 L₁ =  n_то-1 · L_сс  км,

Расчётная величина периодичности  ТО-2 корректируется по кратности  периодичности ТО-1

n_то-2 = L_2 / L₁

где n_то-2 величина кратности (округляется до целого числа), L₁ – скорректированная по кратности величина периодичности ТО-1

Скорректированная по кратности величина периодичности ТО-2 принимает вид

 L₂ = n_то-2 · L₁  км

где n_то-2 величина кратности (округляется до целого числа), L₁ – скорректированная по кратности величина периодичности ТО-1

Внимание! В дальнейшем надо пользоваться только скорректированной по кратности периодичностью L_{1 ,} L₂

Результаты заносим в таблицу 4.

2.1.2. Определение межремонтного пробега автомобиля

Расчёт пробега автомобиля до капитального ремонта L_КР выполняется по формуле:

 LКР = L^Н_КР · К₁ · К₂ · К₃  км,

L^Н_КР – нормативный пробег до капитального ремонта

К₁ – коэффициент учитывающий условия эксплуатации

К₂ – коэффициент, учитывающий модификацию подвижного состава и организацию его работы

К₃ – коэффициент, учитывающий природно-климатические условия;

Расчётная величина пробега до капитального ремонта корректируется по кратности периодичности ТО-2.

Определяем коэффициент кратности между значениями скорректированного пробега до капитального ремонта и принятой периодичности ТО-2 по формуле:

n_КР = L_КР/ L₂

где n_КР величина кратности (округляется до целого числа), L₂ – скорректированная по кратности величина периодичности ТО-2

Скорректированная по кратности величина пробега до капитального ремонта L_КР принимает вид

L_КР = n_КР · L₂   км

Внимание! В дальнейшем надо пользоваться только скорректированным по кратности пробегом L_КР

Результаты заносим в таблицу 4.

2.1.3. Определение расчетной нормы трудоемкости на одно ТО

t(ео,то-1,то-2) = t^н(ео,1,2) · К₂ ·  К₄

где: t^н(ео,1,2) – нормативная трудоёмкость работ ЕО, ТО-1, ТО-2

       К₂  – коэффициент учитывающий модификацию подвижного состава

       К₄ – коэффициент учитывающий трудоёмкость ТО в зависимости от размеров АТП

Трудоемкость ЕО не подлежат корректировке коэффициентом К₄.

Результаты заносим в таблицу 4.

2.1.4. Определение расчетной трудоемкости ТР на 1000 км пробега

t_тр = t^н_тр· К₁ · К₂ · К₃· К₄· К₅

где:  t^н_тр – нормативная трудоёмкость текущего ремонта

      К₁– коэффициент учитывающий категорию условий эксплуатации подвижного состава

      К₂ – коэффициент учитывающий модификацию подвижного состава

      К₃ – коэффициент учитывающий природно-климатические условия 

      К₄ – коэффициент учитывающий количество единиц технологически-совместимого подвижного состава

      К₅ – коэффициент учитывающий условия хранения подвижного состава

Результаты заносим в таблицу 4.

1,2,3,4,5,6,7