Квадра́тное уравне́ние — алгебраическое уравнение второй степени с общим видом
в котором 



Корень уравнения 



Элементы квадратного уравнения имеют собственные названия[1]:
Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице[1]. Такое уравнение может быть получено делением всего выражения на старший коэффициент 
Полным называют такое квадратное уравнение, все коэффициенты которого отличны от нуля.
Неполным называется такое квадратное уравнение, в котором хотя бы один из коэффициентов, кроме старшего (либо второй коэффициент, либо свободный член), равен нулю.
Квадратное уравнение является разрешимым в радикалах, то есть его корни могут быть выражены через коэффициенты в общем виде.
Исторические сведения о квадратных уравнениях[править | править код]
Древний Вавилон[править | править код]
Уже во втором тысячелетии до нашей эры вавилоняне знали, как решать квадратные уравнения[1]. Решение их в Древнем Вавилоне было тесно связано с практическими задачами, в основном такими, как измерение площади земельных участков, земельные работы, связанные с военными нуждами; наличие этих познаний также обусловлено развитием математики и астрономии вообще. Были известны способы решения как полных, так и неполных квадратных уравнений. Приведём примеры квадратных уравнений, решавшихся в Древнем Вавилоне, используя современную алгебраическую запись:
Правила решения квадратных уравнений во многом аналогичны современным, однако в вавилонских текстах не зафиксированы рассуждения, путём которых эти правила были получены.
Индия[править | править код]
Задачи, решаемые с помощью квадратных уравнений, встречаются в трактате по астрономии «Ариабхаттиам», написанным индийским астрономом и математиком Ариабхатой в 499 году нашей эры. Один из первых известных выводов формулы корней квадратного уравнения принадлежит индийскому учёному Брахмагупте (около 598 г.)[1]; Брахмагупта изложил универсальное правило решения квадратного уравнения, приведённого к каноническому виду: 

Корни квадратного уравнения на множестве действительных чисел[править | править код]
I способ. Общая формула для вычисления корней с помощью дискриминанта[править | править код]
Дискриминантом квадратного уравнения 

| Условие | 
|

|

|
| Количество корней | Два корня | Один корень кратности 2 (другими словами, два равных корня) |
Действительных корней нет |
| Формула |  (1) (1)
|

|
— |
Данный метод универсальный, однако не единственный.
II способ. Корни квадратного уравнения при чётном коэффициенте b[править | править код]
Для уравнений вида 

вместо формулы (1) для нахождения корней существует возможность использования более простых выражений[1].
Примечание: данные ниже формулы можно получить, подставив в стандартные формулы выражение b = 2k, через несложные преобразования.
| Дискриминант | Корни | |||
| неприведённое | приведённое | D > 0 | неприведённое | приведённое |
| удобнее вычислять значение
четверти дискриминанта: Все необходимые свойства при этом сохраняются. |
 . .
|

|

|
|
| D = 0 | 
|

|
III способ. Решение неполных квадратных уравнений[править | править код]
К решению неполных квадратных уравнений практикуется особый подход. Рассматриваются три возможных ситуации.
IV способ. Использование частных соотношений коэффициентов[править | править код]
Существуют частные случаи квадратных уравнений, в которых коэффициенты находятся в соотношениях между собой, позволяющих решать их гораздо проще.
Корни квадратного уравнения, в котором сумма старшего коэффициента и свободного члена равна второму коэффициенту[править | править код]
Если в квадратном уравнении 



Доказательство
Способ 1. Сначала выясним, действительно ли такое уравнение имеет два корня (в том числе, два совпадающих):
.
Да, это так, ведь при любых действительных значениях коэффициентов 


Найдём эти корни:
.
В частности, если 

Способ 2.
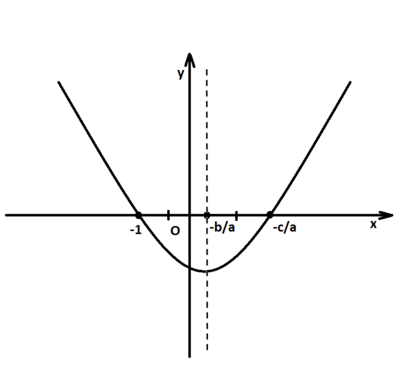
Геометрическая интерпретация: парабола, заданная аналитически указанной формулой, пересекает ось x в двух точках, абсциссами которых и являются корни, хотя бы один из которых равен -1
Используем геометрическую модель корней квадратного уравнения: их мы будем рассматривать как точки пересечения параболы 










- Отсюда следует, что перед решением какого-либо квадратного уравнения целесообразна проверка возможности применения к нему этой теоремы: сравнить сумму старшего коэффициента и свободного члена со вторым коэффициентом.
Корни квадратного уравнения, сумма всех коэффициентов которого равна нулю[править | править код]
Если в квадратном уравнении сумма всех его коэффициентов равна нулю (


Доказательство
Способ 1. Прежде всего заметим, что из равенства 
Установим количество корней:
При любых значениях коэффициентов уравнение имеет хотя бы один корень: действительно, ведь при любых значениях коэффициентов 


Найдём эти корни:
что и требовалось доказать.
- В частности, если
, то уравнение имеет только один корень, которым является число
.
Способ 2. Пользуясь данным выше определением корня квадратного уравнения, обнаруживаем путём подстановки, что число 1 является таковым в рассматриваемом случае: 

- Отсюда следует, что перед решением уравнения стандартными методами целесообразна проверка применимости к нему этой теоремы, а именно сложение всех коэффициентов данного уравнения и установление, не равна ли нулю эта сумма.
V способ. Разложение квадратного трёхчлена на линейные множители[править | править код]
Если трёхчлен вида 





Рассматриваются некоторые частные случаи.
Использование формулы квадрата суммы (разности)[править | править код]
Если квадратный трёхчлен имеет вид 
Выделение полного квадрата суммы (разности)[править | править код]
Также названную формулу применяют, пользуясь методом, получившим названия «выделение полного квадрата суммы (разности)». Применительно к приведённому квадратному уравнению с введёнными ранее обозначениями, это означает следующее:
- прибавляют и отнимают одно и то же число:
.
- применяют формулу к полученному выражению, переносят вычитаемое и свободный член в правую часть:
- извлекают из левой и правой частей уравнения квадратный корень и выражают переменную:
Примечание: данная формула совпадает с предлагаемой в разделе «Корни приведённого квадратного уравнения», которую, в свою очередь, можно получить из общей формулы (1) путём подстановки равенства a = 1. Этот факт не просто совпадение: описанным методом, произведя, правда, некоторые дополнительные рассуждения, можно вывести и общую формулу, а также доказать свойства дискриминанта.
VI способ. Использование прямой и обратной теоремы Виета[править | править код]
Прямая теорема Виета (см. ниже) и обратная ей теорема позволяют решать приведённые квадратные уравнения устно, не прибегая к вычислениям по формуле (1).
Согласно обратной теореме, всякая пара чисел (число) 
- являются корнями уравнения
.
Подобрать устно числа, удовлетворяющие этим уравнениям, поможет прямая теорема. С её помощью можно определить знаки корней, не зная сами корни. Для этого следует руководствоваться правилом:
- 1) если свободный член отрицателен, то корни имеют различный знак, и наибольший по модулю из корней — знак, противоположный знаку второго коэффициента уравнения;
- 2) если свободный член положителен, то оба корня обладают одинаковым знаком, и это — знак, противоположный знаку второго коэффициента.
VII способ. Метод «переброски»[править | править код]
По своей сущности метод «переброски» является просто модификацией теоремы Виета.
Метод «переброски» — это сведение уравнения, которое нельзя привести так, чтобы все коэффициенты остались целыми, к приведённому уравнению с целыми коэффициентами:
- 1) умножаем обе части на старший коэффициент:
- 2) заменяем
Далее решаем уравнение относительно y по методу, описанному выше, и находим x = y/a.
Как можно заметить, в методе «переброски» старший коэффициент как раз «перебрасывается» к свободному члену.
Графическое решение квадратного уравнения[править | править код]
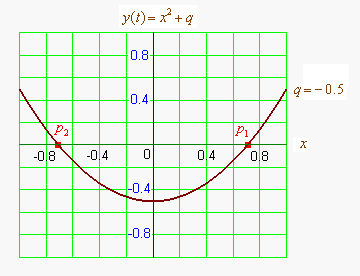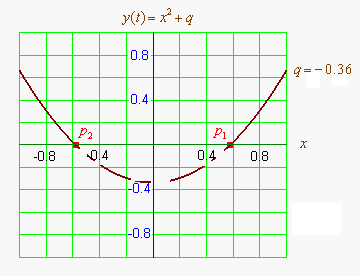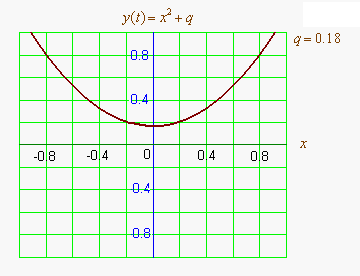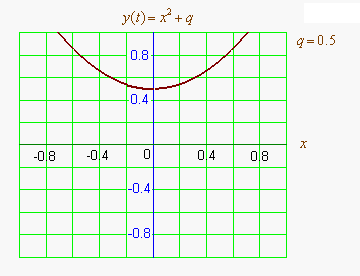
Графиком квадратичной функции является парабола. Решениями (корнями) квадратного уравнения называют абсциссы точек пересечения параболы с осью абсцисс. Если парабола, описываемая квадратичной функцией, не пересекается с осью абсцисс, уравнение не имеет вещественных корней. Если парабола пересекается с осью абсцисс в одной точке (в вершине параболы), уравнение имеет один вещественный корень (также говорят, что уравнение имеет два совпадающих корня). Если парабола пересекает ось абсцисс в двух точках, уравнение имеет два вещественных корня (см. изображение справа.)
Если коэффициент 


Графический способ решения квадратных уравнений[править | править код]
Помимо универсального способа, описанного выше, существует так называемый графический способ. В общем виде этот способ решения рационального уравнения вида 


- Есть всего пять основных способов графического решения квадратных уравнений.
Приём I[править | править код]
Для решения квадратного уравнения 
и отыскиваются абсциссы точек пересечения такого графика с осью 
Приём II[править | править код]
Для решения того же уравнения этим приёмом уравнение преобразуют к виду
и строят в одной системе координат графики квадратичной функции 

Приём III[править | править код]
Данный приём подразумевает преобразование исходного уравнения к виду 





Приём IV[править | править код]
Квадратное уравнение преобразуют к виду 




Приём V[править | править код]
Квадратное уравнение преобразуют к особому виду:
затем
Совершив преобразования, строят графики линейной функции 


Решение квадратных уравнений с помощью циркуля и линейки[править | править код]
Описанные выше приёмы графического решения имеют существенные недостатки: они достаточно трудоёмки, при этом точность построения кривых — парабол и гипербол — низка. Указанные проблемы не присущи предлагаемому ниже методу, предполагающему относительно более точные построения циркулем и линейкой.
Чтобы произвести такое решение, нужно выполнить нижеследующую последовательность действий.
- Построить в системе координат
окружность с центром в точке
, пересекающую ось
в точке
.
- Далее возможны три случая:
Доказательство

Иллюстрация к доказательству.
Рассматриваемый способ предполагает построение окружности, пересекающей ось ординат в точках (точке), абсциссы которых являются корнями (или корнем) решаемого уравнения. Как нужно строить такую окружность? Предположим, что она уже построена. Окружность определяется однозначно заданием трёх своих точек. Пусть в случае, если корня два, это будут точки 









Итак, нами найдены необходимые для построения данные. Действительно, если мы построим окружность с центром в точке 

Корни квадратного уравнения на множестве комплексных чисел[править | править код]
Уравнение с действительными коэффициентами[править | править код]
Квадратное уравнение с вещественными коэффициентами 
Уравнение с комплексными коэффициентами[править | править код]
В комплексном случае квадратное уравнение решается по той же формуле (1) и указанным выше её вариантам, но различимыми являются только два случая: нулевого дискриминанта (один двукратный корень) и ненулевого (два корня единичной кратности).
Корни приведённого квадратного уравнения[править | править код]
Квадратное уравнение вида 

Мнемонические правила:
- Из «Радионяни»:
«Минус» напишем сначала,
Рядом с ним p пополам,
«Плюс-минус» знак радикала,
С детства знакомого нам.
Ну, а под корнем, приятель,
Сводится всё к пустяку:
p пополам и в квадрате
Минус прекрасное[2] q.
- Из «Радионяни» (второй вариант):
p, со знаком взяв обратным,
На два мы его разделим,
И от корня аккуратно
Знаком «минус-плюс» отделим.
А под корнем очень кстати
Половина p в квадрате
Минус q — и вот решенья,
То есть корни уравненья.
- Из «Радионяни» (третий вариант на мотив Подмосковных вечеров):
Чтобы x найти к половине p,
Взятой с минусом не забудь,
Радикал приставь с плюсом минусом,
Аккуратно, не как-нибудь.
А под ним квадрат половины p,
Ты, убавь на q и конец,
Будет формула приведенная,
Рассуждений твоих венец.
Будет формула приведенная,
Рассуждений твоих венец.
Теорема Виета [3][править | править код]
Формулировка для приведённого квадратного уравнения[править | править код]
Сумма корней приведённого квадратного уравнения 


С его помощью приведённые уравнения можно решать устно:
Для неприведённого квадратного уравнения[править | править код]
В общем случае, то есть для неприведённого квадратного уравнения 
На практике (следуя методу «переброски») для вычисления корней применяется модификация теорема Виета:
по которой можно устно находить ax1, ax2, а оттуда — сами корни:
Но у некоторых неприведённых уравнений корни можно устно угадать даже по стандартной теореме Виета:
Разложение квадратного трёхчлена на множители и теоремы, следующие из этого[править | править код]
Если известны оба корня квадратного трёхчлена, его можно разложить по формуле
(2)
Доказательство[править | править код]
Для доказательства этого утверждения воспользуемся теоремой Виета. Согласно этой теореме, корни 



В случае нулевого дискриминанта это соотношение становится одним из вариантов формулы квадрата суммы или разности.
- Из формулы (2) имеются два важных следствия:
Следствие 1[править | править код]
-
- Если квадратный трёхчлен раскладывается на линейные множители с вещественными коэффициентами, то он имеет вещественные корни.
Доказательство[править | править код]
Пусть 
.
Сопоставив полученное выражение с формулой (2), находим, что корнями такого трёхчлена являются 


Следствие 2[править | править код]
-
- Если квадратный трёхчлен не имеет вещественных корней, то он не раскладывается на линейные множители с вещественными коэффициентами.
Доказательство[править | править код]
Действительно, если мы предположим противное (что такой трёхчлен раскладывается на линейные множители), то, согласно следствию 1, он имеет корни в множестве 

Для квадратичной функции:
f (x) = x2 − x − 2 = (x + 1)(x − 2) действительной переменной x, x — координаты точки, где график пересекает ось абсцисс, x = −1 и x = 2, являются решениями квадратного уравнения: x2 − x − 2 = 0.
Уравнения, сводящиеся к квадратным[править | править код]
Алгебраические[править | править код]
Уравнение вида 
В общем случае оно решается методом введения новой переменной, то есть заменой 



Также при решении можно обойтись без замены, решив совокупность двух уравнений:
и
К примеру, если 
Такое уравнение 4-й степени называется биквадратным[4][1].
С помощью замены
к квадратному уравнению сводится уравнение
известное как возвратное или обобщённо-симметрическое уравнение[1].
Дифференциальные[править | править код]
Линейное однородное дифференциальное уравнение с постоянными коэффициентами второго порядка
подстановкой 
Если решения этого уравнения 

, где
и
— произвольные постоянные.
Для комплексных корней 
где A, B, C, φ — любые постоянные. Если решения характеристического уравнения совпадают 
Уравнения такого типа часто встречаются в самых разнообразных задачах математики и физики, например, в теории колебаний или теории цепей переменного тока.
Примечания[править | править код]
Литература[править | править код]
- Квадратное уравнение; Квадратный трёхчлен // Энциклопедический словарь юного математика / Сост. А. П. Савин. — М.: Педагогика, 1985. — С. 133-136. — 352 с.
Ссылки[править | править код]
- Weisstein, Eric W. Quadratic Equation (англ.) на сайте Wolfram MathWorld.
- Вывод формулы корней полного квадратного уравнения. Решение приведённых квадратных уравнений и уравнений с чётным вторым коэффициентом Архивная копия от 28 января 2016 на Wayback Machine / Фестиваль педагогических идей «Открытый урок».
- Математические методы
Теорема Виета для квадратного уравнения

О чем эта статья:
Основные понятия
Квадратное уравнение — это ax 2 + bx + c = 0, где a — первый коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Существует три вида квадратных уравнений:
- не имеют корней;
- имеют один корень;
- имеют два различных корня.
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Формула для его поиска записывается так: D = b 2 − 4ac. Его свойства:
- если D 0, есть два различных корня.
В случае, когда второй коэффициент четный, можно воспользоваться формулой нахождения дискриминанта , где .
В математике теоремой принято называть утверждение, у которого ранее было сформулировано доказательство.
Формула Виета
Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:
Рассмотрим квадратное уравнение, в котором первый коэффициент равен 1: . Такие уравнения называют приведенными квадратными уравнениями. Сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.
Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:
Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.
Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0.
Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:
Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:
Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
2 + 4x + 3 = 0″ height=”215″ src=”https://lh5.googleusercontent.com/E_X403ETh_88EANRWdQN03KRT8yxP2HO4HoCrxj__c8G0DqmNJ1KDRqtLH5Z1p7DtHm-rNMDB2tEs41D7RHpEV5mojDTMMRPuIkcW33jVNDoOe0ylzXdHATLSGzW4NakMkH2zkLE” width=”393″>
Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
2 + 4x + 3 = 0″ height=”52″ src=”https://lh5.googleusercontent.com/VzGPXO9B0ZYrr9v0DpJfXwuzeZtjYnDxE_ma76PUC8o7jVWwa8kZjTJhq2Lof0TiJXAp_ny3yRwI_OyRzeucv9xUZ63yoozGPP4xd4OxvElVT7Pt-d6xL5w17e_mQNs5qZJQiwfG” width=”125″>
Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
2 + 4x + 3 = 0″ height=”52″ src=”https://lh4.googleusercontent.com/Cq-LCFmY3YGNSan1VF3l3CqIeojoJYAvGAiTBWnzyoZu_xJFrF5NfQ3xCe59apJklw6uYbmQ4lAkBTeC-TJmEGicN3rgGtsezhuqdNiOWjZT39NziOB5uOmQr3cr9-5fNnepdZDo” width=”112″>
Результат проделанных вычислений в том, что мы убедились в справедливости выражения:
Обучение на курсах по математике помогает быстрее разобраться в новых темах и подтянуть оценки в школе.
Доказательство теоремы Виета
Дано квадратное уравнение x 2 + bx + c = 0. Если его дискриминант больше нуля, то оно имеет два корня, сумма которых равна второму коэффициенту с противоположным знаком, а произведение корней равно свободному члену:
Докажем, что следующие равенства верны
- x₁ + x₂ = −b,
- x₁ * x₂ = c.
Чтобы найти сумму корней x₁ и x₂ подставим вместо них то, что соответствует им из правой части формул корней. Напомним, что в данном квадратном уравнении x 2 + bx + c = 0 старший коэффициент равен единице. Значит после подстановки знаменатель будет равен 2.
-
Объединим числитель и знаменатель в правой части.
Раскроем скобки и приведем подобные члены:
Сократим дробь полученную дробь на 2, остается −b:
Мы доказали: x₁ + x₂ = −b.
Далее произведем аналогичные действия, чтобы доказать о равенстве x₁ * x₂ свободному члену c.
-
Подставим вместо x₁ и x₂ соответствующие части из формул корней квадратного уравнения:
Перемножаем числители и знаменатели между собой:
Очевидно, в числителе содержится произведение суммы и разности двух выражений. Поэтому воспользуемся тождеством (a + b) * (a − b) = a 2 − b 2 . Получаем:
Далее произведем трансформации в числителе:
Нам известно, что D = b2 − 4ac. Подставим это выражение вместо D.
Далее раскроем скобки и приведем подобные члены:
Сократим:
Мы доказали: x₁ * x₂ = c.
Значит сумма корней приведённого квадратного уравнения x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком (x₁ + x₂ = −b), а произведение корней равно свободному члену (x₁ * x₂= c). Теорема доказана.
Обратная теорема Виета
Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Она формулируется так:
Обратная теорема Виета
Если числа x₁ и x₂ таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа являются корнями x 2 + bx + c = 0.
Обратные теоремы зачастую сформулированы так, что их утверждением является заключение первой теоремы. Так, при доказательстве теоремы Виета стало понятно, что сумма x₁ и x₂ равна −b, а их произведение равно c. В обратной теореме это является утверждением.
Докажем теорему, обратную теореме Виета
Корни x₁ и x₂ обозначим как m и n. Тогда утверждение будет звучать следующим образом: если сумма чисел m и n равна второму коэффициенту x 2 + bx + c = 0, взятому с противоположным знаком, а произведение равно свободному члену, то числа m и n являются корнями x 2 + bx + c = 0.
Зафиксируем, что сумма m и n равна −b, а произведение равно c.
Чтобы доказать, что числа m и n являются корнями уравнения, нужно поочередно подставить буквы m и n вместо x, затем выполнить возможные тождественные преобразования. Если в результате преобразований левая часть станет равна нулю, то это будет означать, что числа m и n являются корнями x 2 + bx + c = 0.
-
Выразим b из равенства m + n = −b. Это можно сделать, умножив обе части на −1:
Подставим m в уравнение вместо x, выражение −m − n подставим вместо b, а выражение mn — вместо c:
При x = m получается верное равенство. Значит число m является искомым корнем.
- Аналогично докажем, что число n является корнем уравнения. Подставим вместо x букву n, а вместо c подставим m * n, поскольку c = m * n.
При x = n получается верное равенство. Значит число n является искомым корнем.
Мы доказали: числа m и n являются корнями уравнения x 2 + bx + c = 0.
Примеры
Для закрепления знаний рассмотрим примеры решения уравнений по теореме, обратной теореме Виета.
Дано: x 2 − 6x + 8 = 0.
Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.
2 − 6x + 8 = 0″ height=”59″ src=”https://lh6.googleusercontent.com/tFokx3SM93Hwlr7ZM9BqX1xiHKv_2dUIB9MoNa8RAwSTmQKXdCcqcFXxTZmxNGw7bOVek-RzRXqBkoCqnYMiqIYVwKhfnHeU-7mA03feEqJTlyKB7e-OsTTKgPaOlddfiaTGszcv” width=”99″>
Имея эти два равенства можно подобрать подходящие корни, которые будут удовлетворять как равенству обоим равенствам системы.
Подбор корней удобнее выполнять с помощью их произведения. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.
Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x₁ + x₂ = 6. Значения 4 и 2 подходят обоим равенствам:
Значит числа 4 и 2 являются корнями уравнения x 2 − 6x + 8 = 0.
2 − 6x + 8 = 0″ height=”57″ src=”https://lh3.googleusercontent.com/rohB7Bvd-elMhTxEUuOhKqLJjqLAvo9VlJxZvOnMeDAHARfKT-SYOWb1WXTTWEN2h0oKbLl6wH7lc0IWL_vH3Si2AJGAGXVn8TPFDT_J1Wu2WeoQ-WP1qgXjCnZ99tWUkK2BOvF2″ width=”64″>
Неприведенное квадратное уравнение
Теорема Виета выполняется только тогда, когда квадратное уравнение является приведённым, то есть его первый коэффициент равен единице:
ax 2 + bx + c = 0, где а = 1.
Если квадратное уравнение не является приведенным, но задание связано с применением теоремы, нужно обе части разделить на коэффициент, который располагается перед x 2 .
- Получилось следующее приведенное уравнение:
-
Получается, второй коэффициент при x равен, свободный член —. Значит сумма и произведение корней будут иметь вид:
Рассмотрим пример неприведенного уравнения: 4x 2 + 5x + 1 = 0. Разделим обе его части на коэффициент перед x 2 , то есть на 4.
Теорема Виета и её применение
Разделы: Математика
Цель:
- Обобщить и закрепить навыки решения квадратных уравнений ах 2 + вх + с = 0, в которых а + в + с = 0; продолжить развивать навыки устного решения таких уравнений.
- Способствовать выработке у школьников желания и потребности обощения изучаемых фактов: развивать самостоятельность и творчество.
- Обеспечить закрепление теоремы на интересных примерах.
Оборудование:
- Кодоскоп
- Карточки тесты
- Карточки с индивидуальными заданиями для учащихся
- Сигнальные карточки.
Ход урока
I Повторение пройденного материала
1) Устная работа через кодоскоп с применением сигнальных карточек. Если ученик готов отвечать, то зеленая, нет – красная. Согласен с ответом – зеленая, не согласен – красная.
| А) 5х 2 – 7х + 2 = 0 | [т.к. а + в + с = 0, то х1 = 1, х2 = ] |
| Б) х 2 – 12х + 35 = 0 | [по обратной теореме Виета х1 = 7, х2 = 5] |
| В) 313х 2 + 326х + 13 = 0 | [а – в + с = 0, то х1 = –1, х2 = –] |
| Г) 4х 2 + 12х + 5 = 0 | [метод переброски х1 = –, х2 = –] |
| Д) Составьте квадратное уравнение, если известны его корни: | |
| х1 = 5, х2 = –6 | [ х 2 + х –30 = 0] |
| х1 = 2, х2 = | [ х 2 – (2 – ) х + 2 = 0] |
Доказательство теоремы Виета и свойств числовых коэффициентов уравнения.
Теорема Виета.
Сумма корней квадратного уравнения равна коэффициенту при х, взятому с противоположным знаком и деленному на коэффициент при х 2 ; произведение корней этого уравнения равно свободному члену деленному на коэффициент при х 2 .
х1 + х2 = –
х1х2 = .
Т.к. квадратное уравнение ах 2 + вх + с = 0 имеет корни х1 и х2, то справедливо тождество ах 2 + вх + с = а(х – х1)(х – х2).
Раскроем скобки в правой части этого тождества:
х 2 + х – х2х + х1х2,
отсюда следует, что х1 + х2 = – и х1* х2 = . Что и требовалось доказать.
Обратная теорема Виета.
Если выполняются равенства х1 + х2 = – и х1х2 = , то числа х1 и х2 являются корнями уравнения ах 2 + вх + с = 0.
Свойства коэффициентов 1.
Пусть дано квадратное уравнение ах 2 + вх + с = 0, где а0. Если а + в + с = 0, то х1 = 1, х2 = .
ах 2 + вх + с = 0, а0
Разделим обе части уравнения на а0, получим приведенное квадратное уравнение х 2 + .
| Согласно теореме Виета | х1 + х2 = – | |
| х1 |
| По условию а + в + с = 0, откуда в = – а – с. Значит | х1 + х2 = – = 1 + | |
| х1* х2 = 1 * |
Получим х1 = 1, х2 = .
Свойство коэффициентов 2.
Если в квадратном уравнении ах 2 + вх + с = 0 а – в + с = 0, то х1 = – 1, х2 = – .
В итоге на доске открывается таблица:
Связь между корнями и коэффициентами квадратного уравнения.
| Уравнение | Условие | Заключение | Пример |
| ах 2 + вх + с = 0 | х1 и х2 | х1 + х2 = – , х1 * х2 = | х1 = 7 + ; х2 = 2 – |
х1 + х2 = 9; х1х2 = 11 – 5
ах 2 + вх + с = 0
х1 + х2 = – , х1 * х2 =
х1 и х2 корни
х 2 + 5х + 6 = 0
х1 = – 2, х2 = – 3
ах 2 + вх + с = 0
а + в + с = 0
х1 = 1, х1 =
1998х 2 – 907х – 1091 = 0
х1 = 1, х2 =
ах 2 + вх + с = 0
а – в + с = 0
х1 = – 1, х1 = –
127х 2 + 250х + 123 = 0
х1 = – 1, х1 = –
ах 2 + вх + с = 0
а 2 х 2 + авх + ас = 0
у1, у2
х1 =
х2 =
4х 2 + 12х + 5 = 0
у 2 + 12у + 20 = 0
х1 = – , х2 = – ;
у1 = – 2, у2 = – 10.
По праву достойна в стихах быть воспета
О свойствах корней теорема Виета.
Что лучше скажи постоянства такого:
Умножишь ты корни – и дробь уж готова?!
В числителе с, в знаменателе а,
А сумма корней тоже дроби равна.
Хоть с минусом дробь, что за беда!
В числителе в, в знаменателе а.
II. Решение интересных заданий с применением теоремы Виета. Классу задается на дом подобрать по три интересных задания. Самые интересные решаются на уроке. №1 и №2 решаются на доске одновременно. №1 решается с полным комментированием, класс работает с учеником, который решает №1. №2 ученик рассказывает основные моменты.
1. Найдите сумму квадратов всех корней уравнения х 2 – 3e х? + 1 = 0.
| х 2 + 3х + 1 = 0; | х1 + х2 = – 3; | х1 * х2 = 1; | |
| х 2 – 3х + 1 = 0; | х3 + х4 = 3; | х1 * х2 = 1; |
х + х + х + х = (х1 + х2) 2 – 2х1х2 + (х3х4) 2 – 2х3х4 = 9 – 2 + 9 – 2 = 14.
2. Пусть х1 и х2 – корни уравнения 2х 2 – 7х + 1 = 0. Составьте квадратное уравнение, корнями которого являются числа и .
Для составления квадратного уравнения с заданными корнями и воспользуемся теоремой, обратной теореме Виета, для этого необходимо найти их сумму и произведение:
+ = = = = 150,5
– = = = 2.
Искомое уравнение имеет вид
х 2 + 150,5 + 2 = 0 или 2х 2 – 301х + 4 = 0.
3. Корни уравнения х 2 – вх – в = 0 таковы, что х + х + хх = 7,5.
х + х = (х)(( х) – 3х) + х = b(b + 3b) – b 3 = b 3 + 3b 2 – b 3 = 3b 2 = 75.
4. Пусть х1и х2 корни уравнения 3х 2 + 14х – 4 = 0.
Установите, больше или меньше единицы значение дроби
.
х1 + х2 = – ;
х1 * х2 = – ;
5. Для каких значений а разность корней уравнения 2х 2 – (а + 1)х + а + 3 = 0 равна единице?
х1 + х2 = = > 1 + х1 + х2 =
х1 * х2 = = > 2х2 + 1 = = > х2 = .
х1 = 1 +
х1 =
= ;
(а + 3)(а – 1) = 8а + 24
а 2 + 3а – а – 3 – 8а – 24 = 0
III. Тест – самостоятельная по карточкам.
Установите верный ответ из числа предложенных А), Б), В), Г).
х 2 + (
А) 2; ;
Б) –;
В); ;
Г) нет правильных ответов.
Не решая квадратного уравнения 3х 2 -х-11 = 0, составьте квадратное уравнение, корнями которого являются числа и .
А) х 2 –
Б) х 2 –
В) х 2 +
Г) х 2 +
Установите верный ответ из числа предложенных А), Б), В), Г).
1) Решите уравнение:
х 2 -(
А) 5; ;
Б) –;
В) -; ;
Г) ; .
Не решая квадратного уравнения 2х 2 -5х-4 = 0, составьте квадратное уравнение, корнями которого являются числа и .
А) х 2 –
Б) х 2 –
В) х 2 +
Г) х 2 +
Проверка ответов через кодоскоп. Учащиеся меняются листочками с ответами, проверяют решение соседа и ставят оценку.
IV. Домашнее задание
Поменяться карточками с творческими заданиями.
Теорема Виета
Что называют теоремой?
Если человек обнаружил в математике какую-нибудь закономерность, позволяющую быстро решить ту или иную задачу, то ему не следует говорить о том, что он сделал открытие. Потому что может случиться так, что эта закономерность работает только для определённых случаев, а для других не работает или вовсе решает задачу неправильно.
Чтобы поделиться своим открытием с другими людьми, найденную закономерность следует сформулировать в виде утверждения, а затем доказать это утверждение, приводя неоспоримые факты.
Сформулированное утверждение называют теоремой. А доказательство теоремы состоит из фактов, логических рассуждений и вычислений, которые не оспариваются.
Например, теоремой можно назвать следующее утверждение:
«Если числитель и знаменатель обыкновенной дроби умнóжить на какое-нибудь число, то значение данной дроби не измéнится».
А затем привести такое доказательство:
Пусть, имеется дробь . Умнóжим числитель и знаменатель этой дроби на число с . Тогда полýчится дробь . Докáжем, что дроби и равны. То есть докажем, что равенство является верным.
Для доказательства этого равенства воспользуемся основным свойством пропорции:
От перестановки мест сомножителей произведение не меняется. Поэтому в получившемся равенстве можно упорядочить правую часть по алфавиту:
Поскольку равенство является пропорцией, а пропорция это равенство двух отношений, то дроби и равны. Теорема доказана.
Теорема Виета
Французский математик Франсуа Виет выявил интересную взаимосвязь между коэффициентами приведённого квадратного уравнения и корнями этого же уравнения. Эта взаимосвязь представлена в виде теоремы и формулируется так:
Сумма корней приведённого квадратного уравнения x 2 + bx + c = 0 равна второму коэффициенту, взятому с противоположным знáком, а произведение корней равно свободному члену.
То есть, если имеется приведённое квадратное уравнение x 2 + bx + c = 0 , а его корнями являются числа x1 и x2 , то справедливы следующие два равенства:
Знак системы (фигурная скобка) говорит о том, что значения x1 и x2 удовлетворяют обоим равенствам.
Покажем теорему Виета на примере приведённого квадратного уравнения x 2 + 4x + 3 = 0 .
Мы пока не знаем какие корни имеет уравнение x 2 + 4x + 3 = 0 . Но по теореме Виета можно записать, что сумма этих корней равна второму коэффициенту 4 , взятому с противоположным знáком. Если коэффициент 4 взять с противоположным знáком, то получим −4 . Тогда:
А произведение корней по теореме Виета будет равно свободному члену. В уравнении x 2 + 4x + 3 = 0 свободным членом является 3 . Тогда:
Теперь проверим действительно ли сумма корней равна −4 , и равно ли произведение 3 . Для этого найдём корни уравнения x 2 + 4x + 3 = 0 . А для удобства воспользуемся формулами для чётного второго коэффициента:
Корнями уравнения являются числа −1 и −3 . По теореме Виета их сумма должна была равняться второму коэффициенту уравнения x 2 + 4x + 3 = 0 , взятому с противоположным знаком. Действительно, так оно и есть. Вторым коэффициентов в уравнении x 2 + 4x + 3 = 0 является 4 . Если взять его с противоположным знаком и приравнять сумму корней x1 + x2 к этому коэффициенту, то получается верное равенство:
А произведение корней −1 и −3 по теореме Виета должно было равняться свободному члену уравнения x 2 + 4x + 3 = 0 , то есть числу 3 . Видим, что это условие тоже выполняется:
Значит выражение является справедливым.
Рассмотрим квадратное уравнение x 2 − 8x + 15 = 0 . По теореме Виета сумма корней этого уравнения равна второму коэффициенту, взятому с противоположным знаком. Второй коэффициент равен −8 . Если взять его с противоположным знаком, то получим 8 . Тогда:
А произведение корней равно свободному члену. В уравнении x 2 − 8x + 15 = 0 свободным членом является 15 . Тогда:
Теперь проверим действительно ли сумма корней равна 8 , и равно ли произведение 15 . Для этого найдём корни данного уравнения. А для удобства воспользуемся формулами для чётного второго коэффициента. В этот раз пропустим нéкоторые подробные записи:
Видим, что корнями уравнения x 2 − 8x + 15 = 0 являются числа 5 и 3 . Их сумма равна 8 . То есть сумма корней равна второму коэффициенту уравнения x 2 − 8x + 15 = 0 , взятому с противоположным знаком.
А произведение чисел 5 и 3 равно 15 . То есть равно свободному члену уравнения x 2 − 8x + 15 = 0 .
Значит выражение является справедливым.
Замечание. Чтобы теорема Виета выполнялась, квадратное уравнение обязательно должно быть приведённым и иметь корни.
Например, рассмотрим квадратное уравнение x 2 − 2x + 4 = 0 . Напишем сумму и произведение корней этого уравнения:
Но уравнение x 2 − 2x + 4 = 0 не имеет корней, сумма которых равна 2, а произведение которых равно 4 . Убедиться в этом можно, вычислив дискриминант:
А значит записывать выражение не имеет смысла.
Теорема Виета полезна тем, что позволяет до начала решения узнать знаки корней уравнения.
Например, запишем для уравнения x 2 − 5x + 6 = 0 сумму и произведение его корней. Сумма корней равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:
Посмотрев на эти два равенства можно сразу понять, что оба корня должны быть положительными. Потому что произведение x1 × x2 = 6 будет выполняться только в двух случаях: если значения x1 и x2 положительны либо они оба отрицательны. Если эти значения будут отрицательными, то не будет выполняться равенство x1 + x2 = 5 , поскольку его правая часть равна положительному числу. А значения x1 и x2 должны удовлетворять как равенству x1 + x2 = 5 , так и равенству x1 × x2 = 6.
Ещё одна польза от теоремы Виета в том, что корни можно найти методом подбора. В данном примере корни должны быть такими, чтобы они удовлетворяли как равенству x1 + x2 = 5 так и равенству x1 × x2 = 6 . Очевидно, что таковыми являются корни 3 и 2
Доказательство теоремы Виета
Пусть дано приведённое квадратное уравнение x 2 + bx + c = 0 . Если его дискриминант больше нуля, то оно имеет два корня, сумма которых равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:
Вспомним формулы корней квадратного уравнения:
Найдём сумму корней x1 и x2 . Для этого подставим в выражение x1 + x2 вместо x1 и x2 соответствующие выражения из правой части формул корней квадратного уравнения. Не забываем, что в приведённом квадратном уравнении x 2 + bx + c = 0 старший коэффициент a равен единице. Тогда в процессе подстановки знаменатель станет равен просто 2
Запишем правую часть в виде дроби с одним знаменателем:
Раскроем скобки в числителе и приведём подобные члены:
Сократим дробь на 2 , тогда получим −b
Теперь аналогично докажем, что произведение x1 × x2 равно свободному члену c .
Подставим вместо x1 и x2 соответствующие выражения из формул корней квадратного уравнения. Не забываем, что коэффициент a всё ещё равен единице:
Чтобы перемнóжить дроби, нужно перемнóжить их числители и знаменатели:
В числителе теперь содержится произведение суммы двух выражений и разности этих же выражений. Воспользуемся тождеством (a + b)(a − b) = a 2 − b 2 . Тогда в числителе полýчится А знаменатель будет равен 4
Теперь в числителе выражение (−b) 2 станет равно b 2 , а выражение станет равно просто D
Но D равно b 2 − 4ac . Подстáвим это выражение вместо D , не забывая что a = 1 . То есть вместо b 2 − 4ac надо подставить b 2 − 4c
В получившемся выражении раскроем скобки в числителе и приведём подобные члены:
Сократим получившуюся дробь на 4
Таким образом, сумма корней приведённого квадратного уравнения x 2 + bx + c = 0 равна второму коэффициенту, взятому с противоположным знáком ( x1 + x2 = −b ), а произведение корней равно свободному члену ( x1 × x2 = c ). Теорема доказана.
Теорема, обратная теореме Виета
Когда записана сумма и произведение корней приведённого квадратного уравнения, обычно начинается подбор подходящих корней к этому уравнению. В этот момент в работу включается так называемая теорема, обратная теореме Виета. Она формулируется так:
Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знáком, а произведение чисел x1 и x2 равно свободному члену уравнения x 2 + bx + c = 0, то числа x1 и x2 являются корнями уравнения x 2 + bx + c = 0.
Обратные теоремы бывают поставлены так, что их утверждением является заключение первой теоремы.
Так, доказывая теорему Виета мы пришли к заключению, что сумма x1 и x2 равна −b , а произведение x1 и x2 равно c . В обратной же теореме это заключение служит утверждением.
Ранее мы решили уравнение x 2 − 5x + 6 = 0 и написали для него такую сумму и произведение корней:
А затем подобрали корни 3 и 2 . По сути мы применили теорему, обратную теореме Виета. Числа 3 и 2 таковы, что их сумма равна второму коэффициенту уравнения x 2 − 5x + 6 = 0 , взятому с противоположным знаком (числу 5 ), а произведение чисел 3 и 2 равно свободному члену (числу 6 ). Значит числа 3 и 2 являются корнями уравнения x 2 − 5x + 6 = 0 .
Пример 2. Решить квадратное уравнение x 2 − 6x + 8 = 0 по теореме, обратной теореме Виета.
В данном уравнении a = 1 . Значит квадратное уравнение является приведённым. Его можно решить по теореме, обратной теореме Виета.
Сначала запишем сумму и произведение корней уравнения. Сумма корней будет равна 6 , поскольку второй коэффициент исходного уравнения равен −6 . А произведение корней будет равно 8
Теперь имея эти два равенства можно подобрать подходящие корни. Они должны удовлетворять как равенству x1 + x2 = 6 , так и равенству x1 × x2 = 8
Подбор корней удобнее выполнять с помощью их произведения. Используя равенство x1 × x2 = 8 нужно найти такие x1 и x2 , произведение которых равно 8.
Число 8 можно получить если перемножить числа 4 и 2 либо 1 и 8.
4 × 2 = 8
1 × 8 = 8
Но значения x1 и x2 надо подбирать так, чтобы они удовлетворяли не только равенству x1 × x2 = 8 , но и равенству x1 + x2 = 6 .
Сразу делаем вывод, что значения 1 и 8 не годятся, поскольку они хоть и удовлетворяют равенству x1 × x2 = 8 , но не удовлетворяют равенству x1 + x2 = 6 .
Зато значения 4 и 2 подходят как равенству x1 × x2 = 8 , так и равенству x1 + x2 = 6 , поскольку эти значения удовлетворяют обоим равенствам:
Значит корнями уравнения x 2 − 6x + 8 = 0 являются числа 4 и 2 .
Обратная теорема, как и любая теорема нуждается в доказательстве. Докажем теорему, обратную теореме Виета. Для удобства корни x1 и x2 обозначим как m и n . Тогда утверждение теоремы, обратной теореме Виета примет следующий вид:
Если числа m и n таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знáком, а произведение чисел m и n равно свободному члену уравнения x 2 + bx + c = 0, то числа m и n являются корнями уравнения x 2 + bx + c = 0
Для начала запишем, что сумма m и n равна −b , а произведение mn равно c
Чтобы доказать, что числа m и n являются корнями уравнения x 2 + bx + c = 0 , нужно поочередно подстáвить буквы m и n в это уравнение вместо x , затем выполнить возможные тождественные преобразования. Если в результате преобразований левая часть станет равна нулю, то это будет означать, что числа m и n являются корнями уравнения x 2 + bx + c = 0 .
Помимо букв m и n нам нужно знать чему равен параметр b . Выразим его из равенства m + n = −b . Легче всего это сделать, умножив обе части этого равенства на −1
Теперь всё готово для подстановок. Подстáвим m в уравнение x 2 + bx + c = 0 вместо x , а выражение −m − n подставим вместо b
Видим, что при x = m получается верное равенство. Значит число m является корнем уравнения x 2 + bx + c = 0 .
Аналогично докажем, что число n является корнем уравнения x 2 + bx + c = 0 . Подставим вместо x букву n , а вместо c подставим mn , поскольку c = mn .
Видим, что при x = n тоже получается верное равенство. Значит число n является корнем уравнения.
Следовательно, числа m и n являются корнями уравнения x 2 + bx + c = 0 .
Примеры решения уравнений по теореме, обратной теореме Виета
Пример 1. Решить квадратное уравнение x 2 − 4x + 4 = 0 по теореме, обратной теореме Виета.
Запишем сумму корней x1 и x2 и приравняем её к второму коэффициенту, взятому с противоположным знаком. Также запишем произведение корней x1 и x2 и приравняем его к свободному члену :
В данном примере очевидно, что корнями являются числа 2 и 2 . Потому что их сумма равна 4 и произведение равно 4
Значение x1 совпадает с x2 . Это тот случай, когда квадратное уравнение имеет только один корень. Если мы попробуем решить данное уравнение с помощью формул корней квадратного уравнения, то обнаружим что дискриминант равен нулю, и корень вычисляется по формуле
Данный пример показывает, что теорема обратная теореме Виета, работает и для уравнений, имеющих только один корень. Признаком того, что квадратное уравнение имеет только один корень является то, что значения x1 и x2 совпадают.
Пример 2. Решить уравнение x 2 + 3x + 2 = 0 по теореме, обратной теореме Виета.
Запишем сумму и произведение корней данного уравнения:
Теперь подберём значения x1 и x2 . Здесь начинается самое интересное. Произведение корней равно 2 . Число 2 можно получить перемножив 1 и 2 . Но сумма корней x1 + x2 равна отрицательному числу −3 . Значит значения 1 и 2 не подходят.
Сумма бывает отрицательной если оба слагаемых отрицательны либо отрицательным является одно слагаемое, модуль которого больше.
Если подберём корни с разными знаками, то не будет выполняться равенство x1 × x2 = 2 .
Если подберем положительные корни, то будет выполняться равенство x1 × x2 = 2 , но не будет выполняться равенство x1 + x2 = −3 .
Очевидно, что корнями являются два отрицательных числа. Произведение отрицательных чисел есть положительное число. А сумма отрицательных чисел есть отрицательное число.
Тогда равенствам будут удовлетворять числа −1 и −2 .
Итак, корнями являются числа −1 и −2
Пример 3. Решить уравнение x 2 + 16x + 15 = 0 по теореме, обратной теореме Виета.
Запишем сумму и произведение корней данного уравнения:
Как и в прошлом примере сумма корней равна отрицательному числу, а произведение корней — положительному числу.
Произведение бывает положительным если оба сомножителя положительны либо оба сомножителя отрицательны. Первый вариант отпадает сразу, поскольку сумма корней равна отрицательному числу. Тогда получается, что оба корня будут отрицательными. Попробуем подобрать их.
Число 15 можно получить, если перемножить числа −1 и −15 или (−3) и (−5) . В данном случае подходит первый вариант, поскольку сумма чисел −1 и −15 равна −16 , а их произведение равно 15 . Значит корнями уравнения x 2 + 16x + 15 = 0 являются числа −1 и −15
Пример 4. Решить уравнение x 2 − 10x − 39 = 0 по теореме, обратной теореме Виета.
Запишем сумму и произведение корней данного уравнения:
Произведение корней равно отрицательному числу. Значит один из корней является отрицательным. Число −39 можно получить если перемножить числа −3 и 13 либо −13 и 3 . Из этих комбинаций больше годится комбинация −3 и 13 , поскольку при перемножении этих чисел получается −39 , а при сложении 10
Значит корнями уравнения x 2 − 10x − 39 = 0 являются числа −3 и 13
Пример 5. Первый корень уравнения x 2 + bx + 45 = 0 равен 15 . Найти второй корень этого уравнения, а также значение коэффициента b .
По теореме Виета произведение корней приведённого квадратного уравнения равно свободному члену. В данном случае это произведение равно 45
При этом один из корней уже известен — это корень 15 .
Тогда второй корень будет равен 3 , потому что число 45 получается, если 15 умножить на 3
Этот второй корень также можно было бы получить, выразив из равенства 15 × x2 = 45 переменную x2
Теперь определим значение коэффициента b . Для этого напишем сумму корней уравнения:
По теореме Виета сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком. Если сумма корней равна 18, а 18 это положительное число, то в самóм уравнении этот коэффициент будет отрицательным:
Обычно решение к такой задаче записывают так. Сначала записывают основную теорему Виета в виде суммы и произведения корней:
Затем в это выражение подставляют имеющиеся известные значения. В нашем случае известно, что первый корень равен 15 , а свободный член уравнения x 2 + bx + 45 = 0 равен 45
Из этой системы следует найти x2 и b . Выразим эти параметры:
Из этой системы мы видим, что x2 равно 3. Подставим его в первое равенство:
Теперь из первого равенства мы видим, что −b равно 18
Но нас интересует b , а не −b . Следует помнить, что −b это −1b . Чтобы найти b нужно 18 разделить на −1 . Тогда b станет равно −18
Этот же результат можно получить если в выражении умножить первое равенство на −1
Теперь возвращаемся к исходному уравнению x 2 + bx + 45 = 0 и подставляем найденное значение b
Выполним умножение −18 на x . Получим −18x
Пример 6. Используя теорему Виета, написать приведённое квадратное уравнение, корнями которых являются числа 2 и 8 .
В этом задании корни уже известны. То есть x1 = 2 , x2 = 8 . По ним надо составить квадратное уравнение вида x 2 + bx + c = 0 .
Запишем сумму и произведение корней:
По теореме Виета сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком. Если сумма корней 2 и 8 равна 10 , то в самóм уравнении число 10 должно быть с противоположным знаком. Значит b = −10 .
Произведение корней по теореме Виета равно свободному члену. У нас это произведение равно 16 .
Значит b = −10 , c = 16 . Отсюда:
Пример 7. Используя теорему Виета, написать приведённое квадратное уравнение, корнями которых являются числа и .
Запишем сумму и произведение корней:
Сумма корней равна 2. Тогда в уравнении второй коэффициент будет равен −2. А произведение корней равно −1. Значит свободный член будет равен −1. Тогда:
Когда квадратное уравнение неприведённое
Теорема Виета выполняется только тогда, когда квадратное уравнение является приведённым.
Если квадратное уравнение не является приведённым, но всё равно возникла необходимость применить теорему Виета, то обе части неприведённого квадратного уравнения следует разделить на коэффициент, который располагается перед x 2 .
Если к примеру в квадратном уравнении a x 2 + bx + c = 0 коэффициент a не равен единице, то данное уравнение является неприведённым. Чтобы сделать его приведённым, надо разделить обе его части на коэффициент, который располагается перед x 2 , то есть на a
Получилось уравнение , которое является приведённым. В нём второй коэффициент равен , а свободный член равен . Тогда сумма и произведение корней будут выглядеть так:
Например, решим квадратное уравнение 4x 2 + 5x + 1 = 0 . Это уравнение не является приведённым. Приведённым оно станет, если разделить обе его части на коэффициент, который располагается перед x 2 , то есть на 4
Получили приведённое квадратное уравнение. В нём второй коэффициент равен , а свободный член . Тогда по теореме Виета имеем:
Отсюда методом подбора находим корни −1 и
Возможно этот метод вы редко будете использовать при решении квадратных уравнений. Но знать о нём не помешает.
Пример 2. Решить квадратное уравнение 3x 2 − 7x + 2 = 0
Данное уравнение не является приведённым, а значит его пока нельзя решить по теореме, обратной теореме Виета.
Сделаем данное уравнение приведенным. Разделим обе части на коэффициент, который располагается перед x 2
Получили уравнение . Запишем сумму и произведение корней этого уравнения:
Отсюда методом подбора находим корни 2 и
Пример 3. Решить квадратное уравнение 2x 2 − 3x − 2 = 0
Это неприведённое квадратное уравнение. Чтобы сделать его приведённым, нужно разделить обе его части на 2 . Сделать это можно в уме. Если 2x 2 разделить на 2 , то полýчится x 2
Далее если −3x разделить на 2 , то полýчится . Чтобы видеть где коэффициент, а где переменная, такое выражение записывают в виде
Далее если −2 разделить на 2 , то полýчится −1
Прирáвниваем получившееся выражение к нулю:
Теперь применяем теорему Виета. Сумма корней будет равна второму коэффициенту, взятому с противоположным знáком, а произведение корней свободному члену:
Отсюда методом подбора находим корни 2 и
[spoiler title=”источники:”]
http://urok.1sept.ru/articles/556279
[/spoiler]
После того, как вы внимательно изучите, как решать квадратные уравнения обычным образом с помощью
формулы для корней
можно рассмотреть другой способ решения квадратных уравнений — с помощью теоремы Виета.
Перед тем, как изучить теорему Виета, хорошо потренируйтесь в
определении коэффициентов
«a», «b» и «с» в квадратных уравнениях.
Без этого вам будет трудно применить теорему Виета.
Когда можно применить теорему Виета
Не ко всем квадратным уравнениям имеет смысл использовать эту теорему.
Применять теорему Виета имеет смысл только к приведённым квадратным уравнениям.
Запомните!
![]()
Приведенное квадратное уравнение — это уравнение, в котором старший
коэффициент «a = 1».
В общем виде приведенное квадратное уравнение выглядит следующим образом:
x2 + px + q = 0
Обратите внимание, что разница с обычным общим видом
квадратного уравнения «ax2 + bx + c = 0» в том, что в
приведённом уравнении «x2 + px + q = 0» коэффициент
«а = 1».
Если сравнить приведенное квадратное уравнение «x2 + px + q = 0» с обычным общим видом квадратного
уравнения «ax2 + bx + c = 0», то становится видно,
что
«p = b», а «q = c».
Теперь давайте на примерах разберем, к каким уравнениям можно применять теорему Виета, а где это не целесообразно.
| Уравнение | Коэффициенты | Вывод |
|---|---|---|
| x2 − 7x + 1 = 0 |
|
Так как «a = 1» можно использовать теорему Виета. |
|
3x2 − 1 + x = 0
Приведем уравнение к общему виду: 3x2 + x − 1 = 0 |
|
Так как «a = 3» не следует использовать теорему Виета. |
|
−x2 = −3 + 2x
Приведем уравнение к общему виду: −x2 + 3 − 2x = 0 |
|
Так как «a = −1» не следует использовать теорему Виета. |
Как использовать теорему Виета
Теперь мы готовы перейти к самому методу Виета для решения квадратных уравнений.
Запомните!
![]()
Теорема Виета для приведённых квадратных уравнений «x2 + px + q = 0» гласит
что справедливо следующее:
, где «x1» и «x2» — корни этого уравнения.
Чтобы было проще запомнить формулу Виета, следует запомнить:
«Коэффициент «p» —
значит плохой, поэтому он берется со знаком минус».
Рассмотрим пример.
x2 + 4x − 5 = 0
Так как в этом уравнении «a = 1», квадратное уравнение
считается приведённым, значит, можно
использовать метод Виета.
Выпишем коэффициенты «p» и «q».
- p = 4
- q = −5
Запишем теорему Виета для квадратного уравнения.
| x1 + x2 = −4 | |
| x1 · x2 = −5 |
Методом подбора мы приходим к тому, что корни уравнения
«x1 = −5» и «x2 = 1». Запишем ответ.
Ответ: x1 = −5; x2 = 1
Рассмотрим другой пример.
x2 + x − 6 = 0
Старший коэффициент «a = 1» поэтому можно применять теорему Виета.
| x1 + x2 = −1 | |
| x1 · x2 = −6 |
Методом подбора получим, что корни уравнения
«x1 = −3» и «x2 = 2». Запишем ответ.
Ответ: x1 = −3; x2 = 2
Важно!

Если у вас не получается решить уравнение с помощью теоремы Виета, не отчаивайтесь.
Вы всегда можете решить любое квадратное уравнение, используя
формулу для нахождения корней.
Деление уравнение на первый коэффициент
Рассмотрим уравнение, которое по заданию требуется решить, используя теорему Виета.
2x2 − 16x − 18 = 0
Сейчас в уравнении «a = 2»,
поэтому перед тем, как использовать теорему Виета нужно сделать так, чтобы «a = 1».
Для этого достаточно разделить все уравнение на «2».
Таким образом, мы сделаем квадратное уравнение приведённым.
2x2 − 16x − 18 = 0 | (:2)
2x2(:2) − 16x(:2) − 18(:2) = 0
x2 − 8x − 9 = 0
Теперь «a = 1» и можно смело записывать формулу Виета и находить корни методом подбора.
| x1 + x2 = −(−8) | |
| x1 · x2 = −9 |
Методом подбора получим, что корни уравнения
«x1 = 9» и «x2 = −1». Запишем ответ.
Ответ: x1 = 9; x2 = −1
Бывают задачи, где требуется найти не только корни уравнения, но и коэффициенты самого уравнения. Например, как в такой задаче.
Корни «x1» и
«x2» квадратного уравнения
«x2 + px + 3 = 0» удовлетворяют
условию «x2 = 3x1».
Найти «p», «x1»,
«x2».
Запишем теорему Виета для этого уравнения.
По условию дано, что
«x2 = 3x1».
Подставим это выражение в систему вместо «x2».
| x1 + 3x1 = −p | |
| x1 · 3x1 = 3 |
Решим полученное квадратное уравнение «x12 = 1»
методом подбора и найдем «x1».
x12 = 1
- (Первый корень) x1 = 1
- (Второй корень) x1 = −1
Мы получили два значения «x1».
Для каждого из полученных значений найдем «p» и запишем все полученные результаты в ответ.
(Первый корень) x1 = 1
Найдем
«x2»
x1 · x2 = 3
1 · x2 = 3
x2 = 3
Найдем «p»
x1 + x2 = −p
1 + 3 = −p
4 = −p
p = −4;
(Второй корень) x1 = −1
Найдем «x2»
x1 · x2 = 3
−1 · x2 = 3
−x2 = 3 | ·(−1)
x2 = −3
Найдем «p»
x1 + x2 = −p
−1 + −3 = −p
−4 = −p
p = 4
Ответ: (x1 = 1; x2 = 3; p = −4) и
(x1 = −1; x2 = −3; p = 4)
Теорема Виета в общем виде
В школьном курсе математики теорему Виета используют только для приведённых уравнений,
где старший коэффициент «a = 1», но, на самом деле, теорему Виета можно применить к любому квадратному уравнению.
В общем виде теорема Виета для квадратного уравнения выглядит так:
Убедимся в правильности этой теоремы на примере. Рассмотрим неприведённое квадратное уравнение.
3x2 + 3x − 18 = 0
Используем для него теорему Виета в общем виде.
| x1 + x2 = −1 | |
| x1 · x2 = −6 |
Методом подбора получим, что корни уравнения
«x1 = −3» и «x2 = 2». Запишем ответ.
Ответ: x1 = −3; x2 = 2
В заданиях школьной математики мы не рекомендуем использовать теорему Виета в общем виде.
Другими словами, реальную пользу теорема Виета приносит только для приведённых квадратных уравнений, в
которых «a = 1».
Именно в таких случаях она не усложняет жизнь, а позволят без дополнительных расчетов быстро найти корни.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
⠀⠀ Всем привет, меня зовут Савин Валерий, я репетитор по физике. Сегодня я решил рассказать вам о всех способах решения квадратных уравнений, которые я знаю. Всего их 6. Знание стольких способов решения позволяет мне крайне быстро решать квадратные уравнения, да и очень удобно проверять себя несколькими способами сразу (например, в стрессовой ситуации) – это минимизирует ошибки.
⠀⠀Для начала совсем немного теории. Квадратное уравнение в самом общем виде выглядит следующим образом:
⠀⠀⠀ Способы решения квадратных уравнений:
Классический способ через дискриминант.
⠀⠀Тут даже описывать ничего не нужно, все знают формулу дискриминанта и как с помощью неё получить ответ. Именно этот способ самый избитый и самый часто применимый. Однако не всегда он самый удобный.
Теорема Виета
⠀⠀Об этом способе тоже знают (или, по крайней мере, слышали) большинство школьников. Нередко в своей репетиторской деятельности встречаю учеников, которые знают эту теорему только для приведённых квадратных уравнений (это где коэффициент а при икс-квадрат равен единице). Однако это теорема справедлива для любого уравнения, т.к. любое квадратное уравнение можно “привести” к приведённому, разделив его на коэффициент а:
⠀⠀Вот, кстати, сама формулировка Теоремы Виета:
- ⠀⠀Сумма корней приведенного квадратного трехчлена равна его второму коэффициенту b с противоположным знаком, а произведение – свободному члену c.
Выделение полного квадрата
⠀⠀Идея данного метода заключается в том, чтобы “объединить” вторую и первую степень неизвестного х в одну (первую) степень в уравнении, т.е. оставить х в одном единственном месте:
⠀⠀Преобразование квадратного трехчлена данному виду называется выделением полного квадрата.
Графический способ
⠀⠀Данный способ рассматривается в школьной программе так же подробно, как и способ решения квадратных уравнений через дискриминант, поэтому я не вижу смысла подробно на этом останавливаться. Отмечу лишь то, что способ действительно очень разнообразный: одно и то же уравнение можно разбить на две части множеством способов, и при этом ответ будет всегда один и тот же. Подробнее со способом можно ознакомиться здесь.
Свойства коэффициентов квадратного уравнения
⠀⠀Такое встречается достаточно редко, но метко. Советую всегда помнить об этом методе и стараться усмотреть его в уравнениях, в которых a, b и с достаточно большие числа (больше 50), и не имеют общего делителя.
Теорема Безу
- ⠀⠀Если число z является корнем квадратного уравнения, то это квадратное уравнение делится на (x-z) без остатка, а число z обязательно должно быть делителем свободного члена с квадратного уравнения.
⠀⠀Данная теорема применима не только для квадратных уравнений, а вообще для многочлена любой степени, и чаще всего эту теорему применяют для многочленов более высокого порядка. Однако мы применим её для квадратного уравнения.
⠀⠀Разделим данное квадратное уравнение на (x-1) в столбик:
⠀⠀Достаточно трудоёмкий способ решения квадратного уравнения, однако имеет место быть.
⠀⠀На этом всё! Читайте и развивайтесь успехов!
Что называют теоремой?
Если человек обнаружил в математике какую-нибудь закономерность, позволяющую быстро решить ту или иную задачу, то ему не следует говорить о том, что он сделал открытие. Потому что может случиться так, что эта закономерность работает только для определённых случаев, а для других не работает или вовсе решает задачу неправильно.
Чтобы поделиться своим открытием с другими людьми, найденную закономерность следует сформулировать в виде утверждения, а затем доказать это утверждение, приводя неоспоримые факты.
Сформулированное утверждение называют теоремой. А доказательство теоремы состоит из фактов, логических рассуждений и вычислений, которые не оспариваются.
Например, теоремой можно назвать следующее утверждение:
«Если числитель и знаменатель обыкновенной дроби умнóжить на какое-нибудь число, то значение данной дроби не измéнится».
А затем привести такое доказательство:
Пусть, имеется дробь ![]() . Умнóжим числитель и знаменатель этой дроби на число с. Тогда полýчится дробь
. Умнóжим числитель и знаменатель этой дроби на число с. Тогда полýчится дробь ![]() . Докáжем, что дроби
. Докáжем, что дроби ![]() и
и ![]() равны. То есть докажем, что равенство
равны. То есть докажем, что равенство ![]() является верным.
является верным.
Для доказательства этого равенства воспользуемся основным свойством пропорции:
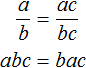
От перестановки мест сомножителей произведение не меняется. Поэтому в получившемся равенстве можно упорядочить правую часть по алфавиту:
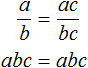
Поскольку равенство ![]() является пропорцией, а пропорция это равенство двух отношений, то дроби
является пропорцией, а пропорция это равенство двух отношений, то дроби ![]() и
и ![]() равны. Теорема доказана.
равны. Теорема доказана.
Теорема Виета
Французский математик Франсуа Виет выявил интересную взаимосвязь между коэффициентами приведённого квадратного уравнения и корнями этого же уравнения. Эта взаимосвязь представлена в виде теоремы и формулируется так:
Сумма корней приведённого квадратного уравнения x2 + bx + c = 0 равна второму коэффициенту, взятому с противоположным знáком, а произведение корней равно свободному члену.
То есть, если имеется приведённое квадратное уравнение x2 + bx + c = 0, а его корнями являются числа x1 и x2, то справедливы следующие два равенства:

Знак системы (фигурная скобка) говорит о том, что значения x1 и x2 удовлетворяют обоим равенствам.
Покажем теорему Виета на примере приведённого квадратного уравнения x2 + 4x + 3 = 0.
Мы пока не знаем какие корни имеет уравнение x2 + 4x + 3 = 0. Но по теореме Виета можно записать, что сумма этих корней равна второму коэффициенту 4, взятому с противоположным знáком. Если коэффициент 4 взять с противоположным знáком, то получим −4. Тогда:
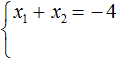
А произведение корней по теореме Виета будет равно свободному члену. В уравнении x2 + 4x + 3 = 0 свободным членом является 3. Тогда:
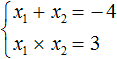
Теперь проверим действительно ли сумма корней равна −4, и равно ли произведение 3. Для этого найдём корни уравнения x2 + 4x + 3 = 0. А для удобства воспользуемся формулами для чётного второго коэффициента:
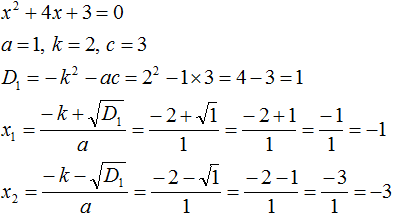
Корнями уравнения являются числа −1 и −3. По теореме Виета их сумма должна была равняться второму коэффициенту уравнения x2 + 4x + 3 = 0, взятому с противоположным знаком. Действительно, так оно и есть. Вторым коэффициентов в уравнении x2 + 4x + 3 = 0 является 4. Если взять его с противоположным знаком и приравнять сумму корней x1 + x2 к этому коэффициенту, то получается верное равенство:
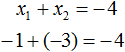
А произведение корней −1 и −3 по теореме Виета должно было равняться свободному члену уравнения x2 + 4x + 3 = 0, то есть числу 3. Видим, что это условие тоже выполняется:
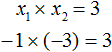
Значит выражение 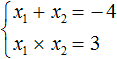 является справедливым.
является справедливым.
Рассмотрим квадратное уравнение x2 − 8x + 15 = 0. По теореме Виета сумма корней этого уравнения равна второму коэффициенту, взятому с противоположным знаком. Второй коэффициент равен −8. Если взять его с противоположным знаком, то получим 8. Тогда:
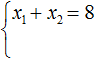
А произведение корней равно свободному члену. В уравнении x2 − 8x + 15 = 0 свободным членом является 15. Тогда:
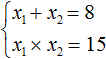
Теперь проверим действительно ли сумма корней равна 8, и равно ли произведение 15. Для этого найдём корни данного уравнения. А для удобства воспользуемся формулами для чётного второго коэффициента. В этот раз пропустим нéкоторые подробные записи:
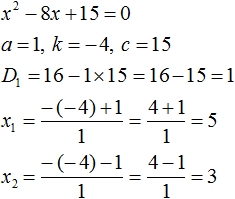
Видим, что корнями уравнения x2 − 8x + 15 = 0 являются числа 5 и 3. Их сумма равна 8. То есть сумма корней равна второму коэффициенту уравнения x2 − 8x + 15 = 0, взятому с противоположным знаком.
А произведение чисел 5 и 3 равно 15. То есть равно свободному члену уравнения x2 − 8x + 15 = 0.
Значит выражение 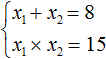 является справедливым.
является справедливым.
Замечание. Чтобы теорема Виета выполнялась, квадратное уравнение обязательно должно быть приведённым и иметь корни.
Например, рассмотрим квадратное уравнение x2 − 2x + 4 = 0. Напишем сумму и произведение корней этого уравнения:
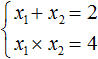
Но уравнение x2 − 2x + 4 = 0 не имеет корней, сумма которых равна 2, а произведение которых равно 4. Убедиться в этом можно, вычислив дискриминант:
D1 = k2 − ac = (−1)2 − 1 × 4 = −3
А значит записывать выражение 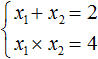 не имеет смысла.
не имеет смысла.
Теорема Виета полезна тем, что позволяет до начала решения узнать знаки корней уравнения.
Например, запишем для уравнения x2 − 5x + 6 = 0 сумму и произведение его корней. Сумма корней равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:
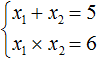
Посмотрев на эти два равенства можно сразу понять, что оба корня должны быть положительными. Потому что произведение x1 × x2 = 6 будет выполняться только в двух случаях: если значения x1 и x2 положительны либо они оба отрицательны. Если эти значения будут отрицательными, то не будет выполняться равенство x1 + x2 = 5, поскольку его правая часть равна положительному числу. А значения x1 и x2 должны удовлетворять как равенству x1 + x2 = 5, так и равенству x1 × x2 = 6.
Ещё одна польза от теоремы Виета в том, что корни можно найти методом подбора. В данном примере корни должны быть такими, чтобы они удовлетворяли как равенству x1 + x2 = 5 так и равенству x1 × x2 = 6. Очевидно, что таковыми являются корни 3 и 2
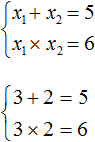
Значит, x1 = 3, x2 = 2
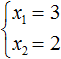
Доказательство теоремы Виета
Пусть дано приведённое квадратное уравнение x2 + bx + c = 0. Если его дискриминант больше нуля, то оно имеет два корня, сумма которых равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:

Докажем, что равенства x1 + x2 = −b и x1 × x2 = c имеют место быть.
Вспомним формулы корней квадратного уравнения:

Найдём сумму корней x1 и x2. Для этого подставим в выражение x1 + x2 вместо x1 и x2 соответствующие выражения из правой части формул корней квадратного уравнения. Не забываем, что в приведённом квадратном уравнении x2 + bx + c = 0 старший коэффициент a равен единице. Тогда в процессе подстановки знаменатель станет равен просто 2
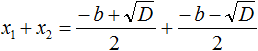
Запишем правую часть в виде дроби с одним знаменателем:
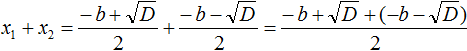
Раскроем скобки в числителе и приведём подобные члены:
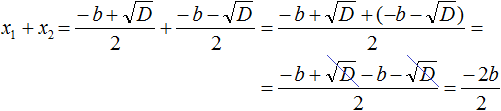
Сократим дробь ![]() на 2, тогда получим −b
на 2, тогда получим −b
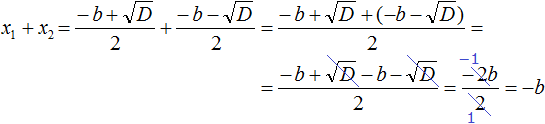
Значит x1 + x2 действительно равно −b
x1 + x2 = −b
Теперь аналогично докажем, что произведение x1 × x2 равно свободному члену c.
Подставим вместо x1 и x2 соответствующие выражения из формул корней квадратного уравнения. Не забываем, что коэффициент a всё ещё равен единице:
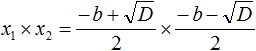
Чтобы перемнóжить дроби, нужно перемнóжить их числители и знаменатели:
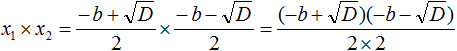
В числителе теперь содержится произведение суммы двух выражений и разности этих же выражений. Воспользуемся тождеством (a + b)(a − b) = a2 − b2. Тогда в числителе полýчится ![]() А знаменатель будет равен 4
А знаменатель будет равен 4
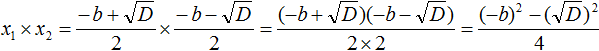
Теперь в числителе выражение (−b)2 станет равно b2, а выражение ![]() станет равно просто D
станет равно просто D
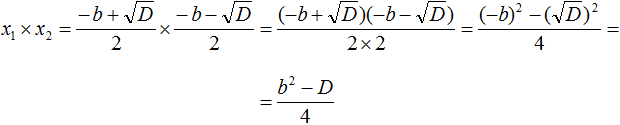
Но D равно b2 − 4ac. Подстáвим это выражение вместо D, не забывая что a = 1. То есть вместо b2 − 4ac надо подставить b2 − 4c
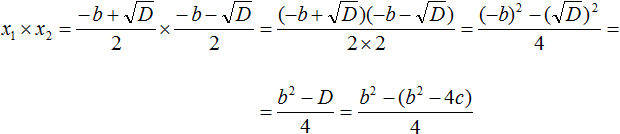
В получившемся выражении раскроем скобки в числителе и приведём подобные члены:
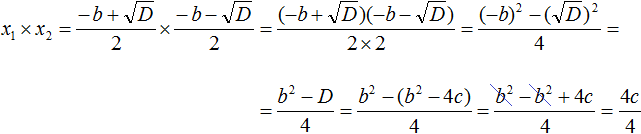
Сократим получившуюся дробь на 4
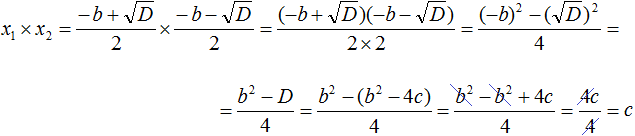
Значит x1 × x2 действительно равно c.
x1 × x2 = c
Таким образом, сумма корней приведённого квадратного уравнения x2 + bx + c = 0 равна второму коэффициенту, взятому с противоположным знáком (x1 + x2 = −b), а произведение корней равно свободному члену (x1 × x2 = c). Теорема доказана.
Теорема, обратная теореме Виета
Когда записана сумма и произведение корней приведённого квадратного уравнения, обычно начинается подбор подходящих корней к этому уравнению. В этот момент в работу включается так называемая теорема, обратная теореме Виета. Она формулируется так:
Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x2 + bx + c = 0, взятому с противоположным знáком, а произведение чисел x1 и x2 равно свободному члену уравнения x2 + bx + c = 0, то числа x1 и x2 являются корнями уравнения x2 + bx + c = 0.
Обратные теоремы бывают поставлены так, что их утверждением является заключение первой теоремы.
Так, доказывая теорему Виета мы пришли к заключению, что сумма x1 и x2 равна −b, а произведение x1 и x2 равно c. В обратной же теореме это заключение служит утверждением.
Ранее мы решили уравнение x2 − 5x + 6 = 0 и написали для него такую сумму и произведение корней:
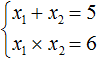
А затем подобрали корни 3 и 2. По сути мы применили теорему, обратную теореме Виета. Числа 3 и 2 таковы, что их сумма равна второму коэффициенту уравнения x2 − 5x + 6 = 0, взятому с противоположным знаком (числу 5), а произведение чисел 3 и 2 равно свободному члену (числу 6). Значит числа 3 и 2 являются корнями уравнения x2 − 5x + 6 = 0.
Пример 2. Решить квадратное уравнение x2 − 6x + 8 = 0 по теореме, обратной теореме Виета.
В данном уравнении a = 1. Значит квадратное уравнение является приведённым. Его можно решить по теореме, обратной теореме Виета.
Сначала запишем сумму и произведение корней уравнения. Сумма корней будет равна 6, поскольку второй коэффициент исходного уравнения равен −6. А произведение корней будет равно 8
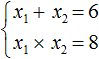
Теперь имея эти два равенства можно подобрать подходящие корни. Они должны удовлетворять как равенству x1 + x2 = 6, так и равенству x1 × x2 = 8
Подбор корней удобнее выполнять с помощью их произведения. Используя равенство x1 × x2 = 8 нужно найти такие x1 и x2, произведение которых равно 8.
Число 8 можно получить если перемножить числа 4 и 2 либо 1 и 8.
4 × 2 = 8
1 × 8 = 8
Но значения x1 и x2 надо подбирать так, чтобы они удовлетворяли не только равенству x1 × x2 = 8, но и равенству x1 + x2 = 6.
Сразу делаем вывод, что значения 1 и 8 не годятся, поскольку они хоть и удовлетворяют равенству x1 × x2 = 8, но не удовлетворяют равенству x1 + x2 = 6.
Зато значения 4 и 2 подходят как равенству x1 × x2 = 8, так и равенству x1 + x2 = 6, поскольку эти значения удовлетворяют обоим равенствам:
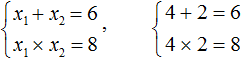
Значит корнями уравнения x2 − 6x + 8 = 0 являются числа 4 и 2.
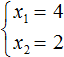
Обратная теорема, как и любая теорема нуждается в доказательстве. Докажем теорему, обратную теореме Виета. Для удобства корни x1 и x2 обозначим как m и n. Тогда утверждение теоремы, обратной теореме Виета примет следующий вид:
Если числа m и n таковы, что их сумма равна второму коэффициенту уравнения x2 + bx + c = 0, взятому с противоположным знáком, а произведение чисел m и n равно свободному члену уравнения x2 + bx + c = 0, то числа m и n являются корнями уравнения x2 + bx + c = 0
Для начала запишем, что сумма m и n равна −b, а произведение mn равно c
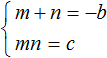
Чтобы доказать, что числа m и n являются корнями уравнения x2 + bx + c = 0, нужно поочередно подстáвить буквы m и n в это уравнение вместо x, затем выполнить возможные тождественные преобразования. Если в результате преобразований левая часть станет равна нулю, то это будет означать, что числа m и n являются корнями уравнения x2 + bx + c = 0.
Помимо букв m и n нам нужно знать чему равен параметр b. Выразим его из равенства m + n = −b. Легче всего это сделать, умножив обе части этого равенства на −1
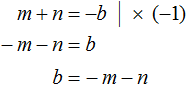
Теперь всё готово для подстановок. Подстáвим m в уравнение x2 + bx + c = 0 вместо x, а выражение −m − n подставим вместо b
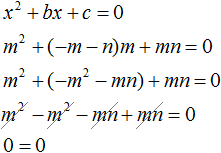
Видим, что при x = m получается верное равенство. Значит число m является корнем уравнения x2 + bx + c = 0.
Аналогично докажем, что число n является корнем уравнения x2 + bx + c = 0. Подставим вместо x букву n, а вместо c подставим mn, поскольку c = mn.
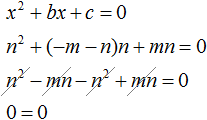
Видим, что при x = n тоже получается верное равенство. Значит число n является корнем уравнения.
Следовательно, числа m и n являются корнями уравнения x2 + bx + c = 0.
Примеры решения уравнений по теореме, обратной теореме Виета
Пример 1. Решить квадратное уравнение x2 − 4x + 4 = 0 по теореме, обратной теореме Виета.
Запишем сумму корней x1 и x2 и приравняем её к второму коэффициенту, взятому с противоположным знаком. Также запишем произведение корней x1 и x2 и приравняем его к свободному члену:
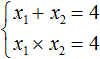
В данном примере очевидно, что корнями являются числа 2 и 2. Потому что их сумма равна 4 и произведение равно 4
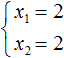
Значение x1 совпадает с x2. Это тот случай, когда квадратное уравнение имеет только один корень. Если мы попробуем решить данное уравнение с помощью формул корней квадратного уравнения, то обнаружим что дискриминант равен нулю, и корень вычисляется по формуле ![]()
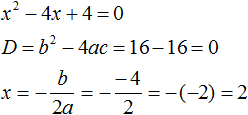
Данный пример показывает, что теорема обратная теореме Виета, работает и для уравнений, имеющих только один корень. Признаком того, что квадратное уравнение имеет только один корень является то, что значения x1 и x2 совпадают.
Пример 2. Решить уравнение x2 + 3x + 2 = 0 по теореме, обратной теореме Виета.
Запишем сумму и произведение корней данного уравнения:
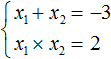
Теперь подберём значения x1 и x2. Здесь начинается самое интересное. Произведение корней равно 2. Число 2 можно получить перемножив 1 и 2. Но сумма корней x1 + x2 равна отрицательному числу −3. Значит значения 1 и 2 не подходят.
Сумма бывает отрицательной если оба слагаемых отрицательны либо отрицательным является одно слагаемое, модуль которого больше.
Если подберём корни с разными знаками, то не будет выполняться равенство x1 × x2 = 2.
Если подберем положительные корни, то будет выполняться равенство x1 × x2 = 2, но не будет выполняться равенство x1 + x2 = −3.
Очевидно, что корнями являются два отрицательных числа. Произведение отрицательных чисел есть положительное число. А сумма отрицательных чисел есть отрицательное число.
Тогда равенствам будут удовлетворять числа −1 и −2.
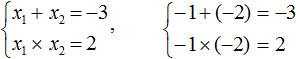
Итак, корнями являются числа −1 и −2
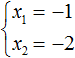
Пример 3. Решить уравнение x2 + 16x + 15 = 0 по теореме, обратной теореме Виета.
Запишем сумму и произведение корней данного уравнения:
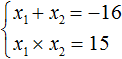
Как и в прошлом примере сумма корней равна отрицательному числу, а произведение корней — положительному числу.
Произведение бывает положительным если оба сомножителя положительны либо оба сомножителя отрицательны. Первый вариант отпадает сразу, поскольку сумма корней равна отрицательному числу. Тогда получается, что оба корня будут отрицательными. Попробуем подобрать их.
Число 15 можно получить, если перемножить числа −1 и −15 или (−3) и (−5). В данном случае подходит первый вариант, поскольку сумма чисел −1 и −15 равна −16, а их произведение равно 15. Значит корнями уравнения x2 + 16x + 15 = 0 являются числа −1 и −15
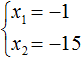
Пример 4. Решить уравнение x2 − 10x − 39 = 0 по теореме, обратной теореме Виета.
Запишем сумму и произведение корней данного уравнения:
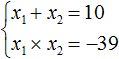
Произведение корней равно отрицательному числу. Значит один из корней является отрицательным. Число −39 можно получить если перемножить числа −3 и 13 либо −13 и 3. Из этих комбинаций больше годится комбинация −3 и 13, поскольку при перемножении этих чисел получается −39, а при сложении 10
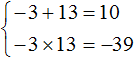
Значит корнями уравнения x2 − 10x − 39 = 0 являются числа −3 и 13
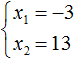
Пример 5. Первый корень уравнения x2 + bx + 45 = 0 равен 15. Найти второй корень этого уравнения, а также значение коэффициента b.
По теореме Виета произведение корней приведённого квадратного уравнения равно свободному члену. В данном случае это произведение равно 45
x1 × x2 = 45
При этом один из корней уже известен — это корень 15.
15 × x2 = 45
Тогда второй корень будет равен 3, потому что число 45 получается, если 15 умножить на 3
15 × 3 = 45
Значит x2 = 3
Этот второй корень также можно было бы получить, выразив из равенства 15 × x2 = 45 переменную x2
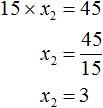
Теперь определим значение коэффициента b. Для этого напишем сумму корней уравнения:
15 + 3 = 18
По теореме Виета сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком. Если сумма корней равна 18, а 18 это положительное число, то в самóм уравнении этот коэффициент будет отрицательным:
x2 − 18x + 45 = 0
Значит b = −18.
Обычно решение к такой задаче записывают так. Сначала записывают основную теорему Виета в виде суммы и произведения корней:

Затем в это выражение подставляют имеющиеся известные значения. В нашем случае известно, что первый корень равен 15, а свободный член уравнения x2 + bx + 45 = 0 равен 45
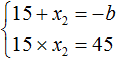
Из этой системы следует найти x2 и b. Выразим эти параметры:
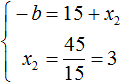
Из этой системы мы видим, что x2 равно 3. Подставим его в первое равенство:
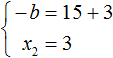
Теперь из первого равенства мы видим, что −b равно 18
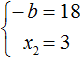
Но нас интересует b, а не −b. Следует помнить, что −b это −1b. Чтобы найти b нужно 18 разделить на −1. Тогда b станет равно −18
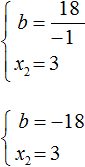
Этот же результат можно получить если в выражении 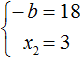 умножить первое равенство на −1
умножить первое равенство на −1
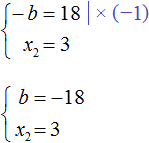
Теперь возвращаемся к исходному уравнению x2 + bx + 45 = 0 и подставляем найденное значение b
![]()
Выполним умножение −18 на x. Получим −18x
![]()
Раскроем скобки:
![]()
Пример 6. Используя теорему Виета, написать приведённое квадратное уравнение, корнями которых являются числа 2 и 8.
В этом задании корни уже известны. То есть x1 = 2, x2 = 8. По ним надо составить квадратное уравнение вида x2 + bx + c = 0.
Запишем сумму и произведение корней:
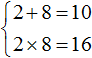
По теореме Виета сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком. Если сумма корней 2 и 8 равна 10, то в самóм уравнении число 10 должно быть с противоположным знаком. Значит b = −10.
Произведение корней по теореме Виета равно свободному члену. У нас это произведение равно 16.
Значит b = −10, c = 16. Отсюда:
x2 − 10x + 16 = 0
Пример 7. Используя теорему Виета, написать приведённое квадратное уравнение, корнями которых являются числа ![]() и
и ![]() .
.
Запишем сумму и произведение корней:
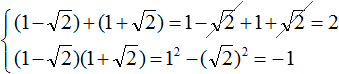
Сумма корней равна 2. Тогда в уравнении второй коэффициент будет равен −2. А произведение корней равно −1. Значит свободный член будет равен −1. Тогда:
x2 − 2x − 1 = 0
Когда квадратное уравнение неприведённое
Теорема Виета выполняется только тогда, когда квадратное уравнение является приведённым.
Если квадратное уравнение не является приведённым, но всё равно возникла необходимость применить теорему Виета, то обе части неприведённого квадратного уравнения следует разделить на коэффициент, который располагается перед x2.
Если к примеру в квадратном уравнении ax2 + bx + c = 0 коэффициент a не равен единице, то данное уравнение является неприведённым. Чтобы сделать его приведённым, надо разделить обе его части на коэффициент, который располагается перед x2, то есть на a
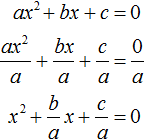
Получилось уравнение ![]() , которое является приведённым. В нём второй коэффициент равен
, которое является приведённым. В нём второй коэффициент равен ![]() , а свободный член равен
, а свободный член равен ![]() . Тогда сумма и произведение корней будут выглядеть так:
. Тогда сумма и произведение корней будут выглядеть так:

Например, решим квадратное уравнение 4x2 + 5x + 1 = 0. Это уравнение не является приведённым. Приведённым оно станет, если разделить обе его части на коэффициент, который располагается перед x2, то есть на 4
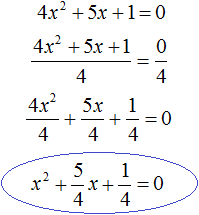
Получили приведённое квадратное уравнение. В нём второй коэффициент равен ![]() , а свободный член
, а свободный член ![]() . Тогда по теореме Виета имеем:
. Тогда по теореме Виета имеем:
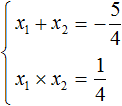
Отсюда методом подбора находим корни −1 и
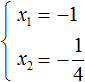
Возможно этот метод вы редко будете использовать при решении квадратных уравнений. Но знать о нём не помешает.
Пример 2. Решить квадратное уравнение 3x2 − 7x + 2 = 0
Данное уравнение не является приведённым, а значит его пока нельзя решить по теореме, обратной теореме Виета.
Сделаем данное уравнение приведенным. Разделим обе части на коэффициент, который располагается перед x2
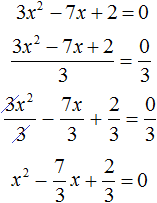
Получили уравнение ![]() . Запишем сумму и произведение корней этого уравнения:
. Запишем сумму и произведение корней этого уравнения:
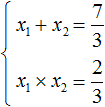
Отсюда методом подбора находим корни 2 и ![]()
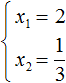
Пример 3. Решить квадратное уравнение 2x2 − 3x − 2 = 0
Это неприведённое квадратное уравнение. Чтобы сделать его приведённым, нужно разделить обе его части на 2. Сделать это можно в уме. Если 2x2 разделить на 2, то полýчится x2
![]()
Далее если −3x разделить на 2, то полýчится ![]() . Чтобы видеть где коэффициент, а где переменная, такое выражение записывают в виде
. Чтобы видеть где коэффициент, а где переменная, такое выражение записывают в виде ![]()
![]()
Далее если −2 разделить на 2, то полýчится −1
![]()
Прирáвниваем получившееся выражение к нулю:
![]()
Теперь применяем теорему Виета. Сумма корней будет равна второму коэффициенту, взятому с противоположным знáком, а произведение корней свободному члену:
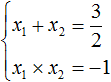
Отсюда методом подбора находим корни 2 и ![]()
Задания для самостоятельного решения
Задание 1. Написать сумму и произведение корней для квадратного уравнения:
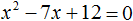
Решение:

Задание 2. Написать сумму и произведение корней для квадратного уравнения:

Решение:

Задание 3. Написать сумму и произведение корней для квадратного уравнения:

Решение:

Задание 4. Решить квадратное уравнение по теореме, обратной теореме Виета:

Решение:

Задание 5. Решить квадратное уравнение по теореме, обратной теореме Виета:

Решение:

Задание 6. Решить квадратное уравнение по теореме, обратной теореме Виета:

Решение:

Задание 7. Решить квадратное уравнение по теореме, обратной теореме Виета:

Решение:

Задание 8. Решить квадратное уравнение по теореме, обратной теореме Виета:

Решение:

Задание 9. Решить квадратное уравнение по теореме, обратной теореме Виета:

Решение:

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже












































