Как найти коэффициент квадратной функции

Алгоритм

нахождения 
значений коэффициентов a,
b,
c

 по
графику квадратичной функции

у=ax²
+bx+c.

Автор: Храмова Ирина Михайловна

МБОУ Луговская ООШ

Источники : алгебра 9 класс, Ю.Н.
Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под редакцией А.С.Теляковского,

 Москва «Просвещение», 2013г.

I.
Нахождение коэффициента a
:

1) по графику
параболы  определяем координаты вершины (m,
n)

2) по графику
параболы  определяем координаты любой точки  А(х₁;у₁)

3) подставляем эти
значения в формулу квадратичной функции, заданной в другом  виде:

y=a(х-m)²+n

4) решаем
полученное уравнение.

II.
Нахождение коэффициента b:

1) Сначала
находим значение коэффициента a(шаг
I,
смотри выше)

2) В
формулу для абсциссы параболы m=
–b/2a
подставляем значения m и
a

3) Находим
значение коэффициента b.

       III.
Нахождение коэффициента с:

1)    Находим
ординату у точки пересечения параболы с осью Оу, это значение равно
коэффициенту с, т.е. точка (0;с) – точка пересечения параболы с
осью Оу.

2)    Если
по графику невозможно найти точку пересечения с осью Оу, то выполняем шаги I,
II (находим
коэффициенты a,
b)

3)    Подставляем
найденные значения a,
b
, А(х_{1 ;}у₁) в  уравнение у=ax²
+bx+c            и находим с.

Предположим, вам попался график функции (y=ax^2+bx+c) и нужно по этому графику определить коэффициенты (a), (b) и (c). В этой статье я расскажу 3 простых способа сделать это.

1 способ – ищем коэффициенты на графике

Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью (y) – целые числа. Если это не так, советую использовать способ 2.

1. Коэффициент (a) можно найти с помощью следующих фактов:

   – Если (a>0), то ветви параболы направленных вверх, если (a<0), то ветви параболы направлены вниз.

   

   – Если (a>1), то график вытянут вверх в (a) раз по сравнению с «базовым» графиком (у которого (a=1)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.

   

   – Аналогично с (a<-1), только график вытянут вниз.

   

   – Если (a∈(0;1)), то график сжат в (a) раз (по сравнению с «базовым» графиком с (a=1)). Вершина при этом остается на месте.

   

   – Аналогично (a∈(-1;0)), только ветви направлены вниз.

   

2. Парабола пересекает ось y в точке (c).

   

3. (b) напрямую по графику не видно, но его можно посчитать с помощью (x_в) – абсциссы (икса) вершины параболы:

   (x_в=-frac{b}{2a})
   (b=-x_вcdot 2a)
   

Пример (ЕГЭ):

Решение:
Во-первых, надо разобраться, где тут (f(x)), а где (g(x)). По коэффициенту (c) видно, что (f(x)) это функция, которая лежит ниже – именно она пересекает ось игрек в точке (4).

Значит нужно найти коэффициенты у параболы, которая лежит повыше.
Коэффициент (c) у неё равен (1).
Ветви параболы направлены вниз – значит (a<0). При этом форма этой параболы стандартная, базовая, значит (a=-1).

Найдем (b). (x_в=-2), (a=-1).

(x_в=-frac{b}{2a})
(-2=-frac{b}{-2})
(b=-4)

Получается (g(x)=-x^2-4x+1). Теперь найдем в каких точках функции пересекаются:

(-x^2-4x+1=-2x^2-2x+4)
(-x^2-4x+1+2x^2+2x-4=0)
(x^2-2x-3=0)
(D=4+4cdot 3=16=4^2)
(x_1=frac{2-4}{2}=-1);    (x_2=frac{2+4}{2}=3).

Ответ: (3).

2 способ – находим формулу по точкам

Это самый надежный способ, потому что его можно применить практически в любой ситуации, но и самый не интересный, потому что думать тут особо не надо, только уметь решать системы линейных уравнений. Алгоритм прост:

1. Ищем 3 точки с целыми координатами, принадлежащие параболе.
   Пример:

   

2. Выписываем координаты этих точек и подставляем в формулу квадратичной функции: (y=ax^2+bx+c). Получится система с тремя уравнениями.

   Пример: (A(-4;5)), (B(-5;5)), (C(-6;3)).

   (begin{cases}5=a(-4)^2+b(-4)+c\5=a(-5)^2+b(-5)+c\3=a(-6)^2+b(-6)+c end{cases})

3. Решаем систему.
   Пример:

   (begin{cases}5=16a-4b+c\5=25a-5b+c\3=36a-6b+c end{cases})

   Вычтем из второго уравнения первое:

   (0=9a-b)
   (b=9a)

   Подставим (9a) вместо (b):

   (begin{cases}5=16a-36a+c\5=25a-45a+c\3=36a-54a+c end{cases})
   (begin{cases}5=-20a+c\5=-20a+c\3=-18a+c end{cases})

   Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки (A) и (B) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:

   (2=-2a)
   (a=-1)

   Найдем (b):

   (b=-9)

   Подставим в первое уравнение (a):

   (5=20+c)
   (c=-15).

   Получается квадратичная функция:   (y=-x^2-9x-15).

Пример (ЕГЭ):

Решение:

Сразу заметим, что по графику можно сразу определить, что (c=4). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: (C(-1;8)), (D(1;2)) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи). 

Таким образом имеем систему:

(begin{cases}8=a(-1)^2+b(-1)+4\2=a+b+4 end{cases})

(begin{cases}8=a-b+4\2=a+b+4 end{cases})

(begin{cases}4=a-b\-2=a+b end{cases})

Сложим 2 уравнения:

(2=2a)
(a=1)

Подставим во второе уравнение:

(-2=1+b)
(b=-3)

Получается:

(g(x)=x^2-3x+4)

Теперь найдем точки пересечения двух функций:

(-3x+13=x^2-3x+4)
(x^2-9=0)
(x=±3)

Теперь можно найти ординату второй точки пересечения:

(f(-3)=-3cdot (-3)+13)
(f(-3)=9+13)
(f(-3)=22)

Ответ:   (22).

3 способ – используем преобразование графиков функций

Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.

Главный недостаток этого способа – вершина должна иметь целые координаты.

Сам способ базируется на следующих идеях:

1. График (y=-x^2) симметричен относительно оси (x) графику (y=x^2).

   

2. – Если (a>1) график (y=ax^2) получается растяжением графика (y=x^2) вдоль оси (y) в (a) раз.
   – Если (a∈(0;1)) график (y=ax^2) получается сжатием графика (y=x^2) вдоль оси (y) в (a) раз.

   

3. – График (y=a(x+d)^2) получается сдвигом графика (y=ax^2) влево на (d) единиц.
   – График (y=a(x-d)^2) получается сдвигом графика (y=ax^2) вправо на (d) единиц. 

   

4. График (y=a(x+d)^2+e) получается переносом графика (y=a(x+d)^2) на (e) единиц вверх.
   График (y=a(x+d)^2-e) получается переносом графика (y=a(x+d)^2) на (e) единиц вниз.

   

У вас наверно остался вопрос – как этим пользоваться? Предположим, мы видим такую параболу:

Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому (a=1). То есть она получена перемещениями графика базовой параболы (y=x^2).

А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на (4).

То есть наша функция выглядит так: (y=(x-5)^2-4).
После раскрытия скобок и приведения подобных получаем искомую формулу:

(y=x^2-10x+25-4)
(y=x^2-10x+21)

Готово.

Пример (ЕГЭ):

Чтобы найти (f(6)), надо сначала узнать формулу функции (f(x)). Найдем её:

1. Парабола растянута на (2) и ветви направлены вниз, поэтому (a=-2). Иными словами, первоначальной, перемещаемой функцией является функция (y=-2x^2).

   

2. Парабола смещена на 2 клеточки вправо, поэтому (y=-2(x-2)^2).

3. Парабола поднята на 4 клеточки вверх, поэтому (y=-2(x-2)^2+4).

4. Получается (y=-2(x^2-4x+4)+4=)(-2x^2+8x-8+4=-2x^2+8x-4).

5. (f(6)=-2cdot 6^2+8cdot 6-4=-72+48-4=-28)

Смотрите также:
Как найти k и b по графику линейной функции?

Нахождение коэффициентов квадратичной функции y=ax² + bx +c

I Нахождение коэффициента а :

1. по графику параболы определяем координаты вершины (m,n)

2. по графику параболы определяем координаты любой точки A (x;y)

3. подставляем эти значения в формулу квадратичной функции, заданной в другом виде:

y=а(х-m)²+n

1. решаем полученное уравнение.

II. нахождение коэффициента b: b= – (х₁ + х₂) это для приведённого уравнения

1. Сначала находим значение коэффициента a (шаг I, смотри выше)

В формулу для абсциссы параболы m = 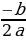подставляем значения m и а

1. Вычисляем значение коэффициента b.

III. нахождение коэффициента с: с = х₁ ∙ х₂ это для приведённого уравнения

1. Находим координату у точки пересечения графика параболы с осью Оу, это значение равно коэффициенту с, т.е. точка (0;C)-точка пересечения графика параболы с осью Оу.

2. Если по графику невозможно найти точку пересечения с осью Оу, то выполняем шаги I, II {находим коэффициенты а,Ь)

3. Подставляем найденные значения а, b ,А(х ; у) в уравнение у=ах² +bх+с и находим с.

I Нахождение коэффициента а :

1. по графику параболы определяем координаты вершины (m,n)

2. по графику параболы определяем координаты любой точки A (x;y)

3. подставляем эти значения в формулу квадратичной функции, заданной в другом виде:

y=а(х-m)²+n

1. решаем полученное уравнение.

II. нахождение коэффициента b:

1. Сначала находим значение коэффициента a (шаг I, смотри выше)

В формулу для абсциссы параболы m = 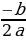подставляем значения m и а

1. Вычисляем значение коэффициента b.

III. нахождение коэффициента с:

1. Находим координату у точки пересечения графика параболы с осью Оу, это значение равно коэффициенту с, т.е. точка (0;C)-точка пересечения графика параболы с осью Оу.

2. Если по графику невозможно найти точку пересечения с осью Оу, то выполняем шаги I, II {находим коэффициенты а,b)

3. Подставляем найденные значения а, b ,А(х ; у) в уравнение у=ах² +bх+с и находим с.

Рассмотрим задачу: где невозможно по графику найти точно m и n необходимо найти все коэффициенты уравнения, задающего график:

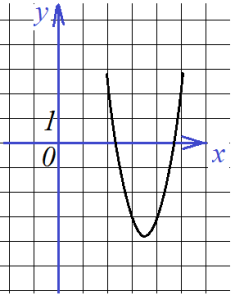
Найти все коэффициенты по графику функции

Подставляем в уравнение: координаты выбранных точек, например, таких: (2;2), (5;2), (4;-3). Получается:

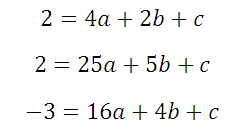
Последние два уравнения вычтем:

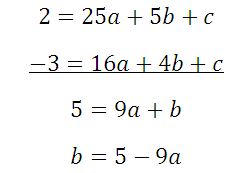
Данное выражение подставим в первое и второе уравнения:

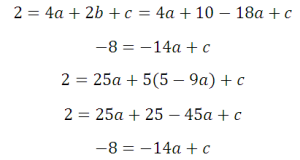
Вычтем два получившихся уравнения:

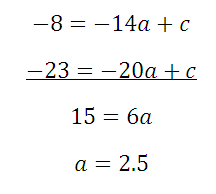Зная а, можем найти и остальные коэффициенты:

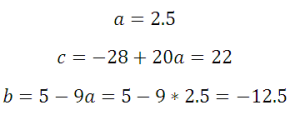
Следующая задача: найти коэффициенты уравнения, задающего график функции, изображенный на рисунке:

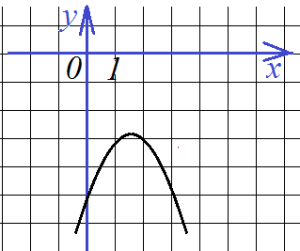
Найти все коэффициенты по графику функции

Здесь будет немного попроще, так как определить коэффициент с можно по рисунку: с=-5. Это значит, что потребуется только две точки, и система будет состоять только из двух уравнений. Возьмем для ее составления точки (1;-3) и (2;-3):

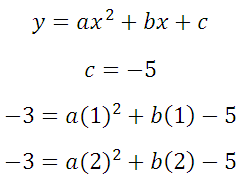
Вычтем получившиеся уравнения (второе – из первого) и определим коэффициенты а и b:

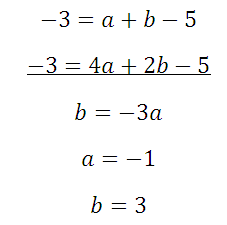
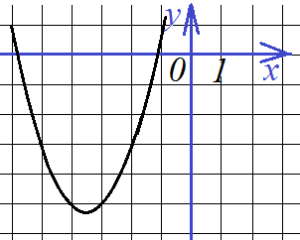
Найти все коэффициенты по графику функции

Наконец, еще одно такое же задание. Снова необходимо определить все коэффициенты функции, график которой представлен на рисунке:

Зададимся точками. Их будет три, уравнений тоже три, так как нам необходимо найти три коэффициента – a, b и c.

Точки будут: (-2; -3),(-5; -3) и  (-3; -5) . Тогда уравнения:

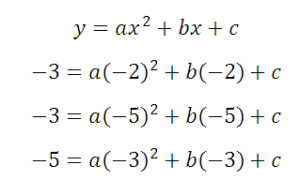
Из первого уравнения вычитаем второе:

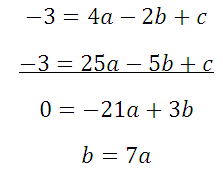
Полученное подставим в первое и третье:

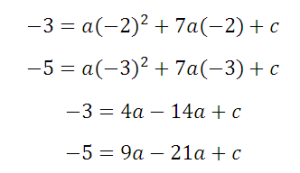
Полученные уравнения вычтем вновь, и найдем искомое:

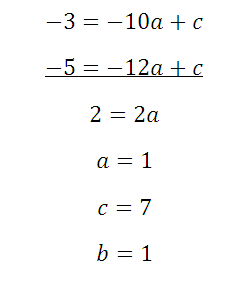
Квадратичная функция — подробнее

Квадратичная функция – это функция вида ( y=a{{x}^{2}}+bx+c), где ( ane 0), ( b) и ( c) ­– любые числа (они и называются коэффициентами). 

Число ( a) называют старшим или первым коэффициентом такой функции, ( b) – вторым коэффициентом, а ( c) – свободным членом.

Другими словами, квадратичная функция – это зависимость, содержащая аргумент в квадрате. Отсюда и ее название.

Как уже говорилось в теме «Функции», важнейшими понятиями, связанными с любой функцией, являются ее область определения ( Dleft( y right)) и область значений( Eleft( y right)).

Какими могут быть значения аргумента квадратичной функции ( y=a{{x}^{2}}+bx+c)? Правильно, любыми. Ведь в эту формулу можно подставить любое число (в отличии, например, от функции ( y=frac{1}{x}) – в нее нельзя подставить ( x=0)).

Значит, область определения – все действительные числа:

( Dleft( y right)=mathbb{R}) или ( Dleft( y right)=left( -infty ;+infty right)).

А теперь множество значений. Все ли значения может принимать функция?

Достаточно рассмотреть самую простую квадратичную функцию ( y={{x}^{2}}) ( left( a=1,text{ }b=0,text{ }c=0 right)~), чтобы убедиться в обратном: ведь какое бы число мы не возводили в квадрат, результат всегда будет больше или равен нулю.

Значит, эта функция всегда не меньше нуля.

А вот больше нуля она может быть сколько угодно: ведь бесконечно большой x в квадрате будет еще больше.

Таким образом, можем написать для ( y={{x}^{2}}:Eleft( y right)=left[ 0;+infty right)).

В каждом отдельном случае область значений будет разная, но всегда – ограниченная.

График квадратичной функции

Наверняка ты слышал, что график квадратичной функции называется параболой. Как она выглядит? Сейчас нарисуем

Кстати мы очень подробно разобрали как быстро и правильно рисовать параболу. Переходи по ссылке и всему научишься.

Начнем с простейшей квадратичной функции – ( y={{x}^{2}}).

Составим таблицу значений:

x	-2	-1	0	1	2
y	4	1	0	1	4

Нарисуем эти точки на координатной плоскости и соединим их плавной линией:

Именно так и выглядит парабола. Самая нижняя ее точка называется вершиной, а части спарва и слева от вершины называем ветвями параболы. Как видим, ветви симметричны относительно вертикали, проходящей через вершину.

Рассмотрим теперь другую функцию: ( y={{x}^{2}}-2{x}-3).

Составим таблицу значений:

x	-2	-1	0	1	2	3	4
y	5	0	-3	-4	-3	0	5

Сравним два рисунка.

Видно, что это как будто одна и та же парабола, просто расположенная в разных местах.

Во второй параболе вершина переместилась в точку ( left( 1;-4 right)), а ветви переехали вместе с ней.

Да, так оно и есть: все параболы с одинаковым старшим коэффициентом, a выглядят одинаково – даже при разных остальных коэффициентах.

Кстати, если хочешь научиться быстро и правильно рисовать график квадратичной функции, то переходи по ссылке, там отличная статья.

Коэффициенты квадратичной функции

Давай разберем, на что влияют коэффициенты квадратичной функции.
Начнем со старшего коэффициента.
Будем рассматривать функции вида ( y=a{{x}^{2}}) (( b=0), ( c=0) – пусть не мешают).

Построим на одном рисунке графики нескольких функций: при ( a= -2,text{ }-1,frac{1}{2},text{ }1,text{ }3:) 

Что ты видишь? Чем они отличаются? Какую закономерность можно заметить?

Во-первых, это невозможно не заметить, если ( displaystyle mathbf{a}<mathbf{0}), ветви парабол направлены вниз, а если ( displaystyle mathbf{a}>mathbf{0}) – вверх.

Так, хорошо.

Значит, если парабола пересекает ось ( displaystyle Ox) в двух точках, то у нас два корня квадратного уравнения.

Если не пересекает – корней нет.

Но бывает ведь, что дискриминант уравнения равен нулю, и тогда только один корень. В этом случае парабола касается оси ( displaystyle Ox) вершиной:

А что такое вершина параболы?

Решения

1. Первое: куда «смотрят» ветви параболы? Вниз. А что это значит? Правильно, ( displaystyle a<0). То есть вариант b) сразу не подходит.

Дальше посмотрим на точку пересечения с осью ( displaystyle Oy:y=4). Что нам дает эта точка? Вспоминай.

Это – свободный член c. Значит, ( displaystyle c=4) – отбросим вариант a).

Ну что же, ( displaystyle a=-1,c=4,) осталось определить b. Тут нам поможет вершина. Напоминаю, что ее координата вычисляется по формуле: ( displaystyle {{x}_{в}}=frac{-b}{2a}).

В нашем случае ( displaystyle {{x}_{в}}=1). Тогда:

( displaystyle 1=frac{-b}{2cdot left( -1 right)}text{ }Rightarrow text{ }b=2).

Итак, наша парабола задается формулой: ( displaystyle y=-{{x}^{2}}+2x+4). Это вариант ответа d)

2. Проще простого: корни – это точки пересечения параболы с осью ( displaystyle Ox).

Смотрим: ( displaystyle {{x}_{1}}=1), ( displaystyle {{x}_{2}}=5). Значит, их сумма ( displaystyle {{x}_{1}}+{{x}_{2}}=6).

3. То же самое: ( displaystyle {{x}_{1}}=-1), ( displaystyle {{x}_{2}}=5). Произведение: ( displaystyle {{x}_{1}}cdot {{x}_{2}}=-5).

4. Хм… Ну, коэффициент с мы бы нашли, да только по оси ( displaystyle Oy) нет обозначений. Зато показаны точки пересечения с осью ( displaystyle Ox). А это ведь корни уравнения ( displaystyle {{x}^{2}}+bx+c=0:{{x}_{1}}=-1,{{x}_{2}}=4).

Как это нам поможет?

Кстати, чему равен старший коэффициент?

Он равен ( displaystyle 1). Как называется такое квадратное уравнение? Вспоминай: оно называется приведенным. Теперь догадался? Можно ведь применить теорему Виета. Точно! Ведь она говорит нам, что сумма корней равна второму коэффициенту с обратным знаком:

( displaystyle {{x}_{1}}+{{x}_{2}}=-b),

а произведение – свободному члену:

( displaystyle {{x}_{1}}cdot {{x}_{2}}=c).

Ну вот и решили: ( displaystyle b=-left( -1+4 right)=-3), ( displaystyle c=-1cdot 4=-4).

Ответ: ( displaystyle -3;text{ -}4.)

Алгоритм

нахождения  значения коэффициентов a,b,c

 по графику квадратичной функции

у=ax2 +bx+c.

Автор: Давыдова  Галина Анатольевна

МКОУ «Кукуйская ООШ №25»

Источники : алгебра 9 класс, под редакцией А.С.Теляковского,

 Москва «Просвещение», 2011г.

I.Нахождение коэффициента a :

1) по графику параболы  определяем координаты вершины (m,n)

2) по графику параболы  определяем координаты любой точки А (х1;у1)

3) подставляем эти значения в формулу квадратичной функции, заданной в другом  виде:

У=a(х-m)2+n  

4) решаем полученное уравнение.

II. нахождение коэффициента b:

1. Сначала находим значение коэффициента a(шаг I, смотри выше)
2. В формулу для абсциссы параболы m= -b/2a подставляем значения m и a
3. Вычисляем значение коэффициента b.

       III. нахождение коэффициента с:

1. Находим координату у точки пересечения графика параболы с осью Оу, это значение равно коэффициенту с, т.е. точка (0;с)-точка пересечения графика параболы с осью Оу.
2. Если по графику невозможно найти точку пересечения с осью Оу, то выполняем шаги I, II(находим коэффициенты a,b)
3. Подставляем найденные значения a, b ,А(х1 ;у1) в  уравнение у=ax2 +bx+c и находим с.