Таблица значений функции Лапласа
В таблице даны значения функции
для положительных значений
и для
;
для
пользуются той же таблицей, так как функция
нечетна, то есть
.
В таблице приведены значения интеграла лишь до
,
так как для
можно принять
.
Эту функцию называют функцией Лапласа.
Таблица значений функции Лапласа в теории вероятностей и математической статистике используется довольно часто. На сайте можно посмотреть примеры ее использования в следующих задачах:
-
Отклонение относительной частоты от постоянной вероятности в независимых испытаниях
-
Интегральная теорема Муавра – Лапласа
-
Доверительные интервалы для среднего и дисперсии
-
Проверка гипотезы о равенстве средних
Цветом в таблице подсвечены аргументы функции Лапласа, рядом, в соседнем столбце – значения функции Лапласа.
| x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) |
| 0,00 | 0,0000 | 0,32 | 0,1255 | 0,64 | 0,2389 | 0,96 | 0,3315 |
| 0,01 | 0,0040 | 0,33 | 0,1293 | 0,65 | 0,2422 | 0,97 | 0,3340 |
| 0,02 | 0,0080 | 0,34 | 0,1331 | 0,66 | 0,2454 | 0,98 | 0,3365 |
| 0,03 | 0,0120 | 0,35 | 0,1368 | 0,67 | 0,2486 | 0,99 | 0,3389 |
| 0,04 | 0,0160 | 0,36 | 0,1406 | 0,68 | 0,2517 | 1,00 | 0,3413 |
| 0,05 | 0,0199 | 0,37 | 0,1443 | 0,69 | 0,2549 | 1,01 | 0,3438 |
| 0,06 | 0,0239 | 0,38 | 0,1480 | 0,70 | 0,2580 | 1,02 | 0,3461 |
| 0,07 | 0,0279 | 0,39 | 0,1517 | 0,71 | 0,2611 | 1,03 | 0,3485 |
| 0,08 | 0,0319 | 0,40 | 0,1554 | 0,72 | 0,2642 | 1,04 | 0,3508 |
| 0,09 | 0,0359 | 0,41 | 0,1591 | 0,73 | 0,2673 | 1,05 | 0,3531 |
| 0,10 | 0,0398 | 0,42 | 0,1628 | 0,74 | 0,2703 | 1,06 | 0,3554 |
| 0,11 | 0,0438 | 0,43 | 0,1664 | 0,75 | 0,2734 | 1,07 | 0,3577 |
| 0,12 | 0,0478 | 0,44 | 0,1700 | 0,76 | 0,2764 | 1,08 | 0,3599 |
| 0,13 | 0,0517 | 0,45 | 0,1736 | 0,77 | 0,2794 | 1,09 | 0,3621 |
| 0,14 | 0,0557 | 0,46 | 0,1772 | 0,78 | 0,2823 | 1,10 | 0,3643 |
| 0,15 | 0,0596 | 0,47 | 0,1808 | 0,79 | 0,2852 | 1,11 | 0,3665 |
| 0,16 | 0,0636 | 0,48 | 0,1844 | 0,80 | 0,2881 | 1,12 | 0,3686 |
| 0,17 | 0,0675 | 0,49 | 0,1879 | 0,81 | 0,2910 | 1,13 | 0,3708 |
| 0,18 | 0,0714 | 0,50 | 0,1915 | 0,82 | 0,2939 | 1,14 | 0,3729 |
| 0,19 | 0,0753 | 0,51 | 0,1950 | 0,83 | 0,2967 | 1,15 | 0,3749 |
| 0,20 | 0,0793 | 0,52 | 0,1985 | 0,84 | 0,2995 | 1,16 | 0,3770 |
| 0,21 | 0,0832 | 0,53 | 0,2019 | 0,85 | 0,3023 | 1,17 | 0,3790 |
| 0,22 | 0,0871 | 0,54 | 0,2054 | 0,86 | 0,3051 | 1,18 | 0,3810 |
| 0,23 | 0,0910 | 0,55 | 0,2088 | 0,87 | 0,3078 | 1,19 | 0,3830 |
| 0,24 | 0,0948 | 0,56 | 0,2123 | 0,88 | 0,3106 | 1,20 | 0,3849 |
| 0,25 | 0,0987 | 0,57 | 0,2157 | 0,89 | 0,3133 | 1,21 | 0,3869 |
| 0,26 | 0,1026 | 0,58 | 0,2190 | 0,90 | 0,3159 | 1,22 | 0,3883 |
| 0,27 | 0,1064 | 0,59 | 0,2224 | 0,91 | 0,3186 | 1,23 | 0,3907 |
| 0,28 | 0,1103 | 0,60 | 0,2257 | 0,92 | 0,3212 | 1,24 | 0,3925 |
| 0,29 | 0,1141 | 0,61 | 0,2291 | 0,93 | 0,3238 | 1,25 | 0,3944 |
| 0,30 | 0,1179 | 0,62 | 0,2324 | 0,94 | 0,3264 | ||
| 0,31 | 0,1217 | 0,63 | 0,2357 | 0,95 | 0,3289 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Продолжение таблицы
| x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) |
| 1,26 | 0,3962 | 1,59 | 0,4441 | 1,92 | 0,4726 | 2,50 | 0,4938 |
| 1,27 | 0,3980 | 1,60 | 0,4452 | 1,93 | 0,4732 | 2,52 | 0,4941 |
| 1,28 | 0,3997 | 1,61 | 0,4463 | 1,94 | 0,4738 | 2,54 | 0,4945 |
| 1,29 | 0,4015 | 1,62 | 0,4474 | 1,95 | 0,4744 | 2,56 | 0,4948 |
| 1,30 | 0,4032 | 1,63 | 0,4484 | 1,96 | 0,4750 | 2,58 | 0,4951 |
| 1,31 | 0,4049 | 1,64 | 0,4495 | 1,97 | 0,4756 | 2,60 | 0,4953 |
| 1,32 | 0,4066 | 1,65 | 0,4505 | 1,98 | 0,4761 | 2,62 | 0,4956 |
| 1,33 | 0,4082 | 1,66 | 0,4515 | 1,99 | 0,4767 | 2,64 | 0,4959 |
| 1,34 | 0,4099 | 1,67 | 0,4525 | 2,00 | 0,4772 | 2,66 | 0,4961 |
| 1,35 | 0,4115 | 1,68 | 0,4535 | 2,02 | 0,4783 | 2,68 | 0,4963 |
| 1,36 | 0,4131 | 1,69 | 0,4545 | 2,04 | 0,4793 | 2,70 | 0,4965 |
| 1,37 | 0,4147 | 1,70 | 0,4554 | 2,06 | 0,4803 | 2,72 | 0,4967 |
| 1,38 | 0,4162 | 1,71 | 0,4564 | 2,08 | 0,4812 | -2,74 | 0,4969 |
| 1,39 | 0,4177 | 1,72 | 0,4573 | 2,10 | 0,4821 | 2,76 | 0,4971 |
| 1,40 | 0,4192 | 1,73 | 0,4582 | 2,12 | 0,4830 | 2,78 | 0,4973 |
| 1,41 | 0,4207 | 1,74 | 0,4591 | 2,14 | 0,4838 | 2,80 | 0,4974 |
| 1,42 | 0,4222 | 1,75 | 0,4599 | 2,16 | 0,4846 | 2,82 | 0,4976 |
| 1,43 | 0,4236 | 1,76 | 0,4608 | 2,18 | 0,4854 | 2,84 | 0,4977 |
| 1,44 | 0,4251 | 1,77 | 0,4616 | 2,20 | 0,4861 | 2,86 | 0,4979 |
| 1,45 | 0,4265 | 1,78 | 0,4625 | 2,22 | 0,4868 | 2,88 | 0,4980 |
| 1,46 | 0,4279 | 1,79 | 0,4633 | 2,24 | 0,4875 | 2,90 | 0,4981 |
| 1,47 | 0,4292 | 1,80 | 0,4641 | 2,26 | 0,4881 | 2,92 | 0,4982 |
| 1,48 | 0,4306 | 1,81 | 0,4649 | 2,28 | 0,4887 | 2,94 | 0,4984 |
| 1,49 | 0,4319 | 1,82 | 0,4656 | 2,30 | 0,4893 | 2,96 | 0,4985 |
| 1,50 | 0,4332 | 1,83 | 0,4664 | 2,32 | 0,4898 | 2,98 | 0,4986 |
| 1,51 | 0,4345 | 1,84 | 0,4671 | 2,34 | 0,4904 | 3,00 | 0,49865 |
| 1,52 | 0,4357 | 1,85 | 0,4678 | 2,36 | 0,4909 | 3,20 | 0,49931 |
| 1,53 | 0,4370 | 1,86 | 0,4686 | 2,38 | 0,4913 | 3,40 | 0,49966 |
| 1,54 | 0,4382 | 1,87 | 0,4693 | 2,40 | 0,4918 | 3,60 | 0,499841 |
| 1,55 | 0,4394 | 1,88 | 0,4699 | 2,42 | 0,4922 | 3,80 | 0,499928 |
| 1,56 | 0,4406 | 1,89 | 0,4706 | 2,44 | 0,4927 | 4,00 | 0,499968 |
| 1,57 | 0,4418 | 1,90 | 0,4713 | 2,46 | 0,4931 | 4,50 | 0,499997 |
| 1,58 | 0,4429 | 1,91 | 0,4719 | 2,48 | 0,4934 | 5,00 | 0,499997 |
Пример решения задачи
Задача
Вероятность того, что
желание, загаданное на Новый год, сбудется, равна 0,7. Найти вероятность того,
что из 100 загаданных желаний сбудется от 60 до 85 желаний.
Решение
Вероятность того, что
событие
появится в
независимых
испытаниях от
до
раз:
В нашем случае
По таблице функции
Лапласа:
Искомая вероятность:
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 7 октября 2022 года; проверки требуют 4 правки.
| Распределение Лапласа | |
|---|---|
 Плотность вероятности Плотность вероятности |
|
 Функция распределения Функция распределения |
|
| Параметры |
 — коэффициент масштаба — коэффициент масштаба — коэффициент сдвига — коэффициент сдвига |
| Носитель |
 |
| Плотность вероятности |
 |
| Функция распределения |
 |
| Математическое ожидание |
 |
| Медиана |
 |
| Мода |
 |
| Дисперсия |
 |
| Коэффициент асимметрии |
 |
| Коэффициент эксцесса |
 |
| Дифференциальная энтропия |
 |
| Производящая функция моментов | ? |
| Характеристическая функция |
 |
Распределе́ние Лапла́са (двойно́е экспоненциа́льное) — в теории вероятностей это непрерывное распределение случайной величины, при котором плотность вероятности есть
где 

Функция распределения[править | править код]
По определению, функция распределения — это интеграл от плотности распределения:
Для интегрирования необходимо рассмотреть два случая:
Проверка свойств полученной функции:
не убывает, так как
положительна.
, следовательно,
непрерывна в точке
ограничена.
- Пределы на бесконечностях:
Математическое ожидание и дисперсия[править | править код]
В показателе экспоненты функции плотности содержится модуль разности, поэтому интервал 




Моменты[править | править код]
,
где 
детали расчёта

Применяя формулу интегрирования по частям несколько раз, получаем:


После подстановок пределов интегрирования:


Так как первый интеграл зависит от чётности k рассматриваются два случая: k — чётное и k — нечётное:

Или, в общем виде:


Характеристическая функция[править | править код]
детали расчёта

Оба интеграла находятся, используя формулу Эйлера 




Окончательно характеристическая функция есть:

Применение [править | править код]
Распределение применяется для моделирования обработки сигналов, в моделировании биологических процессов, экономике и финансах. Распределение можно применить:
- к кредитным рискам;
- к страховым случаям;
- при работе с фильтром Кальмана.
Содержание:
- Объяснение
- Таблица значений функции Лапласа
Таблица значений функции Лапласа – это вероятность того, что случайная величина примет значение,
принадлежащее заданному интервалу. При решении задач по
теории вероятности, как правило, требуется найти значение функции Лапласа по известному значению аргумента
или, наоборот, по известному значению функции Лапласа требуется найти значение аргумента. Для этого пользуются
таблицей значений функции Лапласа.
Таблица значений функции Лапласа незаменима при изучении теории вероятности, так как
решать интеграл (функцию Лапласа) сложно, а запомнить таблицу значений функции Лапласа просто невозможно.
Функцию Лапласа и данную таблицу чаще всего изучают на втором курсе университета, при изучении
математики и теории вероятности, если Вам в данной теме,
что-то не понятно, то Вы всегда можете задать вопрос на нашем
форуме, мы будем рады вам помочь. Пользуйтесь нашим сайтом и таблицей на здоровье.
Функция Лапласа
$$F(t)=frac{2}{sqrt{2 pi}} int_{0}^{t} e^{-frac{t^{2}}{2}} d t=frac{1}{sqrt{2 pi}} int_{-t}^{+infty} e^{-frac{t^{2}}{2}} d t$$
При разных значениях t; F(–t) = –F(t) (функция нормального распределения).
Таблица значений функции Лапласа
|
|
|
|

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Значения функции Лапласа
|
|
|
||||||
|
0,0 |
0,0000 |
1,0 |
0,3413 |
2,0 |
0,4772 |
3,0 |
0,4986 |
|
0,1 |
0398 |
1,1 |
3643 |
2,1 |
4821 |
3,5 |
4998 |
|
0,2 |
0793 |
1,2 |
3849 |
2,2 |
4861 |
4,0 |
4999 |
|
0,3 |
1179 |
1,3 |
4032 |
2,3 |
4893 |
|
0,5 |
|
0,4 |
1554 |
1,4 |
4192 |
2,4 |
4918 |
||
|
0,5 |
1915 |
1,5 |
4332 |
2,5 |
4938 |
||
|
0,6 |
2257 |
1,6 |
4452 |
2,6 |
4953 |
||
|
0,7 |
2580 |
1,7 |
4554 |
2,7 |
4965 |
||
|
0,8 |
2881 |
1,8 |
4641 |
2,8 |
4974 |
||
|
0,9 |
3159 |
1,9 |
4713 |
2,9 |
4981 |
В
интервале

погрешность находится с вероятностью
≈ 0,95 (0,4772·2), в интервале
—
с вероятностью 0,9973, т.е. вероятность
того, что случайная погрешность не
выйдет за пределы
,
составляет 0,9973, или 99,73 %. На практике с
учетом интервала
часто указывают предельную погрешность
для некоторых средств измерений. В ряде
случаев для средства измерения указывают
среднее квадратическое отклонение
случайной погрешности, а доверительную
вероятность выбирают в зависимости
от конкретных условий.
В
производственной практике часто
считается необходимым выполнение
следующего условия: допустимое предельное
отклонение от заданного номинального
размера должно быть не меньше
интервала
.
В этом случае в среднем только одно из
370 изделий будет бракованным.
Область
технологического рассеивания какого-либо
размера (параметра) изделия, как
правило, подчиняется нормальному
закону, и периодически определяемое
среднее квадратическое отклонение
является показателем изменений в
технологическом цикле.
3.4. Обработка результатов измерений, содержащих случайные погрешности
На
практике приходится довольствоваться
ограниченным числом измерений для
того, чтобы оценить истинное значение
измеряемой величины и точность измерения.
Если число измерений велико (более
100), то кривую распределения можно
построить достаточно точно, и если она
соответствует нормальному закону, то
графически определяется математическое
ожидание
и
среднее квадратическое отклонение
.
Результаты
измерений

делят на 10…20 интервалов

и записывают в виде статистического
ряда
|
|
|
… |
|
|
|
|
|
|
… |
|
|
|
|
|
… |
|
Примечание:
—
число результатов в интервале;
—
вычисленная
вероятность попадания в данный
интервал.
При
этом
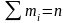
;
.
Статистический
ряд служит основой для построения
гистограммы и статистической функции
распределения (рис. 3.5). При

гистограмма переходит в плавную кривую.
Соответствие
полученной кривой закону нормального
распределения проверяют по критериям
Пирсона или Холмогорова.
Если
измерений меньше 15, то принадлежность
экспериментального распределения
к нормальному не проверяется.
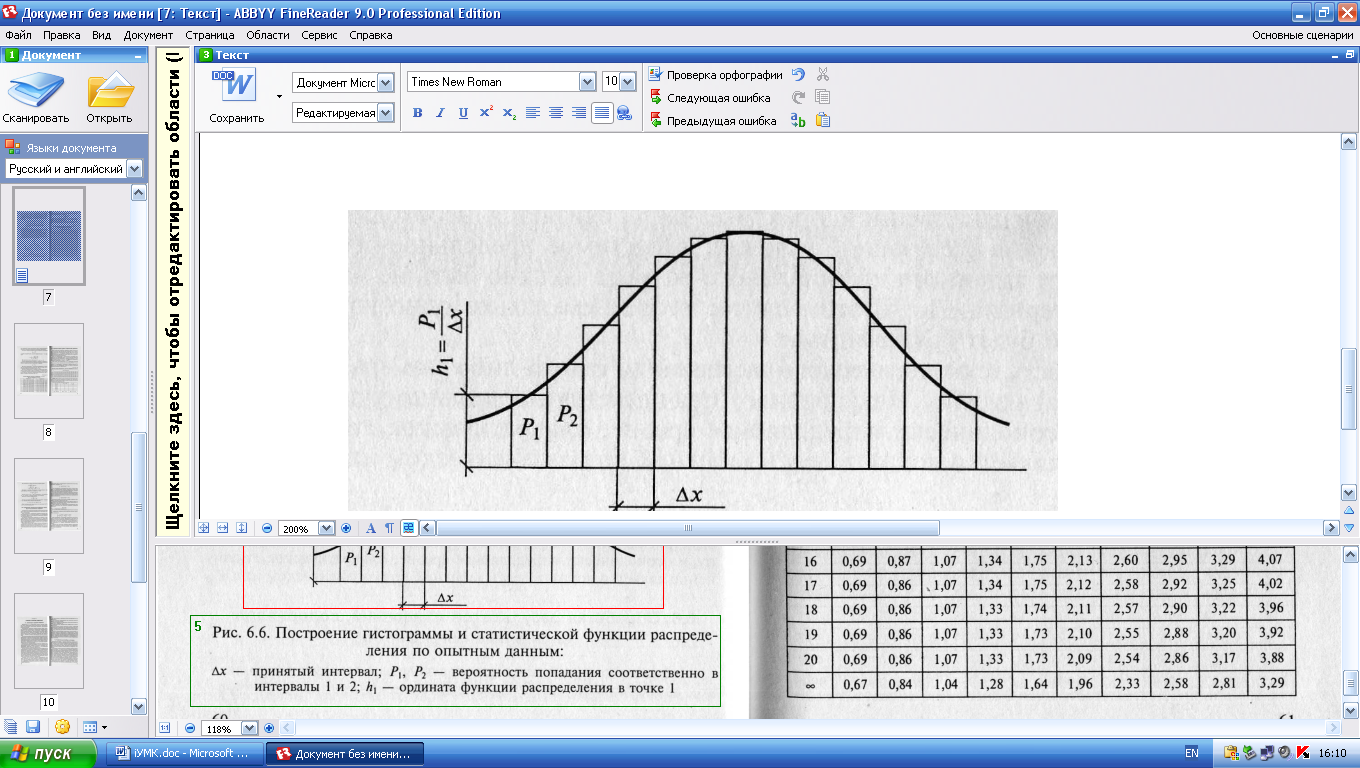
Рис.
3.5. Построение гистограммы и статистической
функции распределения по опытным
данным:
—
принятый интервал;
—
вероятность попадания соответственно
в интервалы 1 и 2;

—
ордината функции распределения в точке
1
При
обработке результатов ограниченного
числа наблюдений в качестве оценки
математического ожидания принимается
среднее арифметическое результатов
наблюдений:
|
|
(3.10) |
Приближенное
значение среднего квадратического
отклонения в
этом
случае вычисляется по формуле:
|
|
(3.11) |
Появление
в знаменателе выражения

вместо
п
связано
с заменой математического ожидания
средним арифметическим незначительного
числа наблюдений.
Среднее
арифметическое отличается от
математического ожидания на величину
случайной погрешности (погрешности
среднего значения), которая подчиняется
тому же закону распределения, что и
погрешности результатов отдельных
наблюдений.
Дисперсия
среднего арифметического вычисляется
по формуле:
|
|
(3.12) |
а
среднее квадратическое среднего
арифметического — по формуле:
|
|
(3.13) |
При
увеличении числа наблюдений

и

.
Границы
доверительного интервала, в котором с
заданной вероятностью (обеспеченностью)
находится случайная погрешность
среднего арифметического, определяют
по формуле:
|
|
(3.14) |
При
числе наблюдений

значения
коэффициента определяют по таблицам
функции Лапласа (см. табл. 3.1), а при

-по
таблицам функции Стьюдента (табл. 3.2,
3.3).
Зная
число наблюдений

и
задавшись доверительной вероятностью

,
можно
найти по табл. 3.2 значение
и, умножив его на

,
определить
границы доверительного интервала. В
тех случаях, когда требуется определить
доверительную вероятность при заданном
,
удобнее пользоваться табл. 3.3.
Таблица
3.2.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Загрузить PDF
Загрузить PDF
Преобразование Лапласа представляет собой интегральное преобразование, которое используют для решения дифференциальных уравнений с постоянными коэффициентами. Это преобразование широко используется в физике и инженерном деле.
Хотя можно использовать соответствующие таблицы, полезно понимать преобразование Лапласа, чтобы при необходимости вы могли провести его самостоятельно.
Предварительные сведения
- Пусть дана функция
, определенная для
Тогда преобразованием Лапласа функции
является следующая функция каждого значения
, при котором интеграл сходится:
- Преобразование Лапласа переводит функцию из t-области (временно́й шкалы) в s-область (область преобразования), где
представляет собой комплексную функцию комплексной переменной. Оно позволяет перевести функцию в ту область, где можно легче найти решение.
- Очевидно, что преобразование Лапласа является линейным оператором, поэтому если мы имеем дело с суммой слагаемых, каждый интеграл можно вычислить отдельно.
- Помните, что преобразование Лапласа работает лишь в тех случаях, если интеграл сходится. Если функция
имеет разрывы, необходимо быть внимательным и правильно расставить пределы интегрирования, чтобы избежать неопределенности.
-
1
-
2
Оцените интеграл с помощью доступных методов. В нашем примере оценка очень проста и можно обойтись простыми вычислениями. В более сложных случаях могут понадобиться более сложные методы, например интегрирование по частям или дифференцирование под знаком интеграла. Ограничивающее условие
означает, что интеграл сходится, то есть его значение стремится к 0 при
-
3
Рассмотрим преобразование Лапласа степенной функции. Для начала следует определить преобразование степенной функции, поскольку свойство линейности позволяет найти преобразование для всех полиномов. Степенной является функция вида
где
— любое положительное целое число. Можно проинтегрировать по частям, чтобы определить рекурсивное правило.
Реклама
-
1
Найдем преобразование Лапласа функции, умноженной на
. Полученные в предыдущем разделе результаты позволили нам выяснить некоторые интересные свойства преобразования Лапласа. Преобразование Лапласа таких функций, как косинус, синус и экспоненциальная функция, кажется более простым, чем преобразование степенной функции. Умножение на
в t-области соответствует сдвигу в s-области:
-
2
Найдем преобразование Лапласа функции, умноженной на
. Сначала рассмотрим умножение на
. Согласно определению, можно продифференцировать функцию под интегралом и получить удивительно простой результат:
-
3
Найдем преобразование Лапласа функции
. Это можно легко сделать с помощью замены переменной на u, используя определение преобразования:
-
4
Найдем преобразование Лапласа производной
. В отличие от предыдущих примеров, в данном случае придется интегрировать по частям:
Реклама
-
1
-
2
Выполните преобразование Лапласа для натурального логарифма. В этом случае интеграл нельзя выразить в виде элементарных функций. Использование гамма-функции и ее разложения в ряд позволяет оценить натуральный логарифм и его степени. Наличие постоянной Эйлера-Маскерони
показывает, что для оценки данного интеграла необходимо использовать разложение в ряд.
-
3
Рассмотрим преобразование Лапласа ненормированной функции sinc. Функция
широко используется для обработки сигналов, в дифференциальных уравнениях она эквивалентна сферической функции Бесселя первого рода и нулевого порядка
Преобразование Лапласа этой функции также невозможно вычислить стандартными методами. В данном случае проводят преобразование отдельных членов ряда, которые представляют собой степенные функции, поэтому их преобразования обязательно сходятся на заданном интервале.
Реклама
Об этой статье
Эту страницу просматривали 12 965 раз.


















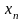














![int _{{0}}^{{infty }}[af(t)+bg(t)]e^{{-st}}{mathrm {d}}t=aint _{{0}}^{{infty }}f(t)e^{{-st}}{mathrm {d}}t+bint _{{0}}^{{infty }}g(t)e^{{-st}}{mathrm {d}}t](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1c8d8faf0a1a517eea7410aa6235a3e4883c4f3)


