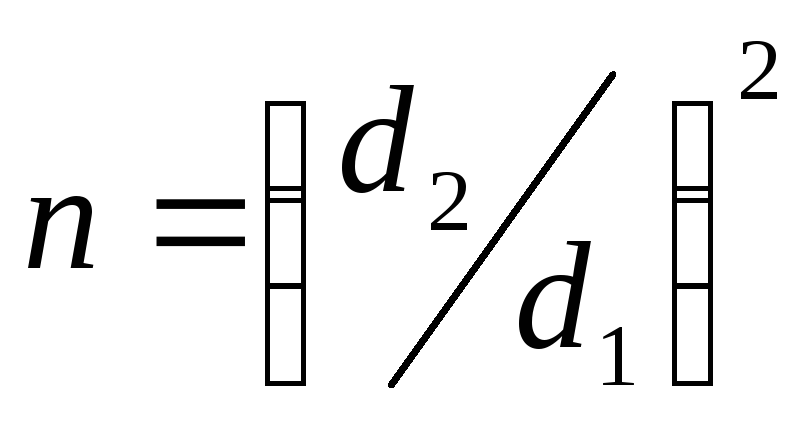Местные
сопротивления представляют короткие
участки трубопроводов, на которых
скорости потока изменяются по значению
или направлению в результате изменения
размеров или формы сечения трубопровода,
а также направления его продольной
оси. Потери давления, возникающие при
‘деформации потока в местных сопротивлениях,
называются местными потерями давления
Δрм.п.
Они определяются
по формуле Вейсбаха
![]()
(10)
где
![]()
— безразмерный
коэффициент местного сопротивления;
w
— средняя скорость потока перед местным
сопротивлением или после него (обычно
берётся скорость за местным сопротивлением).
Значение
коэффициента местных потерь
![]()
в.
общем случае зависит
от пограничной геометрии (формы местного
сопротивления, относительной шероховатости
стенок, распределения скоростей в
граничных сечениях потока перед местным
сопротивлением и после него) и числа
Рейнольдса.
Характер
влияния числа Rе
определяется режимом движения жидкости.
При очень малых числах Rе
(при ламинарном режиме) движение жидкости
происходит без отрыва от стенок, а
местные потери давления, обусловленные
непосредственным действием сил
вязкостного трения, оказываются
пропорциональны первой степени скорости
потока; коэффициент местного сопротивления
при этих значениях числа Rе
выражается формулой
![]() ,
,
(11)
где В
— коэффициент,
зависящий от вида мест .ого сопротивления
и степени стеснения потока (таблица 2)
Таблица
2 – Значения коэффициентов В
для некоторых местных
сопротивлений
|
Сопротивление |
В |
Сопротивление |
В |
|
Пробковый |
150 |
Задвижка: |
|
|
Вентиль |
3000 |
полное |
75 |
|
Колено |
90 |
n |
350 |
|
Угольник |
600 |
n |
1300 |
|
Диафрагма: |
70 |
n |
3000 |
|
n |
120 |
п |
|
|
n |
500 |
Примечание
— Для арматуры при полном открытии и
отсутствии необходимых данных о величине
В можно
принимать приближенно В
= 500![]() кв
кв
.
С
увеличением числа Rе
наряду с потерями на трение возникают
потери, обусловленные отрывом потока
и образованием вихревой зоны (переходная
зона сопротивления). В
переходной зоне
коэффициент местного сопротивления
определяется по формуле
![]() ,
,
(12)
где
![]() кв
кв
—
коэффициент рассматриваемого местного
сопротивления в квадратичной
области.
При
больших числах Rе
основное значение приобретает
вихреобразование, потери давления
становятся пропорциональными квадрату
скорости, т. к. коэффициент
![]() ,
,
перестаёт зависеть
от числа Rе
(так называемая квадратичная или
автомодельная область сопротивления)
и равен ζкв
(ζ=
ζ
кв).
Автомодельность
(независимость) коэффициента местного
сопротивления от числа Rе
при резких переходах в трубопроводе
наступает при Rе
> 3000, а при плавных переходах — при Rе
> 10000.
Влияние
относительной шероховатости стенок
проявляется в местных сопротивлениях
только при больших значениях числа Rе
(в квадратичной области сопротивления).
Увеличение относительной шероховатости
ведёт к возрастанию
![]() ,
,
которое существенно
в тех случаях, когда местные потери
давления обусловлены главным образом
тормозящим действием стенок на поток,
т. е. представляют потери на трение
(колено, диффузор с малым углом раскрытия).
Ниже приводятся значения коэффициента
![]()
=
![]() кв,.для
кв,.для
некоторых местных сопротивлений (более
подробные данные о местных сопротивлениях
в напорных трубах см. [1, 2]). Все коэффициенты
местных сопротивлений отнесены к
динамическому давлению
![]() ,
,
определяемому по скорости за местным
сопротивлением (кроме случаев,
оговариваемых особо),
![]() .
.
(13)
Вентиль

Рисунок 1 — Вентиль
При полном открытии
в зависимости от конструкции следует
принимать:
а) для
вентиля с прямым шпинделем по схеме
рисунок 1 а
ζвен=3÷5,5;
б) для
вентиля с наклонным шпинделем по схеме
рисунок 1 б
ζвен=1,4÷1,85.

П
Коэффициент
![]() кр
кр
зависит
от угла поворота а (рисунок
2) и может быть взят по таблице 3.
робковый кран
Рисунок 2 — Пробковый
кран
|
|
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
|
ζ |
0,05 |
0,29 |
0,75 |
1,56 |
3,1 |
5,47 |
9,68 |
17,3 |
31,2 |
52,6 |
109 |
Таблица 3 —
Значения коэффициентов для пробкового
крана
|
Задвижка
Рисунок |
Коэффициент
от |
|||||||||||||||||
|
Таблица
|
||||||||||||||||||
|
Диафрагма
Р |
Коэффициент
где
|
|||||||||||||||||
|
Внезапное
Значение |
||||||||||||||||||
|
|
где, |
|||||||||||||||||
|
Рисунок 5
Внезапное сужение |
||||||||||||||||||
|
|
Коэффициент
|
|||||||||||||||||
|
Рисунок |
Таблица
5 — Значения коэффициента ζвс
в зависимости от
степени сжатия п
|
ζвс |
0,41 |
0,40 |
0,38 |
0,36 |
0,34 |
0,30 |
0,27 |
0,20 |
0,16 |
0,1 |
|
п |
0 |
0,10 |
0,20 |
0,30 |
0,40 |
0,50 |
0,60 |
0,70 |
0,80 |
0,9 |
Наиболее резкое
сужение трубопровода
 На рисунке 7
На рисунке 7
представлен случай сужения трубопровода,
когда меньшая труба выступает внутрь
большей трубы (случай наиболее резкого
сужения
трубопровода).
Если меньшая труба выступает
на длину, большую половины её диаметра,
то коэффициент сопротивления при таком
внезапном сужении трубопровода может
быть определён по формуле
Рисунок 7 – Наиболее
резкое
сужение трубопровода
 (17)
(17)
Плавный
поворот трубы (закруглённое колено,
отвод)
Д ля
ля
отводов круглого сечения с углом
![]() =90º
=90º
значение коэффициента
ζкол
определяется формулой А.Д. Альтшуля
в зависимости от отношения
радиуса закругления к диаметру
трубы (R/d)
и от значения
коэффициента гидравлического трения
λ
[3].
Рисунок 8 — Плавный
поворот
![]() (18)
(18)
или
(при больших Rе)
— формулой Некрасова
![]() .
.
(19)
При
повороте на любой
угол
![]()
можно приближенно принимать
![]() ,
,
(20)
где ζ
900
—
коэффициент
сопротивления при повороте на 90°;
а —
коэффициент, зависящий от угла поворота
![]() .
.
Величину
коэффициента а при
![]()
< 90º
можно определять
по формуле Миловича А.Я.
![]() ; (21)
; (21)
при
![]()
> 90° — по формуле: Б.Б. Некрасова
![]() . (22)
. (22)
Постепенное
расширение трубопровода (диффузор)
Коэффициент
сопротивления для конически расходящихся
переходных конусов
(диффузоров) зависит от угла конусности
и соотношения диаметров. Для коротких
диффузоров коэффициент сопротивления,
отнесённый
к скорости в узком сечении, определяется
по формуле

 ,
,![]()
(23)
Рисунок
1 — Постепенное рас- где
![]()
— коэффициент смягчения при постепен-
ширение
трубопровода ном
расширении, значения которого приведены
в таблице 6.
Таблица
6 — Средние значения коэффициента
смягчения
![]()
для
диффузоров
|
|
8 |
10 |
12 |
15 |
20 |
25 |
|
|
0,14 |
0,16 |
0,22 |
0,3 |
0,42 |
0,62 |
Постепенное сужение
трубопровода
К оэффициент
оэффициент
сопротивления для сходящихся
переходных конусов (конфузоров) зависит
от угла конусности и соотношения
диаметров. Для
коротких конусов он может быть найден
по формуле
Рисунок
10-
Постепенное суже-
ние
трубопровода
![]() ,
,
(24)
де
![]()
— коэффициент сжатия струи, определяемый
по формуле
 ; (25)
; (25)
φ
— коэффициент смятения при постепенном
сужении, значения которого приведены
в таблице 7 в зависимости от угла
конусности
Таблица
7 — Средние значения коэффициента
смягчения φ
для конфузора
|
|
10 |
20 |
40 |
60 |
80 |
100 |
140 |
|
|
0,40 |
0,25 |
0,20 |
0,20 |
0,30 |
0,40 |
0,60 |
Переходные
конусы (диффузоры и конфузоры) применяются
для соединения
подводящих и отводящих патрубков к
корпусу теплообменника для уменьшения
гидравлических потерь, как это имеет
место, например, в водоводяном
подогревателе
по МВН-2050-62.
Теплообменники
Приведённые
выше данные о коэффициентах местных
сопротивлений относятся
к движению жидкости с нормальным
(выровненным) полем скоростей. В
теплообменных
аппаратах местные сопротивления
расположены настолько близко
одно к другому, что поток между ними не
успевает выравниваться, поскольку
вихреобразования,
возникающие при проходе через местное
сопротивление, сказывается
на значительном протяжении вниз по
потоку. В результате взаимного влияния
местных сопротивлений значения их
коэффициентов сопротивления отличаются
от рассмотренных выше, когда каждое
местное сопротивление исследовалось
отдельно. Значения коэффициентов местных
сопротивлений отдельных элементов
теплообменных аппаратов, полученные
непосредственным измерением в
теплообменных аппаратах, приведены в
таблице 8 (таблица 1-4 [4]).
Таблица
8 — Значения коэффициентов местных
сопротивлений отдельных элементов
теплообменных аппаратов
|
Наименование |
ζ |
Отнесен |
|
Вход |
1,5 |
В |
|
Поворот |
2,5 |
В |
|
Поворот |
2,0 |
В |
|
Вход |
1,0 |
В |
|
Поворот |
0,5 |
В |
|
Вход |
1,5 |
В |
|
Выход |
1,0 |
В |
|
Поворот |
1,5 |
В |
|
Переход |
2,5. |
В |
|
Огибание |
0,5 |
В |
Коэффициенты
потерь входа в камеру через входной
патрубок и выхода из камеры
через выходной патрубок относят к
скорости во входном или выходном
патрубках,
которая определяется по формуле
![]() , (26)
, (26)
где
А
пат=
πd2/4—
площадь проходного сечения патрубка,
м2;
G
—
массовый расход жидкости, кг / с;
— плотность жидкости
(газа), кг / м3.
При
расчёте потерь внутри трубок все
коэффициенты местных потерь относят
к скорости внутри трубок, которая
определяется по формуле
![]() ,
,
(27)
где
![]()
площадь проходного сечения одной трубки;
dв
— внутренний диаметр трубки;
nт
— общее число трубок в теплообменнике;
z
—
число ходов; nт
/ z
— число трубок в одном ходе.
При
продольном омывании пучка труб
сопротивление трения рассчитывается
по формуле (1) для прямых труб,
причём
в этой формуле эквивалентный диаметр
определяется из выражения (5). Средняя
скорость в межтрубном пучке в осевом
направлении определяется по формуле
![]()
(28)
где
![]() –
–
площадь проходного
сечения между трубками, перпендикулярного
оси трубок;
D
—
внутренний диаметр корпуса теплообменника;
d
Н
—
наружный диаметр трубок.
При наличии сегментных
перегородок (рисунок 11) в расчёте потерь
по длине
берётся скорость в сегментном
вырезе перегородки (над перегородками),
которая
определяется по формуле
![]() , (29)
, (29)
где
![]() –
–
площадь
сегмента за вычетом площади трубок (см.
Рисунок 11 а)
Nc
–
количество трубок в сегментном вырезе
перегородки;
![]() с
с
–
центральный угол сегмента в градусах.

сегментная
перегородка
Рисунок
11 – Сегментная перегородка
Эквивалентный
диаметр сечения над перегородкой в этом
случае определяется
по формуле
.
 (30)
(30)
При расчёте местных
сопротивлений в межтрубном пространстве
все коэффициенты местных сопротивлений
относят к максимальной, скорости жидкости
при движении её между перегородками
![]() , (31)
, (31)
где ![]() –
–
площадь минимального
проходного сечения для прохода жидкости
между перегородками (см. рисунок 11
б) в направлении, перпендикулярном оси
трубы;
y0
— зазор между корпусом
и крайней трубкой; у
— зазор между трубками;
h
— расстояние между
перегородками;
т —
количество зазоров между трубками в
ряду у кромки перегородок.
Сопротивление
поперечно омываемых пучков труб.
Коэффициент
сопротивления поперечно омываемого
пучка труб зависит от количества рядов
и расположения труб и от числа Рейнольдса.
Для расчёта коэффициента сопротивления
пучка труб предложено ряд зависимостей
[4, 5, б]. Однако эти зависимости довольно
сложны и применяются для уточнённых
расчётов, когда известна геометрия
пучка труб. Для приближённых расчётов
можно пользоваться формулой [4]
![]() , (32)
, (32)
где К
— количество рядов
трубок, пересекаемых поперечным потоком
(при наличии поперечных перегородок
учитываются все ряды труб, захваченных
перегородкой, и половина рядов труб,
выступающих из неё).
Значение
критерия Rе
здесь определяется по формуле
![]() , (33)
, (33)
где
у —
зазор между трубками;
wмакс
— максимальная скорость потока при
поперечном омьвании пучка труб;
ν
— кинематическая
вязкость. :
На практике встречаются
теплообменники, в межтрубном пространстве
которых устанавливаются кольцевые
и дисковые поперечные перегородки
(например, маслоохладители турбоустановок
завода Пергале). Расчёт площади проходных
сечений для жидкостей в этом случае
производится по следующим формулам:
а) между корпусом и
диском
![]() ; (34)
; (34)
б) в вертикальном
сечении — между перегородками
![]() ; (35)
; (35)
в) внутри кольца
 ,
,
где
D0=(D1+D2)/2
— средний диаметр;
D
— внутренний диаметр
корпуса, м;
D1
и D2
— диаметр
проходного сечения и диаметр диска, м;
d
н
– наружный
диаметр трубки, м;
s
– шаг
между трубками, м;
h
– расстояние
между перегородками, м;
η=0,8![]() 0,85.
0,85.
Диаметр
диска определяется по формуле
![]() ,
,
где
nт
— число трубок в трубной доске; η
имеет
прежнее значение.
Размеры
D0,D2
и h
должны
быть так подобраны, чтобы скорость
жидкости во всех
сечениях была одинаковой:
![]() ,
,
где
Vt=V/t
—
объёмный расход жидкости, м3/с.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
7-я лекция.
7. МЕСТНЫЕ ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ
9.1. Общие сведения о местных сопротивлениях
9.2. Внезапное расширение трубопровода
9.3. Постепенное расширение трубы
9.4. Внезапное сужение трубопровода
9.5. Потери энергии при выходе из резервуара в трубу.
9.6. Потери энергии при постепенном сужении трубы – конфузор.
Рекомендуемые материалы
9.7.Поворот трубы
9.8. Коэффициенты местных сопротивлений.
9.1. Общие сведения о местных сопротивлениях
Местными сопротивлениями называются участки трубопроводов, на которых из-за изменения размеров или направления движения жидкости происходит деформация потока.
Деформация вызывает дополнительное сопротивление, причиной которого являются вихреобразования. Работа, расходуемая на преодоление сопротивлений, превращается в тепловую энергию.
К местным сопротивлениям относятся: внезапные расширения и сужения, “колено” – поворот на некоторый угол, разветвления.
Конструктивно это могут быть: расширения и сужения в трубопроводе, гидрораспределители, клапаны, вентили.
Потери энергии, отнесенные к единице веса потока жидкости, определяются по формуле (Вейсбаха-Дарси):

где V – средняя скорость потока в сечении S, ζ – безразмерный коэффициент местного сопротивления, зависящий от числа Рейнольдса, формы местного сопротивления, шероховатости его поверхностей, степени открытости запорного устройства.
Потеря удельной энергии в местном сопротивлении характеризуется коффициентом ζ – дзета, который определяется в долях удельной кинетической энергии (скоростного напора):
 .
.
Сечения трубопроводов перед местным сопротивлением и за ним могут быть разными. Потери удельной энергии могут быть вычислены через скоростной напор, как перед местным сопротивлением, так и после него. Поэтому коэффициент ζм может быть отнесен к любому из этих скоростных напоров, но будет иметь разные значения, обратно пропорциональные скоростным напорам. За расчетную скорость удобнее принимать большую из скоростей, т.е. ту, которая соответствует меньшему диаметру трубы.
Из сопоставления формул для определения потерь по длине и в местных сопротивлениях следует, что коэффициент ζ эквивалентен λ*(l/d). Поэтому потери энергии в местном сопротивлении можно рассматривать, как потери на эквивалентной длине lэ прямого трубопровода, определяя эквивалентную длину по формуле

Используя эквивалентную длину, можно сравнить потери удельной энергии в местном сопротивлении с потерями на трение по длине.
Местное сопротивление влияет на подведенный и отходящий потоки. Нарушение потока начинается до него и заканчивается после него на значительном расстоянии.
Взаимовлияние соединенных местных сопротивлений проявляется в том, что сумма коэффициентов близко расположенных местных сопротивлений может быть меньше арифметической суммы отдельных коэффициентов. При выполнении расчетов этого не учитывают и складывают коэффициенты.
Коэффициенты сопротивления находят по эмпирическим таблицам для сопротивлений различных типов и конструкций, либо расчетным путем по аналитическим зависимостям. В таблицах приводятся усредненные величины коэффициентов. Если потери напора, отличаются от расчетных, следует проводить эксперименты по определению коэффициентов сопротивления.
При ламинарном режиме движения и малых числах Рейнольдса Re < 2300, когда в потоке преобладают силы вязкостного трения над силами инерции, коэффициенты сопротивления зависят только от числа Re:

В этом случае имеет место ламинарная автомодельность, и потери напора пропорциональны скорости в первой степени.
При турбулентном режиме движения и больших числах Re >> 2300 ÷105 в потоке преобладают силы инерции над силами вязкостного трения, коэффициенты местных сопротивлений практически не зависят от Re:

В этом случае имеет место турбулентная автомодельность, и потери напора пропорциональны квадрату скорости.
Понятие автомодельности относится к области гидродинамического моделирования и означает, сопоставимость коэффициентов сопротивлений местного сопротивления или потерь на трение в трубе при исследованиях на модели и на натуре при соблюдении чисел Рейнольдса.
Автомодельность имеет место, если обеспечено соотношение между вязкостью жидкости, геометрическими размерами потоков, например, диаметрами, кинематическими параметрами, например, скоростями в на модели и на натуре.
9.2. Внезапное расширение трубопровода
При внезапном расширении трубы (рис. 9.1) поток расширяется до большего диаметра не сразу, сначала жидкость выходит из меньшего сечения S1 (обозначено 3 -4) в виде струи. Струя отделена от жидкости, находящейся вокруг ее поверхностью раздела.
Поверхность раздела неустойчива, в кольцевом пространстве между потоком и стенкой трубы образуются вихри. Струя постепенно расширяется и на некотором расстоянии l от начала расширения заполняет все сечение S2 (обозначено 2-2).
В пространстве между струей и стенками жидкость находится в застойной зоне, из-за трения жидкость в этой зоне вовлекается в вихревое движение, затухающее по мере приближения к стенкам. Жидкость из этой зоны вовлекается в центральную струю, а жидкость из струи попадает в вихревую зону. Из-за отрыва потока и вихреобразования происходит потеря энергии.
Обозначим давление, скорость и площадь потока в сечении 1 – 1: Р1 , V1, S1 , а в сечении 2 – 2: Р2 , V2, S2.
 .
.
Сделаем следующие допущения:
1) гидростатическое давление распределяется по сечениям по закону гидростатики:  .
.
2) распределение скоростей в сечениях соответствует турбулентному режиму движения α1 = α2 =1.
3) Трение жидкости о стенки на участке 1-2 не учитываем, ввиду его небольшой длины, учитываем только потери на расширение;
4) движение жидкости является установившимся, в том смысле, что напор истечения постоянен и средние скорости в сечениях S1 и S2 имеют определенное значение и не меняются.
Запишем для сечений 1 – 1 и 2 – 2 уравнение Бернулли с учетом потерь напора на расширение hв.р.  . Выразим потери на расширение
. Выразим потери на расширение

Определим величину потерь на внезапное расширение hв.р. теоремой об изменении количества движения.
Эта теорема формулируется известным образом: “изменению количества движения тела за единицу времени равно силе, действующей на тело».

δq – приращение количества движения объема жидкости “1-1-2-2” в проекции на ось потока равно проекции на ту же ось импульса внешних сил, действующих на этот объем.
За время δt объем “3-4-2-2”, состоящий из элементарных струек, переместится в положение: 3′-4′ -2′-2′. Произойдет изменение количества движения жидкости, заключенной в объеме “1-1-2-2”.
Жидкость в застойной зоне не участвует в главном движении, поэтому приращение количества движения в объеме “1-1-2-2” за время δt будет равно разности количеств движения в объемах: 3-4-3′-4′ и 2-2 -2′-2′. Внутренняя часть объема при вычитании сократится.
Обозначив скорости u1 и u2 в живых сечениях элементарных струек δs1, δs2, можно записать приращение количества движения элементарных масс в струйках:
 ,
,
перейдя к дифференциалу и, интегрируя по площадям, получим
 .
.
Эти интегралы дают количества движения масс жидкости, протекающей через живые сечения S1 и S2 в единицу времени. Они могут быть найдены через средние V1 и V2 скорости в этих сечениях:
 ,
,
получим приращение количества движения потока при расширении за время dt
 .
.
Внешние силы, действующие на рассматриваемый объем:
– сила тяжести G = ρS2l, где l – длина рассматриваемого объема 1-1-2-2;
– силы давления жидкости на поверхность сечения 1-1 – S1 , имея ввиду, что давление Р1 действует по всей площади 1-1 – S1, так как на кольцевую площадь “1-3 и 4-1” действует реакция стенки трубы, а на поверхность сечения 2-2 – S2 действует давление Р2.
Так как давления в сечениях действуют по гидростатическому закону, для определения сил на плоские стенки надо умножить давления в центре тяжести площадей S1 и S2 на их величину. Для проекции импульса получим

Приращение количества движения будет равно импульсу

Используя уравнение неразрывности V1S1 = V2S2 и значение синуса Sinα = (z2–z1)/l и сократив на ρgS2 получим
 (9.4)
(9.4)
Подставляя  в выражение для hв.р. получим
в выражение для hв.р. получим

Потеря напора при внезапном расширении равна скоростному напору, определенному по разность скоростей для турбулентного режима движения.
Эту формулу называют формулой Борда в честь французского ученого, который вывел ее в 1766 г.
Формула хорошо подтверждается при турбулентном режиме течения и используется в расчетах. Явление сопротивления при внезапном расширении используется при конструировании лабиринтных уплотнений.
Определим коэффициенты сопротивления относительно скоростей в узком S2 и широком сечении S1. Уравнение неразрывности


1.Относительно скорости V1 в узком сечении S1:

2.Относительно скорости V2 в широком сечении S2:

9.3. Потери энергии при выходе из трубы в резервуар.

Когда площадь резервуара S2, велика в сравнении с площадью трубопровода S1 , S2/S1→∞ велико, а скорость V2→0 мала, потеря на расширение при выходе из трубы в резервуар

9.3. Постепенное расширение трубы
Местное сопротивление, при котором труба постепенно расширяется, называется диффузором. Течение жидкости в диффузоре сопровождается уменьшением скорости и увеличением давления, происходит преобразование кинетической энергии жидкости в энергию давления.

Частицы движущейся жидкости преодолевает нарастающее давление за счет потери кинетической энергии. Формула для определения сопротивления диффузора похожа на формула для определения потерь при внезапном расширении
 , где φд – коэффициент диффузора.
, где φд – коэффициент диффузора.
Определение коэффициента потерь для диффузора основывано на теореме Борда о внезапном расширении. Выражая коэффициент сопротивления относительно скорости V1 в узком сечении S1, получим

Функция φд =f(α) имеет минимум при угле α = 6º φд =0,2 (рис.9.5), для угла α = 10º φд =0,23-0,25.

Диффузор устанавливают для уменьшения потерь, возникающих при переходе от меньшего к большему диаметра трубы.
а) при 0<α<8-10º на всем протяжении диффузора наблюдается безотрывное движение жидкости;
б) при 8-10º <α<50-60º получается отрыв транзитной струи, с увеличением угла точка начала отрыва перемещается к меньшему сечению трубы;
в) при 50-60º <α отрыв транзитной струи от стенок начинается сразу за меньшим сечением трубы., с увеличением угла точка начала отрыва перемещается к меньшему сечению трубы;
Прямоугольные диффузоры (с расширением в одной плоскости) имеют оптимальный угол больше, чем у круглых и квадратных, около 10 ÷ 12° (плоские диффузоры).
При необходимости перехода на угол α > 15 ÷ 25° применяют специальный диффузор, обеспечивающий постоянный градиент давления вдоль оси dp/dx = const и равномерное нарастание давления, при прямой образующей градиент давления убывает вдоль диффузора, рис.9.6.
Уменьшение потери энергии в таких диффузорах будет тем больше, чем больше угол α, и при углах 40 — 60° доходит до 40 % от потерь в обычных диффузорах. Кроме того, поток в криволинейном диффузоре отличается большей устойчивостью, т. е. в нем меньше тенденций к отрыву потока.

Применяют также ступенчатый диффузор, состоящий из обычного диффузора с оптимальным углом и следующего за ним внезапного расширения.
9.4. Внезапное сужение трубопровода

При внезапном сужении трубы (рис.9.7) потери энергии связаны с трением потока при входе в узкую трубу и с потерями на вихреобразование. Поскольку поток не обтекает входной угол, а срывается с него и сужается, поисходит вихреобразование. Кольцевое пространство вокруг суженной части потока заполнено завихренной жидкостью.
Потеря напора определяется по формуле Идельчика, относительно скорости в необходимом для расчета сечении.
Относительно скорости в узком сечении V1 коэффициент сопротивления равен

 (9.13)
(9.13)
Относительно скорости в широком сечении V2

где ξсуж – коэффициент сопротивления внезапного сужения зависящий от степени сужения и от сечения к которому приводится коэффициент, n = S2/S1 – степень сужения.
9.5. Потери энергии при выходе из резервуара в трубу.

При выходе из резервуара в трубу больших размеров и при отсутствии закруглений входного угла, когда S2>>S1 ,отношение S2/S1→0, для выхода из резервуара в трубу получим, используя формулу Идельчика

коэффициент сопротивления
ξв.р.тр. = 0,5.
Закруглением входного угла (входной кромки) можно значительно уменьшить потерю напора при входе в трубу.
9.6. Потери энергии при постепенном сужении трубы – конфузор. 
Постепенное сужение трубы называется конфузором (рис.9.9). Течение жидкости в конфузоре сопровождается увеличением скорости и падением давления. Давление жидкости в начале конфузора выше, чем в конце, поэтому причин к возникновению вихреобразований и срывов потока, как в диффузоре, нет.
В конфузоре имеются только потери на трение, и поскольку его длина невелика, обычно l/d ≈ 3-4.сопротивление конфузора всегда меньше, чем диффузора и зависит от угла конфузора и его длины, обычные значения коэффициента ζ = 0,06-0,09. Например, для  .
.
Расчет сопротивления конфузора производится по формуле для определения местных сопротивлений

Следует иметь ввиду, что значение ζ обычно связывается с узким сечением конфузора.
9.7.Поворот трубы
Местное сопротивление при повороте трубы на произвольный угол без закругления называется “колено” (рис. 9.10а). В колене имеют место значительные потери энергии, так в нем происходят отрыв потока и вихреобразование, эти потери тем больше, чем больше угол δ. Потерю напора рассчитывают по формуле
h = ξкV2/(2g).
Коэффициенты сопротивления колена круглого сечения определяют экспериментально, ξк возрастает с увеличением угла δ (рис.9.17) и при δ = 90° достигает единицы.
Величина коэффициента сопротивления может быть определена приближенно по формуле
ζк =Sin2δ
Постепенный поворот трубы (рис.9.10в) называется отводом. Плавность поворота значительно уменьшает интенсивность вихреобразования, сопротивление отвода по сравнению с коленом меньше. При достаточно большом его значении относительного радиуса кривизны отвода R/d , срыв потока устраняется полностью. Коэффициент сопротивления отвода ξотв зависит от отношения R/d, угла δ, а также от формы поперечного сечения трубы.

Для отводов круглого сечения при турбулентном режиме течения можно пользоваться эмпирической формулой при R/d>> 1.
Для угла δ= 90° ξ’отв1 = 0,051+0,19*( d/R) (9.16),
для углов меньше δ<< 70° ξотв2 = 0,9* ξ’отв1 *Sinδ, (9.17)
для углов δ >> 100° ξотв3 = (0,7 + (δ/90)*0,35)*ξ’отв1 (9.18)
Потеря напора, определенные по коэффициентам ξотв, учитывают сопротивление, обусловленное кривизной. При расчете трубопроводов, содержащих отводы, следует длины этих отводов включать в общую длину трубопровода для определения потерь на трение, затем к потере на трение нужно прибавить потери, определяемые коэффициентом ξотв.
Ниже в таблицу сведены коэффициенты местных сопротивлений различной конфигурации.
9.8. Коэффициенты местных сопротивлений.
Таблица 1.
|
№ |
Вид местного сопротивления |
Расчетные формулы |
|
Уравнение неразрывности
|
||
|
1 |
Внезапное расширение |
|
|
|
1.Скорости V1 в узком сечении S1:
2.Скорость V2 в широком сечении S2: |
|
|
2 |
Выход из трубы в резервуар |
|
|
|
|
|
|
3 |
Конический диффузор |
|
|
Θ=10º, φД = 0,25 |
1.Относительно скорости V1 в узком сечении S1:
|
|
|
Внезапное сужение |
||
|
|
|
|
|
В лекции “Датчики по отрыву пламени” также много полезной информации. Выход из резервуара в трубу |
||
|
|
|
|
|
Конфузор |
||
|
|
|
ГлавнаяСтатьи и материалыГидравлическое сопротивление труб
Любая трубопроводная коммуникация имеет не только прямолинейные участки, но и повороты, ответвления, для создания которых используются различные фитинги.
А для регулирования потока рабочей среды устанавливается запорная арматура. Всё это создаёт сопротивление, поэтому очень важно перед тем, как приступать к монтажу трубопровода, необходимо выполнить ряд расчётов, в том числе определить гидравлическое сопротивление.
Это позволит в будущем сократить теплопотери и, соответственно, избежать лишних энергозатрат.
Гидравлический расчёт выполняется с целью:
- Вычисления потерь давления на конкретных отрезках системы отопления;
- Определения оптимального диаметра трубопровода с учётом рекомендованной скорости перемещения рабочего потока;
- Расчёта тепловых потерь и величины наименьшего давления в трубопроводе;
- Правильного выполнения увязки параллельно расположенных гидравлических ветвей и закреплённой на ней запорной арматуры.
Во время движения по замкнутому контуру рабочему потоку приходится преодолевать определённое гидравлическое сопротивление. Причём с увеличением его значения, должна увеличиваться мощность насоса.
Только правильные расчёты помогут выбрать оптимальный вариант насоса.
Нет смысла покупать слишком мощное оборудования для трубопроводов с низким гидравлическим сопротивлением, ведь, чем больше мощность, тем выше энергозатраты.
А если мощность будет, наоборот, недостаточной, то насосное оборудование не сможет обеспечить достаточный напор теплоносителя, что приведёт к увеличению тепловых потерь.
- Это безмерная величина, показывающая, каковы потери удельной энергии.
- Ламинарное перемещение рабочего потока
- При ламинарном (равномерном) перемещении рабочей среды по трубопроводу круглого сечения потери давления по длине вычисляется по формуле Дарси-Вейсбаха:

- Где:
- — потери давления по длине;
- — коэффициент гидравлического сопротивления;
- v – скорость движения рабочей среды;
- g – ускорение силы тяжести;
- d – диаметр трубопроводной магистрали.
- Практически определено, что на коэффициент гидравлического сопротивления непосредственное влияние оказывает число Рейнольдса (Re) – безмерная величина, которая характеризует поток жидкости и выражается отношением динамического давления к касательному напряжению.
- Если Re меньше, чем 2300, то для расчёта применяется формула:
- Для трубопроводов в форме круглого цилиндра:
- Для трубопроводных коммуникаций с другим (не круглым) сечением:
- Где А=57 – для квадратных труб.
- Турбулентное течение рабочего потока
- При турбулентном (неравномерном, беспорядочном) перемещении рабочего потока коэффициент сопротивления вычисляют опытным путём, как функцию от Re. Если необходимо определить коэффициент гидравлического сопротивления для магистрали круглого сечения с гладкими поверхностями при
![]()
![]()
- В случае турбулентного перемещения рабочей среды на величину коэффициента трения влияет число Рейнольдса (характер течения) и насколько гладкая внутренняя поверхность трубопроводной коммуникации.
- Коэффициент местного сопротивления
- Это безмерная величина, которая устанавливается экспериментальным путём с помощью формулы:
![]()
- Где:
- – коэффициент местного сопротивления;
- – потеря напора;
- – отношение скорости потока к ускорению силы тяжести – скоростной поток.
- При неизменной скорости перемещения рабочей среды по всему сечению применяется формула:
![]()
– энергия торможения.
Для фитингов из ППР:
ДетальОбозначениеПримечаниеКоэффициент
| Муфта | 0,25 | |
| Муфта переходная | Уменьшение на 1 размер | 0,40 |
| Уменьшение на 2 размер | 0,50 | |
| Уменьшение на 3 размер | 0,60 | |
| Уменьшение на 4 размер | 0,70 | |
| Угольник 90° | 1,20 | |
| Угольник 45° | 0,50 | |
| Тройник | Разделение потока | 1,20 |
| Соединение потока | 0,80 | |
| Крестовина | Соединение потока | 2,10 |
| Разделение потока | 3,70 | |
| Муфта комб. вн. рез. | 0,50 | |
| Муфта комб. нар. рез | 0,70 | |
| Угольник комб. вн. рез. | 1,40 | |
| Угольник комб. нар. рез. | 1,60 | |
| Тройник комб. вн. рез. | 1,40 — 1,80 | |
| Вентиль | 20 мм | 9,50 |
| 25 мм | 8,50 | |
| 32 мм | 7,60 | |
| 40 мм | 5,70 |
Для полиэтиленовых труб
ТрубаРасход, м3/часСкорость, м/сПотери напора в метрах, на 100 метров прямого трубопровода (м/100м)
| Сталь новая 133×5 | 60 | 1,4 | 3,6 |
| Сталь старая 133×5 | 60 | 1,4 | 6,84 |
| ПЭ 100 110×6,6 (5ЭР 17)/td> | 60 | 2,26 | 4,1 |
| ПЭ 80 110×8,1 (ЗйР 13,6) | 60 | 2,41 | 4,8 |
| Сталь новая 245×6 | 400 | 2,6 | 4,3 |
| Сталь старая 245×6 | 400 | 2,6 | 7,0 |
| ПЭ 100 225×13,4 (50 В 17) | 400 | 3,6 | 4,0 |
| ПЭ 80 225×16,6 (ЗЭК 13,6) | 400 | 3,85 | 4,8 |
| Сталь новая 630×10 | 3000 | 2,85 | 1,33 |
| Сталь старая 630×10 | 3000 | 2,85 | 1,98 |
| ПЭ 100 560×33,2 (ЗЭК 17) | 3000 | 4,35 | 1,96 |
| ПЭ 80 560×41,2 (ЗЭК 13,6) | 3000 | 4,65 | 2,3 |
| Сталь новая 820×12 | 4000 | 2,23 | 0,6 |
| Сталь старая 820×12 | 4000 | 2,23 | 0,87 |
| ПЭ100 800×47,4 (ЗЭК 17) | 4000 | 2,85 | 0,59 |
| ПЭ 80 800×58,8 (ЗЭР 13,6) | 4000 | 3,0 | 0,69 |
Для бесшовных стальных труб
Режим движенияЧисло РейнольдсаОпределения λ
| Ламинарный | или | |
| Переходный | Проектирование трубопроводов не рекомендуется | |
| Турбулентный | 1-я область | (ф-ла Блазиуса) |
| 2-я область | ||
| 3-я область |
Для металлопластиковых труб
НаименованиеСимволКоэффициент
| Тройник разделения потока | 7,6 |
| Тройник проходной | 4,2 |
| Тройник противоположные потоки при разделении потока | 8,5 |
| Тройник противоположные потоки при слиянии потока | 8,5 |
| Угол 90° | 6,3 |
| Дуга | 0,9 |
| Редукционный переход | 6,3 |
| Установочный уголок | 5,4 |
С точки зрения гидравлического сопротивления, наиболее оптимальными являются трубопроводные системы с гладкой внутренней стенкой:
Пластиковые трубы произведенные в Германии, широкого спектра применения.
Система отлично подходит для систем горячего и холодного водоснабжения и отопления, как в частных, так и промышленных масштабах. Так же используется для транспортировки химических сред.
Имеет гладкую внутреннюю стенку, что обеспечивает низкий коэффициент гидравлического сопротивления.
- Пластиковые трубы произведенные в Германии, широкого спектра применения.
- Трубопроводная система из инновационного материала fusiolen, специально разработанная для систем холодоснабжения, обогрева поверхностей, транспортировки агрессивных сред и сжатого воздуха, а также для систем геотермальной энергетики.
- Имеет гладкую внутреннюю стенку, что обеспечивает низкий коэффициент гидравлического сопротивления.
Помогите рассчитать потерю давления на газопроводе с начальным диаметром dn80, через 0,1 м становиться dn32 и тянется 10 м Уважаемый Андрей! Информация направлена на вашу почту! Добрый день, помогите рассчитать сопротивление резиновых трубопроводов. Уважаемый Николай! Информация направлена на Вашу почту. Что такое м/100м (в потерях напора)? Уважаемый Павел! Данная колонка с данными отображает потери напора в метрах, на 100 метров прямого трубопровода (м/100м).
Самостоятельный гидравлический расчет трубопровода
- Содержание: [Скрыть]
Постановка задачи
Гидравлический расчёт при разработке проекта трубопровода направлен на определение диаметра трубы и падения напора потока носителя.
Данный вид расчёта проводится с учетом характеристик конструкционного материала, используемого при изготовлении магистрали, вида и количества элементов, составляющих систему трубопроводов(прямые участки, соединения, переходы, отводы и т. д.), производительности,физических и химических свойств рабочей среды.

- минимальное соотношением периметра к площади сечения, т.е. при равной способности, обеспечивать расход носителя, затраты на изолирующие и защитные материалы при изготовлении труб с сечением в виде круга, будут минимальными;
- круглое поперечное сечение наиболее выгодно для перемещения жидкой или газовой среды сточки зрения гидродинамики, достигается минимальное трение носителя о стенки трубы;
- форма сечения в виде круга максимально устойчива к воздействию внешних и внутренних напряжений;
- процесс изготовления труб круглой формы относительно простой и доступный.
Подбор труб по диаметру и материалу проводится на основании заданных конструктивных требований к конкретному технологическому процессу. В настоящее время элементы трубопровода стандартизированы и унифицированы по диаметру. Определяющим параметром при выборе диаметра трубы является допустимое рабочее давление, при котором будет эксплуатироваться данный трубопровод.
Основными параметрами, характеризующими трубопровод являются:
- условный (номинальный) диаметр – DN;
- давление номинальное – PN;
- рабочее допустимое (избыточное) давление;
- материал трубопровода, линейное расширение, тепловое линейное расширение;
- физико-химические свойства рабочей среды;
- комплектация трубопроводной системы (отводы, соединения, элементы компенсации расширения и т.д.);
- изоляционные материалы трубопровода.
 Условный диаметр (проход) трубопровода (DN) – это условная безразмерная величина, характеризующая проходную способность трубы, приблизительно равная ее внутреннему диаметру. Данный параметр учитывается при осуществлении подгонки сопутствующих изделий трубопровода (трубы, отводы, фитинги и др.).
Условный диаметр (проход) трубопровода (DN) – это условная безразмерная величина, характеризующая проходную способность трубы, приблизительно равная ее внутреннему диаметру. Данный параметр учитывается при осуществлении подгонки сопутствующих изделий трубопровода (трубы, отводы, фитинги и др.).
Условный диаметр может иметь значения от 3 до 4000 и обозначается: DN 80.
Условный проход по числовому определению примерно соответствует реальному диаметру определенных отрезков трубопровода.
Численно он выбран таким образом, что пропускная способность трубы повышается на 60-100% при переходе от предыдущего условного прохода к последующему.
Номинальный диаметр выбирается по значению внутреннего диаметра трубопровода. Это то значение, которое наиболее близко к реальному диаметру непосредственно трубы.
Давление номинальное (PN) – это безразмерная величина, характеризующая максимальное давление рабочего носителя в трубе заданного диаметра, при котором осуществима длительная эксплуатация трубопровода при температуре 20°C.
Значения номинального давления были установлены на основании продолжительной практики и опыта эксплуатации: от 1 до 6300.
Номинальное давление для трубопровода с заданными характеристиками определяется по ближайшему к реально создаваемому в нем давлению. При этом,вся трубопроводная арматура для данной магистрали должна соответствовать тому же давлению. Расчет толщины стенок трубы проводится с учетом значения номинального давления.
Основные положения гидравлического расчета
Рабочий носитель (жидкость, газ, пар), переносимый проектируемым трубопроводом, в силу своих особых физико-химических свойств определяет характер течения среды в данном трубопроводе. Одним из основных показателей характеризующих рабочий носитель, является динамическая вязкость, характеризуемая коэффициентом динамической вязкости – μ.
Инженер-физик Осборн Рейнольдс (Ирландия), занимавшийся изучением течения различных сред, в 1880 году провел серию испытаний, по результату которых было выведено понятие критерия Рейнолдса (Re) – безразмерной величины, описывающей характер потока жидкости в трубе. Расчет данного критерия проводится по формуле:

Критерий Рейнольдса (Re) дает понятие о соотношении сил инерции к силам вязкого трения в потоке жидкости. Значение критерия характеризует изменение соотношения указанных сил, что, в свою очередь, влияет на характер потока носителя в трубопроводе. Принято выделять следующие режимы потока жидкого носителя в трубе в зависимости от значения данного критерия:
- ламинарный поток (Re
Коэффициенты местных сопротивлений в таблицах
Все мы прекрасно видели в таблице аэродинамического расчета столбик коэффициента местного сопротивления (КМС).
Постараемся найти ответы на вопросы: Что это? От каких факторов зависит коэффициент местного сопротивления? Зачем вообще его учитывать? И самый главный вопрос: как определить коэффициенты местных сопротивлений воздуховодов? Значение определяется опытным путем и расчетами.
Для стандартных элементов таких как тройник, колено, задвижка, диффузор, решетки и другие уже давно определили коэффициенты местных сопротивлений. Данные со значением коэффициентов можно найти в справочной литературе, или же они указаны в каталоге производителя.
Бывают случаи, когда и нужно воспользоваться калькулятором. Ниже вы можете увидеть таблицы коэффициентов из справочников и каталогов, а также рассмотрим расчет коэффициента местных сопротивлений и от чего он зависит.
Коэффициент местного сопротивления
Сначала дадим определение коэффициенту местного сопротивления. Местными сопротивлениями называются называют точечные потери напора, связанные с изменением структуры потока. В вентиляции существует множество составляющих, что играют роль местного сопротивления:
- поворот воздуховода,
- сужение или расширение потока,
- вход воздуха в воздухозаборную шахту;
- «тройник» и «крестовина»;
- приточные и вытяжные решетки и воздухораспределители;
- воздухораспределители;
- диффузор;
- заслонки и т.д.
Их КМС рассчитываются по определенным формулам, а затем они участвуют в определении местных потерь давления. В математическом понятии коэффициент местных потерь — это отношение потерь известного напора в местном сопротивлении к скоростному напору.

Коэффициент местного сопротивления зависит от формы и вида местного сопротивления, шероховатости воздуховода и как ни странно от числа Рейнольдса. Для заслонок и другой запорной арматуры к перечисленному додается еще степень открытия.
Связанность КМС с числом Рейнольдса выражается в формуле

Значения коэффициентов В для некоторых местных сопротивлений

Чем больше число Rе тем меньше от него зависит коэффициент. Полная независимость коэффициента местного сопротивления от числа Rе в вентиляционной системе происходит для резких переходов при Rе > 3000, а для плавных переходов — при Rе > 10000.
Суммарный коэффициент местных сопротивлений на участке воздуховода равен сумме всех местных коэффициентов на этом участке.
На практике же времени особо для расчета КМС нету, поэтому проектировщики пользуются таблицами со справочников и других источников. Тем более зачем тратить кучу времени на поиски формул и расчеты, если это уже сделали за вас.
Многие производители шумоглушителей, клапанов и решеток с удовольствием указывают значение коэффициента местного сопротивления в каталогах. Но, конечно, уж если совсем никаких данных не нашли, тогда нужно прибегнуть к математике.
Гидравлическое сопротивление
Опубликовано 24 Июн 2018Рубрика: Теплотехника | 26 комментариев

В одной из ранних статей на блоге рассмотрен простой пример расчета трубопровода с параллельными участками с использованием понятия «характеристика сопротивления». В конце статьи я анонсировал: «Можно существенно повысить точность метода…». Под этой фразой подразумевалось учесть зависимость характеристик сопротивления от расхода более точно.
В том расчете характеристики сопротивлений выбирались из таблиц по диаметру трубы и по предполагаемому расходу. Полковов Вячеслав Леонидович написал взамен таблиц пользовательские функции в Excel для более точного вычисления гидравлических сопротивлений, которые любезно предоставил для печати.
Термины «характеристика сопротивления» и «гидравлическое сопротивление» обозначают одно и то же.
Краткая теория
В упомянутой выше статье теория вкратце рассматривалась. Освежим в памяти основные моменты.
- Движение жидкостей по трубам и каналам сопровождается потерей давления, которая складывается из потерь на трение по длине трубопровода и потерь в местных сопротивлениях – в изгибах, отводах, сужениях, тройниках, запорной арматуре и других элементах.
- В гидравлике в общем случае потери давления вычисляются по формуле Вейсбаха:
- ∆Р=ζ·ρ·w²/2, Па, где:
- ζ – безразмерный коэффициент местного сопротивления;
- ρ – объёмная плотность жидкости, кг/м3;
- w – скорость потока жидкости, м/с.
Если с плотностью и скоростью всё более или менее понятно, то определение коэффициентов местных сопротивлений – достаточно непростая задача!
Как было отмечено выше, в гидравлических расчетах принято разделять два вида потерь давления в сетях трубопроводов.
- В первом случае «местным сопротивлением» считается трение по длине прямого участка трубопровода. Перепад давления для потока в круглой трубе рассчитывается по формуле Дарси-Вейсбаха:
∆Ртр=ζтр·ρ·w²/2=λ·L·ρ·w²/(2·D), Па, где:
- L – длина трубы, м;
- D – внутренний диаметр трубы, м;
- λ – безразмерный коэффициент гидравлического трения (коэффициент Дарси).
Таким образом, при учете сопротивления трению коэффициент потерь – коэффициент местного сопротивления – и коэффициент гидравлического трения связаны для круглых труб зависимостью:
ζтр=λ·L/D
- Во втором случае потери давления в местных сопротивлениях вычисляются по классической формуле Вейсбаха:
- ∆Рм=ζм·ρ·w²/2, Па
- Коэффициенты местных сопротивлений определяются для каждого вида «препятствия» по индивидуальным эмпирическим формулам, полученным из практических опытов.
- Выполним ряд математических преобразований. Для начала выразим скорость потока через массовый расход жидкости:
- w=G/(ρ·π·D²/4), м/с, где:
- G – расход жидкости, кг/с;
- π – число Пи.
- Тогда:
- ∆Ртр=8·λ·L·G²/(ρ·π²·D5), Па;
- ∆Рм=8·ζм·G²/(ρ·π²·D4), Па.
- Введем понятие гидравлических сопротивлений:
- Sтр=8·λ·L·/(ρ·π²·D5), Па/(кг/с)²;
- Sм=8·ζм·/(ρ·π²·D4), Па/(кг/с)².
- И получим удобные простые формулы для вычисления потерь давления при прохождении жидкости в количестве G через эти гидравлические сопротивления:
- ∆Ртр=Sтр·G², Па;
- ∆Рм=Sм·G², Па.
- Размерность гидравлического сопротивления (Па/(кг/с)²) определена массовой скоростью (кг/с) движения жидкости, а физические процессы в транспортных системах зависят от её объёмной скорости (м3/с), что учтено в формулах присутствием объёмной плотности ρ транспортируемой жидкости.
- Для удобства последующих расчётов целесообразно введение понятия «гидравлическая проводимость» — а.
- Для последовательного и параллельного соединений гидравлических сопротивлений справедливы формулы:
- Sпосл=S1+S2+…+Sn, Па/(кг/с)²;
- Sпар=1/(а1+a2+…+an)², Па/(кг/с)²;
- ai=(1/Si)0,5, (кг/с)/Па0,5.
Коэффициент гидравлического трения
Для определения гидравлического сопротивления от трения о стенки трубы Sтр необходимо знать параметр Дарси λ – коэффициент гидравлического трения по длине.
В технической литературе приводится значительное количество формул разных авторов, по которым выполняется вычисление коэффициента гидравлического трения в различных диапазонах значений числа Рейнольдса.

Обозначения в таблице:
- Re – число Рейнольдса;
- k – эквивалентная шероховатость внутренней стенки трубы (средняя высота выступов), м.
- В [1] приведена еще одна интересная формула расчета коэффициента гидравлического трения:
- λ=0,11·[(68/Re+k/D+(1904/Re)14)/(115·(1904/Re)10+1)]0,25
- Вячеслав Леонидович выполнил проверочные расчеты и выявил, что вышеприведенная формула является наиболее универсальной в широком диапазоне чисел Рейнольдса!
- Значения, полученные по этой формуле чрезвычайно близки значениям:
- функции λ=64/Re для зоны ламинарного характера потока в диапазоне 10
Местные сопротивления
При движении реальных жидкостей кроме потерь на трение по длине трубопровода, возникающих из-за вязкости жидкости, могут возникать потери напора, связанные с наличием местных сопротивлений (краны, задвижки, сужения, расширения, повороты трубопроводов и проч.), которые вызывают изменения скорости движения или направления потока.
Потери напора в местных сопротивлениях определяются по формуле
где ξ – коэффициент местных потерь; – скоростной напор; – средняя скорость.
Коэффициентом местных потерь ξ называют отношение потери напора в данном местном сопротивлении к скоростному напору
В большинстве случаев диаметр трубопровода до местного сопротивления и после него бывает разным, а поэтому и скорости движения жидкости при этом разные (рис. 6.21).
Очевидно, что и коэффициенты местных потерь, отнесенные к скоростному напору до и после местного сопротивления, будут различными.
Поэтому при пользовании гидравлическими справочниками необходимо всегда обращать внимание, к какому скоростному напору отнесен коэффициент Обычно ξ относят к скоростному напору за местным сопротивлением.
Рис. 6.21. Схема движения жидкости через местное сопротивление
Отсюда
Понятие эквивалентной длины позволяет ввести понятие о приведенной длине трубопровода
где l – действительная длина трубопровода.
Коэффициент местных потерь ξ в общем случае зависит от формы местного сопротивления, числа Re, шероховатости поверхности, а для запорных устройств также от степени их открытия, т.е.
Ввиду большой сложности происходящих в местных сопротивлениях явлений в настоящее время нет надежных методов теоретического определения коэффициента ξ. Он определяется в основном экспериментально.
Имеется попытка теоретически обосновать коэффициент местных потерь на случай внезапного расширения трубопровода (рис. 6.22). Используя аналогию потерь энергии при внезапном расширении с неупругим ударом твердых тел, Ж. III.
Борда из теоремы о приращении количества движения и уравнения Бернулли вывел формулу для местных потерь при внезапном расширении потока в виде
где – скорости потока до и после внезапного расширения, т.е. потеря напора при внезапном расширении равна скоростному напору потерянной скорости, где потерянная скорость. Это утверждение представляет так называемую теорему Борда – Карно.
Однако более детальный анализ явлений показывает, что аналогия потерь напора при внезапном расширении с потерями энергии при неупругом ударе твердых тел далеко неполная. Опытом, в частности, подтверждается, что потери напора, даваемые теоремой Борда – Карно, получаются завышенными.
Поэтому на основании теоретических соображений и эксперимента предложено эту потерю определять по формуле
где k – коэффициент, определяемый опытным путем.
Рис. 6.22. Внезапное расширение потока
Рассмотрим отдельные практически важные типы местных сопротивлений.
1. Внезапное расширение потока (см. рис. 6.22).
Хотя аналогия внезапного расширения потока с неупругим ударом не может служить основой для строгого теоретического обоснования и объяснения физического смысла явления, в первом приближении она достаточна.
Благодаря неупругости удара механическая энергия рассеивается и превращается во внутреннюю энергию жидкости. Этим и объясняется основная доля потерь при внезапном расширении, которые подсчитываются по формуле (6.
26).
Уравнение неразрывности потока для несжимаемой жидкости имеет вид
Отсюда
Подставляя выражение (6.28) в формулу (6.26), получаем
Сравнивая формулы (6.29) и (6.25), находим
Подставляя выражение (6.31) в формулу (6.26), получаем
Сравнивая формулы (6.32) и (6.25), находим
Таким образом, по формулам (6.29), (6.32) можно определить потери напора в местном сопротивлении в случае известных скоростейили. Для приближенных расчетов коэффициент k можно принять равным 1.
2. Выход из трубы в резервуар больших размеров (рис. 6.23).
Рис. 6.23. Выход из трубы в резервуар
В данном случае площадь сечения резервуара поэтому
Тогда из формулы (6.30) следует
3. Внезапное сужение потока (рис. 6.24).
Рис. 6.24. Внезапное сужение потока
В данном случае происходит внезапное увеличение скорости. Удара при этом в плоскости перехода сечения не происходит. Но на некотором расстоянии ниже по течению происходит сжатие струи (сечение с – с), а затем переход от сжатого сечения к нормальному. Этот переход можно рассматривать как удар, что и служит причиной потерь напора.
Таблица 6.1
Значения ξ при внезапном сужении
| 0,01 | 0,1 | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 | |
| ξ | 0,45 | 0,39 | 0,35 | 0,38 | 0,2 | 0,09 | 0,0 |
4. Постепенное расширение потока (диффузор) (рис. 6.25).
Рис. 6.25. Диффузор
При малых углах течение в диффузоре происходит безотрывно. При углах происходит отрыв потока от стенки.
Это объясняется тем, что в диффузоре происходит увеличение давления в направлении движения, вызываемое уменьшением скорости вследствие расширения канала.
Частицы жидкости, движущейся у стенки, сильно затормаживаются силами вязкости, и в определенной точке их кинетическая энергия становится недостаточной для преодоления все возрастающего давления. Поэтому скорость жидкости в пристенном слое в такой точке обращается в нуль, а за этой точкой появляются обратные течения – отрыв потока.
Если безотрывное течение в диффузоре происходит практически без потерь, то течение с отрывом сопровождается значительными потерями энергии на вихреобразование.
Рис. 6.26. Зависимость коэффициента местных сопротивлений от угла Θ для диффузора
При угле коэффициент потерь достигает максимума. Причем при угле
jpg»> потери напора превосходят потери при внезапном расширении потока (). Поэтому вместо переходов в виде диффузоров с углом
jpg»>нужно применять внезапное расширение как переход с меньшими потерями напора.
Для данного местного сопротивления коэффициент ξ будет функцией только от числа Re. В зависимости от влияния числа Re на коэффициент ξ режимы движения жидкости могут быть разделены на следующие зоны.
1. Движение в местном сопротивлении и в трубопроводе ламинарное.
Коэффициент местных сопротивлений в этом случае определяется по формуле
где А – коэффициент, зависящий от типа местного сопротивления.
Так как
то, учитывая формулу (6.33), будем иметь где
Следовательно, потери напора пропорциональны первой степени скорости.
2. Движение в трубопроводе без местного сопротивления ламинарное, а с местным сопротивлением – турбулентное. В этом случае
где В – коэффициент, зависящий от типа местного сопротивления.
Потери напора в данном случае определяют по формуле
3. Движение в трубопроводе без местного сопротивления и при наличии его турбулентное при небольших числах Re > 2300.
Формула для коэффициента местного сопротивления имеет вид
где С – коэффициент, зависящий от типа местного сопротивления.
Подставляя последнее соотношение в формулу (6.34), получаем
4. Развитое турбулентное течение при больших числах Рейнольдса.
Коэффициент ξ здесь не зависит от числа Рейнольдса, и местные потери напора пропорциональны квадрату скорости (квадратичная зона)
Коэффициенты А, В, С для различных типов местных сопротивлений приводятся в учебниках по гидравлике и гидравлических справочниках [3].
Гидравлический расчет системы отопления: цель и ход выполнения, вычисления
- Выражаться гидравлические потери могут по-разному — в единицах давления или линейных единицах столба жидкости, потерях напора.
- Общая формула потери напора выглядит так:
- △H = △P/(pg),
- где △P — потери в единицах давления,
- p — плотность среды,
- g — ускорение свободного падения.
В сфере промышленности, в производственной практике перемещение жидкостей в потоках неразрывно связано с необходимостью преодоления гидравлического сопротивления трубы по всему пути потока.
Кроме этого, гидравлические потери обуславливаются местным сопротивлением встречающихся на пути ответвлений и кранов, задвижек и вентилей, поворотов и диафрагм.
Чтобы преодолевать местные сопротивления, поток затрачивает определенную часть энергии — в этом случае речь идет о потере напора на локальные сопротивления. Как правило, такие потери выражают в долях от скоростного напора, который соответствует средней скорости среды в трубах до местного сопротивления либо после него.
- Найти данные о коэффициентах разных местных сопротивлений можно в соответствующих учебниках, пособиях, справочниках по гидравлике — данные могут быть представлены в разном виде, например как отдельные значения коэффициента гидравлических потерь, в виде диаграмм, таблиц, эмпирических формул.
- При желании или необходимости потери напора на локальные гидравлические сопротивления можно рассчитать самостоятельно. Для этого используется формула:
- hr = ξ υ² / (2g),
- где ξ представляет собой коэффициент местного сопротивления. Как правило, его определяют опытным путем,
- g — ускорение свободного падения.
Местные гидравлические сопротивления: свойства и характеристики
Как мы уже упоминали, потери напора жидкости в случае с местными сопротивлениями определяются в большинстве случаев только опытным путем.
Но и в теоретическом обосновании есть некоторые прорывы — так, местное сопротивление по своим свойствам и характеристикам аналогично сопротивлению, которое наблюдается при внезапном расширении струи.
И это логично, если учитывать, что поведение потока жидкости при преодолении любого локального сопротивления сопровождается сужением или расширением сечения.
1.
При внезапном сужении трубы сопротивление сопровождается появлением водоворотной области в месте сужения, при этом струя уменьшается до размеров меньших, чем сечение наименьшей трубы.
После того как поток проходит участок сужения, струя максимально расширяется, ограничиваясь внутренним сечением трубы. Коэффициент местного сопротивления при резком сужении трубы рассчитывается по формуле: ξвн.суж. = 0,5(1 — (F2/F1)).
Значение коэффициента от отношения F2/F1 несложно найти в соответствующих пособиях по гидравлике.
2.
При изменении направления трубы под углом гидравлические потери рассчитываются по формуле: ξ поворот = 0,946sin(α/2) + 2,047sin(α/2)², где α — это угол поворота трубы. Поток ведет себя следующим образом: сначала струя сжимается, после чего расширяется, так как при повороте по инерции поток отжимается от стенок трубы.
Ремонт системы отопления дома
3.
При входе в трубу цилиндрической формы с острой кромкой, которая наклонена к горизонту под углом α, коэффициент местного сопротивления высчитывается по формуле Вейсбаха: ξвх = 0,505 + 0,303sin α + 0,223sin α².
Иногда труба имеет закругленную форму или в сечении входа стоит диафрагма, которая сужает сечение, — в любом случае сначала струя потока будет сжиматься, потом расширяться, то есть местное сопротивление при входе в водопровод можно свести к внезапному расширению струи потока.
4.
В промышленности, в частности при работе с насосным оборудованием, часто приходится рассчитывать местные сопротивления, которые создаются запорной арматурой — вентилями и клапанами, кранами и задвижками и так далее.
Вне зависимости от того, какую геометрическую форму имеет проточная часть, ограниченная запорной арматурой, гидравлический характер течения при преодолении сопротивлений не меняется. Если мы говорим о полностью открытой запорной арматуре, гидравлическое сопротивление будет колебаться в диапазоне от 2,9 до 4,5.
Коэффициенты для определенного вида запорной арматуры можно найти в соответствующих справочниках.
5.
Гидравлические потери диафрагмы определяются сужением струи потока и последующим ее расширением. Степень сужения потока и его последующего расширения определяется несколькими факторами — это особенности конструкции диафрагмы, отношение диаметров отверстия трубы и диафрагмы, режим движения жидкости и так далее.
6.
Наконец, часто бывает необходимо рассчитать коэффициент местного сопротивления при входе струи потока под уровень жидкости. Впрочем, сложных расчетов проводить не потребуется, коэффициент сопротивления при входе струи в большой резервуар под уровень жидкости или в среду без жидкости связан с потерей кинетической энергии и равен 1.
3Как выбрать материал для трубопровода сжатого воздуха?
Для производства труб системы подготовки и распределения сжатого воздуха используют несколько материалов. Выбор того или иного зависит от нескольких факторов:
- условия эксплуатации (улица, помещение),
- качество сжатого воздуха,
- перепады давления,
- протяженности трубопровода,
- требуемого диаметра трубы,
- стоимости,
- рабочего давления и производительности компрессора,
- износостойкости.
Чаще всего в сетях распределения сжатого воздуха устанавливают трубы, изготовленные из следующих материалов:
- Сталь. К основным преимуществам данного вида труб относятся: бесшовность соединения, наличие резьбовых соединений, разнообразие видов и форм, разнообразие номинальных диаметров, коррозионная стойкость, низкое сопротивление воздушному потоку. Ограничения к выбору данного вида трубопровода: гальванизированное покрытие увеличивает сопротивление воздушному потоку. Также, трубы из нержавеющей стали достаточно дорогие и имеют значительный вес, по сравнению с пластиковыми трубами.
- Медь. Для многих предприятий медный трубопровод для системы распределения сжатого воздуха достаточно дорогостоящий вариант и требует привлечения сторонних специалистов по монтажу высокого технического уровня. Чаще всего такой вид труб используют в медицине или в лабораториях. Медные трубы имеют низкое сопротивление движению потока, устойчивы к коррозии.
- Пластик. Для производства труб используют следующие виды пластика: полипропилен (РPR), полиамид (РА), полиэтилен (РЕ), акрилнитрил-бутадиен-стиролполимер (ABS). Готовые изделия из них не подвержены коррозии, имеют множество форм и соединений, обладают низкой эластичностью, просты в монтаже и обслуживании. Максимальное расчетное давление каждого вида трубы производители указывают в ее спецификации (обозначение PN и далее величина давления в бар, например PN16).
Наиболее распространенным материалом для прокладки пневмопроводов является полипропиленовые трубы. Они просты в установке, имеют приемлемую стоимость и выдерживают давление сжатого воздуха до 20 бар.
Внешние диаметры полипропиленовых труб: 20 мм, 25 мм, 32 мм, 40 мм, 50 мм, 63 мм.
Внутренние диаметры зависят от максимального давления, на которое они рассчитаны и соответственно зависят от толщины стенок труб, поэтому при выборе материалов пневмопровода нужно внимательно ознакомиться с характеристиками выбранной для монтажа PPR-трубы.
Обращаем ваше внимание, что для правильного подбора компрессорной техники наши специалисты предлагают заполнить Опросный Лист, в котором отражаются все наиболее важные нюансы при выборе агрегатов. Также, вы можете обратиться к нашим специалистам за консультацией любым удобным способом:
- По телефону (звонок бесплатный)
- По электронной почте
- Заполнив заявку в нашем онлайн-чате.
О гидравлическом сопротивлении, насосах и кавитации
Работа насосов и гидравлических машин направлена в том числе на преодоление гидравлических потерь. Чтобы снизить влияние таких потерь, при создании трассы стоит избегать узлов, которые будут резко менять направления потока.
Оптимальный вариант — конструкции обтекаемой формы.
Но нужно понимать, что даже максимально гладкие трубы не обеспечат отсутствие потерь: ламинарный режим течения не сопровождается большими потерями из-за шероховатых стенок, но турбулентный режим приводит и к росту гидравлического сопротивления трубы.
Иногда при движении жидкости по закрытым руслам меняется ее агрегатное состояние — она превращается в пар, то есть из жидкости выделяются газы, в ней растворенные. Если скорость небольшая, видимых изменений в ее движении не будет. Но при увеличении скорости движения на узком участке трубы появится отчетливая зона с пузырьками газа.
Далее, когда жидкость подходит к широкой части трубы, пузырьки начинают резко уменьшаться в размерах, а затем исчезать — схлопываться. В месте схлопывания пузырьков резко увеличивается давление, которое затем передается на соседние объемы среды и далее на стенки трубы. Многочисленные местные повышения давлений приводят к вибрации.
Кавитация — нежелательное явление, которое может привести к очень быстрому износу определенных частей трубопроводного и насосного оборудования. Часто она возникает в местах локальных сопротивлений — в вентилях, кранах, задвижках и так далее. При этом кавитация снижает КПД, а в долгосрочной перспективе разрушает детали, стенки трубопроводов, уменьшая их пропускную способность. #ФОРМА#
Расчёт объема воды и вместительность расширительного бака
Объем расширительного бачка должен равняться 1/10 всего объема жидкости
Для расчета рабочих характеристик расширительного бачка, обязательного для любой системы отопления закрытого типа, потребуется разобраться с явлением увеличения объема жидкости в ней.
Этот показатель оценивается с учетом изменения основных рабочих характеристик, включая колебания ее температуры.
Она в этом случае изменяется в очень широком диапазоне – от комнатных +20 градусов и вплоть до рабочих значений в пределах 50-80 градусов.
К местным гидравлическим сопротивлениям относятся различные устройства и элементы, устанавливаемые на трубопроводах, в которых происходит нарушение нормального движения потока в результате его деформации с изменением направления и значения средней скорости и возникновением вихреобразования. В результате деформации турбулентного потока происходит интенсивное перемешивание частиц и обмен количеством движения между частицами жидкости.
К элементам и устройствам относятся фасонная и трубопроводная арматура: отводы (колена), переходники, тройники, крестовины, диафрагмы, сетки, запорные регулирующие вентили (краны), задвижки, затворы, предохранительные и регулирующие клапаны, всасывающие наконечники, устанавливаемые на входе в трубу насосов, и т.д.
Самые простые местные гидравлические сопротивления можно разделить по направлению вектора средней скорости.
1.Скорость переменна при неизменном направлении движения потока жидкости.
Например, расширение трубы (русла) может быть плавное или внезапное; сужение трубы (русла) — плавное или внезапное.
2.Скорость постоянна при изменении направления движения потока.
Например, поворот трубы (русла) в виде плавного или резкого (см. рис.).

К более сложным местным сопротивлениям относятся сопротивления, в которых вектор скорости изменяется по значению и направлению, а также при слиянии или разделении потоков. Например, задвижки, клапаны, вентили и т.д., а также тройники, крестовины (см. рис.).

В таких сопротивлениях в результате резких изменений направления и скорости происходит весьма значительная деформация потока с возникновением интенсивного вихреобразования.
Местными потерями напора называют затраты удельной механической энергии, обусловленные работой сил трения и вихреобразованием на преодоление потоком жидкости местного сопротивления. На поддержание вихрей в определенной зоне затрачивается энергия потока.
Вейсбах предложил местные потери напора определять по формуле:

h-потеря напора здесь она измеряется в метрах.
ζ-Это коэффициент сопротивления, он будет находится дополнительными формулами о которых напишу ниже.
V-скорость потока жидкости. Измеряется [Метр/секунда].
g-ускорение свободного падения равен 9,81 м/с2
Коэффициент ζ, показывает количество скоростного напора, затрачиваемого на преодоление какого-либо местного сопротивления. В местном сопротивлении потери механической энергии при движении потока через него превращаются в тепловую энергию.
Коэффициент местных сопротивлений зависит:
В общем виде коэффициент ζ, можно представить в следующем виде:

В — безразмерный коэффициент, зависящий от вида местного сопротивления при ламинарной и переходной области сопротивления;
Re — число Рейнольдса;
ζкв — коэффициент местных сопротивлений для квадратичной области, т.е. не зависящий от Re.
Для квадратичной области сопротивления ζ = ζкв. Обычно при гидравлических расчетах принимается ζкв.
Квадратичная область – это когда поток имеет турбулентный режим, в таком режиме сопротивление движению жидкости пропорционально квадрату скорости.
Коэффициент ζ, находится опытным путем, а значения ζкв для различных местных сопротивлений, В приводятся в гидравлических справочниках.
На практике сантехника и инженера по монтажу врядли встретится задача которая требует незмедлительно знать эти параметры типа: [ B, ζ, ζкв ]. Вам они понадобятся в случаях, если вы будете защищать кандидатскую или изобретать к примеру особенный кран на высоких скоростях. Поэтому вам это не понадобится. На практике эти цифры обычно очень маленькие и не принимаются в расчет. Но есть исключения.
Ниже мы разберем основные встречающиеся задачи по местным сопротивлениям, которые следует учитывать.
Вообще формул очень много, я не стану вам приводить такое количество, чтоб не грузить вашу голову. К тому же большинство формул на практике даже не пригодятся.
Рассмотрим два варианта местных сопротивлений это варинты закругления трубы:
1. Закругленным углом (а)
2. Прямым углом – коленом (б)
Смотрите рисунок.

Разберем сначала второй вариант, так как он вызывает большое гидравлическое сопротивление нежели с закругленным углом.
Для нахождения коэффициента местного сопротивления ввиде коленного поворота(см.рис.[б]), используем формулу:

Данная формула применима к трубам малого диаметра ну максимум до 50мм. Чем больше диаметр, тем меньши коеффициент местного сопротивления.
ζ-коеффициент местного сопротивления.
β-угол отвода(колена).
Также для наглядного понимания приведу таблицу:

Данная таблица соответствует опытам с трубами диаметром 30мм.
Видно что при 90° коеффициент местного сопротивления приблизительно равен единице.
Полученный коэффициент местного сопротивления вставляем в формулу:

И получаем потерю напора в метрах.
На практике это обычно ну очень маленькая цыфра и существенно бывает не заметно. Но если у вас очень большие скорости движения жидкости и количество таких местных сопротивлений исчисляется десятками, то следует посчитать обязательно. Каждая потеря на местном сопротивление, просто складывается к остальному числу, если они соеденены последовательно(друг за другом).
Не мало важная формула для нахождения местного сопротивления на отводах с закруленным углом(см.рис.[а]). Это могут быть и гнутые трубы под определенным радиусом и определенным углом.
Данная формула справедливо при условии:


d-внутренний диаметр трубы, в переводе на метры.
R-радиус скругления угла, в переводе на метры.
β-угол сгибания трубы.
Данная формула понадобится тем, кто занимается монтажом теплых водяных полов, при котором очень важно понять, что каждое сгибание трубы это дополнительное местное сопротивление. Поэтому чем меньше будет поворотов, тем меньше будет потерь напора, тем легче и быстрее будет проходить жидкость. Поэтому очень целесообразно использовать при раскладке теплых полов метод улитки. Так как метод улитки позволяет разложить на поверхности пола трубу так, чтобы в нем было меньше поворотов, тем самым уменьшая потерю напора.
Для тех, кто хочет сделать теплый водяной пол своими рукам, вот здесь подробнее: Водяной теплый пол своими руками.
Таблица: (Значение коэффициента сопротивления ζ для отвода на 90° при различных закруглениях).

Я думаю вы уже запомнили, что полученный коэффициент вставляем в формулу:

и получаем потерю напора на местном сопротивлении. Если их много, а их много особенно в теплых полах. Просто необходимо найти потерю напора на одном местном сопротивлении и полученный ответ помножить на количество поворотов.
Ну вот собственно и все, что нам пригодится для расчета местного сопротивления. Если что-то не понятно пишите коментарии, обязательно отвечу.
Следующая статья: Профессиональный расчет диаметра трубы для водоснабжения
Все о дачном доме
Водоснабжение
Обучающий курс. Автоматическое водоснабжение своими руками. Для чайников.
Неисправности скважинной автоматической системы водоснабжения.
Водозаборные скважины
Ремонт скважины? Узнайте нужен ли он!
Где бурить скважину – снаружи или внутри?
В каких случаях очистка скважины не имеет смысла
Почему в скважинах застревают насосы и как это предотвратить
Прокладка трубопровода от скважины до дома
100% Защита насоса от сухого хода
Отопление
Обучающий курс. Водяной теплый пол своими руками. Для чайников.
Теплый водяной пол под ламинат
Обучающий Видеокурс: По ГИДРАВЛИЧЕСКИМ И ТЕПЛОВЫМ РАСЧЕТАМ
Водяное отопление
Виды отопления
Отопительные системы
Отопительное оборудование, отопительные батареи
Система теплых полов
Личная статья теплых полов
Принцип работы и схема работы теплого водяного пола
Проектирование и монтаж теплого пола
Водяной теплый пол своими руками
Основные материалы для теплого водяного пола
Технология монтажа водяного теплого пола
Система теплых полов
Шаг укладки и способы укладки теплого пола
Типы водных теплых полов
Все о теплоносителях
Антифриз или вода?
Виды теплоносителей (антифризов для отопления)
Антифриз для отопления
Как правильно разбавлять антифриз для системы отопления?
Обнаружение и последствия протечек теплоносителей
Как правильно выбрать отопительный котел
Тепловой насос
Особенности теплового насоса
Тепловой насос принцип работы
Запас мощности котла. Нужен ли он?
Про радиаторы отопления
Способы подключения радиаторов. Свойства и параметры.
Как рассчитать колличество секций радиатора?
Рассчет тепловой мощности и количество радиаторов
Виды радиаторов и их особенности
Автономное водоснабжение
Схема автономного водоснабжения
Устройство скважины Очистка скважины своими руками
Опыт сантехника
Подключение стиральной машины
Полезные материалы
Редуктор давления воды
Гидроаккумулятор. Принцип работы, назначение и настройка.
Автоматический клапан для выпуска воздуха
Балансировочный клапан
Перепускной клапан
Трехходовой клапан
Трехходовой клапан с сервоприводом ESBE
Терморегулятор на радиатор
Сервопривод коллекторный. Выбор и правила подключения.
Виды водяных фильтров. Как подобрать водяной фильтр для воды.
Обратный осмос
Фильтр грязевик
Обратный клапан
Предохранительный клапан
Смесительный узел. Принцип работы. Назначение и расчеты.
Расчет смесительного узла CombiMix
Гидрострелка. Принцип работы, назначение и расчеты.
Бойлер косвенного нагрева накопительный. Принцип работы.
Расчет пластинчатого теплообменника
Рекомендации по подбору ПТО при проектировании объектов теплоснабжения
О загрязнение теплообменников
Водонагреватель косвенного нагрева воды
Магнитный фильтр – защита от накипи
Инфракрасные обогреватели
Радиаторы. Свойства и виды отопительных приборов.
Виды труб и их свойства
Незаменимые инструменты сантехника
Интересные рассказы
Страшная сказка о черном монтажнике
Технологии очистки воды
Как выбрать фильтр для очистки воды
Поразмышляем о канализации
Очистные сооружения сельского дома
Советы сантехнику
Как оценить качество Вашей отопительной и водопроводной системы?
Профрекомендации
Как подобрать насос для скважины
Как правильно оборудовать скважину
Водопровод на огород
Как выбрать водонагреватель
Пример установки оборудования для скважины
Рекомендации по комплектации и монтажу погружных насосов
Какой тип гидроаккумулятора водоснабжения выбрать?
Круговорот воды в квартире
фановая труба
Удаление воздуха из системы отопления
Гидравлика и теплотехника
Введение
Что такое гидравлический расчет?
Невязка гидравлического расчета
Физические свойства жидкостей
Гидростатическое давление
Поговорим о сопротивлениях прохождении жидкости в трубах
Режимы движения жидкости (ламинарный и турбулентный)
Гидравлический расчет на потерю напора или как рассчитать потери давления в трубе
Местные гидравлические сопротивления
Профессиональный расчет диаметра трубы по формулам для водоснабжения
Как подобрать насос по техническим параметрам
Профессиональный расчет систем водяного отопления. Расчет теплопотерь водяного контура.
Гидравлические потери в гофрированной трубе
Теплотехника. Речь автора. Вступление
Процессы теплообмена
Тплопроводность материалов и потеря тепла через стену
Как мы теряем тепло обычным воздухом?
Законы теплового излучения. Лучистое тепло.
Законы теплового излучения. Страница 2.
Потеря тепла через окно
Факторы теплопотерь дома
Начни свое дело в сфере систем водоснабжения и отопления
Вопрос по расчету гидравлики
Конструктор водяного отопления
Диаметр трубопроводов, скорость течения и расход теплоносителя.
Вычисляем диаметр трубы для отопления
Расчет потерь тепла через радиатор
Мощность радиатора отопления
Расчет мощности радиаторов. Стандарты EN 442 и DIN 4704
Расчет теплопотерь через ограждающие конструкции
Найти теплопотери через чердак и узнать температуру на чердаке
Подбираем циркуляционный насос для отопления
Перенос тепловой энергии по трубам
Расчет гидравлического сопротивления в системе отопления
Распределение расхода и тепла по трубам. Абсолютные схемы.
Расчет сложной попутной системы отопления
Расчет отопления. Популярный миф
Расчет отопления одной ветки по длине и КМС
Расчет отопления. Подбор насоса и диаметров
Расчет отопления. Двухтрубная тупиковая
Расчет отопления. Однотрубная последовательная
Расчет отопления. Двухтрубная попутная
Расчет естественной циркуляции. Гравитационный напор
Расчет гидравлического удара
Сколько выделяется тепла трубами?
Собираем котельную от А до Я…
Система отопления расчет
Онлайн калькулятор Программа расчет Теплопотерь помещения
Гидравлический расчет трубопроводов
История и возможности программы – введение
Как в программе сделать расчет одной ветки
Расчет угла КМС отвода
Расчет КМС систем отопления и водоснабжения
Разветвление трубопровода – расчет
Как в программе рассчитать однотрубную систему отопления
Как в программе рассчитать двухтрубную систему отопления
Как в программе рассчитать расход радиатора в системе отопления
Перерасчет мощности радиаторов
Как в программе рассчитать двухтрубную попутную систему отопления. Петля Тихельмана
Расчет гидравлического разделителя (гидрострелка) в программе
Расчет комбинированной цепи систем отопления и водоснабжения
Расчет теплопотерь через ограждающие конструкции
Гидравлические потери в гофрированной трубе
Гидравлический расчет в трехмерном пространстве
Интерфейс и управление в программе
Три закона/фактора по подбору диаметров и насосов
Расчет водоснабжения с самовсасывающим насосом
Расчет диаметров от центрального водоснабжения
Расчет водоснабжения частного дома
Расчет гидрострелки и коллектора
Расчет Гидрострелки со множеством соединений
Расчет двух котлов в системе отопления
Расчет однотрубной системы отопления
Расчет двухтрубной системы отопления
Расчет петли Тихельмана
Расчет двухтрубной лучевой разводки
Расчет двухтрубной вертикальной системы отопления
Расчет однотрубной вертикальной системы отопления
Расчет теплого водяного пола и смесительных узлов
Рециркуляция горячего водоснабжения
Балансировочная настройка радиаторов
Расчет отопления с естественной циркуляцией
Лучевая разводка системы отопления
Петля Тихельмана – двухтрубная попутная
Гидравлический расчет двух котлов с гидрострелкой
Система отопления (не Стандарт) – Другая схема обвязки
Гидравлический расчет многопатрубковых гидрострелок
Радиаторная смешенная система отопления – попутная с тупиков
Терморегуляция систем отопления
Разветвление трубопровода – расчет
Гидравлический расчет по разветвлению трубопровода
Расчет насоса для водоснабжения
Расчет контуров теплого водяного пола
Гидравлический расчет отопления. Однотрубная система
Гидравлический расчет отопления. Двухтрубная тупиковая
Бюджетный вариант однотрубной системы отопления частного дома
Расчет дроссельной шайбы
Что такое КМС?
Расчет гравитационной системы отопления
Конструктор технических проблем
Удлинение трубы
Требования СНиП ГОСТы
Требования к котельному помещению
Вопрос слесарю-сантехнику
Полезные ссылки сантехнику
—
Сантехник – ОТВЕЧАЕТ!!!
Жилищно коммунальные проблемы
Монтажные работы: Проекты, схемы, чертежи, фото, описание.
Если надоело читать, можно посмотреть полезный видео сборник по системам водоснабжения и отопления

 исунок
исунок ,
, (15)
(15)
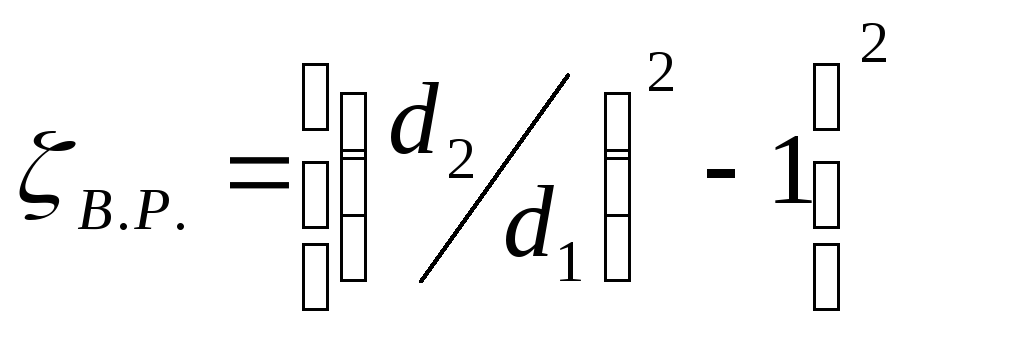 ,
,