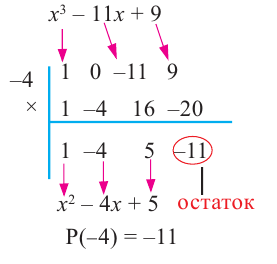
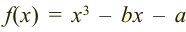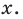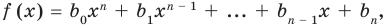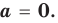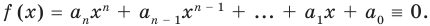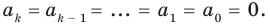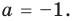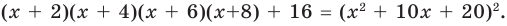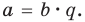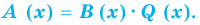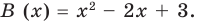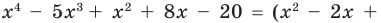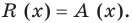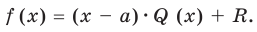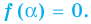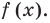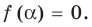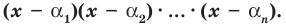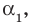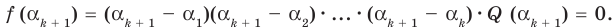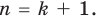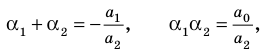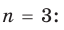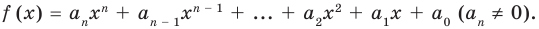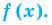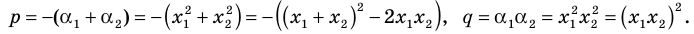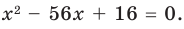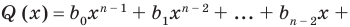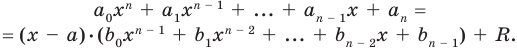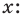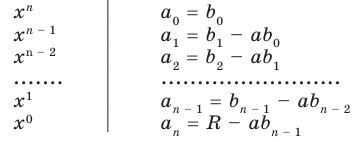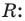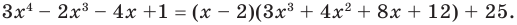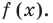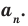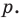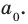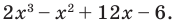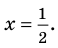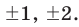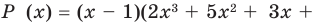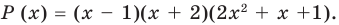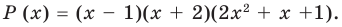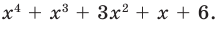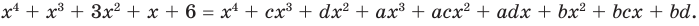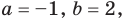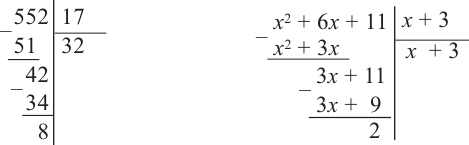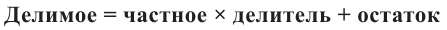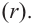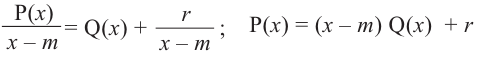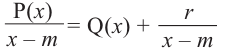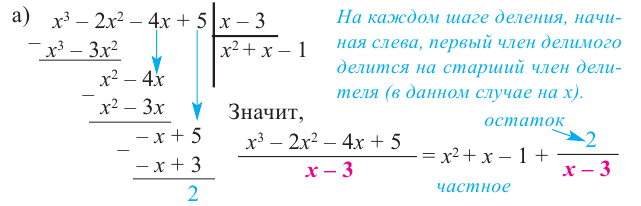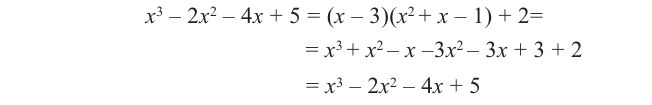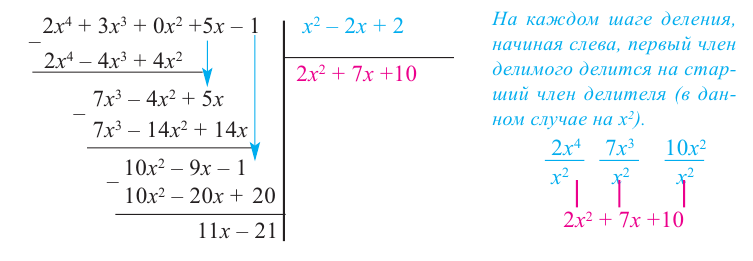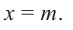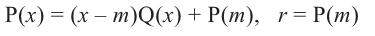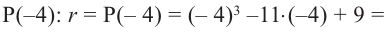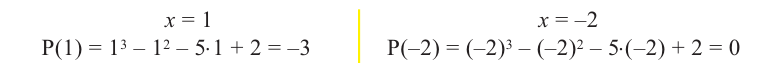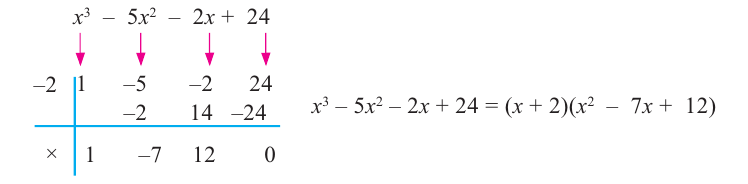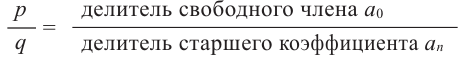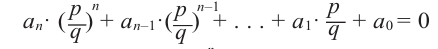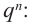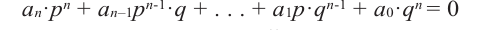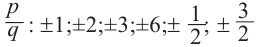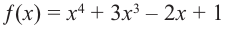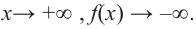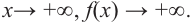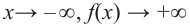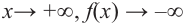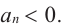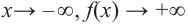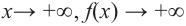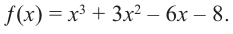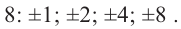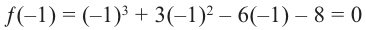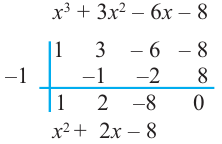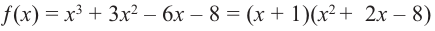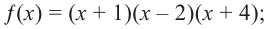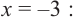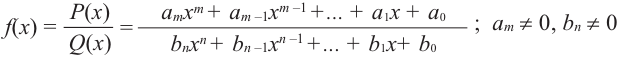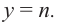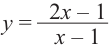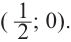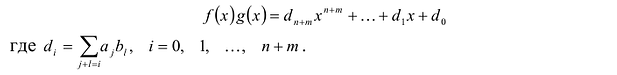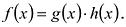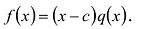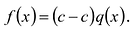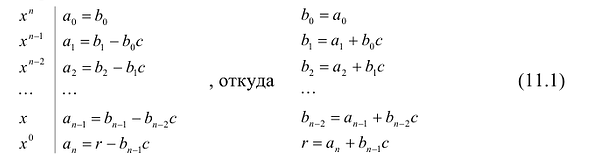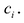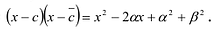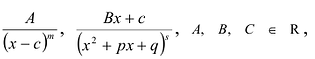После изучения одночленов переходим к многочленам. Данная статья расскажет о всех необходимых сведениях, необходимых для выполнения действий над ними. Мы определим многочлен с сопутствующими определениями члена многочлена, то есть свободный и подобный, рассмотрим многочлен стандартного вида, введем степень и научимся ее находить, поработаем с его коэффициентами.
Многочлен и его члены – определения и примеры
Определение многочлена было дано еще в 7 классе после изучения одночленов. Рассмотрим его полное определение.
Многочленом считается сумма одночленов, причем сам одночлен – это частный случай многочлена.
Из определения следует, что примеры многочленов могут быть различными: 5, 0, −1, x, 5·a·b3, x2·0,6·x·(−2)·y12, -213·x·y2·323·x·x3·y·z и так далее. Из определения имеем, что 1+x, a2+b2 и выражение x2-2·x·y+25·x2+y2+5,2·y·x являются многочленами.
Рассмотрим еще определения.
Членами многочлена называются его составляющие одночлены.
Рассмотрим такой пример, где имеем многочлен 3·x4−2·x·y+3−y3, состоящий из 4 членов: 3·x4, −2·x·y, 3 и −y3. Такой одночлен можно считать многочленом, который состоит из одного члена.
Многочлены, которые имеют в своем составе 2, 3 трехчлена имеют соответственное название – двучлен и трехчлен.
Отсюда следует, что выражение вида x+y – является двучленом, а выражение 2·x3·q−q·x·x+7·b – трехчленом.
По школьной программе работали с линейным двучленом вида a·x+b, где а и b являются некоторыми числами, а х – переменной. Рассмотрим примеры линейных двучленов вида: x+1, x·7,2−4 с примерами квадратных трехчленов x2+3·x−5 и 25·x2-3x+11.
Для преобразования и решения необходимо находить и приводить подобные слагаемые. Например, многочлен вида 1+5·x−3+y+2·x имеет подобные слагаемые 1 и -3, 5х и 2х. Их подразделяют в особую группу под названием подобных членов многочлена.
Подобные члены многочлена – это подобные слагаемые, находящиеся в многочлене.
В примере, приведенном выше, имеем, что 1 и -3, 5х и 2х являются подобными членами многочлена или подобными слагаемыми. Для того, что бы упростить выражение, применяют нахождение и приведение подобных слагаемых.
Многочлен стандартного вида
У всех одночленов и многочленов имеются свои определенные названия.
Многочленом стандартного вида называют многочлен, у которого каждый входящий в него член имеет одночлен стандартного вида и не содержит подобных членов.
Из определения видно, что возможно приведение многочленов стандартного вида, например, 3·x2−x·y+1 и __formula__, причем запись в стандартном виде. Выражения 5+3·x2−x2+2·x·z и 5+3·x2−x2+2·x·z многочленами стандартного вида не является, так как первый из них имеет подобные слагаемые в виде 3·x2 и −x2, а второй содержит одночлен вида x·y3·x·z2, отличающийся от стандартного многочлена.
Если того требуют обстоятельства, иногда многочлен приводится к стандартному виду. Многочленом стандартного вида считается и понятие свободного члена многочлена.
Свободным членом многочлена является многочлен стандартного вида, не имеющий буквенной части.
Иначе говоря, когда запись многочлена в стандартном виде имеет число, его называют свободным членом. Тогда число 5 является свободным членом многочлена x2·z+5, а многочлен 7·a+4·a·b+b3 свободного члена не имеет.
Степень многочлена – как ее найти?
Определение самой степени многочлена базируется на определении многочлена стандартного вида и на степенях одночленов, которые являются его составляющими.
Степенью многочлена стандартного вида называют наибольшую из степеней, входящих в его запись.
Рассмотрим на примере. Степень многочлена 5·x3−4 равняется 3, потому как одночлены, входящие в его состав, имеют степени 3 и 0, а большее из них 3 соответственно. Определение степени из многочлена 4·x2·y3−5·x4·y+6·x равняется наибольшему из чисел, то есть 2+3=5, 4+1=5 и 1, значит 5.
Следует выяснить, каким образом находится сама степень.
Степень многочлена произвольного числа – это степень соответствующего ему многочлена в стандартном виде.
Когда многочлен записан не в стандартном виде, но нужно найти его степень, необходимо приведение к стандартному, после чего находить искомую степень.
Найти степень многочлена 3·a12−2·a·b·c·a·c·b+y2·z2−2·a12−a12.
Решение
Для начала представим многочлен в стандартном виде. Получим выражение вида:
3·a12−2·a·b·c·a·c·b+y2·z2−2·a12−a12= =(3·a12−2·a12−a12)−2·(a·a)·(b·b)·(c·c)+y2·z2= =−2·a2·b2·c2+y2·z2
При получении многочлена стандартного вида получаем, что отчетливо выделяются два из них −2·a2·b2·c2 и y2·z2. Для нахождения степеней посчитаем и получим, что 2+2+2=6 и 2+2=4. Видно, что наибольшая из них равняется 6. Из определения следует, что именно 6 является степенью многочлена −2·a2·b2·c2+y2·z2, следовательно и исходного значения.
Ответ: 6.
Коэффициенты членов многочлена
Когда все члены многочлена являются одночленами стандартного вида, то в таком случаем они имеют название коэффициентов членов многочлена. Иначе говоря, их можно называть коэффициентами многочлена.
При рассмотрении примера видно, что многочлен вида 2·x−0,5·x·y+3·x+7 имеет в своем составе 4 многочлена: 2·x, −0,5·x·y, 3·x и 7 с соответствующими их коэффициентами 2, −0,5, 3 и 7. Значит, 2, −0,5, 3 и 7 считаются коэффициентами членов заданного многочлена вида 2·x−0,5·x·y+3·x+7. При преобразовании важно обращать внимание на коэффициенты, стоящие перед переменными.
Содержание:
Многочлен – это сумма одночленов, причем сам одночлен – это частный случай многочлена.
История многочелена:
Живший в 1050-1122 гг Омар Хаям известен в мире как мастер рубай. Однако имя Омара Хаяма также упоминается наряду с именами гениальных математиков. Именно Омар Хаям впервые представил общую формулу корней уравнения кубического многочлена
Многочлены от одной переменной и действия над ними
Определение многочленов от одной переменной и их тождественное равенство
Рассмотрим одночлен и многочлен, которые зависят только от одной переменной, например, от переменной
По определению одночлена числа и буквы (в нашем случае одна буква — 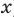
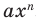
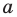
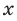
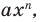
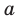
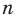
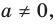
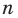
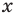
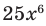
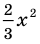
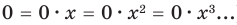
По определению многочлен от одной переменной 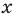
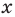
многочленом от одной переменной 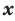
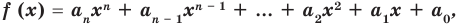
где коэффициенты 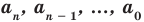
Если 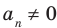
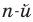
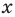
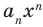
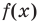
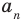
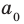
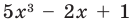
Заметим, что иногда нумерацию коэффициентов многочлена начинают с начала записи выражения (1), и тогда общий вид многочлена 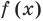
где 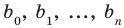
Теорема 1. Одночлены 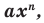
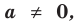
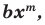
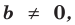
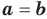
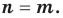
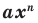
Поскольку равенство одночленов
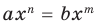
выполняется при всех значениях 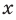
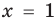
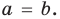
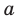
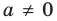
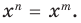
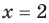
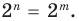
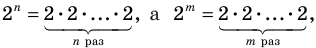
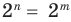
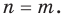
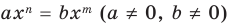
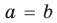
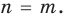
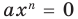
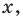
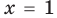
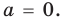
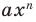
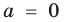
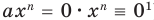
Далее любой одночлен вида 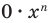
Теорема 2. Если многочлен 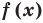
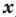
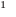
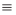
Для доказательства используем метод математической индукции. Пусть
При 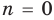
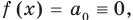
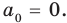
Предположим, что при 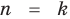
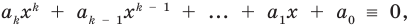
Докажем, что данное утверждение выполняется и при 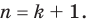
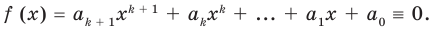
Поскольку равенство (3) выполняется при всех значениях 
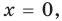
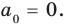
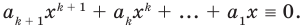

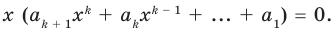
Равенство (4) должно выполняться при всех значениях 
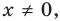
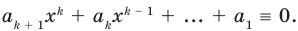
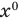
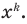
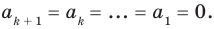
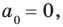
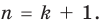
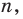
Многочлен, у которого все коэффициенты равны нулю, обычно называют нулевым многочленом, или нуль-многочленом, и обозначают 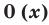
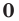
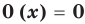
Теорема 3. Если два многочлена 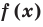
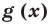
Пусть многочлен 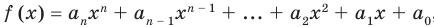
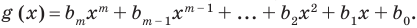
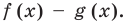
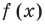
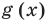
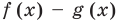
Но 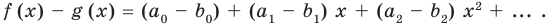
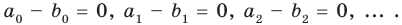
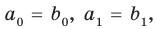
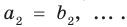
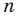
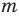
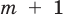
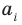
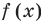
имеют одинаковую степень и соответственно равные коэффициенты при одинаковых степенях.
Теорема 3 является основанием так называемого метода неопределенных коэффициентов. Покажем его применение на следующем примере.
Пример:
Докажите, что выражение
является полным квадратом.
Решение:
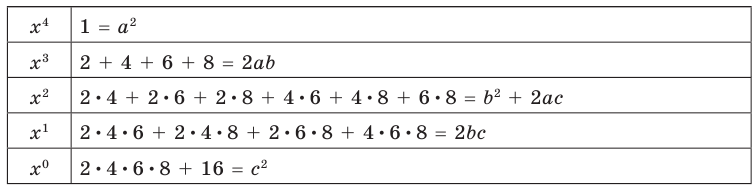
► Данное выражение может быть записано в виде многочлена четвертой степени, поэтому оно может быть полным квадратом только многочлена второй степени вида 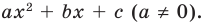
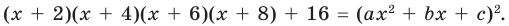
Раскрывая скобки в левой и правой частях этого тождества и приравнивая коэффициенты при одинаковых степенях 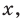
Из первого равенства получаем 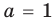
При 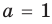
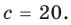
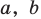
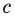
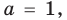
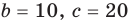
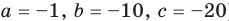
Действия над многочленами. Деление многочлена на многочлен с остатком
Сложение и умножение многочленов от одной переменной выполняется с помощью известных правил сложения и умножения многочленов. В результате выполнения действий сложения или умножения над многочленами от одной переменной всегда получаем многочлен от той же переменной.
Из определения произведения двух многочленов вытекает, что старший член произведения двух многочленов равен произведению старших членов множителей, а свободный член произведения равен произведению свободных членов множителей. Отсюда получаем, что степень произведения двух многочленов равна сумме степеней множителей.
При сложении многочленов одной степени получаем многочлен этой же степени, хотя иногда можно получить многочлен меньшей степени. Например, 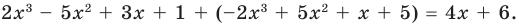
Например, 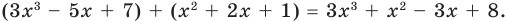
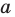
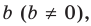
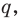
Определение: Многочлен 
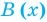
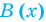

Как и для целых чисел, операция деления многочлена на многочлен выполняется не всегда, поэтому во множестве многочленов вводится операция деления с остатком. Говорят, что
многочлен 








Например, поскольку 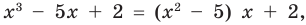
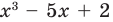
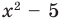
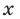
Иногда деление многочлена на многочлен удобно выполнять «уголком», как и деление многозначных чисел, пользуясь следующим алгоритмом.
Пример №1
Разделим многочлен 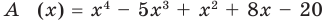
Решение:
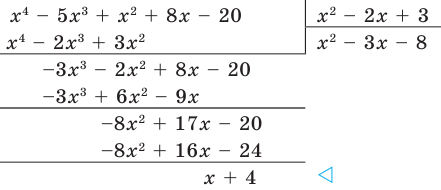
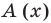
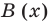
Если обозначить результат выполнения первого шага алгоритма через 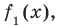
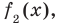
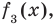
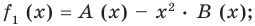
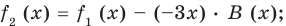
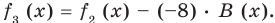
Сложим почленно равенства (1), (2), (3) и получим
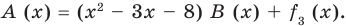
Учитывая, что степень многочлена 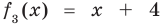
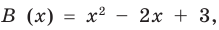
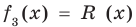
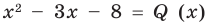
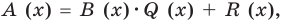
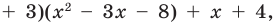
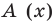
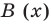
Очевидно, что приведенное обоснование можно провести для любой пары многочленов 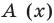
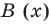
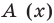
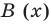
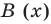
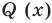
Отметим, что в случае, когда степень делимого 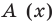
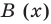
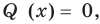
Теорема Безу. Корни многочлена. Формулы Виета
Рассмотрим деление многочлена 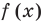
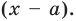
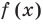
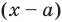
Это равенство выполняется тождественно, то есть при любом значении 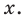
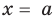
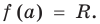
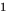
Теорема 1 (теорема Безу). Остаток от деления многочлена 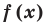
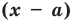
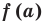
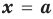
Пример №2
Докажите, что 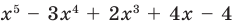
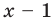
Решение:
► Подставив в 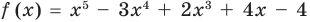
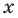
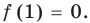
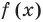

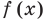

Определение: Число 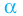
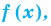
Если многочлен 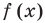

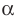
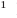
Действительно, если 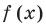
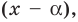

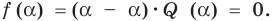
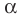
Справедливо и обратное утверждение. Оно является следствием теоремы Безу.
Теорема 2. Если число 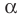
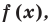
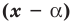
По теореме Безу остаток от деления 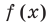

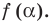
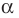
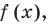
Обобщением теоремы 2 является следующее утверждение.
Теорема 3. Если многочлен 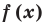
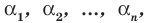
Для доказательства используем метод математической индукции.
При 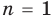
Допустим, что утверждение справедливо при 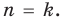
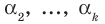
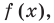
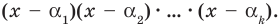
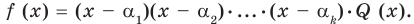
Докажем, что утверждение теоремы справедливо и при 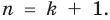
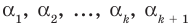
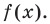
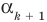
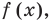
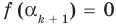
По условию все корни 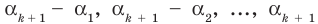
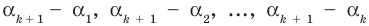
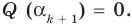
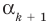
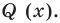
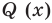
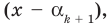
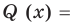
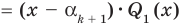
Это означает, что 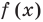
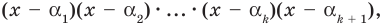
Таким образом, теорема справедлива для любого натурального
Следствие. Многочлен степени 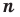
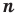
Допустим, что многочлен 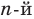
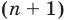
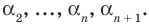
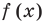
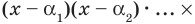
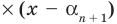
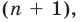
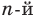
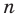
Пусть теперь многочлен 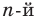
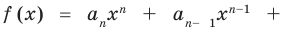
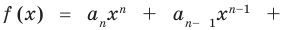
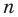
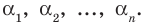
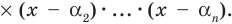
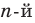
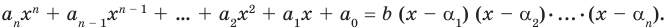
Если раскрыть скобки в правой части равенства (2) и приравнять коэффициенты при старших степенях, то получим, что 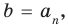
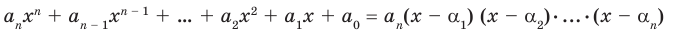
Сравнивая коэффициенты при одинаковых степенях 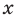
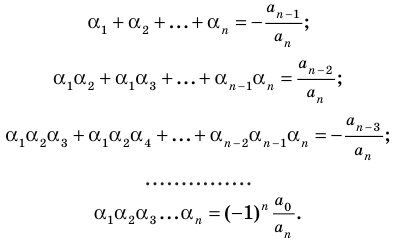
Например, при 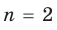
а при
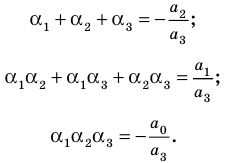
Выполнение таких равенств является необходимым и достаточным
условием того, чтобы числа 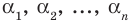
Формулы (3) и (4) справедливы не только для случая, когда все корни многочлена 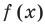
Если многочлен 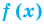
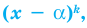
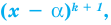


Например, если произведение 
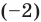
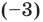
При использовании формул Виета в случае кратных корней необходимо каждый корень записать такое количество раз, которое равно его кратности.
Пример №3
Проверьте справедливость формул Виета для многочлена
Решение:
►
Поэтому 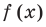
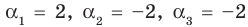
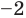
Проверим справедливость формулы (5). В нашем случае: 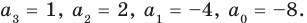
Как видим, все равенства выполняются, поэтому формулы Виета справедливы для данного многочлена.
Пример №4
Составьте квадратное уравнение, корнями которого являются квадраты корней уравнения
Решение:
► Обозначим корни уравнения 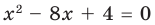
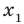
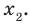
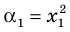
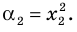
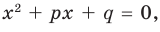
По формулам Виета имеем 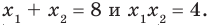
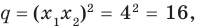
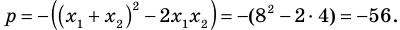
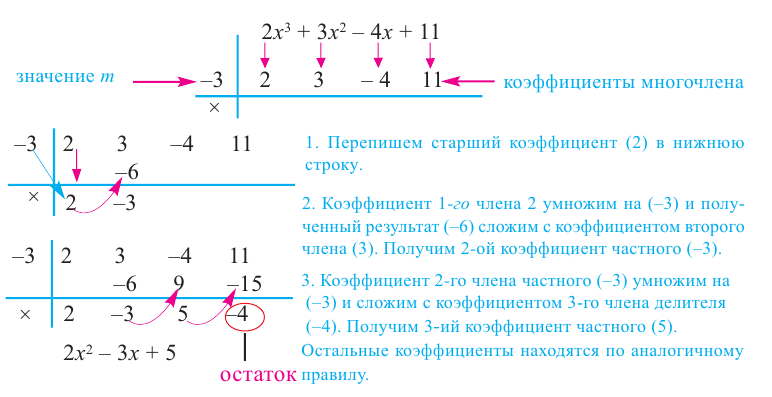
Схема Горнера
Делить многочлен 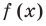
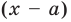
специальной схемы, которую называют схемой Горнера.
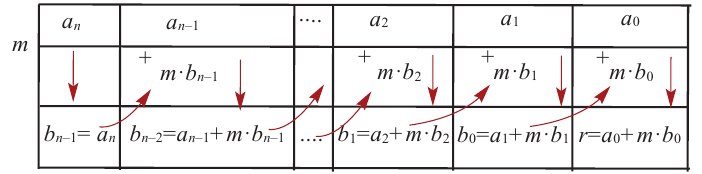
Пусть многочлен 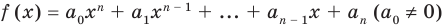
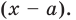
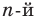
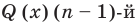
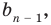
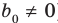
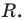
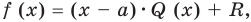
Левая и правая части полученного равенства тождественно равны, поэтому, перемножив многочлены, стоящие в правой части, можем приравнять коэффициенты при соответствующих степенях
Найдем из этих равенств коэффициенты 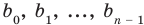
Как видим, первый коэффициент неполного частного равен первому коэффициенту делимого. Остальные коэффициенты неполного частного и остаток находятся одинаково: для того чтобы найти коэффициент 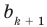
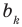
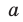
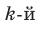
Пример №5
Разделите по схеме Горнера многочлен 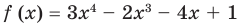
Решение:
► Запишем сначала все коэффициенты многочлена 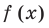
Таким образом,
Пример №6
Проверьте, является ли 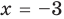
Решение:
► По теореме Безу остаток от деления многочлена 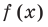
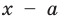
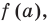
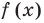
Поскольку 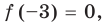
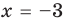
Нахождение рациональных корней многочлена с целыми коэффициентами
Теорема 4. Если многочлен с целыми коэффициентами 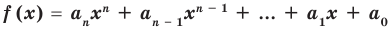
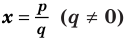
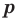
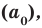
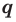
Если 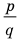
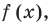
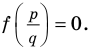
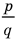
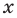
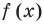
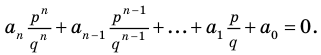
Умножим обе части равенства (1) на 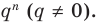
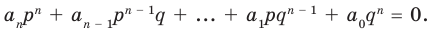
В равенстве (2) все слагаемые, кроме последнего, делятся на 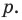
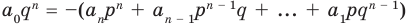
Но когда мы записываем рациональное число в виде 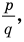
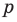
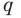
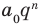
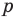
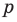
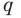
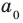
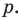
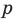
Аналогично все слагаемые равенства (2), кроме первого, делятся на 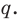
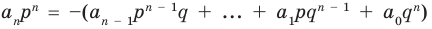
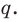
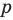
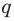
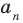
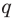
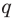
Отметим два следствия из этой теоремы. Если взять 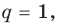
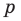
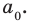
Следствие 1. Любой целый корень многочлена с целыми коэффициентами является делителем его свободного члена.
Если в заданном многочлене 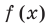
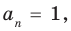
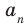
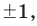
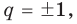
Следствие 2. Если коэффициент при старшем члене уравнения с целыми коэффициентами равен 1, то все рациональные корни этого уравнения (если они существуют) — целые числа.
Пример №7
Найдите рациональные корни многочлена
Решение:
► Пусть несократимая дробь 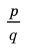
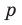
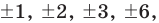
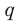
Таким образом, рациональные корни многочлена необходимо искать среди чисел 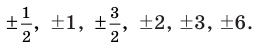
При 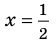
Кроме того, по схеме Горнера можно записать, что
Многочлен 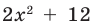
Пример №8
Разложите многочлен 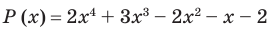
Решение:
► Ищем целые корни многочлена среди делителей свободного члена:
Подходит 1. Делим 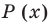

Тогда
Ищем целые корни кубического многочлена 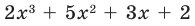
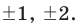
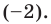
Имеем
Квадратный трехчлен 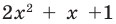
Ответ:
Отметим, что во множестве действительных чисел не всегда можно найти все корни многочлена (например, квадратный трехчлен 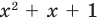
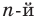
Например, многочлен четвертой степени раскладывается на произведение двух квадратных трехчленов. Для нахождения коэффициентов этого разложения иногда можно применить метод неопределенных коэффициентов.
Пример №9
Разложите на множители многочлен
Решение:
► Попытка найти рациональные корни ничего не дает: многочлен не имеет рациональных (целых) корней.
Попытаемся разложить этот многочлен на произведение двух квадратных трехчленов. Поскольку старший коэффициент многочлена равен 1, то и у квадратных трехчленов возьмем старшие коэффициенты равными 1. То есть будем искать разложение нашего многочлена в виде:
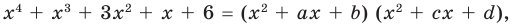
где 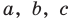
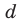
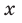
Получаем систему
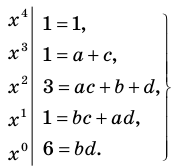
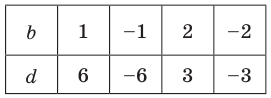
Попытка решить эту систему методом подстановки приводит к уравнению 4-й степени, поэтому попробуем решить систему (4) в целых числах. Из последнего равенства системы (4) получаем, что 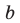
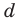
Коэффициенты 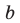
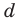
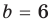
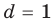
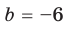
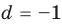
Для каждой пары значений 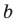
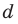
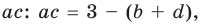
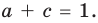
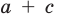
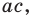
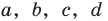
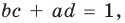
Как видим, системе (4) удовлетворяет набор целых чисел 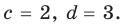
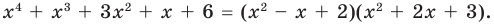
Поскольку квадратные трехчлены 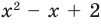
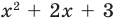
Деление многочлена на многочлен
Задача. Объём подарочных коробок, размеры которых даны в сантиметрах, можно смоделировать функцией 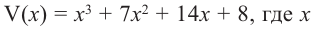
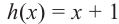
Исследование. Изучите, как правило деления многозначных чисел столбиком можно применить при делении многочлена.
a) Для каждого из двух случаев укажите, какие числа и какие многочлены соответствуют понятиям делимое, делитель и частное.
b) Как был найден первый член при делении многочлена? Каковы сходные и отличительные черты данного деления и деления многозначных чисел?
c) Как вы убедились,что каждое из двух делений выполнено правильно?
Выражение вида 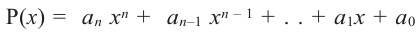
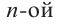
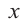
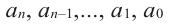
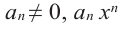
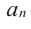
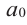
Деление целого числа па целое число можно проверить равенством
Аналогичное правило справедливо и при делении многочлена на многочлен. Если многочлен 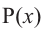
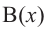
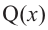
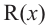
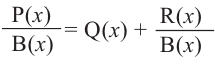
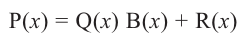
Здесь, степень многочлена 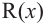
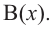
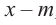
В этом случае:
Пример №10
а) Разделите многочлен 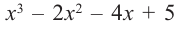
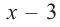
Ответ запишите в виде
b) Определите множество допустимых значений переменной.
c) Выполните проверку.
Решение:
b) При этом 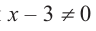
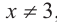
c) Должно выполняться тождество
Пример №11
Разделите 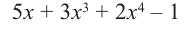
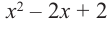
Решение:
запишем делимое в порядке убывания степеней. Введем в запись отсутствующие члены с коэффициентом равным 0.
Пример №12
1) Исследуйте деление столбиком многочлена 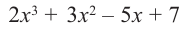
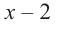
2) На каждом шаге деления делимое делится на старший член делителя, на 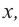
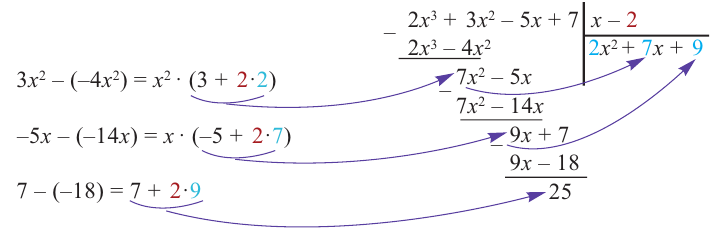
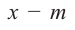
При делении многочлена на двучлен вида 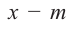
Пример №13
Разделите многочлен 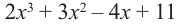
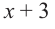
Решение:
коэффициенты делимого записываются в порядке убывания степеней (отсутствующий член записывается с коэффициентом равным нулю). Если двучлен имеет вид 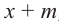
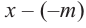
Запишем двучлен 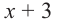
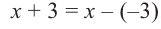
Таким образом, для делимого 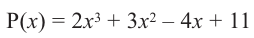
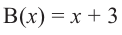
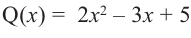
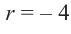
Деление можно записать в виде: 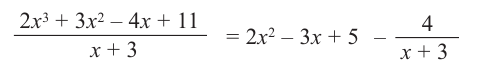
Теорема об остатке
Теорема об остатке (Теорема Безу)
Остаток от деления многочлена 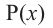
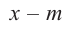
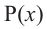
Доказательство: В равенстве 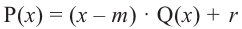
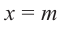
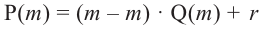
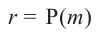
Пример №14
Найдите остаток от деления многочлена 
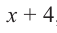
Решение: запишем делитель в виде 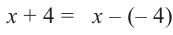
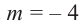
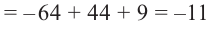
Проверим решение.
Теорема о разложении многочлена на множители
Значения переменной 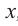
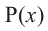
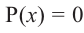
Теорема. Если число 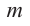
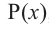
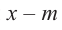
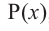
Действительно, если 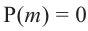
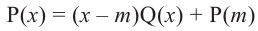
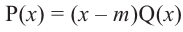
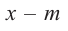
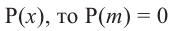
Пример №15
При помощи теоремы о разложении многочлена на множители определите, являются ли двучлены 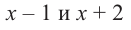
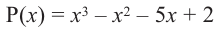
Решение: вычислим значение многочлена 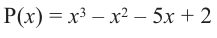
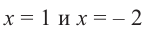
Значит, 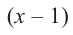
Пример №16
Зная, что 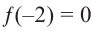
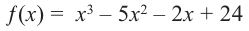
Решение: так как 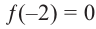
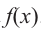
Учитывая, что 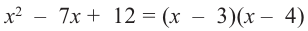
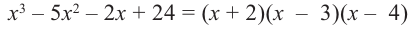
Отсюда получаем, что 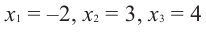
Примечание: Если многочлен задан в виде 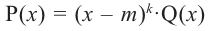
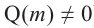
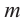
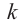
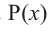
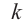
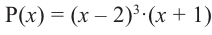
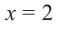
Нахождение рациональных корней
Теорема о рациональных корнях
Если для многочлена 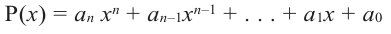
Доказательство. Пусть несократимая дробь 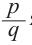
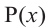
Умножим обе части равенства на
Так как в последнем равенстве каждый член, кроме члена 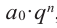
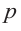
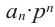
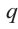
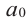
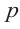
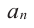
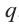
Пример №17
Найдите рациональные корни многочлена 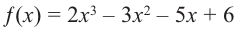
Решение: свободный член 6, старший коэффициент 2.
Для 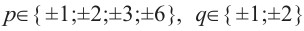
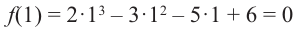
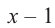
Так как, 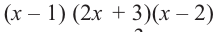
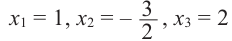
Следствие 1. Если старший коэффициент 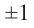
Следствие 2. Целые корни многочлена с целыми коэффициентами (если они имеются) являются делителями свободного члена.
Пример №18
Найдите корни многочлена
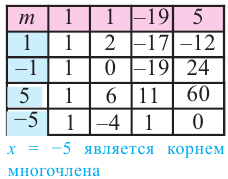
Решение: по теореме о рациональных корнях многочлена, целый корень данного многочлена (если он существует) надо искать среди делителей числа 5. Это числа ±5; ±1.
Запишем это короче при помощи синтетического деления и проверим, являются ли эти числа корнями многочлена.
Так как 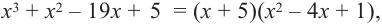
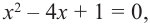
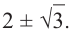
Внимание! Если коэффициенты многочлена являются рациональными числами, то для нахождения рациональных корней уравнения 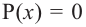
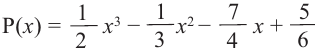
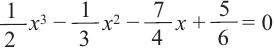
уравнение
Для нахождения рациональных корней выполните следующие действия.
1. Записывается множество всех возможных дробей, числителями которых являются делители свободного члена, а знаменателями являются делители старшего коэффициента.
2. Из этих чисел выбирается число 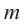
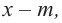
3. Для данного многочлена при помощи синтетического деления на двучлен 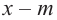
4. Если другой множитель является квадратным трехчленом или его можно разложить при помощи формул сокращенного умножения, находятся другие корни. Иначе все линейные множители находятся синтетическим делением.
5. Возможно, что ни одно число из списка не будет нулем многочлена. В этом случае многочлен не имеет рациональных корней. Например, рациональными корнями многочлена 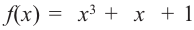
Проверим: 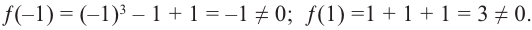
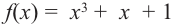
Основная теорема алгебры
Покажем на примере, что многочлен 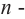
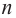
Пример №19
Найдите все корни многочлена
Решение: рациональными корнями данного многочлена (если они существуют), согласно правилу, могут являться числа ±1, ±5. Проверим:
Значит, 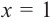
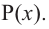
В выражении 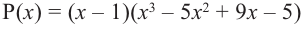
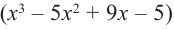
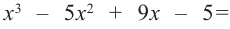
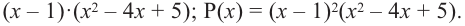
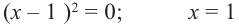
Корни:
Во всех рассмотренных нами примерах уравнение 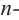
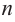
Теорема. Любой многочлен ненулевой степени имеет хотя бы один корень на множестве комплексных чисел.
Если 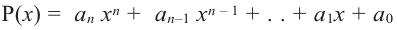
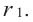
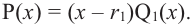
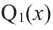
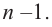
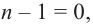
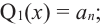
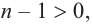
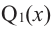
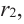
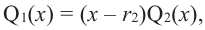
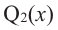
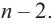
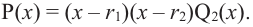
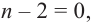
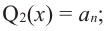
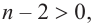
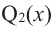
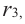
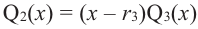
Продолжая процесс 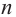
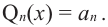
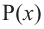
здесь числа 
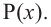
Следствие. Многочлен 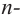
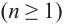
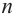
Отметим, что если комплексное число 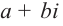
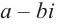
Любой многочлен с действительными коэффициентами можно представить в виде произведения двучленов вида 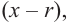
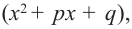
Отсюда можно сделать вывод, что многочлен нечетной степени с действительными коэффициентами всегда имеет действительные корни.
Пример №20
Запишите в виде произведения множителей многочлен наименьшей степени, если коэффициент при старшем члене равен 2, а корни равны 3 и
Решение: так как число 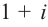
- Заказать решение задач по высшей математике
Пример №21
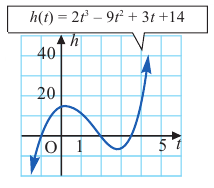
При движении скоростной карусели в Лунапарке изменение высоты (в метрах) кабины от нулевого уровня за первые 5 секунд можно смоделировать функцией 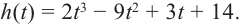
Решение: во всех случаях, кроме значений 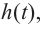
1. Проверим, является ли число 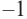
2. Число 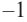
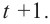
Учитывая, что 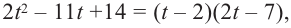
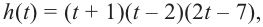
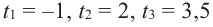
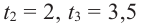
Функция-многочлен
График функции-многочлен
В стандартном виде функция – многочлен записывается как 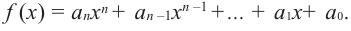
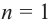
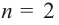
При возрастании значений аргумента по абсолютному значению многочлен ведет себя как функция старшего члена 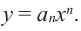
Пример №22
Определите характер поведения функции – многочлен в зависимости от степени и коэффициента при старшем члене при возрастании аргумента по абсолютному значению.
a) 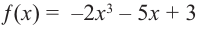
Решение: а) степень многочлена 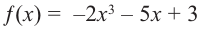
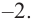
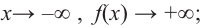
b) степень многочлена 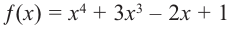
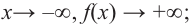
Пример №23
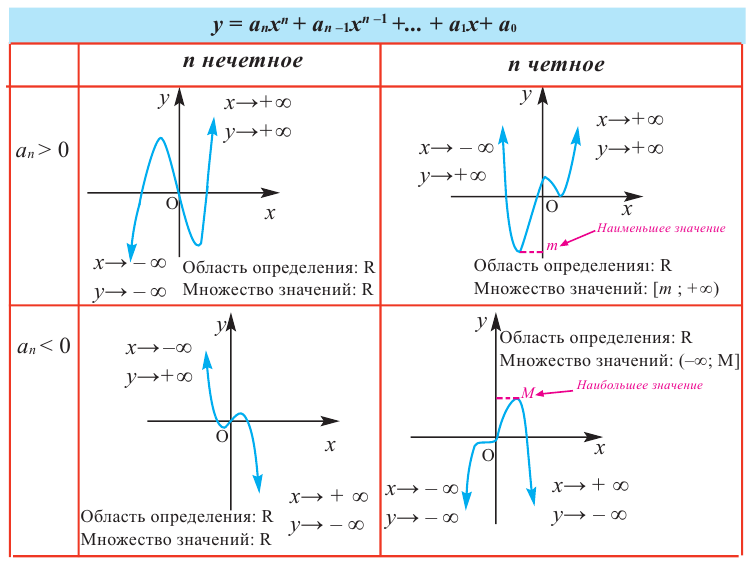
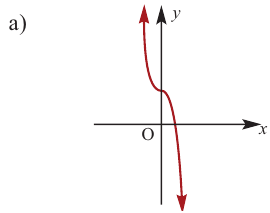
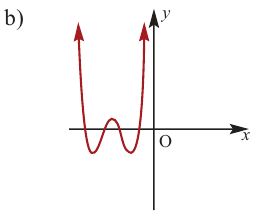
По графику определите как ведет себя функция – многочлен при неограниченном возрастании аргументов но абсолютному значению, четность или нечетность степени многочлена, знак коэффициента старшего члена.
Решение:
при
при
Многочлен нечетной степени
Решение:
при
при
Многочлен четной степени
Отметим, что если 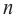
Алгоритм построения эскиза графика функции – многочлен.
1. Находятся точки пересечения графика с осями координат (если они есть). Эти точки отмечаются на координатной плоскости.
2. Вычисляются значения функции в некоторых точках между действительными нулями. Соответствующие точки отмечаются на координатной плоскости.
3. Определяется поведение графика при больших значениях аргумента по абсолютному значению.
4. На основе полученных данных строят схематически график.
Пример №24
Постройте график функции
Решение:
1. Применим теорему о рациональных корнях. Разложим многочлен на множители и найдем нули функции.
По теореме возможные рациональные нули надо искать среди чисел, которые являются делителями числа
Проверим 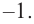
Значит, двучлен 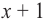
Зная, что 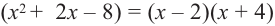
Отсюда находим нули 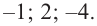
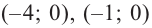
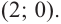
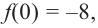
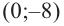
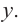
2. Найдем еще несколько значений функции в точках, не требующих сложных вычислений. Например, в точках 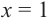
Отметим точки
3. Определим, как меняется график при уменьшении или увеличении значений 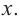
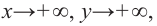
4. Соединим отмеченные точки и получим схематический график функции
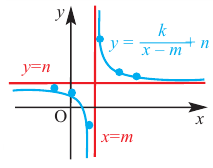
Рациональная функция
Рациональной функцией называется функция, которою можно представить в виде отношения двух многочленов:
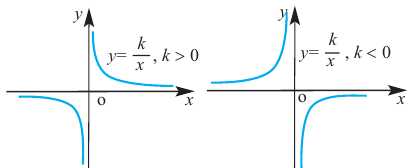
Самым простым примером рациональной функции является функция
График функции 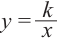
При стремлении значений 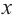
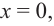
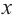
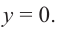
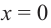
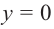
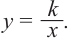
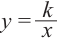
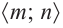
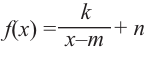
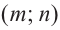
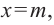
Пример №25
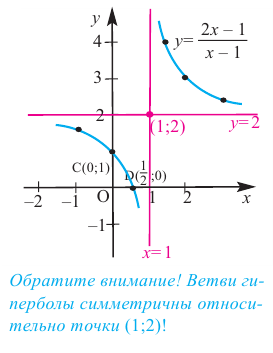
Постройте график функции
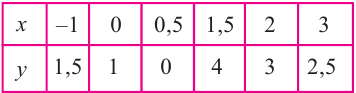
Решение: точки пересечения с осью 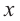
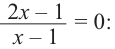
При 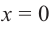
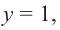
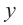
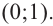
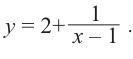
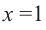
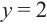
Отметим на координатной плоскости точки, соответствующие парам значений из таблицы и, учитывая горизонтальную и вертикальную асимптоту, изобразим ветви гиперболы, которые пересекают координатные оси в точках 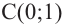
В общем случае, для построения графика рациональной функции надо найти точки пересечения с осями координат (если они есть) и ее асимптоты. Если выражение, которое задает рациональную функцию, имеет вид дроби, знаменатель которой обращается в нуль в точке 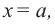
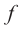
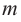
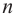
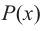
Для 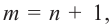
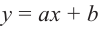
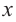
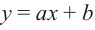
Пример №26
Найдите асимптоты и схематично изобразите график функции
Решение: Точки пересечения с осью 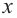
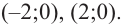
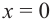
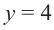
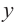
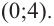
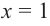
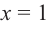
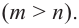
Для больших, но модулю, значений 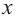
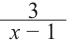
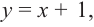
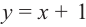
Отметим точки, координаты которых соответствуют парам из таблицы. Учитывая вертикальную и наклонную асимптоту, схематично изобразим график функции.
Многочлены в линейной алгебре
Многочленом от переменной х степени n называется выражение вида:
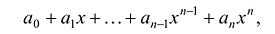
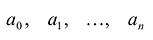
Если коэффициент 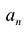
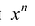
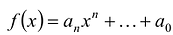
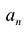
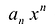
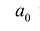
Два многочлена называются равными, если они имеют одинаковую степень и коэффициенты при одинаковых степенях равны.
Суммой многочленов 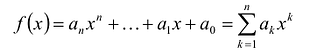
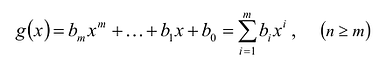
Произведением многочленов 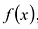
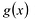
Легко проверить, что сложение и умножение многочленов ассоциативно, коммутативно и связаны между собой законом дистрибутивности.
Многочлен 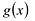
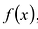
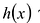
Теорема о делении с остатком
Для любых многочленов 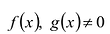
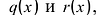
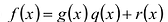
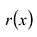
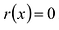
Многочлены g(x) и r(x) называются соответственно частным и остатком. Если g(x) делит 
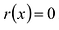
Число с называется корнем многочлена 

Теорема Безу
Число с является корнем многочлена 

Пусть с – корень многочлена 


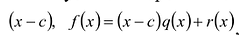
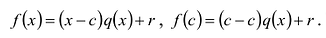

Обратно, пусть (х-с) делит 
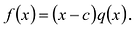
Следствие. Остаток от деления многочлена 
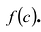
Многочлены первой степени называются линейными многочленами. Теорема Безу показывает, что разыскание корней многочлена 
Многочлен 
Пусть 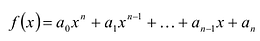
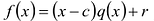
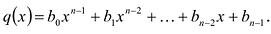
Число с-называется корнем кратности к многочлена 
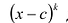

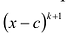

Чтобы поверить, будет ли число с корнем многочлена 

Число различных корней многочлена не превосходит его степени.
Большое значение имеет следующая основная теорема.
Основная теорема. Всякий многочлен с числовыми коэффициентами ненулевой степени имеет хотя бы один корень (может быть комплексный).
Следствие. Всякий многочлен степени 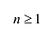
где 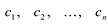

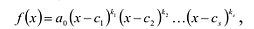
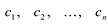

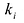
Если многочлен 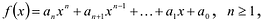
Значит, у многочлена с действительными коэффициентами комплексные корни входят парами.
Следствие. Многочлен с действительными коэффициентами нечетной степени имеет нечетное число действительных корней.
Пусть 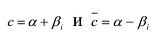


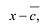
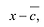

Утверждение 2. Многочлен с действительными коэффициентами степени 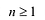
При вычислении интегралов от рациональных функций нам понадобится представление рациональной дроби в виде суммы простейших.
Рациональной дробью называется дробь где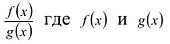
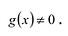

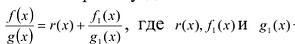
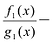
Лемма 1, Если 
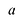
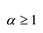
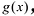
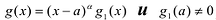
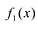
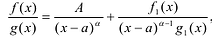
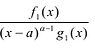
При этом несложно показать, что полученное выражение является рациональной дробью с вещественными коэффициентами.
Лемма 2. Если 
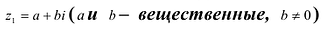
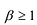
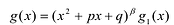
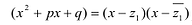
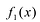
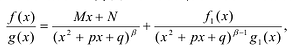
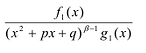
Рациональные дроби вида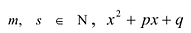
Всякая правильная рациональная дробь представима единственным образом в виде суммы простейших дробей.
При практическом получении такого разложения оказывается удобным так называемый метод неопределенных коэффициентов.
Он состоит в следующем:
При этом если степень многочлена 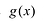
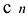
Число неизвестных 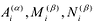
Таким образом, получается система n уравнений с n неизвестными. Существование решения у этой системы следует из приведенной выше теоремы.
- Квадратичные формы – определение и понятие
- Системы линейных уравнений с примерами
- Линейное программирование
- Дифференциальное исчисление функций одной переменной
- Кривые второго порядка
- Евклидово пространство
- Матрица – виды, операции и действия с примерами
- Линейный оператор – свойства и определение
Содержание
- Примеры степени полинома
- Таблица 1. Примеры многочленов и их степеней.
- Порядок работы с многочленами
- Упорядочить, уменьшить и дополнить многочлен
- Важность степени полинома при сложении и вычитании
- Решенные упражнения
- – Упражнение решено 1
- Решение
- – Упражнение выполнено 2
- Решение
- Ссылки
В степень полинома в а переменная задается членом с наибольшим показателем, и если многочлен имеет две или более переменных, то степень определяется суммой показателей каждого члена, причем большая сумма является степенью полинома.
Давайте посмотрим, как определить степень многочлена на практике.
Предположим, что многочлен P (x) = -5x + 8x3 + 7 – 4x2. Этот многочлен является одной переменной, в данном случае это переменная Икс. Этот многочлен состоит из нескольких членов, а именно:
-5x; 8x3; 7; – 4x2
Давайте выберем из четырех членов тот, у которого показатель больше, это член:
8x3
А теперь какой показатель? Ответ: 3. Следовательно, P (x) – многочлен степени 3.
Если рассматриваемый многочлен имеет более одной переменной, то степень может быть:
-Абсолютный
-По отношению к переменной
Абсолютная степень находится, как объяснено в начале: добавление показателей каждого члена и выбор наибольшего.
Вместо этого степень полинома по отношению к одной из переменных или букв является наибольшим значением показателя степени, которое имеет указанная буква. Суть станет яснее с примерами и решенными упражнениями в следующих разделах.
Примеры степени полинома
Многочлены могут быть классифицированы по степени: первая степень, вторая степень, третья степень и так далее. В примере на рисунке 1 энергия является одночленом первой степени массы.
Также важно отметить, что количество членов, которые имеет многочлен, равно класс плюс 1. Так:
-Полиномы первой степени имеют 2 члена:1х + аили
-У полинома второй степени есть 3 члена:2Икс2 + а1х + аили
-Полином третьей степени состоит из 4 членов:3Икс3 + а2Икс2 + а1х + аили
И так далее. Внимательный читатель заметит, что многочлены в предыдущих примерах записаны в виде уменьшение, то есть помещая термин на первое место Высокий класс.
В следующей таблице показаны различные полиномы, как от одной, так и от нескольких переменных, и их соответствующие абсолютные градусы:
Таблица 1. Примеры многочленов и их степеней.
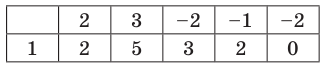
| Полиномиальный | Степень |
|---|---|
| 3x4+ 5x3-2x + 3 | 4 |
| 7x3-2x2+ 3x-6 | 3 |
| 6 | 0 |
| х-1 | 1 |
| Икс5-bx4+ abx3+ab3Икс2 | 6 |
| 3x3Y5 + 5x2Y4 – 7xy2 + 6 | 8 |
Последние два полинома имеют более одной переменной. Из них термин с наивысшей абсолютной степенью был выделен жирным шрифтом, чтобы читатель мог быстро проверить степень. Важно помнить, что если переменная не имеет записанного показателя степени, подразумевается, что указанный показатель равен 1.
Например, в избранном термине ab3Икс2 есть три переменные, а именно: к, б Y Икс. В этот срок к повышается до 1, то есть:
а = а1
Таким образом ab3Икс2 = а1б3Икс2
Поскольку показатель b равен 3, а показатель x равен 2, немедленно следует, что степень этого члена равна:
1+3+2 = 6
Y – это абсолютная степень многочлена, поскольку ни один другой член не имеет более высокой степени.
Порядок работы с многочленами
При работе с многочленами важно обращать внимание на его степень, так как в первую очередь и перед выполнением какой-либо операции удобно выполнить следующие шаги, в которых степень предоставляет очень важную информацию:
-Закажите полином предпочтения в порядке убывания. Таким образом, термин с самой высокой степенью находится слева, а член с самой низкой степенью – справа.
-Уменьшить подобные термины, процедура, которая состоит в алгебраическом сложении всех терминов одной и той же переменной и степени, найденных в выражении.
-Если это точно, полиномы дополняются, вставляя члены с коэффициентом 0, если отсутствуют члены с показателем степени.
Упорядочить, уменьшить и дополнить многочлен
Учитывая многочлен P (x) = 6x2 – 5x4– 2х + 3х + 7 + 2х5 – 3x3 + х7 -12 предлагается расположить его в порядке убывания, сократить аналогичные термины, если они есть, и дополнить отсутствующие термины, если необходимо.
Первое, что нужно искать, – это член с наибольшим показателем, который представляет собой степень многочлена, который оказывается равным:
Икс7
Следовательно, P (x) имеет степень 7. Затем полином упорядочивается, начиная с этого члена слева:
Р (х) = х7 + 2x5 – 5x4 – 3x3 + 6x2 – 2х + 3х + 7-12
Теперь подобные термины уменьшены, а именно: – 2x и 3x с одной стороны. А 7 и -12 с другой. Чтобы уменьшить их, коэффициенты складываются алгебраически, а переменная остается неизменной (если переменная не появляется рядом с коэффициентом, помните, что x0 = 1):
-2x + 3x = х
7 -12 = -5
Замените эти результаты на P (x):
Р (х) = х7 + 2x5 – 5x4 – 3x3 + 6x2 + х -5
И, наконец, проверяется полином на предмет отсутствия какой-либо экспоненты, и действительно, отсутствует член с показателем 6, поэтому он завершается такими нулями:
Р (х) = х7 + 0x6 + 2x5 – 5x4 – 3x3 + 6x2 + х – 5
Теперь можно заметить, что в полиноме осталось 8 членов, поскольку, как было сказано ранее, количество членов равно степени +1.
Важность степени полинома при сложении и вычитании
С полиномами вы можете выполнять операции сложения и вычитания, в которых добавляются или вычитаются только одинаковые члены, которые имеют одинаковую переменную и одинаковую степень. Если одинаковых терминов нет, просто указывается сложение или вычитание.
После того, как было выполнено сложение или вычитание, последнее является суммой противоположных величин, степень полученного многочлена всегда равна или меньше степени многочлена при добавлении наивысшей степени.
Решенные упражнения
– Упражнение решено 1
Найдите следующую сумму и определите ее абсолютную степень:
к3– 8ax2 + х3 + 5а2х – 6ax2 – Икс3 + 3а3 – 5 место2х – х3 + а3+ 14ax2 – Икс3
Решение
Это многочлен с двумя переменными, поэтому его удобно сократить:
к3– 8ax2 + х3 + 5а2х – 6ax2 – Икс3 + 3а3 – 5 место2х – х3 + а3+ 14ax2 – Икс3 =
= а3 + 3а3 + а3 – 8ax2 – 6ax2+ 14ax2 + 5а2x – 5 место2х + х3– Икс3– Икс3– Икс3 =
= 5а3 – 2x3
Оба члена имеют степень 3 по каждой переменной. Следовательно, абсолютная степень полинома равна 3.
– Упражнение выполнено 2
Выразите площадь следующей плоской геометрической фигуры в виде многочлена (рисунок 2 слева). Какова степень полученного многочлена?

Решение
Поскольку это площадь, результирующий многочлен должен иметь степень 2 от переменной x. Чтобы определить подходящее выражение для площади, фигура разбивается на известные области:
Площадь прямоугольника и треугольника соответственно: основание x высота Y основание x высота / 2
К1 = х. 3x = 3x2; К2 = 5. х = 5х; К3 = 5. (2x / 2) = 5x
Заметка: основание треугольника 3x – x = 2x, а его высота 5.
Теперь три полученных выражения складываются, и мы получаем площадь фигуры как функцию от Икс:
3x2 + 5x + 5x = 3x2 + 10x
Ссылки
- Балдор, А. 1974. Элементарная алгебра. Cultural Venezolana S.A.
- Хименес, Р. 2008. Алгебра. Прентис Холл.
- Викиучебники. Полиномы. Получено с: es. wikibooks.org.
- Википедия. Степень (полиномиальная). Получено с: es.wikipedia.org.
- Зилл, Д. 1984. Алгебра и тригонометрия. Мак Гроу Хилл.
9.2.1.
Многочлены с комплексными коэффициентами
от комплексной переменной.
Многочленом -ой
степени называется функция
где
– постоянные комплексные числа
(коэффициенты многочлена), ,
– комплексная переменная. Число ,
в котором многочлен принимает нулевое
значение (),
называется корнем
многочлена.
Справедлива
следующая теорема, которая называется
основной
теоремой алгебры:
любой многочлен степени
имеет комплексный корень.
Пусть
– произвольная точка комплексной
плоскости. Представим
в виде многочлена по степеням
(как мы делали это в разделе 7.7.1.
Формула Тейлора для многочленов):
.
Здесь
– новые значения коэффициентов,
получающиеся после раскрытия степеней
и приведения подобных членов. Очевидно,
,
отсюда следует утверждение: для того,
чтобы число
было корнем многочлена
,
необходимо и достаточно, чтобы коэффициент
при нулевой степени в разложении
по степеням
был равен нулю:
.
Но тогда
.
Таким образом,
доказана теорема
Безу: для
того, чтобы многочлен -ой
степени
имел комплексный корень ,
необходимо и достаточно, чтобы он без
остатка делился на ,
т.е. чтобы
представлялся в виде ,
где
– многочлен -1-ой
степени.
Пусть
– корень многочлена ,
тогда, по теореме Безу, .
Возможны два варианта: 1. Число
не является корнем многочлена ,
в этом случае
называется простым корнем многочлена
.
2. Число
является корнем многочлена ,
тогда, применяя теорему Безу уже к ,
получим ,
.
Применяя к
те же рассуждения, придём к выводу: если
– корень многочлена ,
то
единственным образом представляется
в виде ,
где .
Число
в этом случае называется кратностью
корня .
Согласно основной
теореме алгебры, любой многочлен
при
имеет хотя бы один корень ;
если кратность этого корня равна
,
то, согласно изложенному,
представляется в виде ,
где .
Если ,
то многочлен
имеет корень ,
и представляется в виде .
Если ,
эти выкладки можно продолжить;
окончательный вывод формулируется так:
любой многочлен
степени
при старшем
коэффициенте
единственным (с точностью до порядков
сомножителей) образом может быть
представлен в виде,
где– (попарно различные) корни многочлена,
– их кратности,–
количество различных корней. Общее
число корней многочлена с учётом их
кратностей равна :
.
9.2.2.
Многочлены с действительными
коэффициентами.
В этом разделе мы рассмотрим многочлен
от комплексной переменной ,
в предположении, что его коэффициенты
–
действительные числа. Сформулируем и
докажем ряд свойств такого многочлена.
1.Если
– число, сопряжённое к числу ,
то .
Док-во: Для любого действительного числа
операция сопряжения не меняет это число:
,
поэтому
(см. сформулированные
в разделе 9.
Комплексные числа
свойства операции сопряжения).
2. Если
–
корень многочлена ,
то
– тоже корень этого многочлена. Док-во:
если ,
то
.
3. Если
–
корень многочлена с действительными
коэффициентами ,
то
без остатка делится на квадратный
трёхчлен ,
где .
Док-во: так как числа
– корни ,
то
представляется в виде
.
4. Если
–
корень многочлена
кратности ,
то
– корень этого многочлена той же кратности.
Док-во: непосредственно следует из
утверждений 2,3.
5. Любой многочлен
-ой
степени
может быть представлен, и притом
единственным с точностью до порядка
сомножителей образом, в виде
,
где
– попарно различные
действительные корни этого многочлена,
– их кратности, квадратные трёхчлены
(соответствующие попарно различным
парам сопряжённых корней
кратностей )
с действительными коэффициентами не
имеют действительных корней (т.е. ),
.
Это утверждение непосредственно следует
из результатов этого и предыдущего
разделов.
6. При выводе
предыдущего утверждения мы существенно
использовали тот факт, что
– комплексная переменная (в частности,
когда ссылались на основную теорему
алгебры). В то же время в самом полученном
представлении многочлена все участвующие
величины (кроме )
– действительные числа. Предположим
теперь, чтобы переменная
принимает только действительные
значения, т.е. .
Тогда утверждение 5 можно переформулировать
так: любой многочлен с действительными
коэффициентами
от действительной переменной
может быть представлен, и притом
единственным с точностью до порядка
сомножителей образом, в виде
,
где смысл всех параметров описан выше.
Соседние файлы в папке lec2
- #
- #
- #
- #
- #
Схема Горнера
11 июля 2022
Схема Горнера — это алгоритм для быстрого (счёт идёт на секунды) вычисления значения многочлена
[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]
в точке $x=a$. Также схема Горнера позволяет быстро (быстрее, чем столбиком) делить многочлен $Pleft( x right)$ на линейные двучлены вида $x-a$, искать остатки от деления и многое другое.
Содержание
- Описание Схемы Горнера
- Вычисление значения многочлена
- Деление многочлена с остатком
- Перебор корней уравнения
- Разложение на множители
- Разложение по степеням
- Как всё это работает
1. Описание схемы Горнера
Итак, рассмотрим многочлен
[Pleft( x right)= color{blue}{{a}_{n}}{{x}^{n}}+color{blue}{{a}_{n-1}}{{x}^{n-1}}+ldots +color{blue}{{a}_{1}}x+color{blue}{{a}_{0}}]
Для наглядности коэффициенты выделены синим цветом. Распишем схему Горнера для многочлена $Pleft( x right)$ в точке $x=color{red}{a}$. Для этого заполним таблицу
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}{a} & {} & {} & {} & {} & {} & {} \ end{array}]
В первой строке мы видим коэффициенты многочлена $Pleft( x right)$ в порядке убывания степеней. Таких коэффициентов всегда на один больше, чем степень многочлена: для квадратного многочлена всего 3 коэффициента, для кубического — уже 4, и т.д.
Во второй строке таблицы мы вписываем лишь число $color{red}{a}$ в самой левой клетке. Остальные клетки заполняются последовательно по следующему алгоритму.
В первую свободную клетку мы переносим элемент из верхней строки без изменений. Назовём этот элемент ${{b}_{n-1}}$ — дальше вы поймёте, зачем нужна такая нумерация:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}{a} & {{b}_{n-1}}={{a}_{n}} & {} & {} & {} & {} & {} \ end{array}]
Вторая клетка — элемент ${{b}_{n-2}}$ — считается по формуле ${{b}_{n-2}}={{b}_{n-1}}cdot color{red}{a}+color{blue}{{a}_{n-1}}$. Другими словами, берём элемент слева, умножаем на число $a$ и добавляем элемент сверху:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}{a} & {{b}_{n-1}} & {{b}_{n-2}}={{b}_{n-1}}cdot color{red}{a}+color{blue}{{a}_{n-1}} & {} & {} & {} & {} \ end{array}]
Далее находим элемент ${{b}_{n-3}}$ по аналогичной формуле: ${{b}_{n-3}}={{b}_{n-2}}cdot color{red}{a}+color{blue}{{a}_{n-2}}$. Заносим результат в третью клетку:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}a & {{b}_{n-1}} & {{b}_{n-2}} & {{b}_{n-3}}={{b}_{n-2}}cdot color{red}{a}+color{blue}{{a}_{n-2}} & {} & {} & {} \ end{array}]
Аналогично находим элементы ${{b}_{n-4}}$, ${{b}_{n-5}}$ и далее. Берём элемент слева, умножаем на исходное число $color{red}{a}$, добавляем элемент сверху, результат записываем в клетку:
[{{b}_{k-1}}={{b}_{k}}cdotcolor{red}{a}+color{blue}{{a}_{k}}]
В какой-то момент мы доберёмся до элемента ${{b}_{0}}$, который находится в клетке под коэффициентом $color{blue}{{a}_{1}}$:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}{a} & {{b}_{n-1}} & {{b}_{n-2}} & {{b}_{n-3}} & ldots & {{b}_{0}}={{b}_{1}}cdot color{red}{a}+color{blue}{{a}_{1}} & {} \ end{array}]
Элемент в последней клетке считается по той же схеме: ${{b}_{0}}cdot color{red}{a}+color{blue}{{a}_{0}}$. Обозначим его буквой $r$:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}{a} & {{b}_{n-1}} & {{b}_{n-2}} & {{b}_{n-3}} & ldots & {{b}_{0}} & r={{b}_{0}}cdot color{red}{a}+color{blue}{{a}_{0}} \ end{array}]
Итак, мы заполнили все клетки и получили таблицу:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}{a} & {{b}_{n-1}} & {{b}_{n-2}} & {{b}_{n-3}} & ldots & {{b}_{0}} & r \ end{array}]
Схема заполнения этой таблицы как раз и называется схемой Горнера. Найденные элементы ${{b}_{n-1}}$, …, ${{b}_{0}}$ и $r$ позволяют переписать исходный многочлен $Pleft( x right)$ в виде
[Pleft( x right)=left( {{b}_{n-1}}{{x}^{n-1}}+ldots +{{b}_{1}}x+{{b}_{0}} right)left( x-color{red}{a} right)+r]
Такая запись оказывается грозным оружием для решения задач с многочленами, если знать её свойства. И сегодня мы изучим все эти свойства, но сначала немного практики.
Пример 1. Простой многочлен
Заполните таблицу по схеме Горнера для многочлена
[Pleft( x right)=2{{x}^{4}}-7{{x}^{3}}+{{x}^{2}}+2x-3]
в точке $x=3$.
Решение. Для начала аккуратно запишем коэффициенты исходного многочлена. Для наглядности они вновь помечены синим:
[Pleft( x right)= color{blue}{2}cdot {{x}^{4}}+left( color{blue}{-7} right)cdot {{x}^{3}}+color{blue}{1}cdot {{x}^{2}}+color{blue}{2} cdot x+left( color{blue}{-3} right)]
Составим таблицу. Поскольку степень многочлена $deg Pleft( x right)=4$, в таблице будет пять основных столбцов и один дополнительный столбец слева, в котором мы запишем число $x=color{red}{3}$:
[begin{array}{c|c|c|c|c|c} {} & color{blue}{2} & color{blue}{-7} & color{blue}{1} & color{blue}{2} & color{blue}{-3} \ hlinecolor{red}{3} & {} & {} & {} & {} & {} \ end{array}]
Заполняем пустые клетки во второй строке. В первую клетку переносим без изменений элемент сверху:
[begin{array}{c|c|c|c|c|c} {} & color{blue}{2} & color{blue}{-7} & color{blue}{1} & color{blue}{2} & color{blue}{-3} \ hlinecolor{red}{3} & 2 & {} & {} & {} & {} \ end{array}]
Элемент во второй клетке считается по формуле $2cdot color{red}{3}+left( color{blue}{-7} right)=-1$:
[begin{array}{c|c|c|c|c|c} {} & color{blue}{2} & color{blue}{-7} & color{blue}{1} & color{blue}{2} & color{blue}{-3} \ hlinecolor{red}{3} & 2 & -1 & {} & {} & {} \ end{array}]
Третью и четвёртую клетку заполняем аналогично: сначала $-1cdot color{red}{3}+color{blue}{1}=-2$, затем $-2cdot color{red}{3}+color{blue}{2}=-4$:
[begin{array}{c|c|r|r|r|c} {} & color{blue}{2} & color{blue}{-7} & color{blue}{1} & color{blue}{2} & color{blue}{-3} \ hlinecolor{red}{3} & 2 & -1 & -2 & -4 & {} \ end{array}]
Наконец, последняя клетка: $-4cdot color{red}{3}+left( color{blue}{-3} right)=-15$:
[begin{array}{c|c|r|r|r|r} {} & color{blue}{2} & color{blue}{-7} & color{blue}{1} & color{blue}{2} & color{blue}{-3} \ hlinecolor{red}{3} & 2 & -1 & -2 & -4 & -15 \ end{array}]
Готово! Мы заполнили таблицу по схеме Горнера.
Пример 2. Пропущенные коэффициенты
Заполните таблицу по схеме Горнера для многочлена
[Pleft( x right)={{x}^{4}}+3{{x}^{3}}-4]
в точке $x=1$.
Решение. Обратите внимание: в записи многочлена отсутствуют одночлены ${{x}^{2}}$ и $x$. Другими словами, коэффициенты в этих двух одночленах равны нулю:
[Pleft( x right)= color{blue}{1}cdot {{x}^{4}}+color{blue}{3}cdot {{x}^{3}}+color{blue}{0}cdot {{x}^{2}}+color{blue}{0} cdot x+left( color{blue}{-4} right)]
Для наглядности мы вновь отметили коэффициенты синим цветом — всего их снова пять, т.е. на один больше степени многочлена. И все они переносятся в таблицу. Пропуск нулевых коэффициентов будет грубой ошибкой:
[begin{array}{c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{3} & color{blue}{0} & color{blue}{0} & color{blue}{-4} \ hlinecolor{red}{1} & {} & {} & {} & {} & {} \ end{array}]
Заполняем таблицу по схеме Горнера. Первый элемент переносим сверху:
[begin{array}{c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{3} & color{blue}{0} & color{blue}{0} & color{blue}{-4} \ hlinecolor{red}{1} & 1 & {} & {} & {} & {} \ end{array}]
Второй, третий и четвёртый элемент считаем по формуле: $1cdot color{red}{1}+color{blue}{3}=4$; $4cdot color{red}{1}+color{blue}{0}=4$; $4cdot color{red}{1}+color{blue}{0}=4$:
[begin{array}{c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{3} & color{blue}{0} & color{blue}{0} & color{blue}{-4} \ hlinecolor{red}{1} & 1 & 4 & 4 & 4 & {} \ end{array}]
Наконец, последний элемент таблицы: $4cdot color{red}{1}+left( color{blue}{-4} right)=0$:
[begin{array}{c|c|c|c|c|r} {} & color{blue}{1} & color{blue}{3} & color{blue}{0} & color{blue}{0} & color{blue}{-4} \ hlinecolor{red}{1} & 1 & 4 & 4 & 4 & 0 \ end{array}]
Готово! Таблица заполнена, последний элемент оказался равен нулю. И это не случайно. Скоро узнаем почему.:)
2. Вычисление значения многочлена
Чтобы понять, зачем нужна схема Горнера, давайте вкратце повторим всю цепочку рассуждений. Берём произвольный многочлен
[Pleft( x right)= color{blue}{{a}_{n}}{{x}^{n}}+color{blue}{{a}_{n-1}}{{x}^{n-1}}+ldots +color{blue}{{a}_{1}}x+color{blue}{{a}_{0}}]
и произвольную точку $x=color{red}{a}$. Составляем таблицу:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}{a} & {{b}_{n-1}} & {{b}_{n-2}} & {{b}_{n-3}} & ldots & {{b}_{0}} & r \ end{array}]
Найденные коэффициенты ${{b}_{n-1}}$, …, ${{b}_{0}}$, $r$ позволяют переписать многочлен $Pleft( x right)$ в новом виде:
[Pleft( x right)=left( {{b}_{n-1}}{{x}^{n-1}}+ldots +{{b}_{1}}x+{{b}_{0}} right)left( x-color{red}{a} right)+r]
Но чем так примечательна эта запись? В ближайших четырёх пунктах мы детально разберём все её свойства. И начнём с самого простого. Подставим в эту новую запись число $x=color{red}{a}$, т.е. вычислим $Pleft( color{red}{a} right)$:
[Pleft( color{red}{a} right)=left( {{b}_{n-1}}{color{red}{a}^{n-1}}+ldots +{{b}_{1}}color{red}{a}+{{b}_{0}} right)left( color{red}{a}-color{red}{a} right)+r=r]
Итак, последнее число $r$ в таблице — это значение многочлена $Pleft( x right)$ в точке $x=color{red}{a}$:
[Pleft( color{red}{a} right)=r]
А это значит, что благодаря схеме Горнера можно считать значения многочленов быстро (нет операции возведения в степень) и надёжно (в сложении мы ошибаемся реже, чем в умножении).
Так, из Примера 1 следует, что значение многочлена
[Pleft( x right)=2{{x}^{4}}-7{{x}^{3}}+{{x}^{2}}+2x-3]
в точке $x=3$ равно
[Pleft( 3 right)=r=-15]
Сравните это с прямой подстановкой $x=3$ в многочлен:
[begin{align} Pleft( 3 right) &=2cdot {{3}^{4}}-7cdot {{3}^{3}}+{{3}^{2}}+2cdot 3-3= \ &=2cdot 81-7cdot 27+left( 9+6-3 right)= \ &=162-189+12= \ &=-15 end{align}]
Результат один и тот же, но объём вычислений вырос на порядок.
Пример 3. «Некрасивые» значения
С помощью схемы Горнера найдите значение многочлена
[Pleft( x right)=8{{x}^{4}}-12{{x}^{3}}-24{{x}^{2}}+11x+7]
в точке $x=2,5$.
Решение. Выделим коэффициенты многочлена
[Pleft( x right)= color{blue}{8}cdot {{x}^{4}}+left( color{blue}{-12} right)cdot {{x}^{3}}+left( color{blue}{-24} right)cdot {{x}^{2}}+color{blue}{11} cdot x+color{blue}{7}]
и заполним таблицу для $x=color{red}{2,5}$:
[begin{array}{c|c|c|c|c|c} {} & color{blue}{8} & color{blue}{-12} & color{blue}{-24} & color{blue}{11} & color{blue}{7} \ hlinecolor{red}{2,5} & 8 & 8 & -4 & 1 & 9,5 \ end{array}]
Итого значение многочлена $Pleft( color{red}{2,5} right)=9,5$. Точно такое же значение можно получить прямой подстановкой, но вычисления будут настолько громоздкими, что мы не будем приводить их.
3. Деление многочлена с остатком
Напомню, что разделить многочлен $color{blue}{Pleft( x right)}$ на многочлен $color{red}{Aleft( x right)}$ с остатком — значит найти многочлены $Qleft( x right)$ и $Rleft( x right)$ такие, что
[color{blue}{Pleft( x right)}=Qleft( x right)cdot color{red}{Aleft( x right)}+Rleft( x right)]
причём степень многочлена $Rleft( x right)$ строго меньше степени делителя $color{red}{Aleft( x right)}$:
[deg Rleft( x right) lt deg color{red}{Aleft( x right)}]
Многочлен $Qleft( x right)$ называют неполным частным, $Rleft( x right)$ — остатком от деления. Можно показать, что $Qleft( x right)$ и $Rleft( x right)$ определены однозначно для исходных многочленов $color{blue}{Pleft( x right)}$ и $color{red}{Aleft( x right)}$.
3.1. Случай линейного делителя
Пусть $Aleft( x right)=x- color{red}{a}$ — линейный двучлен. Очевидно, его степень $deg Aleft( x right)=1$.
Рассмотрим произвольный многочлен
[Pleft( x right)= color{blue}{{a}_{n}}{{x}^{n}}+color{blue}{{a}_{n-1}}{{x}^{n-1}}+ldots +color{blue}{{a}_{1}}x+color{blue}{{a}_{0}}]
и составим таблицу для $x=color{red}{a}$ по схеме Горнера:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}{a} & {{b}_{n-1}} & {{b}_{n-2}} & {{b}_{n-3}} & ldots & {{b}_{0}} & r \ end{array}]
Получим новую запись многочлена $Pleft( x right)$:
[Pleft( x right)=left( {{b}_{n-1}}{{x}^{n-1}}+ldots +{{b}_{1}}x+{{b}_{0}} right)left( x-color{red}{a} right)+r]
где $r$ — обычное число, т.е. $deg r=0 lt deg Aleft( x right)$. Но тогда многочлен
[Qleft( x right)={{b}_{n-1}}{{x}^{n-1}}+{{b}_{n-2}}{{x}^{n-1}}+ldots +{{b}_{1}}x+{{b}_{0}}]
является неполным частным при делении $Pleft( x right)$ на двучлен $x-color{red}{a}$, а число $r$ — остаток этого деления:
[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)+r]
Итак, схема Горнера позволяет быстро находить неполное частное и остаток от деления произвольного многочлена $Pleft( x right)$ на двучлен $x-color{red}{a}$.
Пример 4. Деление с остатком
Найдите частное и остаток при делении многочлена
[{{x}^{4}}-2{{x}^{3}}+4{{x}^{2}}-6x+10]
На многочлен $x-1$.
Решение. Выделим синим цветом коэффициенты исходного многочлена:
[color{blue}{1}cdot {{x}^{4}}+left( color{blue}{-2} right)cdot {{x}^{3}}+color{blue}{4}cdot {{x}^{2}}+left( color{blue}{-6} right)cdot x+color{blue}{10}]
Заполним таблицу по схеме Горнера для $x=color{red}{1}$:
[begin{array}{c|c|r|c|r|c} {} & color{blue}{1} & color{blue}{-2} & color{blue}{4} & color{blue}{-6} & color{blue}{10} \ hlinecolor{red}{1} & 1 & -1 & 3 & -3 & 7 \ end{array}]
Первые четыре числа — это коэффициенты многочлена-частного. Отметим их зелёным цветом:
[begin{array}{c|c|r|c|r|c} {} & color{blue}{1} & color{blue}{-2} & color{blue}{4} & color{blue}{-6} & color{blue}{10} \ hlinecolor{red}{1} & color{#green}{1} & color{#green}{-1} & color{#green}{3} & color{#green}{-3} & 7 \ end{array}]
Остаток от деления равен $r=7$. Составим многочлен-частное:
[Qleft( x right)= color{#green}{1}cdot {{x}^{3}}+left( color{#green}{-1} right)cdot {{x}^{2}}+color{#green}{3}cdot x+left( color{#green}{-3} right)]
Очевидно, при делении на линейный двучлен степень частного должна быть на единицу меньше степени исходного многочлена. Так и получилось:
[deg Qleft( x right)=4-1=3]
Пример 5. Проверка делимости
Убедитесь, что многочлен
[{{x}^{5}}-6{{x}^{4}}+16{{x}^{2}}-33{{x}^{2}}+44x-28]
делится на двучлен ${{left( x-2 right)}^{2}}$.
Решение. Многочлен делится без остатка на ${{left( x-2 right)}^{2}}$, если сначала он делится на двучлен $x-2$, а затем частное вновь делится на $x-2$. Следовательно, решение состоит из двух шагов.
Первый шаг: выделим коэффициенты исходного многочлена
[color{blue}{1}cdot {{x}^{5}}+left( color{blue}{-6} right)cdot {{x}^{4}}+color{blue}{16}cdot {{x}^{2}}+left( color{blue}{-33} right)cdot {{x}^{2}}+color{blue}{52} cdot x+left( color{blue}{-36} right)]
[begin{align}color{blue}{1}cdot {{x}^{5}} &+left( color{blue}{-6} right)cdot {{x}^{4}}+color{blue}{16}cdot {{x}^{2}}+ \ &+left( color{blue}{-33} right)cdot {{x}^{2}}+color{blue}{52} cdot x+left( color{blue}{-36} right) \ end{align}]
Составим таблицу для $x=color{red}{2}$. В ней будет 6 основных столбцов:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{-6} & color{blue}{16} & color{blue}{-33} & color{blue}{52} & color{blue}{-36} \ hlinecolor{red}{2} & {} & {} & {} & {} & {} & {} \ end{array}]
Заполним все пустые клетки по схеме Горнера:
[begin{array}{c|c|c|c|r|c|c} {} & color{blue}{1} & color{blue}{-6} & color{blue}{16} & color{blue}{-33} & color{blue}{52} & color{blue}{-36} \ hlinecolor{red}{2} & color{green}{1} & color{green}{-4} & color{green}{8} & color{green}{-17} & color{green}{18} & 0 \ end{array}]
Получили остаток $r=0$, поэтому исходный многочлен действительно делится на $x-color{red}{2}$, а частное равно
[Qleft( x right)= color{green}{1}cdot {{x}^{4}}+left( color{green}{-4} right)cdot {{x}^{3}}+color{green}{8}cdot {{x}^{2}}+left( color{green}{-17} right) cdot x+color{green}{18}]
Следовательно, исходный многочлен можно представить так:
[begin{align} & {{x}^{5}}-6{{x}^{4}}+16{{x}^{2}}-33{{x}^{2}}+44x-28= \ = & left( {{x}^{4}}-4{{x}^{3}}+8{{x}^{2}}-17x+18 right)cdot left( x-color{red}{2} right) \ end{align}]
Второй шаг: выделяем коэффициенты и заполняем ту же самую таблицу, но уже для многочлена $Qleft( x right)$.
[Qleft( x right)= color{blue}{1}cdot {{x}^{4}}+left( color{blue}{-4} right)cdot {{x}^{3}}+color{blue}{8}cdot {{x}^{2}}+left( color{blue}{-17} right) cdot x+color{blue}{18}]
Но все коэффициенты в нужном количестве уже присутствуют в таблице, которую мы получили на предыдущем шаге. А потому достаточно приписать к этой таблице ещё одну строку и вновь заполнить её для $x=color{red}{2}$:
[begin{array}{c|c|c|c|r|c|c} {} & 1 & -6 & 16 & -33 & 52 & -36 \ hlinecolor{red}{2} & color{blue}{1} & color{blue}{-4} & color{blue}{8} & color{blue}{-17} & color{blue}{18} & 0 \ hlinecolor{red}{2} & color{green}{1} & color{green}{-2} & color{green}{4} & color{green}{-9} & 0 & {} \ end{array}]
Остаток от деления равен нулю, поэтому многочлен $Qleft( x right)$ делится на $x-color{red}{2}$, и его можно переписать так:
[Qleft( x right)=left( color{green}{1}cdot {{x}^{3}}+left( color{green}{-2} right){{x}^{2}}+color{green}{4} cdot x+left( color{green}{-9} right) right)cdot left( x-color{red}{2} right)]
Возвращаясь к исходному многочлену, получим
[begin{align} & {{x}^{5}}-6{{x}^{4}}+16{{x}^{2}}-33{{x}^{2}}+44x-28= \ = & left( {{x}^{3}}-2{{x}^{2}}+4x-9 right)cdot {{left( x-color{red}{2} right)}^{2}} \ end{align}]
Такая запись, как и приведённая выше таблица, доказывает, что исходный многочлен делится на ${{left( x-color{red}{2} right)}^{2}}$.
Обратите внимание: на каждом следующем шаге количество коэффициентов уменьшается на единицу:
- В первой строке мы выписали все 6 коэффициентов исходного многочлена.
- Во второй строке осталось лишь 5 коэффициентов, а последнее число — остаток.
- Третья срока — 4 коэффициента и вновь остаток.
Всё это пригодится нам в следующем пункте.
4. Перебор корней уравнения
До сих пор мы применяли схему Горнера для некоторой точки $x=color{red}{a}$, которая была прямо указана в условии задачи. Но что если найти такую точку — как раз и есть условие задачи?
Рассмотрим уравнение
[color{blue}{{a}_{n}}{{x}^{n}}+color{blue}{{a}_{n-1}}{{x}^{n-1}}+ldots +color{blue}{{a}_{1}}x+color{blue}{{a}_{0}}=0]
Число $x=color{red}{a}$ будет корнем этого уравнения, если $Pleft( color{red}{a} right)=0$. Это значит, что последний элемент в схеме Горнера должен быть равен нулю:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}{a} & {{b}_{n-1}} & {{b}_{n-2}} & {{b}_{n-3}} & ldots & {{b}_{0}} & color{green}{0} \ end{array}]
Следовательно, мы можем быстро проверить, является ли число $x=color{red}{a}$ корнем уравнения. Достаточно просто подставить его в таблицу и найти последний элемент.
Кроме того, мы знаем, что последний элемент — это остаток $r$. При $r=color{green}{0}$ исходное уравнение примет вид
[left( {{b}_{n-1}}{{x}^{n-1}}+ldots +{{b}_{1}}x+{{b}_{0}} right)left( x-color{red}{a} right)=0]
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю. Откуда либо $x-color{red}{a}=0$ (этот случай мы уже разобрали), либо
[color{blue}{{b}_{n-1}}{{x}^{n-1}}+ldots +color{blue}{{b}_{1}}x+color{blue}{{b}_{0}}=0]
Получили новое уравнение — меньшей степени, чем исходное. Коэффициенты этого уравнения уже занесены в таблицу, и к нему вновь применима схема Горнера для перебора кандидатов в корни.
Более того: этот перебор можно ускорить. Но об этом чуть позже. Сначала рассмотрим пару простых примеров.
Пример 6. Уравнение третьей степени
Решите уравнение:
[{{x}^{3}}+9{{x}^{2}}+23x+15=0]
Решение. Заметим, что все коэффициенты многочлена положительны, поэтому уравнение не имеет положительных корней. Иначе, если $x gt 0$, левая часть равенства представляет собой сумму положительных чисел, которая никогда не равна нулю.
Рассмотрим отрицательные числа. Начнём с $x=color{red}{-1}$:
[begin{array}{c|c|c|c|c} {} & color{blue}{1} & color{blue}{9} & color{blue}{23} & color{blue}{15} \ hlinecolor{red}{-1} & 1 & 8 & 15 & color{green}{0} \ end{array}]
Получили $r=color{green}{0}$. Следовательно, $x=color{red}{-1}$ — корень, и всё уравнение можно переписать так:
[left( {{x}^{2}}+8x+15 right)left( x+1 right)=0]
Далее уравнение разделяется на линейное $x+1=0$, которое мы уже решили, и квадратное
[{{x}^{2}}+x+15=0]
Такое уравнение можно решить через дискриминант или по теореме Виета. Получим корни $x=-3$ и $x=-5$.
Окончательный ответ: $x=-1$, $x=-3$, $x=-5$.
Впрочем, с тем же успехом мы могли продолжить решение по схеме Горнера:
[begin{array}{r|c|c|c|c} {} & color{blue}{1} & color{blue}{9} & color{blue}{23} & color{blue}{15} \ hlinecolor{red}{-1} & 1 & 8 & 15 & color{green}{0} \ hlinecolor{red}{-3} & 1 & 5 & color{green}{0} & {} \ hlinecolor{red}{-5} & 1 & color{green}{0} & {} & {} \ end{array}]
При этом уравнение примет вид
[left( x+3 right)left( x+5 right)left( x+1 right)=0]
По сути, мы получили разложение на множители. И чуть ниже об этом будет отдельный пункт.
Пример 7. Ещё одно уравнение
Решите уравнение:
[2{{x}^{3}}-{{x}^{2}}-5x-2=0]
Решение. В этот раз мы видим, что корни вполне могут быть положительными. Начнём с $x=color{red}{1}$:
[begin{array}{c|c|r|r|r} {} & color{blue}{2} & color{blue}{-1} & color{blue}{-5} & color{blue}{-2} \ hlinecolor{red}{1} & 2 & 1 & -4 & color{red}{-6} \ end{array}]
Получили $r=color{red}{-6}ne 0$. Следовательно, $x=color{red}{1}$ не является корнем. Проверим $x=color{red}{2}$:
[begin{array}{c|c|r|r|r} {} & color{blue}{2} & color{blue}{-1} & color{blue}{-5} & color{blue}{-2} \ hlinecolor{red}{1} & 2 & 1 & -4 & color{red}{-6} \ hlinecolor{red}{2} & 2 & 3 & 1 & color{green}{0} \ end{array}]
Обратите внимание: при заполнении третьей строки таблицы мы игнорируем вторую строку, где нас постигла неудача. И если бы мы могли стирать строки, то схема Горнера выглядела бы так:
[begin{array}{c|c|r|r|r} {} & color{blue}{2} & color{blue}{-1} & color{blue}{-5} & color{blue}{-2} \ hlinecolor{red}{2} & 2 & 3 & 1 & color{green}{0} \ end{array}]
В любом случае мы получили $r=color{green}{0}$, поэтому $x=color{red}{2}$ — корень, и уравнение примет вид
[left( 2{{x}^{2}}+3x+1 right)left( x-2 right)=0]
Далее можно решить квадратное уравнение через дискриминант, а можно продолжить заполнять таблицу. Например, для $x=color{red}{-1}$:
[begin{array}{r|c|r|r|r} {} & 2 & -1 & -5 & -2 \ hline1 & 2 & 1 & -4 & -6 \ hline2 & color{blue}{2} & color{blue}{3} & color{blue}{1} & color{green}{0} \ hline-1 & 2 & 1 & color{green}{0} & {} \ end{array}]
Вновь получили ноль в последней клетке, поэтому $x=color{red}{-1}$ — тоже корень, а уравнение примет вид
[left( 2x+1 right)left( x+1 right)left( x-2 right)=0]
Теперь ответ очевиден: $x=2$, $x=-1$, $x=-0,5$.
Помните: «неудачные» строки — это нормально. Их бывает много. Главное при переборе корней — игнорировать такие строки и заполнять таблицу так, будто этих строк не существует.
4.1. Теорема Безу
Теорема Безу и следствия из неё позволяет значительно сузить круг потенциальных корней.
Теорема Безу. Остаток от деления многочлена
[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]
на двучлен $x-a$ равен $Pleft( a right)$.
Несложно заметить, что схема Горнера и следующая из неё запись многочлена
[Pleft( x right)=left( {{b}_{n-1}}{{x}^{n-1}}+ldots +{{b}_{1}}x+{{b}_{0}} right)left( x-color{red}{a} right)+r]
является прямым доказательством этой теоремы. Действительно, если подставить в эту запись значение $x=color{red}{a}$, мы получим
[Pleft( color{red}{a} right)=left( {{b}_{n-1}}color{red}{{a}^{n-1}}+ldots +{{b}_{1}}color{red}{a}+{{b}_{0}} right)left( color{red}{a}-color{red}{a} right)+r=r]
У теоремы Безу огромное количество полезных приложений — см. урок «Теорема Безу». Сейчас же нас интересует не сама теорема, а следствие из неё, связанное с корнями многочлена.
Пусть $x=color{red}{a}$ — корень многочлена $Pleft( x right)$. Распишем многочлен по схеме Горнера для $x=color{red}{a}$:
[Pleft( x right)=left( {{b}_{n-1}}{{x}^{n-1}}+ldots +{{b}_{1}}x+{{b}_{0}} right)left( x-color{red}{a} right)]
Поскольку $x=color{red}{a}$ — корень, остаток $r=0$, и мы получили разложение многочлена $Pleft( x right)$ на множители. А теперь выполним обратную операцию — раскроем скобки и приведём подобные слагаемые:
[Pleft( x right)={{b}_{n-1}}{{x}^{n}}+ldots -color{red}{a}cdot {{b}_{0}}]
Получается, что корень $x=color{red}{a}$ является делителем свободного члена $Pleft( x right)$. Более того, можно показать, что в многочлене
[Pleft( x right)= color{blue}{{a}_{n}}{{x}^{n}}+color{blue}{{a}_{n-1}}{{x}^{n-1}}+ldots +color{blue}{{a}_{1}}x+color{blue}{{a}_{0}}]
с целыми коэффициентами $color{blue}{{a}_{n}}$, …, $color{blue}{{a}_{0}}$ все рациональные корни имеют вид
[x=frac{m}{n}]
где $min mathbb{Z}$ — делитель свободного члена $color{blue}{{a}_{0}}$, а $nin mathbb{N}$ — делитель старшего коэффициента $color{blue}{{a}_{n}}$.
И хоть при первом взгляде на все эти рассуждения они могут показаться сложными, на практике теорема Безу значительно упрощает поиск корней. Взгляните на примеры.:)
Пример 8. Сплошной перебор
Решите уравнение:
[{{x}^{5}}+8{{x}^{4}}+24{{x}^{3}}+35{{x}^{2}}+28x+12=0]
Решение. Слева от знака равенства стоит многочлен пятой степени. Старший коэффициент многочлена ${{a}_{5}}=color{blue}{1}$, свободный член ${{a}_{0}}=color{blue}{12}$. Если такой многочлен имеет рациональные корни вида
[x=frac{m}{n}]
то $n=1$ — это единственный натуральный делитель для ${{a}_{5}}=color{blue}{1}$. А вот число $m$ будем искать среди делителей числа ${{a}_{0}}=color{blue}{12}$:
[m=pm 1, pm 2, pm 3, pm 4, pm 6, pm 12.]
Итого 12 вариантов. Далее заметим, что все коэффициенты исходного многочлена положительны, поэтому достаточно проверить лишь отрицательные корни. Начнём с $x=color{red}{-1}$, затем $x=color{red}{-2}$, $x=color{red}{-3}$ и т.д.:
[begin{array}{r|c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{8} & color{blue}{24} & color{blue}{35} & color{blue}{28} & color{blue}{12} \ hline color{red}{-1} & 1 & 7 & 17 & 18 & 10 & color{red}{2} \ hline color{red}{-2} & 1 & 6 & 12 & 11 & 6 & color{green}{0} \ hline color{red}{-3} & 1 & 3 & 3 & 2 & color{green}{0} & {} \ end{array}]
Как видим, вариант $x=color{red}{-1}$ не подошёл, поэму строку с проверкой этого числа можно вычеркнуть. Зато $x=color{red}{-2}$ и $x=color{red}{-3}$ — корни. Более того: можно повторно проверить $x=color{red}{-2}$. Получим интересный результат:
[begin{array}{r|c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{8} & color{blue}{24} & color{blue}{35} & color{blue}{28} & color{blue}{12} \ hline color{red}{-2} & 1 & 6 & 12 & 11 & 6 & color{green}{0} \ hline color{red}{-3} & 1 & 3 & 3 & 2 & color{green}{0} & {} \ hline color{red}{-2} & 1 & 1 & 1 & color{green}{0} & {} & {} \ end{array}]
Другими словами, исходное уравнение можно переписать так:
[left( {{x}^{2}}+x+1 right){{left( x+2 right)}^{2}}left( x+1 right)=0]
Число $x=color{red}{-2}$ оказалось корнем второй кратности, а квадратное уравнение
[{{x}^{2}}+x+1=0]
не имеет корней. Поэтому окончательный ответ: $x=-2$, $x=-3$.
Пример 9. Дробные корни
Решите уравнение:
[3{{x}^{4}}+5{{x}^{3}}-{{x}^{2}}-5x-2=0]
Решение. По теореме Безу получаем, что рациональные корни вида
[x=frac{m}{n}]
должны быть составлены из чисел $min left{ pm 1, pm 2 right}$ и $nin left{ 1,3 right}$. Всего существует восемь таких комбинаций:
[xin left{ pm 1; pm 2; pm frac{1}{3}; pm frac{2}{3} right}]
Рассмотрим самые простые корни: $x=color{red}{1}$ и $x=color{red}{-1}$. Причём на каждом шаге будем проверять возможную кратность:
[begin{array}{r|c|c|c|c|c} {} & color{blue}{3} & color{blue}{5} & color{blue}{-1} & color{blue}{-5} & color{blue}{-2} \ hline color{red}{1} & 3 & 8 & 7 & 2 & color{green}{0} \ hline color{red}{1} & 3 & 11 & 18 & color{red}{20} & {} \ hline color{red}{-1} & 3 & 5 & 2 & color{green}{0} & {} \ hline color{red}{-1} & 3 & 2 & color{green}{0} & {} & {} \ end{array}]
Получили корень $x=color{red}{1}$ (первой кратности) и $x=color{red}{-1}$ (как минимум второй кратности), а само уравнение можно переписать так:
[left( 3x+2 right){{left( x+1 right)}^{2}}left( x-1 right)=0]
Теперь очевидно, что всего уравнение имеет три корня: $x=1$, $x=-1$ и $x=-{2}/{3};$.
4.2. Учёт кратности корней
Как видим, схема Горнера позволяет не просто перебирать корни, но и определять их кратность. Это особенно важно при решении неравенств и задач с параметрами.
Чтобы определить кратность корня $x=color{red}{a}$, достаточно подставлять его в таблицу до тех пор, пока не появится остаток, отличный от нуля. Либо пока исходный многочлен не будет полностью разложен на множители.
Пример 10. Корень четвёртой кратности
Решите уравнение и определите кратность корней:
[{{x}^{5}}-10{{x}^{3}}-20{{x}^{2}}-15x-4=0]
Решение. Слева стоит многочлен с целыми коэффициентами. Выпишем потенциальные корни по теореме Безу:
[xin left{ pm 1; pm 2; pm 4 right}]
Начнём с самых простых чисел: $x=color{red}{1}$ и $x=color{red}{-1}$. Проверим их по схеме Горнера:
[begin{array}{r|c|r|r|r|r|r} {} & color{blue}{1} & color{blue}{0} & color{blue}{-10} & color{blue}{-20} & color{blue}{-15} & color{blue}{-4} \ hlinecolor{red}{1} & 1 & 1 & -9 & -29 & -44 & color{red}{-48} \ hlinecolor{red}{-1} & 1 & -1 & -9 & -11 & -4 & color{green}{0} \ hlinecolor{red}{-1} & 1 & -2 & -7 & -4 & color{green}{0} & {} \ hlinecolor{red}{-1} & 1 & -3 & -4 & color{green}{0} & {} & {} \ hlinecolor{red}{-1} & 1 & -4 & color{green}{0} & {} & {} & {} \ end{array}]
Перепишем исходное уравнение:
[{{left( x+1 right)}^{4}}left( x-1 right)left( x-4 right)=0]
Итого уравнение имеет три различных корня: $x=-1$ (четвёртой кратности), $x=1$ (первой кратности) и $x=4$ (тоже первой кратности).
Ключевая мысль: с помощью схемы Горнера можно решать даже уравнения высших степеней. Поэтому если при решении текстовой задачи (и особенно задачи с параметром) возникло уравнение 3-й степени и выше, это вовсе не означает, что вы где-то ошиблись. Вполне возможно, что составители задачи хотят проверить, умеете ли вы решать уравнения высших степеней.
5. Разложение на множители
Схему Горнера часто применяют для разложения многочлена на множители. Мы знаем, что для всякого $x=color{red}{a}$ такого, что последний элемент таблицы $r=color{green}{0}$, можно переписать исходный многочлен $Pleft( x right)$ в виде
[Pleft( x right)=left( x-color{red}{a} right)cdot Qleft( x right)]
Коэффициенты многочлена $Qleft( x right)$ будут также даны в таблице, и к нему тоже применима схема Горнера.
Пример 11. Простой многочлен
Разложите на множители многочлен
[{{x}^{4}}+2{{x}^{3}}+4{{x}^{2}}+3x-10]
Решение. Рассмотрим многочлен
[Pleft( x right)= color{blue}{1}cdot {{x}^{4}}+color{blue}{2}cdot {{x}^{3}}+color{blue}{4}cdot {{x}^{2}}+color{blue}{3}cdot x+left( color{blue}{-10} right)]
Будем выделять из него двучлены вида $left( x-color{red}{a} right)$, где $x=color{red}{a}$ — корни многочлена $Pleft( x right)$. Рассмотрим в качестве таких корней делители свободного члена ${{a}_{0}}=color{blue}{-10}$. Начнём с $x=color{red}{1}$ и $x=color{red}{-1}$:
[begin{array}{r|c|c|c|c|c} {} & color{blue}{1} & color{blue}{2} & color{blue}{4} & color{blue}{3} & color{blue}{-10} \ hlinecolor{red}{1} & 1 & 3 & 7 & 10 & color{green}{0} \ hlinecolor{red}{-1} & 1 & 2 & 5 & color{red}{5} & {} \ hlinecolor{red}{-2} & 1 & 1 & 5 & color{green}{0} & {} \ end{array}]
Итого одна неудачная попытка и две удачных. Получили разложение многочлена
[Pleft( x right)=left( x-1 right)left( x+2 right)left( {{x}^{2}}+x+5 right)]
Квадратный трёхчлен в третьей скобке всегда положителен:
[{{x}^{2}}+x+5 gt 0]
Его нельзя разложить на множители, поэтому указанное разложение $Pleft( x right)$ — окончательное.
Пример 12. Сложный многочлен
Разложите на множители многочлен
[{{x}^{5}}-6{{x}^{4}}+2{{x}^{3}}+36{{x}^{2}}-27x-54]
Решение. Рассмотрим многочлен
[Pleft( x right)= color{blue}{1}cdot {{x}^{5}}+left( color{blue}{-6} right)cdot {{x}^{4}}+color{blue}{2}cdot {{x}^{3}}+color{blue}{36}cdot {{x}^{2}}+left( color{blue}{-27} right)cdot x+left( color{blue}{-54} right)]
[begin{align}Pleft( x right)= color{blue}{1}cdot {{x}^{5}} &+left( color{blue}{-6} right)cdot {{x}^{4}}+color{blue}{2}cdot {{x}^{3}}+ \ &+color{blue}{36}cdot {{x}^{2}}+left( color{blue}{-27} right) cdot x+left( color{blue}{-54} right) \ end{align}]
Проверим делители свободного члена ${{a}_{0}}=color{blue}{-54}$. Таких делителей очень много, поэтому начнём с самых простых: $x=color{red}{1}$ и $x=color{red}{-1}$:
[begin{array}{r|c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{-6} & color{blue}{2} & color{blue}{36} & color{blue}{-27} & color{blue}{-54} \ hlinecolor{red}{1} & 1 & -5 & -3 & 33 & 6 & color{red}{-48} \ hlinecolor{red}{-1} & 1 & -7 & 9 & 27 & -54 & color{green}{0} \ hlinecolor{red}{-1} & 1 & -8 & 17 & 10 & color{red}{-64} & {} \ hlinecolor{red}{2} & 1 & -5 & -1 & 25 & color{red}{-4} & {} \ hlinecolor{red}{-2} & 1 & -9 & 27 & -27 & color{green}{0} & {} \ hlinecolor{red}{3} & 1 & -6 & 9 & color{green}{0} & {} & {} \ hlinecolor{red}{3} & 1 & -3 & color{green}{0} & {} & {} & {} \ hlinecolor{red}{3} & 1 & color{green}{0} & {} & {} & {} & {} \ end{array}]
Получили три неудачных попытки и пять удачных. В целом многочлен привет вид
[Pleft( x right)=left( x+1 right)left( x+2 right){{left( x-3 right)}^{3}}]
Это и есть искомое разложение на множители.
Обратите внимание: после проверки корня $x=color{red}{-2}$ в таблице возникла формула сокращённого умножения — куб разности:
[{{x}^{3}}-9{{x}^{2}}+27x-27={{left( x-3 right)}^{3}}]
С этим замечанием дальше можно было вообще не заполнять таблицу, поскольку многочлен сразу примет вид
[Pleft( x right)=left( x+1 right)left( x+2 right){{left( x-3 right)}^{3}}]
6. Разложение по степеням
Наконец, ещё одно применение схемы Горнера — это разложение многочлена по степеням двучлена $left( x-color{red}{a} right)$. Для этого достаточно составлять таблицу с указанным $x=color{red}{a}$ до тех пор, пока не закончатся столбцы с коэффициентами.
Полученные остатки будут коэффициентами искомого разложения. Взгляните на примеры.
Пример 13. Разложение многочлена
Разложите по степеням $left( x-1 right)$ многочлен
[{{x}^{4}}-6{{x}^{3}}+16{{x}^{2}}-17x-5]
Решение. Выделим коэффициенты многочлена:
[Pleft( x right)= color{blue}{1}cdot {{x}^{4}}+left( color{blue}{-6} right)cdot {{x}^{3}}+color{blue}{16}cdot {{x}^{2}}+left( color{blue}{-17} right)cdot x+left( color{blue}{-5} right)]
[begin{align}Pleft( x right)= color{blue}{1}cdot {{x}^{4}} &+left( color{blue}{-6} right)cdot {{x}^{3}}+color{blue}{16}cdot {{x}^{2}}+ \ &+left( color{blue}{-17} right) cdot x+left( color{blue}{-5} right) \ end{align}]
Занесём эти коэффициенты в таблицу и будем заполнять её по схеме Горнера для $x=color{red}{1}$ до тех пор, пока не вычеркнем все столбцы:
[begin{array}{c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{-6} & color{blue}{16} & color{blue}{-17} & color{blue}{-5} \ hlinecolor{red}{1} & 1 & -5 & 11 & -6 & color{green}{-11} \ hlinecolor{red}{1} & 1 & -4 & 7 & color{green}{1} & {} \ hlinecolor{red}{1} & 1 & -3 & color{green}{4} & {} & {} \ hlinecolor{red}{1} & 1 & color{green}{-2} & {} & {} & {} \ hlinecolor{red}{1} & color{green}{1} & {} & {} & {} & {} \ end{array}]
Числа, выделенные зелёным — это остатки от деления в каждой новой строке. Они и будут коэффициентами разложения в порядке возрастания степеней. Внизу таблицы находится старший коэффициент, а в первой строке — свободный член:
[Pleft( x right)= color{green}{1}cdot {{left( x-1 right)}^{4}}+left( color{green}{-2} right)cdot {{left( x-1 right)}^{3}}+color{green}{4}cdot {{left( x-1 right)}^{2}}+color{green}{1}cdot left( x-1 right)+left( color{green}{-11} right)]
[begin{align}Pleft( x right) &=color{green}{1}cdot {{left( x-1 right)}^{4}}+left( color{green}{-2} right)cdot {{left( x-1 right)}^{3}}+ \ &+color{green}{4}cdot {{left( x-1 right)}^{2}}+color{green}{1}cdot left( x-1 right)+left( color{green}{-11} right) \ end{align}]
Представим эту запись более компактно:
[Pleft( x right)={{left( x-1 right)}^{4}}-2{{left( x-1 right)}^{3}}+4{{left( x-1 right)}^{2}}+left( x-1 right)-11]
[begin{align}Pleft( x right) &={{left( x-1 right)}^{4}}-2{{left( x-1 right)}^{3}}+ \ &+4{{left( x-1 right)}^{2}}+left( x-1 right)-11 \ end{align}]
Это и есть искомое разложение.
Пример 14. Финал
Разложите по степеням $left( x-2 right)$ многочлен
[{{x}^{4}}-8{{x}^{3}}+24{{x}^{2}}-50x+48]
Решение. В раз не будем переписывать многочлен с выделением коэффициентов, а сразу составим таблицу:
[begin{array}{c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{-8} & color{blue}{24} & color{blue}{-50} & color{blue}{48} \ hlinecolor{red}{2} & 1 & -6 & 12 & -26 & color{green}{-4} \ hlinecolor{red}{2} & 1 & -4 & 4 & color{green}{-18} & {} \ hlinecolor{red}{2} & 1 & -2 & color{green}{0} & {} & {} \ hlinecolor{red}{2} & 1 & color{green}{0} & {} & {} & {} \ hlinecolor{red}{2} & color{green}{1} & {} & {} & {} & {} \ end{array}]
Запишем найденное разложение в порядке убывания степеней:
[color{green}{1}cdot {{left( x-2 right)}^{4}}+color{green}{0}cdot {{left( x-2 right)}^{3}}+color{green}{0}cdot {{left( x-2 right)}^{2}}+left( color{green}{-18} right)cdot left( x-2 right)+left( color{green}{-4} right)]
[begin{align}color{green}{1}cdot {{left( x-2 right)}^{4}}&+color{green}{0}cdot {{left( x-2 right)}^{3}}+color{green}{0}cdot {{left( x-2 right)}^{2}}+ \ &+left( color{green}{-18} right)cdot left( x-2 right)+left( color{green}{-4} right) \ end{align}]
То же самое разложение, но более компактно:
[{{left( x-2 right)}^{4}}-18left( x-2 right)-4]
Это окончательный ответ.
7. Как работает Схема Горнера
Очень просто. Вернёмся к исходному многочлену:
[Pleft( x right)= color{blue}{{a}_{n}}{{x}^{n}}+color{blue}{{a}_{n-1}}{{x}^{n-1}}+ldots +color{blue}{{a}_{1}}x+color{blue}{{a}_{0}}]
Вынесем за скобки множитель $x$ из всех слагаемых, кроме последнего:
[Pleft( x right)=left( color{blue}{{a}_{n}}{{x}^{n-1}}+color{blue}{{a}_{n-1}}{{x}^{n-2}}+ldots +color{blue}{{a}_{1}} right)cdot x+color{blue}{{a}_{0}}]
В скобках стоит новый многочлен. Вновь вынесем за скобки $x$. Сделаем так много раз и в какой-то момент получим запись вида
[Pleft( x right)=left( ldots left( left( color{blue}{{a}_{n}} right)cdot x+color{blue}{{a}_{n-1}} right)cdot x+ldots +color{blue}{{a}_{1}} right)cdot x+color{blue}{{a}_{0}}]
Мы видим множество скобок. Обозначим элемент в самой внутренней скобке через ${{b}_{n-1}}$:
[{{b}_{n-1}}=color{blue}{{a}_{n}}]
Элемент в предыдущей скобке обозначим ${{b}_{n-2}}$:
[{{b}_{n-2}}={{b}_{n-1}} cdot x+color{blue}{{a}_{k}}]
И так далее по уже известной формуле
[{{b}_{k-1}}={{b}_{k}} cdot x+color{blue}{{a}_{k}}]
В какой-то момент мы находим ${{b}_{0}}$ и $r$:
[begin{align} {{b}_{0}} &={{b}_{1}}cdot x+color{blue}{{a}_{1}} \ r &={{b}_{0}}cdot x+color{blue}{{a}_{0}} end{align}]
Собираем все найденные значения в таблицу:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hline x & {{b}_{n-1}} & {{b}_{n-2}} & {{b}_{n-3}} & ldots & {{b}_{0}} & r \ end{array}]
Легко показать, что $r=Pleft( x right)$. Кроме того, согласно теореме Безу, при подстановке $x=color{red}{a}$ найденное число $r=Pleft( color{red}{a} right)$ есть остаток от деления многочлена $Pleft( x right)$ на двучлен $x-color{red}{a}$:
[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)+r]
В частности, при $r=0$ деление выполнено без остатка, поэтому многочлен $Pleft( x right)$ раскладывается на множители:
[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)]
Далее по индукции или прямым вычислением можно показать, что коэффициенты $Qleft( x right)$ — это те самые числа ${{b}_{n-1}}$, …, ${{b}_{0}}$ из таблицы. Поскольку $deg Qleft( x right)=n-1$, на каждом шаге степень этого многочлена будет уменьшаться.
В какой-то момент окажется, что $Qleft( x right)= color{blue}{{a}_{n}}$ — константа, и дальнейшее заполнение таблицы по схеме Горнера невозможно. Вот и всё.:)
Смотрите также:
- Бином Ньютона
- Теорема Безу и корни многочленов
- Решение задач B12: №448—455
- Задача B3 — работа с графиками
- Пример решения задачи 15
- Задача B15: частный случай при работе с квадратичной функцией