Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.
Определения и понятия
Угол наклона прямой y=kx+b называется угол α, который отсчитывается от положительного направления оси ох к прямой y=kx+b в положительном направлении.
На рисунке направление ох обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.
Угловой коэффициент прямой y=kx+b называют числовым коэффициентом k.
Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k=tg α.
- Угол наклона прямой равняется 0 только при параллельности ох и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0. Значит, вид уравнения будет y=b.
- Если угол наклона прямой y=kx+b острый, тогда выполняются условия 0<α<π2 или 0°<α<90°. Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию tg α>0, причем имеется возрастание графика.
- Если α=π2, тогда расположение прямой перпендикулярно ох. Равенство задается при помощи равенства x=c со значением с, являющимся действительным числом.
- Если угол наклона прямой y=kx+b тупой, то соответствует условиям π2<α<π или 90°<α<180°, значение углового коэффициента k принимает отрицательное значение, а график убывает.
Секущей называют прямую, которая проходит через 2 точки функции f(x). Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.
По рисунку видно, что АВ является секущей, а f(x) – черная кривая, α – красная дуга, означающая угол наклона секущей.
Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника АВС можно найти по отношению противолежащего катета к прилежащему.
Получаем формулу для нахождения секущей вида:
k=tg α=BCAC=f(xB)-fxAxB-xA, где абсциссами точек А и В являются значения xA, xB, а f(xA), f(xB) – это значения функции в этих точках.
Очевидно, что угловой коэффициент секущей определен при помощи равенства k=f(xB)-f(xA)xB-xA или k=f(xA)-f(xB)xA-xB, причем уравнение необходимо записать как y=f(xB)-f(xA)xB-xA·x-xA+f(xA) или
y=f(xA)-f(xB)xA-xB·x-xB+f(xB).
Секущая делит график визуально на 3 части: слева от точки А, от А до В, справа от В. На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.
По определению видно, что прямая и ее секущая в данном случае совпадают.
Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у=0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.
Касательная к графику функции f(x) в точке x0; f(x0) называется прямая, проходящая через заданную точку x0; f(x0), с наличием отрезка, который имеет множество значений х, близких к x0.
Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y=x+1, считается касательной к y=2x в точке с координатами (1; 2). Для наглядности, необходимо рассмотреть графики с приближенными к (1; 2) значениями. Функция y=2x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.
Очевидно, что y=2x сливается с прямой у=х+1.
Для определения касательной следует рассмотреть поведение касательной АВ при бесконечном приближении точки В к точке А. Для наглядности приведем рисунок.
Секущая АВ, обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной αx.
Касательной к графику функции y=f(x) в точке А считается предельное положение секущей АВ при В стремящейся к А, то есть B→A.
Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.
Геометрический смысл производной функции в точке
Перейдем к рассмотрению секущей АВ для функции f(x), где А и В с координатами x0, f(x0) и x0+∆x, f(x0+∆x), а ∆x обозначаем как приращение аргумента. Теперь функция примет вид ∆y=∆f(x)=f(x0+∆x)-f(∆x). Для наглядности приведем в пример рисунок.
Рассмотрим полученный прямоугольный треугольник АВС. Используем определение тангенса для решения, то есть получим отношение ∆y∆x=tg α. Из определения касательной следует, что lim∆x→0∆y∆x=tg αx. По правилу производной в точке имеем, что производную f(x) в точке x0 называют пределом отношений приращения функции к приращению аргумента, где ∆x→0, тогда обозначим как f(x0)=lim∆x→0∆y∆x.
Отсюда следует, что f'(x0)=lim∆x→0∆y∆x=tg αx=kx, где kx обозначают в качестве углового коэффициента касательной.
То есть получаем, что f’(x) может существовать в точке x0 причем как и касательная к заданному графику функции в точке касания равной x0, f0(x0), где значение углового коэффициента касательной в точке равняется производной в точке x0. Тогда получаем, что kx=f'(x0).
Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.
Уравнение касательной прямой
Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x0 при пересечении.
Уравнение касательной к графику функции y=f(x) в точке x0, f0(x0) принимает вид y=f'(x0)·x-x0+f(x0).
Имеется в виду, что конечным значением производной f'(x0) можно определить положение касательной, то есть вертикально при условии limx→x0+0f'(x)=∞ и limx→x0-0f'(x)=∞ или отсутствие вовсе при условии limx→x0+0f'(x)≠limx→x0-0f'(x).
Расположение касательной зависит от значения ее углового коэффициента kx=f'(x0). При параллельности к оси ох получаем, что kk=0, при параллельности к оу – kx=∞, причем вид уравнения касательной x=x0 возрастает при kx>0, убывает при kx<0.
Произвести составление уравнения касательной к графику функции y=ex+1+x33-6-33x-17-33 в точке с координатами (1; 3) с определением угла наклона.
Решение
По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, (1; 3) является точкой касания, тогда x0=-1, f(x0)=-3.
Необходимо найти производную в точке со значением -1. Получаем, что
y’=ex+1+x33-6-33x-17-33’==ex+1’+x33′-6-33x’-17-33’=ex+1+x2-6-33y'(x0)=y'(-1)=e-1+1+-12-6-33=33
Значение f’(x) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.
Тогда kx=tg αx=y'(x0)=33
Отсюда следует, что αx=arctg33=π6
Ответ: уравнение касательной приобретает вид
y=f'(x0)·x-x0+f(x0)y=33(x+1)-3y=33x-9-33
Для наглядности приведем пример в графической иллюстрации.
Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.
Выяснить наличие существования касательной к графику заданной функции
y=3·x-15+1 в точке с координатами (1;1). Составить уравнение и определить угол наклона.
Решение
По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.
Перейдем к нахождению производной
y’=3·x-15+1’=3·15·(x-1)15-1=35·1(x-1)45
Если x0=1, тогда f’(x) не определена, но пределы записываются как limx→1+035·1(x-1)45=35·1(+0)45=35·1+0=+∞ и limx→1-035·1(x-1)45=35·1(-0)45=35·1+0=+∞, что означает существование вертикальной касательной в точке (1;1).
Ответ: уравнение примет вид х=1, где угол наклона будет равен π2.
Для наглядности изобразим графически.
Найти точки графика функции y=115x+23-45×2-165x-265+3x+2, где
- Касательная не существует;
- Касательная располагается параллельно ох;
- Касательная параллельна прямой y=85x+4.
Решение
Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x∈-∞; 2 и [-2; +∞). Получаем, что
y=-115×3+18×2+105x+176, x∈-∞; -2115×3-6×2+9x+12, x∈[-2; +∞)
Необходимо продифференцировать функцию. Имеем, что
y’=-115×3+18×2+105x+176′, x∈-∞; -2115×3-6×2+9x+12′, x∈[-2; +∞)⇔y’=-15(x2+12x+35), x∈-∞; -215×2-4x+3, x∈[-2; +∞)
Когда х=-2, тогда производная не существует, потому что односторонние пределы не равны в этой точке:
limx→-2-0y'(x)=limx→-2-0-15(x2+12x+35=-15(-2)2+12(-2)+35=-3limx→-2+0y'(x)=limx→-2+015(x2-4x+3)=15-22-4-2+3=3
Вычисляем значение функции в точке х=-2, где получаем, что
- y(-2)=115-2+23-45(-2)2-165(-2)-265+3-2+2=-2, то есть касательная в точке (-2;-2) не будет существовать.
- Касательная параллельна ох, когда угловой коэффициент равняется нулю. Тогда kx=tg αx=f'(x0). То есть необходимо найти значения таких х, когда производная функции обращает ее в ноль. То есть значения f’(x) и будут являться точками касания, где касательная является параллельной ох.
Когда x∈-∞; -2, тогда -15(x2+12x+35)=0, а при x∈(-2; +∞) получаем 15(x2-4x+3)=0.
Решим:
-15(x2+12x+35)=0D=122-4·35=144-140=4×1=-12+42=-5∈-∞; -2×2=-12-42=-7∈-∞; -2 15(x2-4x+3)=0D=42-4·3=4×3=4-42=1∈-2; +∞x4=4+42=3∈-2; +∞
Вычисляем соответствующие значения функции
y1=y-5=115-5+23-45-52-165-5-265+3-5+2=85y2=y(-7)=115-7+23-45(-7)2-165-7-265+3-7+2=43y3=y(1)=1151+23-45·12-165·1-265+31+2=85y4=y(3)=1153+23-45·32-165·3-265+33+2=43
Отсюда -5; 85, -4; 43, 1; 85, 3; 43 считаются искомыми точками графика функции.
Рассмотрим графическое изображение решения.
Черная линия – график функции, красные точки – точки касания.
- Когда прямые располагаются параллельно, то угловые коэффициенты равны. Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 85 . Для этого нужно решить уравнение вида y'(x)=85. Тогда, если x∈-∞; -2, получаем, что -15(x2+12x+35)=85, а если x∈(-2; +∞), тогда 15(x2-4x+3)=85.
Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что
-15×2+12x+35=85×2+12x+43=0D=122-4·43=-28<0
Другое уравнение имеет два действительных корня, тогда
15(x2-4x+3)=85×2-4x-5=0D=42-4·(-5)=36×1=4-362=-1∈-2; +∞x2=4+362=5∈-2; +∞
Перейдем к нахождению значений функции. Получаем, что
y1=y(-1)=115-1+23-45(-1)2-165(-1)-265+3-1+2=415y2=y(5)=1155+23-45·52-165·5-265+35+2=83
Точки со значениями -1; 415, 5; 83 являются точками, в которых касательные параллельны прямой y=85x+4.
Ответ: черная линия – график функции, красная линия – график y=85x+4, синяя линия – касательные в точках -1; 415, 5; 83.
Возможно существование бесконечного количества касательных для заданных функций.
Написать уравнения всех имеющихся касательных функции y=3cos32x-π4-13, которые располагаются перпендикулярно прямой y=-2x+12.
Решение
Для составления уравнения касательной необходимо найти коэффициент и координаты точки касания, исходя из условия перпендикулярности прямых. Определение звучит так: произведение угловых коэффициентов, которые перпендикулярны прямым, равняется -1, то есть записывается как kx·k⊥=-1. Из условия имеем, что угловой коэффициент располагается перпендикулярно прямой и равняется k⊥=-2, тогда kx=-1k⊥=-1-2=12.
Теперь необходимо найти координаты точек касания. Нужно найти х, после чего его значение для заданной функции. Отметим, что из геометрического смысла производной в точке
x0 получаем, что kx=y'(x0). Из данного равенства найдем значения х для точек касания.
Получаем, что
y'(x0)=3cos32x0-π4-13’=3·-sin32x0-π4·32×0-π4’==-3·sin32x0-π4·32=-92·sin32x0-π4⇒kx=y'(x0)⇔-92·sin32x0-π4=12⇒sin32x0-π4=-19
Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.
32×0-π4=arcsin-19+2πk или 32×0-π4=π-arcsin-19+2πk
32×0-π4=-arcsin19+2πk или 32×0-π4=π+arcsin19+2πk
x0=23π4-arcsin19+2πk или x0=235π4+arcsin19+2πk, k∈Z
Z- множество целых чисел.
Найдены х точек касания. Теперь необходимо перейти к поиску значений у:
y0=3cos32x0-π4-13
y0=3·1-sin232x0-π4-13 или y0=3·-1-sin232x0-π4-13
y0=3·1–192-13 или y0=3·-1–192-13
y0=45-13 или y0=-45+13
Отсюда получаем, что 23π4-arcsin19+2πk; 45-13, 235π4+arcsin19+2πk; -45+13 являются точками касания.
Ответ: необходимы уравнения запишутся как
y=12x-23π4-arcsin19+2πk+45-13,y=12x-235π4+arcsin19+2πk-45+13, k∈Z
Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.
Рисунок показывает, что расположение функции идет на промежутке [-10;10], где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y=-2x+12. Красные точки – это точки касания.
Касательная к окружности, эллипсу, гиперболе, параболе
Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.
Касательная к окружности
Для задания окружности с центром в точке xcenter; ycenter и радиусом R применяется формула x-xcenter2+y-ycenter2=R2.
Данное равенство может быть записано как объединение двух функций:
y=R2-x-xcenter2+ycentery=-R2-x-xcenter2+ycenter
Первая функция располагается вверху, а вторая внизу, как показано на рисунке.
Для составления уравнения окружности в точке x0; y0, которая располагается в верхней или нижней полуокружности, следует найти уравнение графика функции вида y=R2-x-xcenter2+ycenter или y=-R2-x-xcenter2+ycenter в указанной точке.
Когда в точках xcenter; ycenter+R и xcenter; ycenter-R касательные могут быть заданы уравнениями y=ycenter+R и y=ycenter-R, а в точках xcenter+R; ycenter и
xcenter-R; ycenter будут являться параллельными оу, тогда получим уравнения вида x=xcenter+R и x=xcenter-R.
Касательная к эллипсу
Когда эллипс имеет центр в точке xcenter; ycenter с полуосями a и b, тогда он может быть задан при помощи уравнения x-xcenter2a2+y-ycenter2b2=1.
Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что
y=ba·a2-(x-xcenter)2+ycentery=-ba·a2-(x-xcenter)2+ycenter
Если касательные располагаются на вершинах эллипса, тогда они параллельны ох или оу. Ниже для наглядности рассмотрим рисунок.
Написать уравнение касательной к эллипсу x-324+y-5225=1 в точках со значениями x равного х=2.
Решение
Необходимо найти точки касания, которые соответствуют значению х=2. Производим подстановку в имеющееся уравнение эллипса и получаем, что
x-324x=2+y-5225=114+y-5225=1⇒y-52=34·25⇒y=±532+5
Тогда 2; 532+5 и 2; -532+5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.
Перейдем к нахождению и разрешению уравнения эллипса относительно y. Получим, что
x-324+y-5225=1y-5225=1-x-324(y-5)2=25·1-x-324y-5=±5·1-x-324y=5±524-x-32
Очевидно, что верхний полуэллипс задается с помощью функции вида y=5+524-x-32, а нижний y=5-524-x-32.
Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2; 532+5 будет иметь вид
y’=5+524-x-32’=52·124-(x-3)2·4-(x-3)2’==-52·x-34-(x-3)2⇒y'(x0)=y'(2)=-52·2-34-(2-3)2=523⇒y=y'(x0)·x-x0+y0⇔y=523(x-2)+532+5
Получаем, что уравнение второй касательной со значением в точке
2; -532+5 принимает вид
y’=5-524-(x-3)2’=-52·124-(x-3)2·4-(x-3)2’==52·x-34-(x-3)2⇒y'(x0)=y'(2)=52·2-34-(2-3)2=-523⇒y=y'(x0)·x-x0+y0⇔y=-523(x-2)-532+5
Графически касательные обозначаются так:
Касательная к гиперболе
Когда гипербола имеет центр в точке xcenter; ycenter и вершины xcenter+α; ycenter и xcenter-α; ycenter, имеет место задание неравенства x-xcenter2α2-y-ycenter2b2=1, если с вершинами xcenter; ycenter+b и xcenter; ycenter-b, тогда задается при помощи неравенства x-xcenter2α2-y-ycenter2b2=-1.
Гипербола может быть представлена в виде двух объединенных функций вида
y=ba·(x-xcenter)2-a2+ycentery=-ba·(x-xcenter)2-a2+ycenter или y=ba·(x-xcenter)2+a2+ycentery=-ba·(x-xcenter)2+a2+ycenter
В первом случае имеем, что касательные параллельны оу, а во втором параллельны ох.
Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.
Составить уравнение касательной к гиперболе x-324-y+329=1 в точке 7; -33-3.
Решение
Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что
x-324-y+329=1⇒y+329=x-324-1⇒y+32=9·x-324-1⇒y+3=32·x-32-4 или y+3=-32·x-32-4⇒y=32·x-32-4-3y=-32·x-32-4-3
Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7; -33-3.
Очевидно, что для проверки первой функции необходимо y(7)=32·(7-3)2-4-3=33-3≠-33-3, тогда точка графику не принадлежит, так как равенство не выполняется.
Для второй функции имеем, что y(7)=-32·(7-3)2-4-3=-33-3≠-33-3, значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.
Получаем, что
y’=-32·(x-3)2-4-3’=-32·x-3(x-3)2-4⇒kx=y'(x0)=-32·x0-3×0-32-4×0=7=-32·7-37-32-4=-3
Ответ: уравнение касательной можно представить как
y=-3·x-7-33-3=-3·x+43-3
Наглядно изображается так:
Касательная к параболе
Чтобы составить уравнение касательной к параболе y=ax2+bx+c в точке x0, y(x0), необходимо использовать стандартный алгоритм, тогда уравнение примет вид y=y'(x0)·x-x0+y(x0). Такая касательная в вершине параллельна ох.
Следует задать параболу x=ay2+by+c как объединение двух функций. Поэтому нужно разрешить уравнение относительно у. Получаем, что
x=ay2+by+c⇔ay2+by+c-x=0D=b2-4a(c-x)y=-b+b2-4a(c-x)2ay=-b-b2-4a(c-x)2a
Графически изобразим как:
Для выяснения принадлежности точки x0, y(x0) функции, нежно действовать по стандартному алгоритму. Такая касательная будет параллельна оу относительно параболы.
Написать уравнение касательной к графику x-2y2-5y+3, когда имеем угол наклона касательной 150°.
Решение
Начинаем решение с представления параболы в качестве двух функций. Получим, что
-2y2-5y+3-x=0D=(-5)2-4·(-2)·(3-x)=49-8xy=5+49-8x-4y=5-49-8x-4
Значение углового коэффициента равняется значению производной в точке x0 этой функции и равняется тангенсу угла наклона.
Получаем:
kx=y'(x0)=tg αx=tg 150°=-13
Отсюда определим значение х для точек касания.
Первая функция запишется как
y’=5+49-8x-4’=149-8x⇒y'(x0)=149-8×0=-13⇔49-8×0=-3
Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150° для такой функции не существует.
Вторая функция запишется как
y’=5-49-8x-4’=-149-8x⇒y'(x0)=-149-8×0=-13⇔49-8×0=-3×0=234⇒y(x0)=5-49-8·234-4=-5+34
Имеем, что точки касания – 234; -5+34.
Ответ: уравнение касательной принимает вид
y=-13·x-234+-5+34
Графически изобразим это таким образом:
Геометрический смысл производной
Если плохо разбираешься в производной, то вот тебе полноценный гид по ней, с текстом, примерами и вебинарами: «Производная функции – геометрический смысл и правила дифференцирования»!
Рассмотрим график какой-то функции ( y=fleft( x right)):
Выберем на линии графика некую точку ( A). Пусть ее абсцисса ( {{x}_{0}}), тогда ордината равна ( fleft( {{x}_{0}} right)).
Затем выберем близкую к точке ( A) точку ( B) с абсциссой ( {{x}_{0}}+Delta x); ее ордината – это ( fleft( {{x}_{0}}+Delta x right)):
Проведем прямую через эти точки. Она называется секущей (прямо как в геометрии).
Обозначим угол наклона прямой к оси ( Ox) как ( alpha ).
Как и в тригонометрии, этот угол отсчитывается от положительного направления оси абсцисс против часовой стрелки.
Какие значения может принимать угол ( alpha )?
Как ни наклоняй эту прямую, все равно одна половина будет торчать вверх. Поэтому максимально возможный угол – ( 180{}^circ ), а минимально возможный – ( 0{}^circ ).
Значит, ( alpha in left[ 0{}^circ ;180{}^circ right)). Угол ( 180{}^circ ) не включается, поскольку положение прямой в этом случае в точности совпадает с ( 0{}^circ ), а логичнее выбирать меньший угол.
Возьмем на рисунке такую точку ( C), чтобы прямая ( AC) была параллельна оси абсцисс, а ( BC) – ординат:
По рисунку видно, что ( AC=Delta x), а ( BC=Delta f).
Тогда отношение приращений:
( frac{Delta f}{Delta x}=frac{BC}{AC}={tg}alpha )
(так как ( angle C=90{}^circ ), то ( triangle ABC) – прямоугольный).
Давай теперь уменьшать ( Delta x).
Тогда точка ( B) будет приближаться к точке ( A). Когда ( Delta x) станет бесконечно малым ( left( Delta xto 0 right)), отношение ( frac{Delta f}{Delta x}) станет равно производной функции в точке ( {{x}_{0}}).
Что же при этом станет с секущей?
Точка ( B) будет бесконечно близка к точке ( A), так что их можно будет считать одной и той же точкой.
Но прямая, имеющая с кривой только одну общую точку – это ни что иное, как касательная (в данном случае это условие выполняется только на небольшом участке – вблизи точки ( A), но этого достаточно).
Говорят, что при этом секущая занимает предельное положение.
Угол наклона секущей к оси ( displaystyle Ox) назовем ( varphi ). Тогда получится, что производная
( {f}’left( {{x}_{0}} right)underset{Delta xto 0}{mathop{=}},frac{Delta f}{Delta x}= {tg}varphi ),
то есть
Производная равна тангенсу угла наклона касательной к графику функции в данной точке
Поскольку касательная – это прямая, давай теперь вспомним уравнение прямой:
( y=kx+b).
За что отвечает коэффициент ( displaystyle k)? За наклон прямой. Он так и называется: угловой коэффициент.
Что это значит? А то, что равен он тангенсу угла между прямой и осью ( displaystyle Ox)!
То есть вот что получается:
( {f}’left( {{x}_{0}} right)= {tg}varphi =k).
Но мы получили это правило, рассматривая возрастающую функцию. А что изменится, если функция будет убывающей?
Посмотрим: Теперь углы ( alpha ) и ( displaystyle varphi ) тупые. А приращение функции ( Delta f) – отрицательное.
Снова рассмотрим ( triangle ABC): ( angle B=180{}^circ -alpha text{ }Rightarrow text{ } {tg}angle B=- {tg}alpha ).
С другой стороны, ( {tg}angle B=frac{AC}{BC}=frac{-Delta f}{Delta x}).
Получаем: ( frac{-Delta f}{Delta x}=- {tg}alpha text{ }Rightarrow text{ }frac{Delta f}{Delta x}= {tg}alpha ), то есть все, как и в прошлый раз.
Снова устремим точку ( displaystyle B) к точке ( displaystyle A), и секущая ( displaystyle AB) примет предельное положение, то есть превратится в касательную к графику функции в точке ( displaystyle A).
Итак, сформулируем окончательно полученное правило:
Производная функции в данной точке равна тангенсу угла наклона касательной к графику функции в этой точке, или (что то же самое) угловому коэффициенту этой касательной:
( {f}’left( {{x}_{0}} right)= {tg}varphi =k)
Это и есть геометрический смысл производной.
Окей, все это интересно, но зачем оно нам? Вот пример:
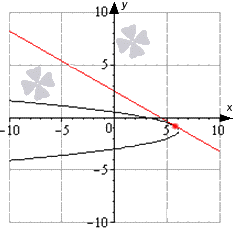
На рисунке изображен график функции ( displaystyle y=mathsf{f}left( x right)) и касательная к нему в точке с абсциссой ( {{x}_{0}}).
Найдите значение производной функции ( displaystyle mathsf{f}left( x right)) в точке ( {{x}_{0}}).
Решение.
Как мы недавно выяснили, значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс:
( displaystyle f’left( x right)=k= {tg}varphi).
Значит, для нахождения значения производной нам нужно найти тангенс угла наклона касательной.
На рисунке у нас отмечено две точки, лежащие на касательной, координаты которых нам известны. Так давай достроим прямоугольный треугольник, проходящий через эти точки, и найдем тангенс угла наклона касательной!
Угол наклона касательной к оси ( displaystyle Ox) – это ( displaystyle angle BAC). Найдем тангенс этого угла:
( displaystyle {tg}angle BAC=frac{BC}{AC}=frac{6}{5}=1,2).
Таким образом, производная функции ( displaystyle mathsf{f}left( x right)) в точке ( {{x}_{0}}) равна ( displaystyle 1,2).
Ответ: ( displaystyle 1,2).
Теперь попробуй сам.
Уравнение касательной к графику функций
А сейчас сосредоточимся на произвольных касательных.
Предположим, у нас есть какая-то функция, например, ( fleft( x right)=left( {{x}^{2}}+2 right)). Мы нарисовали ее график и хотим провести касательную к нему в какой-нибудь точке ( {{x}_{0}}). Например, в точке ( {{x}_{0}}=2).
Берем линейку, пристраиваем ее к графику и чертим:
Что мы знаем об этой прямой? Что самое важное нужно знать о прямой на координатной плоскости?
Поскольку прямая – это изображение линейной функции, очень удобно было бы знать ее уравнение. То есть коэффициенты ( k) и ( b) в уравнении
( y=kx+b).
Но ведь ( k) мы уже знаем! Это угловой коэффициент касательной, который равен производной функции в этой точке:
( k={f}’left( {{x}_{0}} right)).
В нашем примере будет так:
( {f}’left( x right)={{left( {{x}^{2}}+2 right)}^{prime }}=2x;)
( k={f}’left( {{x}_{0}} right)={f}’left( 2 right)=2cdot 2=4.)
Теперь остается найти ( b) . Это проще простого: ведь ( b) – значение ( y) при ( displaystyle x=0).
Графически ( b) – это координата пересечения прямой с осью ординат (ведь ( displaystyle x=0) во всех точках оси ( displaystyle Oy)):
Проведём ( BCparallel Ox) (так, что ( triangle ABC) – прямоугольный).
Тогда ( angle ABC=alpha )(тому самому углу между касательной и осью абсцисс). Чему равны ( displaystyle AC) и ( displaystyle BC)?
По рисунку явно видно, что ( BC={{x}_{0}}), а ( AC=fleft( {{x}_{0}} right)-b). Тогда получаем:
( {f}’left( {{x}_{0}} right)= {tg}alpha =frac{AC}{BC}=frac{fleft( {{x}_{0}} right)-b}{{{x}_{0}}}text{ }Rightarrow text{ }b=fleft( {{x}_{0}} right)-{{x}_{0}}cdot {f}’left( {{x}_{0}} right)).
Соединяем все полученные формулы в уравнение прямой:
( y=kx+b={f}’left( {{x}_{0}} right)cdot x+fleft( {{x}_{0}} right)-{{x}_{0}}cdot {f}’left( {{x}_{0}} right);)
( y={f}’left( {{x}_{0}} right)cdot left( x-{{x}_{0}} right)+fleft( {{x}_{0}} right))
Это и есть уравнение касательной к графику функции ( fleft( x right)) в точке ( {{x}_{0}}).
Пример:
Найди уравнение касательной к графику функции ( fleft( x right)={{x}^{2}}-2x+3) в точке ( {{x}_{0}}=3).
Решение:
На этом примере выработаем простой…
Бонус: Вебинар из нашего курса по подготовке к ЕГЭ по математике
ЕГЭ №7. Производная функции — геометрический смысл, дифференцирование
На этом видео мы вспомним, что такое функция и её график, научимся искать производную некоторых функций, например, такой: y = 2×3 – 3×2 + x + 5.
Мы разберём от А до Я все 7 типов задач, которые могут попасться в задаче №7 из ЕГЭ. Узнаем, на какие 3 фразы в условии задачи нужно обратить особое внимание, чтобы с лёгкостью решить задачу и не потерять баллы на ровном месте.
Разберём все возможные ошибки, которые можно допустить в этих задачах. Мы поймём, что многие из этих задач решаются обычным подсчётом клеточек на графике! Главное – не перепутать, что нужно считать.
P.S. Не забудьте потом посмотреть родственную тему: «Интегралы на ЕГЭ. Первообразные элементарных функций».
Касательная к графикам функции в точке
Угол наклона прямой линии [y=k x+b] — это угол [a], который берет свой отсчет от положительного направления оси координат ox по направлению к прямой. Угол наклона может иметь значение как со знаком плюс, так и со знаком минус.
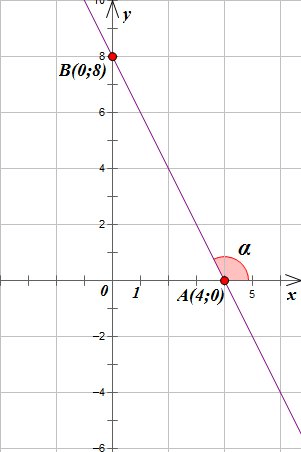
На расположенном рис.1 показана прямая и угол наклона относительно оси.
Для каждого угла наклона характерен угловой коэффициент прямой.
Определение
Угловой коэффициент — это числовой коэффициент прямой вида [boldsymbol{y=k x+b}]. В уравнение он обозначается буквой k.
Угловой коэффициент равен значению тангенса наклона заданной прямой линии: [k=operatorname{tg} alpha].
Основные значения угла наклона прямой
- Угол наклона прямой линии будет иметь нулевое значение, только в случае, когда параллельна ось Ox, и значение углового коэффициента равняется нулю. Потому что [operatorname{tg} 0=0]. Следовательно уравнение прямой будет записываться следующим образом: [y=b].
- В случае, когда угол наклона будет острым, то должно выполняться два следующих условия: [0<alpha<frac{pi}{2}] или [0^{circ}<alpha<90^{circ}]. Отсюда следует, что значение углового коэффициента будет являться положительным значением. Потому что значение тангенса удовлетворяет следующему условию, где показатель тангенса больше нулевого значения: [t g>0]. При этом будет наблюдаться возрастание графика функции на протяжении всей координатной прямой.
- При условии, что угол [alpha=frac{pi}{2}], из этого следует, что прямая будет располагаться относительно оси Ox в перпендикулярном положении. Условие задается следующим равенством [x=c]. Где с — это простое действительное число.
- Если угол наклона прямой, является тупым, то будет применяться следующее условие: [frac{pi}{2}<alpha<pi] или [90^{circ}<alpha<180^{circ}] . Для данного случая характерно отрицательное значение углового коэффициента и убывание функции.
Определение
Секущая прямая — это прямая, которая проходит через две точки заданной функции. Иными словами, можно сказать, что секущая — это прямая, которую можно провести через две любые точки графика.
На графике показана секущая, которая обозначена красным цветом и точками А и В.
Если угловой коэффициент прямой линии равен тангенсу угла наклона, то используя прямоугольный треугольник можно найти значение тангенса. Сделать это можно вычислением по правилу: тангенс равен отношению противолежащего катета к прилежащему.
Чтобы определить значение секущий, нужно использовать следующую формулу:
[k=operatorname{tg} alpha=frac{B C}{A C}=frac{fleft(chi_{B}right)-fleft(chi_{A}right)}{chi_{B}-chi_{A}}], где:
[chi_{B}, chi_{A}] — абсциссы точек А и В;
[fleft(chi_{B}right), fleft(chi_{A}right)] — значения функции, в заданных точках.
Значение секущий определяется, используя следующее неравенство:
[k=frac{fleft(chi_{B}right)-fleft(chi_{A}right)}{chi_{B}-chi_{A}}] либо [k=frac{fleft(chi_{A}right)-fleft(chi_{B}right)}{chi_{A}-chi_{B}}]
Уравнение записывается следующим образом:
[k=frac{fleft(chi_{B}right)-fleft(chi_{A}right)}{chi_{B}-chi_{A}} cdotleft(chi-chi_{A}right)+fleft(chi_{A}right)]
[k=frac{fleft(chi_{A}right)-fleft(chi_{B}right)}{chi_{A}-chi_{B}} cdotleft(chi-chi_{B}right)+fleft(chi_{B}right)]
Определение
Касательная к графику функции — это прямая, которая проходит через определенную заданную точку, которая в свою очередь имеет отрезок с множеством числовых значений x.
Пример:
Прямая задана следующей функцией: [y=x+1]. Данная функция считается касательной к графику [y=2 sqrt{x}] с координатными точками (1;2).
Рассмотрим графики со значениями (1;2). Функция обозначается черным цветом, а касательная линия соответственно синим цветом.
Чтобы определить касательную к функции, нужно исследовать поведение касательной АВ. При этом должно быть бесконечное приближение точки В к точке А.
Значение производной функции в точке и ее геометрический смысл
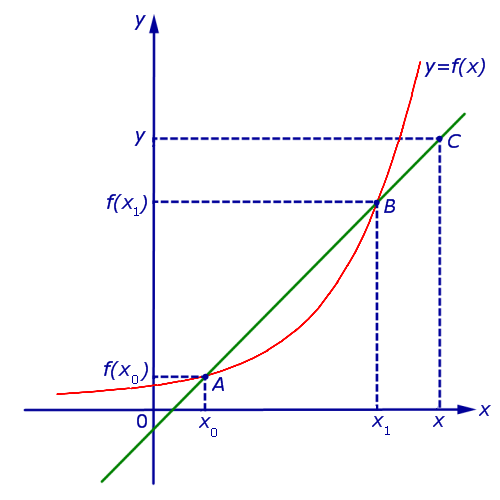
Для заданной функции [f(chi)] рассмотрим секущую АВ. Точки А и В заданы следующими значениями: [left(chi_{0}, fleft(chi_{0}right)right)] и [left(chi_{0}+Delta chi ,left(chi_{0}+Delta chiright)right.].
[Delta chi] — это показатель приращения значения аргумента.
Подставив все значения в исходную функцию получим следующий вид:
[Delta y=Delta f(chi)=fleft(chi_{0}+Delta chiright)-f(Delta chi)].
Для более лучшего восприятия решения, построим график.
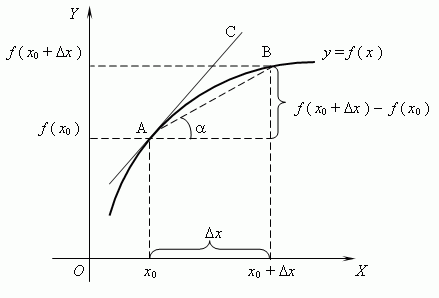
Из графика видно, что образуется прямоугольный треугольник ABC. Составим соотношение [frac{Delta y}{Delta x}=operatorname{tg} alpha], для этого необходимо применить основное определение тригонометрической функции, а именно тангенса.
Исходя из основного определения касательной, запишем следующее выражение:
[lim _{Delta x rightarrow 0} frac{Delta y}{Delta x}=operatorname{tg} alpha_{x}]
Используя правило производной, имеем следующее:
- производная [f(x)] в точке [x_{0}] — является пределом отношения приращения функции к аргументу.
- [Delta_{chi} rightarrow 0 text { и } fleft(x_{0}right)=lim _{Delta x rightarrow 0} frac{Delta y}{Delta x}].
Следовательно:
[f^{prime}left(x_{0}right)=lim _{Delta x rightarrow 0} frac{Delta y}{Delta x}=operatorname{tg} alpha_{x}=k_{z}]
[k_{z}] — это угловой коэффициент касательной функции.
Из данной функции можно сделать следующий вывод:
- функция [f(x)] может находится в точке со значением [x_{0}]
- функция может быть касательной к графику в некой точке касания, где угловой коэффициент равняется производной.
Понятие уравнения касательной прямой
Чтобы составить уравнение прямой, нужно знать угловой коэффициент с заданной точкой. Это точка, через которую проходит прямая. При пересечении угловой коэффициент записывается как значение [x_{0}].
Уравнение касательной записывается следующим образом:
[y=f^{prime}left(x_{0}right) cdotleft(x-x_{0}right)+fleft(x_{0}right)]
График функции [y=f(x)].
Расположение касательной прямой непосредственно зависит от значения углового коэффициента. Если прямая параллельна оси Ox, то значение коэффициента равно нулевому значению. При параллельном расположении относительно оси Oy, коэффициент угловой принимает значение бесконечности. При это уравнение касательной записывается как: [x=x_{0}].Также угловой коэффициент будет возрастать при значении больше нуля, а если коэффициент меньше нуля, то функция соответственно будет убывать.
Примеры
Нужно составить уравнение касательной к графику функции.
[y=e^{x+1}+frac{x^{3}}{3}-frac{6-sqrt{3}}{3} x-frac{17-sqrt{3}}{3}]
Порядок решения:
Из условия задачи следует, что функция может быть определенной для всех действительных значений. Точка,
которая задана с координатами (1;3) будет являться точкой касания, следовательно , [x_{0}=-1,
fleft(x_{0}right)=-3].
Для точки со значение равным -1, нужно определить производную.
Для этого составим уравнение:
[y^{prime}=left(e^{x+1}+frac{x^{3}}{3}-frac{6-sqrt{3}}{3}
x-frac{17-sqrt{3}}{3}right)^{prime}=\left(e^{x+1}right)^{prime}+left(frac{x^{3}}{3}right)^{prime}-left(frac{6-sqrt{3}}{3}
xright)^{prime}-left(frac{17-sqrt{3}}{3}right)^{prime}=e^{x+1}+x^{2}-frac{6-sqrt{3}}{3};]
[y^{prime}left(x_{0}right)=y^{prime}(-1)=e^{-1+1}+(-1)^2-frac{6-sqrt{3}}{3}=frac{sqrt{3}}{3}]
Показатель [f^{prime}(x)] в точке, которая является касательной, будет равен угловому коэффициенту.
Угловой коэффициент равен наклону тангенса. Отсюда следует, что:
[k_{x}=operatorname{tg} alpha_{x}=y^{prime}left(x_{0}right)=frac{sqrt{3}}{3}Rightarrow alpha_{chi}=operatorname{arctg} frac{sqrt{3}}{3}=frac{pi}{6}]
Подведем итоги, и запишем ответ:
[y=f^{prime}left(x_{0}right) cdotleft(x-x_{0}right)+fleft(x_{0}right);\y=frac{sqrt{3}}{3}(x+1)-3
; y=frac{sqrt{3}}{3} x-frac{9-sqrt{3}}{3}]
По условию задачи нужно определить касательную к графику функции [y=3 cdot sqrt[5]{x-1}+1]. Точки
координат равны (1;1). Также нужно составить уравнение и определить значение угла наклона.
Согласно условию задачи, область определения функции — это простые действительные числа.
Определим значение производной.
[y^{prime}=(3 cdot sqrt[5]{x-1}+1)^{prime}=3 cdot frac{1}{5} cdot(x-1)^{frac{1}{5}} 1=frac{3}{5}
cdot frac{1}{(x-1)^{frac{4}{5}}}]
При условии, что [x_{0}=1] тогда функция будет не определенной, но пределы ее можно записать как:
[lim _{x rightarrow 1+0}left(frac{3}{5} cdot frac{1}{(x-1)^{frac{4}{5}}}right)=frac{3}{5} cdot
frac{1}{(+0)^{frac{4}{5}}}=frac{3}{5} cdot frac{1}{+0}=infty]
[lim _{x rightarrow 1-0}left(frac{3}{5} cdot frac{1}{(x-1)^{frac{4}{5}}}right)=frac{3}{5} cdot
frac{1}{(-0)^{frac{4}{5}}}=frac{3}{5} cdot frac{1}{+0}=+infty]
Это значит, что вертикальная касательная в точке существует.
Ответ: после всех проведенных вычислений уравнение приобретает вид x=1, где угол наклона будет равен
[frac{pi}{2}].
Нет времени решать самому?
Наши эксперты помогут!
Касательная линия к окружности
Для того чтобы задать окружность с центром в следующих точках:
[text {(Xcenter;Ycenter)}] и радиусом R, нужно воспользоваться формулой.
[(x-x_{center})^2+(y+y_{center})^2=R^2]
Данное выражение можно представить как две функции:
[y=sqrt{R^{2}-(x-x_{center})^2+y_{center}}]
[y=-sqrt{R^{2}-(x-x_{center})^2+y_{center}}]
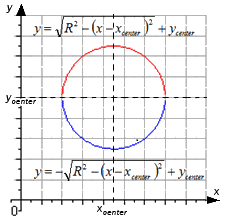
Из рисунка видно, что первая функция расположена в верхней части координатной плоскости. Вторая функция, соответственно в нижней части.
Чтобы составить уравнение окружности в точке, которая находится в верхней или нижней полуокружности, нужно составить уравнение для графика функции следующего вида:
[y=sqrt{R^{2}-left(x-x_{text {center }}right)^2 +y_{text {center }}}] и [y=-sqrt{R^{2}-left(x-x_{c e n t e r}right)+y_{c e n t e r}}], для конкретной точки.
Если в точках (xcenter;ycenter +R) и (xcenter;ycenter -R) касательные к окружности задаются выражением [y=y_{text {center }}+R ] и [y=y_{text {center }}-R], то они будут параллельны оси Oy. Из этого следует следующее уравнение [x=x_{text {center }}+R] и [x=x_{text {center }}-R].
Касательная к геометрической фигуре эллипс
Геометрическая фигура эллипс может быть задана следующей функцией:
[frac{left(x-x_{text {center }}right)^2}{a^{2}}+frac{left(y-y_{text {center }}right)^2}{b^{2}}=1]
Данное уравнение можно применять при следующих условиях:
- эллипс имеет в центре следующие точки: xcenter; ycenter
- a и b — это значение полуосей.
Используя два вида функций можно обозначить эллипс и окружность:
[y=frac{b}{a} cdot sqrt{a^{2}-left(x-x_{text {center }}right)+y_{text {center }}}]
[y=-frac{b}{a} cdot sqrt{a^{2}-left(x-x_{text {center }}right)+y_{text {center }}}]
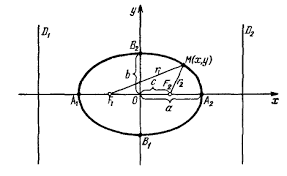
Пример
Необходимо составить уравнение касательной к эллипсу [frac{(x-3)^2}{4}+frac{(y-5)^2}{25}=1]. При этом
значение точки x будет равняться двум.
Порядок решения задачи:
Нужно определить точки касания, которые приближены к значению равным двум.
В уравнение подставляем данные.
[left|left(frac{(x-3)^{2}}{4}right)right|_{x=2}+frac{(y-5)^{2}}{25}=1]
[frac{1}{4}+frac{(y-5)^{2}}{25}=1 Rightarrow(y-5)^{2}=frac{3}{4} cdot 25 Rightarrow y=pm frac{5
sqrt{3}}{2}+5]
Точки касания, принадлежащие верхнему и нижнему полуэллипсу:
[left(2 ; frac{5 sqrt{3}}{2}+5right) и left(2 ;-frac{5 sqrt{3}}{2}+5right)].
Составим уравнение эллипса для координатной оси Oy.
[frac{(x-3)^{2}}{4}+frac{(y-5)^{2}}{25}=1];
[frac{(y-5)^{2}}{25}=1-frac{(x-3)^{2}}{4}];
[(y-5)^{2}=25 cdotleft(1-frac{(x-3)^{2}}{4}right)];
[y-5=pm 5 cdot sqrt{1-frac{(x-3)^{2}}{4}};]
[y=5 pm frac{5}{2} sqrt{4-(x-3)^{2}}];
Функция верхнего полуэллипса будет задаваться следующим видом:
[y=5+frac{5}{2} sqrt{4-(x-3)^{2}}];
Нижний полуэллипс можно записать как:
[y=5-frac{5}{2} sqrt{4-(x-3)^{2}}].
Для того чтобы составить уравнение касательной в точке, нужно применить стандартный алгоритм решения.
Для первой касательной в точке [left(2 ; frac{5 sqrt{3}}{2}+5right)] уравнение будет выглядеть
следующим образом:
[y^{prime}=left(5+frac{5}{2} sqrt{4-(x-3)^{2}}right)^{prime}=frac{5}{2} cdot frac{1}{2
sqrt{4-(x-3)^{2}}} cdotleft(4-(x-3)^{2}right)^{prime}=\=-frac{5}{2} cdot
frac{x-3}{sqrt{4-(x-3)^{2}}} Rightarrow y^{prime}left(x_{0}right)=y^{prime}(2)=-frac{5}{2} cdot
frac{2-3}{sqrt{4-(2-3)^{2}}}=frac{5}{2 sqrt{3}} Rightarrow\y=y^{prime}left(x_{0}right)
cdotleft(x-x_{0}right)+y_{0} Rightarrow y=frac{5}{2 sqrt{3}}(x-2)+frac{5}{2 sqrt{3}}+5]
Для второй касательной с точкой функция будет иметь следующий вид:
[y^{prime}=left(5-frac{5}{2} sqrt{4-(x-3)^{2}}right)^{prime}=-frac{5}{2} cdot frac{1}{2
sqrt{4-(x-3)^{2}}} cdotleft(4-(x-3)^{2}right)^{prime}=\=frac{5}{2} cdot
frac{x-3}{sqrt{4-(x-3)^{2}}} Rightarrow y^{prime}left(x_{0}right)=y^{prime}(2)=-frac{5}{2} cdot
frac{2-3}{sqrt{4-(2-3)^{2}}}=-frac{5}{2 sqrt{3}} Rightarrow\y=y^{prime}left(x_{0}right) cdotleft(x-x_{0}right)+y_{0} Rightarrow y=-frac{5}{2 sqrt{3}}(x-2)-frac{5}{2 sqrt{3}}+5]
Касательная к гиперболе. Основные функции
Чтобы составить уравнение касательной к геометрической фигуре гипербола, нужно применять основной алгоритм решения задач подобного типа.
Для гиперболы будет характерно следующее неравенство:
[frac{left(x-x_{text {center }}right)^2}{a^{2}}+frac{left(y-y_{text {center }}right)^2}{b^{2}}=1]
При этом должны выполняться следующие условия:
- центр в точке xcenter;ycente
- вершины точки (xcenter+ [a]; ycenter) и (xcenter-[a]; ycenter)
Если вершины имеют значения: (xcenter;ycenter+b) и (xcenter;ycenter-b), то функция задается следующим образом: [frac{left(x-x_{text {center }}right) 2}{a^{2}}+frac{left(y-y_{text {center }}right) ^2}{b^{2}}=-1].
Гиперболу можно определить, используя две пары уравнений, которые записываются в следующем виде:
[y=frac{b}{a} cdot sqrt{left(x-x_{text {center }}right)^2}-a^{2}+y_{text {center }}]
[y=-frac{b}{a} cdot sqrt{left(x-x_{text {center }}right)^2}-a^{2}+y_{text {center }}]
или
[y=frac{b}{a} cdot sqrt{left(x-x_{text {center }}right) ^2+a^{2}}+y_{text {center }}]
[y=-frac{b}{a} cdot sqrt{left(x-x_{text {center }}right)^2}+a^{2}+y_{text {center }}]
Для первых уравнение характерно параллельное расположение касательной относительно оси Oy. Соответственно для второй пары уравнений: параллельное расположение относительно оси Ox.
Пример
Составим уравнение касательной к гиперболе следующего вида: [frac{(x-3)^{2}}{4}-frac{(x+3)^{2}}{9}], в
характерных точках [(7 ;-3 sqrt{3}-3)].
Преобразование заданное уравнение при помощи двух функций.
[frac{(x-3)^{2}}{4}-frac{(x+3)^{2}}{9}=1 Rightarrow frac{(x+3)^{2}}{9}=frac{(x-3)^{2}}{4}-1
Rightarrow(y-3)^{2}=\9 cdotleft(frac{(x-3)^{2}}{4}-1right) Rightarrow y+3=frac{3}{2} cdot sqrt{(x-3)^{2}-4}] или [y+3=-frac{3}{2}]
[sqrt{(x-3)^{2}-4} Rightarrow\y=frac{3}{2} cdot sqrt{(x-3)^{2}-4}-3\y=-frac{3}{2} cdot sqrt{(x-3)^{2}-4}-3]
Далее нужно определить к какой из двух функций относится точка с координатами: [(7 ;-3 sqrt{3}-3)].
Проверим первую функцию [y(7)=frac{3}{2} cdot sqrt{(7-3)^{2}-4}-3=3 sqrt{3}-3 neq-3 sqrt{3}-3], из уравнения следует, что заданная точка не принадлежит графику, потому что равенство не выполняется.
Следовательно, нужно определить угловой коэффициент:
[y^{prime}=left(-frac{3}{2} cdot sqrt{(x-3)^{2}-4}-3right)^{prime}=-frac{3}{2} cdot frac{x-3}{sqrt{(x-3)^{2}-4}} Rightarrow\k_{x}=y^{prime}left(x_{0}right)=left(-frac{3}{2} cdot frac{x_{0}-3}{sqrt{left(x_{0}-3right)^{2}-4}}right)=-frac{3}{2} cdot frac{7-3}{sqrt{(7-3)^{2}-4}}=-sqrt{3}]
Ответ: уравнение касательной записывается следующим образом: [y=-sqrt{3} cdot(x-7)-3 sqrt{3}-3=-sqrt{3} cdot x+4 sqrt{3}-3]
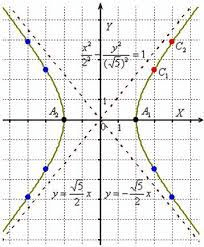
Касательная к параболе. Основные правила решения
Используя стандартный алгоритм решения, можно составить уравнение касательной к параболе [y=a x^{2}+b x+c] в точках [left(x_{0}, yleft(x_{0}right)right)]. Данное уравнение после преобразования будет иметь следующий вид:
[y=y^{prime}left(x_{0}right) cdotleft(x-x_{0}right)+yleft(x_{0}right)].
Необходимо задать параболу [x=a y^{2}+b y+c] как общая функция двух уравнений. Затем решить уравнение относительно оси Oy.
[x=a y^{2}+b y+c Rightarrow a y^{2}+b y+1-x=0;\D=b^{2}-4 a(c-x)\y=frac{-b+sqrt{b^{2} 4 a(c-x)}}{2 a};\y=frac{-b-sqrt{b^{2} 4 a(c-x)}}{2 a}.]
Чтобы определить принадлежность заданных точек [left(x_{0}, yleft(x_{0}right)right)], необходимо руководствоваться стандартным решением согласно алгоритма. Данная касательная будет иметь параллельное расположение относительно параболы.
Пример
Необходимо составить уравнение к графику касательной: [x-2 y^{2}-5 y+3] при угле наклона равным [150^{circ}]
Для решения будем применять стандартный алгоритм решения задач.
Для начала данную параболу нужно расписать и составить две функции, следующего вида:
[-2 y^{2}+5 y+3-x=0;\D=(-5)^{2}-4 cdot(-2) cdot(3-x)=49-8 x;\y=frac{5+sqrt{49-8 x}}{-4};\y=frac{5-sqrt{49-8 x}}{-4}.]
Значение углового коэффициента будет равняться значению производной в конкретной точке [x_{0}] для этой функции. И будет равен значению тангенса угла наклона.
[k_{x}=y^{prime}left(x_{0}right)=operatorname{tg} alpha_{x}=operatorname{tg} 150^{circ}=-frac{1}{sqrt{3}}];
Из уравнения сможем определить значение x для всех точек касания.
Функции будут записываться следующим образом:
[y^{prime}=left(frac{5+sqrt{49-8 x}}{-4}right)^{prime}=frac{1}{sqrt{49-8 x}} Rightarrow y^{prime}left(x_{0}right)=\frac{1}{sqrt{49-8 x_{0}}}=-frac{1}{sqrt{3}} Leftrightarrow sqrt{49-8 x_{0}}=-sqrt{3}]
В данном уравнении действительных корней нет. Так как ответ получился отрицательный.
Отсюда делаем вывод, что касательной линии с углом равным [150^{circ}] для функции такого вида не существует.
Функция второго вида:
[y^{prime}=left(frac{5-sqrt{49-8 x}}{-4}right)^{prime}=-frac{1}{sqrt{49-8 x}} Rightarrow y^{prime}left(x_{0}right)=-frac{1}{sqrt{49-8 x_{0}}}=\-frac{1}{sqrt{3}} Leftrightarrow sqrt{49-8 x_{0}}=-sqrt{3}\x_{0}=frac{23}{4} Rightarrow yleft(x_{0}right)=frac{5-sqrt{49-8 cdot frac{23}{4}}}{-4}=frac{-5+sqrt{3}}{4}]
Точки касания: [left(frac{23}{4} ; frac{-5+sqrt{3}}{4}right)].
Ответ: уравнение касательной имеет вид: [y=-frac{1}{sqrt{3}} cdotleft(x-frac{23}{4}right)+frac{-5+sqrt{3}}{4}].
Cправочник репетитора по математике предназначен для учащихся 5-11 классов и для преподавателей математики. Последние найдут в нем несколько оригинальных подходов к подаче и оформлению теоретических конспектов, упрощающих работу школьников с математическими понятиями и законами.
Касательная к графику функции.
Школьное определение касaтельной: прямая y=f (x) называется касательной к графику функции f (x) в точке 
если она проходит через точку 
и имеет угловой коэффициент 
.
Строгое определение касательной (из курса математического анализа) : прямая 
называется касательной к графику функции 
в точке , если при 
разность 
есть бесконечно малая величина, более высокого порядка малости чем 
Иллюстрация касательной m к графику функции 
в точке 
:
Геометрический смысл производной: Значение производной функции в точке равнo угловому коэффициенту касательной, проведенной к в точке , то есть 
, где k — угловой коэффициент касательной.
Комментарий репетитора по математике: угол наклона касательной определяется как направленный положительный угол, то есть тот самый угол, который вы привыкли откладывать на тригонометрическом круге от положительного направления оси OX против часовой стрелки. Поэтому, если если касательная отклонена влево от вертикального положения, ваш угол наклона окажется тупым, то есть принадлежащим промежутку ![[0;pi]](https://ankolpakov.ru/wp-content/plugins/easy-latex2/cache/tex_81caf8e5ffcc03c07b3aa0041092b867.png "[0;pi]")
. Так как тангенс любого такого угла (угла второй четверти) отрицательный, то отрицательной окажется и производная.
Общая форма уравнения касательной: 
Окончательная форма уравнения касательной :
Полезные факты для решения задач на касательную:
1) две наклонный прямые параллельны, тогда и только тогда, когда их угловые коэффициенты равны.
2) две наклонный прямые перпендикулярны тогда и только тогда, когда произведение их угловых коэффициентов равно -1.
Как найти угол наклона касательной по ее угловому коэффициенту:
Если 
, то 
Если 
, то 
Достаточный признак возрастания функции: если все значения производной некоторой функции положительны внутри промежутка, то функция внутри него строго возрастает.
Замечание репетитора по математике: если концы промежутка являются точками непрерывности функции (один или оба), то их можно присоденить к указанному промежутку возрастания.
Достаточный признак убывания функции: если все значения производной некоторой функции отрицательны внутри промежутка, то функция внутри него строго убывает.
Замечание репетитора по математике: если функция непрерывна на концах промежутка (на одном или на обоих), то эти концы можно присоединить к указанному промежутку убывания.
Блиц вопросы к репетитору:
Что такое критическая точка? Внутренняя точка области определения функции называется критической, если производная в этой точке либо не сущуствует, либо она равна нулю.
Что такое стационарная точка: Если у критической точки производная равна нулю — она называется стационарной точной.
Экстремумы
Минимум функции.
Определение: Точка называется точкой минимума функции , если в некотором промежутке I оси ОХ, содержащем для всех точек 
выполняется неравенство 
. В этом случае число 
называется минимумом функции в точке (или локальным минимумом).
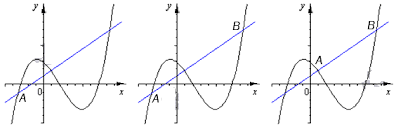
Фрагмент графика функции, имеющей точку минимума:
Комментарий репетитора по математики к рисунку: знаки — и + на оси OХ показывают на отрицательные/положитлеьные значения производной в левой/правой окрестности точки . Стрелки указывают на возрастание и убывание функции в этих крестностях. Я советую репетиторам математики включать в теоретические памятки для учеником именно такую (интегрированную) иллюстрацию минимума.
Максимум функции.
Определение:Точка называется точкой максимума функции , если в некотором промежутке I оси ОХ, содержащем для всех точек выполняется неравенство 
. В этом случае число называется максимумом функции в точке (или локальным максимумом).
Фрагмент графика функции, имеющей точку максимума:
Комментарий репетитора по математике: все обозначения и опорные знаки для подачи материала преподавателем аналогичны случаю с минимумом.
Экстремум – общее название минимума и максимума. Точка экстремума – общее название для точки минимума и точки максимума. На всех рисунках — экстремум, а — точка экстремума.
Необходимое условие существования экстремума: если — точка экстремума и в этой точке существует производная, то она равна нулю, то есть 
. В этом случае касательная, проведенная к графику функции будет параллельна оси ОХ.
Достаточное условие существования экстремума: если функция y=f (x) непрерывна в точке и при переходе через производная меняет знак , то — точка экстремума.
Признак минимума функции: если функция y=f (x) непрерывна в точке и производная меняет знак с минуса на плюс, то — точка минимума.
Признак максимума функции: если функция y=f (x) непрерывна в точке и производная меняет знак с плюса на минус , то — точка максимума.
Алгоритм нахождения наибольшего и наименьшего значения функции y=f (x) на отрезке [a;b], на которм она непрерывна
1) Найдите производную 
от данной функции
2) Найдите стационарные точки, решив уравнение 
2*) В редких случаях функция может иметь точки, в которых производной не существует. Их тоже нужно выявить.
3) Выберите из всех найденных точек те, которые попадают в исследуемый отрезок
4) Найдите значения данной функции в выбранных точках
5) Выберите среди них наименьшее и наибольшее
План исследования функции с применением производной. Построение графика.
1) Найдите производную 
2) Разложите ее на множители (если это возможно) или приведите все ее дроби к общему знаменателю, а затем разложите числитель. Тем самым вы ее готовите к дальнейшему исследованию методом интервалов
2) Определите у функции критические и стационарные точки, приравнивая числитель и знаменатель ее производной к нулю
2*) Точки, в которых производной не существует (обычно это нули знаменателя) отесите в группу тех, в которых функция будет иметь вертикальные асимптоты
3) Отметьте все найденные точки на оси Х и раставьте методом интервалов на образовавшихся промежутках знаки производной
4) Определите промежутки монотонности (промежутки возрастания и убывания) и над каждым из них поставьте соответствующую стрелку в соответствии с видом этой монотонности
5) Определите через признак минимума и максимума (или по характеру расположения стрелок) соответствующие точки экстремумов и найдите значения функции в этих точках
6) Нанесите их на координатной плоскости и также по характеру стрелок проведите через эти точки график.
Замечание репетитора по математике: аккуратнее выполняйте рисунок вблизи асимптот. График функции не должен их пересекать и обрываться рядом с ними. Плавно приближайте его к асимтоте пока на это хватает выделенного пространства системы координат.
Удачи в изучении математики!
Колпаков Александр Николаевич, репетитор по математике, Москва, Строгино.
Виртуальный математический справочник профессионального репетитора — преподавателя.
Касательная к графику функции f, дифференцируемой в точке xо, – это прямая, проходящая через точку (xо; f(xо)) и имеющая угловой коэффициент f ′(xо).
Угловой коэффициент имеет прямая вида y = kx + b. Коэффициент k и является угловым коэффициентом этой прямой.
Угловой коэффициент равен тангенсу острого угла, образуемого этой прямой с осью абсцисс: k = tgα
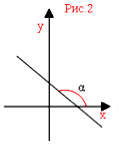
Здесь угол α – это угол между прямой y = kx + b и положительным (то есть против часовой стрелки) направлением оси абсцисс. Он называется углом наклона прямой (рис.1 и 2).
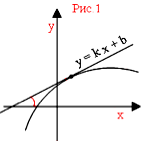
Если угол наклона прямой y = kx + b острый, то угловой коэффициент является положительным числом. График возрастает (рис.1).
Если угол наклона прямой y = kx + b тупой, то угловой коэффициент является отрицательным числом. График убывает (рис.2).
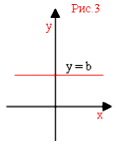
Если прямая параллельна оси абсцисс, то угол наклона прямой равен нулю. В этом случае угловой коэффициент прямой тоже равен нулю (так как тангенс нуля есть ноль). Уравнение прямой будет иметь вид y = b (рис.3).
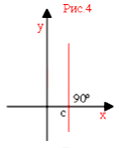
Если угол наклона прямой равен 90º (π/2), то есть она перпендикулярна оси абсцисс, то прямая задается равенством x = c, где c – некоторое действительное число (рис.4).
Уравнение касательной к графику функции y = f(x) в точке xо:
y = f(xо) + f ′(xо) (x – xо)
Алгоритм решения уравнения касательной к графику функции y = f(x):
- Вычислить f ( x0 )
- Вычислить производные f ‘( x) и f ‘( x0 )
- Внести найденные числа x0, f ( x0 ) ,f ‘( x0 ) в уравнение касательной и решить его
Пример: Найдем уравнение касательной к графику функции f(x) = x3 – 2x2 + 1 в точке с абсциссой 2.
Решение.
Следуем алгоритму.
1) Точка касания xо равна 2. Вычислим f(xо):
f(xо) = f(2) = 23 – 2 ∙ 22 + 1 = 8 – 8 + 1 = 1
2) Находим f ′(x). Для этого применяем формулы дифференцирования, изложенные в предыдущем разделе. Согласно этим формулам, х2 = 2х, а х3 = 3х2. Значит:
f ′(x) = 3х2 – 2 ∙ 2х = 3х2 – 4х.
Теперь, используя полученное значение f ′(x), вычислим f ′(xо):
f ′(xо) = f ′(2) = 3 ∙ 22 – 4 ∙ 2 = 12 – 8 = 4.
3) Итак, у нас есть все необходимые данные: xо = 2, f(xо) = 1, f ′(xо) = 4. Подставляем эти числа в уравнение касательной и находим окончательное решение:
у = f(xо) + f ′(xо) (x – xо) = 1 + 4 ∙ (х – 2) = 1 + 4х – 8 = –7 + 4х = 4х – 7.
Ответ: у = 4х – 7.
Найти угловой коэффициент касательной к графику функции в точке с абсциссой x0 =
Найдите угловой коэффициент касательной к графику функции в точке с абсциссой x0 = 2
Найдите тангенс угла наклона касательной, проведенной к графику функции в его точке с абсциссой (-1)
Дана функция f(x)=х2- 4x+1. Найдите координаты точки, в которой угловой коэффициент касательной к графику функции равен 2
Укажите абсциссу точки графика функции у = 12 -3х + х2 в которой угловой коэффициент касательной равен 2.
