Как найти коэффициент направленного действия

Аннотация

Перед тем как перейти к рассмотрению конструкции и работы разного типа антенн, рассмотрим одну из важнейших характеристик антенны – диаграмму направленности и те параметры, которые из нее напрямую вытекают.
Рекомендую, также, ознакомиться с предыдущей статьёй – Ликбез: основы теории по антеннам.

Введение

Антенна, вне зависимости от конструкции, обладает свойством обратимости (может работать как на прием, так и на излучение). Часто в радиорелейных трактах одна и та же антенна может быть подключена одновременно к приемнику и передатчику. Это позволяет излучать и принимать сигнал в одном направлении на разных частотах.

Почти все параметры приемной антенны соответствуют параметрам передающей антенны, но иногда имеют несколько другой физический смысл.

Несмотря на то, что приемная и передающая антенны обладают принципом двойственности, в конструктивном отношении они могут существенно отличаться. Связано это с тем, что передающая антенна должна пропускать через себя значительные мощности для передачи электромагнитного сигнала на большие (максимально возможные) расстояния. Если же антенна работает на прием, то она взаимодействует с полями очень малой напряженности. Вид токопередающей конструкции антенны часто определяет ее конечные габариты.

Пожалуй, основная характеристика любой антенны это диаграмма направленности. Из нее вытекает множество вспомогательных параметров и такие важные энергетические характеристики как коэффициент усиления и коэффициент направленного действия.

Диаграмма направленности

Диаграмма направленности (ДН) – это зависимость напряженности поля, создаваемого антенной на достаточно большом расстоянии, от углов наблюдения в пространстве. В объеме диаграмма направленной антенны может выглядеть так, как показано на рисунке 1.

Рисунок 1

То, что изображено на рисунке выше также еще называют пространственной диаграммной направленностью, которая является поверхностью объема и может иметь несколько максимумов. Главный максимум, выделенный на рисунке красным цветом, называется главным лепестком диаграммы и соответствует направлению главного излучения (или приема). Соответственно первые минимальные или (реже) нулевые значения напряженности поля вокруг главного лепестка определяют его границу. Все остальные максимальные значения поля называются боковыми лепестками.

На практике встречаются различные антенны, которые могут иметь несколько направлений максимального излучения, или не иметь боковых лепестков вовсе.

Для удобства изображения (и технического применения) ДН их принято рассматривать в двух перпендикулярных плоскостях. Как правило, это плоскости электрического вектора E и магнитного вектора H (которые друг другу в большинстве сред перпендикулярны), рисунок 2.

Рисунок 2

В некоторых случаях ДН рассматривают в вертикальной и горизонтальной плоскостях по отношению к плоскости Земли. Плоские диаграммы изображают полярной или декартовой (прямоугольной) системами координат. В полярных координатах диаграмма более наглядна, и при наложении ее на карту можно получить представление о зоне действия антенны радиостанции, рисунок 3.

Рисунок 3

Представление диаграммы направленности в прямоугольной системе координат более удобно для инженерных расчетов, такое построение чаще применяется для исследования самой структуры диаграммы. Для этого диаграммы строят нормированными, с главным максимумом, приведенным к единице. На рисунке ниже приводится типичная нормированная диаграмма направленности зеркальной антенны.

Рисунок 4

В том случае, когда интенсивность бокового излучения довольно небольшая и в линейном масштабе измерение бокового излучения затруднительно, применяют логарифмический масштаб. Как известно децибелы маленькие значения делают большими, а большие – маленькими, поэтому та же самая диаграмма в логарифмическом масштабе выглядит так, как показано ниже:

Рисунок 5

Из одной только диаграммы направленности можно вытащить довольно большое количество важных для практики характеристик. Исследуем подробнее диаграмму, изображенную выше.

Один из наиболее важных параметров – это ширина главного лепестка по нулевому излучению θ₀ и ширина главного лепестка по уровню половинной мощности θ_0,5. Половина мощности соответствует уровню 3 дБ, или уровню 0,707 по напряженности поля.

Рисунок 6

Из рисунка 6 видно, что ширина главного лепестка по нулевому излучению составляет θ₀ = 5,18 град, а ширина по уровню половины мощности θ_0,5 = 2,15 град.

Также диаграммы оценивают по интенсивности бокового и обратного излучения (мощности боковых и задних лепестков), отсюда вытекает еще два важных параметры антенны – это коэффициент защитного действия, и уровень боковых лепестков.

Коэффициент защитного действия – это отношение напряженности поля, излученного антенной в главном направлении к напряженности поля, излученного в противоположном направлении.  Если рассматривают ориентацию главного лепестка диаграммы в направлении на 180 градусов, то обратного – на 0 градусов. Возможны и любые другие направления излучения. Найдем коэффициент защитного действия рассматриваемой диаграммы. Для наглядности изобразим ее в полярной системе координат (рисунок 7):

Рисунок 7

На диаграмме маркерами m1,m2 изображены уровни излучения в обратном и прямом направлениях соответственно. Коэффициент защитного действия определяется как:

 

– в относительных единицах. То же самое значение в дБ: 

. 

Уровень боковых лепестков (УБЛ) принято указывать в дБ, показывая тем самым, насколько уровень бокового излучения слаб по сравнению с уровнем главного лепестка, рисунок 8.

Рисунок 8

УБЛ в районе -18 дБ считается довольно хорошим показателем для высоконаправленной антенны. На рисунке изображены уровни первых боковых лепестков. Аналогично можно указывать также уровни всех последующих, но практической ценности их значение имеет мало, а представляет скорее академический интерес. Дело в том, что первые боковые лепестки находятся как правило “ближе всех остальных” к максимуму диаграммы направленности и могут оказывать помехи. Например, если сопровождение объекта происходит на уровне главного лепестка диаграммы -3дБ, а уровень первого бокового лепестка близок к этому значению (например -5:7 дБ), то велика вероятность начать цеплять объект боковым излучением со всеми вытекающими отсюда последствиями (неправильное позиционирование, потеря объекта и др.). Низкий УБЛ необходим не только для радиолокации, но и для области связи, ведь наличие паразитного излучения это всегда дополнительные помехи.

Коэффициент направленного действия и коэффициент усиления

Это два немаловажных параметра любой антенной системы, которые напрямую вытекают из определения диаграммы направленности. КНД и КУ часто путают между собой. Перейдем к их рассмотрению.

Коэффициент направленного действия

Коэффициент направленного действия (КНД) – это отношение квадрата напряженности поля, созданного в главном направлении (Е₀²), к среднему значению квадрата напряженности поля по всем направлениям (Е_ср²). Как понятно из определения, КНД характеризует направленные свойства антенны. КНД не учитывает потери, так как определяется по излучаемой мощности. Из сказанного выше можно указать формулу для расчета КНД:

D=E₀²/E_ср²

Если антенна работает на прием, то КНД показывает, во сколько раз улучшится отношение сигнал/шум по мощности, при замене направленной антенны ненаправленной, если помехи приходят равномерно со всех направлений.

Для передающей антенны КНД показывает, во сколько раз нужно уменьшить мощность излучения, если ненаправленную антенну заменить направленной, при сохранении одинаковых напряженностей поля в главном направлении.

КНД абсолютно ненаправленной антенны, очевидно, равно единице. Физически пространственная диаграмма направленности такой антенны выглядит в виде идеальной сферы:

Рисунок 9

Такая антенна одинаково хорошо излучает во всех направлениях, но на практике нереализуема. Поэтому это своего рода математическая абстракция.

Коэффициент усиления

Как уже было сказано выше, КНД не учитывает потери в антенне. Параметр, который характеризует направленные свойства антенны и учитывает потери в ней, называется коэффициентом усиления.

Коэффициент усиления (КУ) G – это отношение квадрата напряженности поля, созданного антенной в главном направлении (Е₀²), к среднему значению квадрата напряженности поля (Е_оэ²), созданного эталонной антенной, при равенстве подводимых к антеннам мощностей. Также отметим, что при определении КУ учитываются КПД эталонной и измеряемой антенны.

Понятие эталонной антенны очень важно в понимании коэффициента усиления, и в разных частотных диапазонах используют разные типы эталонных антенн. В диапазоне длинных/средних волн за эталон принят вертикальный несимметричный вибратор длиной четверть волны (рисунок 10).    

Рисунок 10

Для такого эталонного вибратора D_э=3,28, поэтому коэффициент усиления длинноволновой/средневолновой антенны определяется через КНД так: G=D*ŋ/3,28,  где ŋ – КПД антенны.

В диапазоне коротких волн в качестве эталонной антенны принимают симметричный полуволновый вибратор, для которого Dэ=1,64, тогда КУ:

G=D*ŋ/1,64

В диапазоне СВЧ (а это почти все современные Wi-Fi, LTE и др. антенны) за эталонный излучатель принят изотропный излучатель, дающий D_э=1, и имеющий пространственную диаграмму, изображенную на рисунке 9.

Коэффициент усиления является определяющим параметром передающих антенн, так как показывает, во сколько раз необходимо уменьшить мощность, подводимую к направленной антенне, по сравнению с эталонной, чтобы напряженность поля в главном направлении осталась неизменной.

КНД и КУ в основном выражают в децибелах: 10lgD, 10lgG.

Заключение

Таким образом, мы рассмотрели некоторые полевые характеристики антенны, вытекающие из диаграммы направленности и энергетические характеристики (КНД и КУ). Коэффициент усиления антенны всегда меньше коэффициента направленного действия, так как КУ учитывает потери в антенне. Потери могут возникать из-за отражения мощности обратно в линию питания облучателя, затекания токов за стенки (например, рупора), затенение диаграммы конструктивными частями антенны и др. В реальных антенных системах разница между КНД и КУ может составлять 1.5-2 дБ.    

Коэффицие́нт напра́вленного де́йствия (КНД) антенны — отношение квадрата напряженности поля, создаваемого антенной в данном направлении, к среднему значению квадрата напряженности поля по всем направлениям^[1].

КНД является безразмерной величиной, может выражаться в децибелах (дБ, дБи, дБд). Для обозначения КНД используют латинскую букву D (от англ. Directivity).

Обычно оперируют значением КНД D₀ в направлении максимального излучения антенны, а для описания угловой зависимости КНД используют нормированную диаграмму направленности (ДН) антенны по мощности. При этом КНД становится мерой способности антенны концентрировать энергию электромагнитного излучения в узком луче. Согласно определению, КНД однозначно связан с формой ДН антенны (более строго — с характеристикой направленности антенны).

Следует различать КНД и коэффициент усиления (КУ) антенны: КНД целиком и полностью определяется формой ДН антенны и не учитывает КПД антенны и потери на отражение, то есть не учитывает потери энергии в элементах конструкции антенны и объектах, расположенных в ближней зоне антенны.

Значения КНД[править | править код]

В зависимости от конструкции и рабочей длины волны значение КНД реальной антенны в направлении максимума излучения превышает единицу и может достигать миллионов. КНД абстрактного изотропного излучателя равен единице. Чем у́же главный лепесток ДН и меньше уровень боковых лепестков, тем больше КНД.

КНД линейной антенны (модели в виде расположенных непрерывно вдоль отрезка прямой длиной L>>λ изотропных источников с одинаковой амплитудой; λ — длина волны в свободном пространстве)^[2]:

• D₀ = 2L/λ — в режиме поперечного и наклонного излучения (пока луч отстоит от оси антенны на 2-3 ширины по уровню −3 дБ; при этом КНД не зависит от направления сканирования);
• D₀ = 4L/λ — в режиме осевого излучения;
• D₀ ≈ 7.2L/λ — в режиме осевого излучения с оптимальным замедлением.

КНД линейной антенной решетки изотропных излучателей с одинаковой амплитудой (при Nd = L>>λ и отсутствии дифракционных лепестков диаграммы направленности в области видимости; N — число элементов; d — период решетки)^[2]:

• D₀ ≈ 2Nd/λ — в режиме поперечного и наклонного излучения (пока луч отстоит от оси антенны на 2-3 ширины по уровню −3 дБ; при этом КНД не зависит от направления сканирования); в частности, в пределе при большом N и d = λ/2 D₀ = N;
• D₀ ≈ 4Nd/λ — в режиме осевого излучения;
• D₀ ≈ 7.2Nd/λ — в режиме осевого излучения с оптимальным замедлением.

КНД плоской апертуры^[2]:

• D₀ = (4πSK_и.п./λ²)cosθ₀ (при условии, что луч отстоит от плоскости апертуры на 2-3 ширины по уровню −3 дБ; S — площадь апертуры; K_и.п. — апертурный коэффициент использования поверхности; θ₀ — направление сканирования луча, угол места в сферической системе координат, отсчитываемый от нормали к апертуре). Уменьшение КНД при сканировании (множитель cosθ₀) обусловлено расширением луча;
• D₀ ≠ 0 при θ₀ → 90°.

Примечания[править | править код]

Коэффициент направленного действия (КНД) ‒ первым словом стоит коэффициент, то есть это безразмерная величина, он показывает во сколько раз в данном направлении антенна излучает больше, чем средняя мощность, излучаемая по всем направлениям. 

Давайте теперь визуализируем это определение, чтобы было более понятно. Проще всего показать на графике.

Рисунок 1. График диаграммы направленности

Итак, на рисунке 1 показано нулевое направление, и вид диаграммы направленности F(θ,φ). Поскольку это диаграмма направленности, то максимум у нее нормирован на единицу.

Рисунок 2

Теперь, если меня интересует коэффициент направленного действия, то я хочу узнать, насколько, например, в данном направлении, в единицу телесного угла (рисунок 2 – выделенная полоса), антенна излучает сильнее, нежели средняя мощность излучения по всем направлениям. Средняя, то есть это что? Значит надо взять и как-то усреднить эту всю функцию – примерно по горизонтальной прямой функции F_средн. Поэтому коэффициент направленного действия – это отношение мощности, излучаемой в верхней точке единицы телесного угла, к F_средн (рисунок 2). 

КНД, обозначается буквой D, это как раз и есть отношение мощности, излучаемой в некотором заданном направлении F(θ,φ) к средней мощности, излучаемой по всем направлениям F_средн. Средняя мощность, излучаемая по всем направлениям определяется по формуле: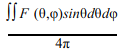, соответственно:

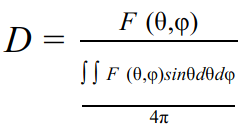— коэффициент направленности действия.

— в данном случае суммирование, суммируем всю эту функцию F(θ,φ), 4π -интервал (полный телесный угол).

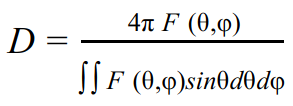— коэффициент направленности действия (КНД).

Но в выражении для мощности  стоит не КНД, а G  — коэффициент усиления. Коэффициент усиления – это что? Если это коэффициент, то соответственно это безразмерная величина. Что она характеризует? Коэффициент усиления — это отношение, которое показывает, во сколько раз наша реальная антенна с потерями в данном направлении излучает больше, чем некоторая изотропная антенна, к которой подведена та же самая мощность.

Фактически, изотропную антенну мы уже увидели. Когда я говорил про F_средн, про среднюю мощность излучения, я нарисовал линию, которая не зависит от углов, то есть, фактически, – это мощность излучения изотропной антенны. А когда мы говорим про нашу антенну, к которой подведена та же самая мощность, но реальную антенну, то в этом случае мы обязательно учитываем потери в антенне. Поэтому коэффициент усиления (КУ) обозначается буквой G, и G = D × η , где – это коэффициент полезного действия (КПД). 

Характеристика G для нас самая главная. Коэффициент усиления показывает во сколько раз наша антенна излучает сильнее, нежели изотропная антенна, в данном направлении, при условии, что к нашей реальной антенне и изотропной антенне подведена одна и та же самая мощность. То есть фактически наша антенна характеризуется этим коэффициентом усиления, это во сколько раз она энергию концентрирует эффективнее, чем излучает изотропная антенна.

Для размышления

Подумайте, будет ли влиять на коэффициент усиления антенны увеличение подаваемой мощности в 10 раз? А если увеличить подаваемую мощность в 1000 раз?

Материалы

• Достаточно подробная статья о коэффициенте направленного действия и коэффициенте усиления, подробно рассказывающая об этих вещах на реальных примерах

Коэффициент
направленного действия (КНД)
характеризует способ­ность
антенны концентрировать ЭМП ее излучения
в каком-либо
определенном направлении. Это понятие
было введено в 1929 г. советским ученым
А.А. Пистолькорсом. Коэффициентом
направленного действия называется
отношение среднего за период высокой
частоты значения плотности активного
пото­ка мощности
(среднего значения вектора Пойнтинга),
излучаемого антенной в
данном направлении

,
к усредненному по
всем направлениям значе­нию
плотности потока мощности П_Σ
[2, 5, 11]:

,

(2.11)

где

,
|
|
— амплитудное значение на­пряженности
электрического поля в направлении,
характеризуемом углами

;
А — амплитудный коэффициент;

—
нормированная ДН антенны по напряженности
поля.

Из сказанного выше
следует еще одно определение КНД антенны:
это число, которое показывает, во сколько
раз надо уменьшить излучаемую мощность
при замене изотропной антенны данной
антенной, чтобы среднее значение
плотности по­тока
мощности (значение напряженности
электрического поля) в одной и той же
точке наблюдения в дальней зоне осталось
неизменным.

Таким образом, при
определении КНД антенна сравнивается
с воображаемой абсолютно ненаправленной
(изотропной) антенной с равномерной
диаграммой направленности

,
излучаю­щей ту же мощность

.
Усредненное значение плотности потока
мощности

,
(2.12)

где

— мощность излучения; r
— радиус воображаемой сферы, охватываю­щей
антенну, причем величина r
должна быть такой, чтобы поверхность
сфе­ры находилась
в дальней зоне поля антенны. Тогда

.
(2.13)

С другой стороны,
мощность излучения антенны в соответствии
с методом вектора Пойнтинга определяется
выражением [11]

.
(2.14)

Подставив (2.14) в
(2.13), получаем общее выражение, определяющее
КНД антенны [2—5, 9—13]:

.

(2.15)

На практике чаще всего требуется знать
максимальное значение КНД антенны

в направлении максимального излучения,
в котором значение нормированной ДН

.
Тогда формула для расчета максимального
КНД принимает вид

.

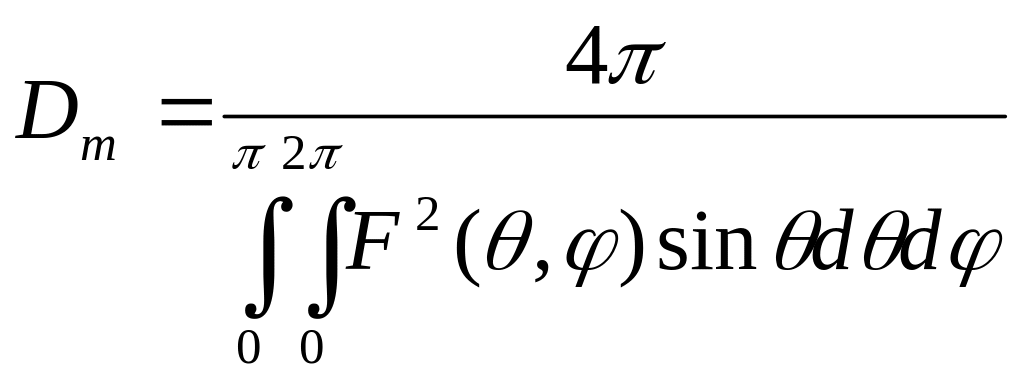
(2.16)

Учитывая, что квадрат нормированной
ДН по полю

есть нормированная ДН по мощности,
выражение (2.16) можно записать в виде

.

Из выражения (2.16) следует важный вывод:
чем уже главный лепесток и чем ниже УБЛ
ДН антенны, тем выше будет ее КНД.

В случае антенны с
осесимметричной ДН (форма которой не
зависит от азимутального угла φ)
выражение (2.16) приобретает вид [2, 5, 11]

.

(2.17)

В частности, в случае
элементарного электрического вибратора
(диполя Герца)

и D_m=1,5.

На практике КНД часто выражают в
логарифмических единицах (дБ):

.

В приведенных выше
определениях КНД реальная антенна
сравнивалась с воображаемой изотропной
антенной с равномерным излучением во
всех направлениях в пространстве.
Поскольку такая антенна является
физически нереализуемой, для практических
целей, в частности для измерения КНД,
вместо нее используют другой эталон —
любую реальную антенну, КНД которой
заранее известен (рассчитан или измерен).

Полученные выше
результаты справедливы для антенн с
линейной поляризацией излучения.
Выражения, определяющие КНД антенн с
эллиптической (круговой) поляризацией
излучения, приведены, например, в [10].

Для практических
расчетов полезно выразить максимальный
КНД антенны через амплитудное значение
напряженности поля в направлении
максимального излучения в дальней зоне.
Так, если антенна находится в свободном
пространстве с волновым сопротивлением
W₀=120π
Ом, то из (2.13) можно получить новое
выражение [10]:

,
(2.18)

где

.
Соответственно,

.

В частности, для
элементарного электрического вибратора
в эту формулу вместо

можно подставить выражение (2.1) в квадрате
(без фазовых множителей) и учесть,
что

,
где

— сопротивление излучения
элементарного электрического вибратора.
В результате КНД эле­ментарного
вибратора D_m=1,5
(1,76 дБ).

КНД можно выразить
с помощью еще одного параметра,
назы­ваемого действующей
длиной

или высотой

антенны. Этот
параметр особенно часто используют при
анализе приемных антенн.

В случае реальной линейной антенны ток
по ее длине l
распределен неравномерно. Од­нако
реальную антенну можно заменить
воображаемой антенной длиной l_Д
≤l (действующей длиной)
с равномерным синфазным распределением
тока, создающим в направлении
максимального излучения такую же
напряженность электрического поля, как
и данная антенна в направлении
максимального излучения. При этом
амплитуда тока в точках питания
воображаемой
антенны счи­тается
равной амплитуде тока на входе реальной
антенны. По
аналогии с (2.1)
(диполь Герца с равномерным распределением
тока) напряженность поля, создаваемую
реальной антенной в главном направлении,
можно определить с помощью выражения
[10, 11]

(2.19)

где I₀
— амплитуда
тока в точках питания антенны. Запишем
выражение для величины напряженно­сти
поля любой антенны в произвольном
направлении [10, 11]

.
(2.20)

Подставляя в
(2.18) вместо

выражение (2.19) и учитывая, что

(
—
сопротивление излучения антенны,
отнесенное к току в точках питания),
получаем [2, 10, 11]

или

(м) . (2.21)

Формально параметром
«действующая длина» можно пользоваться
в случае любой
антенны, так как
этот параметр выражается через КНД, а
последний определяется только
характеристикой направленности.

Из определения КНД
следует, что он не учитывает потери
энергии
электромагнитных колебаний в антенне.
В связи с этим для более полного
описания свойств антенны как преобразователя
энергии подводимых к ее входу направляемых
ЭМВ в излучаемые в окружающее пространство
вводится параметр, учитывающий тепловые
потери, — коэффициент
усиления (КУ).

Определим коэффициент
полезного действия антенны
η
в режиме излучения как отношение мощности
излучения к мощности колебаний на входе
антенны [2—5, 10—12]:

,

(2.22)

где Р_п
— мощность
потерь в реальных проводниках и
диэлектриках конструкции антенны,
рассеиваемая в виде тепла. Из закона
сохранения энергии следует, что η≤1.

По аналогии с КНД
коэффициентом
усиления называется отношение среднего
за период высокой частоты значения
плотности активного пото­ка
мощности (среднего значения вектора
Пойнтинга), излучаемого антенной в
данном направлении

,
к среднему значению
плотности пото­ка
мощности

,
создаваемого воображаемой идеальной
(имеющей КПД η=1)
антенной в том же направлении при
условии, что мощности колебаний на
входах обеих антенн равны и обе антенны
согласованы с питающими линиями передачи
(фидерами). При этом предполагается, что
точка наблюдения находится в дальней
зоне на одинаковом
расстоянии от обеих антенн [2—5, 9—12].

.
(2.23)

Иными словами,
коэффициент усиления антенны показывает,
во сколько раз следует увеличить
мощность, подводимую к идеальной
изотропной антенне с КПД, равным еди­нице,
по сравнению с данной антенной, чтобы
среднее значение плотности потока
мощности (напряженности электрического
поля) в одной и
той же точке наблюдения в дальней зоне
осталось неизменным.

Отличие КУ от КНД
состоит в том, что при определении КУ
исходят из
равенства мощностей, подводимых к
исследуемой и эталонной антеннам
Р_вх,
а не из равенства мощностей излучения
P

этих антенн.

Таким образом, КУ
антенны однозначно связан с ее КПД и
КНД выражением

и

.
(2.24)

Учитывая, что D=G/
,
можно записать полезное для практики
выражение, определяющее амплитуду
напряженности электрического поля в
направлении максимального излучения
антенны через ее КУ [10, 11]:

.
(2.25)

Под КНД антенны с
эллиптической поляризаци­ей
поля при полном поляризационном приеме
подразумевают величину [10, 11]

(2.26)

где

—
пар­циальные
КНД для каждой из ортогональных
составляющих поля; П_уср
— ус­редненное
по всем направлениям значение плотности
потока мощности пол­ного
поля;

.
Здесь

— полная мощность излуче­ния;

и

—
мощности излучения, соответствующие
ортогональным ком­понентам
поля.

В качестве примера
простейшей антенны, создающей вращающееся
поле, рассмотрим два линейных излучателя
1 и 2 (для простоты считаем их эле­ментарными),
расположенных крестообразно в плоскости
xoy
и питаемых токами равной ам­плитуды,
но сдвинутых по фазе на

,

.
Такой излучатель
час­то называют
турникетным
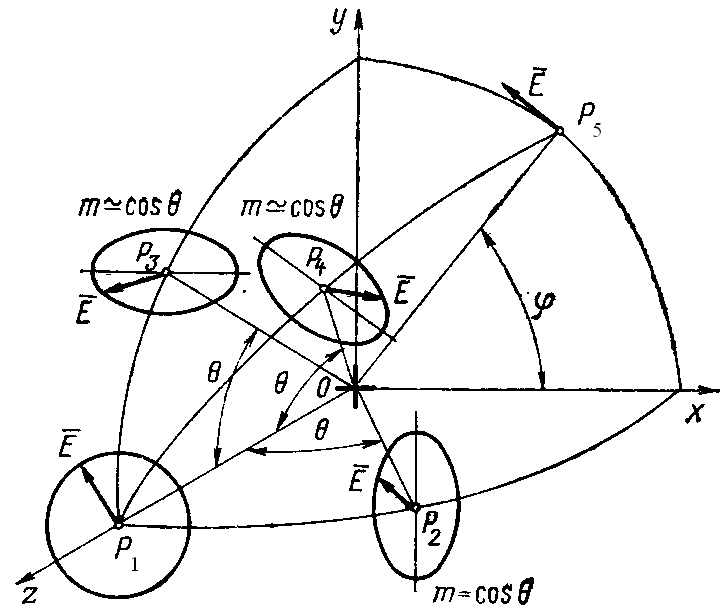
(рис. 2.8) [10, 11].

а
б

Рис. 2.8. Турникетный излучатель

В точке Р₁,
лежа­щей на нормали (ось z)
к плоскости расположения вибраторов,
первый создаёт
электрическое поле
c
линейной горизонтальной,
второй — с
линейной вертикальной поляризацией.
Поскольку оба вектора Е
равны по
амплитуде, сдвинуты по фазе друг
относи­тельно
друга на 90° и взаимно перпендикулярны,
в направлении
нормали z
к плоскости вибраторов
xoy
имеет место круговая поляриза­ция
излучаемых ЭМВ. Вращение плоскости
поляризации происходит в сторону
вибратора, ток в котором отстает по фазе
от тока в другом вибраторе.

В произвольной точке наблюдения,
расположенной в плоскости xoz
(P₂ на рис.
2.8, б) электрическое поле излучаемых ЭМВ
оказывается эллиптически поляризованным
с вертикальной ориентацией большей оси
поляризационного эллипса и коэффициентом
эллиптичности

[10].

В произвольной точке наблюдения,
расположенной в плоскости yoz
(P₃ на рис.
2.8, б) электрическое поле излучаемых ЭМВ
также оказывается эллиптически
поляризованным, но с горизонтальной
ориентацией большей оси поляризационного
эллипса.

В любой промежуточной
плоскости, проходящей через ось z,
электрическое поле будет иметь
эллиптическую поляризацию, но, в
зависимости от направления, изменяется
ориентация большей оси поляризационного
эллипса (точка Р₄
на рис. 2.8, б).

В плоскости
расположения вибраторов xoy
результирующий вектор напряженности
электрического поля излучения имеет
линейную поляризацию,
причем его амплитуда не зависит от
направления.
Результирующая напряженность
электрического поля в произвольной
точке Р₅ в плоскости
вибраторов xoy
(θ=90°) с учетом
фазового сдвига токов ±90°
описывается выражением [10]

,

из которого следует, что ДН антенны в
плоскости вибраторов является круговой,
излучаемые ЭМВ имеют линейную поляризацию,
причем фаза ЭМВ зависит от направления,
т.е.

,
следовательно, турникетный излучатель
не имеет фазового центра [10, 11].

Турникетные излучатели широко применяются
на практике, например, в виде скрещенных
полуволновых СЭВ, как самостоятельные
антенны, так и в составе решеток
(директорные антенны с круговой
поляризацией). В УВЧ и СВЧ диапазонах
такие скрещенные вибраторы (обычно с
дисковыми контррефлекторами) используются
в качестве облучателей зеркальных
антенн с круговой поляризацией.

Другой известный способ получения ЭМВ
с эллиптической (круговой) поляризацией
предусматривает использование, например,
крестообразной щели в широкой стенке
прямоугольного металлического волновода
с волной Н₁₀. Из электродинамики
известно, что в таком волноводе на
одинаковых расстояниях от его продольной
оси существуют сечения, в которых вектор
Н волны Н₁₀ имеет
круговую поляризацию противоположных
направлений вращения [6, 7]. Следовательно,
крестообразная щель в виде двух одинаковых
перпендикулярных щелей в направлении
нормали к плоскости широкой стенки
будет излучать волны с круговой
поляризацией [3—5].

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Сразу хочу сказать, что здесь никакой воды про рупорные антенны, и только нужная информация. Для того чтобы лучше понимать что такое
рупорные антенны, рупорная антенна , настоятельно рекомендую прочитать все из категории Устройства СВЧ и антенны.

рупорная антенна — металлическая конструкция, состоящая из волновода переменного (расширяющегося) сечения с открытым излучающим концом. Как правило, рупорную антенну возбуждают волноводом, присоединенным к узкому концу рупора. По форме рупора различают E-секториальные, H-секториальные, пирамидальные и конические
рупорные антенны .

Обобщенная модель рупорной антенны показана на рис. 14.1. а)

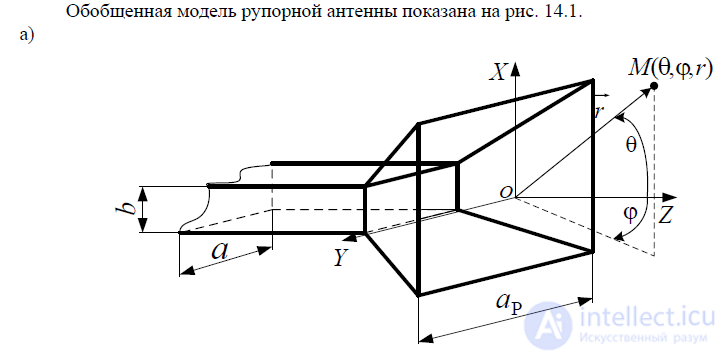
На основе модели, показанной на рис. 14.1., можно рассмотреть следующие варианты апертурных излучателей:

— Е-секториальный рупор, при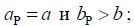

— Н-секториальный рупор, при

пирамидальный остроконечный рупор, при

Отметим следующие закономерности вхарактере поведения поляврупоре.  Тип волны в рупоре является таким же, каки в возбуждающем рупор волноводе.  В отличие от волновода,поверхностью равных фаз в рупоре является не плоскость,

а поверхность цилиндра с центром в вершине О для секториального рупора и поверхность сфероидадля пирамидального рупора.  Фазовая скорость волны в рупоре непостоянна. Она больше в горловине рупора и приближается к скорости света C вего раскрыве.  В рупоре, в отличие от волновода, отсутствует критическая длина волны.Это объясняется тем, что у бесконечного рупора всегда можно найти такое сечение, которое

окажетсядостаточным для распространения любого типа волны.

 Локальное поверхностное сопротивление WS в раскрыве рупора приближенно равно волновому сопротивлению свободного пространства W0.

Излучающей поверхностью рупора является поверхность его раскрыва. Особое внимание уделяется амплитудно-фазовому распределению поля в апертуре рупорной антенны.Амплитудное распределение поля на раскрыве совпадает с распределением поля в поперечном сечении волновода для основного типа волны. В плоскости Е наблюдается равномерноеамплитудное распределение поля, в плоскости Н — косинусоидальное

где E0 — напряженность электрического поля в середине раскрыва; (x, y) — фазовая ошибка враскрыве рупора,получающаяся из-за неплоскости фазового фронта врупоре. Фронт волны в процессе ее движения в рупоре преобразуется из плоского вцилиндрический (всекториальныхрупорах) или всферический (в пирамидальных рупорах). Проанализируем более подробно характер фазовойошибки в секториальном рупоре, продольное сечение которого показано на рис. 14.2.

Рис.14.2 — Продольное сечение Н-секториального рупора

Дуга окружности KML с центром в вершине рупора О является линией равных фаз. В произвольной точке M, имеющей координату x, фаза поля отстает от фазы в середине раскрыва(вточке О) на угол

Раскладывая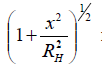 в ряд Тейлора и ограничиваясь при первыми двумя членами, получаем

Фазовое распределение имеет квадратичный характер в плоскости, в которой производится раскрыв рупора . Об этом говорит сайт https://intellect.icu . Максимальная фазовая ошибка (максимальный сдвиг по фазе по отношениюк центру раскрыва) определяется соотношением

— в Е-плоскости:

— в Н-плоскости:

где R — длина рупора (см. рис. 2.1). Максимальная фазовая ошибка, достигаемая в углах пирамидального рупора определяется соотношением

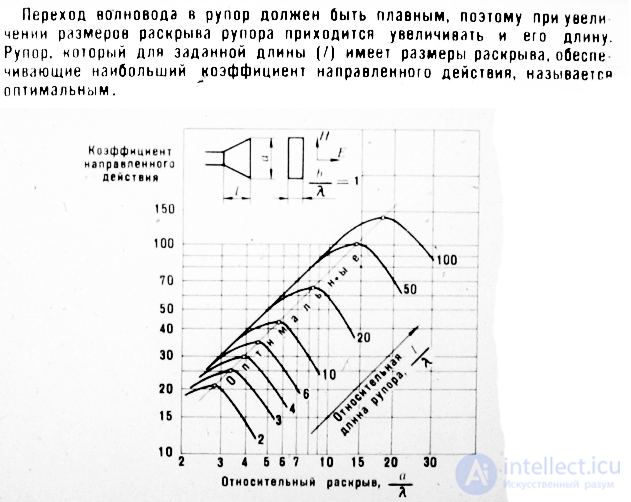
Если максимальные фазовыеошибки в раскрыве рупора не превышают допустимых

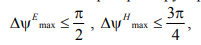
то коэффициент направленного действия (КНД) рупорной антенны при заданной длине будет максимальным. Рупоры, размеры которыхсоответствуют максимальным значениям КНД, называются «оптимальными». Их размеры связаны с длиной рупора следующими соотношениями:

Перейдем к изучению диаграммы направленности секториального рупора. С учетом (14.1), (14.2) в раскрыве секториального рупора

Множитель направленности вычисляется следующим образом. В плоскости H:

Аналогично в плоскости E:

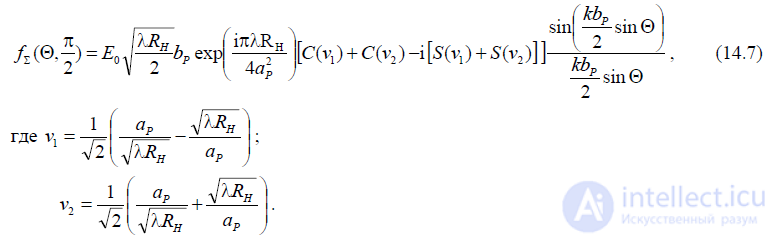
Нормированные диаграммы направленности (ДН) рупорной антенны в предложении синфазного раскрыва

(при фазовых ошибках, не превышающих допустимые значения) можнорассчитать по формулам:

— в E-плоскости: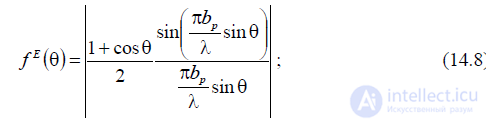

— в Н-плоскости: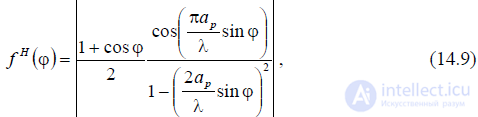

Ширина главного луча диаграммы направленности рупорных антенн в Е-и Н плоскостях 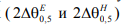определяется по уровню половинной мощности по формулам:

Коэффициент направленного действия Н-секториального рупора DH определяется по формуле

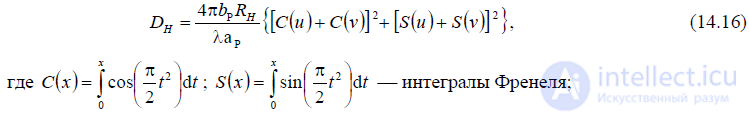
На рис. 14.3 показаны построенные по (14.16) графики зависимости КНД DН от aP относительного размера раскрыва H-секториального рупора для различных длин рупора

Коэффициент направленного действия Е-секториального рупора DE определяется по формуле

Коэффициент направленного действия пирамидального рупора D с учетом (14.16, 14.17) определяется по следующей формуле

Коэффициент направленного действия (КНД) оптимальной рупорной антенны вычисляется по формуле:

где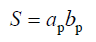 — геометрическая площадь раскрыва;

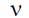— коэффициент использования поверхности, определяемый амплитудным и фазовым распределением поля в раскрыве антенны: а .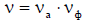

Для оптимальных секториальных рупоров учитывает косинусоидальный характер амплитудного распределения поля в Н-плоскости;

— несинфазность

раскрыва в однойиз плоскостей при условии

Поэтому для секториальных рупорных антенн

Для оптимальных пирамидальных рупоров при тех же условиях 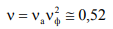(учтена несинфазность раскрыва в обеихплоскостях).

Рупорные антенны используются на практике как самостоятельные направленные антенны, так и в качестве облучателей зеркальных и линзовых антенн, а также в качестве излучателейФАР. Особенно широко рупорные антенны используются в лабораторных установках при измерении диаграммы направленности и коэффициента усиления других антенн. Достоинствомрупорных антенн является простота их конструкции и хорошие диапазонные свойства. Практически рабочая полоса частот рупорной антенны ограничивается полосой питающего его волноводаи составляет около 100%.

Недостаток рупорных антенн заключается в необходимости выбора слишком большой длины рупора для получения остронаправленного излучения.

Определение длины рупора

Как следует из формул (14.3), (14.4),оптимальная длина рупора пропорциональна квадрату размеров раскрыва aP и bP , а ширина диаграммы направленности обратно пропорциональна aP и bP в первой степени. Поэтому для сужения диаграммы направленности рупорной антенны в n раз размер ее апертуры долженбыть увеличен в n раз, а длина рупора — в n2 раз.

Это обстоятельство накладывает ограничения на ширину диаграммы направленности рупорных антенн. Так, при длине рупора, примерно равной размеру одной из сторон его раскрыва,ширина диаграммы направленности составляет около 2025 . При сужении ширины диаграммы направленности до 10 длина рупора приблизительно в 4…5 раз больше размера большейстороны его раскрыва.

Существуют различные способы уменьшения длины рупора. Суть этих способов заключается в компенсации или уменьшении фазовой ошибки в раскрыве рупора. Одним из наиболеечасто используемых на практике способов уменьшения длины рупора является установкавего раскрыве линзы, котораяустраняетфазовые ошибки (рис. 14.4, a).

При этом длина рупора выбирается уже из условий хорошего согласования питающего рупор волновода со свободным пространством и приблизительно равна (1…0,5) ширине егораскрыва.

На рис. 14.4, б показан другой способ выравнивания фазового фронта в раскрыве рупора за счет выравнивания длины пути, проходимого волной от вершины рупора до различных точек нараскрыве. Для получения в раскрыве синфазного поля кривая ABC, образующая профильстенки согнутого рупора, должна иметь форму параболы.

Рупорно-параболические антенны KS-15676 C-диапазона (4-6 ГГц) радиорелейных линий AT&T Long-Lines на крыше центра телефонных коммуникаций AT&T, Сиэттл, Вашингтон, США

Виды рупоров

многорупорные антенны

свернутый рупор

Применение рупорных антенн

Статью про рупорные антенны я написал специально для тебя. Если ты хотел бы внести свой вклад в развии теории и практики,
ты можешь написать коммент или статью отправив на мою почту в разделе контакты.
Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое рупорные антенны, рупорная антенна
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Устройства СВЧ и антенны