|
Коэффициент подобия треугольников – что это? Как его найти?
Коэффициент подобия треугольников, определение. Подобные треугольники имеют равные углы и пропорциональные сходственные стороны. Сходственные стороны (другое название – соответственные) – это стороны, которые лежат напротив равных углов.
На рисунке представлены подобные треугольники ABC и A1B1C1. Для их сторон выполняется следующее равенство:
Величина, которая равна отношению сходственные сторон треугольников, называется коэффициентом подобия. Коэффициент подобия треугольников обозначается буквой k, k > 0. Таким образом, приведённое выше равенство можно записать в виде:
Найти коэффициент подобия треугольников можно несколькими способами. 1) Через отношение сходственных сторон (например, AB / A1B1). 2) Этот коэффициент также равен отношению периметров подобных треугольников. P(ABC) = A + B + C, P(A1B1C1) = A1 + B1 + C1. k = P(ABC) / P(A1B1C1). 3) Через площади подобных треугольников. k² = S(ABC) / S(A1B1C1). 4) Отношение длин высот, медиан, биссектрис подобных треугольников также равно коэффициенту подобия. Пример. Даны подобные треугольники DEC и AON.
Коэффициент подобия = 1,5, а сторона DE = 12 см. Требуется найти сторону AO. _ По определению коэффициента подобия k = DE / AO = 1,5. Так как DE = 12 см, то можно записать: 12 / AO = 1,5. AO = 12 / 1,5 = 8 см. Значит, длина стороны AO составляет 8 см. модератор выбрал этот ответ лучшим
smile6008 3 года назад Для того чтобы найти коэффициент подобия треугольников необходимо сначала определиться что же это понятие значит. Итак, подобный треугольник, это треугольник, геометрическая фигура, у которой одинаковые углы и одинаковые стороны, которые находятся напротив друг друга. То есть называются подобными. Для того чтобы найти коэффициент подобия треугольников обратимся к формуле.
Для вычисления коэффициент используют разные способы расчёта. Проще всего найти коэффициент, если вычислить площади треугольников. Другой способ расчёта коэффициента примениние расчёта через отношение сходственных сторон подобных треугольников.
Дублон 2 месяца назад Говоря о коэффициенте подобия треугольников, необходимо знать, что есть подобные фигуры, а точнее подобные треугольники. Под таковыми являются треугольники, чьи углы равные, а сходственные стороны этих треугольников пропорциональны. Так вот, отношение этих сходственных сторон и есть коэффициент подобия. Коэффициент подобия можно определить, зная величину как сходственных сторон, так и величину периметров подобных треугольников, так и величину площади подобных треугольников.
Бутафога 2 месяца назад Говоря простым языком, подобные треугольники называют такие геометрические фигуры, у которых углы одинаковые, а стороны пропорциональные. Стоит отметить как понятие соответственных сторон, лежащих напротив одинаковых углов. Отсюда вытекает коэффициент подобия, равный отношению соответственных сторон подобных треугольников.
КорнетОболенский 3 месяца назад Подобными называются фигуры, одинаковые по форме, но разные по размеру. Треугольники считаются подобными, если у них углы равны, а их соответственные стороны пропорциональны друг другу. Рассмотрим рисунок:
Изображённые на нем треугольники подобны, поскольку у них соответствующие углы равны между собой, а соответственные (второе название сходственные) стороны пропорциональны. Коэффициент подобия равняется отношению сходственных сторон имеющихся подобных треугольников, т.е. сторон, лежащих напротив равных углов. Простыми словами, Коэффициент подобия показывает, в какое количество раз один треугольник больше другого, обозначается буквой k, при этом k>0. Т.е. коэффициент подобия всегда является положительной величиной. Коэффициент подобия можно найти несколькими способами:
Ellic 8 месяцев назад Подобными фигурами называются фигуры, одинаковые по форме, но разные по величине. Треугольники подобны, если их углы равны, а стороны пропорциональны друг другу. Также есть три признака, которые позволяют определить сходство без выполнения всех условий. Первый признак состоит в том, что в подобных треугольниках два угла одного равны двум углам другого. Второй признак подобия треугольников состоит в том, что две стороны одного пропорциональны двум сторонам другого и углы между этими сторонами равны. Третий признак сходства — пропорциональность трех сторон одного по отношению к трем сторонам другого. Треугольники называются подобными, если они имеют равные углы и соответствующие стороны пропорциональны. Число k, равное отношению соответствующих сторон треугольников, называется коэффициентом подобия.
Давайте вспомним, какие треугольники называются подобными. Треугольники считаются подобными, если у них:
Выделяют три признаки по добия треугольников:
Коэффициент подобия треугольников равен отношению соответственных ( сходственных ) сторон этих треугольников.
Вычислить этот коэффициент можно несколькими путями, в основе которых, по сути, лежит пропорциональность их сходственных сторон: 1.) Непосредственно как отношение сторон. 2.) Через периметры этих треугольников ( то есть через суммы длин их сторон ). 3.) Через площади этих фигур. 4.) Как отношение их биссектрис, высот или медиан. Сергей Гориинов 5 лет назад Коэффициент подобия треугольников – это безразмерная величина, равная отношению соответствующих сторон подобных треугольников: К=a1/a2=b1/b2=c1/c2, где a1,b1,c1 – стороны первого подобного треугольника, а a2,b2,c2 – стороны второго подобного треугольника. Также существует коэффициент подобия площадей подобных треугольников, равный квадрату коэффициента подобия треугольника. Лара Изюминка 2 года назад При изучении темы “Подобие треугольников” очень важно понимание , что такое коэффициент подобия траугольников. Итак, коэффициент подобия – это отношение сходственных сторон в подобных треугольниках. Сходственные стороны, это стороны, которые лежат против равных углов. Коэффициент подобия помогает найти площадь подобного треугольника, если известна площадь другого. Здесь пользуемся тем , что отношение площадей подобных треугольников равно квадрату коэффициента подобия. Также можно найти стороны одного подобного треугольника, если есть стороны другого и известен коэффициент подобия. Ьема изучается в 8 классе в курсе геометрии.
Nastya Chuk 3 года назад Актуальный вопрос на самом деле, поскольку он необходим для понимания различий между видами треугольников и их пропорциями.Предназначение коэффициента подобия : показывает во сколько раз стороны нашего треугольника соответственно больше сторон другого треугольника и какую же часть составляют они от сходственных стороны.Коэффициент подобия обозначается как “к” и выражается всегда через некое соотношение 2-х или 3-х треугольников. Знаете ответ? |
Подобные треугольники
Определение
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.
Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.
Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.
Признаки подобия треугольников
I признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
II признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Свойства подобных треугольников
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
- Отношение периметров подобных треугольников равно коэффициенту подобия.
- Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.
Примеры наиболее часто встречающихся подобных треугольников
1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.
2. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –
3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.
Здесь вы найдете подборку задач по теме «Подобные треугольники» .
Геометрия
План урока:
Пропорциональные отрезки
Если известна длина двух отрезков, то можно узнать, во сколько раз один из них больше другого. Например, если некоторый отрезок NM = 24 см, а другой отрезок KP = 4 см, то можно утверждать, что NM в 6 раз длиннее, так как
Величину NM/KP именуют отношением отрезков NM и KP. Надо заметить, что в ряде случаев отношение отрезков можно найти, не зная их длины. Пусть в ∆МКР проведена медиана МН. Очевидно, что отрезок КР будет вдвое длиннее КН, ведь Н – середина КР:
Другой пример – это отношение между диагональю квадрата и его стороной.
Используя теорему Пифагора, несложно показать, что в любом квадрате АВСD
Наконец, в прямоугольном треуг-ке, один из углов которого равен 30°, гипотенуза всегда вдвое длиннее меньшего из катетов:
Если отношение отрезка AB к А1В1 равно отношению отрезка СD к С1D1, то говорят, что отрезки AB и CD пропорциональны отрезкам А1В1 и С1D1. Например, пусть
Получается, AВ и CD пропорциональны А1В1 и С1D1. Важно отметить, что пропорциональны могут быть также сразу три и более отрезка.
Определение подобных треугольников
В жизни нередко можно наблюдать объекты, у которых совпадает форма, но отличаются размеры. В качестве примера можно привести мяч для настольного тенниса и баскетбольный мяч. Оба этих предмета имеют форму шара, на баскетбольный мяч значительно больше. Другой пример – настоящий танк и игрушка, изображающая его. Часто подобны друг другу матрешки, которые вкладываются друг в друга – все они выглядят одинаково, а отличаются только общим размером. Наконец, подобны и знаменитые египетские пирамиды:
Такие объекты в геометрии именуют подобными. Подобны друг другу любые две окружности и любые два квадрата. Но особо важную роль в геометрии играют подобные треугольники. Рассмотрим это понятие подробнее.
Пусть есть два треуг-ка, ∆AВС и ∆А1В1С1, у которых соответственно равны углы:
Стороны, которые лежат против одинаковых углов в таких треуг-ках, именуют сходственными. Ими являются стороны AВ и А1В1, ВС и В1С1, АС и А1С1.
Можно дать такое определение подобных треугольников:
Таким образом, подобие треугольников (оно обозначается символом ∾) обозначает выполнение сразу нескольких равенств:
Отношение между сходственными сторонами подобных треуг-ков именуется коэффициентом подобия и обозначается буквой k:
Грубо говоря, подобие треуг-ков означает, что их форма одинакова, но один из них в несколько раз больше или меньше другого. Чтобы получить, из одного треуг-ка другой, равный ему по размерам, его надо просто «масштабировать». Например, на этом рисунке все стороны исходного треуг-ка просто увеличили в три раза:
Это значит, что коэффициент подобия в данном случае равен 3. Однако важно понимать, что в различных геометрических задачах подобные треуг-ки также могут быть повернуты друг относительно друга:
Задание. ∆AВС подобен ∆DEF. Известно, что
Найдите длину ЕF.
Решение. Как только в задаче появляются подобные треуг-ки, стоит сразу же определить их коэффициент подобия, а для этого надо разобраться, какие стороны будут сходственными. Так как∠А = ∠Е, то лежащие против них стороны DF и ВС– сходственные. Их отношение и будет равно коэффициенту подобия:
Получили, что стороны ∆DEF вдвое длиннее сходственных им сторон ∆AВС. У подобных треуг-ков углы одинаковы, поэтому∠С = ∠D. Отсюда следует, что стороны AВ и ЕF сходственны, а потому ЕF вдвое больше:
Задание. ∆AВС и∆DEF – подобные. Известно, что
Найдите длину ЕF.
Решение. По сравнению с предыдущей задачей изменилось только одно условие, теперь∠А = ∠D. Однако это меняет сходственные стороны. Из подобия треуг-ков следует, что∠С = ∠Е. Тогда сходственными оказываются уже стороны AВ и DF. Найдем коэффициент подобия треугольников:
Сходственными являются также стороны ВС и ЕF (ведь∠А = ∠D), поэтому ЕF в 1,25 раза длиннее:
Эти две задачи показывают, как важно правильно определять сходственные стороны подобных треугольников.
Естественно, что все равные друг другу треуг-ки являются одновременно и подобными, причем их коэффициент подобия равен единице.
Задание. Докажите, что у подобных треуг-ков отношение их периметров равно коэффициенту подобия.
Решение. Пусть подобны ∆ AВС и ∆А1В1С1, причем
Периметр ∆AВС можно вычислить так:
Мы доказали утверждение, сформулированное в условии.
Первый признак подобия треугольников
Оказывается, для того, чтобы доказать подобие треуг-ков, не требуется сравнивать все их углы и находить соотношение всех сторон. Существуют три простых признака подобия треугольников.
Однако прежде, чем сформулировать их, нам придется доказать отдельное утверждение, которое известно как обобщенная теорема Фалеса («обычную», не обобщенную теорему мы уже изучали ранее).
Если прямые ВВ1 и СС1 (показаны красным цветом)параллельны, то отрезки AВ и АС пропорциональны отрезкам AВ1 и АС1, то есть справедливо соотношение:
Доказывать будем от противного. Пусть отрезки AВ и АС непропорциональны AВ1 и АС1. Тогда отметим наАС такую точку Н, которая разобьет АС на пропорциональные отрезки, то есть
Естественно, эта точка не будет совпадать с С1. Рассмотрим случай, когда она окажется правее, чем С1:
Теперь поступим следующим образом. Проведем через стороны угла большое число прямых, параллельных ВС, которые будут разбивать АС на одинаковые отрезки. По теореме Фалеса эти же прямые отсекут одинаковые отрезки и на AВ. При этом мы проведем настолько много параллельных прямых, что хотя бы одна из них пересечет отрезок С1Н:
Пусть эта прямая пересечет отрезок С1Н в некоторой точке С2, а сторону AВ в точке В2. Ясно, что отрезки AВ и АВ2 пропорциональны отрезкам АС и АС2, так как они состоят из одинакового количества одинаковых отрезков. Например, на построенном рисунке отношение AB2 к AB равно 5/8, так как AB2 состоит из 5 отрезков, отсеченных зелеными параллельными прямыми, а AB состоит из 8 таких отрезков. Аналогично и отношение АС2 к АС также равно 5 к 8. Таким образом, можно записать:
Здесь мы рассмотрели случай, когда точка Н лежит правее С1, то есть АН >C1. Случай, когда АН 2 раз. Докажем это.
Пусть ∆AВС и ∆А1В1С1 подобны с коэффициентом подобия k. Снова проведем в них высоты СН и СН1:
Запишем очевидные равенства:
В итоге получили, что площади подобных треугольников отличаются в k 2 раз.
Задание. Известно, у ∆AВС площадь составляет 10, а отрезок AВ имеет длину 5. ∆DEF подобен ∆AВС, причем сторона DE, сходственная AВ, равна 15. Вычислите площадь ∆DEF.
Решение. По условию задачи легко найти коэффициент подобия ∆AВС и ∆DEF, надо лишь поделить одну сходственную сторону на другую:
Задание. Площади двух подобных треуг-ков составляют 75 м 2 и 300 м 2 . Одна из сторон второго треуг-ка равна 9 м. Вычислите сходственную ей сторону первого треуг-ка.
Решение. Зная площади треуг-ков, легко найдем коэффициент их подобия:
Если коэффициент равен 2, то стороны первого многоугольника вдвое меньше сторон второго, поэтому интересующая нас сторона равна
Отношение площадей подобных треугольников
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На данном уроке мы введем понятие подобных треугольников и рассмотрим теорему об отношении их площадей. Затем будет рассмотрен ряд примеров на применение этой теоремы.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Измерение»
[spoiler title=”источники:”]
http://100urokov.ru/predmety/urok-6-podobnye-treugolniki
http://interneturok.ru/lesson/geometry/8-klass/podobnye-treugolniki/otnoshenie-ploschadey-podobnyh-treugolnikov
[/spoiler]
22
Авг 2013
Категория: Справочные материалы
Подобные треугольники
2013-08-22
2014-01-31
Определение
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

Коэффициентом подобия называют число k, равное отношению сходственных сторон подобных треугольников.
Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.

Признаки подобия треугольников
I признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
 II признак подобия треугольников
II признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

III признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Свойства подобных треугольников
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
- Отношение периметров подобных треугольников равно коэффициенту подобия.

- Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.
Примеры наиболее часто встречающихся подобных треугольников
1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.

2. Треугольники и
, образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –

3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.


Здесь вы найдете подборку задач по теме «Подобные треугольники».
Автор: egeMax |
комментариев 50
Подобные треугольники
3 октября 2022
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны соответственным сторонам другого.
Подобные треугольники — ключевая тема геометрии 8 класса. Они будут преследовать нас до самого конца школы. И сегодня мы разберём всё, что нужно знать о них.
План такой:
- Основное определение
- Лемма о подобных треугольниках
- Свойства подобных треугольников
- Разбор задач
1. Основное определение
Определение. Треугольники называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны соответственным сторонам другого.
Рассмотрим треугольники $ABC$ и $MNK$:
У них есть равные углы: $angle A=angle M$, $angle B=angle N$, $angle C=angle K$. И пропорциональные стороны:
[frac{AB}{MN}=frac{BC}{NK}= frac{AC}{MK}= frac{color{red}{3}}{color{red}{2}}]
Следовательно, треугольники $ABC$ и $MNK$ подобны. Записывается это так:
[Delta ABCsim Delta MNK]
Число $k={color{red}{3}}/{color{red}{2}};$ называется коэффициентом подобия. К нему мы ещё вернёмся.
Пропорциональные стороны подобных треугольников (например, $AB$ и $MN$, либо $BC$ и $NK$) в некоторых учебниках называют сходственными. На практике этот термин применяется редко. Мы будем говорить просто «соответственные стороны».
Дальше идёт очень важное замечание.
1.1. Обозначение подобных треугольников
В геометрии один и тот же треугольник можно называть по-разному. Например, $Delta ABC$, $Delta BCA$ или $Delta CAB$ — это всё один и тот же треугольник. То же самое касается и углов.
Но в подобных треугольниках есть негласное правило:
При обозначении подобных треугольников порядок букв выбирают так, чтобы равные углы перечислялись в одной и той же последовательности.
Вернёмся к нашим треугольникам $ABC$ и $MNK$:
Поскольку $anglecolor{red}{A}=anglecolor{red}{M}$ и $anglecolor{blue}{B}=anglecolor{blue}{N}$, можно записать $Deltacolor{red}{A}color{blue}{B}Csim Deltacolor{red}{M}color{blue}{N}K$. Или $Delta Ccolor{red}{A}color{blue}{B}sim Delta Kcolor{red}{M}color{blue}{N}$. Но никак не $Deltacolor{red}{A}color{blue}{B}Csim Delta Kcolor{red}{M}color{blue}{N}$.
Да, это негласное правило. И если вы нарушите последовательность букв, это не ошибка. Никто не снизит вам за это баллы. А если снизит — добро пожаловать на апелляцию.
Правильная запись позволяет быстро и безошибочно выписывать пропорциональные стороны треугольников. Рассмотрим два подобных треугольника:
[Delta ABCsim Delta MNK]
Берём две первые буквы из каждого треугольника: ${AB}/{MN};$. Затем две последние буквы: ${BC}/{NK};$. Наконец, вычёркиваем «центральную» букву: ${AC}/{MK};$.
Приравниваем полученные три дроби:
[frac{AB}{MN}=frac{BC}{NK}=frac{AC}{MK}]
Вот и всё! Даже рисунок не нужен! Этот приём настолько прост и эффективен, что его в обязательном порядке изучают на моих занятиях, курсах и вебинарах.
В будущем мы увидим, что подобные треугольники чаще всего ищут как раз для составления таких пропорций.
2. Лемма о подобных треугольниках
Подобные треугольники появляются всякий раз, когда прямая, параллельная стороне треугольника, пересекает его стороны.
Теорема 1. Прямая, пересекающая две стороны треугольника и параллельная третьей стороне, отсекает треугольник, подобный исходному.
Доказательство. Рассмотрим треугольник $ABC$. Пусть прямая $MNparallel AB$ отсекает треугольник $MNC$:
Докажем, что $Delta ABCsim Delta MNC$. Рассмотрим треугольники $ABC$ и $MNC$. У них есть общий угол $ACB$.
Углы $ABC$ и $MNC$ — соответственными при $MNparallel AB$ и секущей $BC$. Следовательно, они равны: $angle ABC=angle MNC$.
Аналогично равны углы $BAC$ и $NMC$. Следовательно, треугольники $ABC$ и $MNC$ имеют три соответственно равных угла.
Докажем теперь, что соответственные стороны пропорциональны. Т.е. докажем пропорцию
[frac{AB}{MN}=frac{BC}{NC}=frac{AC}{MC}]
Рассмотрим угол $ACB$. Параллельные прямые $AB$ и $MN$ пересекают стороны этого угла. По теореме о пропорциональных отрезках:
[frac{AC}{MC}=frac{BC}{NC}]
Это равенство — второе в искомом:
[frac{AB}{MN}= color{red}{frac{BC}{NC}=frac{AC}{MC}}]
Осталось доказать первое равенство. Дополнительное построение: прямая $KNparallel AC$:
Поскольку $AMparallel KN$ (по построению) и $AKparallel MN$ (по условию), четырёхугольник $AKNM$ — параллелограмм. Поэтому $AK=MN$.
Рассмотрим угол $ABC$. Параллельные прямые $AC$ и $KN$ пересекают стороны этого угла. По теореме о пропорциональных отрезках:
[frac{AB}{AK}=frac{BC}{NC}]
Учитывая, что $AK=MN$, получаем
[frac{AB}{MN}=frac{BC}{NC}=frac{AC}{MC}]
Итак, соответственные углы треугольников $ABC$ и $MNC$ равны, а их стороны пропорциональны. Следовательно, по определению подобных треугольников
[Delta ABCsim Delta MNC]
Что и требовалось доказать.
Эта лемма — не признак подобия. Это самостоятельная теорема, которая ускоряет решение многих задач.
Признаки подобия разобраны в отдельном уроке — см. «Признаки подобия треугольников».
Частный случай этой леммы — средняя линия. Она отсекает треугольник со сторонами в два раза меньше, чем у исходного:
Оформляется это так. Поскольку $AM=MC$ и $BN=NC$, то $MN$ — средняя линия треугольника $ABC$. Следовательно, прямые $AB$ и $MN$ параллельны, откуда
[Delta ABCsim Delta MNC]
3. Свойства подобных треугольников
Два важнейших свойства: связь периметров и связь площадей.
3.1. Периметры подобных треугольников
Теорема 2. Отношение периметров подобных треугольников равно коэффициенту подобия.
Доказательство. Рассмотрим подобные треугольники $ABC$ и $MNK$:
Запишем равенство из определения подобия. Поскольку $Delta ABCsimDelta MNK$, стороны этих треугольников пропорциональны:
[frac{AB}{MN}=frac{BC}{NK}=frac{AC}{MK}=color{red}{k}]
Здесь число $color{red}{k}$ — коэффициент подобия. Полученное тройное равенство можно переписать так:
[frac{AB}{MN}=color{red}{k}; frac{BC}{NK}=color{red}{k}; frac{AC}{MK}=color{red}{k}]
Или, что то же самое:
[begin{align}AB&=color{red}{k}cdot MN \ BC &=color{red}{k}cdot NK \ AC &=color{red}{k}cdot MK \ end{align}]
Периметр треугольника $MNK$:
[{{P}_{Delta MNK}}=MN+NK+MK]
Периметр треугольника $ABC$:
[begin{align}{{P}_{Delta ABC}} &=AB+BC+CD= \ &=color{red}{k}cdot MN+color{red}{k}cdot NK+color{red}{k}cdot MK= \ &=color{red}{k}cdot left( MN+NK+MK right)= \ &=color{red}{k}cdot {{P}_{Delta MNK}} end{align}]
Итого получаем равенство
[{{P}_{Delta ABC}}=color{red}{k}cdot {{P}_{Delta MNK}}]
Обычно именно в таком виде это равенство и применяют. Но можно записать его и как отношение:
[frac{{{P}_{Delta ABC}}}{{{P}_{Delta MNK}}}=color{red}{k}]
В любом случае, мы получили отношение, которое и требовалось доказать.
3.2. Площади подобных треугольников
Теорема 3. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Доказательство. Первые шаги очень похожи на доказательство предыдущей теоремы. Вновь рассмотрим подобные треугольники $ABC$ и $MNK$:
Поскольку $Delta ABCsimDelta MNK$, углы $ABC$ и $MNK$ равны. Следовательно, равны синусы этих углов:
[begin{align}angle ABC &=angle MNK=color{blue}{alpha} \ sin angle ABC &=sin angle MNK=sin color{blue}{alpha} end{align}]
Кроме того, стороны подобных треугольников пропорциональны:
[frac{AB}{MN}=frac{BC}{NK}=frac{AC}{MK}=color{red}{k}]
В частности, из этого равенства следует, что
[frac{AB}{MN}=color{red}{k}; frac{BC}{NK}=color{red}{k}]
Или, что то же самое:
[begin{align}AB &= color{red}{k}cdot MN \ BC &= color{red}{k}cdot NK \ end{align}]
Площадь треугольника $MNK$:
[{{S}_{Delta MNK}}=frac{1}{2}cdot MNcdot NKcdot sin color{blue}{alpha} ]
Площадь треугольника $ABC$:
[begin{align}{{S}_{Delta ABC}} &=frac{1}{2}cdot ABcdot BCcdot sincolor{blue}{alpha} = \ &=frac{1}{2}cdotcolor{red}{k}cdot MNcdotcolor{red}{k}cdot NKcdot sincolor{blue}{alpha} = \ &={color{red}{k}^{2}}cdot frac{1}{2}cdot MNcdot NKcdot sin alpha = \ &={color{red}{k}^{2}}cdot {{S}_{Delta MNK}} end{align}]
Получаем равенство
[{{S}_{Delta ABC}}={color{red}{k}^{2}}cdot {{S}_{Delta MNK}}]
Перепишем в виде отношения:
[frac{{{S}_{Delta ABC}}}{{{S}_{Delta MNK}}}={color{red}{k}^{2}}]
Что и требовалось доказать.
Для доказательства теоремы мы использовали формулу площади треугольника:
[{{S}_{Delta }}=frac{1}{2}absin alpha ]
Тригонометрию проходят после подобия, поэтому мы опираемся на ещё не изученный материал.
Впрочем, ничто не мешает взять уже известную формулу:
[{{S}_{Delta }}=frac{1}{2}ah]
Здесь $a$ — сторона треугольника, $h$ — высота, проведённая к этой стороне. Дело в том, что высоты в подобных треугольниках тоже пропорциональны. И не только высоты. Назовём это Свойством 3.3.:)
3.3. Элементы подобных треугольников
Теорема 4. Отношение высот, биссектрис и медиан, проведённых к соответствующим сторонам подобных треугольников, равно коэффициенту подобия.
Проиллюстрируем это на высотах. Пусть треугольники $ABC$ и $MNK$ подобны:
В этом случае высоты $CDbot AB$ и $KLbot MN$ относятся как
[frac{CD}{KL}=frac{AB}{MN}= color{red}{k}]
Для доказательства этой теоремы нужно знать признаки подобия. Поэтому оставим его до следующего урока. А сейчас переходим к задачам.
4. Задачи на подобие
Здесь разобрано пять задач на подобие треугольников. Все они довольно простые. За сложными задачами добро пожаловать в задачник.:)
Задача 1. Готовые треугольники
Известно, что треугольники $ABC$ и $MNK$ подобны, причём $angle A=angle M$, $angle B=angle N$, $angle C=angle K$. Кроме того, стороны $AB=6$, $BC=7$, $AC=10$ и $MN=9$. Найдите стороны $NK$ и $MK$.
Решение. Построим треугольники $ABC$ и $MNK$, отметим известные стороны:
Из условия $Delta ABCsim Delta MNK$ следует, что верно равенство
[frac{AB}{MN}=frac{BC}{NK}=frac{AC}{MK}]
Подставим в это равенство всё, что нам известно:
[frac{color{red}{6}}{color{red}{9}}=frac{color{red}{7}}{NK}=frac{color{red}{10}}{MK}]
Опустим последнюю дробь и получим пропорцию
[frac{color{red}{6}}{color{red}{9}}=frac{color{red}{7}}{NK}]
Найдём сторону $NK$:
[NK=frac{color{red}{9}cdot color{red}{7}}{color{red}{6}}=10,5]
Аналогично, убирая среднюю дробь, получим пропорцию
[frac{color{red}{6}}{color{red}{9}}=frac{color{red}{10}}{MK}]
Найдём сторону $MK$:
[NK=frac{color{red}{9}cdot color{red}{10}}{color{red}{6}}=15]
Ответ: $NK=10,5$, $MK=15$.
Задача 2. Прямая, параллельная стороне
Прямая, параллельная стороне $AC$ треугольника $ABC$, пересекает сторону $AB$ в точке $D$, а сторону $BC$ — в точке $E$. Найдите:
а) Отрезок $BD$, если $AB=16$, $AC=20$, $DE=15$.
б) Отрезок $AD$, если $AB=28$, $BC=63$, $BE=27$.
Решение. Для начала построим рисунок. Он будет общий для обоих пунктов.
Из условия следует, что прямая $DE$ пересекает стороны треугольника $ABC$:
Поскольку $DEparallel AC$, по лемме о подобных треугольниках прямая $DE$ отсекает от треугольника $ABC$ новый треугольник, подобный исходному:
[Delta ABCsim Delta DBE]
Из подобия треугольников $ABC$ и $DBE$ следует равенство
[frac{AB}{DB}=frac{BC}{BE}=frac{AC}{DE}]
Решаем пункт а). Подставляем в это равенство всё, что нам известно:
[frac{color{red}{16}}{DB}=frac{BC}{BE}=frac{color{red}{20}}{color{red}{15}}]
Вычёркиваем среднюю дробь и получаем пропорцию
[frac{color{red}{16}}{DB}=frac{color{red}{20}}{color{red}{15}}]
Отсюда легко найти $DB$ (или, что то же самое, $BD$):
[DB=frac{color{red}{16}cdotcolor{red}{15}}{color{red}{20}}=12]
Аналогично решаем пункт б). Подставляем в исходное равенство известные величины:
[frac{color{red}{28}}{DB}=frac{color{red}{63}}{color{red}{27}}=frac{AC}{DE}]
Первые две дроби образуют пропорцию, из которой вновь легко найти $DB$:
[DB=frac{color{red}{28}cdotcolor{red}{27}}{color{red}{63}}=12]
Осталось найти $AD$:
[begin{align}AD &=AB-BD= \ &=color{red}{28}-color{red}{12}=16 end{align}]
Ответ: а) $BD=12$; б) $AD=16$.
Важное замечание по работе с пропорциями. Ни в коем случае не нужно перемножать числа в числителе.
Напротив: нужно разложить их на множители и сократить!
Взгляните:
[DB=frac{color{red}{28}cdotcolor{red}{27}}{color{red}{63}}=frac{4cdotcolor{blue}{7}cdot 3cdotcolor{green}{9}}{color{blue}{7}cdotcolor{green}{9}}=12]
Так вы сэкономите время, избежите умножения столбиком и защитите себя от множества ошибок. Никогда не умножайте большие числа, если дальше их нужно будет сокращать.
Задача 3. Доказательство подобия
Точки $M$ и $K$ — середины сторон $CD$ и $AD$ квадрата $ABCD$ соответственно. Докажите, что треугольники $MDK$ и $BCD$ подобны.
Решение. Сделаем первоначальный рисунок по условию задачи:
Здесь нет прямых, параллельных сторонам треугольника, поэтому лемма о подобных треугольниках не поможет. Докажем подобие по определению.
Сначала разберёмся с углами. Поскольку $ABCD$ — квадрат, и $KD=MD$ — половина стороны квадрата, треугольники $MDK$ и $BCD$ — прямоугольные и равнобедренные.
Все острые углы треугольников $MDK$ и $BCD$ равны 45°. Можем записать это так:
[begin{align}angle BCD &=angle MDK={90}^circ \ angle CBD &=angle DMK={45}^circ \ angle CDB &=angle DKM={45}^circ \ end{align}]
Дополнительное построение: диагональ квадрата $color{red}{AC}$:
Рассмотрим треугольник $ACD$. Отрезок $KM$ — средняя линия, поэтому $KM={color{red}{AC}}/{2};$. С другой стороны, $AC=BD$ как диагонали квадрата. Поэтому верно равенство
[frac{KM}{BD}=frac{KM}{color{red}{AC}}=frac{1}{2}]
Но тогда выполняется следующее равенство:
[frac{MD}{BC}=frac{DK}{CD}=frac{MK}{BD}=frac{1}{2}]
А это вместе с равенством углов как раз и означает, что треугольники $MDK$ и $BCD$ подобны:
[Delta MDKsim Delta BCD]
Доказательство завершено.
Мы доказали подобие треугольников по определению. Если пользоваться признаками подобия, всё будет намного быстрее. Но пока мы не вправе пользоваться этими признаками.
Задача 4. Вписанный ромб
В треугольник $ABC$ вписан ромб $BDEK$ так, как показано на рисунке. Найдите сторону ромба, если $AB=10$, $BC=15$.
Решение. Пусть искомая сторона ромба равна $color{red}{x}$. Из условия задачи получим такой рисунок:
Зная, что $AB=10$ и $BC=15$, выразим $AK$ и $CD$:
[begin{align}AK &=10-color{red}{x} \ CD &=15-color{red}{x} \ end{align}]
Далее рассмотрим треугольник $ABC$. Поскольку $BDEK$ — ромб, то $KEparallel BC$. По лемме о подобных треугольниках имеем:
[Delta ABCsim Delta AKE]
В подобных треугольниках подобные стороны пропорциональны, поэтому
[frac{AB}{AK}=frac{BC}{KE}=frac{AC}{AE}]
Подставим в это равенство всё, что нам известно или выражено через $color{red}{x}$:
[frac{10}{10-color{red}{x}}=frac{15}{color{red}{x}}=frac{AC}{AE}]
Последняя дробь оказалась бесполезной. Вычеркнем её и получим пропорцию:
[frac{10}{10-color{red}{x}}=frac{15}{color{red}{x}}]
Применяем основное свойство пропорции и уравнение:
[begin{align}10cdotcolor{red}{x} &=15cdot left( 10- color{red}{x} right) \ 2cdotcolor{red}{x} &=3cdot left( 10- color{red}{x} right) \ &cdots\ color{red}{x} &=6 end{align}]
Это и есть искомая сторона ромба. Она равна $color{red}{x}=6$.
Ответ: $BD=6$.
Задача 5. Свойства биссектрисы
В треугольнике $ABC$ стороны $AB=8$, $BC=12$, угол $ABC={120}^circ $. Отрезок $BD$ — биссектриса. Найдите длину $BD$.
Решение. Из условия задачи можно сделать вот такой рисунок:
Поскольку $BD$ — биссектриса угла в треугольнике, точка $D$ делит сторону $AC$ на отрезки, пропорциональные сторонам $AB$ и $BC$. Это можно записать так:
[frac{AD}{CD}=frac{AB}{CB}=frac{color{red}{8}}{color{red}{12}}=frac{color{red}{2}}{color{red}{3}}]
Обозначим пропорциональные отрезки переменными. Пусть $AD=color{blue}{2x}$, $CD=color{blue}{3x}$.
Дополнительное построение: прямая $DMparallel AB$:
Рассмотрим угол $ACB$. Поскольку $DMparallel AB$, по теореме о пропорциональных отрезках получаем, что
[frac{BM}{CM}=frac{AD}{CD}=frac{color{red}{2}}{color{red}{3}}]
Вновь обозначим пропорциональные отрезки переменными. Пусть $BM=color{blue}{2y}$, $CM=color{blue}{3y}$. Но тогда
[BC=BM+MC=color{blue}{5y}=color{red}{12}]
Получаем, что $color{blue}{y}=color{red}{2,4}$. Отсюда легко найти длину $BM$:
[BM=color{blue}{2y}=2cdotcolor{red}{2,4}= color{red}{4,8}]
Далее заметим, что если угол $ABC$ равен 120°, то
[angle ABD=angle CBD={60}^circ ]
С другой стороны, прямые $AB$ и $MD$ параллельны по построению. Прямая $BD$ — секущая для этих параллельных прямых.
Следовательно, углы $ABD$ и $BDM$ — внутренние накрест лежащие, поэтому
[angle BDM=angle ABD={60}^circ ]
Рассмотрим треугольник $BDM$. В нём есть два угла по 60°. Следовательно, это равносторонний треугольник:
[BD=BM=color{red}{4,8}]
Мы нашли длину отрезка $BD$. Задача решена.
Ответ: $BD=4,8$.
Итак, с определением разобрались. В следующем уроке разберём признаки подобия.:)
Смотрите также:
- Как применяется теорема косинусов и подобие треугольников для решения широкого класса задач в планиметрии.

- Теорема менелая

- Комбинаторика в задаче B6: легкий тест

- Введение системы координат

- Четырехугольная пирамида: как найти координаты вершин

- Нестандартная задача B5 на площадь круга

Подобные треугольники. Признаки подобия треугольников
Содержание
- Определение подобных треугольников
- Коэффициент подобия треугольников
- Перый признак подобия треугольников
- Второй признак подобия треугольников
- Третий признак подобия треугольников
- Отношение площадей подобных треугольников
Определение подобных треугольников
Определение 1. Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
Определение 2. Сходственными называются стороны подобных треугольников, лежащих напротив равных углов.
На рисунке 1 углы треугольников ( small ABC ) и ( small A_1B_1C_1 ) соответственно равны:
Тогда стороны ( small AB ) и ( small A_1B_1 ), ( small BC ) и ( small B_1C_1 ), ( small AC ) и ( small A_1C_1 ) называются сходственными.
Определение 1 можно понимать так: два треугольника подобны, если для них можно ввести обозначения  и
и  (Рис.1) так, что
(Рис.1) так, что
Если два треугольника  и
и  подобны, то это обозначают так:
подобны, то это обозначают так:
Коэффициент подобия треугольников
Коэффициентом подобия треугольников k − это число, равное отношению сходственных сторон (см. формулу (2)).
Перый признак подобия треугольников
Теорема 1. Если два угла одного треугольника соответсвенно равны двум углам другого треугольника, то такие треугольники подобны.
Доказательство. Пусть заданы два треугольника  и
и  и пусть
и пусть  ,
, 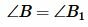 . Докажем, что
. Докажем, что 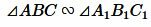 (Рис.2).
(Рис.2).
Поскольку сумма углов треугольника равна 180°, то можно записать:
и, так как  ,
, 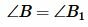 , получим:
, получим:
Таким образом углы треугольника  соответственно равны углам треугольника
соответственно равны углам треугольника  . Покажем, теперь, что стороны одного треугольника пропорциональны сходственным сторонам другого треугольника, т. е. выполнено равенство (2).
. Покажем, теперь, что стороны одного треугольника пропорциональны сходственным сторонам другого треугольника, т. е. выполнено равенство (2).
Площади треугольников  и
и  по двум сторонам и углу между ними можно вычислить формулами:
по двум сторонам и углу между ними можно вычислить формулами:
Из (3) и (4), и из  следует:
следует:
С другой стороны:
Из (6) и (7), и из 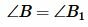 следует:
следует:
Левые части уравнения (5) и (8) равны. Следовательно равны и правые части:
Умножая левую и правую части уравнения (9) на 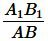 , получим:
, получим:
Продолжая аналогичные рассуждения, получим:
Сравнивая (8) и (11), получим:
Умножая левую и правую части уравнения (12) на 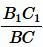 , получим:
, получим:
Из (10) и (13), получим:
То есть стороны треугольника  пропорциональны сходственным сторонам треугольника
пропорциональны сходственным сторонам треугольника  . Что и требовалось доказать.
. Что и требовалось доказать.
Второй признак подобия треугольников
Теорема 2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны, то такие треугольники подобны.
Доказательство. Пусть заданы два треугольника  и
и  и пусть
и пусть  ,
, 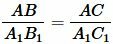 . Докажем, что
. Докажем, что 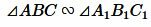 (Рис.3).
(Рис.3).
Рассмотрим треугольник 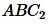 у которого
у которого
Из условия (15) следует, что треугольники 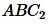 и
и  подобны (по первому признаку подобия треугольников). Следовательно:
подобны (по первому признаку подобия треугольников). Следовательно:
Но по условию теоремы 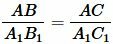 . Поэтому
. Поэтому 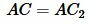 . Треугольники
. Треугольники 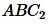 и
и  равны по двум сторонам и углу между ними (сторона AB общая,
равны по двум сторонам и углу между ними (сторона AB общая, 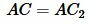 ,
, 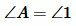 (поскольку
(поскольку  и
и 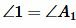 )). Следовательно
)). Следовательно 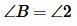 и поскольку
и поскольку 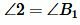 , то
, то 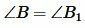 .
.
Получили, что  и
и 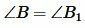 . Тогда по первому признаку подобия треугольников
. Тогда по первому признаку подобия треугольников 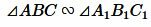 .
.
Третий признак подобия треугольников
Теорема 3. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Доказательство. Пусть стороны треугольников пропорциональны:
Докажем, что 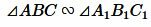 . Рассотрим треугольник
. Рассотрим треугольник 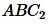 у которого
у которого 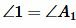 ,
, 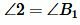 (Рис.3). Треугольники
(Рис.3). Треугольники 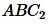 и
и  подобны по первому признаку подобия треугольников. Тогда выполнено следующее равенство:
подобны по первому признаку подобия треугольников. Тогда выполнено следующее равенство:
Сравнивая равенства (16) и (17) получаем: 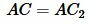 ,
, 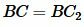 .
.
Из этих рассуждений следует, что треугольники 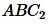 и
и  равны по трем сторонам (см. статью Треугольники. Признаки равенства треугольников). Тогда
равны по трем сторонам (см. статью Треугольники. Признаки равенства треугольников). Тогда 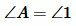 , а поскольку
, а поскольку 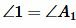 , то
, то  . Следовательно, по второму признаку подобия треугольников, треугольники
. Следовательно, по второму признаку подобия треугольников, треугольники  и
и  подобны:
подобны: 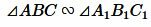 .
.
Отношение площадей подобных треугольников
Теорема 4. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Доказательство. Пусть треугольники  и
и  подобны. Тогда
подобны. Тогда
и
где 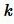 -коэффициент подобия.
-коэффициент подобия.
Площади треугольников 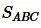 и
и 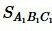 по двум сторонам и углу между ними равны:
по двум сторонам и углу между ними равны:
Тогда























