Как найти коэффициент отражения поверхности

Коэффициент отражения (оптика)

Размерность	безразмерная
Примечания
скалярная величина

Коэффицие́нт отраже́ния — безразмерная физическая величина, характеризующая способность тела отражать падающее на него излучение. В качестве буквенного обозначения используется греческая rho или латинская ^[1].

Определения[править | править код]

Количественно коэффициент отражения равен отношению потока излучения, отраженного телом, к потоку, упавшему на тело^[1]:

$rho ={frac {Phi }{Phi _{0}}}.$

Сумма коэффициента отражения и коэффициентов поглощения, пропускания и рассеяния равна единице. Это утверждение следует из закона сохранения энергии.

В тех случаях, когда спектр падающего излучения настолько узок, что его можно считать монохроматическим, говорят о монохроматическом коэффициенте отражения. Если спектр падающего на тело излучения широк, то соответствующий коэффициент отражения иногда называют интегральным.

В общем случае значение коэффициента отражения тела зависит как от свойств самого тела, так и от угла падения, спектрального состава и поляризации излучения. Вследствие зависимости коэффициента отражения поверхности тела от длины волны падающего на него света визуально тело воспринимается как окрашенное в тот или иной цвет.

Коэффициент зеркального отражения $rho _{r}~(R_{r})$ [править | править код]

Характеризует способность тел зеркально отражать падающее на них излучение. Количественно определяется отношением зеркально отраженного потока излучения $Phi _{r}$ к падающему потоку:

$rho _{r}={frac {Phi _{r}}{Phi _{0}}}.$

Зеркальное (направленное) отражение происходит в тех случаях, когда излучение падает на поверхность, размеры неровностей которой пренебрежимо малы по сравнению с длиной волны излучения.

Различают отражение от электропроводных поверхностей, например, металлических зеркал и отражение от диэлектрических поверхностей, например, стеклянных. При отражении от раздела двух диэлектрических сред с показателями преломления $n_{1}$ и ${displaystyle n_{2}}$ в случае нормального падения коэффициент отражения $rho _{r}$ выражается:

${displaystyle rho _{r}=left({frac {n_{1}-n_{2}}{n_{1}+n_{2}}}right)^{2},}$

причём его значение при нормальном падении не зависит от направления распространения излучения — из среды с бо́льшим показателем преломления в среду с меньшим показателем преломления или наоборот.

При косом падении излучения на плоскую поверхность раздела двух диэлектрических сред коэффициент отражения зависит от угла падения, в частности, при полном внутреннем отражении становится равным 1. Соотношения мощностей отраженного и проходящего потоков даются формулами Френеля.

Коэффициент диффузного отражения $rho _{d}~(R_{d})$ [править | править код]

Характеризует способность тел диффузно отражать падающее на них излучение — отражение от матовых поверхностей. Количественно определяется отношением диффузно отраженного потока излучения $Phi _{d}$ к падающему потоку:

$rho _{d}={frac {Phi _{d}}{Phi _{0}}}.$

Если одновременно происходят и зеркальное, и диффузное отражения, то коэффициент отражения rho является суммой коэффициентов зеркального $rho _{r}$ и диффузного $rho _{d}$ отражений:

$rho =rho _{r}+rho _{d}.$

См. также[править | править код]

Коэффициент поглощения
Коэффициент рассеяния
Коэффициент пропускания
Коэффициент ослабления

Примечания[править | править код]

↑ ¹ ² ГОСТ 26148—84. Фотометрия. Термины и определения. Дата обращения: 28 ноября 2020. Архивировано из оригинала 16 марта 2020 года.

Источник

Определение коэффициента отражения рабочей поверхности субъективным и объективным методами.
1. Определения коэффициента отражения рабочих поверхностей субъективным методом.

Для определения коэффициента отражения рабочих поверхностей пользуются готовыми шкалами сравнения. Шкалу накладывают на исследуемую поверхность и подбирают подходящую по густоте окраски полоску. Таким образом определяется, хотя приблизительно, но с достаточной для практических целей точностью, коэффициент отражения данной поверхности.

I. Шкала сравнения для определения коэффициентов отражения черных, серых и белых поверхностей (коэффициенты отражений выражены в процентах).

II. Шкала сравнения для определения коэффициентов отражения цветных поверхностей (коэффициенты отражения выражены в процентах).

2. Определения коэффициента отражения рабочих поверхностей объективным методом.

ГОСТ Р 50923-96. Дисплеи. Рабочее место оператора. Общие эргономические требования и требования к производственной среде. Методы измерения
Приложение В (рекомендуемое). измерение (определение) коэффициентов отражения поверхностей.

B.1 Коэффициенты отражения поверхностей (стол, пюпитр и др.) измеряют с помощью фотометра и других средств измерения, предназначенных для измерения коэффициентов диффузного отражения.
Для измерения используют образцы, окрашенные в цвет, соответствующий цвету измеряемых поверхностей. Размеры образцов должны соответствовать размерам средств измерения.

В.2 Коэффициенты отражения поверхностей допускается определять визуально сравнением отражающих свойств исследуемых поверхностей с эталонной шкалой коэффициентов отражения, изготавливаемой специально.
Эталонная шкала должна состоять из квадратных или прямоугольных эталонных пластин одинакового размера и цветового тона, но разного коэффициента отражения от 0,1 до 0,9. Эталонные пластины располагают рядом таким образом, чтобы в одном направлении шкалы их коэффициент отражения убывал или увеличивался с постоянным шагом 0,1. Коэффициент отражения эталонных пластин измеряют также с помощью фотометра или других средств измерения коэффициентов диффузного отражения.

В.3 Коэффициенты отражения поверхностей определяют также косвенным методом, исходя из результатов измерений освещенности и яркости исследуемых поверхностей.
При измерении освещенности исследуемую поверхность освещают источником света типа А по ГОСТ 7721и проводят измерения, как указано в 6.2 настоящего стандарта.
При измерении яркости яркомер устанавливают под углом 45° к нормали фотометрируемой поверхности и измеряют ее яркость в соответствии с 6.3.2 настоящего стандарта.
Коэффициент отражения поверхности рассчитывают по формуле

Источник

Коэффициент
отражения поверхности. Средневзвешенный
коэффициент отражения внутренных
поверхностей помещения. Коэффицент
пропускания.

Важнейшим
свойством поверхности объекта,
определяющий его цвет и яркость, является
коэффициент отражения поверхности на
различных частотах: в видимом, инфракрасном
и радиодиапазоне.
Коэффициент отражения поверхности
(р) характеризует способность поверхности
отражать падающий на нее световой поток;
определяется отношением светового
потока отраженного от поверхности, к
падающему на нее световому потоку

Средневзвешенный
коэффициент отражения внутренных
поверхностей помещения (р_ср)

где S_ст,
S_пот,
S_пол–
соответственно площади стен, потолка
и пола, м²
а Р_ст,
Р_пот,
Р_пол–
соответственно коэффиценты отражения
стен, потолка и пола.

Коэффицент
пропускания, –
отношение светового потока, прошедшего
через слой, к световому потоку, падающему
на слой: τ=F/F. Коэффициент пропускания
является мерой прозрачности слоя. В
зависимости от характера изменения
пучка при прохождении через слой
различают пропускание направленное,
рассеянное, направленно-рассеянное и
смешанное .
Совершенно очевидно, что коэффициент
пропускания всегда меньше единицы,
поскольку все тела более или менее
поглощают проходящий через них свет и
поглощение тем больше, чем толще слой.

3. Естественное освещение кео

Что
такое коэффициент естественной
освещенности (КЕО)?

Это
выраженное в процентах отношение
естественной освещенности Е_Вв
какой либо точке на рабочей поверхности
внутри помещении к одновременному
значению наружной горизонтальной
освещенности Е_н,
создаваемой рассеяным светом полностьь
открытого небосвода. е = Е_в/Е_н*100%

КЕО
показывает, какую долю освещенность в
данной точке помещения составляет от
одновременной освещенности горизонтальной
поверхности на открытом месте при
диффузном свете неба

Какие
факторы влияют на значения коэффициента
естественной освещенностив расчетной
точке помещения?

Неравномерная
яркость небосвода
Влияние
остекления оконных проемов
Усиление
освещенности отраженным светом

4. Нормирование коэффициента естественной освещенности.

От
каких факторов зависит нормативное
значение коэффициента естественной
освещенности?

Кроме
назначения помещения( характера
пыполняемой в помещении зрительной
работы), при нормировании естественного
освещения учитывается так же световой
климат района строительства (т.е
превалирующие условия наружной
освещенности, количество солнечных
лучей, устойчивость снежного покрова)
и ориентация светового проема по сторонам
горизонта. В силу этого нормированное
з начение КЕО определяют по формуле

Принципы
нормирования коэффициента естественной
освещенности.

5. Геометрические кео

Принцип
расчета геометрического КЕО

Учитывается
только диффузный свет неба и не учитываются
реальные условия освящения: неравномерность,
яркость небосвода, влияние остекления
оконных проемов, отраженный свет.
Определяется с помощью гр.Данилюка. при
построение небосвод представляют в
виде равномерно яркой полусферы с
центром в расчетной точке, светящаяся
сферическая пов-ть небосвода разбита
на 10⁴
участков, площади проэкций которых на
горизонтальную пов-ть основания
одинаковы. От каждого участка небосвода
в расчетную точку приводит один луч.
Освещенность в точке на горизонт. пов-ти
плоскостью открытия небосводом Е_н
соответствует 10⁴лучей.
Внутри помещения Е_в
соответствует числу лучей N, поподающих
через световой проем.

Порядок
расчета (по гр. Данилюка):

Вычертить
план и разрез в одном масштабе
Определить
положение расчетной точки и плоскости.
На
разрезе соединить расчетную точку с
гранями светопро ема через которые
видна небесная сфера
По
гр.1 определить количество лучей, для
этого расчетную точку совместить с
полюсом графика, расчётную плоскость
с горизонтальной осью грани. Лучами
считать расстояния между сплошными
линиями. Пунктирные линии на графике
1 – 10ые доли луча.
Поставить
точку С, разделив участок пополам.
По
гр.1 определить номер полуокружности
проходящей вблизи точки С.
На
плане(2ой график) разместить вертикальную
ось графика совпадающую с характерным
расчетным разрезом.
Номер
горизонтали соответствует номеру
полуокружности, совместить с наружной
гранью.
Определить
количество лучей
Вычисляем
геометрический коэффициент естественной
освещенности

График
Данилюка накладывается на поперечный
разрез здания, центр графика совмещается
с точкой. подсчитывается количество
лучей n1, отмечается номер полуокружности,
которая проходит через точку С-середина
светового проема. График 2 накладывается
на план. Его ось совпадает с горизонтом
и проходит через точку С. По номеру
полуокружности, подсчитываем количество
лучей проходящее через световой проем.

Вычисленный
по гр. Данилюка КЕО совпадает с расчетным,
если небосвод равномерно яркий , в
световом проеме нет заполнения(рам,стекол,
и т. п. ), подстилающий слой земл и
поверхности помещения абсолютно черные.

Графики
Данилюка

Каждый
график содержит 100 лучей. Нумерация
лучей идет от оси графика в обе стороны.
Луч- это промежуток между сплошными
линиями. Пунктирные линии на графике 1
– 10ые доли луча(50). Каждой дуге
(полуокружности) на гр.1 соответствует
горизонталь(горизонтальная линия) на
графике 2. Дуги и горизонтали на графиках
пронумерованы. Разработаны на основе
закона телесного угла.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

From Wikipedia, the free encyclopedia

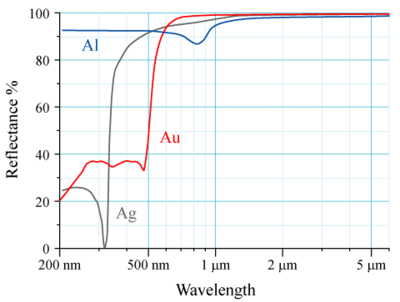
The reflectance of the surface of a material is its effectiveness in reflecting radiant energy. It is the fraction of incident electromagnetic power that is reflected at the boundary. Reflectance is a component of the response of the electronic structure of the material to the electromagnetic field of light, and is in general a function of the frequency, or wavelength, of the light, its polarization, and the angle of incidence. The dependence of reflectance on the wavelength is called a reflectance spectrum or spectral reflectance curve.

Mathematical definitions[edit]

Hemispherical reflectance[edit]

The hemispherical reflectance of a surface, denoted R, is defined as^[1]

${displaystyle R={frac {Phi _{mathrm {e} }^{mathrm {r} }}{Phi _{mathrm {e} }^{mathrm {i} }}},}$

where Φ_e^r is the radiant flux reflected by that surface and Φ_eⁱ is the radiant flux received by that surface.

Spectral hemispherical reflectance[edit]

The spectral hemispherical reflectance in frequency and spectral hemispherical reflectance in wavelength of a surface, denoted R_ν and R_λ respectively, are defined as^[1]

${displaystyle R_{nu }={frac {Phi _{mathrm {e} ,nu }^{mathrm {r} }}{Phi _{mathrm {e} ,nu }^{mathrm {i} }}},}$

${displaystyle R_{lambda }={frac {Phi _{mathrm {e} ,lambda }^{mathrm {r} }}{Phi _{mathrm {e} ,lambda }^{mathrm {i} }}},}$

where

Φ_e,ν^r is the spectral radiant flux in frequency reflected by that surface;
Φ_e,νⁱ is the spectral radiant flux in frequency received by that surface;
Φ_e,λ^r is the spectral radiant flux in wavelength reflected by that surface;
Φ_e,λⁱ is the spectral radiant flux in wavelength received by that surface.

Directional reflectance[edit]

The directional reflectance of a surface, denoted R_Ω, is defined as^[1]

${displaystyle R_{Omega }={frac {L_{mathrm {e} ,Omega }^{mathrm {r} }}{L_{mathrm {e} ,Omega }^{mathrm {i} }}},}$

where

L_e,Ω^r is the radiance reflected by that surface;
L_e,Ωⁱ is the radiance received by that surface.

This depends on both the reflected direction and the incoming direction. In other words, it has a value for every combination of incoming and outgoing directions. It is related to the bidirectional reflectance distribution function and its upper limit is 1. Another measure of reflectance, depending only on the outgoing direction, is I/F, where I is the radiance reflected in a given direction and F is the incoming radiance averaged over all directions, in other words, the total flux of radiation hitting the surface per unit area, divided by π.^[2] This can be greater than 1 for a glossy surface illuminated by a source such as the sun, with the reflectance measured in the direction of maximum radiance (see also Seeliger effect).

Spectral directional reflectance[edit]

The spectral directional reflectance in frequency and spectral directional reflectance in wavelength of a surface, denoted R_Ω,ν and R_Ω,λ respectively, are defined as^[1]

${displaystyle R_{Omega ,nu }={frac {L_{mathrm {e} ,Omega ,nu }^{mathrm {r} }}{L_{mathrm {e} ,Omega ,nu }^{mathrm {i} }}},}$

${displaystyle R_{Omega ,lambda }={frac {L_{mathrm {e} ,Omega ,lambda }^{mathrm {r} }}{L_{mathrm {e} ,Omega ,lambda }^{mathrm {i} }}},}$

where

L_e,Ω,ν^r is the spectral radiance in frequency reflected by that surface;
L_e,Ω,νⁱ is the spectral radiance received by that surface;
L_e,Ω,λ^r is the spectral radiance in wavelength reflected by that surface;
L_e,Ω,λⁱ is the spectral radiance in wavelength received by that surface.

Again, one can also define a value of I/F (see above) for a given wavelength.^[3]

Reflectivity[edit]

Fresnel reflection coefficients for a boundary surface between air and a variable material in dependence of the complex refractive index and the angle of incidence.

For homogeneous and semi-infinite (see halfspace) materials, reflectivity is the same as reflectance.
Reflectivity is the square of the magnitude of the Fresnel reflection coefficient,^[4]
which is the ratio of the reflected to incident electric field;^[5]
as such the reflection coefficient can be expressed as a complex number as determined by the Fresnel equations for a single layer, whereas the reflectance is always a positive real number.

For layered and finite media, according to the CIE,^{[citation needed]} reflectivity is distinguished from reflectance by the fact that reflectivity is a value that applies to thick reflecting objects.^[6] When reflection occurs from thin layers of material, internal reflection effects can cause the reflectance to vary with surface thickness. Reflectivity is the limit value of reflectance as the sample becomes thick; it is the intrinsic reflectance of the surface, hence irrespective of other parameters such as the reflectance of the rear surface. Another way to interpret this is that the reflectance is the fraction of electromagnetic power reflected from a specific sample, while reflectivity is a property of the material itself, which would be measured on a perfect machine if the material filled half of all space.^[7]

Surface type[edit]

Given that reflectance is a directional property, most surfaces can be divided into those that give specular reflection and those that give diffuse reflection.

For specular surfaces, such as glass or polished metal, reflectance is nearly zero at all angles except at the appropriate reflected angle; that is the same angle with respect to the surface normal in the plane of incidence, but on the opposing side. When the radiation is incident normal to the surface, it is reflected back into the same direction.

For diffuse surfaces, such as matte white paint, reflectance is uniform; radiation is reflected in all angles equally or near-equally. Such surfaces are said to be Lambertian.

Most practical objects exhibit a combination of diffuse and specular reflective properties.

Water reflectance[edit]

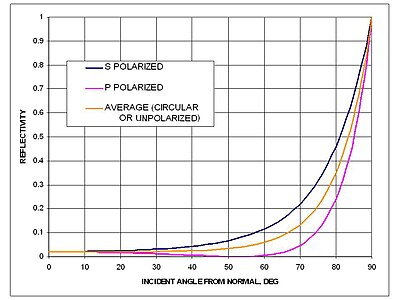
Reflectance of smooth water at 20 °C (refractive index 1.333).

Reflection occurs when light moves from a medium with one index of refraction into a second medium with a different index of refraction.

Specular reflection from a body of water is calculated by the Fresnel equations.^[8] Fresnel reflection is directional and therefore does not contribute significantly to albedo which primarily diffuses reflection.

A real water surface may be wavy. Reflectance, which assumes a flat surface as given by the Fresnel equations, can be adjusted to account for waviness.

Grating efficiency[edit]

The generalization of reflectance to a diffraction grating, which disperses light by wavelength, is called diffraction efficiency.

Other radiometric coefficients[edit]

Radiometry coefficients

Quantity	SI units	Notes
Name	Sym.
Hemispherical emissivity	ε	—	Radiant exitance of a surface, divided by that of a black body at the same temperature as that surface.
Spectral hemispherical emissivity	ε_ν ε_λ	—	Spectral exitance of a surface, divided by that of a black body at the same temperature as that surface.
Directional emissivity	ε_Ω	—	Radiance emitted by a surface, divided by that emitted by a black body at the same temperature as that surface.
Spectral directional emissivity	ε_Ω,ν ε_Ω,λ	—	Spectral radiance emitted by a surface, divided by that of a black body at the same temperature as that surface.
Hemispherical absorptance	A	—	Radiant flux absorbed by a surface, divided by that received by that surface. This should not be confused with “absorbance”.
Spectral hemispherical absorptance	A_ν A_λ	—	Spectral flux absorbed by a surface, divided by that received by that surface. This should not be confused with “spectral absorbance”.
Directional absorptance	A_Ω	—	Radiance absorbed by a surface, divided by the radiance incident onto that surface. This should not be confused with “absorbance”.
Spectral directional absorptance	A_Ω,ν A_Ω,λ	—	Spectral radiance absorbed by a surface, divided by the spectral radiance incident onto that surface. This should not be confused with “spectral absorbance”.
Hemispherical reflectance	R	—	Radiant flux reflected by a surface, divided by that received by that surface.
Spectral hemispherical reflectance	R_ν R_λ	—	Spectral flux reflected by a surface, divided by that received by that surface.
Directional reflectance	R_Ω	—	Radiance reflected by a surface, divided by that received by that surface.
Spectral directional reflectance	R_Ω,ν R_Ω,λ	—	Spectral radiance reflected by a surface, divided by that received by that surface.
Hemispherical transmittance	T	—	Radiant flux transmitted by a surface, divided by that received by that surface.
Spectral hemispherical transmittance	T_ν T_λ	—	Spectral flux transmitted by a surface, divided by that received by that surface.
Directional transmittance	T_Ω	—	Radiance transmitted by a surface, divided by that received by that surface.
Spectral directional transmittance	T_Ω,ν T_Ω,λ	—	Spectral radiance transmitted by a surface, divided by that received by that surface.
Hemispherical attenuation coefficient	μ	m⁻¹	Radiant flux absorbed and scattered by a volume per unit length, divided by that received by that volume.
Spectral hemispherical attenuation coefficient	μ_ν μ_λ	m⁻¹	Spectral radiant flux absorbed and scattered by a volume per unit length, divided by that received by that volume.
Directional attenuation coefficient	μ_Ω	m⁻¹	Radiance absorbed and scattered by a volume per unit length, divided by that received by that volume.
Spectral directional attenuation coefficient	μ_Ω,ν μ_Ω,λ	m⁻¹	Spectral radiance absorbed and scattered by a volume per unit length, divided by that received by that volume.

References[edit]

^ ^a ^b ^c ^d “Thermal insulation — Heat transfer by radiation — Physical quantities and definitions”. ISO 9288:1989. ISO catalogue. 1989. Retrieved 2015-03-15.
^ Jeffrey Cuzzi, Lindsey Chambers, and Amanda Hendrix (Oct 21, 2016). “Rough Surfaces: is the dark stuff just shadow?”. Icarus. 289: 281–294. doi:10.1016/j.icarus.2016.10.018. PMC 6839776. PMID 31708591.{{cite journal}}: CS1 maint: multiple names: authors list (link)
^ See for example P.G.J Irwin; et al. (Jan 12, 2022). “Hazy Blue Worlds: A Holistic Aerosol Model for Uranus and Neptune, Including Dark Spots”. Journal of Geophysical Research: Planets. 127 (6): e2022JE007189. arXiv:2201.04516. Bibcode:2022JGRE..12707189I. doi:10.1029/2022JE007189. hdl:1983/65ee78f0-1d28-4017-bbd9-1b49b24700d7. PMC 9286428. PMID 35865671. S2CID 245877540.
^ E. Hecht (2001). Optics (4th ed.). Pearson Education. ISBN 0-8053-8566-5.
^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the “Gold Book”) (1997). Online corrected version: (2006–) “Reflectance”. doi:10.1351/goldbook.R05235
^ “CIE International Lighting Vocabulary”. Archived from the original on 2016-06-16. Retrieved 2010-12-04.
^ Palmer and Grant, The Art of Radiometry
^ Ottaviani, M. and Stamnes, K. and Koskulics, J. and Eide, H. and Long, S.R. and Su, W. and Wiscombe, W., 2008: ‘Light Reflection from Water Waves: Suitable Setup for a Polarimetric Investigation under Controlled Laboratory Conditions. Journal of Atmospheric and Oceanic Technology, 25 (5), 715–728.

External links[edit]

Look up reflectance in Wiktionary, the free dictionary.

Reflectivity of metals Archived 2016-03-04 at the Wayback Machine.
Reflectance Data.

Источник

Тепловизор регистрирует инфракрасное излучение от всех объектов, расположенных в поле его зрения. Это излучение состоит из трех частей:
– излучаемого объектом;
– отраженного от объекта;
– проходящего через объект.

Что такое коэффициент излучения

Коэффициент излучения (КИ) — это степень способности материала излучать инфракрасное излучение.

КИ изменяется в зависимости от материала, свойств поверхности и для некоторых материалов — от температуры измеряемого объекта.

Максимальное значение коэффициента излучения = 1 (100%), в реальных условиях КИ всегда меньше 1.

У живых тел КИ также меньше 1, т. к. живые тела также отражают и пропускают излучение.

Многие неметаллические материалы, например, органические вещества, бетон, ПВХ, имеют высокую излучательную способность (от 0,8 до 0,95). Коэффициент излучения у таких материалов от температуры не зависит.

Металлы, особенно материалы с блестящей поверхностью, имеют низкую излучательную способность. У таких металлических материалов коэффициент излучения зависит от температуры.

Коэффициент излучения ε можно задать в тепловизоре вручную. О способах определения КИ читайте здесь.

Что такое коэффициент отражения

Коэффициент отражения — это степень способности материала отражать инфракрасное излучение.

Коэффициент отражения зависит от свойств поверхности, температуры и типа материала.

Как правило, гладкие, полированные поверхности имеют большую отражательную способность, чем шероховатые, матовые поверхности, изготовленные из того же материала.

Компенсацию отраженной температуры (КОТ) можно настроить в тепловизоре вручную.

В большинстве случаев отраженная температура равна температуре окружающей среды. Вы можете измерить ее, например, с помощью воздушного термометра Testo 810.

КОТ также можно определить излучателем Ламберта (см. Определение КОТ).

Что такое коэффициент пропускания

Коэффициент пропускания — это степень способности материала пропускать (проводить через себя) инфракрасное излучение.

Коэффициент пропускания зависит от типа материала и его толщины.

Большинство материалов не пропускают инфракрасное излучение.

Закон теплового излучения Кирхгофа

Инфракрасное излучение, регистрируемое тепловизором, состоит из:
– излучаемого объектом (ε),
– отраженного излучения других объектов (ρ),
– проходящего через объект (τ).

Сумма трех видов излучения всегда принимается равной 1 ( 100%):
ε + ρ + τ = 1
Поскольку коэффициент пропускания на практике редко играет значительную роль, τ опускается, и формула упрощается до
ε + ρ = 1

Для термографии это означает:
чем ниже коэффициент излучения,
тем выше уровень отраженного инфракрасного излучения,
тем сложнее осуществить точное измерение температуры и
тем более важным фактором становится правильная настройка компенсации отраженной температуры (КОТ).

Как влияет коэффициент излучения на точность измерений

1. Объекты измерений с высоким коэффициентом излучения (больше 0,8) имеют низкий коэффициент отражения (ρ = 1 – ε). Температуру таких объектов можно очень легко измерить с помощью тепловизора.

2. Объекты измерений со средним коэффициентом излучения (от 0,6 до 0,8) имеют средний коэффициент отражения. Температуру таких объектов можно измерить с помощью тепловизора.

3. Объекты измерений с низким коэффициентом излучения (меньше 0,6) имеют высокий коэффициент отражения. Измерение температуры таких объектов тепловизором возможно, но результаты необходимо тщательно проверять.

очень важна корректная настройка компенсации отраженной температуры (КОТ), поскольку это является одним из основных факторов при расчете температуры.

Измерения при различной температуре объекта и окружающей среды

Корректная настройка коэффициента излучения очень важна при значительной разнице между температурой объекта и температурой окружающей среды.

Когда температура измеряемого объекта выше температуры окружающей среды (радиатор на рисунке):
чрезмерно высокий коэффициент излучения приведет к завышенным показаниям температуры (тепловизор 1);
чрезмерно низкий коэффициент излучения приведет к заниженным показаниям температуры (тепловизор 2).

Когда температура измеряемого объекта ниже температуры окружающей среды (дверь, изображенная на том же рисунке):
чрезмерно высокий коэффициент излучения приведет к заниженным показаниям температуры (тепловизор 1);
чрезмерно низкий коэффициент излучения приведет к завышенным значениям температуры.

Обратите внимание: чем больше разница между температурой измеряемого объекта и температурой окружающей среды и чем ниже коэффициент излучения, тем больше вероятность возникновения ошибок.

Количество ошибок возрастет, если КИ задан неверно.

Резюме

Тепловизор позволяет измерить только поверхностную температуру объекта; с помощью данного прибора Вы не можете «заглянуть внутрь» объекта или увидеть его насквозь.

Несмотря на то, что многие материалы, например, стекло, кажутся прозрачными, они проявляют себя как материалы непропускающего типа, т.е. они устойчивы к длинноволновому инфракрасному излучению.

При необходимости снимите с измеряемого объекта чехол (упаковку), т.к. при наличии последних тепловизор измерит поверхностную температуру чехла (упаковки).

Если компоненты, расположенные внутри объекта, влияют на распределение температуры по его поверхности через проводимость, то на тепловом снимке можно рассмотреть внутреннюю структуру объекта .

Тем не менее, тепловизор может измерять только поверхностную температуру объекта. Точную температуру внутренних элементов с помощью тепловизора определить невозможно.

Следующий материал: Размеры и расстояния

Недорогой тепловизор Testo с цифровой камерой, выпущен взамен модели 875, самый дешевый прибор, который годится для энергоаудита. Подходит для решения большинства стандартных задач термографии, сегодня это наиболее востребованная модель линейки тепловизоров Testo.

– матрица детектора 160 x 120
– температура -30°C..+350°C
– чувствительность 50 mK
– поле зрения 32° x 23°
– дисплей 3,5″, 320 x 240
– цифровая камера 640 x 480

Источник

Определения[править | править код]

Коэффициент зеркального отражения $rho _{r}~(R_{r})$ [править | править код]

Коэффициент диффузного отражения $rho _{d}~(R_{d})$ [править | править код]

См. также[править | править код]

Примечания[править | править код]

3. Естественное освещение кео

4. Нормирование коэффициента естественной освещенности.

5. Геометрические кео