Коэффицие́нт переда́чи (также коэффициент преобразова́ния, крутизна преобразова́ния) — отношение приращения некоторой физической величины на выходе некоторой системы 


Величину на входе системы часто называют возмущающим воздействием или просто возмущением, а выходную
величину — откликом системы.
В общем случае размерности возмущения и отклика не совпадают, например, звуковое давление, развиваемое электродинамическим громкоговорителем и подводимая к нему электрическая мощность, или ЭДС термопары и температура, в этом случае отношение выходной величины к входной часто называют коэффициентом преобразования или крутизной преобразования, при этом коэффициент передачи размерный в приведённых примерах — Па/Вт или В/К.
Если входная и выходная величины имеют одинаковую размерность, то коэффициент передачи — безразмерная величина и его обычно называют коэффициентом усиления. При этом если выходная величина больше по модулю входной величины, то коэффициент усиления больше 1. Если коэффициент усиления меньше 1 то часто используют обратную ему величину 
В линейных системах коэффициент передачи не зависит от величины возмущения, то есть является постоянной величиной, и связь между откликом и воздействием выражается формулой:
В нелинейных системах связь между откликом и возмущением является некоторой нелинейной функцией, при этом вводят понятие дифференциального коэффициента передачи — производной отклика по возмущению 
Обычно коэффициент передачи не зависит от предыстории системы, но в некоторых системах текущий коэффициент передачи зависит от предыдущий воздействий, например, в электрических цепях с катушками индуктивности с ферромагнитными сердечниками или в цепях с электрохимическими элементами[1]
Логарифмический коэффициент передачи[править | править код]
Пример логарифмической амплитудно-частотной характеристики фильтра нижних частот 1-го порядка. В показанной на графике полосе частот коэффициент передачи по мощности изменяется на 6 порядков.
Безразмерный коэффициент передачи часто численно выражают в виде логарифма по некоторому оговорённому основанию 
Для коэффициентов передачи, имеющих размерность, логарифмический коэффициент передачи не имеет смысла, так как будет зависеть от системы выбранных единиц, в отличие от безразмерных коэффициентов передачи инвариантных относительно выбранной системы единиц. Для размерных коэффициентов передачи имеют смысл только логарифмы их отношений, например, на двух разных частотах или при двух разных условиях.
Применение логарифмического коэффициента передачи обусловлено во-первых тем, что при последовательном соединении нескольких систем (звеньев, цепей) с коэффициентами передачи 
При замене на логарифмы коэффициентов передачи результирующий логарифмический коэффициент передачи 

то есть, перемножение чисел заменяется их сложением, что на практике при расчётах удобнее.
И, во-вторых, коэффициент передачи может изменяться на много порядков, например, при изменении частоты гармонического возбуждающего воздействия и на графиках выражение коэффициентов передачи в виде логарифмов получается нагляднее.
В качестве основания логарифма практически используются три числа, это логарифмы по основанию числа Эйлера 

Энергетические и силовые логарифмические коэффициенты передачи[править | править код]
Энергетические величины 

Соответственно, логарифмические коэффициенты передачи:
Поэтому логарифмические коэффициенты передачи для энергетических величин в 2 раза больше логарифмических коэффициентов передачи для силовых величин.
Пример. Электрическая мощность на сопротивлении нагрузки 
Соотношения между силовыми и энергетическими логарифмическими коэффициентами передачи выраженные в белах, децибелах и неперах приведены в таблице.
| Единица | Обозначение | Изменение энергетической величины в … раз |
Изменение силовой величины в … раз |
Пересчёт в … | ||
|---|---|---|---|---|---|---|
| дБ | Б | Нп | ||||
| децибел | дБ, dB | ![sqrt[10]{10}](https://wikimedia.org/api/rest_v1/media/math/render/svg/640a47a05663578069ba03cd5ebb8ec412d4131e) ≈ 1,259 ≈ 1,259 |
![{displaystyle {sqrt[{20}]{10}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cba419e91dd4b2131d31468bd0b1353a869cfb4) ≈ 1,122 ≈ 1,122 |
1 | 0,1 | ≈0,1151 |
| бел | Б, B | 10 |  ≈ 3,162 ≈ 3,162 |
10 | 1 | ≈1,151 |
| непер | Нп, Np | e2 ≈ 7,389 | e ≈ 2,718 | ≈8,686 | ≈0,8686 | 1 |
Если коэффициент передачи больше 1, то логарифмический коэффициент передачи положителен, отрицателен при
коэффициенте передачи меньше 1 и равен нулю, если коэффициент передачи равен 1.
Также в виде логарифмического коэффициента передачи обычно указывается затухание (ослабление) сигнала в электрических и оптоволоконных линиях передачи, часто в виде удельного ослабления на единицу длины линии, например, в дБ/км, при этом знак минус у логарифмического коэффициента передачи, как правило, не указывается, а подразумевается.
Комплексный коэффициент передачи и модуль коэффициента передачи[править | править код]
Большинство изучаемых систем нелинейны, то есть для них не выполняется принцип суперпозиции. Практически при анализе многие системы поддаются линеаризации — они ведут себя как приближённо линейные для малых изменений возмущающих входных воздействий. Для линейных и линеаризованных систем вводят понятие комплексного коэффициента передачи.
Если на вход линейной или приближённо линейной системы подать гармоническое воздействие 





Гармонические входное возмущение и выходной отклик можно записать в виде комплексных амплитуд, буквой 
По определению коэффициент передачи равен отношению выходного и входного сигналов, в теории автоматического регулирования, теории электрических цепей комплексный коэффициент передачи обычно обозначают как 

В этом выражении отношение 

Или в других обозначениях, если записать комплексный коэффициент передачи в нормализованном виде комплексного числа 




Зависимость комплексного коэффициента передачи линейной системы от частоты возмущения графически можно изобразить в виде амплитудно-фазовой частотной характеристики, где на одном из графиков строится зависимость модуля коэффициента передачи от частоты, а на другом графике — зависимость фазового сдвига от частоты. Обычно для наглядности на оси частот и на оси модуля коэффициента передачи применяют логарифмические координаты, в этом случае такой график называют логарифмической амплитудно-фазовой частотной характеристикой, ось модуля коэффициента передачи обычно оцифровывается в децибелах.
Также комплексный коэффициент передачи графически может изображаться в виде годографа на комплексной плоскости — траектории конца вектора векторного представления комплексного коэффициента передачи при изменении частоты, на этой траектории в виде засечек указывается частота. Графическое представление удобно при анализе устойчивости систем автоматического регулирования, в частности, если годограф коэффициента передачи системы с разомкнутой обратной связью не охватывает точку комплексной плоскости −1, то такая системы при замыкании контура обратной связи будет устойчива.
Другие виды коэффициента передачи[править | править код]
В общем случае отношение выходного сигнала к вызвавшему его входному сигналу любой системы можно назвать коэффициентом передачи. В зависимости от конкретной системы коэффициент передачи может называться по-разному. Например, отношение приращения тока через активный электронный прибор (например, электровакуумный триод, транзистор) в вызвавшему это приращение изменению напряжения на управляющем электроде прибора называют крутизной передаточной характеристики, имеющей размерность электрической проводимости. В измерительных стрелочных приборах отношение отклонения стрелки к вызвавшему это отклонение изменению измеряемой величины называют чувствительностью прибора или ценой деления шкалы.
Применение понятия[править | править код]
В основном термин «коэффициент передачи» используется в электротехнике, электронике, оптике, акустике. Например, коэффициент усиления усилителей, коэффициент затухания сигнала в линиях передачи, ослабление электромагнитного излучения в поглощающих средах, или наоборот, усиление света в активных средах лазеров, в описании поглощения и отражения звуковых волн и поглощении механических вибраций, и т. п.
Методы измерения коэффициента передачи[править | править код]
- Прямое измерение — производится прямым измерением амплитуды сигнала на входе и выходе системы с последующим вычислением. Существуют специализированные оптические и электрические приборы для выполнения такого измерения.
- Измерение методом сравнения — производится с помощью аттенюатора, являющегося мерой ослабления. Например, с помощью аттенюатора ослабляют выходной сигнал усилителя до достижения равенства с входным сигналом, сравнение сигналов производится каким либо компаратором. По степени ослабления калиброванного аттенюатора определяют коэффициент усиления усилителя.
- Для измерения комплексных коэффициентов передачи применяются измерители импеданса и комплексных коэффициентов передачи, или, на сверхвысоких частотах, измерители комплексных коэффициентов и измерители коэффициента стоячей волны.
Примечания[править | править код]
- ↑ Боровков В. С., Графов Б. М. и др. Электрохимические преобразователи первичной информации. М. Машиностроение. 1969. 196 с., ил.
См. также[править | править код]
- Ослабление электромагнитного сигнала
- Усилитель
- Лазерные материалы
- Волоконно-оптический усилитель
- Четырёхполюсник
Литература[править | править код]
- Хлытчиев С. М. Основы автоматики и автоматизации производственных процессов. — 1985.
- Словарь радиолюбителя — Л.: Энергия, 1979.
- Гусев В. Г. Электроника. — 1991.
Ссылки[править | править код]
- Синтез корреляционных алгоритмов идентификации в частотной области.
- Вывод комплексного коэффициента передачи системы каскадно-соединённых взаимодействующих четырёхполюсников.
- О методах описания линейных систем.
- Динамика линейных систем автоматического управления.
Содержание:
Частотные методы анализа электрических цепей:
Частотные характеристики являются компонентами комплексных функций цепи.
Комплексная функция цепи (КФЦ)
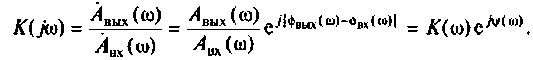
Амплитудно-частотная характеристика (АЧХ)
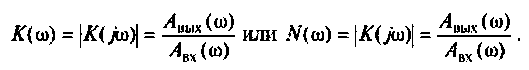
Фазочастотная характеристика (ФЧХ)
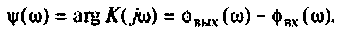
Амплитудно-фазовая частотная характеристика (АФЧХ) (комплексная функция цепи)
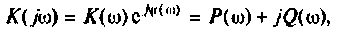
где 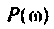 — вещественная частотная характеристика (ВЧХ);
— вещественная частотная характеристика (ВЧХ); 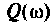 — мнимая частотная характеристика (МЧХ).
— мнимая частотная характеристика (МЧХ).
Комплексные функции простых цепей можно рассчитать непосредственно по закону Ома.
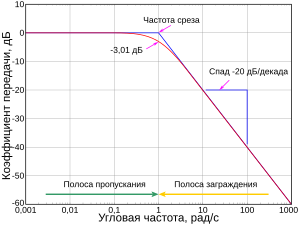
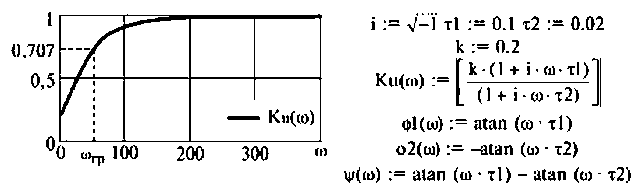
На рис.4.1 показаны АЧХ и ФЧХ, а на рис.4.2 — АФЧХ простейшей интегрирующей цепи (апериодического звена). По АЧХ определяют полосу пропускания
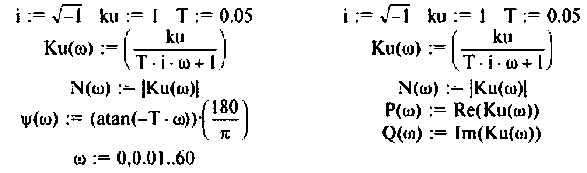
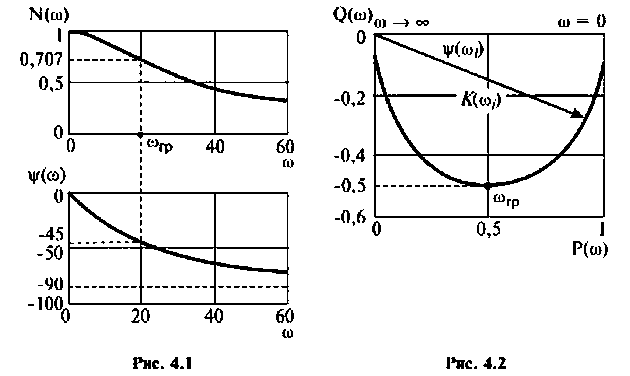
Полосой пропускания П называется диапазон частот, на границах которого мощность сигнала уменьшается в 2 раза, а амплитуда (действующее значение) напряжения (тока) — в 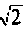 раз по сравнению с максимальными значениями.
раз по сравнению с максимальными значениями.
Полоса пропускания может измеряться в радианах в секунду 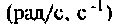 или в герцах (Гц).
или в герцах (Гц).
Например, для простой интегрирующей цепи полоса пропускания (см. рис. 4.1)
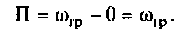
Для сложных цепей КФЦ рассчитывают по MKT или МУН. В табл. 4.1 приведены соотношения для расчета КФЦ, выраженные через определитель и алгебраические дополнения матрицы контурных сопротивлений и узловых проводимостей.
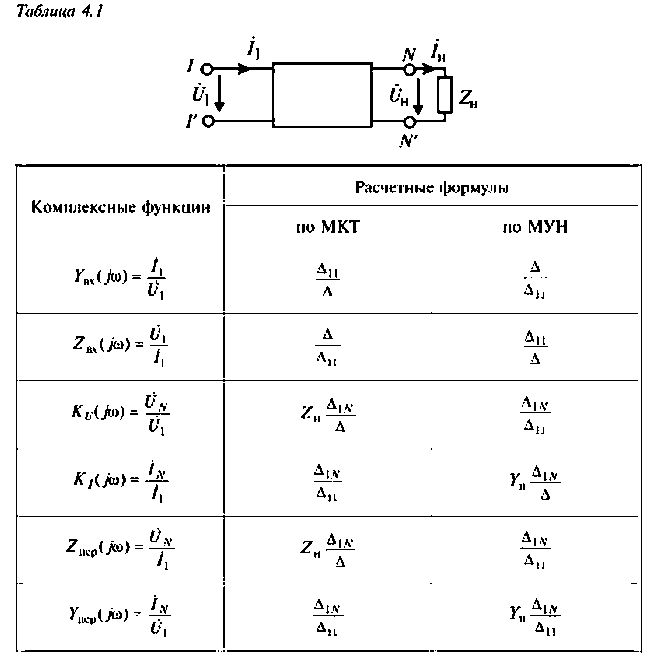
Частотные характеристики цепей с одним реактивным элементом
Примеры решения типовых задач:
Пример 4.2.1.
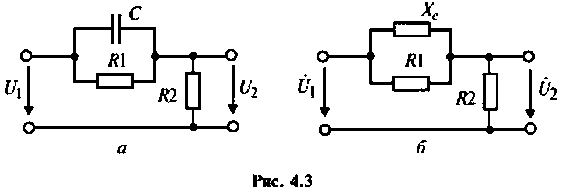
Определить комплексный коэффициент передачи по напряжению для дифференцирующего RC-контура (рис.4.3, а), рассчитать и построить графики АЧХ и ФЧХ.
Решение
1. Изобразим комплексную схему замещения цепи (рис. 4.3, б).
2. Определим комплексное напряжение на выходе цепи в виде
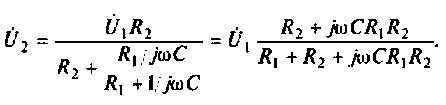
Преобразуем полученное выражение, вынеся зa скобки в числителе и знаменателе члены, не содержащие  . После преобразований получим
. После преобразований получим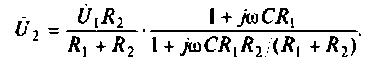
Следовательно.
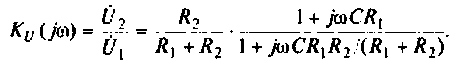
Введем обозначения:
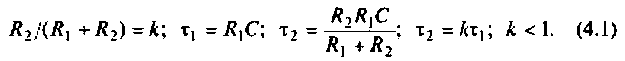
Величина 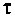 называется постоянной времени цепи и измеряется в секундах. Величина
называется постоянной времени цепи и измеряется в секундах. Величина 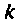 имеет смысл коэффициента усиления по напряжению на постоянном токе, т. е. на частоте
имеет смысл коэффициента усиления по напряжению на постоянном токе, т. е. на частоте 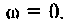
С учетом принятых обозначений
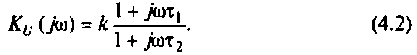
Для получения аналитических выражений АЧХ и ФЧХ запишем комплексную функцию в показательной форме.
Так как выражение (4.2) есть отношение двух полиномов, то удобно числитель и знаменатель записать отдельно в показательной форме, а затем разделить:
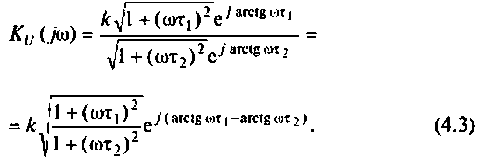
3. Из (4.3) запишем АЧХ и ФЧХ соответственно:
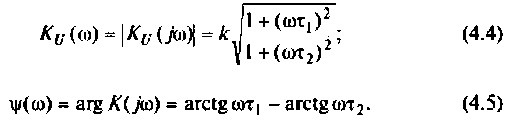
4. Построим график АЧХ и ФЧХ качественно по двум точкам. Для этого рассчитаем значения 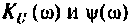 для крайних значений частот:
для крайних значений частот:
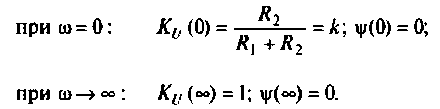
График АЧХ  (рис. 4.4, а) является кривой, монотонно возрастающей от значения
(рис. 4.4, а) является кривой, монотонно возрастающей от значения 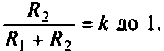
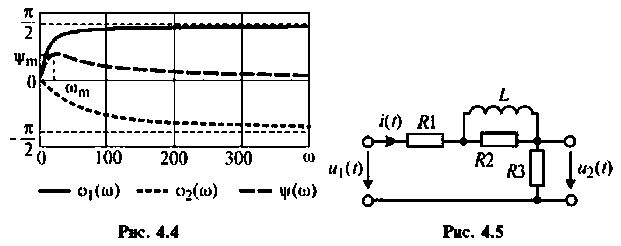
График функции ФЧХ  можно построить качественно как сумму двух графиков (рис. 4.4). Из рис. 4.4,б видно, что оба слагаемых монотонно увеличиваются: первое от нуля до +90° и вносит опережение по фазе. Второе до -90° и вносит отставание по фазе. Но первое слагаемое растет быстрее, так как
можно построить качественно как сумму двух графиков (рис. 4.4). Из рис. 4.4,б видно, что оба слагаемых монотонно увеличиваются: первое от нуля до +90° и вносит опережение по фазе. Второе до -90° и вносит отставание по фазе. Но первое слагаемое растет быстрее, так как 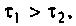 что следует из формулы (4.1). Поэтому функция
что следует из формулы (4.1). Поэтому функция 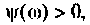 следовательно, дифференцирующий RС-контур вносит опережение по фазе.
следовательно, дифференцирующий RС-контур вносит опережение по фазе.
Исследуя функцию (4.5) на экстремум, можно показать, что она имеет максимум на частоте
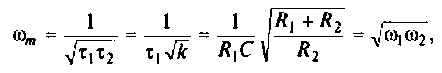
где 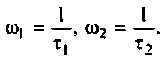
Подставляя 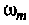 в (4.5), получим
в (4.5), получим
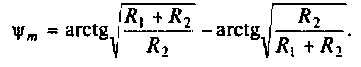
Графики АЧХ и ФЧХ изображены на рис. 4.4.
Пример 4.2.2.
Для электрической цепи, изображенной на рис. 4.5, определить АЧХ 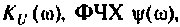 граничную частоту полосы пропускания. Рассчитать АЧХ, ФЧХ и построить графики, если параметры цепи:
граничную частоту полосы пропускания. Рассчитать АЧХ, ФЧХ и построить графики, если параметры цепи: 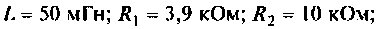
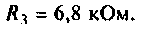
Решение
1. Найдем комплексную функцию К(; (/ш) но формуле делителя напряжения
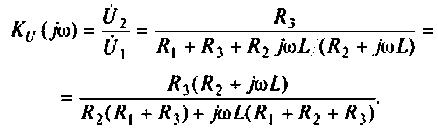
Преобразуем полученное выражение к виду
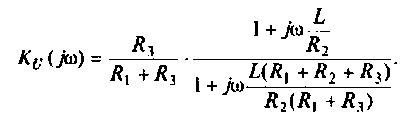
Обозначим:
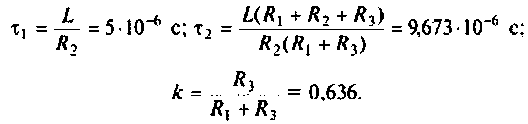
Следовательно,
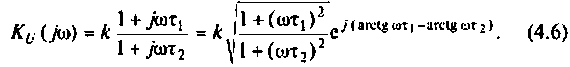
Отсюда: АЧХ
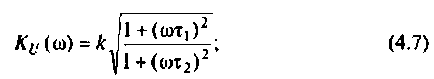
ФЧХ
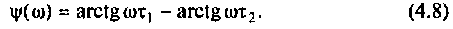
2. Рассчитаем граничную частоту. По определению
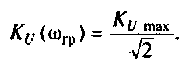
Из (4.7) найдем
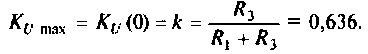
Следовательно,
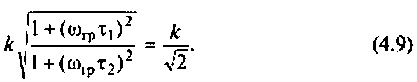
Из уравнения (4.9) получаем, что
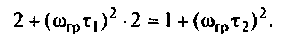
Отсюда 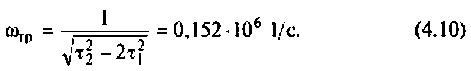
3. Построим график функций.
Вычислим значения (4.7) и (4.8) для частот с дискретностью 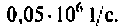
Графики и таблицы выполним в среде Mathcad (рис. 4.6).
Пример 4.2.3.
Определить комплексный коэффициент передачи интегрирующей цепи (рис. 4.7, а), используя метод контурных токов. Построить в среде Mathcad график АЧХ, определить полосу пропускания.
Параметры цепи: 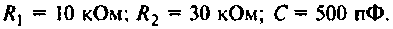
Решение
1. Представим цепь комплексной схемой замещения (рис. 4.7, б). Данная цепь имеет два независимых контура. Ток 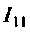 в первом контуре замыкается через источник, который на схеме не изображен. Направления контурных токов выбираем одинаковыми.
в первом контуре замыкается через источник, который на схеме не изображен. Направления контурных токов выбираем одинаковыми.
2.Составим матрицы контурных сопротивлений для двух независимых контуров
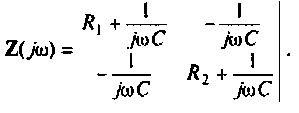
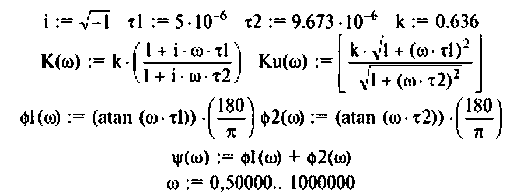
3.Определим комплексный коэффициент передачи, используя соотношение, приведенное в табл. 4.1.
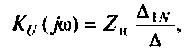
где сопротивление нагрузки равно 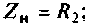
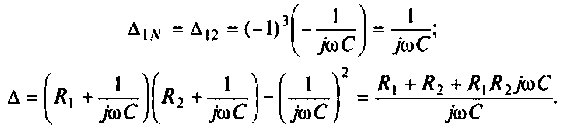
Подставляя найденные выражения, получаем
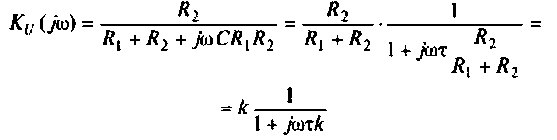
или 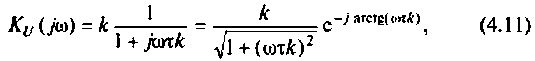
где 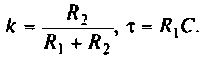
4. Рассчитаем 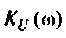 для крайних значений частоты
для крайних значений частоты 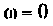 и
и 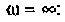
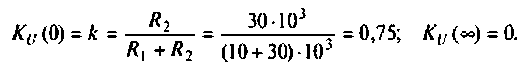
Объяснить полученные результаты можно, рассуждая так: на нулевой частоте (режим постоянного тока) сопротивление емкости бесконечно велико, ток в ней равен нулю, что эквивалентно разрыву этой ветви. При этом цепь становится резистивным делителем напряжения с передаточной функцией 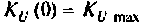
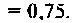 С ростом частоты емкостное сопротивление уменьшается. Если
С ростом частоты емкостное сопротивление уменьшается. Если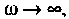 то
то 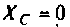 и шунтирует сопротивление
и шунтирует сопротивление  . При этом
. При этом
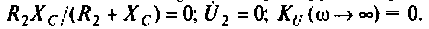 = 0.
= 0.
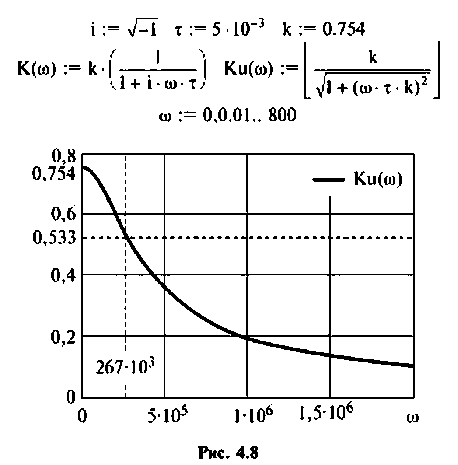
По полученным выражениям строим график АЧХ (рис. 4.8) и среде Mathcad.
5. Определяем полосу пропускания. По определению
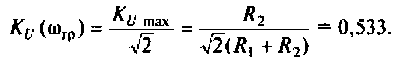
Поэтому из (4.11) имеем
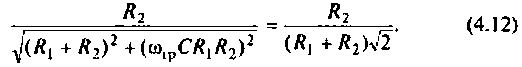
После преобразований уравнения (4.12) получаем
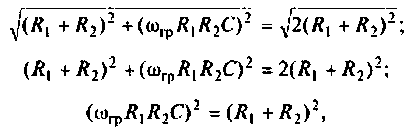
откуда
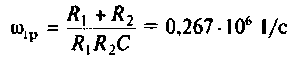
или
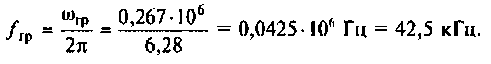
Следовательно, цепь имеет полосу пропускания
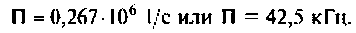
На рис. 4.8 указана граничная частота 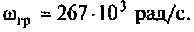
Данная цепь представляет собой фильтр нижних частот с полосой пропускания 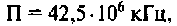 сигналы на частотах
сигналы на частотах  проходят с большим затуханием.
проходят с большим затуханием.
Пример 4.2.4.
Найти комплексную передаточную проводимость 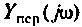 для цепи, изображенной на рис. 4.9, а методом узловых напряжений.
для цепи, изображенной на рис. 4.9, а методом узловых напряжений.
Параметры цепи: 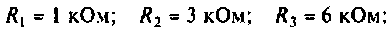
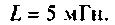
Определить АЧХ и ФЧХ, построить их графики в среде Mathcad.
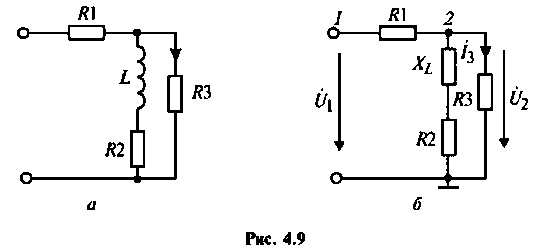
Решение
1. Изобразим комплексную схему замещения цепи (рис. 4.9, б). Схема имеет два независимых узла. В данном случае 
2. Составим матрицу узловых проводимостей. При определении собственной проводимости узлов необходимо помнить, что собственная проводимость ветви, состоящей из последовательно включенных пассивных элементов, находится из соотношения 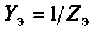 , где
, где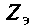 — эквивалентное сопротивление ветви. Как найти проводимость ветви с последовательно включенными
— эквивалентное сопротивление ветви. Как найти проводимость ветви с последовательно включенными 
В начале рассчитывают комплексное сопротивление этой ветви, 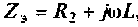 , а затем комплексную проводимость
, а затем комплексную проводимость
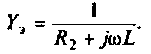
Составим матрицу проводимостей цепи 1 2
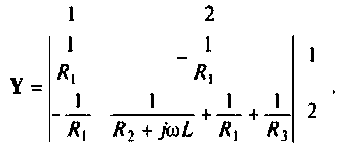
Как видим, общие проводимости узлов взяты со знаком минус, так как узловые напряжения  направлены одинаково, к базисному yзлy.
направлены одинаково, к базисному yзлy.
3.Определим комплексную передаточную проводимость по соотношению, приведенному в табл. 4.1
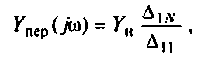
где 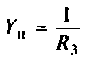 -комплексная проводимость ветви, по которой протекает ток
-комплексная проводимость ветви, по которой протекает ток 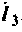 ,так как по определению
,так как по определению
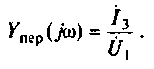
Найдем алгебраические дополнения:
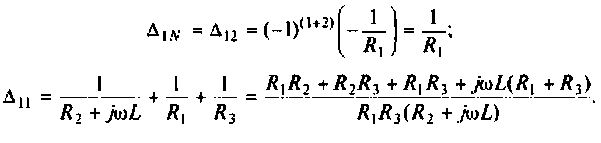
После подстановки найденных значений получим
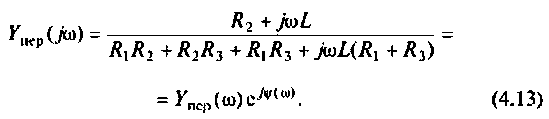
Для определении АЧХ и ФЧХ запишем выражения для модуля и аргумента 
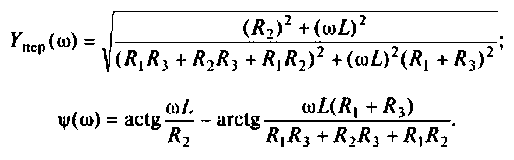
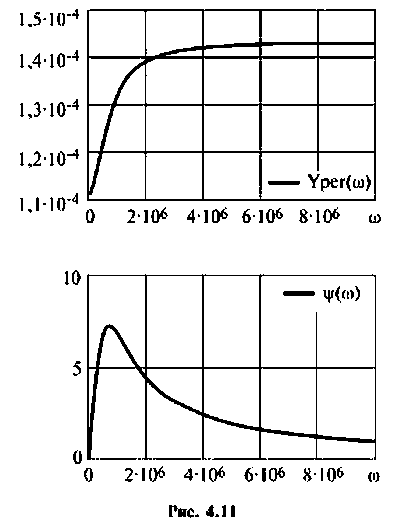
4. Рассчитаем значения 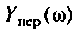 на частотах
на частотах 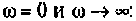
Примечание. Эти значения можно найти без вывода аналитического выражения для  Для этого достаточно воспользоваться эквивалентными схемами цепи на рассматриваемых частотах.
Для этого достаточно воспользоваться эквивалентными схемами цепи на рассматриваемых частотах.
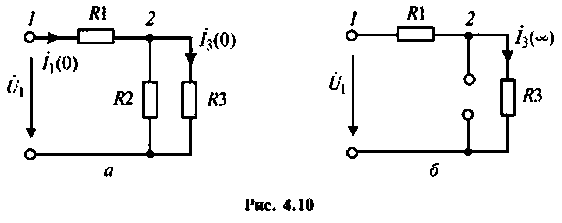
Учитывая, что 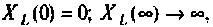 получим две схемы, показанные на рис. 4.10. а, б, соответственно.
получим две схемы, показанные на рис. 4.10. а, б, соответственно.
Для первой схемы:
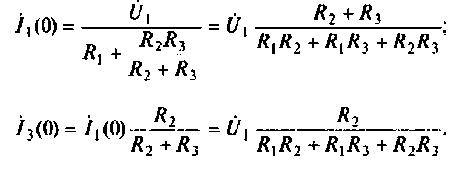
Следовательно,
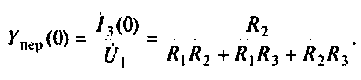
Аналогично для второй схемы получим
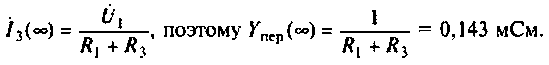
При расчете сложных схем такой прием можно применять для проверки правильности полученного аналитического выражения КФЦ.
Из (4.13) видно, что функция наметен монотонной, но для качественного построения графика АЧХ (рис. 4.11) необходимо воспользоваться ПЭВМ, например построить функцию в среде Mathcad.
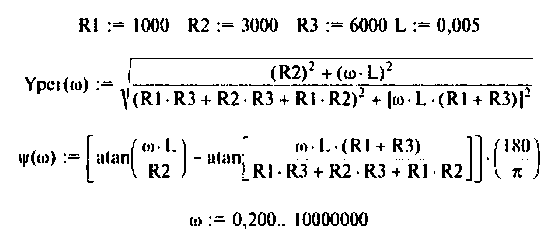
Пример 4.2.5.
Для интегрирующего RС-контура (рис.4.12,а) определить комплексный коэффициент передачи по напряжению, рассчитать АЧХ, ФЧХ, ВЧХ, МЧХ. Построить графики АЧХ, ФЧХ. АФЧХ, если
Решение
1. Составим комплексную схему замещения цепи (рис. 4.12, б).
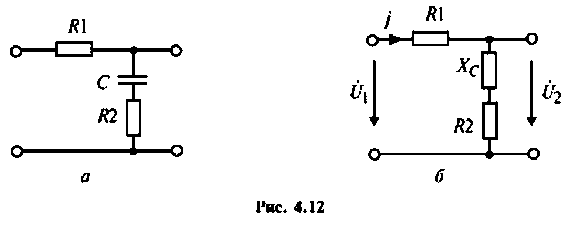
2. Определим  из соотношения
из соотношения  где
где
Следовательно.
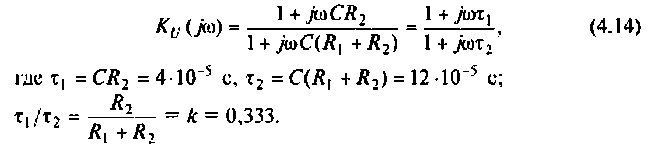
3. Для нахождения АЧХ и ФЧХ комплексную функцию 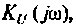 представленную в виде отношения двух полиномов мнимой частоты
представленную в виде отношения двух полиномов мнимой частоты 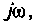 записывают в показательной форме
записывают в показательной форме
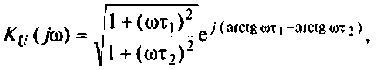
Найдем модуль (АЧХ) и аргумент (ФЧХ) комплексной функции;
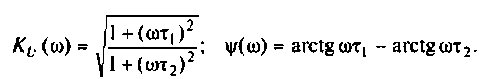
Для определения вещественной и мнимой частотных характеристик запишем КФЦ в алгебраической форме. Для этого умножим и разделим (4.14) на комплексно-сопряженный знаменатель:
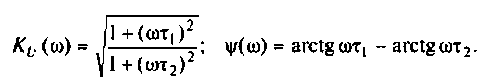
4. Для приближенного построения графиков АЧХ, ФЧХ. АФХ найдем значения  для трех значений частот:
для трех значений частот: 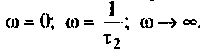 Результаты расчетов для удобства построения графиков сведем в табл. 4.2.
Результаты расчетов для удобства построения графиков сведем в табл. 4.2.

Для более точного и наглядного представления графиков воспользуемся ПЭВМ и математической средой Mathcad.
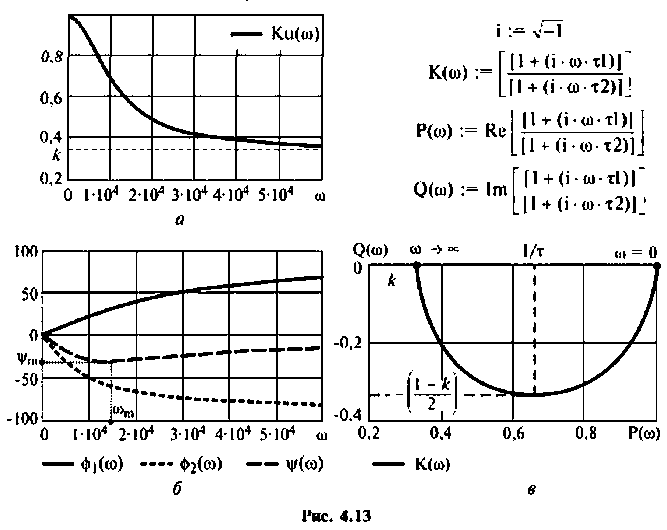
Графики характеристик приведены на рис. 4.13.
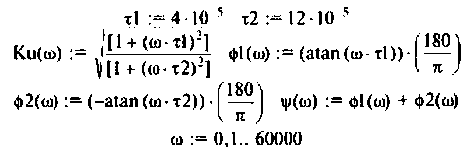
АЧХ представляет монотонно убывающую функцию (рис. 4.13, а).
ФЧХ принимает отрицательные значения, т.е. контур вносит фазовое отставание, а на частоте  ФЧХ имеет экстремум (рис.4.13, б). Найдем из соотношения
ФЧХ имеет экстремум (рис.4.13, б). Найдем из соотношения
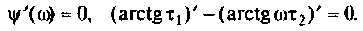
Взяв производную, получим
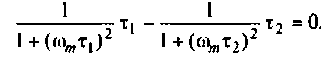
Решая полученное уравнение относительно  , найдем
, найдем
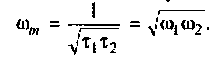
Подставляя  в выражение
в выражение 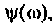 определим максимальное значение фазовой частотной характеристики.
определим максимальное значение фазовой частотной характеристики.
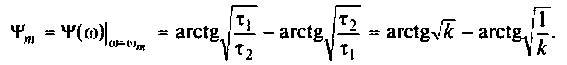
АФХ (рис. 4.13, в) представляет собой полуокружность, расположенную в 4-м квадрате. Центр окружности находится на оси  в точке с абсциссой, равной
в точке с абсциссой, равной
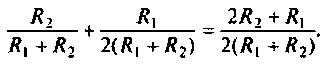
Радиус окружности нетрудно определить из соотношения:
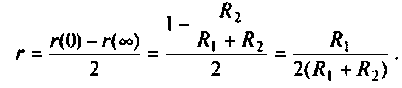
МЧХ:
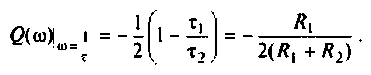
Отрицательное значение  свидетельствует о том, что
свидетельствует о том, что
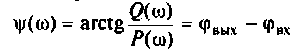 принимает отрицательное значения, т.е. интегрирующий контур вносит запаздывание по фазе.
принимает отрицательное значения, т.е. интегрирующий контур вносит запаздывание по фазе.
5. Проверка расчетов АЧХ. Воспользуемся эквивалентными схемами цепи для частот  (рис. 4.14).
(рис. 4.14).
На частоте  цепь разомкнута (рис. 4.14, а), поэтому
цепь разомкнута (рис. 4.14, а), поэтому
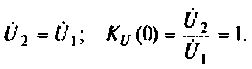
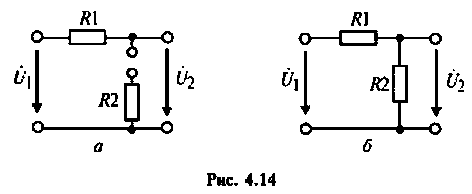
При  схема представляет собой резистивный делитель напряжения (рис. 4.14, б) с коэффициентом передачи
схема представляет собой резистивный делитель напряжения (рис. 4.14, б) с коэффициентом передачи
Подставляя эти значения частот в аналитическое выражение (4.14) для  получаем
получаем
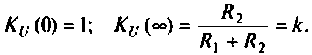
Следовательно, расчет АЧХ выполнен верно.
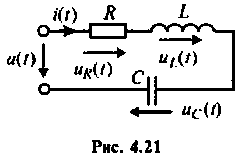
Частотные характеристики последовательного колебательного контура
Основные теоретические сведения:
В последовательном колебательном контуре (рис. 4.21) возникает резонанс напряжений, если выполняется условие
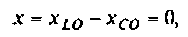
т. е. 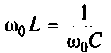
Резонансная частота
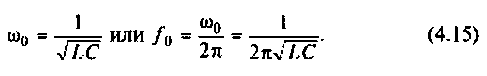
Волновое сопротивление контура 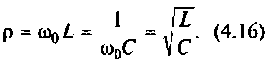
Сопротивление контура при резонансе 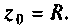
Собственная добротность контура 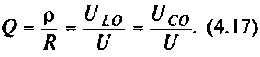
Добротность нагруженного контура 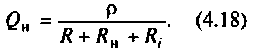
Затухание контура 
Абсолютная расстройка 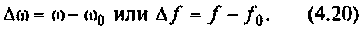
Относительная расстройка 
Обобщенная расстройка
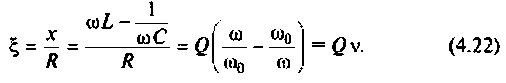
Фактор расстройки: 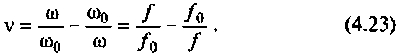
Абсолютная полоса пропускания (рис. 4.22)
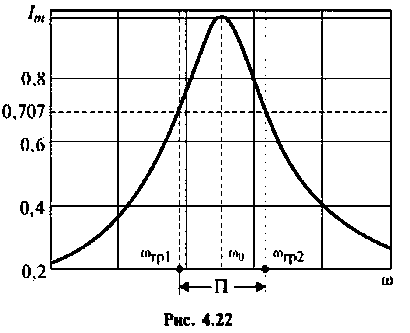
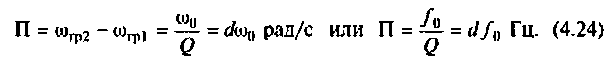
Относительная полоса пропускания

Для нагруженного контура:
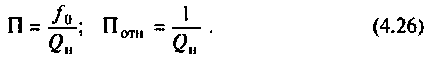
Комплексные коэффициенты передачи по напряжению:
на активном сопротивлении
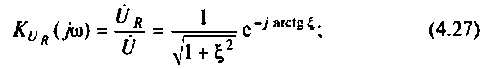
на индуктивности
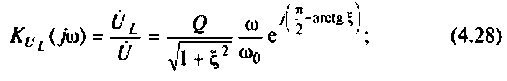
на емкости
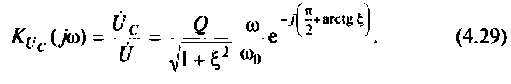
Примеры решения типовых задач:
Пример 4.3.1.
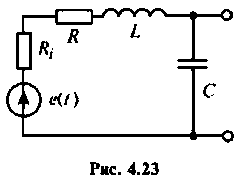
Последовательный колебательный контур (рис. 4.23) подключен к источнику напряжению. Контур настроен в резонанс.
Параметры цепи: 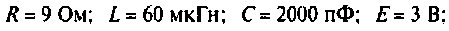
Определить резонансную частоту, волновое сопротивление. добротность и полосу пропускания, ток и напряжения на элементах контура.
Построить АЧХ и ФЧХ по напряжению на конденсаторе в среде Mathcad.
Решение
1. Определяем резонансную частоту контура
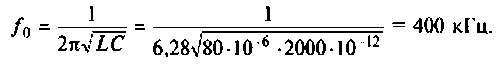
2. Находим волновое сопротивление контура
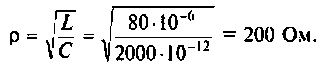
3. Вычисляем добротность нагруженного контура
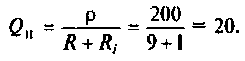
4. Определяем полосу пропускания
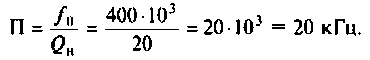
5. Рассчитываем ток и напряжения на элементах контура при резонансе
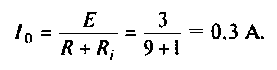
Напряжение на R равно
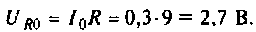
Напряжения на реактивных элементах
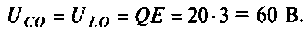
6. Рассчитаем АЧХ и ФЧХ комплексного коэффициента передачи напряжения с емкости.
Учитывая (4.22), из (4.29) получим:
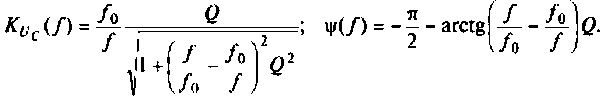
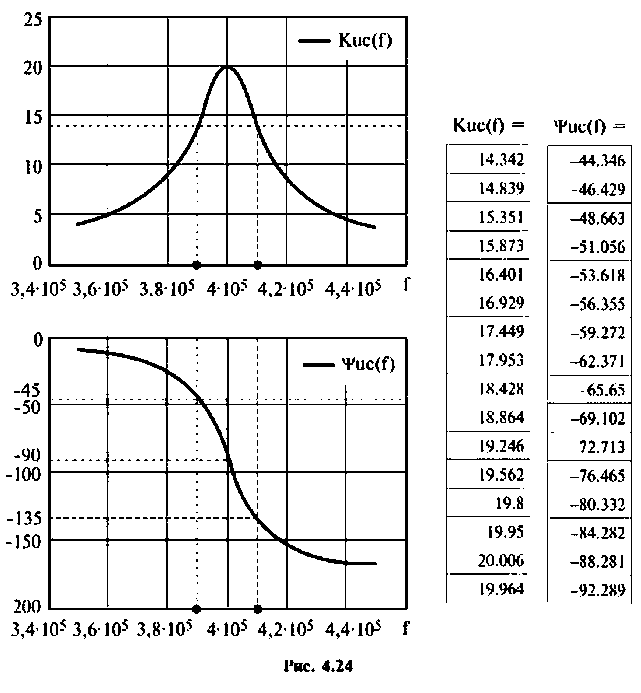
Для построения графиков АЧХ и ФЧХ, выполнения расчетов используем среду Mathcad. АЧХ, ФЧХ в виде графиков и таблиц приведены на рис. 4.24.
Следует заметить, что максимум А11Х достигается на частоте
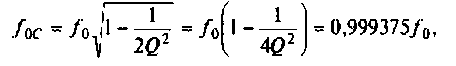
т.е. при 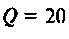 смещение максимума мало, тогда
смещение максимума мало, тогда 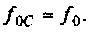
Задача 4.3.2.
К последовательному колебательному контуру (рис. 4.25) с параметрами  подключена нагрузка
подключена нагрузка 
Определить собственную добротность и добротность нагруженного контура, полосу пропускания нагруженного и ненагруженного контура.
Решение
1. Рассчитаем вторичные параметры ненагруженного контура:
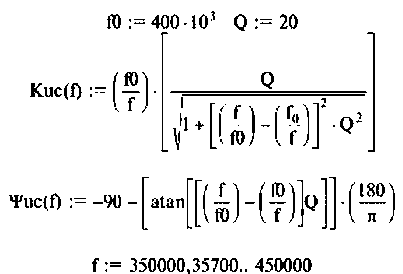
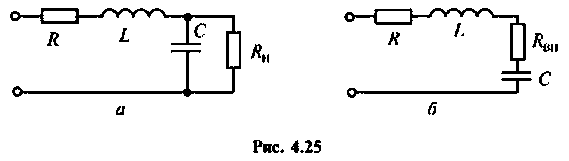
2.Определим вторичные параметры наруженного контура. Так как сопротивление нагрузки активное, причем 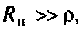 то согласно (4.15) и (4.16) резонансная частота и волновое сопротивление не изменяются.
то согласно (4.15) и (4.16) резонансная частота и волновое сопротивление не изменяются.
Для определения добротности рассчитаем сопротивление 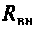 , вносимое в контур за счет нагрузки, и построим эквивалентную схему нагруженного контура (рис. 4.25, б). Так как
, вносимое в контур за счет нагрузки, и построим эквивалентную схему нагруженного контура (рис. 4.25, б). Так как 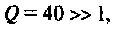 то
то
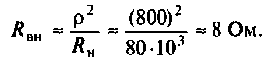
Следовательно,
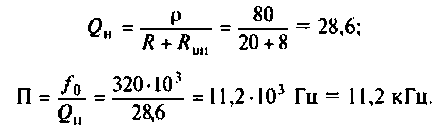
Вывод. Подключение нагрузки ухудшает добротность контура, что приводит к расширению полосы пропускания.
Пример 4.3.3.
На рис. 4.26, а изображена входная цепь приемника, а на рис. 4.26, б — ее эквивалентная схема. Известны входное сопротивление и входная емкость транзистора входного каскада УВЧ:  . На резонансной частоте антенна наводит в контуре ЭДС
. На резонансной частоте антенна наводит в контуре ЭДС 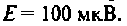 Емкость конденсатора
Емкость конденсатора 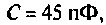 катушка индуктивности имеет
катушка индуктивности имеет 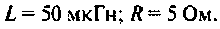
Определить абсолютную полосу пропускания и ток в контуре на резонансной частоте.
Решение
1. Определяем эквивалентную емкость контура
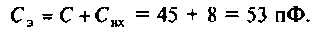
2. Рассчитываем резонансную частоту контура
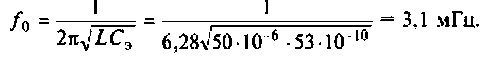
3. Находим волновое сопротивление и сопротивление, вносимое в контур за счет транзистора усилителя (рис. 4.26, в):
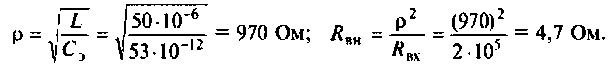
4. Определяем добротность нагруженного контура
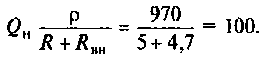
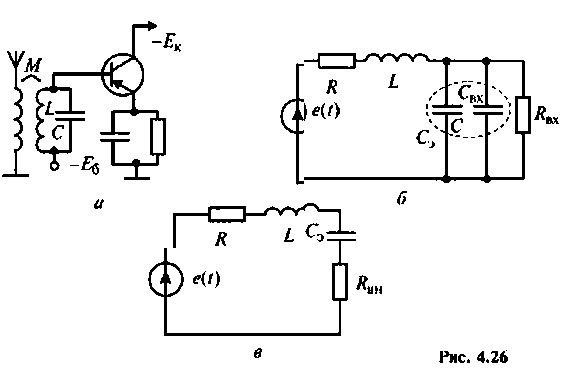
5. Рассчитаем абсолютную полосу пропускания нагруженного контура
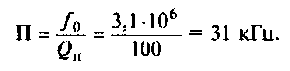
6. Находим ток в контуре
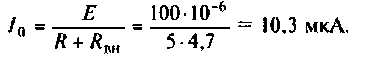
Пример 4.3.4.
Рассчитать емкость последовательного колебательного контура, если резонансная частота контура 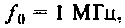 полоса пропускания
полоса пропускания 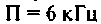 при сопротивлении потерь 0,5 Ом.
при сопротивлении потерь 0,5 Ом.
Построить АЧХ и ФЧХ комплексного коэффициента передачи напряжения с индуктивности в среде Mаthcad.
Решение
1. Определим требуемую добротность контура
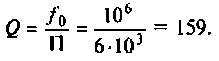
2. Рассчитаем емкость конденсатора. Из формулы 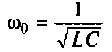 найдем
найдем
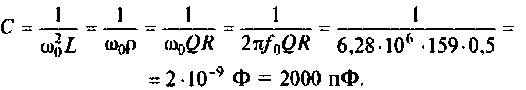
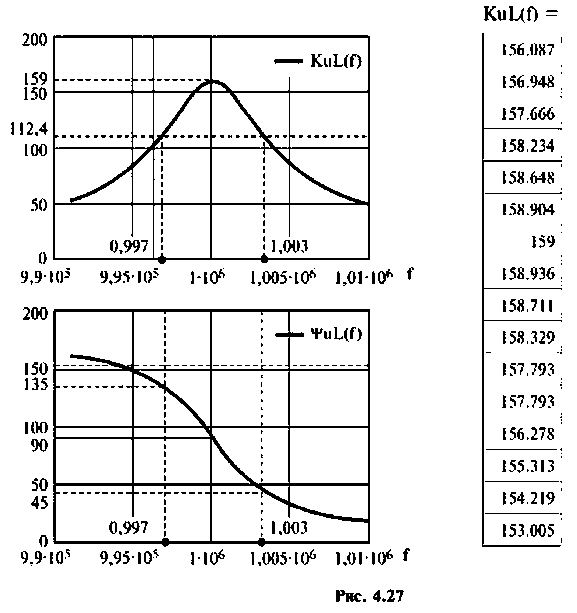
3. Рассчитаем АЧХ и ФЧХ.
Воспользуемся комплексным коэффициентом передачи напряжения с индуктивности по формуле (4.28). Учитывая 4.22), запишем:
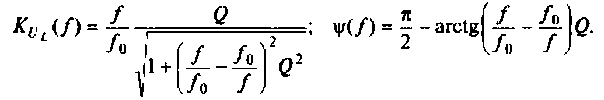
Вычислим значения функций на частотах:
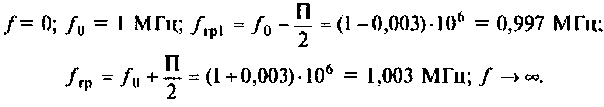
Определим частоту, при которой АЧХ имеет максимум
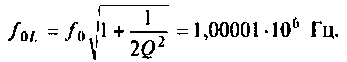
Смещением частоты  можно пренебречь.
можно пренебречь.
Результаты расчетов АЧХ и ФЧХ б графическом и табличном видах приведены на рис. 4.27.
Частотные характеристики параллельного колебательного контура
Основные теоретические сведения:
Параллельный колебательный контур образуется путем параллельного соединения катушки индуктивности и конденсатора. Оба элемента, кроме основного эффекта (запасания энергии), имеют потери энергии. В расчетной схеме (рис. 4.29, а) тепловые потери в элементах учтены включением условных сопротивлений 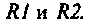
где резонансная частота колебаний
Для реального контура  поэтому при расчете можно полагать, что
поэтому при расчете можно полагать, что
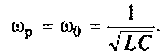
При резонансе сопротивление контура является активным, поэтому ток 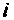 в цепи и напряжение
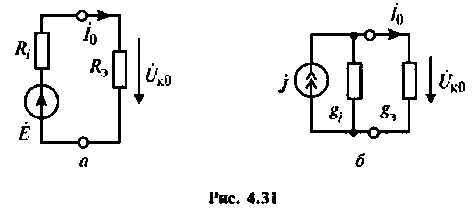
в цепи и напряжение 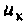 в контуре синфазны. Эквивалентные схемы цепи в режиме резонанса токов показаны на рис. 4.31, а, б.
в контуре синфазны. Эквивалентные схемы цепи в режиме резонанса токов показаны на рис. 4.31, а, б.
Сопротивление параллельного колебательного контура при резонансе максимально и равно (без учета внешней цепи)
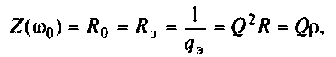
где 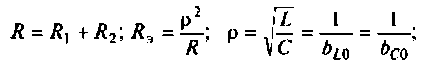
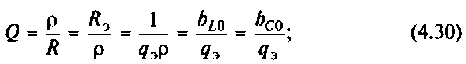
Добротность  нагруженного контура меньше собственной добротности
нагруженного контура меньше собственной добротности  Ее можно выразить через сопротивления элементов цепи
Ее можно выразить через сопротивления элементов цепи
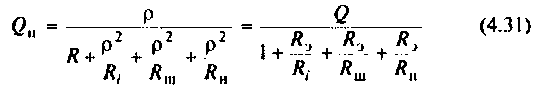
или через их проводимости
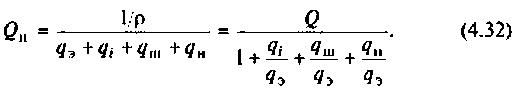
Важными параметрами цепи при резонансе являются токи в ветвях и напряжение на контуре. Ток в обшей ветви (ток источника) при резонансе минимален и равен (см. рис. 4.31)
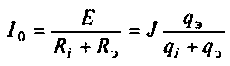
При этом напряжение на контуре максимально и равно
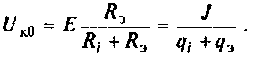
Токи в индуктивности и в емкости при резонансе равны по значению и противоположны по направлению. Они образуют замкнутый ток в контуре, равный
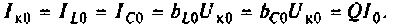
Частотные свойства параллельного колебательного контура обычно оценивают по нормированной АЧХ
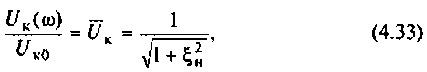
где 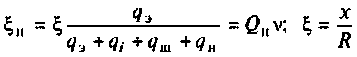 -обобщенная расстройка контура без учета внешних цепей;
-обобщенная расстройка контура без учета внешних цепей; 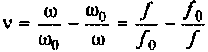 — фактор расстройки.
— фактор расстройки.
Параллельный контур, показанный на рис. 4.29, имеет по одной реактивности в ветвях. Такой контур называется простым или контуром I вида. Для уменьшения шунтирующего действия внешних цепей часто применяют сложные параллельные контуры.
На рис. 4.32, а, б, в показаны контуры II, (III и IV) видов, соответственно.
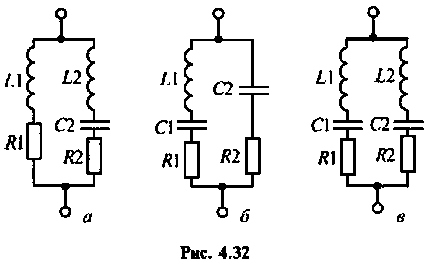
Главной особенностью этих контуров является то, что их резонансное сопротивление меньше резонансного сопротивления простого контура с такими же параметрами.
Сопротивление контуров (рис.4.32) при резонансе рассчитывается по формулам, соответственно:
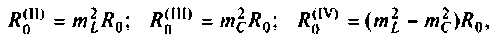
где 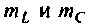 — коэффициенты включения:
— коэффициенты включения:
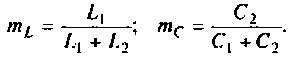
Примеры решения типовых задач:
Пример 4.4.1.
Параллельный контур (см. рис. 4.29, а) подключен к источнику с параметрами 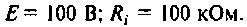 Контур настроен в резонанс на длину волны, равную 1000 м.
Контур настроен в резонанс на длину волны, равную 1000 м.
Параметры катушки индуктивности: 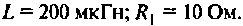
Определить действующие значения тока в контуре, тока на входе цепи и напряжения на контуре при резонансе, абсолютную и относительную полосы пропускания контура, добавочное сопротивление необходимое для расширения полосы пропускания в 2 раза.
Решение
1. Определим резонансную частоту колебания
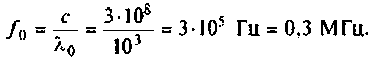
2. Рассчитаем волновое сопротивление
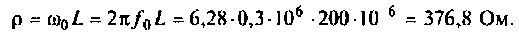
3. Определим сопротивление контура при резонансе
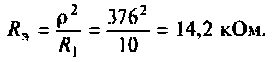
4. Найдем действующее значение тока на входе контура (см. рис. 4.31, а) при резонансе
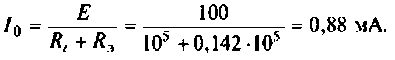
5. Определим соответственную добротность контура
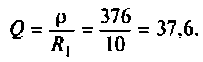
6. Найдем ток в контуре и напряжение на нем:
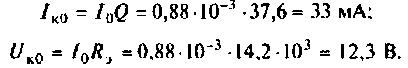
7. Определим добротность нагруженного контура
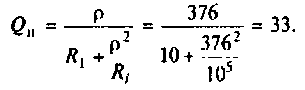
8. Рассчитаем абсолютную и относительную полосы пропускания:
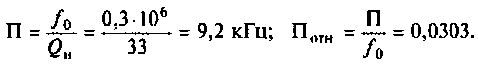
9. Определяем добавочное cопротивление 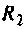 из (4.31)
из (4.31)
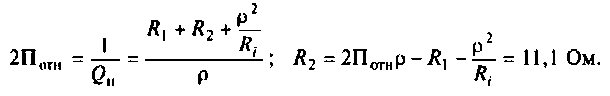
Пример 4.4.2.
Рассчитать полосу пропускания колебательного контура (см. рис. 4.30, а).
Дано: 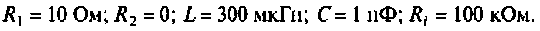
Определить сопротивление  шунта, необходимого для расширения полосы пропускания до 10 кГц.
шунта, необходимого для расширения полосы пропускания до 10 кГц.
Решение
1. Рассчитаем волновое сопротивление и резонансную частоту контура:
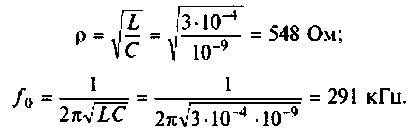
2.Рассчитаем добротность цепи без шунта. Воспользуемся трехветвевой эквивалентной схемой цепи и соотношением (4.32). Найдем проводимость элементов схемы:
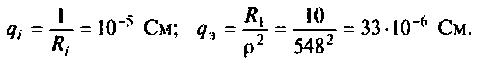
Тогда
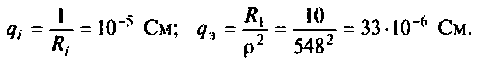
3. Определим полосу пропускания
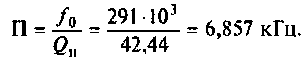
4. Найдем сопротивление шунта, необходимою для расширения полосы до 10 кГц,
В этом случае добротность цепи должна быть равна
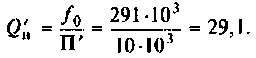
Тогда из (4.32) получаем
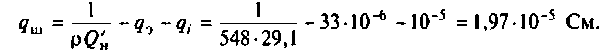
Следовательно, сопротивление шунта должно быть равно
Пример 4.4.3.
Параллельный колебательный контур с параметрами: 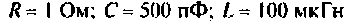 подключен к источнику
подключен к источнику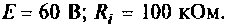
Определить собственную добротность контура, добротность нагруженного контура, абсолютную полосу пропускания и граничные частоты полосы пропускания. Построить резонансную кривую по напряжению на ЭВМ.
Решение
1. Определим волновое сопротивление контура
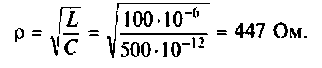
2. Рассчитаем собственную добротность контура
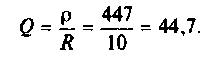
3. Найдем сопротивление контура при резонансе
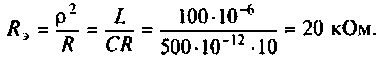
4. Определим добротность нагруженного контура по формуле (4.31)
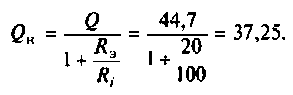
5. Рассчитаем резонансную частоту
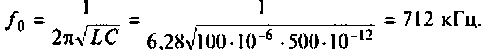
6. Найдем полосу пропускания
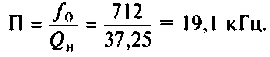
7. Определим граничные частоты полосы пропускания:
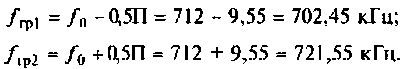
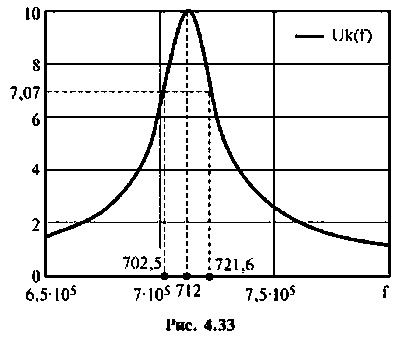
8. Построим резонансную характеристику контура но напряжению. Из выражения (4.33) запишем
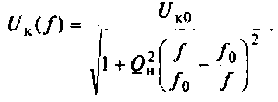
Напряжение па контуре при резонансе
Для построения резонансной характеристики задаемся характерными значениями частот:  Результаты расчетов в графическом виде представлены на рис. 4.33.
Результаты расчетов в графическом виде представлены на рис. 4.33.
Пример 4.4.4.
Определить резонансную частоту, эквивалентное сопротивление при резонансе и добротность сложного контура (рис. 4.32, а), подключенного к источнику напряжения.
Дано: 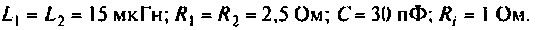
Решение
1. Определим резонансную частоту и сопротивление параллельного контура при резонансе:
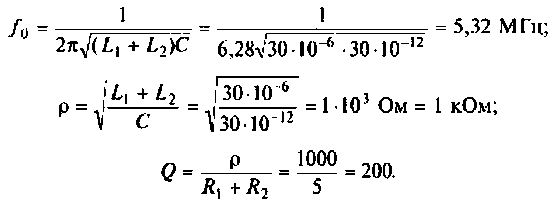
Сопротивление контура при резонансе
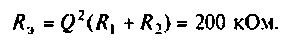
2. Рассчитаем эквивалентное сопротивление сложного контура II вида
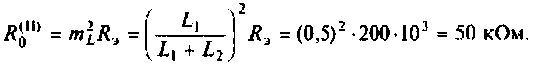
3. Найдем добротность нагруженного контура II вида
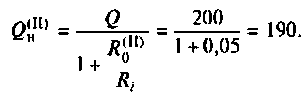
Сравним значения 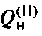 с добротностью простого нагруженного контура
с добротностью простого нагруженного контура
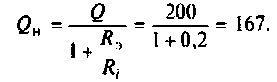
Вывод. За счет неполного включения индуктивности 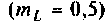 уменьшилось шунтирующее действие источника. Поэтому добротность сложного контура больше, чем простого с теми же параметрами элементов.
уменьшилось шунтирующее действие источника. Поэтому добротность сложного контура больше, чем простого с теми же параметрами элементов.
Частотные характеристики связанных колебательных контуров
Основные теоретические сведения:
С целью повышения коэффициента прямоугольности АЧХ контуров применяют связанные контуры последовательного и параллельного питания (рис. 4.37, а, б).
Частотные характеристики связанных контуров рассмотрим на примере системы из двух контуров.
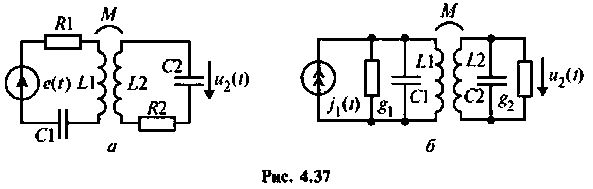
Эквивалентные схемы связанных контуров
Во всех случаях систему связанных контуров можно представить в виде Т- или П-образной эквивалентной схемы (рис. 4.38).
Количественной характеристикой связи является сопротивление связи 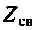 в Т-образной эквивалентной схеме (рис. 4.38,а) или проводимость связи
в Т-образной эквивалентной схеме (рис. 4.38,а) или проводимость связи 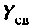 в П-образной эквивалентной схеме (рис. 4.38, б).
в П-образной эквивалентной схеме (рис. 4.38, б).
Удобным параметром для оценки связи является коэффициент связи
В случае реактивной связи для Т-образной схемы
Для П-образной схемы
где — сопротивление (проводимость) связи;
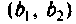 — сопротивления (проводимости) контуров, однотипные элементу связи. Для анализа связанных контуров удобно применять схемы, приведенные к первичному (рис. 4.39, а) или ко вторичному (рис. 4.39, б) контуру.
— сопротивления (проводимости) контуров, однотипные элементу связи. Для анализа связанных контуров удобно применять схемы, приведенные к первичному (рис. 4.39, а) или ко вторичному (рис. 4.39, б) контуру.
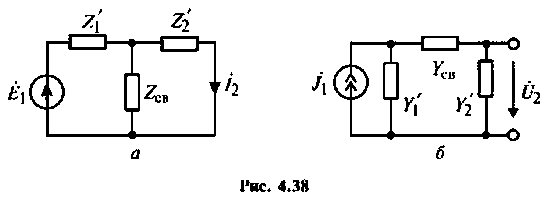
Для этого используют понятия вносимого сопротивления  и вносимой проводимости
и вносимой проводимости 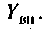 Эти схемы представляют собой одиночные последовательные (параллельные) контуры с параметрами:
Эти схемы представляют собой одиночные последовательные (параллельные) контуры с параметрами:
Резонансы в связанных контурах:
При настройке контуров в резонанс добиваются максимального тока (напряжения) во вторичном контуре.
Настройка связанных контуров может производиться различными способами, поэтому различают шесть резонансов. В табл. 4.3, 4.4 приведены виды и условия резонансов, способы настройки и соотношения для токов (напряжений) в связанных контурах последовательного (параллельного) питания.


Резонансные характеристики связанных контуров:
Для двух неидентичных связанных контуров: последовательного питания
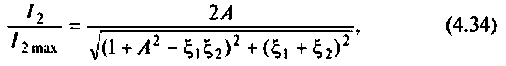
где 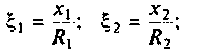
параллельного питания:
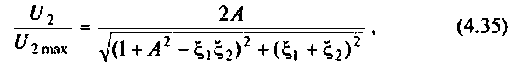
где 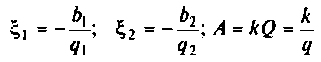 — параметр связи.
— параметр связи.
Если контуры идентичны, то обобщенная расстройка 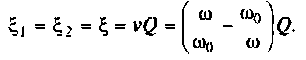
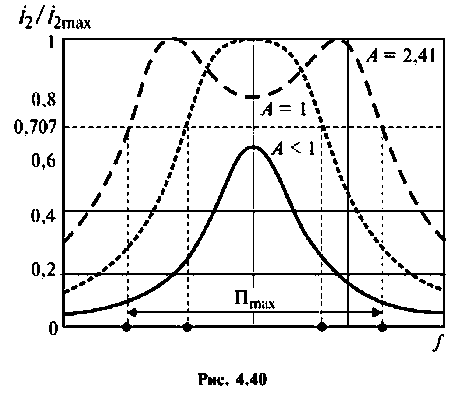
На рис. 4.40 приведены резонансные характеристики при различных факторах связи.
Относительная полоса пропускания:
а) связь слабая 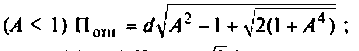
б) связь критическая 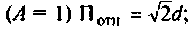
в) связь сильная 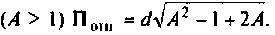
При 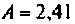 достигается максимально возможная полоса пропускания
достигается максимально возможная полоса пропускания 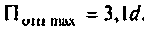
Примеры решения типовых задач:
Пример 4.5.1.
В системе двух индуктивно связанных контуров (см. рис.4.37,а) известны следующие параметры: коэффициент связи
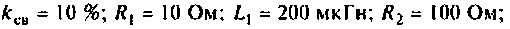
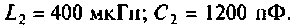
Определить емкость 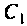 при которой в системе наступает первый частный резонанс, если частота источника равна 500 кГц.
при которой в системе наступает первый частный резонанс, если частота источника равна 500 кГц.
Решение
Емкость конденсатора 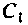 определим но реактивному сопротивлению первого контура:
определим но реактивному сопротивлению первого контура:
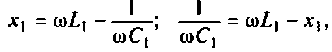
отсюда
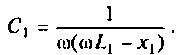
Определим реактивное сопротивление 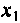 , первого контура из условия первого частного резонанса (см. табл. 4.3)
, первого контура из условия первого частного резонанса (см. табл. 4.3)
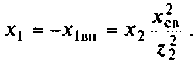
Peaктивное сопротивление второго контура
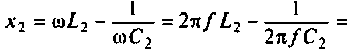
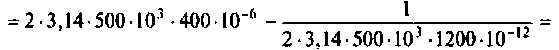
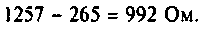
Рассчитаем полное сопротивление второго контура
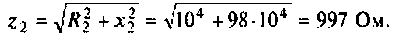
Определим сопротивление связи контуров
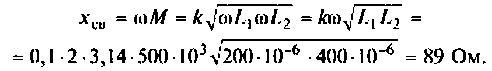
Следовательно
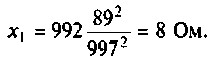
Находим емкость первого контура
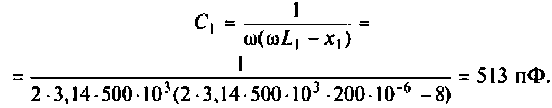
Пример 4.5.2.
Рассчитать емкости связанных контуров (см. рис. 4.37,а) и оптимальное сопротивление связи, если система настроена и полный резонанс. Определить токи, мощности в контурах при этом режиме, а также КПД системы.
Дано: 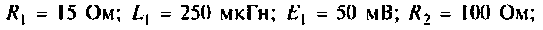
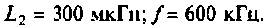
Решение
1. Определим емкость конденсатора 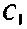 , полагая, что
, полагая, что
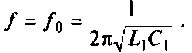
Отсюда
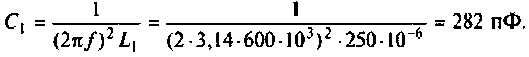
2. Сопротивление оптимальной связи при полном резонансе
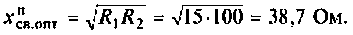
3. Рассчитаем токи в первом и втором контурах при полном резонансе
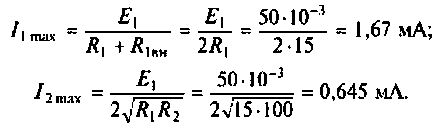
4. Определим активные мощности в первом и втором контурах и КПД связанных контуров:
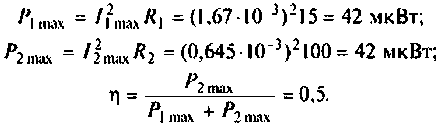
Пример 4.5.3.
На рис. 4.37, а показана система из двух идентичных связанных контуров с параметрами: 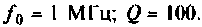 Рассчитать полосы пропускания одиночного контура и связанных контуров при различной связи:
Рассчитать полосы пропускания одиночного контура и связанных контуров при различной связи: 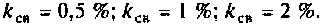
Решение
1. Определим полосу пропускания одиночного контура
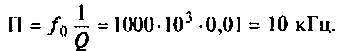
2. Рассчитаем полосу пропускания системы связанных контуров:
1) определим параметр связи для 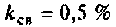
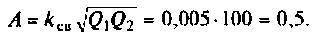
Таким образом при 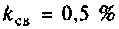 связь меньше критической
связь меньше критической 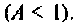 При этом относительная полоса пропускания
При этом относительная полоса пропускания
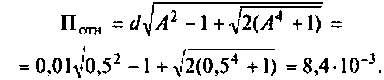
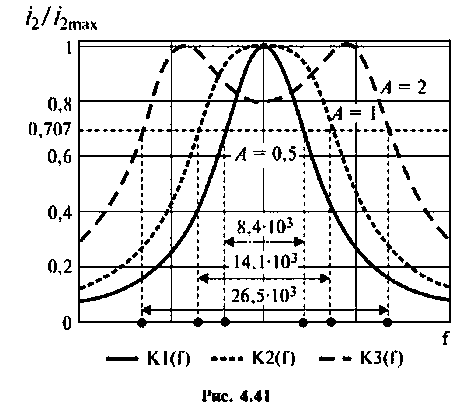
Абсолютная полоса пропускания (рис. 4.41, резонансная кривая А = 0,5)
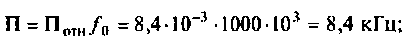
2) при 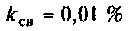 параметр связи
параметр связи 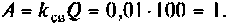 Таким образом, коэффициент связи является оптимальным, а связь критическая, система настроена в полный резонанс. Полоса пропускания в этом случае
Таким образом, коэффициент связи является оптимальным, а связь критическая, система настроена в полный резонанс. Полоса пропускания в этом случае
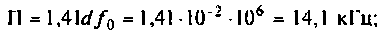
3) если 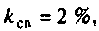 то параметр связи
то параметр связи 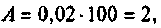 следовательно, связь больше критической.
следовательно, связь больше критической.
Рассчитаем полосу пропускания для этого случая.
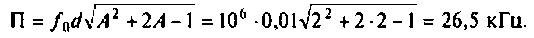
Вид резонансных кривых по току и полоса пропускания для критической и сильной связи показаны на рис. 4.41, кривые А = 1 и А = 2.

Пример 4.5.4.
Антенный контур (см. рис. 4.37,б) индуктивно связан с входным контуром усилителя высокой частоты. Оба контура настроены в резонанс на частоту 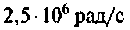 принимаемого сигнала. В антенном контуре наводится
принимаемого сигнала. В антенном контуре наводится 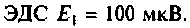
Дано: 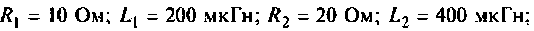
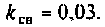
Входное сопротивление УВЧ считать бесконечно большим.
Определить емкости и добротности контуров, их взаимную индуктивность, а также ток и напряжение на емкости во вторичном контуре.
Решение
1.Емкости контуров определим из формулы резонансной частоты. Емкость конденсатора первого контура
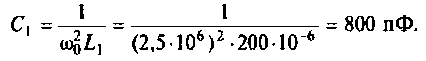
Емкость конденсатора второго контура
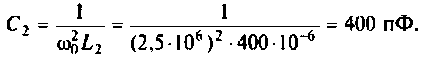
2. Рассчитаем волновое сопротивление контуров:
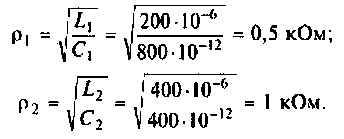
3. Рассчитаем добротности контуров и параметр связи:
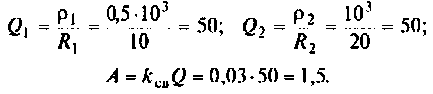
4. Определим взаимную индуктивность двух связанных контуров
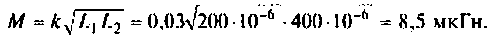
5. Рассчитаем ток во вторичном контуре. Известно (см. табл. 4.3), что при полном резонансе 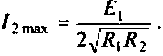
Тогда, учитывая, что контуры настроены в резонанс, то из (4.34) получаем
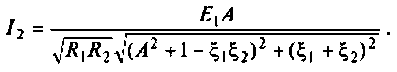
Оба контура по условию настроены в резонанс, поэтому расстройки равны нулю:
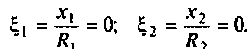
С учетом этого рассчитаем ток во втором контуре
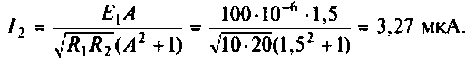
6. Найдем напряжение на конденсаторе вторичного контура
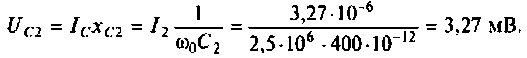
Пример 4.5.5.
На рис. 4.42 приведена схема одного каскада УПЧ радиоприемника, в котором избирательность обеспечивается двумя связанными контурами с емкостной связью. Оба контура настроены в резонанс на промежуточную частоту 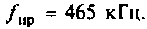
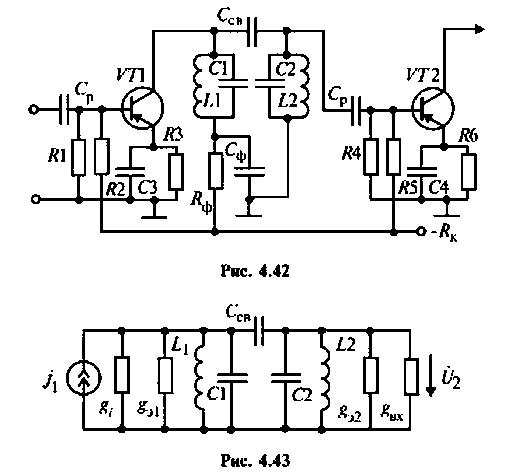
Эквивалентная схема этого каскада (рис. 4.43) имеет следующие параметры: 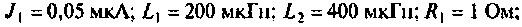
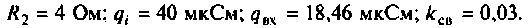
Определить емкости и добротности контуров, емкость связи, напряжение на емкости во вторичном контуре, а также полосу пропускания каскада УПЧ.
Решение
1. Из формулы резонансной частоты найдем емкость первого контура. С учетом влияния выходной емкости транзистора 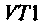 и емкости монтажа получаем
и емкости монтажа получаем
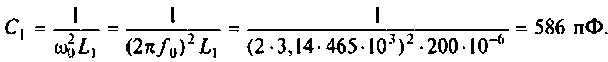
Емкость второго контура с учетом влияния входной емкости транзистора 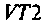 и емкости монтажа
и емкости монтажа
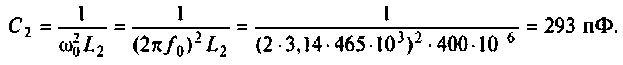
2. Определим емкость связи
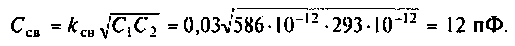
3. Рассчитаем добротности нагруженных контуров при отсутствии связи между ними. Для расчета воспользуемся формулой (4.31)
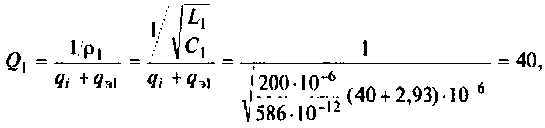
где
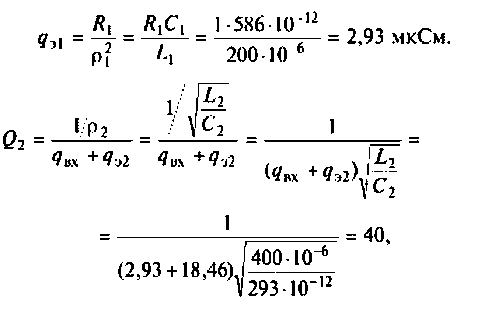
где
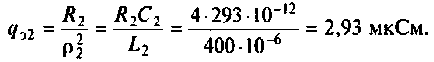
4. Рассчитаем параметр связи 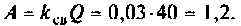
5. Рассчитаем напряжение на втором контуре. Известно (см. табл. 4.4), что при полном резонансе
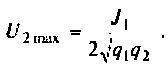
Тогда, учитывая, что контуры настроены в резонанс 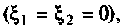 из (4.35) получаем
из (4.35) получаем
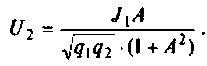
Найдем проводимость контуров
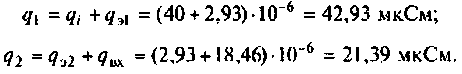
Тогда
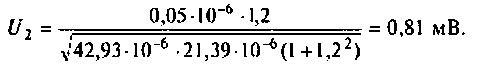
6. Рассчитаем полосу пропускания каскадов УПЧ. учитывая, что А = 1,2.
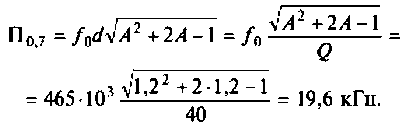
Частотные методы расчета и построения переходных и установившихся процессов в электрических цепях
Основные теоретические сведения:
Зная частотную характеристику электрической цепи 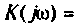
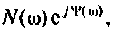 можно определить ее выходную величину при подаче на вход синусоидального (гармонического) сигнала. Действительно, если на вход цепи подано синусоидальное напряжение комплексное изображение которого
можно определить ее выходную величину при подаче на вход синусоидального (гармонического) сигнала. Действительно, если на вход цепи подано синусоидальное напряжение комплексное изображение которого 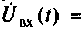
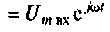 то в установившемся режиме комплексное изображение выходного напряжения
то в установившемся режиме комплексное изображение выходного напряжения
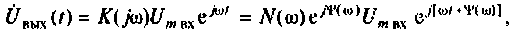
где 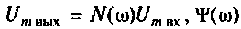 амплитуда и сдвиг по фазе выходных колебаний соответственно.
амплитуда и сдвиг по фазе выходных колебаний соответственно.
С помощью частотной характеристики электрической цели можно не только определить выходную величину цепи в установившемся режиме при гармоническом входном воздействии, но и найти реакцию цепи в переходном процессе на произвольное воздействие  . Действительно, представляя это воздействие в зависимости от того, является оно периодической или непериодической функцией, в виде ряда или интеграла Фурье, т.е. в виде бесконечной суммы гармонических колебаний. По частотной характеристике можно определить реакцию электрической цепи на каждое из этих элементарных колебаний, а затем, просуммировав все реакции, найти результирующую реакцию в виде суммы или интеграла [4].
. Действительно, представляя это воздействие в зависимости от того, является оно периодической или непериодической функцией, в виде ряда или интеграла Фурье, т.е. в виде бесконечной суммы гармонических колебаний. По частотной характеристике можно определить реакцию электрической цепи на каждое из этих элементарных колебаний, а затем, просуммировав все реакции, найти результирующую реакцию в виде суммы или интеграла [4].
Найдем реакцию цепи на единичную ступенчатую функцию (т.е. найдем переходную функцию цепи), используя ее частотную характеристику. Как известно, интеграл Фурье для единичной ступенчатой функции имеет вид
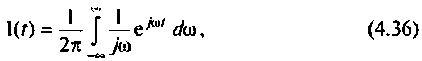
т.е. единичная ступенчатая функция может быть представлена как бесконечная сумма элементарных колебаний вида 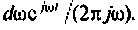
Каждому из этих колебаний соответствует выходное колебание 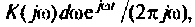 а реакция системы на единичную ступенчатую функцию выражается интегралом
а реакция системы на единичную ступенчатую функцию выражается интегралом
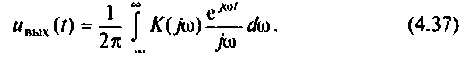
Представляя 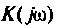 в алгебраической форме
в алгебраической форме 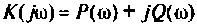 и преобразуя выражение (4.37), получаем следующую формулу для переходной функции |4, 6|:
и преобразуя выражение (4.37), получаем следующую формулу для переходной функции |4, 6|:
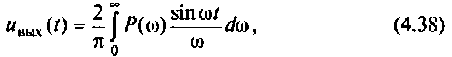
где 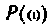 — вещественная частотная характеристика (ВЧХ) КФ электрической цепи. Полученное выражение связывает ВЧХ КПФ цепи с ее переходной функцией. Таким образом, при частотном методе анализа косвенной характеристикой переходной функции является вещественная частотная характеристика КФ электрической цепи.
— вещественная частотная характеристика (ВЧХ) КФ электрической цепи. Полученное выражение связывает ВЧХ КПФ цепи с ее переходной функцией. Таким образом, при частотном методе анализа косвенной характеристикой переходной функции является вещественная частотная характеристика КФ электрической цепи.
Построение переходной функции с помощью вещественной частотной характеристики методами численного интегрирования:
Выражение (4.38) позволяет вычислить переходную функцию ЭЦ и определить качество переходного процесса. Однако интегрирование этого выражения аналитическими методами — задача весьма трудоемкая, а чаще всего просто практически невыполнимая. С применением современных ЭВМ и методов численного интегрирования (метод прямоугольников, трапеций, метод Симпсона и др.) эта задача существенно упрощается, ее решение сводится к составлению программы для ПЭВМ. В инженерной практике интегрирование достаточно осуществлять в области существенных частот от 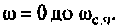 В области частот
В области частот  влияние ВЧХ
влияние ВЧХ 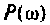 на переходную функцию (4.38) мало и им можно пренебречь. В dtom случае используют модифицированное выражение от (4.38) [4]
на переходную функцию (4.38) мало и им можно пренебречь. В dtom случае используют модифицированное выражение от (4.38) [4]
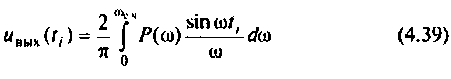
В результате интегрирования получают совокупность значений 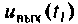 переходной функции системы и исследуемом интервале времени и строят график переходной функции, по которой определяют показатели качества переходного процесса.
переходной функции системы и исследуемом интервале времени и строят график переходной функции, по которой определяют показатели качества переходного процесса.
В качестве примера построения алгоритма численного интегрирования рассмотрим интегрирование с точки зрения простоты вычислений и точности результата. Сущность метода заключается в следующем. Пусть необходимо вычислить определенный интеграл
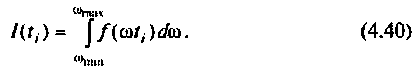
Вид подынтегральной функции, соответствующей выражению
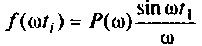
при фиксированном времени 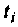 приведен на рис. 4.47, кривая
приведен на рис. 4.47, кривая 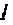 для t = 10 с, кривая 2 для
для t = 10 с, кривая 2 для 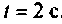 , а кривая 3 изображает ВЧХ электрической цепи. Функция
, а кривая 3 изображает ВЧХ электрической цепи. Функция 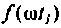 представляет функцию
представляет функцию 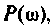 модулированную «замечательным» синусом. Известно, что интеграл (4.40) численно равен площади под кривой функции
модулированную «замечательным» синусом. Известно, что интеграл (4.40) численно равен площади под кривой функции 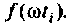 Если интервал аргумента
Если интервал аргумента 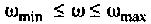 разбить на
разбить на 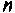 равных частей, то длина одного интервала будет равна
равных частей, то длина одного интервала будет равна 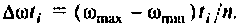 Площадь под кривой можно аппроксимировать суммой площадей прямоугольных трапеций с основаниями
Площадь под кривой можно аппроксимировать суммой площадей прямоугольных трапеций с основаниями 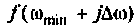
 и высотой
и высотой  Тогда интеграл (4.40) можно представить как сумму площадей прямоугольных трапеций:
Тогда интеграл (4.40) можно представить как сумму площадей прямоугольных трапеций:
Очевидно, что погрешность численного интегрирования зависит и от выбора числа интервалов 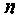 разбиения аргумента
разбиения аргумента  при конкретном времени
при конкретном времени 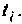 При увеличении времени , как видно из рис. 4.47, период подынтегральной функции уменьшается. Следовательно, необходимо увеличивать число интервалов, которое определился выражением
При увеличении времени , как видно из рис. 4.47, период подынтегральной функции уменьшается. Следовательно, необходимо увеличивать число интервалов, которое определился выражением

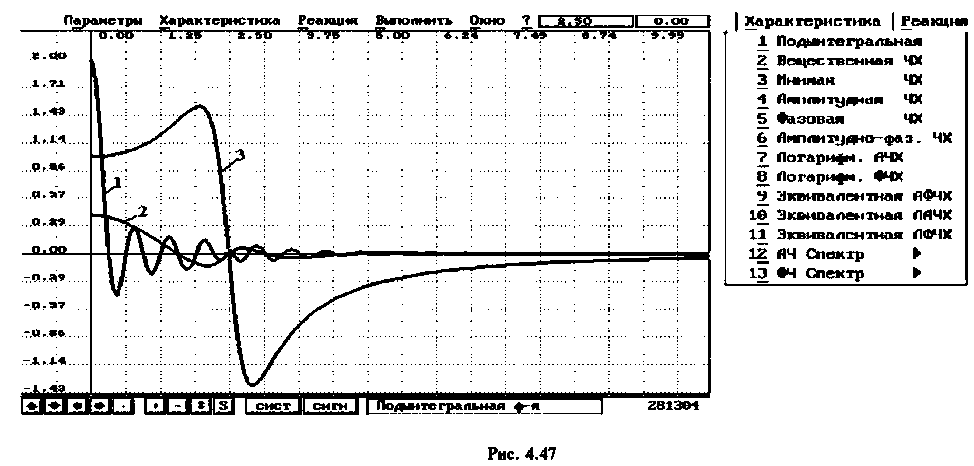
При этом одно полное колебание подынтегральной функции представляется не менее чем шестнадцатью трапециями.
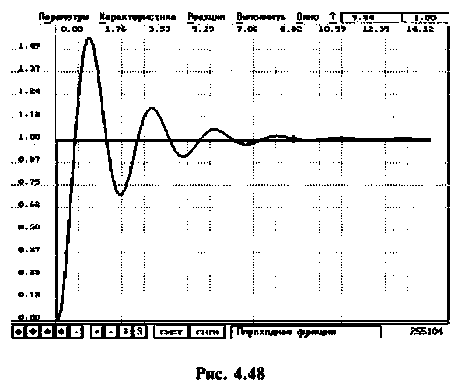
В качестве примера для построения переходной функции возьмем электрическую цепь, ВЧХ которой была построена и приведена на рис. 4.47 (кривая 3). На рис. 4.48 приведена переходная функция этой сложной электрической цепи.
Переходная функция на рис. 4.48 получена с помощью пакета ПП «Сигнал» [5].
Для вычисления интеграла (4.39) необходимо определить значение частоты для верхнего предела интегрирования  Это значение легко может быть определено из кривой вещественной частотной характеристики (ВЧХ) КФ электрической цепи. В качестве примера возьмем простую интегрирующую цепь (см. рис. 4.1), КФ которой имеет вид
Это значение легко может быть определено из кривой вещественной частотной характеристики (ВЧХ) КФ электрической цепи. В качестве примера возьмем простую интегрирующую цепь (см. рис. 4.1), КФ которой имеет вид
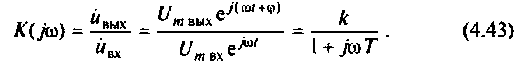
Алгебраическая форма КФ
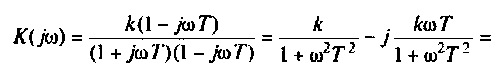
где 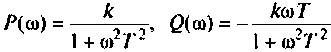 — вещественная и мнимая части КФ. Построим кривую
— вещественная и мнимая части КФ. Построим кривую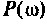 (рис. 4.49) в среде Mathcad, если
(рис. 4.49) в среде Mathcad, если 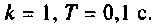 .
.
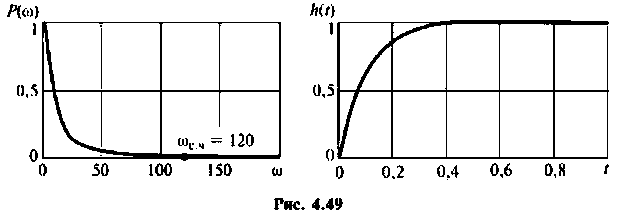
Из графика ВЧХ видно, что при 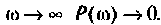 Влияние ВЧХ в области больших частот на переходную функцию несущественно, поэтому за частоту
Влияние ВЧХ в области больших частот на переходную функцию несущественно, поэтому за частоту 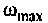 можно принять частоту, при которой ВЧХ принимает значение
можно принять частоту, при которой ВЧХ принимает значение 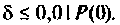 Эту частоту принято называть «существенной частотой» и обозначать
Эту частоту принято называть «существенной частотой» и обозначать 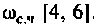 . В нашем примере
. В нашем примере 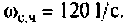 Переходная функция, вычисленная по выражению (4.39), приведена на рис. 4.49.
Переходная функция, вычисленная по выражению (4.39), приведена на рис. 4.49.
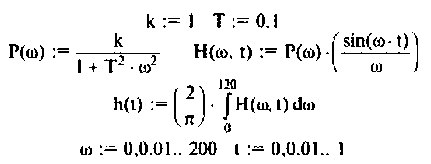
Для случая электрических цепей с дифференцирующими свойствами может оказаться, что при  ВЧХ КФ этой цепи
ВЧХ КФ этой цепи  Тогда для расчета переходной функции необходимо использовать мнимую частотную характеристику (МЧХ) в соответствии с выражением
Тогда для расчета переходной функции необходимо использовать мнимую частотную характеристику (МЧХ) в соответствии с выражением
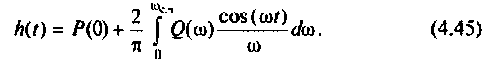
Приведенный пример наглядно показывает, что использование частотных характеристик для построения временных характеристик с помощью ЭВМ существенно расширяет возможности частотных методов анализа электрических цепей.
Спектральный метод расчета и построения выходных величин электрических цепей при сложных входных воздействиях:
Применение частотных методов при анализе и синтезе электрических цепей с требуемыми динамическими характеристиками и использованием ЭВМ позволяет не только строить переходные характеристики, но и строить реакцию цепи на любые детерминированные воздействия, оценивать их в установившихся режимах.
Математической основой частотных методов анализа электрических цепей и систем автоматического управления является обратное преобразование Фурье, позволяющее получать изображение выходного сигнала системы y(t) с помощью вещественной и мнимой частотных характеристик систем. В свою очередь, по вещественной или мнимой частотным характеристикам можно построить переходный процесс выходной величины и оценить реакцию цепи в переходном и установившемся режимах.
Как известно, реакция системы определяется по формуле обратного преобразования Фурье [4]
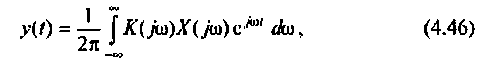
где 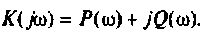
После соответствующих преобразований выражение (4.46) примет вид:
I) для ступенчатой входной функции 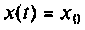 спектром
спектром 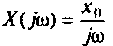
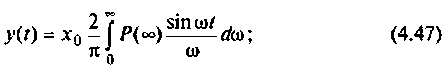
2) для линейной входной функции 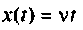 со спектром
со спектром 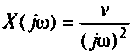
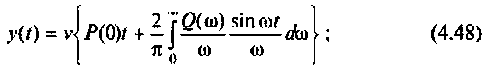
y{t) = vP(0)t+±l
2 r0(
Л» И
(4.48)
О)
3) для параболической входной функции 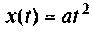 со спектром
со спектром 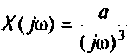
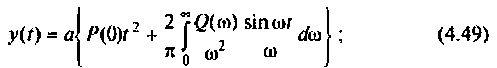
4) для полиномиального воздействия вида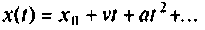
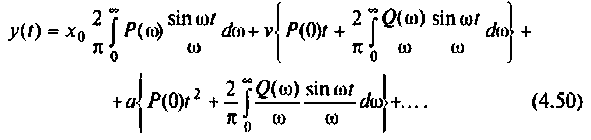
Применение ЭВМ и численных методов интегрирования позволяет отказаться от графических и табличных методов построения переходных и других необходимых функций в электрических цепях.
Примеры решения типовых задач:
Пример 4.6.1.
Определить комплексный коэффициент передачи по напряжению для дифференцирующего 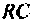 -контура (рис. 4.50,а), рассчитать и построить переходную функцию контура с помощью ВЧХ.
-контура (рис. 4.50,а), рассчитать и построить переходную функцию контура с помощью ВЧХ.
Решение
1. Изобразим комплексную схему замещения цепи (рис. 4.50, б).
2. Определим комплексное напряжение на выходе цепи в виде
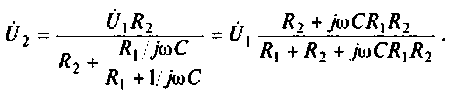
Преобразуем полученное выражение, вынеся за скобки в числителе и знаменателе члены, не содержащие 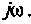 После преобразований получим
После преобразований получим
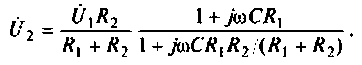
Следовательно
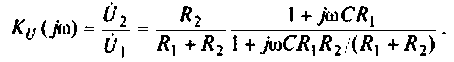
Введем обозначения:
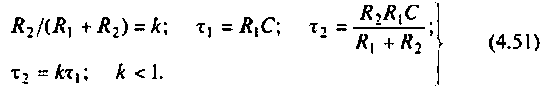
Величина 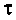 называется постоянной времени цепи и измеряется в секундах. Величина k имеет смысл коэффициента усиления по напряжению на постоянном токе, т. е. на частоте
называется постоянной времени цепи и измеряется в секундах. Величина k имеет смысл коэффициента усиления по напряжению на постоянном токе, т. е. на частоте 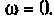 С учетом принятых обозначений
С учетом принятых обозначений
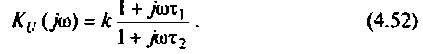
Для получения аналитических выражений ВЧХ и МЧХ запишем комплексную функцию и алгебраической форме
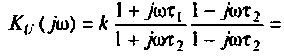
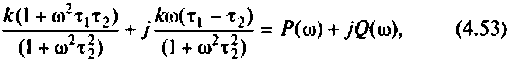
где 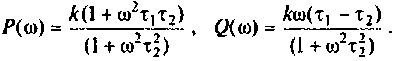
Примем: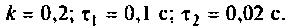
Для определения частоты 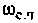 в среде Mathcad построим кривые ВЧХ и МЧХ (рис. 4.51).
в среде Mathcad построим кривые ВЧХ и МЧХ (рис. 4.51).
Из частотных характеристик КПФ принимаем 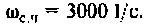 Для построения переходной функции воспользуемся выражением (4.45). Построение проведем также в среде Mathcad.
Для построения переходной функции воспользуемся выражением (4.45). Построение проведем также в среде Mathcad.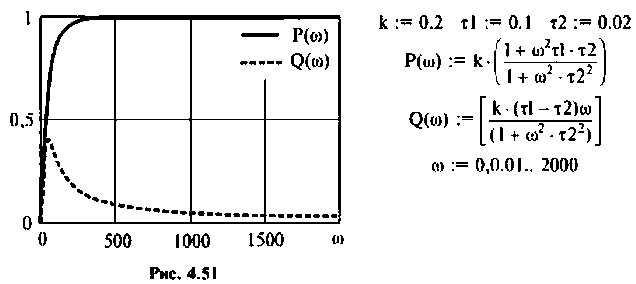
Переходная функция, показанная на рис.4.52, соответствует дифференцирую щему фазоопережающему контуру, который широко применяется в электронных и радиотехнических устройствах, системах автоматического управления.
Пример 4.6.2.
Для электрической цепи, изображенной на рис, 4.53, определить КПФ  построить ВЧХ
построить ВЧХ 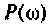 и МЧХ
и МЧХ 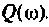 . Рассчитать и построить график переходной функции. Параметры цепи:
. Рассчитать и построить график переходной функции. Параметры цепи: 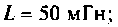
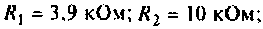
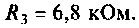
Решение
1. Найдем комплексную функцию 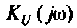 по формуле делителя напряжения
по формуле делителя напряжения
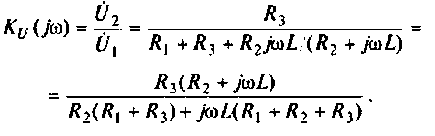
Преобразуем полученное выражение к виду
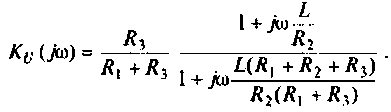
Обозначим:
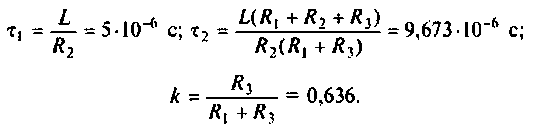
Следовательно,
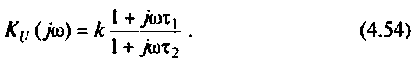
Для получения аналитических выражений ВЧХ и МЧХ запишем комплексную функцию и алгебраической форме
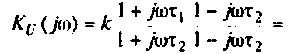
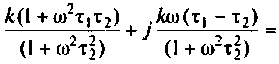
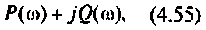
где 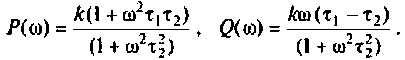
Для определения частоты 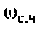 в среде Mathcad построим кривые ВЧХ и МЧХ (рис. 4.54).
в среде Mathcad построим кривые ВЧХ и МЧХ (рис. 4.54).
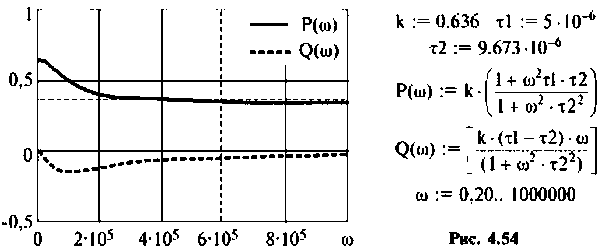
По виду ВЧХ и МЧХ определяем, что для построения переходной функции необходимо применить МЧХ. Примем из графика МЧХ 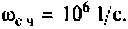 Переходная функция и программа для ее вычисления и построения приведена на рис. 4.55.
Переходная функция и программа для ее вычисления и построения приведена на рис. 4.55.
Из рис. 4.55 видно, что переходная функция соответствует интегрирующему контуру.
Пример 4.6.3.
Определить комплексный коэффициент передачи интегрирующей цепи (рис. 4.56, а), используя метод контурных токов. Построить в среде Mathcad графики АЧХ, ВЧХ, МЧХ. Рассчитать и построить эпюру входного и выходного напряжения, если на вход цепи поступает напряжение вида  где
где 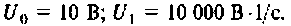
Параметры цепи: 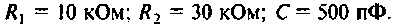
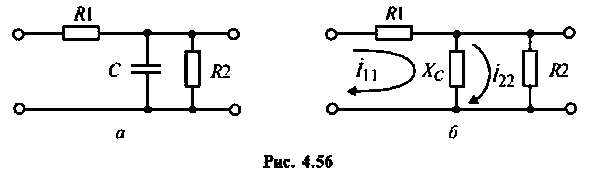
Решение
1.Представим цепь комплексной схемой замещения (рис. 4.56, б). Данная цепь имеет два независимых контура. Ток 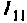 в первом контуре замыкается через источник, который на схеме не изображен. Направление контурных тиков выбираем одинаковым.
в первом контуре замыкается через источник, который на схеме не изображен. Направление контурных тиков выбираем одинаковым.
2.Составим матрицы контурных сопротивлений для двух независимых контуров
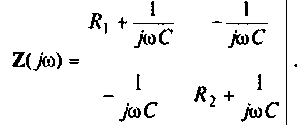
3.Определим комплексный коэффициент передачи, используя соотношение, приведенное в табл. 4.1.
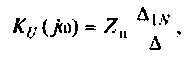
где сопротивление нагрузки 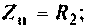
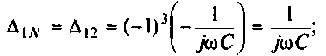
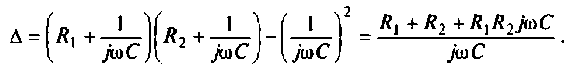
Подставляя найденные выражения, получаем
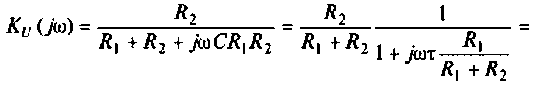
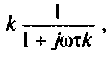
т.е. 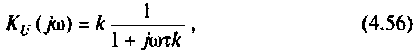
где 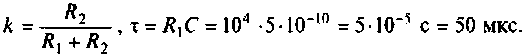
4. Рассчитаем 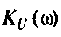 для крайних значений частоты
для крайних значений частоты 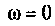 и
и 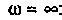
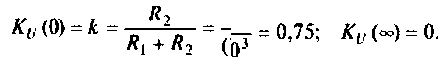
Объяснить полученные результаты можно, рассуждая так: на нулевой частоте (режим постоянного тока) сопротивление емкости бесконечно велико, ток в ней равен нулю, что эквивалентно разрыву этой ветви. При этом цепь становится резистивным делителем напряжения с передаточной функцией 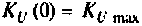 = = 0,75. С ростом частоты емкостное сопротивление уменьшается. Если
= = 0,75. С ростом частоты емкостное сопротивление уменьшается. Если 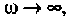 то
то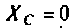 и шунтирует сопротивление
и шунтирует сопротивление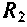 . При этом
. При этом
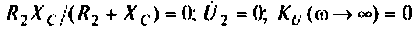
5.Определим выражения для АЧХ, ВЧХ, МЧХ. Представим КГ1Ф (4.55) в алгебраической форме
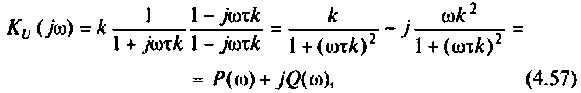
где 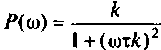 вещественная частотная характеристика:
вещественная частотная характеристика:
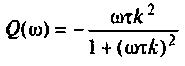 — мнимая частотная характеристика.
— мнимая частотная характеристика.
Амплитудно-частотную характеристику запишем в виде
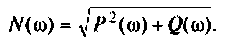
6. В среде Mathcad построим частотные характеристики и определим 
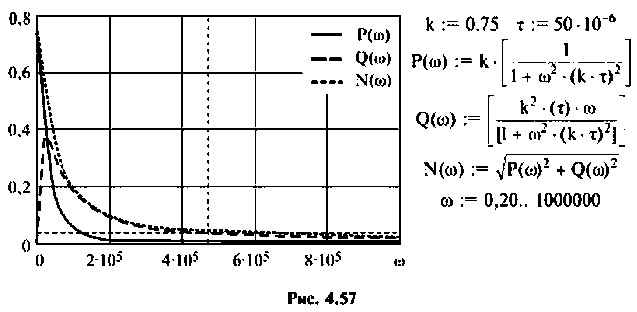
По ВЧХ на рис. 4.57 определяем, что существенная частота 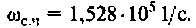
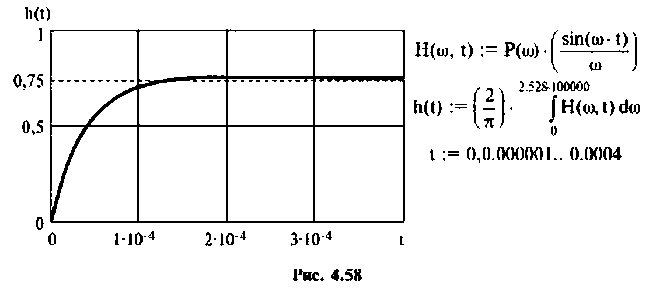
7. Построим переходную функцию электрической цепи, которая представлена на рис. 4.58.
Переходная функция электрической цепи соответствует апериодическому звену.
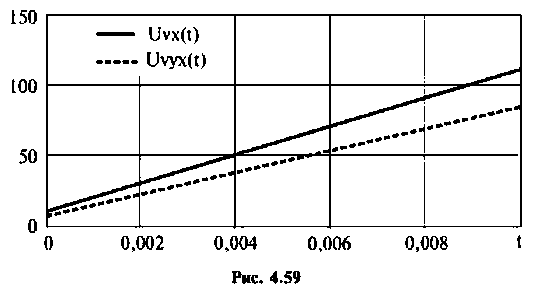
8. Построим реакцию электрической цепи на напряжение, изменяющееся но линейному закону (рис. 4.59).
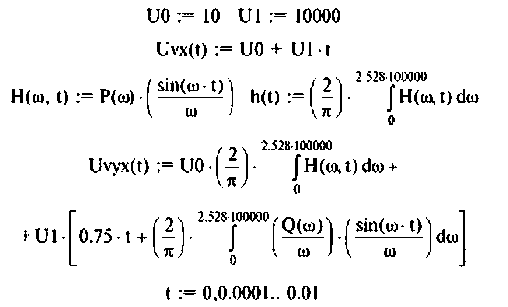
- Операторные передаточные функции
- Свободные колебания в пассивных электрических цепях
- Цепи с распределёнными параметрами
- Волновые параметры длинной линии
- Энергетические характеристики двухполюсников
- Комплексные функции электрических цепей
- Гармонические колебания в колебательном контуре
- Частотные характеристики линейных электрических цепей
Демьян Бондарь
Эксперт по предмету «Электроника, электротехника, радиотехника»
преподавательский стаж — 5 лет
Задать вопрос автору статьи
Комплексный коэффициент передачи
Определение 1
Комплексный коэффициент передачи – это отношение комплексного сигнала на выходе к комплексному сигналу на входе при установившемся режиме работы устройства или системы (сигнал на входе действует бесконечно долго).
Формула для определения комплексного коэффициента передачи выглядит следующим образом:
$W(jw) = Y(jw) / X(jw)$
где, Y(jw) – комплексная амплитуда выходного сигнала; X(jw) – комплексная амплитуда входного сигнала.
Понятие комплексного коэффициента передачи, как правило, используется в акустике, оптике, электротехнике, электронике. Например, коэффициент усиления усилителей, ослабление электромагнитного излучения в поглощающих средах, коэффициент затухания сигнала в линиях электропередачи, усиление света в активных средах лазера.
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Существуют следующие методы измерения коэффициента передачи:
- Использование измерителя комплексных коэффициентов передачи и импеданса (комплексное сопротивление между двумя узлами электрической цепи).
- Прямое измерение, заключающееся в измерении амплитуды сигнала на выходе и входе системы и последующее вычисление. Для этого применяются специальные электрические и оптические приборы.
- Измерение методом сравнения, которое осуществляется при помощи аттенюатора (прибор для фиксированного понижения интенсивности электрических и электромагнитных колебаний).
Амплитудно-частотная характеристика и фазо-частотная характеристика цепи
Определение 2
Амплитудно-частотная характеристика – это зависимость амплитуды колебаний (установившихся) выходного сигнала системы от частоты входного гармонического сигнала.
Понятие амплитудно-частотной широко используется в средствах связи, радиолокации и других радиотехнических приложениях. Данный показатель характеризует степень защищенности системы от помех. В многоканальных системах, таких как цифровые антенны, важная роль принадлежит межканальная идентичность амплитудно-частотной характеристики с коэффициентом корреляции, значение которого может достигать 0,999. Чем выше данный показатель (и чем шире полоса частот), тем лучше и проще можно минимизировать мультипликативные помехи, возникающие во время межканальной обработки сигналов.
«Комплексный коэффициент передачи. АЧХ и ФЧХ цепи» 👇
Традиционный метод измерения амплитудно-частотной характеристики заключается в подаче на вход исследуемого объекта гармонического сигнала с изменяемой частотой и с известной или постоянной амплитудой. В этом случае измерению подвергаются отношение модулей амплитуды выходного и выходного сигналов (коэффициент передачи) для разных значений частоты.
Для того, чтобы сократить время, за которое формируется амплитудно-частотная характеристика, используются специальный генератор, способный перестраивать частоту собственного сигнала с не меняющейся во времени амплитудой (генератор качающейся частоты). Данные генераторы плавно изменяют частоту генерации от низких до высоких, после чего переключают частоту на низшую, данный процесс повторяется периодически. Недостатками данных методов являются:
- Они являются непригодными для устройств с функционирующей регулировкой усиления, задача которой заключается в выравнивании различий в значениях амплитудно-частотных характеристик.
- Они не позволяют произвести оценку интермодуляционных искажений, возникающих между сигналами разных частот.
- Они не позволяют когерентное накопление во времени напряжений сигнала для частотных компонентов.
Существуют измерители амплитудно-частотной характеристики, которые подают на вход рассматриваемой системы широкополосные сигнал или импульс с коротким фронтом, а также измерители с шумовым сигналом, имеющий постоянную спектральную плотность мощности. Отклик анализируется анализатором спектра или фурье-измерителем амплитудно-частотной характеристики, который автоматически выполняет фурье-преобразование.
Фазо-частотная характеристика представляет собой зависимость между частотой сдвига выходного напряжения (сигнала) и входным напряжением при усилении гармонических колебаний.
Если фазо-частотная характеристика не искажает форму усиливаемых колебаний, то она представляет собой линейную зависимость фазового сдвига от частоты:
$j(f) = –t3 • 2 • p • f$
где, j(f) – фазовый сдвиг между входным и выходным напряжением; t3 – время задержки; f – частота, на которой осуществляется измерение фазового сдвига.
Для идеальной фазо-частотной характеристики сдвиг j прямо пропорционален частоте. Угол наклона такой фазо-частотной характеристики определяет время запаздывания сигнала на выходе. Если данный угол равен нулю, то это означает, что выходной сигнал появляется одновременно с входным. По графику фазо-частотной характеристики производится оценка фазовых искажений, вносящихся усилителем. Пример фазо-частотной характеристики изображен на рисунке ниже.
Рисунок 1. Фазо-частотная характеристика. Автор24 — интернет-биржа студенческих работ
Фазовые искажения должны обязательно учитываться в устройствах, которые охвачены глубокой обратной связью, а также в усилителях высококачественного воспроизведения, стереофонических усилителях и т.п.
Амплитудно-частотная и фазо-частотная характеристики представляют собой одни из самых важнейших характеристик систем и приборов, использующихся в радиотехнике, электротехнике и электронике.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Характеристики линейной цепи
Передаточная
функция А(јω)
определяется
как отношение комплексных амплитуд
выходного и входного сигнала
соответственно.
![]() А(јω)
А(јω)
= Uвых(ј![]() )/Uвх(j
)/Uвх(j![]() )=
)=
![]() ej
ej![]()
(1)
Коэффициент
передачи
![]() –модуль
–модуль
передаточной функции, обозначается
обычно К(![]() )
)
и называется амплитудно-частотной
характеристикой (АЧХ) цепи. Содержит
информацию о степени передачи различных
частотных составляющих сигнала.
Фазочастотная
характеристика (ФЧХ)
цепи – это частотная зависимость
разности фаз между выходным и входным
испытательными гармоническими сигналами.
![]() =arctg
=arctg
(А(јω)) (2)
Переходная
характеристика h(t)
– это
отклик линейной цепи на входной
испытательный сигнал, представляющий
собой единичный скачок 1(t).
Эти характеристики позволяют оценить
условия приемлемого качества прохождения
сигнала через различные простейшие
линейные цепи и линейный усилитель с
резистивной и резонансной нагрузкой.
Коэффициент
усиления в дБ:
К(дБ) = 20 lg
К
ЛАБОРАТОРНАЯ
РАБОТА №1.
Резистивный
делитель
напряжения
Целью
настоящей работы является изучение
характеристик и области применения
линейного четырехполюсника изображенного
на рис.1.1.
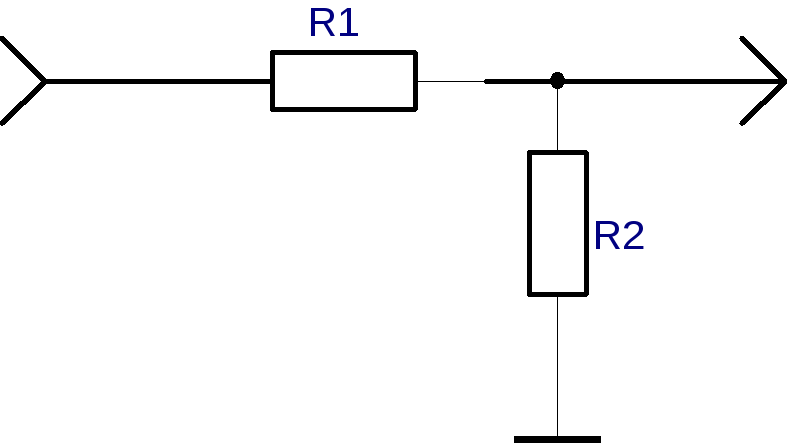
Uвх
Uвых
Рис.1.1.
Резистивный делитель напряжения.
-
Коэффициент
передачи
по напряжению определяем согласно (1)
и получим
Кu
= Uвых
/ Uвх
= R2/
(R1+R2),
(1.1)
откуда видно, что
он не зависит от частоты. Это естественно,
так как цепь не содержит реактивных
элементов.
-
Сдвига по фазе
выходного
сигнала относительно входного, по
причине, указанной выше, так же не
происходит. -
Рассматриваемая
схема является пассивным
четырехполюсником.
Его входное сопротивление
rвх
= Uвх
/ iвх
= R1
+ R2,
(1.2)
а выходное
rвых
= Uхх
/ iкз
= R1∙
R2/
(R1+R2).
(1.3) Если
ко входу делителя «навсегда» присоединить
постоянный источник э.д.с., то получим
активный
двухполюсник
с некоторым напряжением на зажимах и
выходным сопротивлением (Рис.1.2).
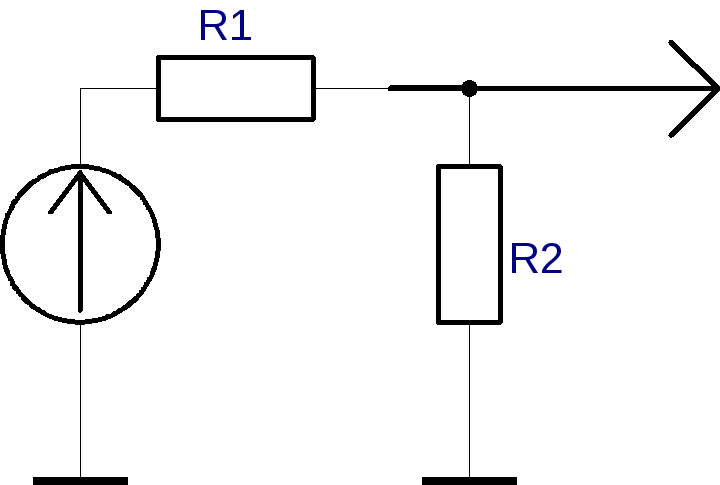
Uэ
Еп
Рис.1.2. Активный
двухполюсник.
Uэ
rэ
 Эту
Эту
схему можно использовать как источник
э.д.с. с любым заданным значением выходного
напряженияUэ
и внутреннего сопротивления rэ
(Рис.1.3).

Рис.1.3. Эквивалентный
источник э.д.с.
При заданных Uэ
и rэ
, и подходящим
выбором Еп
, решая систему (1.4)
Uэ
= Еп
∙R2/
(R1+R2)![]()
rэ
= R1∙R2/
(К1+К2) (1.4)
можно рассчитать
значения сопротивлений резисторов R1
и R2.
Порядок
выполнения работы.
-
Подберите два
любых резистора с величиной сопротивления
одного порядка (единицы кОм или десятки
кОм) и соберите схему делителя (рис.1.1). -
По
формулам (1.1)–(1.3) рассчитайте характеристики
четырехполюсника, результаты занесите
в рабочую тетрадь. -
Ко
входу схемы подключите генератор
гармонических колебаний, а к выходу
осциллограф. -
В интервале частот
20Гц – 100 кГц, измеряя осциллографом
входное и выходное напряжение, построить
по экспериментальным значениям
зависимость Кu(f)
= K(lg(f/fо)),
fo
= 10Гц. -
Соберите схему
для измерения внутреннего сопротивления
(Рис.1.4) и
rэ
Uэ
R
Рис.1.4. Схема для
измерения внутреннего (выходного)
сопротивления.
вычислите
внутреннее сопротивление по формуле
rэ
= (Uэ
/UR
– 1)R, (1.5)
где UR
– падение
напряжения на резисторе R
измеренное вольтметром.
-
Вывести выражения
(1.1) – (1.3) и 1.5. -
Будьте готовы
решить задачу с использованием системы
(1.4). -
Результаты
измерений представьте в виде таблицы.
|
Измер. величина |
Ku |
rвх, |
rвых, |
|
Расчет |
|||
|
Опыт |
ЛАБОРАТОРНАЯ
РАБОТА №2.
Фильтр нижних частот (ФНЧ)
Целью настоящей
работы является изучение характеристик
и области применения линейного
четырехполюсника изображенного на
рис.2.1, который называется фильтром
нижних частот (ФНЧ).
R
Uвх
Uвых
C
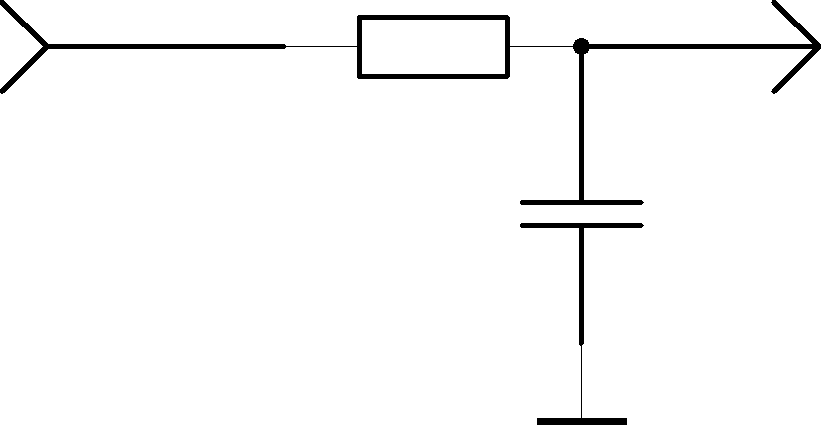
Рис.2.1. Фильтр
нижних частот.
-
Передаточная
функция
A(j![]() )=
)=
Uвых
/ Uвх
=
![]() (2.1)
(2.1)
-
Коэффициент
передачи
по напряжению определяем согласно (1)
и получим
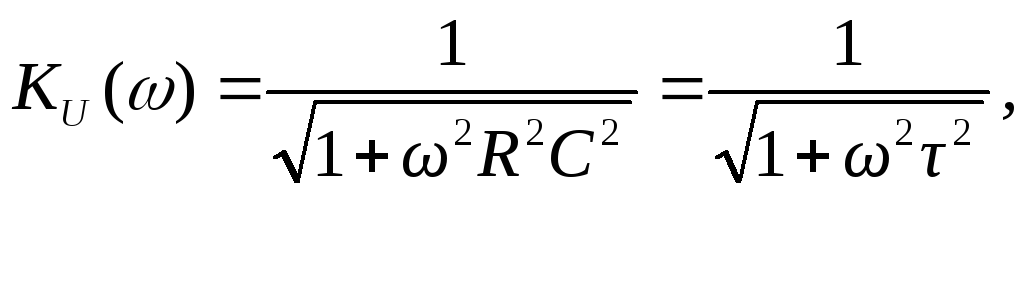
(2.2)
где
![]() RC.
RC.
Из (2.2) видно, что в области малых частот
коэффициент передачи близок к единице,
а при неограниченном увеличении частоты
– стремится к нулю.
-
Фазочастотная
характеристика (ФЧХ)
![]() = -arctg(
= -arctg(![]() )
)
(2.3)
Частота,
![]() для
для
которой выполняется условиеR
= 1/![]() С,
С,
называется частотой среза фильтра и
является одной из его граничных частот.
Для ее определения опытным путем можно
воспользоваться соотношениями
К(![]() )
)
= 0,707 и![]() (
(![]() )
)
= –![]() (2.4)
(2.4)
-
Переходную
характеристику h(t)
легко определить аналитически, поскольку
для сигнала
Uвх
=
 ,
,
выходное напряжение
будет функцией заряда конденсатора
Uвых
= Uвх
(1- e
– t/
![]() )
)
и, следовательно,
h(t)
= 1 – e
–t/![]() .
.![]() (2.5)
(2.5)
Заметим, что h(![]() )
)
= 0,63. Это позволяет определить
![]() из переходной характеристики.
из переходной характеристики.
Порядок
выполнения работы.
-
Так как приборы
измеряют частоту f
, а не
 , подберите номиналы конденсатора С и
, подберите номиналы конденсатора С и
резистораR
такими, чтобы fср
= 1,5 – 2,0
кГц. По формулам (2.1)–(2.3) рассчитайте
характеристики четырехполюсника,
результаты занесите в рабочую тетрадь. -
Ко входу схемы
подключите генератор гармонических
колебаний, а к выходу осциллограф. -
В интервале частот
20Гц – 100 кГц, измеряя осциллографом
входное значениям зависимость К(f)
= K(lg(f/fо)),
fo
= 10Гц. -
Из экспериментально
полученой АЧХ определите частоту среза
фильтра fср1. -
Подайте на вход
фильтра последовательность прямоугольных
импульсов с некоторой амплитудой Uвх.
Частоту следования подберите так,
чтобы форма выходного сигнала выглядела
так, как показано на рис.2.2.

Рис.2.2. Переходная
характеристика ФНЧ.
-
Из переходной
характеристики ( она выделена жирной
линией ) определите частоту среза
fср2. -
Подайте на вход
схемы гармонический сигнал и, меняя
частоту ге нератора, добейтесь, чтобы
отношение амплитуд выходного и входного
сигналов было равно 0,707. При этом разность
фаз между выходным и входным сигналом
должна соответствовать (2.4), а частота
– fср3.
В отчете представьте изображения
входного и выходного сигналов для этого
случая. -
Сравните значения
fср1,
fср2
и fср3.
В пределах погрешности они должны
совпасть, т. к. характеризуют одну и ту
же схему. . Результаты представьте в
виде таблицы.
|
Частота среза |
fср1,кГц |
fср2,кГц |
fср3,кГц |
|
Расчет |
|||
|
Опыт |
-
Выведите выражения
(2.1) – (2.5).
ЛАБОРАТОРНАЯ
РАБОТА №3.
Фильтр верхних частот (ФВЧ)
Целью настоящей
работы является изучение характеристик
и области применения линейного
четырехполюсника изображенного на
рис.3.1, который называется фильтром
верхних частот (ФВЧ).
C
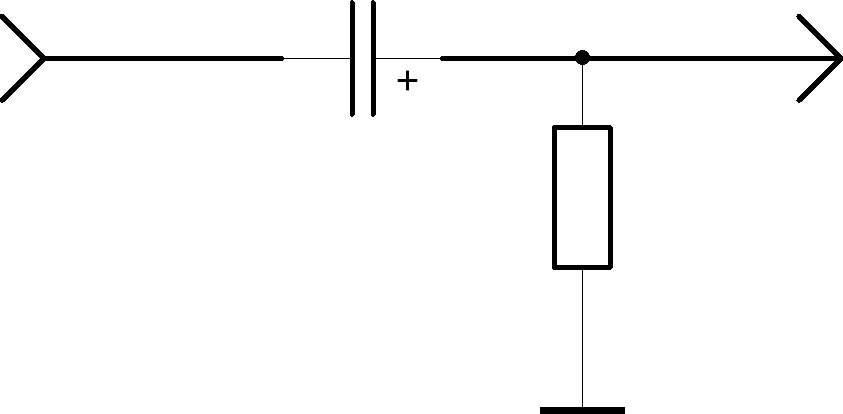
R
Uвх
Uвых
Рис.3.1. Фильтр
верхних частот.
-
Передаточная
функция
A(j![]() )=
)=
Uвых
/ Uвх
=
![]() (3.1)
(3.1)
-
Коэффициент
передачи
по напряжению определяем согласно (1)
и получим
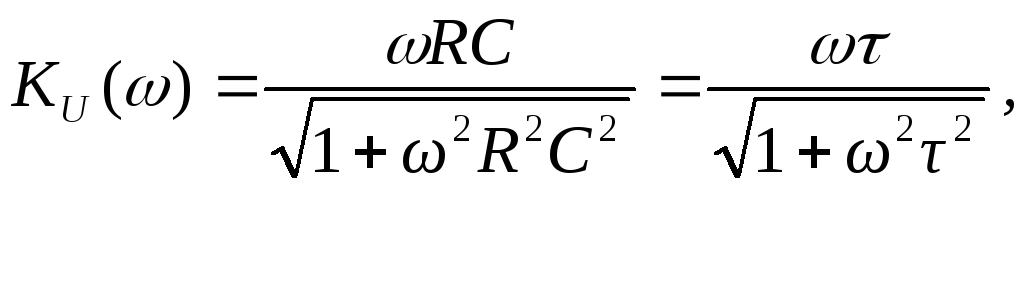
(3.2)
где
![]() RC.
RC.
Из (3.2) видно, что в области малых частот
коэффициент передачи близок к нулю, а
при неограниченном увеличении частоты
– стремится к единице.
-
Фазочастотная
характеристика (ФЧХ)
![]() =
=
arctg(![]() )
)
(3.3)
Частота,
![]() для
для
которой выполняется условиеR
= 1/![]() С,
С,
называется частотой среза фильтра и
является одной из его граничных частот.
Для ее определения опытным путем можно
воспользоваться соотношениями
К(![]() )
)
= 0,707 и![]() (
(![]() )
)
=![]() (3.4)
(3.4)
-
Переходную
характеристику h(t)
легко определить аналитически, поскольку
для сигнала
Uвх
=
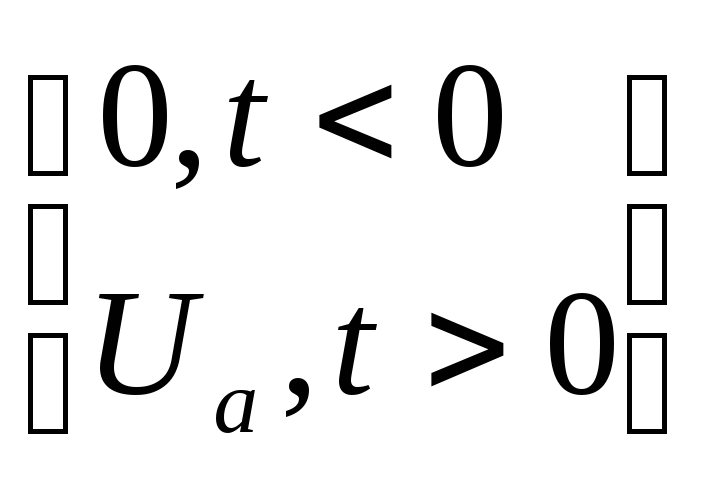 ,
,
выходное напряжение
будет функцией разряда конденсатора
Uвых
= Uвх
e
– t/
![]()
и, следовательно,
h(t)
= e
–t/![]() .
.![]() (3.5)
(3.5)
Заметим, что h(![]() )
)
= 0,37. Это позволяет определить
![]() также и из переходной характеристики.
также и из переходной характеристики.
Порядок
выполнения работы.
1.
Подберите номиналы конденсатора С и
резистора R
такими, чтобы fср
=
3,5 – 5,0 кГц. Ко
входу схемы подключите генератор
гармонических колебаний, а к
выходу осциллограф.
2. В
интервале частот 20Гц – 100 кГц, измеряя
осциллографом входное и выходное
напряжение, построить по экспериментальным
значениям зависимость К(f)
= K(lg(f/fо)),
fo
= 10Гц.
3. Из
полученой АЧХ определите частоту среза
фильтра fср1,
воспользовавшись соотношением (3.4).
-
Подайте на вход
фильтра последовательность прямоугольных
импульсов с некоторой амплитудой Uвх.
Частоту следования подберите так, чтобы
форма выходного сигнала выглядела
так, как показано на рис.3.2.
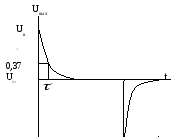
Рис.3.2. Переходная
характеристика ФВЧ.
-
Из переходной
характеристики (она выделена жирной
линией ) определите частоту среза fср2. -
Подайте на вход
схемы гармонический сигнал и, меняя
частоту генератора, добейтесь, чтобы
Uвых
/ Uвх
= 0,707, тогда разность фаз между выходным
и входным сигналами должна быть
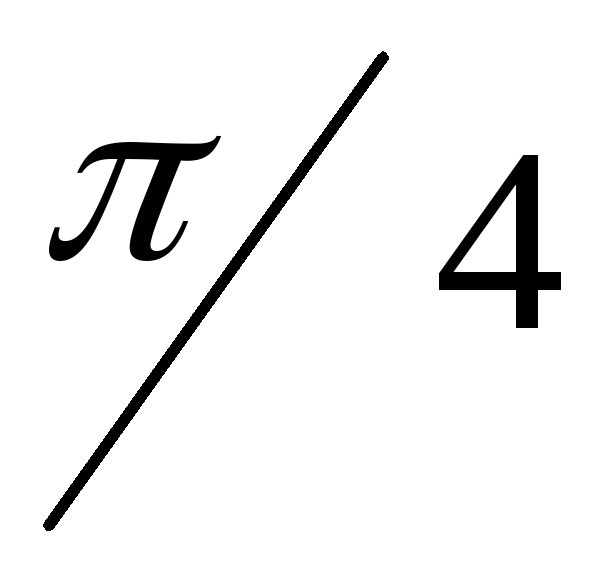 ,
,
а частота –fср3.
В отчете представьте изображения
входного и выходного сигналов для этого
случая. Сравните значения fср1,
fср2
и fср3.
В пределах погрешности они должны
совпасть. Результаты представьте в
виде таблицы.
|
Частота среза |
fср1,кГц |
fср2,кГц |
fср3,кГц |
|
Расчет |
|||
|
Опыт |
-
Выведите выражения
(3.1), (3.2) и (3.4)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Коэффициент передачи
Коэффициент передачи (также коэффициент преобразования) — отношение напряжения на выходе той или иной системы, предназначенной для передачи электрических сигналов, к напряжению на входе. В частном случае, когда значения выходного и входного сигнала являются однородными, коэффициент передачи называют коэффициентом усиления. KП = UВЫХ / UВХ. Коэффициент передачи часто выражают в логарифмическом виде, как 20 lg (UВЫХ / UВХ), дБ.
Содержание
Коэффициент усиления и ослабления сигнала
- В усилительных устройствах коэффициент передачи больше единицы (больше нуля в логарифмическом масштабе) называют коэффициентом усиления (не путать с коэффициентом усиления антенны).
- При рассмотрении пассивных устройств, а также линий передачи, когда выходное напряжение меньше входного, употребляют понятие ослабление сигнала.
Комплексный коэффициент передачи
При анализе частотнозависимых устройств часто возникает необходимость в векторном представлении коэффициента передачи
- Комплексный коэффициент передачи K(jω) — отношение комплексной амплитуды (КА)Y выходной величины системы к комплексной амплитуде X входной величины синусоидальной формы при заданном значении её частоты ω.
Также ещё используется (в основном на практике в теории передачи сигналов по каналу связи) обратный комплексный коэффициент передачи (1/K(jω)). Так как ККП в этом случае меньше единицы и имеет дробный вид, что усложняет расчёты, комплексную амплитуду выходного сигнала Y можно вычислить умножением КА входного сигнала X на K(jω), если комплексный коэффициент передачи априори известен. Комплексный коэффициент передачи является комплексной величиной, а его компоненты зависят от частоты входного сигнала. Может быть представлен вектором на комплексной плоскости (построенная таким образом кривая называется годографом коэффициента передачи).
Измерения
- Прямое измерение — производится с помощью установок для измерения ослаблений или измерителей коэффициента передачи, в том числе панорамных.
- Совокупное измерение — производится с помощью измерения мощности или напряжения сигнала на выходе и на входе, и последующего расчета.
- Измерение методом сравнения — производится с помощью аттенюатора, являющегося мерой ослабления. В качестве меры коэффициента усиления, в принципе, можно применить откалиброванный измерительный усилитель, однако на практике это, как правило, не используется.
- Для измерения комплексных коэффициентов передачи применяются измерители импеданса и комплексных коэффициентов передачи, или, на сверхвысоких частотах, измерители комплексных коэффициентов и КСВ.
Литература
- Хлытчиев С. М. Основы автоматики и автоматизации производственных процессов. — 1985
- Словарь радиолюбителя — Л.: Энергия, 1979
- Гусев В. Г. Электроника. — 1991
Ссылки
- Добавить иллюстрации.
- Радиотехнические величины и параметры
Wikimedia Foundation . 2010 .
Полезное
Смотреть что такое «Коэффициент передачи» в других словарях:
коэффициент передачи — Отношение комплексной амплитуды сигнала на выходе системы (усилителя, фильтра и т.п) к комплексной амплитуде сигнала на ее входе. Часто используют модуль коэффициента передачи, являющийся действительной величиной. [Система неразрушающего контроля … Справочник технического переводчика
коэффициент передачи — perdavimo koeficientas statusas T sritis automatika atitikmenys: angl. transfer coefficient; transfer gain; transmission gain vok. Übertragungskoeffizient, m; Übertragungsmaß, n rus. коэффициент передачи, m pranc. coefficient de transfert, m;… … Automatikos terminų žodynas
коэффициент передачи — perdavimo faktorius statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, lygus elektrinės grandinės išėjimo ir įėjimo signalų įtampų, srovių arba galių dalmeniui. atitikmenys: angl. transfer coefficient; transfer factor;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
коэффициент передачи — perdavimo faktorius statusas T sritis fizika atitikmenys: angl. transfer factor; transfer ratio vok. Übertragungsfaktor, m; Übertragungsverhältnis, n rus. коэффициент передачи, m pranc. facteur de transmission, m; rapport de transfert, m … Fizikos terminų žodynas
коэффициент передачи при виброизоляции — коэффициент передачи Ндп коэффициент амортизации Отношение амплитуды виброперемещения (виброскорости, виброускорения защищаемого объекта или действующей на него силы) к амплитуде той же величины источника возбуждения при гармонической вибрации.… … Справочник технического переводчика
коэффициент передачи между оптическими полюсами — коэффициент передачи между полюсами Отношение мощности оптического излучения на одном из оптических полюсов компонента ВОСП к мощности оптического излучения на другом из его оптических полюсов, выраженное в децибелах. [ГОСТ 26599 85] Тематики… … Справочник технического переводчика
коэффициент передачи интегральной микросхемы — коэффициент передачи Отношение абсолютного значения изменения выходного напряжения усилителя рассогласования интегральной микросхемы к абсолютному изменению входного напряжения. Обозначение KUP [ГОСТ 19480 89] Тематики микросхемы Синонимы… … Справочник технического переводчика
коэффициент передачи модуля СВЧ — коэффициент передачи Кпер Отношение мощности на выходе модуля СВЧ к мощности на его входе при согласовании входа и выхода по заданному коэффициенту стоячей волны. [ГОСТ 23221 78] Тематики компоненты техники связи Обобщающие термины модули СВЧ,… … Справочник технического переводчика
коэффициент передачи мощности преобразовательного прибора СВЧ — коэффициент передачи мощности Кпер Отношение мощности преобразованного сигнала прибора СВЧ к мощности входного сигнала. [ГОСТ 23769 79] Тематики приборы и устройства защитные СВЧ Синонимы коэффициент передачи мощности … Справочник технического переводчика
коэффициент передачи по напряжению интегральной микросхемы — коэффициент передачи по напряжению Отношение напряжения на выходе интегральной микросхемы к заданному значению коммутируемого напряжения при включенном канале. Обозначение Кп KU [ГОСТ 19480 89] Тематики микросхемы Синонимы коэффициент передачи по … Справочник технического переводчика
Коэффициент передачи
Форма представления коэффициента передачи зависит от формы математического представления сигналов входа и выхода. Это могут быть, например, операторы Лапласа или Фурье, тогда коэффициенты передачи называют операторными.
Коэффициент передачи и коэффициент усиления
В частности, если величины входного и выходного сигналов однородны, тогда коэффициент передачи называют коэффициентом усиления. Так, коэффициентом усиления по напряжению (![]() ) называют физическую величину, равную отношению амплитуды переменной компоненты выходного напряжения (
) называют физическую величину, равную отношению амплитуды переменной компоненты выходного напряжения (![]() ) к амплитуде входного напряжения (
) к амплитуде входного напряжения (![]() ):
):
![]()
В выражении для коэффициента усиления можно использовать не только амплитуды, но и действующие значения напряжения.
Если коэффициенты усиления выражают в децибелах, то определением коэффициента преобразования (усиления) по напряжению будет выражение:
![]()
Коэффициенты усиления по току и мощности в децибелах выражают как:
![]()
Коэффициент усиления каскада равен произведению отдельных элементов каскада, если он выражен в относительных единицах:
![]()
Общий коэффициент усиления каскада равен сумме отдельных элементов каскада, если он выражен в децибелах.
K(дб)=![]()
Если в усилителе коэффициент передачи больше единицы для безразмерного коэффициента или больше нуля для коэффициента, представленного в децибелах, то коэффициент называют коэффициентом усиления.
Коэффициент передачи может быть представлен в комплексном виде. Он используется для анализа устройств, которые зависят от частоты сигналов.
Комплексный коэффициент передачи линейного звена находят как отношение комплексной амплитуды выходного сигнала к комплексной амплитуде входного сигнала:
![]()
где ![]() — комплексная амплитуда выходного сигнала,
— комплексная амплитуда выходного сигнала, ![]() — комплексная амплитуда сигнала на входе,
— комплексная амплитуда сигнала на входе, ![]() — частота.
— частота.
Единицы измерения
Коэффициент усиления — может быть величиной безразмерной. При решении задач следует обратить внимание на то, чтобы величины входных и выходных сигналов были выражены в одних единицах.
Или коэффициент усиления может выражаться в логарифмических единицах — децибелах.
Примеры решения задач
| Задание | Что такое частотный годограф? |
| Решение | Комплексный коэффициент передачи применяют для графического изображения свойств звена. С этой целью строят частотный годограф. Частотным годографом называют геометрическое место точек, которое создает конец вектора комплексного коэффициента передачи, если частота сигнала изменяется от 0 до |

Для узла, к которому подключен инвертирующий выход, запишем закон Кирхгофа для токов:
![]()
Рассмотрим контур, который включает источник напряжения, вход усилителя, и сопротивление ![]() , запишем второй закон Кирхгофа для этого контура:
, запишем второй закон Кирхгофа для этого контура:
![]()
Рассмотрим контур, который включает вход усилителя, сопротивление ![]() и выход схемы, получаем:
и выход схемы, получаем:
![]()
Выразим из (2.3) выходное напряжение и учтем, что: если усилитель работает в линейном режиме, то входные токи в рассматриваемый усилитель равны нулю (в нашем случае ![]() ); напряжение на входе в такой усилитель равно нулю
); напряжение на входе в такой усилитель равно нулю ![]() =0. Тогда:
=0. Тогда:
Коэффициент передачи
- Коэффициент передачи (также коэффициент преобразования) — отношение мощности, напряжения или тока на выходе той или иной системы, предназначенной для передачи электрических сигналов, соответственно, к мощности, напряжению или току на входе системы. Например, выражение для коэффициента передачи по напряжению: KV = V2 / V1.
Коэффициент передачи часто выражают в децибелах (дБ, dB), в основе которых лежит десятичный логарифм отношения величин. Например: KV (дБ) = 20 lg (V2 / V1). В случае, когда значения рассматриваемых величин уже представлены в децибелах: KV (дБ) = V2 (дБ) − V1 (дБ). Коэффициент передачи, выраженный в децибелах, может иметь знак плюс или минус в зависимости от соотношения величин на выходе и на входе.
Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
В статье описаны некоторые типовые применения операцио́нных усили́телей (ОУ) в аналоговой схемотехнике.
При включении биполярного транзистора по схеме с общим эмиттером (ОЭ) входной сигнал подаётся на базу относительно эмиттера, а выходной сигнал снимается с коллектора относительно эмиттера. При этом выходной сигнал инвертируется относительно входного (для гармонического сигнала фаза выходного сигнала отличается от входного на 180°). Данное включение транзистора позволяет получить наибольшее усиление по мощности, потому что усиливается и ток, и напряжение.













![{displaystyle H(jomega )={frac {Y[j(omega t+varphi )]}{X(jomega t)}}={frac {A_{o}e^{j(omega t+varphi )}}{A_{i}e^{jomega t}}}={frac {A_{o}}{A_{i}}}e^{jvarphi }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce61b9e0c838cfdff5d3ca9d1a1859244996819e)


