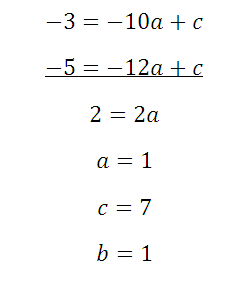Как найти коэффициент по графику зависимости

Предположим, вам попался график функции (y=ax^2+bx+c) и нужно по этому графику определить коэффициенты (a), (b) и (c). В этой статье я расскажу 3 простых способа сделать это.

1 способ – ищем коэффициенты на графике

Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью (y) – целые числа. Если это не так, советую использовать способ 2.

1. Коэффициент (a) можно найти с помощью следующих фактов:

   – Если (a>0), то ветви параболы направленных вверх, если (a<0), то ветви параболы направлены вниз.

   

   – Если (a>1), то график вытянут вверх в (a) раз по сравнению с «базовым» графиком (у которого (a=1)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.

   

   – Аналогично с (a<-1), только график вытянут вниз.

   

   – Если (a∈(0;1)), то график сжат в (a) раз (по сравнению с «базовым» графиком с (a=1)). Вершина при этом остается на месте.

   

   – Аналогично (a∈(-1;0)), только ветви направлены вниз.

   

2. Парабола пересекает ось y в точке (c).

   

3. (b) напрямую по графику не видно, но его можно посчитать с помощью (x_в) – абсциссы (икса) вершины параболы:

   (x_в=-frac{b}{2a})
   (b=-x_вcdot 2a)
   

Пример (ЕГЭ):

Решение:
Во-первых, надо разобраться, где тут (f(x)), а где (g(x)). По коэффициенту (c) видно, что (f(x)) это функция, которая лежит ниже – именно она пересекает ось игрек в точке (4).

Значит нужно найти коэффициенты у параболы, которая лежит повыше.
Коэффициент (c) у неё равен (1).
Ветви параболы направлены вниз – значит (a<0). При этом форма этой параболы стандартная, базовая, значит (a=-1).

Найдем (b). (x_в=-2), (a=-1).

(x_в=-frac{b}{2a})
(-2=-frac{b}{-2})
(b=-4)

Получается (g(x)=-x^2-4x+1). Теперь найдем в каких точках функции пересекаются:

(-x^2-4x+1=-2x^2-2x+4)
(-x^2-4x+1+2x^2+2x-4=0)
(x^2-2x-3=0)
(D=4+4cdot 3=16=4^2)
(x_1=frac{2-4}{2}=-1);    (x_2=frac{2+4}{2}=3).

Ответ: (3).

2 способ – находим формулу по точкам

Это самый надежный способ, потому что его можно применить практически в любой ситуации, но и самый не интересный, потому что думать тут особо не надо, только уметь решать системы линейных уравнений. Алгоритм прост:

1. Ищем 3 точки с целыми координатами, принадлежащие параболе.
   Пример:

   

2. Выписываем координаты этих точек и подставляем в формулу квадратичной функции: (y=ax^2+bx+c). Получится система с тремя уравнениями.

   Пример: (A(-4;5)), (B(-5;5)), (C(-6;3)).

   (begin{cases}5=a(-4)^2+b(-4)+c\5=a(-5)^2+b(-5)+c\3=a(-6)^2+b(-6)+c end{cases})

3. Решаем систему.
   Пример:

   (begin{cases}5=16a-4b+c\5=25a-5b+c\3=36a-6b+c end{cases})

   Вычтем из второго уравнения первое:

   (0=9a-b)
   (b=9a)

   Подставим (9a) вместо (b):

   (begin{cases}5=16a-36a+c\5=25a-45a+c\3=36a-54a+c end{cases})
   (begin{cases}5=-20a+c\5=-20a+c\3=-18a+c end{cases})

   Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки (A) и (B) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:

   (2=-2a)
   (a=-1)

   Найдем (b):

   (b=-9)

   Подставим в первое уравнение (a):

   (5=20+c)
   (c=-15).

   Получается квадратичная функция:   (y=-x^2-9x-15).

Пример (ЕГЭ):

Решение:

Сразу заметим, что по графику можно сразу определить, что (c=4). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: (C(-1;8)), (D(1;2)) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи). 

Таким образом имеем систему:

(begin{cases}8=a(-1)^2+b(-1)+4\2=a+b+4 end{cases})

(begin{cases}8=a-b+4\2=a+b+4 end{cases})

(begin{cases}4=a-b\-2=a+b end{cases})

Сложим 2 уравнения:

(2=2a)
(a=1)

Подставим во второе уравнение:

(-2=1+b)
(b=-3)

Получается:

(g(x)=x^2-3x+4)

Теперь найдем точки пересечения двух функций:

(-3x+13=x^2-3x+4)
(x^2-9=0)
(x=±3)

Теперь можно найти ординату второй точки пересечения:

(f(-3)=-3cdot (-3)+13)
(f(-3)=9+13)
(f(-3)=22)

Ответ:   (22).

3 способ – используем преобразование графиков функций

Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.

Главный недостаток этого способа – вершина должна иметь целые координаты.

Сам способ базируется на следующих идеях:

1. График (y=-x^2) симметричен относительно оси (x) графику (y=x^2).

   

2. – Если (a>1) график (y=ax^2) получается растяжением графика (y=x^2) вдоль оси (y) в (a) раз.
   – Если (a∈(0;1)) график (y=ax^2) получается сжатием графика (y=x^2) вдоль оси (y) в (a) раз.

   

3. – График (y=a(x+d)^2) получается сдвигом графика (y=ax^2) влево на (d) единиц.
   – График (y=a(x-d)^2) получается сдвигом графика (y=ax^2) вправо на (d) единиц. 

   

4. График (y=a(x+d)^2+e) получается переносом графика (y=a(x+d)^2) на (e) единиц вверх.
   График (y=a(x+d)^2-e) получается переносом графика (y=a(x+d)^2) на (e) единиц вниз.

   

У вас наверно остался вопрос – как этим пользоваться? Предположим, мы видим такую параболу:

Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому (a=1). То есть она получена перемещениями графика базовой параболы (y=x^2).

А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на (4).

То есть наша функция выглядит так: (y=(x-5)^2-4).
После раскрытия скобок и приведения подобных получаем искомую формулу:

(y=x^2-10x+25-4)
(y=x^2-10x+21)

Готово.

Пример (ЕГЭ):

Чтобы найти (f(6)), надо сначала узнать формулу функции (f(x)). Найдем её:

1. Парабола растянута на (2) и ветви направлены вниз, поэтому (a=-2). Иными словами, первоначальной, перемещаемой функцией является функция (y=-2x^2).

   

2. Парабола смещена на 2 клеточки вправо, поэтому (y=-2(x-2)^2).

3. Парабола поднята на 4 клеточки вверх, поэтому (y=-2(x-2)^2+4).

4. Получается (y=-2(x^2-4x+4)+4=)(-2x^2+8x-8+4=-2x^2+8x-4).

5. (f(6)=-2cdot 6^2+8cdot 6-4=-72+48-4=-28)

Смотрите также:
Как найти k и b по графику линейной функции?

Как найти k и b по графику линейной функции?

В новой 9 задаче профильного ЕГЭ много заданий на линейные функции. Самое сложное, что нужно сделать, решая эти задачи – определить формулу линейной функции , т.е. найти (k) и (b) по графику. Примеры таких заданий (решения будут внизу статьи):

В статье я расскажу про два простых способа найти (k) и (b), если известен график линейной функции.

Способ 1

Первый способ основывается на трех фактах:

Линейная функция пересекает ось (y) в точке (b).
Примеры:

Но не советую определять так (b), если прямая пересекает ось не в целом значении или если точка пересечения вообще не видна на графике. Для таких случаев пользуйтесь вторым способом.

Если функция возрастает, то знак коэффициента (k) плюс, если убывает – минус, а если постоянна, то (k=0).

Чтоб конкретнее определить (k) надо построить на прямой прямоугольный треугольник так, чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Далее, чтоб определить (k) нужно вертикальную сторону треугольника поделить на горизонтальную и поставить знак согласно возрастанию/убыванию функции.

Давайте пока что не будем искать формулу иррациональной функции, сосредоточимся только на линейной функции.

(b=3) – это сразу видно. Функция идет вниз, значит (k 0). (k=+frac=frac<4><4>=1,b=1). (f(x)=x+1).

Теперь перейдем к функции (g(x)). Найдем координаты точек (D) и (E): (D(-2;4)), (E(-4;1)). Можно составить систему:

Вычтем второе уравнение из первого, чтоб убрать (b):

(g(x)=1,5x+7). Обе функции найдены, теперь можно найти абсциссу (икс) точки пересечения. Приравняем (f(x)) и (g(x)).

Картинку в хорошем качестве, можно скачать нажав на кнопку “скачать статью”.

Коэффициенты k и b

Содержание

Положение прямой на графике зависит от величины коэффициентов $k$ и $b$

Коэффициент $k$ называют угловым, так как он показывает угол наклона линейной функции на графике относительно оси $Ox$

При $k > 0$ угол между графиком и осью $Ox$ меньше $90 degree$ (острый)

При $k

Коэффициент b

Коэффициент $b$ называют свободным. На графике он показывает длину отрезка, который отсекает линия функции по оси ординат относительно начала координат.

Другими словами, коэффициент $b$ показывает, насколько график сдвинут вдоль оси $Oy$. Если $b > 0$, то график будет сдвинут вверх, и если $b

Так на нашем графике функции из примера про копилку видно, что прямая пересекает ось $Oy$ выше начала координат на $500$ единиц (этому числу и равен коэффициент $b$).

График функции $y=50x + 500$

Частные случаи. b = 0

В случае, когда коэффициент $b = 0$, а функция прямо пропорциональна, ее график будет проходить через начало координат $O(0;0)$. Ведь при подставлении в формулу $x = 0$ получим и $y = 0$.

Для построения графика такой функции достаточно найти одну точку, вторая – начало координат $О(0;0)$.

Важно: график в виде вертикальной прямой, параллельной оси $Oy$, не является графиком функции. В таком случае одному значению аргумента соответствует множество значений $y$. Это не наш случай, потому что он не соответствует самому определению функции.

При этом прямой, параллельной оси $Ox$, график функции может быть. Это возможно, когда коэффициент $k = 0$. Угол наклона также будет равен $0$. Формула принимает вид $y = b$.

График линейной функции, его свойства и формулы

О чем эта статья:

Понятие функции

Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, следуя которому по значениям независимой переменной можно найти соответствующие значения функции. Вот какими способами ее можно задать:

Табличный способ помогает быстро определить конкретные значения без дополнительных измерений или вычислений.

Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.

Словесный способ.

Графический способ — наглядно. Его мы и разберем в этой статье.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Понятие линейной функции

Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.

Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.

Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.

Если известно конкретное значение х, можно вычислить соответствующее значение у.

Нам дана функция: у = 0,5х – 2. Значит:

если х = 0, то у = -2;

если х = 2, то у = -1;

если х = 4, то у = 0 и т. д.

Для удобства результаты можно оформлять в виде таблицы:

Графиком линейной функции является прямая. Для ее построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.

Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.

k и b — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.

Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты k и b.

Функция	Коэффициент k	Коэффициент b
y = 2x + 8	k = 2	b = 8
y = −x + 3	k = −1	b = 3
y = 1/8x − 1	k = 1/8	b = −1
y = 0,2x	k = 0,2	b = 0

Может показаться, что в функции y = 0,2x нет числового коэффициента b, но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа y = kx + b есть коэффициенты k и b.

Свойства линейной функции

Область определения функции — множество всех действительных чисел.

Множеством значений функции является множество всех действительных чисел.

График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.

Функция не имеет ни наибольшего, ни наименьшего значений.

Четность и нечетность линейной функции зависят от значений коэффициентов k и b:

b ≠ 0, k = 0, значит, y = b — четная;

b = 0, k ≠ 0, значит, y = kx — нечетная;

b ≠ 0, k ≠ 0, значит, y = kx + b — функция общего вида;

b = 0, k = 0, значит, y = 0— как четная, так и нечетная функция.

Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.

График функции пересекает оси координат:

ось абсцисс ОХ — в точке (−b/k; 0);

ось ординат OY — в точке (0; b).

x = −b/k — является нулем функции.

Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.

Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.

Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0 функция принимает отрицательные значения на промежутке (−∞; −b/k) и положительные значения на промежутке (−b/k; +∞).

При k 0, то этот угол острый, если k

Построение линейной функции

В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида у = kx + b, достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.

Например, чтобы построить график функции y = 1/3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:

В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:

если k > 0, то график наклонен вправо;

если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;

если b 0, то график функции y = kx + b выглядит так:

0″ src=”https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png” style=”height: 600px;”>

Если k > 0 и b > 0, то график функции y = kx + b выглядит так:

0 и b > 0″ src=”https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png” style=”height: 600px;”>

Если k > 0 и b

В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.

Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.

Например, график уравнения х = 3:

Условие параллельности двух прямых:

График функции y = k₁x + b₁ параллелен графику функции y = k₂x + b₂, если k₁ = k₂.

Условие перпендикулярности двух прямых:

График функции y = k₁x + b₁ перпендикулярен графику функции y = k₂x + b₂, если k₁k₂ = −1 или k₁ = −1/k₂.

Точки пересечения графика функции y = kx + b с осями координат:

С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.

Координаты точки пересечения с осью OY: (0; b).

С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = −b/k.

Координаты точки пересечения с осью OX: (−b/k; 0).

Решение задач на линейную функцию

Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!

Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.

В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.

Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.

Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:

Таким образом, нам надо построить график функции y = -4x – 10

Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).

Поставим эти точки в координатной плоскости и соединим прямой:

Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).

Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.

Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.

Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.

Вычтем из второго уравнения системы первое, и получим k = 3.

Подставим значение k в первое уравнение системы, и получим b = -2.

Ответ: уравнение прямой y = 3x – 2.

[spoiler title=”источники:”]

http://obrazavr.ru/algebra/7-klass-algebra/linejnaya-funktsiya-i-eyo-grafik/linejnaya-funktsiya/koeffitsienty-k-i-b/

http://skysmart.ru/articles/mathematic/grafik-linejnoj-funkcii

[/spoiler]

На прошлых уроках мы рассмотрели линейную функцию и научились строить ее график на координатной плоскости. На этом уроке мы углубимся в теорию и разберем, почему график выглядит именно так.

Вспомним, что линейная функция имеет вид $y = kx+b$, где $x$ – переменная, а $k$ и $b$ – некоторые числа, называемые коэффициентами.

Например,

• $y = textcolor{blue}{5}x + color{green}{10}$ – линейная функция
• $color{blue} k = 5$
• $color{green} b = 10$.

График линейной функции – прямая линия, а ее положение на плоскости зависит от того, какие у функции $k$ и $b$.

Коэффициент $k$ называют угловым, так как он показывает угол наклона линейной функции на графике относительно оси $Ox$

Коэффициент b

Коэффициент $b$ называют свободным. На графике он показывает длину отрезка, который отсекает линия функции по оси ординат относительно начала координат. 

Другими словами, коэффициент $b$ показывает, насколько график выше или ниже оси $Oy$.

• Если $b > 0$, график сдвинут вверх,
• если $b < 0$, то график сдвинут вниз.

На нашем графике функции из примера про копилку видно, что прямая пересекает ось $Oy$ выше начала координат на $500$ единиц (этому числу и равен коэффициент $b$).

Частные случаи. b = 0

Если коэффициент $b = 0$, функция приобретает вид $y = kx + 0$, что можно сократить до $y = kx$.

Подставим в формулу $x = 0$, получим: $$y = k times 0$$

Значит, график будет проходить через начало координат $O(0;0)$.

Для построения графика функции вида $y = kx$ достаточно найти одну точку, вторая – начало координат.

k = 0

Если коэффициент $k = 0$, угол наклона также будет равен $0$.

Функция при этом принимает вид $y = 0 times x + b$, то есть $y = b$.

Куда делась переменная $x$? Она нам больше не нужна, так как какой бы $x$ мы не подставили, значение $y$ не изменится.

Таблица

Нахождение коэффициентов квадратичной функции y=ax² + bx +c

I Нахождение коэффициента а :

1. по графику параболы определяем координаты вершины (m,n)

2. по графику параболы определяем координаты любой точки A (x;y)

3. подставляем эти значения в формулу квадратичной функции, заданной в другом виде:

y=а(х-m)²+n

1. решаем полученное уравнение.

II. нахождение коэффициента b: b= – (х₁ + х₂) это для приведённого уравнения

1. Сначала находим значение коэффициента a (шаг I, смотри выше)

В формулу для абсциссы параболы m = 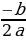подставляем значения m и а

1. Вычисляем значение коэффициента b.

III. нахождение коэффициента с: с = х₁ ∙ х₂ это для приведённого уравнения

1. Находим координату у точки пересечения графика параболы с осью Оу, это значение равно коэффициенту с, т.е. точка (0;C)-точка пересечения графика параболы с осью Оу.

2. Если по графику невозможно найти точку пересечения с осью Оу, то выполняем шаги I, II {находим коэффициенты а,Ь)

3. Подставляем найденные значения а, b ,А(х ; у) в уравнение у=ах² +bх+с и находим с.

I Нахождение коэффициента а :

1. по графику параболы определяем координаты вершины (m,n)

2. по графику параболы определяем координаты любой точки A (x;y)

3. подставляем эти значения в формулу квадратичной функции, заданной в другом виде:

y=а(х-m)²+n

1. решаем полученное уравнение.

II. нахождение коэффициента b:

1. Сначала находим значение коэффициента a (шаг I, смотри выше)

В формулу для абсциссы параболы m = 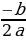подставляем значения m и а

1. Вычисляем значение коэффициента b.

III. нахождение коэффициента с:

1. Находим координату у точки пересечения графика параболы с осью Оу, это значение равно коэффициенту с, т.е. точка (0;C)-точка пересечения графика параболы с осью Оу.

2. Если по графику невозможно найти точку пересечения с осью Оу, то выполняем шаги I, II {находим коэффициенты а,b)

3. Подставляем найденные значения а, b ,А(х ; у) в уравнение у=ах² +bх+с и находим с.

Рассмотрим задачу: где невозможно по графику найти точно m и n необходимо найти все коэффициенты уравнения, задающего график:

Найти все коэффициенты по графику функции

Подставляем в уравнение: координаты выбранных точек, например, таких: (2;2), (5;2), (4;-3). Получается:

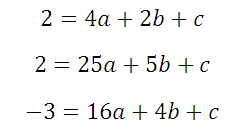
Последние два уравнения вычтем:

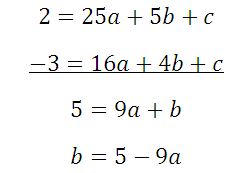
Данное выражение подставим в первое и второе уравнения:

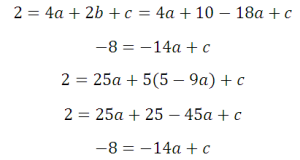
Вычтем два получившихся уравнения:

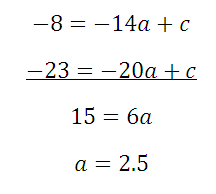Зная а, можем найти и остальные коэффициенты:

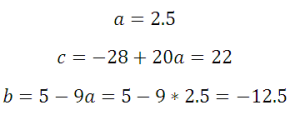
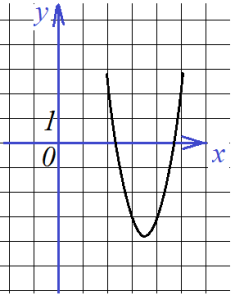
Следующая задача: найти коэффициенты уравнения, задающего график функции, изображенный на рисунке:

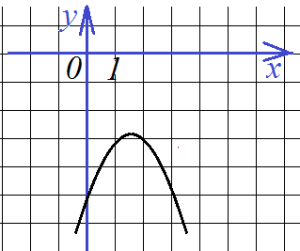
Найти все коэффициенты по графику функции

Здесь будет немного попроще, так как определить коэффициент с можно по рисунку: с=-5. Это значит, что потребуется только две точки, и система будет состоять только из двух уравнений. Возьмем для ее составления точки (1;-3) и (2;-3):

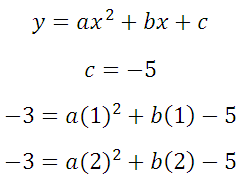
Вычтем получившиеся уравнения (второе – из первого) и определим коэффициенты а и b:

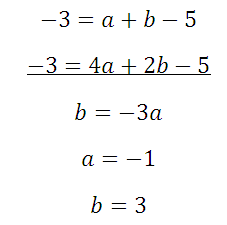
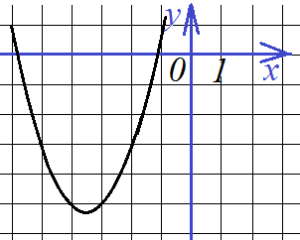
Найти все коэффициенты по графику функции

Наконец, еще одно такое же задание. Снова необходимо определить все коэффициенты функции, график которой представлен на рисунке:

Зададимся точками. Их будет три, уравнений тоже три, так как нам необходимо найти три коэффициента – a, b и c.

Точки будут: (-2; -3),(-5; -3) и  (-3; -5) . Тогда уравнения:

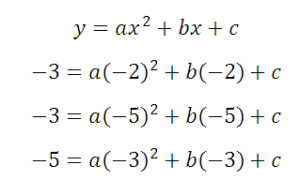
Из первого уравнения вычитаем второе:

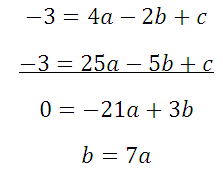
Полученное подставим в первое и третье:

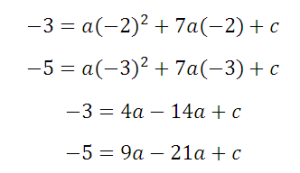
Полученные уравнения вычтем вновь, и найдем искомое: