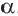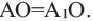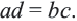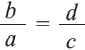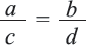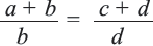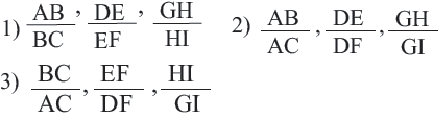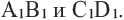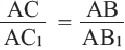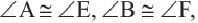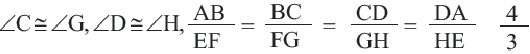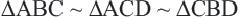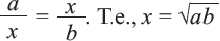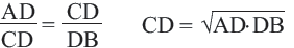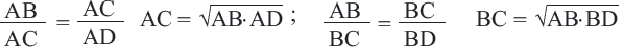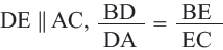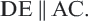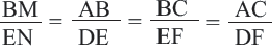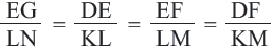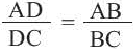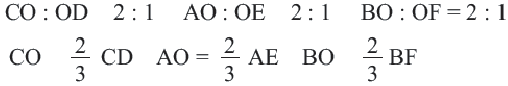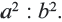Подобные треугольники
Определение
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.
Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.
Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.
Признаки подобия треугольников
I признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
II признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Свойства подобных треугольников
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
- Отношение периметров подобных треугольников равно коэффициенту подобия.
- Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.
Примеры наиболее часто встречающихся подобных треугольников
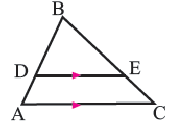
1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.
2. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –
3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.
Здесь вы найдете подборку задач по теме «Подобные треугольники» .
Математика
252. Понятие о подобии треугольников распространяется и на многоугольники. Пусть дан многоугольник ABCDE (чер. 245); выполним построение аналогичное п. 206. Построим диагонали AC и AD и, выбрав какую-либо точку K на стороне AB между точками A и B или вне отрезка AB, построим KL || BC до пересечения с диагональю AC, затем LM || CD до пересечения с AD и, наконец, MN || DE до пересечения с AE. Тогда получится многоугольник AKLMN, который связан с ABCD следующими зависимостями:
1) Углы одного многоугольника равны попарно углам другого: угол A у них общий, ∠K = ∠B (как соответственные), ∠KLM = ∠BCD, ибо ∠KLA = ∠BCA и ∠ALM = ∠ACD и т. д.
2) Сходственные стороны этих многоугольников пропорциональны, т. е. отношение одной пары сходственных сторон равно отношению другой пары, равно отношению третьей пары и т. д.
«Сходственные» стороны здесь надо понимать несколько иначе, чем для треугольников: здесь считаем сходственными сторонами те, которые заключены между равными углами, например, BC и KL.
Справедливость указанной пропорциональности видна следующим образом:
∆ABC, следовательно, AK/AB = KL/BC = AL/AC
∆ALM
∆ACD, следовательно, AL/AC = LM/CD = AM/AD
∆AMN
∆ADE, следовательно, AM/AD = MN/DE = AN/AE
Мы видим, что среди первых трех равных отношений и среди вторых трех равных отношений имеется одно одинаковое AL/AC; также и последние три отношения связываются с предыдущими отношением AM/AD. Поэтому, пропуская отношения диагоналей, получим:
AK/AB = KL/BC = LM/CD = MN/DE = AN/AE
Все это остается, как легко видеть, справедливым и для многоугольника с большим, чем у нас, числом сторон.
Если мы многоугольник AKLMN перенесем в другое место плоскости, то найденные выше 2 соотношения этого многоугольника с ABCDE останутся в силе; такие многоугольники называются подобными. Итак, два многоугольника называются подобными, если углы одного равны попарно углам другого и если сходственные стороны их пропорциональны .
Мы, следовательно, умеем строить многоугольник, подобный данному. Мы построили AKLMN
Мы видим еще, что в многоугольниках ABCDE и AKLMN построены диагонали из их соответственных вершин,причем получилось два ряда подобных треугольников: ∆AKL
∆ADE — треугольники эти одинаково расположены в обоих многоугольниках.
Возникает вопрос, останется ли в силе последнее свойство, если мы построим многоугольник, подобный данному, каким-либо еще способом, не тем, которым мы пользовались здесь.
253. Пусть как-либо построен многоугольник A’B’C’D’E’ подобный многоугольнику ABCDE (чер. 246), т. е. так, что
∠A’ = ∠A, ∠B’ = ∠B, ∠C’ = ∠C, ∠D’ = ∠D, ∠E’ = ∠E (1)
A’B’/AB = B’C’/BC = C’D’/CD = D’E’/DE = E’A’/EA (2)
Вопрос конца предыдущего п. равносилен другому: можно ли привести эти два многоугольника в положение, чтобы, например, точка A’ совпала с A, а остальные вершины были бы расположены попарно на прямых, идущих из этой общей точки, и чтобы сходственные стороны их или были параллельны, или сторона одного многоугольника расположилась бы на стороне другого.
Решим этот вопрос. Для этого отложим на стороне AB от точки A отрезок AK = A’B’ и, пользуясь предыдущим п., построим многоугольник AKLMN
Остается выяснить, может ли многоугольник A’B’C’D’E’ совпасть при наложении с AKLMN.
Мы имеем: AK/AB = KL/BC = LM/CD = MN/DE = NA/EA.
Сравнивая эти равенства с равенствами (2) и принимая во внимание, что AK = A’B’, легко получаем KL = B’C’, LM = C’D’ и т. д., т. е. все стороны многоугольников A’B’C’D’E’ и AKLMN попарно равны. Наложим многоугольник A’B’C’D’E’ на AKLMN так, чтобы A’ попала в A и сторона A’B’ совпала бы с AK (мы ведь строили AK = A’B’); тогда, в силу равенства углов B’ и K, сторона B’C’ пойдет по KL, в силу равенства сторон KL и B’C’, точка C’ попадет в L и т. д.
Итак, A’B’C’D’E’ совпадает с AKLMN, а следовательно, если построим диагонали A’C’ и A’D’, получим ряд треугольников, подобных и одинаково расположенных с ∆ABC, ∆ACD и т. д.
Поэтому заключаем: Если построить в подобных многоугольниках диагонали из соответственных вершин, то получим 2 ряда подобных и одинаково расположенных треугольников.
Легко увидать справедливость и обратного заключения: если, ∆A’B’C’
∆ADE, то многоугольник A’B’C’D’E’
многоугольнику ABCDE. Тогда ∆A’B’C’ = ∆AKL, ∆A’C’D’ = ∆ALM и ∆A’D’E’ = ∆AMN, откуда следует равенство многоугольников A’B’C’D’E’ и AKLMN и, следовательно, подобие A’B’C’D’E’ и ABCDE.
254. То положение (две соответственных вершины сливаются в одной точке, остальные вершины попарно лежат на прямых, проходящих чрез эту точку, а сходственные стороны параллельны), в которое нам удалось привести два подобных многоугольника, является частным случаем другого более общего положения двух подобных многоугольников.
Пусть имеем KLMN
ABCD (чер. 247). Возьмем какую-либо точку S и соединим ее со всеми вершинами A, B, C и D первого многоугольника. Постараемся построить многоугольник, равный многоугольнику KLMN, так, чтобы его вершины лежали на прямых SA, SB, SC и SD и стороны были бы параллельны сторонам многоугольника ABCD.
Для этого отложим на стороне AB отрезок AP = KL (полагаем, что KL и AB сходственные стороны) и построим PB’ || AS (на чертеже точка P и прямая PB’ не даны). Чрез точку B’, где SB пересекается с PB’, построим B’A’ || AB. Тогда A’B’ = AP = KL, затем построим B’C’ || BC, чрез точку C’, где B’C’ пересекается с SC, проведем C’D’ || CD и точку D’, где C’D’ пересекается с SD, соединим с A’. Получим многоугольник A’B’C’D’, который, как это сейчас увидим, подобен многоугольнику ABCD.
Так как A’B’ || AB, то ∆SA’B’
SA’/SA = A’B’/AB = SB’/SB (1)
Так как B’C’ || BC, то ∆SB’C’
SB’/SB = B’C’/BC = SC’/SC (2)
Так как C’D’ || CD, то ∆SC’D’
SC’/SC = C’D’/CD = SD’/SD (3)
Отсюда можно вывести, что SA’/SA = SD’/SD, а следовательно ∆SA’D’
∆SAD, так как две стороны одного пропорциональны двум сторонам другого и углы между ними равны (∠S общий), – A’D’ || AD и
SD’/SD = D’A’/DA = SA’/SA (4)
Из равенств отношений (1), (2), (3) и (4) легко получаем:
A’B’/AB = B’C’/BC = C’D’/CD = D’A’/DA (5)
Кроме того, ∠A’ = ∠A, ∠B’ = ∠B и т. д., как углы с параллельными сторонами. Следовательно, A’B’C’D’
Далее легко увидать, что KLMN = A’B’C’D’. В самом деле, ∠K = ∠A, но ∠A = ∠A’, следовательно, ∠K = ∠A’; также ∠L = ∠B’ и т. д. – углы у наших многоугольников равны. Креме того, из подобия KLMN
KL/AB = LM/BC = MN/CD = NK/DA.
Сравнивая эти равные отношения с равенствами (5) и имея в виду, что A’B’ = KL, находим: B’C’ = LM, C’D’ = MN, D’A’ = NK. Теперь легко, как это делали выше, увидать, что KLMN при наложении совместится с A’B’C’D’. Следовательно, нам удалось поместить данные подобные многоугольники в такое положение, что их вершины расположены попарно на прямых, проходящих чрез точку S и их сходственные стороны параллельны, к чему мы и стремились.
Заметим еще, что соответственные вершины в наших многоугольниках следуют друг за другом в одном направлении (см. стрелки около многоугольников ABCD, KLMN и A’B’C’D’) — по часовой стрелке.
Если бы вершины одного многоугольника, соответствующие последовательным вершинам другого, шли друг за другом в направлении, обратном тому, как они расположены в другом, то удалось бы поместить наши многоугольники так, чтобы соответствующие вершины располагались по разные стороны от точки S (см. чер. 248).
Точка S, где сходятся прямые, соединяющие пары соответственных вершин многоугольников, называется центром подобия; в первом случае (чер. 247), когда обе соответственные вершины (например, A и A’) расположены в одной стороне от S, центр подобия называется внешним , а во втором (чер. 248), когда соответствующие вершины расположены по разные стороны точки S, центр подобия называется внутренним . Если подобные многоугольники расположены так, что они имеют центр подобия, то говорят, что они подобно расположены .
255. Если нам дан многоугольник ABCD (чер. 247 или 248), – будем данный многоугольник называть оригиналом , – мы можем, выбрав произвольную точку S, получать его изображения, подобные ему в каком угодно масштабе , – этим именем называют отношение какого-либо отрезка изображения к соответствующему отрезку в оригинале (в данном многоугольнике). Это отношение называют еще коэффициентом подобия — обозначим его через k. Пока еще для нас коэффициентом подобия является отношение стороны изображения к стороне оригинала, т. е.
A’B/AB = B’C/BC = … = k.
В дальнейшем мы распространим это понятие на отношение всяких двух отрезков изображения и оригинала, сходственных между собою.
Из равенства (1), (2), (3) и (4) предыдущего п., имеем:
SA’/SA = SB’/SB = SC’/SC = SD’/SD = A’B’/AB = k,
т. е. отношение расстояний от центра подобия соответственных вершин изображения и оригинала = коэффициенту подобия.
Под именем фигура (плоская) мы понимаем совокупность точек и линий плоскостей. Многоугольники ABCD — есть фигура. Присоединим еще одну точку (выбранную по произволу) E — получим новую фигуру состоящую из многоугольника ABCD и точки E, – найдем изображение точки E. Для этого построим прямую SE и на ней отложим отрезок SE так, чтобы SE’/SE = k (такой отрезок легко построить, пользуясь п. 214); этот отрезок мы можем отложить по направлению SE (чер. 247); или в обратном направлении (чер. 248). Полученная точка E’ и есть изображение точки E — другими словами точки E’ и E суть соответственные точки в наших двух подобных и подобно расположенных фигурах.
Соединив точку E, например, с B и точку E’ с B’ (B и B’ суть тоже соответственные точки), получим два соответствующих друг другу отрезка BE и B’E’.
Легко увидать, что ∆SBE
∆SB’E’ (так как ∠BSE = ∠B’SE и стороны, составляющие эти углы, пропорциональны: SB’/SB = k и SE’/SE = k, – следовательно, SB’/SB = SE’/SE), отсюда вытекает:
1) B’E’ || BE и 2) B’E’/BE = SB’/SB = k
т. е. соответствующие друг другу отрезки в изображении и оригинале 1) параллельны между собою и 2) их отношение равно коэффициенту подобия .
Отсюда вытекает возможность следующего построения для нахождения точки, соответствующей данной в оригинале точке, если уже имеем одну пару соответствующих точек и известен центр подобия: пусть имеем пару соответствующих точек B и B’ и требуется найти точку, соответствующую точке E, – строим прямые SE и BE и чрез B’ строим прямую, параллельную BE, ее точка пересечения E’ с SE и даст искомую точку.
256. Построим для какой-либо фигуры, одна точка которой есть A (чер. 249), ее изображения, принимая две произвольных точки S1 и S2 за внешние центры подобия и числа k1 и k2 за коэффициенты подобия. Пусть в первом изображении точке A соответствует точка A’ и во втором изображении этой же точке соответствует точка A”.
Присоединим еще к данной фигуре какую-либо точку B, лежащую на прямой S1S2; тогда этой точке B соответствуют в первом изображении точка B’ и во втором точка B”, причем точки B’ и B” должны лежать на той же прямой S1S2 и прямые AB, A’B’ и A”B” должны быть параллельны и одинаково направлены.
Соединим точки A’ и A”, найдем точку пересечения S3 прямых A”A’ и S2S1. Тогда из подобия треугольников S3A’B’ и S2A”B” находим:
Соединив точки A’ и A”, найдем точку пересечения S3 прямых A”A’ и S2S1. Тогда из подобия треугольников S3A’B’ и S2A”B” находим:
т. е. точка S2 должна делить отрезок B’B” внешним образом в отношении, равном данному числу k1/k2. Мы знаем (п. 217), что существует только одна точка, которая делит данный отрезок B’B” в данном отношении внешним образом. Если мы возьмем какую-либо еще точку C данной фигуры и построим ее изображения C’ и C”, то, соединив точки C’ и C” и взяв точку пересечения, назовем ее опять S3, прямой C’C” с прямой S1S2, получим, что ∆S3B’C’
∆S3B”C” (B”C” || BC и B’C’ || BC, следовательно, B”C” || B’C’), откуда опять найдем, что S3B’/S3B” = k1/k2, т. е. новая точка S3 совпадает с прежнею. Следовательно, S3 есть центр подобия фигур (A’B’C’. ) и (A”B”C”. ) и притом внешний, ибо направления, в котором следуют друг за другом соответствующие точки в обеих фигурах, одинаковы. Из этого заключаем, что фигуры (A’B’C’. ) и (A”B”C”. ) также имеют внешний центр подобия и он расположен на одной прямой с центрами S1 и S2.
Если одни из центров подобия S1 взять внешний, а другой S2 внутренний (чер. 250), то направления соответствующих отрезков таковы: A’B’ одинаково с направлением AB, но A”B” обратно направлению AB, – следовательно, направление A”B” обратно A’B’ и S3 является внутренним центром подобия фигур (A’B’. ) и (A”B”. ).
Если взять оба центра подобия внутренними (например, S2 и S3 на чер. 250), то легко увидать, что третий центр подобия окажется внешним. Итак, вообще:
Если три фигуры попарно подобно расположены, то три центра подобия расположены на одной прямой, причем или все три они внешние, или два из них внутренних, а один внешний.
257. Отношение периметров и площадей подобных многоугольников.
Пусть имеем два подобных многоугольника ABCDEF и A’B’C’D’E’F’ (чер. 251). Назовем коэффициент подобия чрез k.
A’B’/AB = k, B’C’/BC = k и т. д.,
A’B’ = k · AB, B’C’ = k · BC, C’D’ = k · CD, …
Сложив эти равенства по частям и вынеся множитель k во второй части за скобку, получим:
A’B’ + B’C’ + C’D’ + … = k(AB + BC + CD + …),
(A’B’ + B’C’ + C’D’ …) / (AB + BC + CD + …) = k = A’B’/AB,
т. е. отношение периметров подобных треугольников равно отношению сходственных сторон (или равно коэффициенту подобия).
Выберем две соответственных вершины, напр., A и A’, и построим проходящие чрез них диагонали. Тогда мы знаем: 1) (из п. 253) ∆ABC
∆A’C’D’ и т. д. 2) (из п. 212). Отношение площадей подобных треугольников равно квадрату отношения их сходственных сторон, следовательно,
пл. ∆A’B’C’ / пл. ∆ABC = (A’B’/AB) 2 = k 2 ; пл. ∆A’C’D’ / пл. ∆ACD = (C’D’/CD) 2 = k 2 и т. д.,
пл. ∆A’B’C’ = k 2 · пл. ∆ABC; пл. ∆A’C’D’ = k 2 · пл. ∆ACD;
пл. ∆A’D’E’ = k 2 · пл. ∆ADE .
Сложив эти равенства по частям и вынеся общего множителя k 2 во второй части за скобку получим:
пл. ∆A’B’C’ + пл. ∆A’C’D’ + ∆A’D’E’ + … = k 2 (пл. ∆ABC + пл. ∆ACD + пл. ∆ADE + …),
пл. A’B’C’D’E’F’ / пл. ABCDEF = k 2 = (A’B’/AB) 2 ,
т. е. отношение площадей подобных многоугольников равно квадрату отношения их сходственных сторон (или равно квадрату коэффициента подобия).
258. Два правильных одноименных многоугольника всегда подобны. В самом деле, углы у одноименных многоугольников одинаковы (п. 248), а так как все стороны каждого равны между собою, то, очевидно, отношение любой стороны одного к любой стороне другого есть число постоянное.
Если в круг впишем какой-либо правильный многоугольник (чер. 252) и чрез середины дуг, стягиваемых его сторонами, построим касательные к кругу, то получим правильный одноименный многоугольник, описанный около этого круга. Не трудно выяснить (предоставляем это желающим), что полученные два правильные многоугольника подобно расположены, и центр круга служит их внешним центром подобия, – внешним потому, что каждая пара соответствующих точек (напр., A и A’) расположена в одном направлении от центра (если многоугольник имеет четное число сторон, то центр круга можно считать и внутренним центром подобия, надо лишь считать, что, например, точке A соответствует точка A”).
259. Упражнения.
1. Стороны одного пятиугольника равны соответственно 12, 14, 10, 8 и 16 дм. Найти стороны другого пятиугольника, подобного первому, если его периметр = 80 дм.
2. Сумма площадей двух подобных многоугольников равна 250 кв. дм., а отношение двух сходственных сторон = ¾. Вычислить площадь каждого из них.
3. Показать, что если в круг вписан правильный многоугольник с нечетным числом сторон и в его вершинах построены касательные к кругу, то получится описанный многоугольник, подобно расположенный с вписанным, – центр круга служит их внутренним центром подобия.
4. Дан треугольник; построить другой треугольник, подобно расположенный с первым так, чтобы центр тяжести первого служил внутренним центом подобия и чтобы коэффициент подобия = ½. Выяснить при помощи этого, как расположены точки высот, центр тяжести и центр описанного круга данного треугольника.
5. В данный треугольник вписан квадрат.
Пусть ABC данный треугольник (чер. 253) и DEFK искомый квадрат. Построим еще квадрат MNPQ, чтобы одна сторона MQ лежала на стороне AC треугольника и точка N на стороне AB. Легко видеть, что квадрат MNPQ подобно расположен с искомым квадратом DEFK и внешним их центром подобия является точка A; следовательно, точка F лежит на прямой AP. После нахождения точки F искомый квадрат легко построить.
6. Дан угол и точка внутри его. Найти на одной стороне угла точку, равноудаленную от данной точки и от другой стороны.
Задача решается тем же приемом.
7. Построить треугольник по его высотам.
Легко получить, называя стороны треугольника чрез a, b и c и соответствующие высоты чрез ha, hb и hc, следующую зависимость:
Легко построить отрезок x = (hbha)/hc (x/ha = hb/hc — построение 4-го пропорционального), после чего построим треугольник со сторонами hb, ha и x. Этот треугольник подобен искомому, так как a : h : c = hb : ha : x; остается построить треугольник подобный только что построенному так, чтобы одна его высота была равна данной.
Подобие фигур
Подобие фигур — это две геометрические фигуры или два геометрических тела называются подобными, если одно представляет собой уменьшенную модель другого.
Содержание:
Понятие подобия фигур
В окружающем мире часто встречаются предметы, одинаковые по форме, но различные по размерам: мыльный пузырь и футбольный мяч, небольшая модель ледокола и сам корабль, карты, фотоснимки различных размеров одного и того же здания. В геометрии такие фигуры называют подобными.
Существуют фигуры, которые всегда подобны друг другу, например, круги, квадраты, кубы.
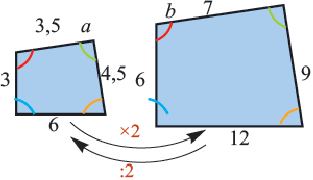
Для обозначения подобия фигур употребляется знак . На рисунке 2.434 изображены подобные фигуры . Запись читается: фигура подобна фигуре
Для подобных фигур вводится понятие — коэффициент подобия, он обозначается k; k всегда больше нуля. Коэффициент подобия показывает, в каком отношении находятся соответствующие расстояния между точками фигур. На рисунке 2.434 коэффициент подобия можно определить, найдя отношения сторон квадратиков изображенной сетки.
Подобие фигур широко используется при разработке планов построек зданий или при изображении на картах городов или других участков земной поверхности. Всякий план или карта является подобным изображением реального объекта или участка земной поверхности, т. е. фигурой, подобной реальному объекту. При этом план или карта может изображать реальный объект в разном масштабе.
Определение. Масштаб — это коэффициент подобия соответствующих фигур.
Подобие треугольников
На рисунке 2.435 изображены два чертежных прямоугольных треугольника с острыми углами в 60° и 30°. Стороны второго треугольника по сравнению с первым уменьшены в два раза: У этих треугольников углы попарно равны. Стороны, лежащие против разных углов, пропорциональны: Такие треугольники называют подобными. Стороны, лежащие против равных углов, называют сходственными.
Определение. Подобными называют треугольники, у которых углы попарно равны, а сходственные стороны пропорциональны.
Подобие треугольников записывается так: Отношение сходственных сторон подобных треугольников называется коэффициентом подобия. В случае, изображенном на рисунке 2.435, коэффициентом подобия треугольников будет число 2. Если же взять отношения , коэффициент подобия будет равен .
Подобные треугольники могут быть произвольно расположены как на плоскости, так и в пространстве.
Если фигуры равны, то они подобны с коэффициентом подобия, равным 1. Если фигуры подобны, то они не обязательно равны.
Теорема 1. (Лемма о подобии треугольников). Прямая, пересекающая две стороны треугольника и проведенная параллельно третьей стороне, отсекает треугольник, подобный данному.
Для выявления подобия треугольников существуют признаки подобия треугольников.
Теорема 2. (Первый признак — по двум равным углам.) Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого.
Следствия из этой теоремы.
1. Равносторонние треугольники подобны.
2. Равнобедренные треугольники подобны, если они имеют по равному углу при вершине или при основании.
3. Два прямоугольных треугольника подобны, если они имеют по равному острому углу.
4. Равнобедренные прямоугольные треугольники подобны.
Теорема 3. (Второй признак — по пропорциональности двух сторон и равенству углов между ними.) Два треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, лежащие между ними, равны.
Следствие. Прямоугольные треугольники подобны, если катеты одного из них пропорциональны катетам другого.
Теорема 4. (Третий признак — по пропорциональности трех сторон.) Два треугольника подобны, если три стороны одного треугольника пропорциональны трем сторонам другого треугольника.
Теорема 5. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Подобие многоугольников
Определение. Если стороны одного многоугольника пропорциональны сторонам другого многоугольника и соответственные углы этих многоугольников равны, то такие многоугольники подобны.
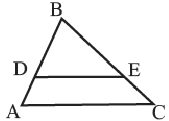
На рисунке 2.436 изображены два подобных пятиугольника , у них а также k – коэффициент подобия.
Для многоугольников с числом сторон больше трех признак подобия, аналогичный третьему признаку подобия треугольников, будет неверен. Например, квадрат и ромб, отличный от квадрата, не будут подобны, хотя их стороны пропорциональны (рис. 2.437). Недостаточно для подобия двух прямоугольников и равенства их соответствующих углов. Например, квадрат не подобен четырехугольнику, не все стороны которого равны (рис. 2.438).
Теорема 6. Отношение периметров подобных многоугольников равно отношению их сходственных сторон (коэффициенту подобия).
Теорема 7. Отношение площадей подобных многоугольников равно квадрату коэффициента подобия.
Эта лекция взята со страницы полного курса лекций по изучению предмета “Математика”:
Смотрите также дополнительные лекции по предмету “Математика”:
[spoiler title=”источники:”]
http://maths-public.ru/planimetry/polygons-similarity
http://natalibrilenova.ru/podobie-figur/
[/spoiler]
Вступление
Думаю много кого интересовал факт того, что у подобных фигур площади соотносятся как квадрат коэффициента подобия соответственно. Сегодня я покажу как это доказывается.
Квадрат коэффициента подобия.
У нас есть два треугольника, они подобны с коэффициентом k – а это значит, что у большого треугольника все соответственные стороны, высоты, биссектрисы, и т.д. увеличены в k раз.
Как видно, основание большого треугольника увеличено в k раз.
Давайте теперь к основаниям этих треугольников опустим высоты.
Как опять видно, высота тоже будет увеличена в k раз, т.к. она опущена на соответственную сторону.
Ну и теперь посчитаем площадь этих треугольников через основание и высоту(моя статья где есть док-во этой формулы).
Для удобства запишем формулы рядом.
И теперь сделаем вот такой трюк, мы возьмем и разделим два этих равенства друг на друга.(так можно делать, если они, конечно, не равны нулю, про это я писал статью).
Ну а далее сокращаем одинаковые множители.
Вот и всё, для удобства можно перевернуть дроби
Этот факт очень часто используется на ЕГЭ, он особенно полезен в задачах, связанных с окружностью, здесь есть разбор подобного задания(пример 1).
Спасибо за просмотр, подписывайтесь, ставьте лайки 🙂
Подобие фигур — это две геометрические фигуры или два геометрических тела называются подобными, если одно представляет собой уменьшенную модель другого.
Содержание:
- Понятие подобия фигур
- Подобие треугольников
- Подобие многоугольников
Понятие подобия фигур
В окружающем мире часто встречаются предметы, одинаковые по форме, но различные по размерам: мыльный пузырь и футбольный мяч, небольшая модель ледокола и сам корабль, карты, фотоснимки различных размеров одного и того же здания. В геометрии такие фигуры называют подобными.
Существуют фигуры, которые всегда подобны друг другу, например, круги, квадраты, кубы.
Для обозначения подобия фигур употребляется знак 



Для подобных фигур вводится понятие — коэффициент подобия, он обозначается k; k всегда больше нуля. Коэффициент подобия показывает, в каком отношении находятся соответствующие расстояния между точками фигур. На рисунке 2.434 коэффициент подобия можно определить, найдя отношения сторон квадратиков изображенной сетки.
Подобие фигур широко используется при разработке планов построек зданий или при изображении на картах городов или других участков земной поверхности. Всякий план или карта является подобным изображением реального объекта или участка земной поверхности, т. е. фигурой, подобной реальному объекту. При этом план или карта может изображать реальный объект в разном масштабе.
Определение. Масштаб — это коэффициент подобия соответствующих фигур.
Подобие треугольников
На рисунке 2.435 изображены два чертежных прямоугольных треугольника с острыми углами в 60° и 30°. Стороны второго треугольника по сравнению с первым уменьшены в два раза: 

Определение. Подобными называют треугольники, у которых углы попарно равны, а сходственные стороны пропорциональны.
Подобие треугольников записывается так: 



Подобные треугольники могут быть произвольно расположены как на плоскости, так и в пространстве.
Если фигуры равны, то они подобны с коэффициентом подобия, равным 1. Если фигуры подобны, то они не обязательно равны.
Теорема 1. (Лемма о подобии треугольников). Прямая, пересекающая две стороны треугольника и проведенная параллельно третьей стороне, отсекает треугольник, подобный данному.
Для выявления подобия треугольников существуют признаки подобия треугольников.
Теорема 2. (Первый признак — по двум равным углам.) Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого.
Следствия из этой теоремы.
1. Равносторонние треугольники подобны.
2. Равнобедренные треугольники подобны, если они имеют по равному углу при вершине или при основании.
3. Два прямоугольных треугольника подобны, если они имеют по равному острому углу.
4. Равнобедренные прямоугольные треугольники подобны.
Теорема 3. (Второй признак — по пропорциональности двух сторон и равенству углов между ними.) Два треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, лежащие между ними, равны.
Следствие. Прямоугольные треугольники подобны, если катеты одного из них пропорциональны катетам другого.
Теорема 4. (Третий признак — по пропорциональности трех сторон.) Два треугольника подобны, если три стороны одного треугольника пропорциональны трем сторонам другого треугольника.
Теорема 5. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Подобие многоугольников
Определение. Если стороны одного многоугольника пропорциональны сторонам другого многоугольника и соответственные углы этих многоугольников равны, то такие многоугольники подобны.
На рисунке 2.436 изображены два подобных пятиугольника 


Для многоугольников с числом сторон больше трех признак подобия, аналогичный третьему признаку подобия треугольников, будет неверен. Например, квадрат и ромб, отличный от квадрата, не будут подобны, хотя их стороны пропорциональны (рис. 2.437). Недостаточно для подобия двух прямоугольников и равенства их соответствующих углов. Например, квадрат не подобен четырехугольнику, не все стороны которого равны (рис. 2.438).
Теорема 6. Отношение периметров подобных многоугольников равно отношению их сходственных сторон (коэффициенту подобия).
Теорема 7. Отношение площадей подобных многоугольников равно квадрату коэффициента подобия.
Эта лекция взята со страницы полного курса лекций по изучению предмета “Математика”:
- Математика решение заданий и задач
Смотрите также дополнительные лекции по предмету “Математика”:
Лекции:
- Элементарные функции
- Пересекающиеся плоскости
- Как найти производную: примеры решения
- Дифференциальные уравнения примеры решения
- Решение кубических уравнений
- Многоугольники
- Арифметические операции над пределами
- Метод Гаусса: пример решения
- Производные показательной и логарифмической функций
- Вычислить площадь фигуры ограниченной линиями
Найдите коэффициент подобия четырёхугольников сплошадьми 6 м ^ 2 и 24 м ^ 2.
На этой странице сайта, в категории Геометрия размещен ответ на вопрос
Найдите коэффициент подобия четырёхугольников сплошадьми 6 м ^ 2 и 24 м ^ 2?. По уровню сложности вопрос рассчитан на учащихся
5 – 9 классов. Чтобы получить дополнительную информацию по
интересующей теме, воспользуйтесь автоматическим поиском в этой же категории,
чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы
расположена кнопка, с помощью которой можно сформулировать новый вопрос,
который наиболее полно отвечает критериям поиска. Удобный интерфейс
позволяет обсудить интересующую тему с посетителями в комментариях.
Содержание:
Отображение плоскости на себя, которое сохраняет расстояния между точками, называется движением. Примерами движения являются такие преобразования, как центральная симметрия, осевая симметрия, поворот (вращение), скольжение.
Поворот:
Пусть, заданы точка О и угол
1. Если точка А не совпадает с точкой О, то
2. Если точка А совпадает с точкой О, то точки 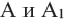
Пример 1. Угол поворота 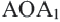
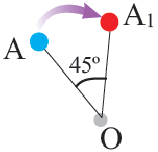
Пример 2. Проанализируйте последовательность шагов, при котором совершается поворот треугольника 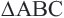
Примечание. Центральная симметрия является поворотом плоскости относительно центра симметрии на 180°.
Исследуйте и начертите в тетради:
На рисунке показана последовательность шагов, которые выполняются при повороте треугольника 
При повороте на угол 90″ в направлении по часовой стрелке координаты вершин изменяются следующим образом.
Отношения, пропорция
Свойства пропорции
Если 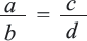
Если 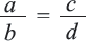
Если 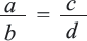
Если 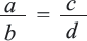
Пропорциональные отрезки
Практическая работа. Пропорциональные отрезки.
1. Начертите в тетради 3 параллельные прямые.
2. Проведите 3 секущие, которые пересекают эти прямые.
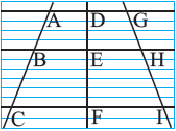
3. Измерьте отрезки АВ, ВС, AC, DE, EF, DF, GH, HI и GI.
4. Запишите и вычислите следующие отношения
5. Можно ли по результатам сказать, что параллельные линии делят секущие на пропорциональные отрезки? Пропорциональные отрезки
Если для отрезков АВ, CD, 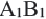
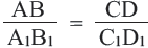
Теорема. Параллельные линии, пересекающие стороны угла, отсекают от них пропорциональные отрезки.
Доказательство. Допустим, что параллельные прямые пересекают стороны угла А в точках В и С, 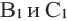
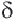
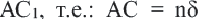
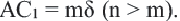
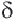
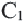
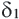
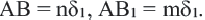
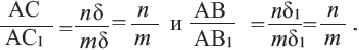
Подобные четырехугольники, подобные треугольники
Подобными называются фигуры одинаковые по форме и у которых соответствующие размеры пропорциональны. Например, все квадраты подобны друг другу, так же как и окружности разных радиусов.
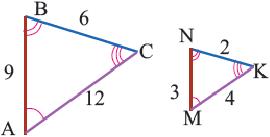
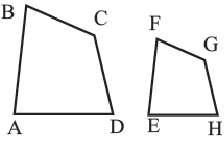
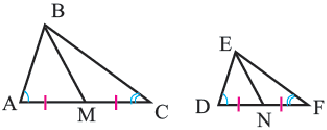
Подобными называются многоугольники, у которых соответствующие углы конгруэнтны, а соответствующие стороны являются пропорциональными отрезками. Например, на рисунке четырёхугольники ABCD и EFGH являются подобными четырёхугольниками. Так как,
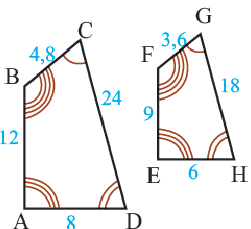
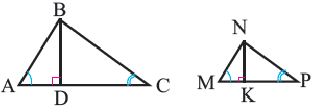
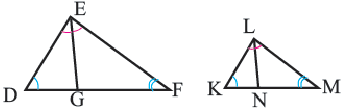
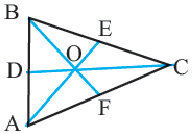
У подобных треугольников соответствующие углы конгруэнтны, а соответствующие стороны являются пропорциональными отрезками. Здесь, говоря о соответствующих сторонах, имеются в виду стороны, которые находятся напротив конгруэнтных углов. На рисунке для 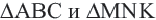
Так как 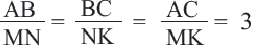
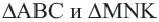
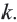
Периметр подобных многоугольников
Теорема. Отношение периметров двух подобных многоугольников равно отношению соответствующих сторон (или коэффициенту подобия)
Если 
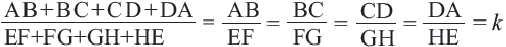
Запишите доказательство теоремы, приняв коэффициент подобия за 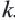
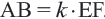
Признаки подобия треугольников
Признак подобия УУ (угол угол)
Если два угла одного треугольника конгруэнтны двум углам другого треугольника, то такие треугольники подобны. Этот признак подобия коротко записывается как УУ.
Признак подобия ССС
Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого треугольника, то такие треугольники подобны. Этот признак подобия коротко записывается как ССС.
Признак подобия СУС
Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами конгруэнтны, то такие треугольники подобны. Этот признак подобия коротко записывается как СУС.
Подобие прямоугольных треугольников
Высота, проведенная к гипотенузе
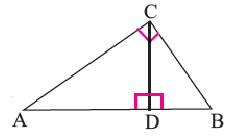
Теорема. Высота, проведённая из вершины прямого угла прямоугольного треугольника, делит его на два подобных треугольника, каждый из которых подобен данному треугольнику.
Доказательство данной теоремы проводится на основании признака подобия УУ Для каждого из трёх треугольников нужно определить два конгруэнтных угла.
Среднее геометрическое
Среднее геометрическое. Для положительных чисел а и b средним геометрическим называется положительное число 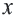
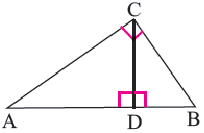
Высота, проведённая из вершины прямого угла на гипотенузу, делит её на два отрезка (на рисунке AD и DB) Здесь отрезки AD и DB являются проекциями катетов АС и ВС на гипотенузу, соответственно.
Следствие 1. Высота прямоугольного треугольника, опущенная из вершины прямого угла есть среднее геометрическое отрезков, на которые она делит гипотенузу.
Следствие 2. Каждый катет прямоугольного треугольника есть среднее геометрическое между гипотенузой и проекцией этого катета на гипотенузу.
Применение подобия треугольников
Пропорциональные отрезки
Теорема. Прямая, пересекающая две стороны треугольника, и параллельная третьей стороне делит стороны на пропорциональные отрезки.
Если
Обратная теорема. Если прямая, пересекающая две стороны треугольника делит их на пропорциональные отрезки, то эта прямая параллельна третьей стороне.
Если 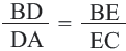
Высоты, медианы и биссектрисы подобных треугольников
Теорема 1. Если два треугольника подобны, то отношение длин соответствующих высот равны отношению длин соответствующих сторон.
Теорема 2. Если два треугольника подобны, то отношение длин соответствующих медиан равны отношению длин д соответствующих сторон.
Теорема 3. Если два треугольника подобны, то отношение длин соответствующих биссектрис равны отношению длин соответствующих сторон.
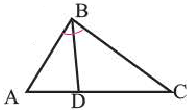
Свойство биссектрисы треугольника
Теорема. Биссектриса треугольника делит противоположную сторону на отрезки пропорциональные двум другим сторонам.
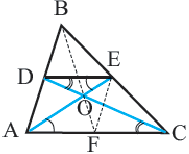
Теорема. Свойство медиан треугольника
Медианы треугольника пересекаются в одной точке и делятся в точке пересечения в отношении 2:1, начиная от вершины.
Точка пересечения медиан называется центром тяжести треугольника.
Доказательство теоремы представлено в виде двухстолбчатой таблицы.
Дано: 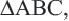
Доказать: AO:OE=CO:OD=BO:OF=2:1
Доказательство: соединим точки O и E.
Преобразование подобия, гомотетия
Гомотетия
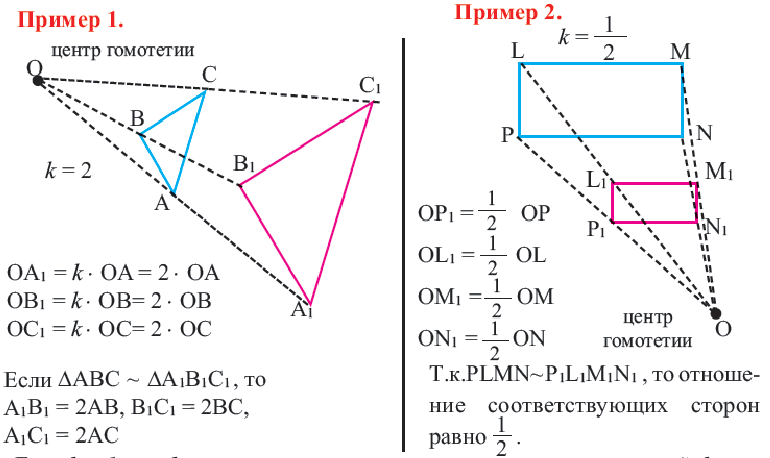
Преобразование плоскости на себя, при котором расстояние между любыми двумя точками изменяется в одно и то же число раз называется преобразованием подобия. Фигуры называются подобными, если одна фигура переводится в другую преобразованием подобия. Если при преобразовании подобия точки А и В на плоскости соответственно преобразованы в точки 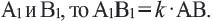
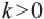
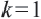
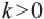
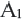
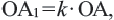
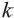
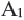
Если 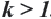
Если 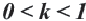
Если 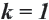
Площади подобных фигур
Теорема. Отношение площадей подобных фигур равно квадрату коэффициента подобия. Например, если отношение соответствующих сторон двух подобных четырёхугольников равно 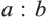
- Многоугольник
- Площадь многоугольника
- Правильные многоугольники
- Вписанные и описанные многоугольники
- Четырехугольник
- Площади фигур в геометрии
- Площади поверхностей геометрических тел
- Вычисление площадей плоских фигур