Как найти коэффициент подобия кругов

Математика

260. Возьмем два круга O и O₁ (чер. 254 и 255). Построим радиус OA и параллельный ему радиус другого круга O₁A₁, который имеет одинаковое направление с OA, или O₁A₁₁ тоже параллельный OA, но имеющий обратное с ним направление. Построим затем прямые AA₁ и AA₁₁, проходящие чрез концы этих радиусов. Тогда представляется следующая задача:

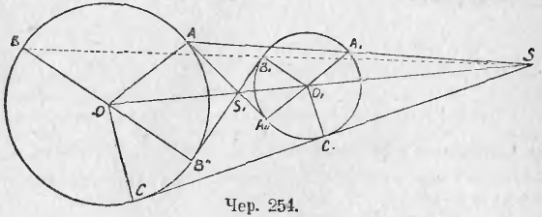
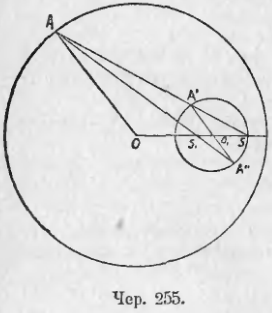
По данным радиусам R и r кругов и по расстоянию их центров OO₁ = d найти расстояние от одного из центров (напр., от O) точек пересечения линий центров с прямою AA₁ и с прямою AA₁₁.

Назовем OS чрез x; тогда O₁S = x – d. ∆OAS

∆O₁A₁S, следовательно, OS/O₁S = OA/O₁A₁ или x/(x – d) = R/r, откуда rx = Rx – dR.
Определяя отсюда x, получим

Отсюда мы видим, что положение точки пересечения S прямых OO₁ и AA₁ не зависит от того, в каком направлении от центра мы построили параллельные радиусы OA и O₁A₁, так что прямая BB₁, соединяющая концы другой пары параллельных радиусов OB и O₁B₁, должна пройти чрез точку S и, кроме того, имеем (∆O₁SB₁

∆OSB): SB₁/SB = r/R. Таким образом точка S обладает всеми свойствами внешнего центра подобия двух подобно расположенных фигур.

Также, называя OS₁ чрез y, получим S₁O₁ = d – y и из подобия ∆OAS₁ и ∆O₁A₁₁S₁: y(d – y) = R/r. Отсюда находим yr = dR – yR и

Отсюда видим, что положение точки S₁ также не зависит от того, какую именно пару параллельных, но идущих в обратных направлениях, радиусов мы взяли. Чрез эти же точку S₁ должна пройти прямая B₁B₁₁, соединяющая концы радиусов OB₁₁ и O₁B₁ параллельных, но имеющих обратные направления. Кроме того, имеем (∆O₁B₁S₁

Таким образом точка S₁ обладает всеми свойствами внутреннего центра подобия двух кругов.

Если один круг лежит внутри другого (чер. 255), то оба центра подобия расположены внутри меньшего круга: внешний лежит вне отрезка OO1, а внутренний — внутри его.

Центры O и O₁ также соответствуют друг другу, так как SO₁/SO = r/R (из подобия ∆OAS и ∆O₁A₁S) и S₁O₁/S₁O = r/R (из подобия ∆S₁O₁A₁₁ и ∆S₁OA).

Итак, всякие два круга подобно расположены и имеют два центра подобия — внутренний и внешний; центру одного круга соответствует центр другого и любой точке одного соответствует та точка другого, которая расположена на радиусе, параллельном радиусу первого круга, идущему чрез взятую точку, и имеющем то же или обратное направление. Обратно: если чрез S построить любую прямую A и соответствующие точки пересечения соединить с центрами, то полученные радиусы должны быть параллельны между собою.

261. Если окажется, что радиус, напр., O₁C₁ (чер. 254), перпендикулярен к прямой SC₁, то и радиус OC, соединяющий центр O другого круга с его точкою C, соответствующей точке C₁, должен быть также перпендикулярен к SC. Отсюда следует, что касательная из точки S к одному из наших кругов должна касаться и другого круга. Точно так же, если построим касательную к одному кругу чрез точку S₁, то она должна касаться и другого круга.

Этим пользуются для решения задачи: построить общую касательную к двум данным кругам .

Надо найти сначала их центры подобия, для чего надо построить радиус OA и параллельный ему диаметр A₁A₁₁ второго круга (чер. 254). Соединив концы A и A₁, найдем внешний центр подобия S и соединив A и A₁₁, найдем внутренний центр подобия S₁. Затем чрез найденные центры подобия S и S₁ построим касательные к одному кругу — они и должны быть общими касательными. Всего общих касательных у двух кругов может быть 4. Если два круга имеют внешнее касание, то точка касания служит их внутренним центром подобия, и общих касательных тогда будем иметь 3; если два круга пересекаются, то внутренний ценр подобия лежит внутри обоих кругов, и из него нельзя построить касательных, – тогда получим только две общих касательных чрез внешний центр подобия; если 2 круга имеют равные радиусы, то внешний центр подобия удаляется в бесконечность и тогда две внешних касательных параллельны линии центров; если два круга имеют внутреннее касание, то точка касания служит их внешним центром подобия, – тогда возможна лишь одна общая касательная; если, наконец, один круг внутри другого, то оба центра подобия расположены внутри обоих кругов, и общих касательных вовсе не существует.

262. Можно применить понятие о центре подобия кругов к решению задачи, которую раньше мы решили другим способом (п. 227 зад. 3): построить круг, касающийся двух пересекающихся прямых и проходящий чрез данную точку .

Точка пересечения данных прямых является внешним центром подобия искомого круга и какого-либо еще касающегося данных прямых и расположенного внутри того же угла, где лежит данная точка, но не проходящего чрез эту точку. Последний круг легко построить. Затем найдем на нем точку, соответствующую данной, построим чрез найденную точку радиус построенного круга, а чрез данную точку построим прямую, параллельную этому радиусу, – точка пересечения ее с биссектором угла и должна быть центром искомого круга. Задача имеет 2 решения, так как у построенного сначала круга можно найти 2 точки, любую из которых можно принять за соответствующую данной.

263. Если возьмем три каких-либо круга O, O₁ и O₂ (чер. 256), то они попарно подобно расположены и к ним применимо свойство п. 256. У этих трех кругов всего 6 центров подобия и они располагаются на четырех прямых: UST, US₁T₁, SU₁T₁ и TS₁U₁. Чрез каждый центр подобия проходят 2 из этих четырех прямых.

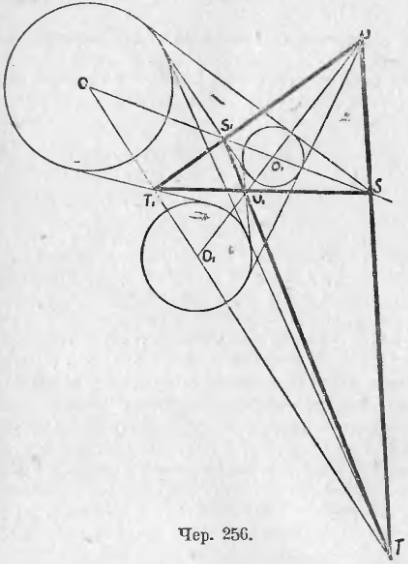
264. Степень точки относительно круга . В п. 222 мы познакомились с понятием о степени точки относительно круга. Этим именем называется, как мы знаем, произведение отрезков какой-либо прямой, проходящей чрез эту точку и пересекающей круг, от этой точки до точек пересечения прямой с кругом. Если точка вне круга, то это произведение равно квадрату касательной из нашей точки к ругу; если точка внутри круга, то это произведение равно квадрату половины хорды, делящейся в этой точке пополам. Чтобы отличить первый случай от второго, считают степень точки во втором случае отрицательною и перед указанным квадратом половины хорды ставят знак минус.

Пусть имеем круг O (чер. 257) и точку M вне его. Построив касательную MA и прямые MO и OA, найдем из прямоугольного треугольника AOM, что степень точки M = MA 2 = OM 2 – OA 2 = OM 2 – R 2 , где OA обозначаем чрез R.

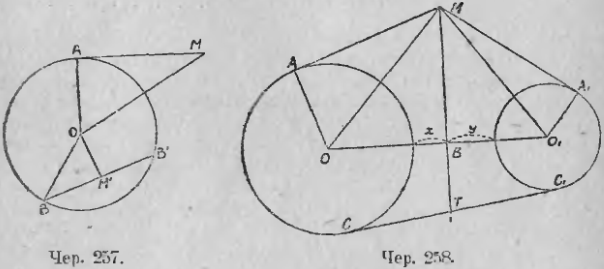
Возьмем теперь точку M₁ внутри круга. Степень этой точки равна произведению отрезков хорды M₁B и M₁B’, взятому со знаком минус. Если эта хорда перпендикулярна к прямой OM₁, соединяющей точку M₁ с центром, то хорда делится в точке M₁ пополам и M₁B₁ = M1B и, следовательно, степень точки M₁ = –M₁B 2 . Из прямоугольного треугольника OM₁B найдем: M₁B 2 = OB 2 – OM₁ 2 = R 2 – OM₁ 2 , а, следовательно, степень точки M₁ = – M₁B 2 = –(R 2 – OM₁ 2 ) = OM₁ 2 – R 2 .

В обоих случаях степень точки выражается одинаково: она равна квадрату расстояния точки от центра минус квадрат радиуса.

Если точка лежит на круге, то легко увидим, что ее степень равна нулю.

265. Пусть теперь имеем 2 круга O и O₁ (чер. 258). Возникает вопрос, не существует ли таких точек, степени которых относительно обоих кругов равны между собой. Если такие точки существуют, то где они расположены? Допустим, что M такая точка. Называя радиус OA чрез R и радиус O₁A₁ чрез r, имеем для этой точки M

Из этого равенства и их равенства OB + O₁B = d мы можем определить отрезки OB и O₁B, – получим для каждого одно решение (уравнения первой степени), откуда заключаем, что точка B вполне определена. Отсюда выводим: если бы мы нашли другую точку M₁, степени которой относительно наших кругов равны, и на нее опустим перпендикуляр на линию центров, то он должен пройти чрез ту же точку B и, следовательно, слиться с MB. Следовательно, все точки, степени которых относительно двух кругов равны, расположены на перпендикуляре к линии центров. Этот перпендикуляр носит название — радикальная ось двух кругов. Обратно, легко показать, что всякая точка перпендикуляра MB имеет равные степени относительно наших кругов.

Из равенства (2) видим: 1) если R = r, то OB – O₁B = 0 и OB = O₁B, т. е. радикальная ось двух равных кругов делит расстояние между их центрами пополам; 2) если R > r, то OB > O₁B, т. е. радикальная ось расположена ближе к центру меньшего круга.

Но, если мы назовем чрез x и y расстояния точки B от круга O и от круга O₁ (мы применяемся к случаю данному на чертеже: круги расположены один вне другого), то OB = R + x, O₁B = r + y и, подставив в равенство (2), найдем:
f48

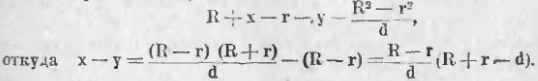
У нас R + r 0 (ибо считаем, что R > r). Тогда из последнего равенства вытекает x 2 = TC₁ 2 , или TC = TC₁, т. е. общая касательная двух кругов делится радикальною осью пополам.

Если два круга пересекаются, то радикальная ось должна пройти чрез точки пересечения, так как степень каждой из этих точек одинакова относительно каждого круга (она равна нулю); для построения радикальной оси в этом случае следует лишь построить прямую, определяемую этими точками пересечения.

Если два круга касаются, то радикальная ось есть перпендикуляр к линии центров чрез точку касания.

266. Пусть имеем 3 круга O, O₁ и O₂ (чер. 259). Построив радикальные ости mn и m₁n₁ двух пар кругов, мы найдем, что они пересекаются в какой-либо точке C, если только центры всех трех кругов не расположены на одной прямой. Так как точка C лежит на оси m₁n₁, то степени ее относительно кругов O₁ и O₂ одинаковы. Отсюда следует, что точка C имеет одинаковые степени и относительно кругов O и O₂, т. е. она должна лежать на радикальной оси последней пары кругов. Итак,

Радикальные оси трех кругов, взятых попарно, пересекаются в одной точке, которая называется радикальным центром трех рассматриваемых кругов.

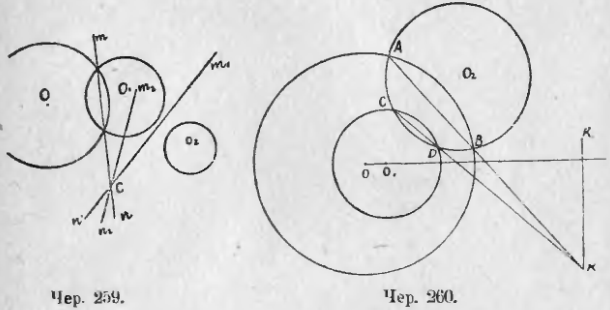
Если из радикального центра построить касательные ко всем трем кругам, то они равны между собою.

Если три круга попарно пересекаются, то их общие хорды проходят чрез одну точку (общая хорда двух пересекающихся кругов есть их радикальная ось).

267. Свойством предыдущего п. можно воспользоваться для построения радикальной оси для двух непересекающихся кругов . Пусть даны круги O и O₁ (чер. 260). Построим третий круг O₂ чтобы его центр не лежал на линии центров OO₁ и чтобы он пересекался с каждым из данных кругов: с кругом O и точках A и B и с кругом O1 в точках C и D. Тогда AB есть радикальная ось кругов O и O₂, CD — радикальная ось кругов O₁ и O₂, точка пересечения K прямых AB и CD есть радикальный центр наших трех кругов. Построив прямую KK₁ ⊥ OO₁, получим радикальную ось кругов O и O₁.

268. Построить круг, касающийся данного круга и проходящий чрез две данных точки .

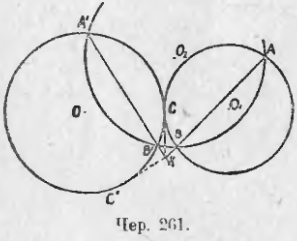
Пусть дан круг O и точки A и B (чер. 261). Воспользуемся предыдущею задачею. Искомый круг должен касаться данного; следовательно, радикальною осью этой пары кругов должна служить их общая касательная. Если бы ее удалось построить, то легко было бы построить и искомый круг. Для построения этой радикальной оси воспользуемся, как в предыдущем п., третьим кругом O₂, пересекающим и данный и искомый круг. Но у искомого круга мы знаем пока только 2 точки A и B; следовательно, и этот третий круг O₂ мы можем построить лишь так, чтобы он проходил чрез точки A и B. Итак, построим любой круг O₂, проходящий чрез точки A и B и пересекающий круг O, напри., в точках A’ и B’. Тогда прямая AB есть радикальная ось искомого круга и круга O₂, прямая A’B’ есть радикальная ось кругов O и O₂, а точка их пересечения K есть радикальный центр всех трех кругов. Теперь нетрудно построить радикальную ось круга O и искомого, так как она должна касаться круга O: надо чрез точку K построить касательную к кругу O, а их можно построить две KC и KC’ (C и C’ точки касания). Тогда получим два решения: 1) искомый круг определяется точками A, B и C и 2) искомый круг определяется точками A, B и C’.

269. Мы имеем в виду решить еще две задачи на построение кругов: 1) построить круг, касающий двух данных кругов и проходящий чрез данную точку; и 2) построить круг, касающийся трех данных кругов (задача Аполлонин). Для этого надо познакомиться еще с некоторыми свойствами центра подобия и радикальной оси двух кругов.

Чрез центр подобия S кругов O и O₁ (чер. 262) построена общая касательная SCC₁ к этим кругам и секущая SB, соответственные точки которой суть A и A₁, B и B₁.

270. Пусть круг M касается кругов O и O₁ (чер. 263), обоих внешним образом в точках A и B. Построим прямую AB и пусть эта прямая пересекает еще круг O в точке B₁ и круг O₁ в A₁. Тогда OAM есть прямая, – следовательно, углы при основаниях в равнобедренных треугольниках OAB₁ и MAB равны; также O₁BM есть прямая и, следовательно, углы при основании в равнобедренном треугольнике O₁A₁B равны углам в ∆MAB (на чертеже равные углы отмечены). Отсюда заключаем, что O₁A₁ || OA и O₁B || OB₁, откуда следует, что прямая B₁ABA₁ проходит чрез внешний центр подобия кругов O и O₁. Итак, если круг касается двух других, то точки касания расположены на прямой, проходящей чрез центр подобия, но не суть соответственные точки .

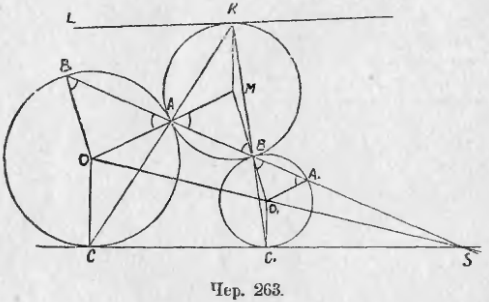
Мы разобрали случай, когда M с O и с O₁ имеет внешнее касание; также будет и для случая, когда M с O и с O₁ имеет внутреннее касание; но если M имеет с одним из кругов внешнее касание, а с другим внутреннее, то вместо внешнего центра подобия надо взять внутренний. Поэтому в предыдущем заключении мы и не указали, чрез какой именно центр подобия проходит прямая, соединяющая точки касания.

Если построить еще общую касательную SC₁C, то прямые CA и C₁B, как мы знаем, пересекаются в точке K, лежащей на радикальной оси кругов O и O₁. Но можно выяснить еще, что точка K лежит на круге M.

Точка A есть внутренний центр подобия кругов O и M, причем точке O соответствует точка M, радиус OC (который ⊥ SC) соответствует некоторый радиус MX круга M, который параллелен OC, но имеет обратное с ним направление. Точка B есть внутренний центр подобия кругов O₁ и M, причем точке O₁ соответствует точка M и радиус O₁C₁ круга O₁ соответствует некоторый радиус MY круга M, который параллелен радиусу O₁C₁, но имеет обратное с ним направление. Отсюда следует, что радиусы MX и MY параллельны друг другу (ибо O₁C₁ || OC) и одинаково направлены, но они имеют общую точку M, – следовательно, они совпадают. С другой стороны, точка X должна лежать на прямой CA и точка Y на прямой C₁B. Поэтому совпадение радиусов MX и MY требует, чтобы точка X и точка Y совпали с точкою K, где пересекаются прямые CA и C₁B. Следовательно, точка K есть конец радиуса MK круга, и M, и K лежит на круге M.

Далее прямой SC относительно центра подобия A должна соответствовать прямая KL, проходящая чрез K (ибо SC проходит чрез C) и параллельная SC. Кроме того, прямая KL ⊥ MK, ибо SC ⊥ OC (радиусы OC и MK соответствуют друг другу). Поэтому прямая KL касается круга M в точке K. К тому же результату придем, рассматривая соответствие относительно центра подобия B.

271. Теперь мы можем приступить к решению первой из намеченных задач: даны круги O и O₁ и точка P (чер. 264). Требуется построить круг, касающийся кругов O и O₁ и проходящий чрез P.

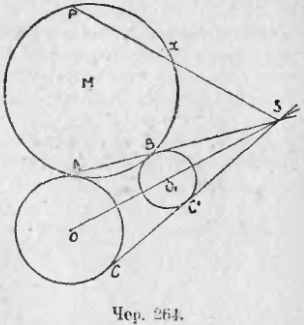
Пусть M искомый круг и точки A и B суть точки касания. Тогда легко найти точку X, где луч SP (S центр подобия кругов O и O1) пересекает круг M. Мы имеем:

SP · SX = SA · SB = SC · SC₁ (п. 269)

Отсюда SX/SC = SC1/SP, т. е. отрезок SX есть четвертый пропорциональный к трем известным отрезкам SC, SC1 и SP, – построить его мы умеем. Тогда задача сведется к задаче п. 268.

272. Задача Апполония . Даны три круга O₁, O₂ и O₃ (чер. 265). Построить круг, касающийся трех данных.

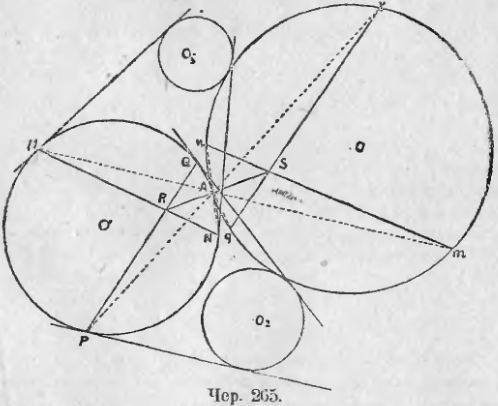
Мы будем рассуждать лишь в предположении, что мы ищем круг, касающийся каждого из данных внешним образом. Применить к другим случаям не представит затруднений (всего задача имеет 8 решений).

Пусть круг O есть искомый и A есть точка касания кругов O и O₁; тогда прямой MN, соединяющей точки касания M и N общих касательных для кругов O₁ и O₃, соответствует относительно центра подобия A (точка A есть внутренний центр подобия кругов O₁ и O) радикальная ось mn кругов O₁ и O₃: точке M соответствует точка m, лежащая на круге O и на радикальной оси кругов O₁ и O₃ (п. 270) и также точке N соответствует точка n, лежащая на радикальной оси кругов O₁ и O. Точно так же прямой PQ, соединяющей точки касания круга O₁ с общими касательными для кругов O₁ и O₂, соответствует радикальная ось pq кругов O₁ и O₂.

Точке R, где MN и PQ пересекаются, соответствует точка S, где mn и pq пересекаются, т. е. радикальный центр кругов O₁, O₂ и O₃. Поэтому точки R и S лежат на одной прямой с A.

Точки R и S мы можем построить; соединив их, получим (между ними) точку касания искомого круга с кругом O₁, после чего задача легко решается.

Подобные треугольники

Определение

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.

Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.

Признаки подобия треугольников

I признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

II признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Свойства подобных треугольников

• Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
• Отношение периметров подобных треугольников равно коэффициенту подобия.
• Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.

Примеры наиболее часто встречающихся подобных треугольников

1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.

2. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –

3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.

Здесь вы найдете подборку задач по теме «Подобные треугольники» .

Объем пространственных фигур – определение и вычисление с примерами решения

Содержание:

Исследование. Соберите не менее 4 призм различных размеров из кубиков и изобразите полученные призмы.

1. Предположим, что ребро каждого кубика, из которых состоит призма, равна 1 единице, площадь грани равна 1 квадратной единице, а объём равен 1 кубической единице.
2. Данные для каждой призмы запишите в таблицу.
3. Какая связь существует между площадью основания призмы и высотой?
4. Вытащите один кубик из угла конструкции и изобразите вид впереди, сверху и сбоку каждого кубоида.

Если тело можно разделить на конченое число треугольных пирамид, то оно называется простым телом. Для простых тел объём – положительная величина, численное значение которой удовлетворяет следующим свойствам.

1. Объёмы конгруэнтных тел равны.
2. Объём куба, ребро которого равно единице, равен кубической единице.
3. Если тело можно разделить на простые части, то его объём равен сумме объёмов полученных частей.

Тела, имеющие одинаковые объёмы называются равновеликими. Объём прямоугольного параллелепипеда, размеры которого являются натуральными числами, равен

количеству кубических единиц, из которых он состоит. Можно также показать, что объём прямоугольного параллелепипеда, размеры которого заданы любыми действительными числами равен произведению трёх измерений: . Формулу объёма можно записать как произведение площади основания и высоты с. Объём прямоугольного параллелепипеда равен произведению площади основания и высоты:

Следствие: Объём куба с ребром а равен:

Объём любой прямой призмы равен произведению площади основания и высоты. Справедливость данного утверждения проверим на прямой призме, в основании которой лежит прямоугольный треугольник.

Достроим основание призмы до прямоугольника, получим призму, достроенную до прямоугольного параллелепипеда. Объём полученной призмы равен .

Плоскость , проходящая через диагональ параллелепипеда делит призму на две конгруэнтные треугольные призмы. Значит, объём прямой призмы, в основании которой лежит прямоугольный треугольник будет:

В треугольнике ABC, являющимся основанием прямой призмы, проведём высоту так, чтобы она пересекала противоположную сторону во внутренней области: . Плоскость, проходящая через ребро АА’ перпендикулярно ребру ВС имеет одинаковую высоту с призмой, и делит её на две призмы, в основании которых лежат прямоугольные треугольники. Объём заданной призмы равен сумме объёмов полученных призм. Значит, объём прямой призмы с произвольным треугольником в основании равен произведению площади основания и высоты.

Если основанием прямой призмы является произвольный многоугольник, то её также можно разделить на треугольные призмы и найти её объём как сумму объёмов данных призм. Наклонную призму АВСА’В’С’ преобразуем в прямую призму равного объёма. Для этого:

1. проведём плоскость перпендикулярную боковым рёбрам;
2. отделим оставшуюся при сечении верхнюю часть призмы;
3. переместим и соединим её с оставшейся внизу частью;
4. высота полученной прямой призмы является боковым ребром наклонной призмы, т.е. , основание же является перпендикулярным сечением наклонной призмы. Объём данной прямой призмы является также объёмом наклонной призмы.

Следствие. Объём наклонной призмы равен произведению перпендикулярного сечения и ребра призмы: . Угол между перпендикулярным сечением и основанием равен углу между боковым ребром и высотой призмы.

Поэтому, .

Таким образом объём призмы равен произведению площади основания и высоты.

Принцип Кавальери для нахождении объёмов

Если площади сечений параллельных основаниям двух тел равны, то равны и их объёмы, при условии, что основания лежат в одной плоскости, а высоты равны. Этот принцип открыл итальянский математик Бонавентура Кавальери (1598 – 1647).

Объем призмы

Объем призмы равен произведению площади основания и высоты.

Пример №1

Найдём объём правильной пятиугольной призмы, стороны основания которой равны 4 см, а длина бокового ребра 9 см. Центральный угол правильного пятиугольника равен 360 : 5 = 72° значит апофема равна:

Площадь правильного многоугольника равна полупроизведению периметра и апофемы.

Исследование. 1. Диагонали куба деляг его на 6 конгруэнтных пирамид. Основание каждой пирамиды – грань куба, а высота

каждой пирамиды равна

а)Докажите, что объём каждой пирамиды равен

б)Докажите, что объём каждой пирамиды равен

Объём пирамиды

Объем пирамиды равен одной третьей произведения площади основанию на высоту.

Пусть, ТАВС – треугольная пирамида с вершиной Т и основанием ABC. Достроим эту пирамиду до треугольной призмы. Полученная призма состоит из трёх пирамид:

1)заданной пирамиды ТАВС;

Основания 2-ой и 3-ей пирамид конгруэнтны: и высота, проведённая из вершины Т общая. Поэтому их объёмы равны. Основания 1-ой и 3-ей пирамид конгруэнтны: и высота, проведённая из вершины С общая. Поэтому и их объёмы равны. Тогда объём заданной пирамиды равен . Основание любой пирамиды всегда можно разделить на треугольники и найти объём пирамиды суммировав объёмы всех полученных пирамид. Таким образом, объём любой пирамиды равен одной третьей произведения площади основания на высоту: .

Подобие фигур в пространстве

Подобные фигуры имеют одинаковую форму и пропорциональные размеры.

Например, прямоугольные треугольники на рисунке подобны, так как отношения соответствующих сторон равны.

Прямоугольные параллелепипеды на рисунке подобны, так как отношения соответствующих линейных размеров равны и соответствующие грани являются подобными четырёхугольниками. Правильные многогранники подобны. В частном случае подобными являются все кубы, правильные тетраэдры и т.д.

Подобные фигуры

Если при преобразовании расстояние между любыми двумя точками, меняется в одинаковое число раз, то такое преобразование называется подобием. Одна и другая, полученная при преобразовании подобием, фигура называются подобными фигурами. Коэффициент подобия равен отношению расстояний между парой любых двух соответсвующих точек.

Пример №2

Определим подобны или нет фигуры на рисунке.

Площади поверхностей и объёмы подобных фигур

Исследование. Покажите подобны или нет следующие фигуры.

Призмы А и В (прямоугольные параллелепипеды) подобные призмы

с коэффициентом подобия равным .

Для данных призм найдите:

а)отношение площадей полных поверхностей;

а)площадь полной поверхности призмы А

площадь полной поверхности призмы В

Отношение полной поверхности призмы А к полной поверхности призмы В

б)объём призмы А

объём призмы В

Отношение объёма призмы А к объёму призмы В

Если коэффициент подобия двух пространственных фигур равен , то отношение площадей (боковых, полных, оснований) равно , а отношение объемов равно Коэффициент подобия:

Пирамида, полученная сечением плоскости параллельной основанию, подобна данной. Коэффициент подобия можно найти из отношения соответствующих линейных размеров.

Например, на рисунке даны высоты. Тогда, отношения их боковых поверхностей, основании и полных поверхностей равно квадрату отношения высот.

Объём усечённой пирамиды

Исследование. В древнем Египте объём правильной усечённой четырёхугольной пирамиды вычисляли по формуле . Однако доподлинно не известно каким образом эта формула была получена. Выведите формулу, выполнив следующие шаги:

• а)Запишите объём правильной четырёхугольной пирамиды, со стороной основания у ед.
• б)Запишите объём правильной четырёхугольной пирамиды, со стороной основания х ед.
• в)Покажите зависимость между высотами Н и h, как
• г)Покажите, что объём усечённой пирамиды находится по формуле .

Объём усечённой пирамиды можно также найти как разность объёмов пирамид, при сечении плоскостью параллельной основанию.

Здесь V – объём усечённой пирамиды, S₂ и S₁ площади нижнего и верхнего оснований. h – высота усечённой пирамиды, h₁ – высота меньшей пирамиды.

Так как эти пирамиды подобны, то отношение площадей равно квадрату отношений высот. Запишем это равенство и найдём высоту меньшей пирамиды.

Учитывая выражение

в равенстве

Объём усечённой призмы

Объём усечённой пирамиды с площадями оснований и , и высотой вычисляется по формуле

Задачи на сечение плоскостью

Пример:

На рисунке показано сечение куба, с ребром а, плоскостью АВDО. Точки D и С являются серединами рёбер. Найдём площадь сечения.

Решение:

Дано: куб, длина ребра которого равна а точки D и С середины рёбер.

Найдите:

Для удобства повернём куб и отметим данные задачи на рисунке. Из по теореме Пифагора:

Ответ:

Симметрия в пространстве

В пространственных фигурах также можно наблюдать различную симметрию. Известно, что в параллелепипеде диагональные сечения являются параллелограммами и диагонали ВD₁ и DВ₁ пересекаясь в точке О делятся пополам.

Можно показать, что другие диагонали также пересекаются в точке О и делятся пополам. Значит, точка пересечения диагоналей параллелепипеда является центром его симметрии.

В пространстве, помимо симметрии относительно точки и прямой, рассматривается симметрия относительно плоскости.

Если отрезок АА’ пересекает плоскость а посередине, и перпендикулярен плоскости, то говорят, что точки А и А’ симметричны относительно плоскости а.

Если точки фигуры, симметричные некоторой плоскости, также принадлежат этой фигуре,то эту плоскость называют плоскостью симметрии, а фигуру называют симметричной относительно плоскости.

Прямоугольный параллелепипед, у которого все линейные размеры разные, кроме центра симметрии имеет ещё три оси и три плоскости симметрии. Прямая, проходящая через точку пересечения диагоналей противоположных граней, называется осью симметрии,а плоскость, проходящая перпендикулярно через середину рёбер называется плоскостью симметрии. Параллелепипед, у которого два линейных размера равны, имеет 5 плоскостей симметрии. Данные изображения нарисуйте в тетрадь.

Точка пересечения диагоналей куба является его центром симметрии. Прямые, проходящие через середину параллельных рёбер, не принадлежащих одной грани (их всего 6) и прямые, проходящие через центры противоположных граней(их всего три), являются осями симметрии куба. У куба 9 плоскостей симметрии. Они изображены на следующих рисунках.

Вращательная симметрии

Вращательная симметрия пространственных фигур похожа на вращательную симметрию плоских фигур. Однако, для объёмных фигур она определяется при помощи оси вращения.

Вращательная и осевая симметрия широко применяется при изучении строения молекул веществ.

Пример №3

На рисунке показан вид сверху деталей, в виде правильных треугольных призм. Из них сконструирована правильная шестиугольная призма с центром основания О. Сколько деталей понадобилось для этого?

Основанием призмы является правильный шестиугольник, состоящий их 6 конгруэнтных треугольников. Каждый треугольник заполнен призмами. По изображению видно, что в один треугольник помещено 1+3 + 5 + 7 + 9 = 25 призм . Для правильной шестиугольной призмы таких призм нужно будет 6 • 25 = 150.

Рекомендую подробно изучить предметы:

Геометрия Аналитическая геометрия Начертательная геометрия

Ещё лекции с примерами решения и объяснением:

• Объёмы поверхностей геометрических тел
• Фигуры вращения: цилиндр, конус, шар
• Объем фигур вращения
• Длина дуги кривой
• Площадь многоугольника
• Правильные многоугольники
• Вписанные и описанные многоугольники
• Площадь прямоугольника

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

[spoiler title=”источники:”]

http://www.evkova.org/obem-prostranstvennyih-figur

[/spoiler]

Подобие фигур — это две геометрические фигуры или два геометрических тела называются подобными, если одно представляет собой уменьшенную модель другого.

Содержание:

1. Понятие подобия фигур
2. Подобие треугольников
3. Подобие многоугольников

Понятие подобия фигур

В окружающем мире часто встречаются предметы, одинаковые по форме, но различные по размерам: мыльный пузырь и футбольный мяч, небольшая модель ледокола и сам корабль, карты, фотоснимки различных размеров одного и того же здания. В геометрии такие фигуры называют подобными.

Существуют фигуры, которые всегда подобны друг другу, например, круги, квадраты, кубы.

Для обозначения подобия фигур употребляется знак . На рисунке 2.434 изображены подобные фигуры . Запись читается: фигура подобна фигуре 

Для подобных фигур вводится понятие — коэффициент подобия, он обозначается k; k всегда больше нуля. Коэффициент подобия показывает, в каком отношении находятся соответствующие расстояния между точками фигур. На рисунке 2.434 коэффициент подобия можно определить, найдя отношения сторон квадратиков изображенной сетки.

Подобие фигур широко используется при разработке планов построек зданий или при изображении на картах городов или других участков земной поверхности. Всякий план или карта является подобным изображением реального объекта или участка земной поверхности, т. е. фигурой, подобной реальному объекту. При этом план или карта может изображать реальный объект в разном масштабе.

Определение. Масштаб — это коэффициент подобия соответствующих фигур.

Подобие треугольников

На рисунке 2.435 изображены два чертежных прямоугольных треугольника с острыми углами в 60° и 30°. Стороны второго треугольника по сравнению с первым уменьшены в два раза:  У этих треугольников углы попарно равны. Стороны, лежащие против разных углов, пропорциональны:  Такие треугольники называют подобными. Стороны, лежащие против равных углов, называют сходственными.

Определение. Подобными называют треугольники, у которых углы попарно равны, а сходственные стороны пропорциональны.

Подобие треугольников записывается так:  Отношение сходственных сторон подобных треугольников называется коэффициентом подобия. В случае, изображенном на рисунке 2.435, коэффициентом подобия треугольников  будет число 2. Если же взять отношения , коэффициент подобия будет равен .

Подобные треугольники могут быть произвольно расположены как на плоскости, так и в пространстве.

Если фигуры равны, то они подобны с коэффициентом подобия, равным 1. Если фигуры подобны, то они не обязательно равны.

Теорема 1. (Лемма о подобии треугольников). Прямая, пересекающая две стороны треугольника и проведенная параллельно третьей стороне, отсекает треугольник, подобный данному.

Для выявления подобия треугольников существуют признаки подобия треугольников.

Теорема 2. (Первый признак — по двум равным углам.) Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого.

Следствия из этой теоремы.

1.    Равносторонние треугольники подобны.

2.    Равнобедренные треугольники подобны, если они имеют по равному углу при вершине или при основании.

3.    Два прямоугольных треугольника подобны, если они имеют по равному острому углу.

4.    Равнобедренные прямоугольные треугольники подобны.

Теорема 3. (Второй признак — по пропорциональности двух сторон и равенству углов между ними.) Два треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, лежащие между ними, равны.

Следствие. Прямоугольные треугольники подобны, если катеты одного из них пропорциональны катетам другого.

Теорема 4. (Третий признак — по пропорциональности трех сторон.) Два треугольника подобны, если три стороны одного треугольника пропорциональны трем сторонам другого треугольника.

Теорема 5. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Подобие многоугольников

Определение. Если стороны одного многоугольника пропорциональны сторонам другого многоугольника и соответственные углы этих многоугольников равны, то такие многоугольники подобны.

На рисунке 2.436 изображены два подобных пятиугольника , у них  а также  k – коэффициент подобия.

Для многоугольников с числом сторон больше трех признак подобия, аналогичный третьему признаку подобия треугольников, будет неверен. Например, квадрат и ромб, отличный от квадрата, не будут подобны, хотя их стороны пропорциональны (рис. 2.437). Недостаточно для подобия двух прямоугольников и равенства их соответствующих углов. Например, квадрат не подобен четырехугольнику, не все стороны которого равны (рис. 2.438).

Теорема 6. Отношение периметров подобных многоугольников равно отношению их сходственных сторон (коэффициенту подобия).

Теорема 7. Отношение площадей подобных многоугольников равно квадрату коэффициента подобия.

Эта лекция взята со страницы полного курса лекций по изучению предмета “Математика”:

• Математика решение заданий и задач

Смотрите также дополнительные лекции по предмету “Математика”:

Говорят, что треугольник FGH
подобен треугольнику АВС с
коэффициентом k ,
когда 
F = 
A , 
G = 
B, 
H = 
C, а также FG
/ AB = FH
/ AC = GH
/ BC = k.
Если в ходе решения задания не важен
коэффициент подобия k
, то просто говорят, что треугольники
FGH и АВС
подобны и пишут 
АВС  
FGH . Необходимо знать
три признака подобия треугольников: по
двум пропорциональным соответствующим
сторонам и равным углам между ними; по
двум равным соответствующим углам; по
трем пропорциональным соответствующим
сторонам. Так же необходимо помнить,
что коэффициент подобия треугольников
может быть найден как отношение их
соответствующих компонент, имеющих
линейные размеры (например, как отношение
соответствующих высот, медиан или
биссектрис, а также как отношение
периметров, радиусов вписанных или
радиусов описанных окружностей и т.
п.). Квадрат коэффициента подобия
треугольников равен отношению площадей
соответствующих фигур, связанных с
этими треугольниками (например, отношению
площадей самих треугольников, отношению
площадей, вписанных в них кругов, и
т.п.). Часто встречаются ситуации, когда
подобные треугольники расположены как
на рис. 6 при 
ABC = 
ADE или на рис.
7 при 
GKL = 
FGK . В этих ситуациях
имеем 
ABC 

ADE и 
HKL 

HGF соответственно.

А
F
G

D
H

E

B
K
L

Рис. 6 C
Рис. 7

П

одобные
треугольники встречаются и при решении
заданий, связанных с окружностью. На
рис. 8 – 11 приведены такие ситуации.

В
A B

С
F

F A

D B
(касательная) C

А B

F C

D
Рис. 10
D

Рис. 8 C

D
A

Рис. 9
Рис. 11

На каждом из рисунков 8 – 10 подобие
треугольников AFD и
CFB является
необходимым и достаточным условием для
того, чтобы точки A,
B, C
и D лежали на
одной окружности.

Из подобия этих треугольников следуют
полезные соотношения: AFFC
= BFFD
на рисунке 8, CB
: AD = FB
: FD на рисунке 9, а
если к тому же на этом рисунке угол DBF
прямой, то есть FB
: FD = Cos
 ВFD,
то получаем равенство СВ : АD
= Cos 
AFD. На рисунке 10 из
подобия треугольников AFD
и CFB следует,
что FBFA
= FDFC
. На рисунке 11 подобными являются
треугольники АВС и BDC
(величины углов BAD и
CBD равны половине
угловой величины одной дуги BD
, а угол С общий). Откуда получается
полезное равенство для отрезка касательной
ВС, имеющее вид ВС =

.

Теперь можно переходить к решению
заданий 2.1 – 2.5.

7.1. Стороны АВ и ВС треугольника
АВС пересекает прямая, параллельная
АС, соответственно в точках D
и E . Периметр и
площадь треугольника АВС равны 12
(ед. и ед.²).

Найдите радиус окружности, вписанной
в треугольник BDE, если
DA + AC
+ CE = 6+ DE.

7.2. Около треугольника АВС описана
окружность. Продолжение медианы АD
пересекает окружность в точке Е
. Найдите длину отрезка СЕ, если
AB = 8, AD
= 12, AE = 15.

7.3. В треугольнике АВС точка
D лежит на стороне
АС, причем АD
= 2, DС = 7 и 
А = 45⁰. Найдите площадь
треугольника АВD,
если  АВD
=  АСВ .

7.4. В треугольнике АВС проведены
высоты ВD и
СЕ. Найдите DЕ,
если AB / AD
= 3 и ВС = 15.

7.5. На стороне АС треугольника
АВС как на диаметре построена
окружность, пересекающая прямые АВ
и ВС в двух точках D
и E соответственно.
Найдите сторону ВС, если известно,
что АВ = 1 и АС = 2DE
=

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #

  06.09.2019647.68 Кб2ПЗ.doc

• #
• #
• #
• #
• #
• #
• #
• #

Коэффициент подобия треугольников – что это? Как его найти? Коэффициент подобия треугольников, определение. Подобные треугольники имеют равные углы и пропорциональные сходственные стороны. Сходственные стороны (другое название – соответственные) – это стороны, которые лежат напротив равных углов. На рисунке представлены подобные треугольники ABC и A1B1C1. Для их сторон выполняется следующее равенство: Величина, которая равна отношению сходственные сторон треугольников, называется коэффициентом подобия. Коэффициент подобия треугольников обозначается буквой k, k > 0. Таким образом, приведённое выше равенство можно записать в виде: Найти коэффициент подобия треугольников можно несколькими способами. 1) Через отношение сходственных сторон (например, AB / A1B1). 2) Этот коэффициент также равен отношению периметров подобных треугольников. P(ABC) = A + B + C, P(A1B1C1) = A1 + B1 + C1. k = P(ABC) / P(A1B1C1). 3) Через площади подобных треугольников. k² = S(ABC) / S(A1B1C1). 4) Отношение длин высот, медиан, биссектрис подобных треугольников также равно коэффициенту подобия. Пример. Даны подобные треугольники DEC и AON. Коэффициент подобия = 1,5, а сторона DE = 12 см. Требуется найти сторону AO. _ По определению коэффициента подобия k = DE / AO = 1,5. Так как DE = 12 см, то можно записать: 12 / AO = 1,5. AO = 12 / 1,5 = 8 см. Значит, длина стороны AO составляет 8 см. модератор выбрал этот ответ лучшим smile­6008 [28.5K] 3 года назад  Для того чтобы найти коэффициент подобия треугольников необходимо сначала определиться что же это понятие значит. Итак, подобный треугольник, это треугольник, геометрическая фигура, у которой одинаковые углы и одинаковые стороны, которые находятся напротив друг друга. То есть называются подобными. Для того чтобы найти коэффициент подобия треугольников обратимся к формуле. Для вычисления коэффициент используют разные способы расчёта. Проще всего найти коэффициент, если вычислить площади треугольников. Другой способ расчёта коэффициента примениние расчёта через отношение сходственных сторон подобных треугольников. Дубло­н [176K] 2 месяца назад  Говоря о коэффициенте подобия треугольников, необходимо знать, что есть подобные фигуры, а точнее подобные треугольники. Под таковыми являются треугольники, чьи углы равные, а сходственные стороны этих треугольников пропорциональны. Так вот, отношение этих сходственных сторон и есть коэффициент подобия. Коэффициент подобия можно определить, зная величину как сходственных сторон, так и величину периметров подобных треугольников, так и величину площади подобных треугольников. Бутаф­ога [31.1K] 2 месяца назад  Говоря простым языком, подобные треугольники называют такие геометрические фигуры, у которых углы одинаковые, а стороны пропорциональные. Стоит отметить как понятие соответственных сторон, лежащих напротив одинаковых углов. Отсюда вытекает коэффициент подобия, равный отношению соответственных сторон подобных треугольников. Корне­тОбол­енски­й [160K] 3 месяца назад  Подобными называются фигуры, одинаковые по форме, но разные по размеру. Треугольники считаются подобными, если у них углы равны, а их соответственные стороны пропорциональны друг другу. Рассмотрим рисунок: Изображённые на нем треугольники подобны, поскольку у них соответствующие углы равны между собой, а соответственные (второе название сходственные) стороны пропорциональны. Коэффициент подобия равняется отношению сходственных сторон имеющихся подобных треугольников, т.е. сторон, лежащих напротив равных углов. Простыми словами, Коэффициент подобия показывает, в какое количество раз один треугольник больше другого, обозначается буквой k, при этом k>0. Т.е. коэффициент подобия всегда является положительной величиной. Коэффициент подобия можно найти несколькими способами: поделить одну сходственную сторону на другую. Это правило работает, если известны длины сторон треугольников. Можно вычислить также коэффициент подобия треугольников в случае, если по условию задачи известны их площади. Существует свойство подобных треугольников, говорящее, что отношение их площадей равняется коэффициента подобия, умноженному на себя, т.е. собственному квадрату. Тогда, разделив значения площадей у подобных треугольников и, извлекши квадратный корень из результата, получим коэффициент подобия. Также k находится через отношение длин медиан, биссектрис или серединных перпендикуляров, проведенных к соответственным сторонам, если длины этих медиан, серединных перпендикуляров или биссектрис известны по условию задачи. Если известны периметры подобных треугольников, то их отношение будет давать всё тот же коэффициент подобия. Если в подобные треугольники вписаны окружности, то отношение их радиусов или диаметров также даст коэффициент подобия. У подобных треугольников отношение диаметров или радиусов описанных вокруг них окружностей равно коэффициенту подобия. Если по условиям задачи известны диаметры или радиусы этих окружностей, либо есть возможность каким-либо способом вычислить из площадей окружностей, то коэффициент подобия ищется и таким способом. Krust­all [125K] 8 месяцев назад  Подобными фигурами называются фигуры, одинаковые по форме, но разные по величине. Треугольники подобны, если их углы равны, а стороны пропорциональны друг другу. Также есть три признака, которые позволяют определить сходство без выполнения всех условий. Первый признак состоит в том, что в подобных треугольниках два угла одного равны двум углам другого. Второй признак подобия треугольников состоит в том, что две стороны одного пропорциональны двум сторонам другого и углы между этими сторонами равны. Третий признак сходства — пропорциональность трех сторон одного по отношению к трем сторонам другого. Треугольники называются подобными, если они имеют равные углы и соответствующие стороны пропорциональны. Число k, равное отношению соответствующих сторон треугольников, называется коэффициентом подобия. Давайте вспомним, какие треугольники называются подобными. Треугольники считаются подобными, если у них: равны углы, пропорциональны соответственные стороны. Выделяют три признаки по добия треугольников: по трем сторонам, по двум сторонам и углу между ними, по двум углам. Коэффициент подобия треугольников равен отношению соответственных ( сходственных ) сторон этих треугольников. Вычислить этот коэффициент можно несколькими путями, в основе которых, по сути, лежит пропорциональность их сходственных сторон: 1.) Непосредственно как отношение сторон. 2.) Через периметры этих треугольников ( то есть через суммы длин их сторон ). 3.) Через площади этих фигур. 4.) Как отношение их биссектрис, высот или медиан. Серге­й Гории­нов [5.5K] 5 лет назад  Коэффициент подобия треугольников – это безразмерная величина, равная отношению соответствующих сторон подобных треугольников: К=a1/a2=b1/b2=c1/c2, где a1,b1,c1 – стороны первого подобного треугольника, а a2,b2,c2 – стороны второго подобного треугольника. Также существует коэффициент подобия площадей подобных треугольников, равный квадрату коэффициента подобия треугольника. Лара Изюми­нка [59.8K] 2 года назад  При изучении темы “Подобие треугольников” очень важно понимание , что такое коэффициент подобия траугольников. Итак, коэффициент подобия – это отношение сходственных сторон в подобных треугольниках. Сходственные стороны, это стороны, которые лежат против равных углов. Коэффициент подобия помогает найти площадь подобного треугольника, если известна площадь другого. Здесь пользуемся тем , что отношение площадей подобных треугольников равно квадрату коэффициента подобия. Также можно найти стороны одного подобного треугольника, если есть стороны другого и известен коэффициент подобия. Ьема изучается в 8 классе в курсе геометрии. Nasty­a Chuk [6.8K] 3 года назад  Актуальный вопрос на самом деле, поскольку он необходим для понимания различий между видами треугольников и их пропорциями.Предназн­ачение коэффициента подобия : показывает во сколько раз стороны нашего треугольника соответственно больше сторон другого треугольника и какую же часть составляют они от сходственных стороны.Коэффициент подобия обозначается как “к” и выражается всегда через некое соотношение 2-х или 3-х треугольников. Знаете ответ?