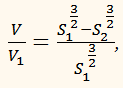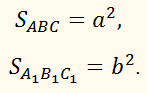Как найти коэффициент подобия кубов

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

OBRAZOVALKA.COM

OBRAZOVALKA.COM – образовательный портал
Наш сайт это площадка для образовательных консультаций, вопросов и ответов для школьников и студентов .

На вопросы могут отвечать также любые пользователи, в том числе и педагоги.

Консультацию по вопросам и домашним заданиям может получить любой школьник или студент.

Если вам необходимо получить ответ на вопрос Как найти коэффициент подобия у кубов 8см кубических и 27 см кубических?, относящийся
к уровню подготовки учащихся 5 – 9 классов, вы открыли нужную страницу.
В категории Математика вы также найдете ответы на похожие вопросы по
интересующей теме, с помощью автоматического «умного» поиска. Если после
ознакомления со всеми вариантами ответа у вас остались сомнения, или
полученная информация не полностью освещает тематику, создайте свой вопрос с
помощью кнопки, которая находится вверху страницы, или обсудите вопрос с
посетителями этой страницы.

Подобность многогранников.

Два многогранника называются подобными, если они имеют соответственно
равные многогранные углы и соответственно подобные грани.

Соответственные элементы подобных многогранников называются сходственными. У подобных многогранников
двугранные углы равны и одинаково расположены; сходственные рёбра пропорциональны.

Если в пирамиде проведём секущую площадь параллельно
основанию, то она отсечёт от неё другую пирамиду, подобную данной.

Поверхности подобных многогранников относятся, как
квадраты сходственных линейных элементов многогранников.

Объёмы подобных многогранников относятся как кубы
сходственных линейных элементов этих многогранников.

Квадраты объёмов подобных многогранников относятся как
кубы площадей сходственных граней.

Подобные цилиндры и конусы.

Два цилиндра, конуса
или усечённых конуса называются подобными, если подобны их осевые сечения.

Боковые и полные поверхности подобных цилиндров, конусов и
усечённых конусов относятся, как квадраты их сходственных линейных элементов. (радиусов оснований, высот, образующих).

Объёмы подобных тел.

Пусть  Т  и  Т‘ – два простых подобных тела. Это означает, что существует
преобразования подобия, при котором тело 
Т  переходить в тело  Т‘. Обозначим через  k  коэффициент
подобия.

Разобьём тело  Т  на треугольные пирамиды  


Р₁, Р₂,
…, Р_n … 


Преобразования подобия, которое переводит тело  Т  в  тело  Т‘  переводит пирамиды  


Р₁, Р₂,
…, Р_n  в пирамиды  Р₁‘, Р₂‘, …, Р_n‘. 


Эти пирамиды составляют тело  Т‘  и поэтому объём тела  Т‘  равен сумме объёмов пирамид  


Р₁‘, Р₂‘, …, Р_n‘.  

Так как пирамиды  Р₁‘  и  Р₁  подобны и коэффициент подобия равен  k,
то и отношение их высот равно  k, а отношение площадей их оснований равно  k². Поэтому, отношение объёмов пирамид равно  k³. Так как тело  Т  состоит из пирамид  Р₁, а тело  Т‘  состоит из пирамид  Р₁‘,
то отношение объёмов тел  Т‘  и  Т  тоже равно 
k³.  

Число  k  – коэффициент подобия – равен отношению расстояний
между любыми двумя соответствующими парами точек при преобразования подобия. Поэтому,
это число равно отношению любых двух соответствующих линейных размеров тел  Т‘  и 
Т.
Таким образом, мы приходим к следующему выводу: 

Объёмы двух подобных
тел относятся как кубы их соответствующих линейных размеров.

Квадраты объёмов
подобных тел относятся, как кубы площадей соответствующих граней.

Объёмы подобных цилиндров, конусов и усечённых конусов относятся,
как кубы их соответствующих линейных элементов (радиусов оснований,
высот, образующих).

Объёмы шаров относятся, как кубы их радиусов или диаметров.

ЗАДАЧА:

Площади оснований усечённой пирамиды  S₁  и  S₂, а её объём равен 
V. Определить объём полной пирамиды.

РЕШЕНИЕ:

Пусть  S₁ > S₂. Обозначим
объём полной пирамиды через  V₁, а объём пирамиды, дополняющей данную усечённую пирамиду
до полной, через  V₂

Тогда:

или

Составляя производную пропорцию, получим:

С учётом   V₁ –
V₂ = V, находим:

откуда:

ОТВЕТ:

ЗАДАЧА:

Площади оснований усечённой пирамиды
равны  а²  и  b². Найти площадь сечения, которое параллельно площадям
оснований усечённой пирамиды и делящего её объём пополам.

РЕШЕНИЕ:

В усечённой пирамиде  АС₁  (для простоты
рисунка рассматривается треугольная пирамида) дано:

Необходимо найти площадь сечения  А‘‘ё  (пл. АВС ∥ пл. А‘‘ё), которое делит усечённую
пирамиду на равновеликие по объёму части.

Дополним усечённую пирамиду до полной. Пирамиды

SАВС, SА‘‘ё, SA₁B₁C₁ – 


подобные.

Обозначим площадь искомого сечения  А‘‘ё  через  х², а объёмы пирамид  


SАВС, SА‘‘ё  и  SA₁B₁C₁  


соответственно
V_a, V_x, V_b.
Тогда:

или

где  t –
некоторое число, которое обозначает величину этих отношений. Тогда:

V_a = a³t,  V_x
= x³t,  V_b = b³t.

По условию задачи:

V_a – V_x =
V_x – V_b,

или

a³t – x³t = x³t – b³t,

откуда:

2x³ = a³ + b³.

поэтому,

ОТВЕТ:

Задания к уроку 19