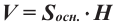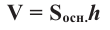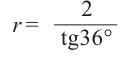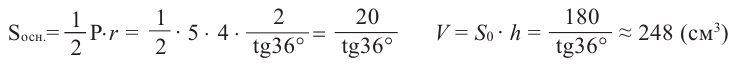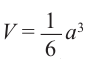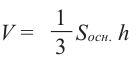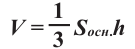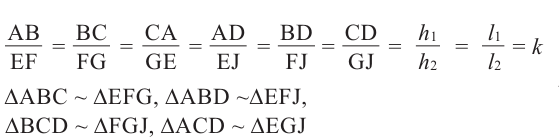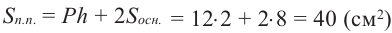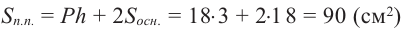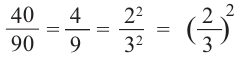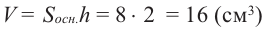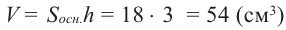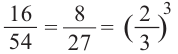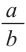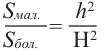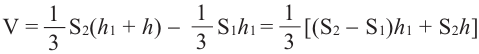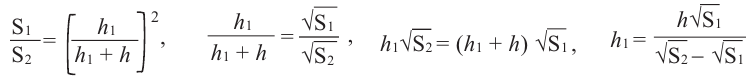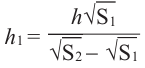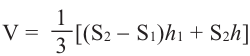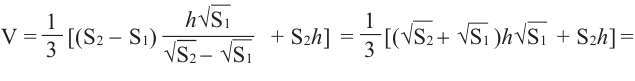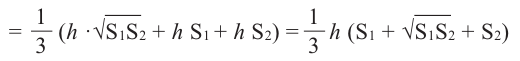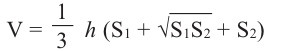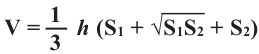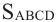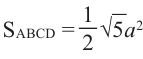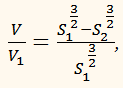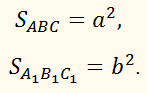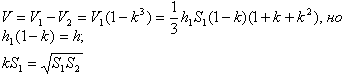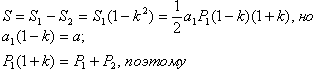Содержание:
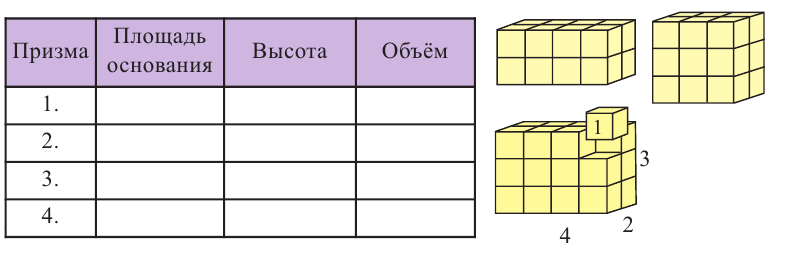
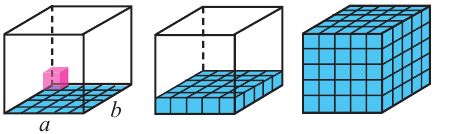
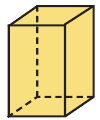
Исследование. Соберите не менее 4 призм различных размеров из кубиков и изобразите полученные призмы.
- Предположим, что ребро каждого кубика, из которых состоит призма, равна 1 единице, площадь грани равна 1 квадратной единице, а объём равен 1 кубической единице.
- Данные для каждой призмы запишите в таблицу.
- Какая связь существует между площадью основания призмы и высотой?
- Вытащите один кубик из угла конструкции и изобразите вид впереди, сверху и сбоку каждого кубоида.
Если тело можно разделить на конченое число треугольных пирамид, то оно называется простым телом. Для простых тел объём – положительная величина, численное значение которой удовлетворяет следующим свойствам.
- Объёмы конгруэнтных тел равны.
- Объём куба, ребро которого равно единице, равен кубической единице.
- Если тело можно разделить на простые части, то его объём равен сумме объёмов полученных частей.
Тела, имеющие одинаковые объёмы называются равновеликими. Объём прямоугольного параллелепипеда, размеры которого являются натуральными числами, равен
количеству кубических единиц, из которых он состоит. Можно также показать, что объём прямоугольного параллелепипеда, размеры которого заданы любыми действительными числами равен произведению трёх измерений: 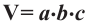
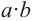
Следствие: Объём куба с ребром а равен:
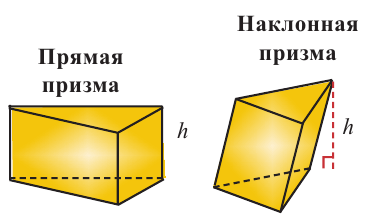
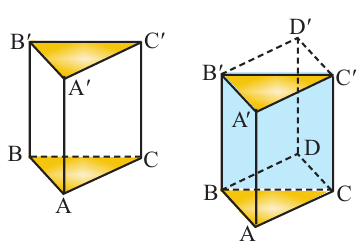
Объём любой прямой призмы равен произведению площади основания и высоты. Справедливость данного утверждения проверим на прямой призме, в основании которой лежит прямоугольный треугольник.
Достроим основание призмы до прямоугольника, получим призму, достроенную до прямоугольного параллелепипеда. Объём полученной призмы равен 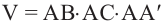
Плоскость 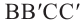
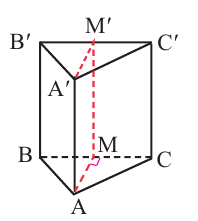
В треугольнике ABC, являющимся основанием прямой призмы, проведём высоту так, чтобы она пересекала противоположную сторону во внутренней области: 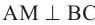
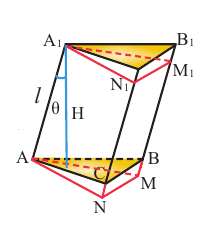
Если основанием прямой призмы является произвольный многоугольник, то её также можно разделить на треугольные призмы и найти её объём как сумму объёмов данных призм. Наклонную призму АВСА’В’С’ преобразуем в прямую призму равного объёма. Для этого:
- проведём плоскость перпендикулярную боковым рёбрам;
- отделим оставшуюся при сечении верхнюю часть призмы;
- переместим и соединим её с оставшейся внизу частью;
- высота полученной прямой призмы является боковым ребром наклонной призмы, т.е.
, основание же является перпендикулярным сечением наклонной призмы. Объём данной прямой призмы является также объёмом наклонной призмы.
Следствие. Объём наклонной призмы равен произведению перпендикулярного сечения и ребра призмы: 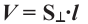
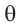
Поэтому, 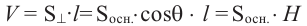
Таким образом объём призмы равен произведению площади основания и высоты.
Принцип Кавальери для нахождении объёмов
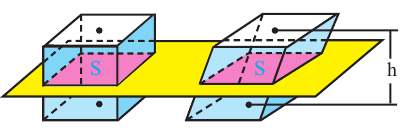
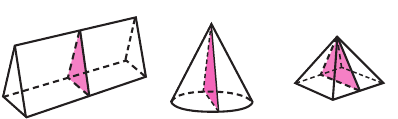
Если площади сечений параллельных основаниям двух тел равны, то равны и их объёмы, при условии, что основания лежат в одной плоскости, а высоты равны. Этот принцип открыл итальянский математик Бонавентура Кавальери (1598 – 1647).
Объем призмы
Объем призмы равен произведению площади основания и высоты.
Пример №1
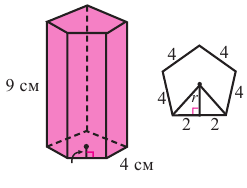
Найдём объём правильной пятиугольной призмы, стороны основания которой равны 4 см, а длина бокового ребра 9 см. Центральный угол правильного пятиугольника равен 360 : 5 = 72° значит апофема равна:
Площадь правильного многоугольника равна полупроизведению периметра и апофемы.
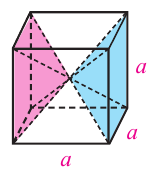
Исследование. 1. Диагонали куба деляг его на 6 конгруэнтных пирамид. Основание каждой пирамиды – грань куба, а высота
каждой пирамиды равна
а)Докажите, что объём каждой пирамиды равен
б)Докажите, что объём каждой пирамиды равен
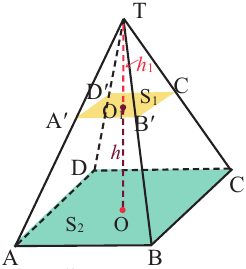
Объём пирамиды
Объем пирамиды равен одной третьей произведения площади основанию на высоту.
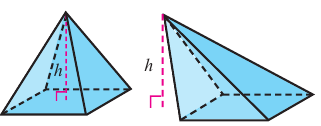
1)заданной пирамиды ТАВС;
2)пирамиды TCNM;
3)пирамиды ТМВС.
Основания 2-ой и 3-ей пирамид конгруэнтны: 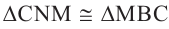
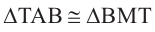
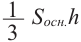
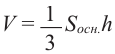
Подобие фигур в пространстве
Подобные фигуры имеют одинаковую форму и пропорциональные размеры.
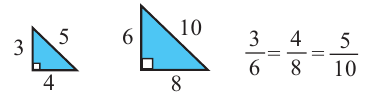
Например, прямоугольные треугольники на рисунке подобны, так как отношения соответствующих сторон равны.
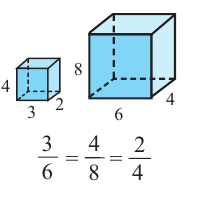
Прямоугольные параллелепипеды на рисунке подобны, так как отношения соответствующих линейных размеров равны и соответствующие грани являются подобными четырёхугольниками. Правильные многогранники подобны. В частном случае подобными являются все кубы, правильные тетраэдры и т.д.
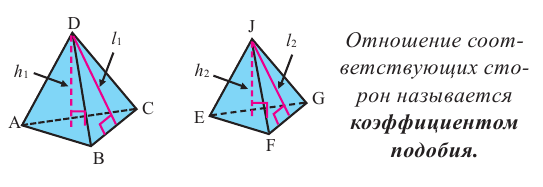
Подобные фигуры
Если при преобразовании расстояние между любыми двумя точками, меняется в одинаковое число раз, то такое преобразование называется подобием. Одна и другая, полученная при преобразовании подобием, фигура называются подобными фигурами. Коэффициент подобия равен отношению расстояний между парой любых двух соответсвующих точек.
Пример №2
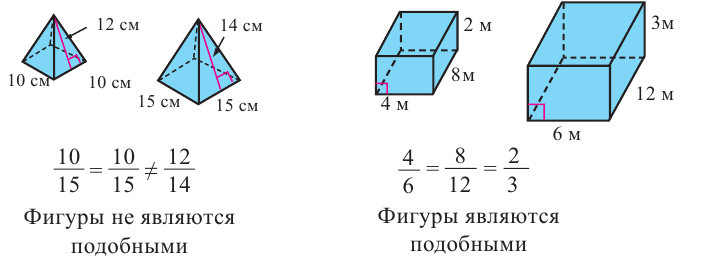
Определим подобны или нет фигуры на рисунке.
Площади поверхностей и объёмы подобных фигур
Исследование. Покажите подобны или нет следующие фигуры.
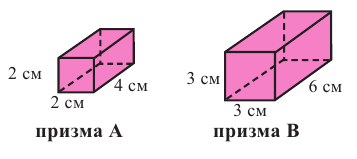
Призмы А и В (прямоугольные параллелепипеды) подобные призмы
с коэффициентом подобия равным 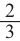
Для данных призм найдите:
а)отношение площадей полных поверхностей;
б)отношение объёмов.
а)площадь полной поверхности призмы А
площадь полной поверхности призмы В
Отношение полной поверхности призмы А к полной поверхности призмы В
б)объём призмы А
объём призмы В
Отношение объёма призмы А к объёму призмы В
Если коэффициент подобия двух пространственных фигур равен 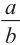
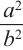
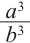
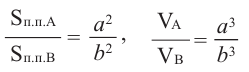
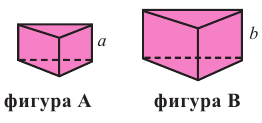
Пирамида, полученная сечением плоскости параллельной основанию, подобна данной. Коэффициент подобия можно найти из отношения соответствующих линейных размеров.
Например, на рисунке даны высоты. Тогда, отношения их боковых поверхностей, основании и полных поверхностей равно квадрату отношения высот.
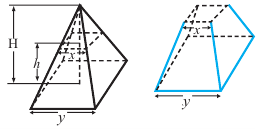
Объём усечённой пирамиды
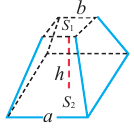
Исследование. В древнем Египте объём правильной усечённой четырёхугольной пирамиды вычисляли по формуле 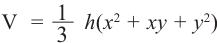
Объём усечённой пирамиды можно также найти как разность объёмов пирамид, при сечении плоскостью параллельной основанию.
Здесь V – объём усечённой пирамиды, S2 и S1 площади нижнего и верхнего оснований. h – высота усечённой пирамиды, h1 – высота меньшей пирамиды.
Так как эти пирамиды подобны, то отношение площадей равно квадрату отношений высот. Запишем это равенство и найдём высоту меньшей пирамиды.
Учитывая выражение
в равенстве
получим:
Объём усечённой призмы
Объём усечённой пирамиды с площадями оснований 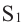
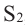
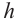
Задачи на сечение плоскостью
Пример:
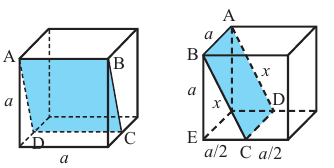
На рисунке показано сечение куба, с ребром а, плоскостью АВDО. Точки D и С являются серединами рёбер. Найдём площадь сечения.
Решение:
Дано: куб, длина ребра которого равна а точки D и С середины рёбер.
Найдите:
Для удобства повернём куб и отметим данные задачи на рисунке. Из 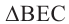
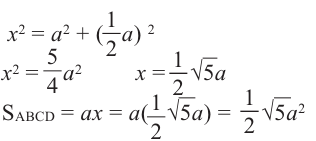
Симметрия в пространстве
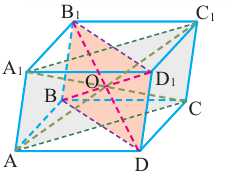
В пространственных фигурах также можно наблюдать различную симметрию. Известно, что в параллелепипеде диагональные сечения являются параллелограммами и диагонали ВD1 и DВ1 пересекаясь в точке О делятся пополам.
Можно показать, что другие диагонали также пересекаются в точке О и делятся пополам. Значит, точка пересечения диагоналей параллелепипеда является центром его симметрии.
В пространстве, помимо симметрии относительно точки и прямой, рассматривается симметрия относительно плоскости.
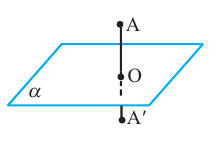
Если отрезок АА’ пересекает плоскость а посередине, и перпендикулярен плоскости, то говорят, что точки А и А’ симметричны относительно плоскости а.
Если точки фигуры, симметричные некоторой плоскости, также принадлежат этой фигуре,то эту плоскость называют плоскостью симметрии, а фигуру называют симметричной относительно плоскости.
Прямоугольный параллелепипед, у которого все линейные размеры разные, кроме центра симметрии имеет ещё три оси и три плоскости симметрии. Прямая, проходящая через точку пересечения диагоналей противоположных граней, называется осью симметрии,а плоскость, проходящая перпендикулярно через середину рёбер называется плоскостью симметрии. Параллелепипед, у которого два линейных размера равны, имеет 5 плоскостей симметрии. Данные изображения нарисуйте в тетрадь.
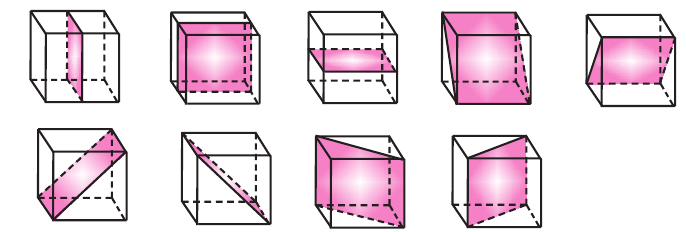
Точка пересечения диагоналей куба является его центром симметрии. Прямые, проходящие через середину параллельных рёбер, не принадлежащих одной грани (их всего 6) и прямые, проходящие через центры противоположных граней(их всего три), являются осями симметрии куба. У куба 9 плоскостей симметрии. Они изображены на следующих рисунках.
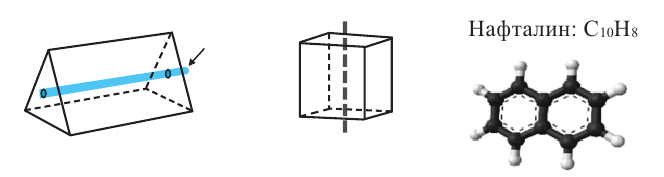
Вращательная симметрии
Вращательная симметрия пространственных фигур похожа на вращательную симметрию плоских фигур. Однако, для объёмных фигур она определяется при помощи оси вращения.
Вращательная и осевая симметрия широко применяется при изучении строения молекул веществ.
Пример №3
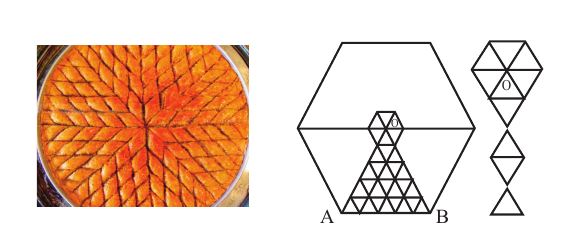
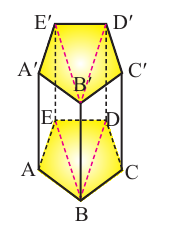
На рисунке показан вид сверху деталей, в виде правильных треугольных призм. Из них сконструирована правильная шестиугольная призма с центром основания О. Сколько деталей понадобилось для этого?
Основанием призмы является правильный шестиугольник, состоящий их 6 конгруэнтных треугольников. Каждый треугольник заполнен призмами. По изображению видно, что в один треугольник помещено 1+3 + 5 + 7 + 9 = 25 призм . Для правильной шестиугольной призмы таких призм нужно будет 6 • 25 = 150.
- Объёмы поверхностей геометрических тел
- Фигуры вращения: цилиндр, конус, шар
- Объем фигур вращения
- Длина дуги кривой
- Площадь многоугольника
- Правильные многоугольники
- Вписанные и описанные многоугольники
- Площадь прямоугольника
Подобность многогранников.
Два многогранника называются подобными, если они имеют соответственно
равные многогранные углы и соответственно подобные грани.
Соответственные элементы подобных многогранников называются сходственными. У подобных многогранников
двугранные углы равны и одинаково расположены; сходственные рёбра пропорциональны.
Если в пирамиде проведём секущую площадь параллельно
основанию, то она отсечёт от неё другую пирамиду, подобную данной.
Поверхности подобных многогранников относятся, как
квадраты сходственных линейных элементов многогранников.
Объёмы подобных многогранников относятся как кубы
сходственных линейных элементов этих многогранников.
Квадраты объёмов подобных многогранников относятся как
кубы площадей сходственных граней.
Подобные цилиндры и конусы.
Два цилиндра, конуса
или усечённых конуса называются подобными, если подобны их осевые сечения.
Боковые и полные поверхности подобных цилиндров, конусов и
усечённых конусов относятся, как квадраты их сходственных линейных элементов. (радиусов оснований, высот, образующих).
Объёмы подобных тел.
Пусть Т и Т‘ – два простых подобных тела. Это означает, что существует
преобразования подобия, при котором тело
Т переходить в тело Т‘. Обозначим через k коэффициент
подобия.
Разобьём тело Т на треугольные пирамиды
Р1, Р2,
…, Рn …
Преобразования подобия, которое переводит тело Т в тело Т‘ переводит пирамиды
Р1, Р2,
…, Рn в пирамиды Р1‘, Р2‘, …, Рn‘.
Эти пирамиды составляют тело Т‘ и поэтому объём тела Т‘ равен сумме объёмов пирамид
Р1‘, Р2‘, …, Рn‘.
Так как пирамиды Р1‘ и Р1 подобны и коэффициент подобия равен k,
то и отношение их высот равно k, а отношение площадей их оснований равно k2. Поэтому, отношение объёмов пирамид равно k3. Так как тело Т состоит из пирамид Р1, а тело Т‘ состоит из пирамид Р1‘,
то отношение объёмов тел Т‘ и Т тоже равно
k3.
Число k – коэффициент подобия – равен отношению расстояний
между любыми двумя соответствующими парами точек при преобразования подобия. Поэтому,
это число равно отношению любых двух соответствующих линейных размеров тел Т‘ и
Т.
Таким образом, мы приходим к следующему выводу:
Объёмы двух подобных
тел относятся как кубы их соответствующих линейных размеров.
Квадраты объёмов
подобных тел относятся, как кубы площадей соответствующих граней.
Объёмы подобных цилиндров, конусов и усечённых конусов относятся,
как кубы их соответствующих линейных элементов (радиусов оснований,
высот, образующих).
Объёмы шаров относятся, как кубы их радиусов или диаметров.
ЗАДАЧА:
Площади оснований усечённой пирамиды S1 и S2, а её объём равен
V. Определить объём полной пирамиды.
РЕШЕНИЕ:
Пусть S1 > S2. Обозначим
объём полной пирамиды через V1, а объём пирамиды, дополняющей данную усечённую пирамиду
до полной, через V2
Тогда:
или
Составляя производную пропорцию, получим:
С учётом V1 –
V2 = V, находим:
откуда:
ОТВЕТ:
ЗАДАЧА:
Площади оснований усечённой пирамиды
равны а2 и b2. Найти площадь сечения, которое параллельно площадям
оснований усечённой пирамиды и делящего её объём пополам.
РЕШЕНИЕ:
В усечённой пирамиде АС1 (для простоты
рисунка рассматривается треугольная пирамида) дано:
Необходимо найти площадь сечения А‘‘ё (пл. АВС ∥ пл. А‘‘ё), которое делит усечённую
пирамиду на равновеликие по объёму части.
Дополним усечённую пирамиду до полной. Пирамиды
SАВС, SА‘‘ё, SA1B1C1 –
подобные.
Обозначим площадь искомого сечения А‘‘ё через х2, а объёмы пирамид
SАВС, SА‘‘ё и SA1B1C1
соответственно
Va, Vx, Vb.
Тогда:
или
где t –
некоторое число, которое обозначает величину этих отношений. Тогда:
Va = a3t, Vx
= x3t, Vb = b3t.
По условию задачи:
Va – Vx =
Vx – Vb,
или
a3t – x3t = x3t – b3t,
откуда:
2x3 = a3 + b3.
поэтому,
ОТВЕТ:
Задания к уроку 19
Задача 8 в ЕГЭ по математике посвящена стереометрии и обычно вызывает у ребят панику. Да, нужно знать много формул и свойств пирамид, призм и тел вращения. Но сегодня мы предлагаем тебе лайфхак, делающий подобные задачи элементарными. Ты знаешь, что такое подобные фигуры? Сразу вспоминается планиметрия восьмого и девятого класса, где вы подробно проходили подобные треугольники. Наверняка ты помнишь, как найти коэффициент подобия, посмотрев на соотношения сторон. Также должно быть известно, что отношение площадей равно коэффициенту подобия в квадрате.
Внимание! Новость! В стереометрии тоже существуют подобные фигуры. Отношение радиусов – это коэффициент подобия. Отношение площадей поверхности – это квадрат коэффициента подобия, а отношение объемов – это коэффициент подобия в кубе. Посмотри на картинку: видишь в задаче дано отношение объемов? Получи коэффициент подобия (линейное соотношение), а из него найди отношение площадей. Ты получил балл за задачу по грозной стереометрии.
Обрати внимание, что это отношение будет верно не только для площадей поверхности, но и одинаковых сечений и граней подобных фигур. Сказанное справедливо в том случае, когда мы имеем дело с подобными фигурами. Без этого простого правила нам бы пришлось составлять уравнения, находить отношения. А это бывает долго и муторно.
Сдай ЕГЭ на максимальный балл!
Видео по теме
Задача 1. В правильной четырехугольной пирамиде точка
– центр основания,
– вершина,
Найдите длину отрезка
.
Решение: + показать
Задача 2. В правильной четырехугольной пирамиде точка
– центр основания,
– вершина,
Найдите боковое ребро
Решение: + показать
Задача 3. Стороны основания правильной четырехугольной пирамиды равны боковые ребра равны
Найдите площадь поверхности этой пирамиды.
Решение: + показать
Задача 4. В правильной четырёхугольной пирамиде точка
— центр основания,
— вершина,
Найдите длину отрезка
Решение: + показать
Задача 5. Основанием пирамиды является прямоугольник со сторонами и
Ее объем равен
Найдите высоту этой пирамиды.
Решение: + показать
Задача 6. В правильной четырёхугольной пирамиде с основанием
боковое ребро
равно
сторона основания равна
Найдите объём пирамиды.
Решение: + показать
Задача 7. В правильной четырёхугольной пирамиде все рёбра равны Найдите площадь сечения пирамиды плоскостью, проходящей через середины боковых рёбер.
Решение: + показать
Задача 8. Даны две правильные четырёхугольные пирамиды. Объём первой пирамиды равен У второй пирамиды высота в
раза больше, а сторона основания в
раза больше, чем у первой. Найдите объём второй пирамиды.
Решение: + показать
Задача 9. В правильной четырёхугольной пирамиде боковое ребро равно а тангенс угла между боковой гранью и плоскостью основания равен
Найти сторону основания пирамиды.
Решение: + показать
Задача 10. Основанием пирамиды является прямоугольник со сторонами и
Ее объем равен
Найдите высоту этой пирамиды.
Решение: + показать
Задача 11. Стороны основания правильной четырехугольной пирамиды равны боковые ребра равны
Найдите площадь поверхности этой пирамиды.
Решение: + показать
Задача 12. В правильной треугольной пирамиде медианы основания
пересекаются в точке
. Площадь треугольника
равна
объем пирамиды равен
Найдите длину отрезка
.
Решение: + показать
Задача 13. В правильной треугольной пирамиде точка
— середина ребра
— вершина. Известно, что
а
. Найдите площадь боковой поверхности пирамиды.
Решение: + показать
Задача 14. Найдите объем правильной треугольной пирамиды, стороны основания которой равны а высота равна
Решение: + показать
Задача 15. Найдите высоту правильной треугольной пирамиды, стороны основания которой равны а объем равен
Решение: + показать
Задача 16. Стороны основания правильной шестиугольной пирамиды равны боковые ребра равны
Найдите площадь боковой поверхности этой пирамиды.
Решение: + показать
Задача 17. Объем правильной шестиугольной пирамиды Сторона основания равна
Найдите боковое ребро.
Решение: + показать
Задача 18. Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в два раза?
Решение: + показать
Задача 19. Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в раз?
Решение: + показать
Задача 20. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в пять раз?
Решение: + показать
Задача 21. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом °. Высота пирамиды равна
Найдите объем пирамиды.
Решение: + показать
Задача 22. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно Найдите объем пирамиды.
Решение: + показать
Задача 23. От треугольной призмы, объем которой равен отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.
Решение: + показать
Задача 24. Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен Найдите объем шестиугольной пирамиды. Видео по теме 1 2
Решение: + показать
Задача 25. Сторона основания правильной шестиугольной пирамиды равна 8, боковое ребро равно 16. Найдите объём пирамиды.
Решение: + показать
Задача 26. Сторона основания правильной шестиугольной пирамиды равна а угол между боковой гранью и основанием равен
Найдите объем пирамиды.
Решение: + показать
Задача 27. Найдите объём правильной шестиугольной пирамиды если объём треугольной пирамиды
равен
Решение: + показать
Задача 28. Объем параллелепипеда равен
Найдите объем треугольной пирамиды
Решение: + показать
Задача 29. Объем куба равен Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
Решение: + показать
Задача 30. Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно
Решение: + показать
Задача 31. Объем правильной четырехугольной пирамиды равен
Точка
— середина ребра
. Найдите объем треугольной пирамиды
.
Решение: + показать
Задача 32. От треугольной пирамиды, объем которой равен отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
Решение: + показать
Задача 33. Ребра тетраэдра равны Найдите площадь сечения, проходящего через середины четырех его ребер.
Решение: + показать

Усеченная пирамида
Определение . Часть пирамиды, образованная при сечении пирамиды плоскостью, параллельной её основанию, заключенная между секущей плоскостью и основанием, называется усеченной пирамидой.
На рисунке показана пирамида, отбрасывая её часть, лежащую выше секущей плоскости, получаем усеченную пирамиду. Ясно, что малая отбрасываемая пирамида гомотетична большой пирамиде с центром гомотетии в вершине. Коэффициент подобия равен отношению высот: k=h2/h1, или боковых ребер, или других соответствующих линейных размеров обеих пирамид. Мы знаем, что площади подобных фигур относятся, как квадраты линейных размеров; так площади оснований обеих пирамид (т.е. пощади оснований усеченной пирамиды) относятся, как 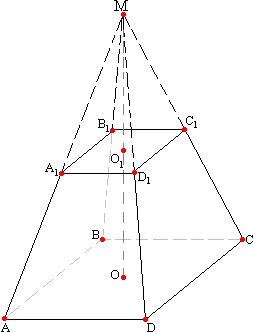
Здесь S1 – площадь нижнего основания, а S2 – площадь верхнего основания усеченной пирамиды. В таком же отношении находятся и боковые поверхности пирамид. Сходное правило имеется и для объемов.
Объемы подобных тел относятся, как кубы их линейных размеров; например, объемы пирамид относятся, как произведения их высот на площади оснований, откуда наше правило получается сразу. Оно имеет совершенно общий характер и прямо следует из того, что объем всегда имеет размерность третей степени длины. Пользуясь этим правилом, выведем формулу, выражающую объем усеченной пирамиды через высоту и площади оснований.
Пусть дана усеченная пирамида с высотой h и площадями оснований S1 и S2. Если представить себе, что она продолжена до полной пирамиды, то коэффициент подобия полнорй пирамиды и малой пирамиды легко найти, как корень из отношения S2/S1. Высота усеченной пирамиды выражается как h = h1 – h2 = h1(1 – k). Теперь имеем для объема усеченной пирамиды (через V1 и V2 обозначены объемы полной и малой пирамид)
k2S1=S2, поэтому
Теорема. Объем усеченной пирамиды можно вычислить по формуле:
При нахождении площади боковой поверхности усеченной пирамиды принципы нахождения ПБП обычной пирамиды не теряют актуальности:
Теорема . Если все апофемы усеченной пирамиды равны, то площадь её боковой поверхности можно вычислить по формуле:
Из этой теоремы можно получить подобные:
Теорема. Если все боковые грани усеченной пирамиды наклонены к плоскости основания под одинаковым углом, то площадь её боковой поверхности можно вычислить по формуле:
Теорема. Если пирамида правильная, то площадь её боковой поверхности можно вычислить по формуле:
При нахождении площади поверхности усеченной пирамиды, необладающей ни одним из перечисленных признаков, осуществляется вычисление площадей отдельных граней, а затем производится их суммирование.
Выведем эту формулу. Пусть S – площадь боковой поверхности усеченной пирамиды, обладающей одним из вышеперечисленных признаков, Р1 и Р2 – периметры оснований и а – длина апофемы. Рассуждаем точно так же, как и при выводе формулы для объема. Дополняем пирамиду верхней частью, имеем P2 = kP1, S2=k2S1, где k – коэффициент подобия, P1 и P2 – периметры оснований, а S1 и S2 – лощади боковых поверхностей всей полученной пирамиды и её верхней части соответственно. Для боковой поверхности найдем
(а1 и а2 – апофемы пирамид, а = а1 – а2 = а1(1-k)):
Правильная усеченная пирамида также как и обычная правильная пирамида имеет особенности:
Теорема. В правильной усеченной n-угольной пирамиде все боковые ребра равны между собой.
Теорема. Все боковые грани правильной усеченной n-угольной пирамиды суть равные равнобедренные трапеции (углы при основаниях рабнобедренной трапеции равны), поэтому:
Теорема. В правильной усеченной n-угольной пирамиде все плоские углы при основаниях равны.
Теорема. В правильной усеченной n-угольной пирамиде все двугранные углы при основаниях равны.
Теорема. В правильной усеченной n-угольной пирамиде все двугранные углы при боковых ребрах равны.
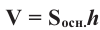
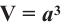
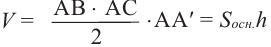
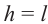 , основание же является перпендикулярным сечением наклонной призмы. Объём данной прямой призмы является также объёмом наклонной призмы.
, основание же является перпендикулярным сечением наклонной призмы. Объём данной прямой призмы является также объёмом наклонной призмы.