Как найти коэффициент подобия прямоугольника

Вы открыли страницу вопроса Как найти коэффициент подобия прямоугольника?. Он относится к категории
Математика. Уровень сложности вопроса – для учащихся 5 – 9 классов.
Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие
ответы по интересующей теме. Чтобы получить наиболее развернутый ответ,
можно просмотреть другие, похожие вопросы в категории Математика,
воспользовавшись поисковой системой, или ознакомиться с ответами других
пользователей. Для расширения границ поиска создайте новый вопрос, используя
ключевые слова. Введите его в строку, нажав кнопку вверху.

Сегодня мы поговорим о подобии произвольных фигур.

Треугольник —
это та фигура, которую мы уже изучили достаточно подробно. Вам уже известны
признаки равенства и признаки подобия треугольников.

Повторим признаки равенства треугольников. Они могут
быть равны по двум равным сторонам и углу между ними, по стороне и двум
прилежащим углам, по трём равным сторонам.

Повторим признаки подобия. Треугольники подобны по
двум пропорциональным сторонам и углу между ними, по двум углам, по трём
пропорциональным сторонам.

Проведём аналогию с треугольником и рассмотрим равные
фигуры. Понятно, что они должны быть одинаковой формы и одинакового размера.

Если же форму оставить той же, а размер изменить, то
мы как раз таки получим подобные фигуры.

Определение.
Фигуры F и F₁
называются подобными, если каждой точке фигуры F
можно сопоставить точку фигуры F₁
так, что для любых двух точек М и N
фигуры F
и
сопоставленных им точек M₁
и N₁
фигуры F₁
выполняется такое равенство , .
Число коэффициент
подобия фигур  и
.
При этом предполагается, что каждая точка фигуры F1
оказывается сопоставленной какой-то точке фигуры F.

Такое сопоставление точек подобных фигур можно
наблюдать при проявлении фотографий. Каждой точке кадра соответствует одна
точка на готовой фотографии. Если бы подобие не выполнялось, то фото не могло
бы достоверно передавать пропорции тех или иных объектов и искажало бы
действительную картину.

Приведём ещё несколько примеров подобия из
окружающего нас мира. Матрёшки. Объект и его изображение в лупе.

Изображение той или иной местности на картах
различного масштаба.

Примерами подобных геометрических фигур являются два
любых круга, два любых квадрата, два любых равносторонних треугольника, два
куба. А так же, например, два треугольника, соответствующие стороны которых
отличаются ровно в k
раз. Два прямоугольника будут подобны, если отношение длины и ширины одного из
них равно отношению длины и ширины другого.

Вспомним свойства периметров и площадей подобных фигур.

Рассмотрим, например, два подобных прямоугольника,
отношение соответствующих сторон которого равно коэффициенту подобия k.

Записав периметр каждого прямоугольника, не трудно
выяснить, что их отношение равно коэффициенту k.

Аналогично, записав площади прямоугольников,
получаем, что их отношение равно квадрату коэффициента пропорциональности.

А сейчас рассмотрим два подобных прямоугольных
параллелепипеда.

По известной вам формуле объёма, найдём его значение
для каждой из фигур.

Воспользовавшись подобием, выразим измерения первого
параллелепипеда через измерения второго с помощью коэффициента подобия.

Запишем отношение объёмов. Получаем, что оно равно
кубу коэффициента подобия.

Теперь в вашем арсенале не только свойства
периметров и площадей подобных фигур, а ещё и их объёмов.

Задача. Даны два
подобных пятиугольника. Найдите ,
если ,
,
.

Решение.

 

 

 

Ответ: .

Задача. Эйфелева башня,
высотою  м,
весит  кг.
Сколько весит точная модель этой башни, из того же материала, высотой  м?

Решение.

Из физики вам
известно, что масса равна произведению плотности и объёма .
 Запишем отношение масс.

Плотность можно сократить, так как копию башни
делают из того же материала, что и оригинал.

Ответ: .

Подведём итоги урока.

Сегодня вы познакомились с подобием произвольных
фигур. Фигуры F и F₁
называются подобными, если каждой точке фигуры F
можно сопоставить точку фигуры F₁
так, что для любых двух точек М и N
фигуры F и
сопоставленных им точек M₁
и N₁
фигуры F₁
выполняется такое равенство ,  k
— одно и то же положительное число для всех точек. При этом предполагается, что
каждая точка фигуры F₁
оказывается сопоставленной какой-то точке фигуры F.
Число k
называется
коэффициентом подобия фигур F
и F₁.

Также мы рассмотрели примеры подобных фигур и с
помощью свойств периметров, площадей и объёмов подобных фигур решили несколько
задач.

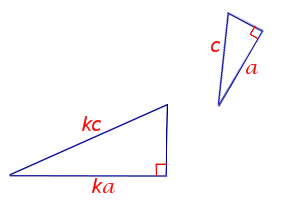
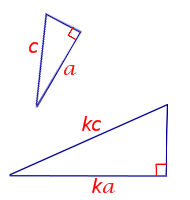
Формулировка признака подобия прямоугольных треугольников:

Если гипотенуза и катет одного прямоугольного треугольника пропорциональны гипотенузе и катету другого прямоугольного треугольника, то такие прямоугольные треугольники подобны.

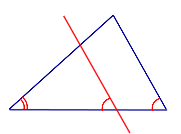
Следствие 1 . Прямая, пересекающая треугольник и параллельная стороне треугольника, отсекает от этого треугольника подобный треугольник (рис. 3).

Следствие 2 . Отношение площадей подобных треугольников равно квадрату коэффициента подобия (рис. 4)

Подобные треугольники

Определение

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.

Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.

Признаки подобия треугольников

I признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

II признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Свойства подобных треугольников

• Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
• Отношение периметров подобных треугольников равно коэффициенту подобия.
• Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.

Примеры наиболее часто встречающихся подобных треугольников

1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.

2. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –

3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.

Здесь вы найдете подборку задач по теме «Подобные треугольники» .

Коэффициент подобия прямоугольных треугольников

Признака подобия треугольников

Две фигуры `F` и `F’` называются подобными, если они переводятся друг в друга преобразованием подобия, т. е. таким преобразованием, при котором расстояния между точками изменяются (увеличиваются или уменьшаются) в одно и то же число раз. Если фигуры `F` и `F’` подобны, то пишется `F

F’`. Напомним, что запись подобия треугольников `Delta ABC

Delta A_1 B_1 C_1` означает, что вершины, совмещаемые преобразованием подобия, стоят на соответствующих местах, т. е. `A` переходит в `A_1`, `B` – в `B_1`, `C` – в `C_1`.

Из свойств преобразования подобия следует, что у подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны. В частности, если `Delta ABC

Delta A_1B_1C_1`, то `/_ A = /_ A_1`, `/_ B = /_ B_1`, `/_ C = /_ C_1`,

`A_1B_1 : AB = B_1C_1 : BC = C_1A_1 : CA`.

Два треугольника подобны, если:

1. два угла одного соответственно равны двум углам другого;

2. две стороны одного пропорциональны двум сторонам другого и углы, образованные этими сторонами, равны;

3. три стороны одного треугольника пропорциональны трём сторонам другого.

В решении задач и доказательстве теорем часто используется утверждение, которое, чтобы не повторять каждый раз, докажем сейчас отдельно.

Если две стороны треугольника пересекает прямая, параллельная третьей стороне (рис. 9), то она отсекает треугольник, подобный данному.

Действительно, из параллельности `MN` и `AC` следует, что углы `1` и `2` равны. Треугольники `ABC` и `MBN` имеют два равных угла: общий угол при вершине `B` и равные углы `1` и `2`. По первому признаку эти треугольники подобны.

И сразу применим это утверждение в следующем примере, в котором устанавливается важное свойство трапеции.

Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках `M` и `N`. Найти длину отрезка `MN`, если основания трапеции равны `a` и `b`.

1. Пусть `O` – точка пересечения диагоналей, `AD = a`, `BC = b`. Прямая `MN` параллельна основанию `AD` (рис. 10а), следовательно, $$ MOparallel AD$$, треугольники `BMO` и `BAD` подобны, поэтому

2. $$ ADparallel BC$$, `Delta AOD

Delta COB` по двум углам (рис. 10б):

`(OD)/(OB) = (AD)/(BC)`, то есть `(OD)/(OB) = a/b`.

3. Учитывая, что `BD = BO + OD` находим отношение

`(BO)/(BD) = (BO)/(BO + OD) = 1/(1 + OD//BO) = b/(a + b)`.

Подставляя это в (1), получаем `MO = (ab)/(a + b)`; аналогично устанавливаем, что `ON = (ab)/(a + b)`, таким образом `MN = (2ab)/(a + b)`.

Точки `M` и `N` лежат на боковых сторонах `AB` и `CD` трапеции `ABCD` и $$ MNparallel AD$$ (рис. 11а). Найти длину `MN`, если `BC = a`, `AD = 5a`, `AM : MB = 1:3`.

1. Пусть $$ BFVert CD$$ и $$ MEVert CD$$ (рис. 11б), тогда `/_ 1 = /_ 2`, `/_ 3 = /_ 4` (как соответствующие углы при пересечении двух параллельных прямых третьей) и `Delta AME

Delta MBF`. Из подобия следует `(AE)/(MF) = (AM)/(MB) = 1/3`.

2. Обозначим `MN = x`. По построению `BCNF` и `MNDE` – параллелограммы, `FN = a`, `ED = x` и, значит, `MF = x – a`; `AE = 5a – x`. Итак, имеем `(5a – x)/(x – a) = 1/3`, откуда находим `x = 4a`.

Напомним, что отношение периметров подобных треугольников равно отношению их сходственных сторон. Верно также следующее утверждение: отношение медиан, биссектрис и высот, проведённых к сходственным сторонам в подобных треугольниках, равно отношению сходственных сторон.

Отношение радиусов вписанных окружностей, как и отношение радиусов описанных окружностей, в подобных треугольниках также равно отношению сходственных сторон.

Попытайтесь доказать это самостоятельно.

Прямоугольные треугольники подобны, если:

1. они имеют по равному острому углу;

2. катеты одного треугольника пропорциональны катетам другого;

3. гипотенуза и катет одного треугольника пропорциональны гипотенузе и катету другого.

Два первых признака следуют из первого и второго признаков подобия треугольников, поскольку прямые углы равны. Третий признак следует, например, из второго признака подобия и теоремы Пифагора.

Заметим, что высота прямоугольного треугольника, опущенная на гипотенузу, разбивает его на два прямоугольных треугольника, подобных между собой и подобных данному. Доказанные в § 1 метрические соотношения Свойств 1, 2, 3 можно доказать, используя подобие указанных треугольников.

СВОЙСТВА ВЫСОТ И БИССЕКТРИС

Если в треугольнике `ABC` нет прямого угла, `A A_1` и `BB_1` – его высоты, то `Delta A_1B_1C

Delta ABC` (этот факт можно сформулировать так: если соединить основания двух высот, то образуется треугольник, подобный данному).

Как всегда, полагаем `AB = c`, `BC = a`, `AC = b`.
а) Треугольник `ABC` остроугольный (рис. 12а).

В треугольнике `A A_1C` угол `A_1` – прямой, `A_1C = AC cos C = ul (b cos C)`.

В треугольнике `B B_1C` угол `B_1` – прямой, `B_1C = BC cos C = ul (a cos C)`.

В треугольниках `A_1 B_1C` и `ABC` угол `C` общий, прилежащие стороны пропорциональны: `(A_1C)/(AC) = (B_1C)/(BC) = cos C`.

Таким образом, `Delta A_1 B_1 C

Delta ABC` с коэффициентом подобия `ul (cos C)`. (Заметим, что `/_ A_1 B_1 C = /_B`).
б) Треугольник `ABC` – тупоугольный (рис. 12б), угол `C` – острый, высота `A A_1` проведена из вершины тупого угла.

$$left.begin
Delta AA_1C, angle A_1 =90^circ Rightarrow A_1C=ACcdot cos C =b cos C;\
Delta BB_1C, angle B_1 =90^circ Rightarrow B_1C=BCcdot cos C =a cos C,
end
right>Rightarrow Delta A_1B_1Csim Delta ABC,$$

коэффициент подобия `ul (cos C)`, `/_ A_1 B_1 C = /_B`.

Случай, когда угол `B` тупой, рассматривается аналогично.
в) Треугольник `ABC` – тупоугольный (рис. 12в), угол `C` – тупой, высоты `A A_1` и `B B_1` проведены из вершин острых углов.

`varphi = /_ BCB_1 = /_ ACA_1 = 180^@ – /_ C`, `cos varphi = – cos C = |cos C|`.

$$left.begin
Delta AA_1C, angle A_1 =90^circ Rightarrow A_1C=ACcdot cosvarphi =b |cos C|;\
Delta BB_1C, angle B_1 =90^circ Rightarrow B_1C=BCcdot cosvarphi =b |cos C|,
end
right>Rightarrow Delta A_1B_1Csim Delta ABC$$

с коэффициентом подобия `ul (k = |cos C|`, `(/_A_1B_1C=/_B)`.

В остроугольном треугольнике `ABC` проведены высоты `A A_1`, `B B_1`, `C C_1` (рис. 13).

Треугольник, вершинами которого служат основания высот, называется «высотным» треугольником (или ортотреугольником).

Доказать, что лучи `A_1 A`, `B_1 B` и `C_1 C` являются биссектрисами углов высотного треугольника `A_1 B_1 C_1` (т. е. высоты остроугольного треугольника являются биссектрисами ортотреугольника).

По первой лемме о высотах `Delta A_1 B_1 C

Delta ABC`, `/_ A_1 B_1 C = /_ B`.

Аналогично `Delta AB_1C_1

Delta ABC`, `/_ AB_1 C_1 = /_ B`, т. е. `/_A_1 B_1C = /_ AB_1 C_1`.

Так как `BB_1` – высота, то `/_AB_1B = /_CB_1B = 90^@`.

Поэтому `/_C_1B_1B = /_A_1B_1B = 90^@ – /_B`, т. е. луч `B_1B` – биссектриса угла `A_1B_1C_1`.

Аналогично доказывается, что `A A_1` – биссектриса угла `B_1 A_1 C_1` и `C_1C` – биссектриса угла `B_1 C_1 A_1`.

Высоты `A A_1`, `B B_1` треугольника `ABC` пересекаются в точке `H` (рис. 14). Доказать, что имеет место равенство `AH * H A_1 = BH * HB_1`, т. е. произведение отрезков одной высоты равно произведению отрезков другой высоты.

Delta BHA_1`, имеют по равному острому углу при вершине `H` (заметим, что этот угол равен углу `C`). Из подобия следует `(AH)/(BH) = (HB_1)/(HA_1)`, откуда `AH * HA_1 = BH * HB_1`. Для тупоугольного треугольника утверждение также верно. Попробуйте доказать самостоятельно.

Высоты `A A_1` и `B B_1` треугольника `ABC` пересекаются в точке `H`, при этом `BH = HB_1` и `AH = 2 HA_1` (рис. 15). Найти величину угла `C`.

1. По условию пересекаются высоты, поэтому треугольник остроугольный. Положим `BH = HB_1 = x` и `HA_1 = y`, тогда `AH = 2y`. По второй лемме о высотах `AH * HA_1 = BH * HB_1`, т. е. `x^2 = 2y^2`, `x = y sqrt 2`.
2. В треугольнике `AHB_1` угол `AHB_1` равен углу `C` (т. к. угол `A_1 AC` равен `90^@ – C`), поэтому `cos C = cos (/_ AHB_1) = x/(2y) = sqrt 2/ 2`. Угол `C` – острый, `/_ C = 45^@`.

Установим ещё одно свойство биссектрисы угла треугольника.

Биссектриса внутреннего угла треугольника делит противолежащую этому углу сторону на отрезки, пропорциональные прилежащим сторонам, т. е. если `AD` – биссектриса треугольника `ABC`, то `(BD)/(DC) = (AB)/(AC)`.

Проведём через точку `B` прямую параллельно биссектрисе `DA`, пусть `K` – её точка пересечения с прямой `AC` (рис. 16).

Параллельные прямые `AD` и `KB` пересечены прямой `KC`, образуются равные углы `1` и `3`. Те же прямые пересечены и прямой `AB`, здесь равные накрест лежащие углы `2` и `4`. Но `AD` – биссектриса, `/_1 = /_2`, следовательно `/_3 = /_4`. Отсюда следует, что треугольник `KAB` равнобедренный, `KA = AB`.
По теореме о пересечении сторон угла параллельными прямыми из $$ ADVert KB$$ следует `(BD)/(DC) = (KA)/(AC)`. Подставляя сюда вместо `KA` равный ему отрезок `AB`, получим `(BD)/(DC) = (AB)/(AC)`. Теорема доказана.

Биссектриса треугольника делит одну из сторон треугольника на отрезки длиной `3` и `5`. Найти в каких пределах может изменяться периметр треугольника.

Пусть `AD` – биссектриса и `BD = 3`, `DC = 5` (рис. 17).

По свойству биссектрисы `AB : AC = 3:5`. Положим `AB = 3x`, тогда `AC = 5x`. Каждая сторона треугольника должна быть меньше суммы двух других сторон, т. е. `ul (5x 1`.

Периметр треугольника `P = 8 + 8x = 8(1 + x)`, поэтому `ul (16

[spoiler title=”источники:”]

http://zftsh.online/articles/5599

[/spoiler]