Перед началом обращусь к вам с просьбой. Я пытаюсь помочь вам, а вы помогайте мне 🙂 Обязательно дочитывайте до конца, подписывайтесь на канал, задавайте свои вопросы по математике в комментарии или в соцсетях по ссылкам на канале. Помогайте мне продвинуть канал 🙂
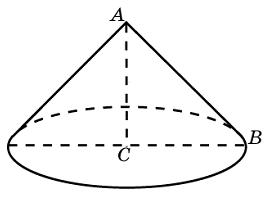
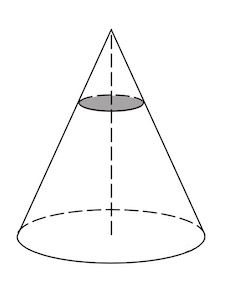
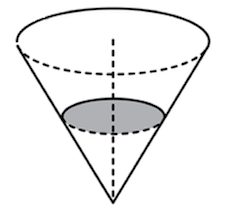
Сейчас научимся решать задачи на объём конуса. Кстати, странно, что задачи заявлены на объём конуса, но представлены на площадь сечения. Но не будем спорить, им виднее.
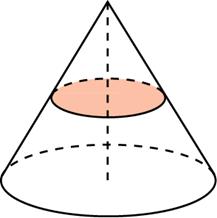
Такие задачки решаются через коэффициент подобия. Находим, чему равен коэффициент подобия с помощью высот. Маленькая высота равна 1, большая 3, значит коэффициент равен 1/3. Как работать с коэффициентом подобия? Если сравниваем величины одномерные, то берём просто коэффициент подобия, если площади, то в квадрате, если объемы, то в кубе. В данном случае у нас площадь, значит 63 два раза умножаем на 1/3 и получаем 7. Значит площадь второго сечения равна 7.
Записывайтесь на семинар по базе ЕГЭ
Успейте записаться на интенсив ОГЭ
↓ ↓ ↓ ↓ ↓ За помощью обращайся сюда ↓ ↓ ↓ ↓ ↓
89174639366 (звонки, СМС) WA 89174639366 ВК Никита Тюрин
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
2
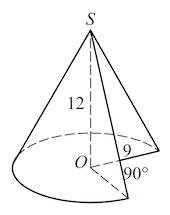
Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30°. В ответе укажите
3
Во сколько раз уменьшится объем конуса, если его высота уменьшится в 3 раза, а радиус основания останется прежним?
4
Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 1,5 раза, а высота останется прежней?
5
Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на
Пройти тестирование по этим заданиям
09
Сен 2013
Категория: 02 Стереометрия
02. Конус
2013-09-09
2022-09-11
Задача 1. Высота конуса равна , образующая равна
Найдите его объем, деленный на
.
Решение: + показать
Задача 2. Конус получается при вращении равнобедренного прямоугольного треугольника вокруг катета, равного
Найдите его объем, деленный на
.
Решение: + показать
Задача 3. Высота конуса равна а диаметр основания –
Найдите образующую конуса.
Задача 4. Найдите объем конуса, образующая которого равна
и наклонена к плоскости основания под углом
В ответе укажите
Решение: + показать
Задача 5. Длина окружности основания конуса равна образующая равна
Найдите площадь боковой поверхности конуса.
Решение: + показать
Задача 6. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в раз?
Решение: + показать
Задача 7. Во сколько раз уменьшится объем конуса, если его высоту уменьшить в раз?
Решение: + показать
Задача 8. Во сколько раз увеличится объем конуса, если радиус его основания увеличится в раз, а высота останется прежней?
Решение: + показать
Задача 9. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
Решение: + показать
Задача 10. Объем конуса равен Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Решение: + показать
Задача 11. Площадь полной поверхности конуса равна Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Решение: + показать
Задача 12. Найдите объем конуса, образующая которого равна
и наклонена к плоскости основания под углом
В ответе укажите
.
Решение: + показать
Задача 13. Диаметр основания конуса равен а угол при вершине осевого сечения равен
°. Вычислите объем конуса, деленный на
.
Решение: + показать
Задача 14. Площадь основания конуса равна , высота —
Найдите площадь осевого сечения конуса.
Решение: + показать
Задача 15. Площадь основания конуса равна Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной
и
считая от вершины. Найдите площадь сечения конуса этой плоскостью.
Решение: + показать
Задача 16. Найдите объем части конуса, изображенной на рисунке. В ответе укажите
.
Решение: + показать
Задача 17. Найдите объем части конуса, изображенной на рисунке. В ответе укажите
.
Решение: + показать
Задача 18. В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объём жидкости равен
мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Решение: + показать
Вы можете пройти тест
Автор: egeMax |
комментариев 10
Печать страницы
Скачать материал
без ожидания

Скачать материал
без ожидания


- Сейчас обучается 26 человек из 18 регионов


- Сейчас обучается 956 человек из 80 регионов


- Сейчас обучается 105 человек из 36 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Подготовка к ЕГЭ, подборка задач
по теме “Конус” (базовый уровень) -
2 слайд
Содержание
Задача №1
Задача №2
Задача №3
Задача №4
Задача №5
Задача №6
Задача №7
Задача №8
Задача №9
Задача №10
Задача №11
Задача №12
Задача №13
Задача №14
Задача №15
Задача №16
Задача №17
Задача №18
Задача №19
Задача №20
Задача №21 -
3 слайд
Задача №1
Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 3 и 9, а второго — 6 и 9. Во сколько раз площадь боковой поверхности второго конуса больше площади боковой поверхности первого?
Решение.
Т.к. площадь боковой поверхности конуса: S=πrl.
Значит S1= π·3·9= 27π, S2= π·6·9= 54π.
Тогда S2: S1= 54π : 27π = 2 -
4 слайд
Задача №2
Объём конуса равен 135. Через точку, делящую высоту конуса в отношении 1:2, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.
Отношение объемов конусов равно кубу их коэффициента подобия. Высоты конусов относятся как 1:3, поэтому их объемы относятся как 1:27. Следовательно, объем отсекаемого конуса равен 135 : 33 = 5. -
5 слайд
К задаче №2
Объём конуса равен 32. Через середину высоты конуса проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.
Решение.
Отношение объемов конусов равно кубу их коэффициента подобия k. Так как высоты конусов относятся как 1:2, то k равно одной второй, а значит объем отсекаемого конуса будет равен 32 : 2³ = 4. -
6 слайд
Задача №3
Объём конуса равен 50π а его высота равна 6 . Найдите радиус основания конуса.
Найдём радиус основания конуса по формуле: V=1/3·πR²h
Откуда R²=3V:πh => R²= 150π : 6π = 25. Тогда R=5 -
7 слайд
Задача №4
Во сколько раз уменьшится объем конуса, если
его высоту уменьшить в 3 раза?
Объем конуса вычисляется по формуле V=1/3·Soc.·h .
Значит, если высоту увеличить в 3 раза, то и объём увеличится в 3 раза -
8 слайд
Задача №5
Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 1,5 раза?
Объем конуса вычисляется по формуле
V=1/3·Soc.·h = 1/3·πR²·h.
Значит, если радиус основания увеличить в 1,5 раза, то и объём конуса увеличится в 2,25 раза -
9 слайд
Задача №6
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза?
Площадь боковой поверхности конуса вычисляется по формуле
S= πR·L, где L-образующая.
Значит если увеличить L в 3 раза, то площадь боковой поверхности конуса тоже увеличится в 3 раза. -
10 слайд
Задача №7
Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 1,5 раза, а образующая останется прежней?Площадь боковой поверхности конуса вычисляется по формуле S= πR·L. Значит, если радиус основания уменьшится в 1,5 раза, то площадь боковой поверхности конуса тоже уменьшится в 1,5 раза.
-
11 слайд
Задача №8
Высота конуса равна 4, а диаметр основания — 6. Найдите образующую конуса.
По теореме Пифагора -
12 слайд
Задача №9
Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса.
По теореме Пифагора….
Ответ: 6. -
13 слайд
Задача №10
Диаметр основания конуса равен 6, а длина образующей — 5. Найдите высоту конуса.
По теореме Пифагора….
Ответ: 4. -
14 слайд
Задача №11
В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём жидкости равен 70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Меньший конус подобен большему с коэффициентом 0,5. Объемы подобных тел относятся как куб коэффициента подобия. Поэтому объем большего конуса в 8 раз больше объема меньшего конуса, он равен 560 мл. Следовательно, необходимо долить 560 − 70 = 490 мл жидкости. -
15 слайд
Задача №12
В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём сосуда 1600 мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах. -
16 слайд
Решение
Пусть х — высота налитой жидкости, у — радиус окружности в основании конуса. Тогда 2х — высота сосуда, 2у — радиус окружности в основании сосуда (так как поверхность жидкости отсекает от конического сосуда конус подобный данному). Найдем отношения объёмов конусов,
Таким образом, объём сосуда в 8 раз больше объёма налитой жидкости: 1600 : 8 = 200 -
17 слайд
Задача №13
Объём конуса равен 96π, а его высота равна 8. Найдите радиус основания конуса.
Найдём радиус основания конуса из формулы: V=1/3·πR²h
Откуда R²=3V:πh => -
18 слайд
Задача №14
Даны два конуса. Радиус основания и образующая первого конуса равны, соответственно, 2 и 4, а второго — 6 и 8. Во сколько раз площадь боковой поверхности второго конуса больше площади боковой поверхности первого? -
19 слайд
Решение
Найдём площадь боковой поверхности первого конуса: S1=π·R1·L1 = π·2·4=8π
2) Найдём площадь боковой поверхности второго конуса: S2=π·R2·L2 = π·6·8=48π
3) Найдём отношение площадей этих конусов:
S2 : S1 = 48π : 8π = 6 -
20 слайд
Задача №15
Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна 3√2. Найдите площадь боковой поверхности конуса. -
21 слайд
Решение
Заметим, что конус и цилиндр имеют общую высоту и равные радиусы основания. Площадь боковой поверхности цилиндра равна Sб.п.= 2πR·h, но R=h следовательно Sб.п.= 2πR² и =3√2 => πR² =1,5√2
2) Площадь боковой поверхности конуса равна S=πR·L, Но L² = R²+h², но R=h => L² = 2R² => L = R√2.
Значит Sб.п.= πR·L= πR· R√2 = πR²·√2 =
= 1,5√2·√2 = 3 -
22 слайд
Задача №16
Диаметр основания конуса равен 12, а длина образующей — 10. Найдите площадь осевого сечения этого конуса.
Осевым сечением конуса является равнобедренный треугольник, основание которого —это диаметр основания конуса, а высота совпадает с высотой конуса.
Но L² = R²+h² => h = √100-36=√64=8
Следовательно, площадь осевого сечения
равна 0,5 · 12 · 8 = 48. -
23 слайд
Задача №17
Высота конуса равна 8, а длина образующей — 10. Найдите площадь осевого сечения этого конуса.
Осевым сечением конуса является равнобедренный треугольник, основание которого — диаметр основания конуса, а высота совпадает с высотой конуса.
Но L² = R²+h² => R=√100-64=√36=6
Следовательно, диаметр осевого сечения конуса равен 12, а площадь осевого сечения равна 0,5 · 12 · 8 = 48. -
24 слайд
Задача №18
Площадь основания конуса равна 18. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 3 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью -
25 слайд
Решние
Сечение плоскостью, параллельной основанию, представляет собой круг, радиус которого относится к радиусу основания конуса как 3 : 9. Площади подобных фигур относятся как квадрат коэффициента подобия, поэтому площадь сечения в 9 раз меньше площади основания. Тем самым, она равна 2. -
26 слайд
Задача №19
Площадь основания конуса равна 16π, высота — 6. Найдите площадь осевого сечения конуса.Осевым сечением конуса является равнобедренный треугольник, высота которого совпадает с высотой конуса, а основание является диаметром основания конуса. Поэтому площадь осевого сечения равна половине произведения высоты конуса на диаметр его основания или произведению высоты конуса на радиус основания R. Поскольку по условию πR²=16π, то радиус основания конуса равен 4, а тогда искомая площадь осевого сечения равна 24.
-
27 слайд
Задача №20
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен 10√2. Найдите образующую конуса.
Высота конуса перпендикулярна основанию и равна радиусу сферы. Тогда по теореме Пифагора получаем: -
28 слайд
Задача №21
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса.
Формулу для объёма шара:
V=4/3 ·πR³, а формула объёма конуса: V=1/3 ·πR³.
Значит объём конуса в 4 раза меньше объёма шара.
Тогда объём конуса равен 28 : 4 = 7
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 255 667 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
-
«Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
Тема
§ 2. Конус
Больше материалов по этой теме
Другие материалы


Все о конусе (теория)
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
- Тема: § 2. Конус
- 14.03.2019
- 2068
- 28


Урок по теме “Конус”
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
- Тема: § 2. Конус
- 12.12.2018
- 351
- 1

Презентация по теме “Конус. Площадь поверхности конуса”
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
- Тема: § 2. Конус
Рейтинг:
4 из 5
- 22.11.2018
- 4019
- 684

Открытый урок по теме “Конус”.
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
- Тема: § 2. Конус
- 23.10.2018
- 1090
- 7

Презентация по геометрии на тему “Конус”
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
- Тема: § 2. Конус
- 10.07.2018
- 3266
- 14

Вам будут интересны эти курсы:
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Управление персоналом и оформление трудовых отношений»
-
Курс повышения квалификации «Организация научно-исследовательской работы студентов в соответствии с требованиями ФГОС»
-
Курс повышения квалификации «Экономика предприятия: оценка эффективности деятельности»
-
Курс профессиональной переподготовки «Логистика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Финансы: управление структурой капитала»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»
-
Курс профессиональной переподготовки «Организация и управление службой рекламы и PR»
-
Курс профессиональной переподготовки «Информационная поддержка бизнес-процессов в организации»
Формулировка задачи: Объём конуса равен N. Через точку, делящую высоту конуса в отношении A:B, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13 (Задачи по стереометрии).
Рассмотрим, как решаются подобные задачи на примере и выведем общий способ решения.
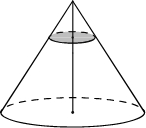
Пример задачи:
Объём конуса равен 27. Через точку, делящую высоту конуса в отношении 1:2, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.
Решение:
По условию задачи дано 2 конуса: большой и малый, отсеченный плоскостью от большого. Большой конус подобен малому с коэффициентом подобия, равным:
K = H / h = (1 + 2)x / 1x = 3 / 1 = 3
где H – высота большого конуса, а h – высота малого конуса. Получается, что высота большого конуса в 3 раза больше высоты малого конуса, так как высота большого конуса составляет 3 части (1 + 2), а высота малого только одну.
Поскольку в задаче дан объем большего конуса и по нему нужно получить объем меньшего, а объемы любых двух подобных объемных фигур относятся как куб коэффициента подобия, можно составить следующее соотношение:
Vбол.кон. / Vмал.кон. = 33 / 1
Выразим из этого соотношения объем малого конуса и вычислим его:
Vбол.кон. = Vмал.кон. ⋅ 33
Vмал.кон. = Vбол.кон. / 33 = 27 / 27 = 1
Ответ: 1
В общем виде решение данной задачи по стереометрии выглядит следующим образом:
K = (A + B) / A – коэффициент подобия
ОБЪЕМ МАЛОГО КОНУСА = N / K3
где N – объем большего конуса, а A:B – отношение высот конуса, считая от вершины.
Остается лишь подставить конкретные значения и подсчитать результат.