Как найти коэффициент поглощения излучения

Коэффициент поглощения (оптика)

Размерность	безразмерная
Примечания
скалярная величина

Коэффицие́нт поглоще́ния — безразмерная физическая величина, характеризующая способность тела поглощать падающее на него излучение. В качестве буквенного обозначения используется греческая alpha ^[1].

Определения[править | править код]

Численно коэффициент поглощения равен отношению потока излучения Phi , поглощенного телом, к потоку излучения $Phi _{0}$ , упавшего на тело^[1]^[2]:

$alpha ={frac {Phi }{Phi _{0}}}.$

Сумма коэффициента поглощения и коэффициентов отражения, пропускания и рассеяния равна единице. Это утверждение следует из закона сохранения энергии.

В тех случаях, когда спектр падающего излучения настолько узок, что излучение можно считать монохроматическим, говорят о монохроматическом коэффициенте поглощения. Другое используемое в таких обстоятельствах наименование, имеющее то же значение, — поглощательная способность^[3] тела.

Если спектр падающего на тело излучения широк, то соответствующий коэффициент поглощения называют интегральным.

В общем случае значение коэффициента поглощения тела зависит как от свойств самого тела, так и от угла падения, спектрального состава и поляризации излучения.

Коэффициент внутреннего поглощения [править | править код]

В бо́льшей степени характеризует способность поглощать излучение материалами, а не телами. Соответственно, в отличие от коэффициента поглощения в его определении используется не падающий на поверхность тела поток $Phi _{0}$ , а поток $Phi _{{in}}$ , прошедший через входную поверхность тела.

Таким образом, коэффициент внутреннего поглощения alpha_i определяется из соотношения^[1]:

$alpha _{i}={frac {Phi }{Phi _{{in}}}}.$

Поток $Phi _{{in}}$ при этом связан с $Phi _{0}$ равенством:

$Phi _{{in}}=(1-rho )Phi _{0},$

где rho — коэффициент отражения.

В общем случае, при распространении параллельного пучка излучения в среде, где одновременно имеет место поглощение и рассеяние излучения, коэффициент внутреннего поглощения связан с натуральными показателями поглощения и рассеяния соотношением:

$alpha _{i}={frac {a'}{a'+r'}}left[1-e^{{-(a'+r')l}}right],$

где — расстояние, пройденное излучением в среде.

См. также[править | править код]

Показатель поглощения
Коэффициент отражения
Коэффициент рассеяния
Коэффициент ослабления
Коэффициент пропускания

Примечания[править | править код]

↑ ¹ ² ³ ГОСТ 26148—84. Фотометрия. Термины и определения. Дата обращения: 28 ноября 2020. Архивировано из оригинала 16 марта 2020 года.
↑ Статья «Коэффициент поглощения» в Физической энциклопедии. Дата обращения: 3 июня 2012. Архивировано 6 февраля 2020 года.
↑ Статья «Поглощательная способность» в Физической энциклопедии. Дата обращения: 3 июня 2012. Архивировано 8 января 2020 года.

Источник

Первые исследования поглощения света
относятся ещё к 1729 г., когда Пьер Бугер
открыл закон экспоненциального убывания
интенсивности в прозрачных поглощающих
телах. В то время отсутствовали измерители
оптического излучения. Поэтому опыты
основывались на способности глаза
человека с довольно высокой точностью
устанавливать равенство освещенностей
близко расположенных друг к другу
поверхностей дощечек. Дощечки, освещались
свечками и помещались на разных
расстояниях от наблюдателя вдоль линии
наблюдения. В своих рассуждениях Бугер
воспользовался идеей Кеплера о том, что
интенсивность света при удалении от
точечного источника убывает обратно
пропорционально квадрату расстояния.
Бугер установил, что интенсивность
света, распространяющегося в прозрачной
поглощающей среде в виде плоской волны,
убывает по экспоненциальному закону –
это и есть закон Бугера в интегральной
форме.

, (4)

где I
– интенсивность света прошедшего слой,
толщиной d, I₀
– интенсивность падающего на слой
света, k – коэффициент
поглощения.

Коэффициент поглощения определяется
свойствами поглощающих свет частиц и
зависит от длины волны излучения. В
классической оптике он считается не
зависящим от интенсивности света. C.И.
Вавилов установил, что постоянство
коэффициента поглощения сохраняется
при изменении спектральной плотности
излучения на 20 порядков. Однако он все
же обнаружил первый нелинейный
оптический эффект – насыщение
коэффициента усиления или просветление
вещества под действием света для
долгоживущих атомных состояний.

( Как известно, при использовании
лазерного излучения насыщение усиления
и поглощения становится скорее правилом,
чем уникальным явлением.)

Закон Бугера в интегральной форме
следует из закона Бугера, записанного
в дифференциальной форме:

dI = I(x) k dx. (5)

Использование закона Бугера в
дифференциальной форме позволяет
рассчитывать пропускание вещества и
при наличии насыщения, то есть зависимости
коэффициента поглощения от интенсивности
излучения k(I).

Прозрачная поглощающая среда представляет
собой атомные пары, газы, активированные
кристаллы и стекла или жидкости с
растворенными в них поглощающими
молекулами. Поэтому поглощение света
определяется не только толщиной слоя,
но и концентрацией активных частиц. Это
означает, что коэффициент поглощения
равен произведению концентрации частиц
c на коэффициент,
называемый сечением поглощения 
активных частиц. При этом обобщенный
закон Бугера (его иногда называют законом
Бугера-Ламберта-Бера) принимает вид

I = I₀
exp (- 
c d). (6)

(Следует отметить, что в приведенных
формулах коэффициент поглощения следует
называть показателем поглощения. Однако
в оптике традиционно закрепились
нелогичные термины: «коэффициент
поглощения» вместо «показатель
поглощения» и «показатель преломления»
вместо «коэффициент преломления».)

Поглощение света обусловлено переходами
атомов, из которых состоит среда, на
более высокие энергетические уровни.
Экспоненциальность затухания света по
мере его распространения в среде
фактически отражает тот факт, что процесс
поглощения и испускания света отдельным
атомом подчиняется статистическим
закономерностям. Свет малой интенсивности
поглощается в некоторый произвольный
момент времени не всеми атомами
одновременно, а случайно отдельными
атомами системы, при этом энергия поля
скачком уменьшается на величину кванта.
Средняя суммарная мощность поглощенной
световой энергии при этом оказывается
пропорциональной концентрации поглощающих
примесей в веществе.

Экспоненциальный характер затухания
света в среде, а также послесвечения
тела после прекращения его возбуждения
светом, может служить экспериментальным
свидетельством отсутствия взаимодействия
испускающих свет атомов друг с другом.
В этих случаях атомы испускают и поглощают
свет случайным образом независимо друг
от друга.

Однако, необходимо ясно понимать, что
в случае взаимодействия с веществом
мощного квазимонохроматического
лазерного излучения нельзя пренебрегать
эффектами коллективной реакции системы
атомов на световое возмущение. Поглощение
света в этом случае подчиняется совершенно
другим динамическим закономерностям,
описывающим эффекты когерентного
поглощения света.

Еще одно ограничение классического
закона поглощения света связано с
конечным временем релаксации атомных
переходов. В квантовой механике
предполагается мгновенность процессов
поглощения и испускания квантов света.
Это позволяет описывать стационарные
процессы испускания и поглощения света
пользуясь понятием «вероятность
перехода», которая не зависят от
интенсивности света.

В общем случае вероятность поглощения
и испускания лазерного света атомной
системы зависит от времени, интенсивности
излучения и концентрации активных
частиц, а установление стационарного
режима поглощения и испускания света
согласно квантовым закономерностям
никогда не наступает.

1.4. Насыщение
поглощения (усиления)

Из
квантовых представлений с очевидностью
следует, что увеличение плотности
излучения на резонансной частоте для
системы двухуровневых атомов должно
приводить к росту населенности
возбужденного состояния. А это означает,
что коэффициент поглощения вещества
при этом должен уменьшаться. В пределе
при бесконечно больших мощностях
возбуждения населенности верхнего и
нижнего уровней становятся одинаковыми
и поглощение света исчезает. Это и есть
явление просветления среды. При меньших
мощностях коэффициент поглощения
уменьшается – наступает насыщения
поглощения. По аналогии должно наблюдаться
и симметричное явление – насыщение
усиления.

При
достаточно высоких мощностях возбуждающего
света закон Бугера должен нарушаться.
Детальное исследование справедливости
закона Бугера проводилось С.И. Вавиловым
в 1920 г. [1]. По его данным закон Бугера
выполнялся при изменении плотность
мощности света на 15 порядков вплоть до
~ 10 Вт/см²
. В кристаллических фосфорах, время
жизни возбужденного состояния которых
очень велико по атомным масштабам и
может достигать секунд. В таких средах
оказалось возможным наблюдать насыщение
поглощения при возбуждении достаточно
интенсивным светом от дуговой лампы
[2]. Это были первые наблюдение нелинейного
оптического явления.

Характерные
особенности явлений насыщения поглощения
и усиления легко понять на примере
рассмотрения простейшей модели системы
двухуровневых атомов. Пусть система
атомов с концентрацией n
[1/см³],
находится в стационарном состоянии
термодинамического равновесия с
излучением с объемной плотностью U.
Для упрощения рассмотрения предполагаем,
что в системе отсутствуют безизлучательные
переходы, а расстояние между уровнями
так велико, что можно пренебрегать
влиянием температуры на населенность
возбужденного состояния.

В
рассматриваемой системе в стационарном
состоянии число переходов 1 –2 и 2 –1 в
единицу времени одинаково. Следовательно:

n₁
BU
= n₂
(A
+ BU);

n₁
+ n₂
= n. (7)

Для
простоты записи индексы у коэффициента
Эйнштейна для спонтанного перехода –
А₂₁
и вынужденных переходов В₂₁
и В₁₂
здесь опущены.

Решение
этой системы уравнений имеет вид:

.
(8)

Из
приведенных формул легко видеть, что в
пределе U


n₁
= n₂
= n/2,
то есть населенности уровней выравниваются,
а вещество «просветляется» – поглощение
света исчезает.

Описание
процессов насыщения усиления и поглощения
становится особенно наглядным при
введении параметра, названного В.П.
Грибковским и Б.И. Степановым [3] параметром
нелинейности .
Для рассмотренной выше модели вещества

= 2В/А. Тогда населенности уровней можно
записать в виде:

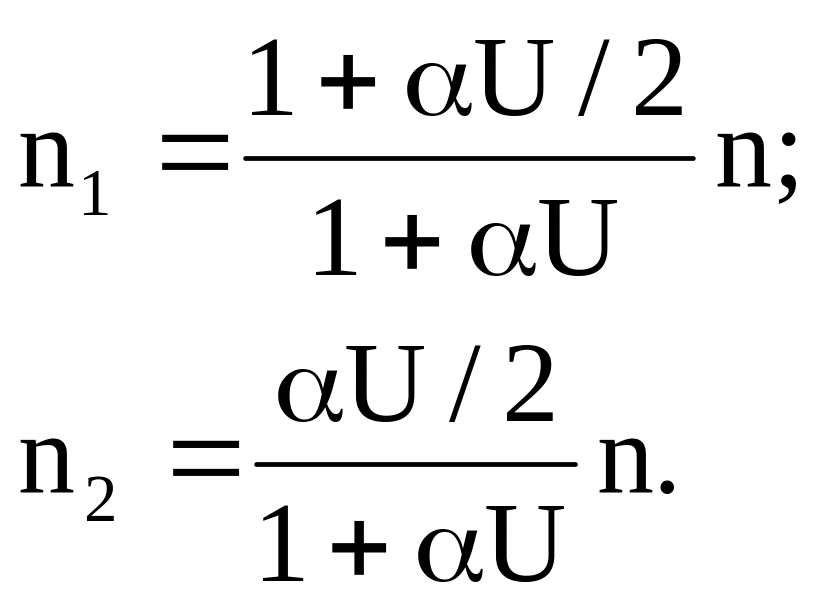
(9)

При
этом выражения для мощности поглощения
W_погл[Вт]
и коэффициента поглощения k[см^-1]
приобретают простой вид:

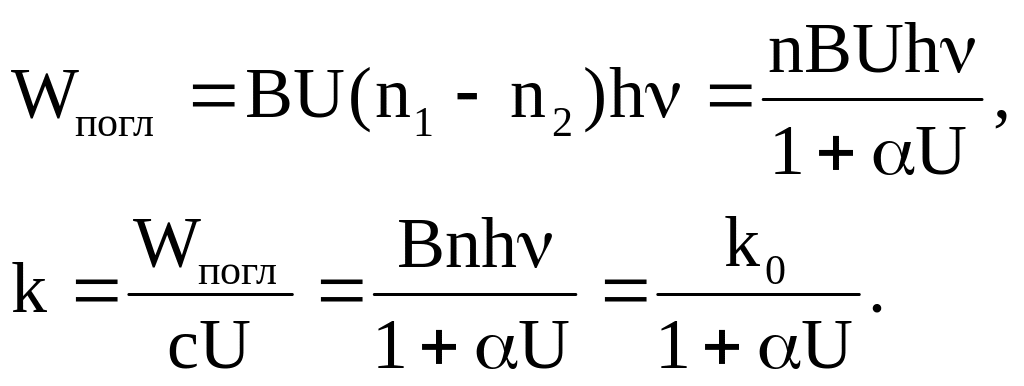
(10)

Здесь
k₀
– коэффициент поглощения вещества при
малых мощностях возбуждения, когда U

0. Это обычно измеряемый с помощью
спектрофотометра коэффициент поглощения
вещества. Насыщение поглощения будет
ясно наблюдаться, когда U
становится соизмеримым с единицей.

Коэффициенты
Эйнштейна связаны друг с другом.
Спонтанные переходы происходят под
действием нулевых колебаний вакуума.
Объемная плотность нулевого
электромагнитного поля вакуума
определяется из формулы Планка как
коэффициент между вероятностями
спонтанных и вынужденных переходов А
и В. Поэтому параметр нелинейности в
рассматриваемом случае зависит только
от частоты излучения, резонансно
взаимодействующего с веществом:

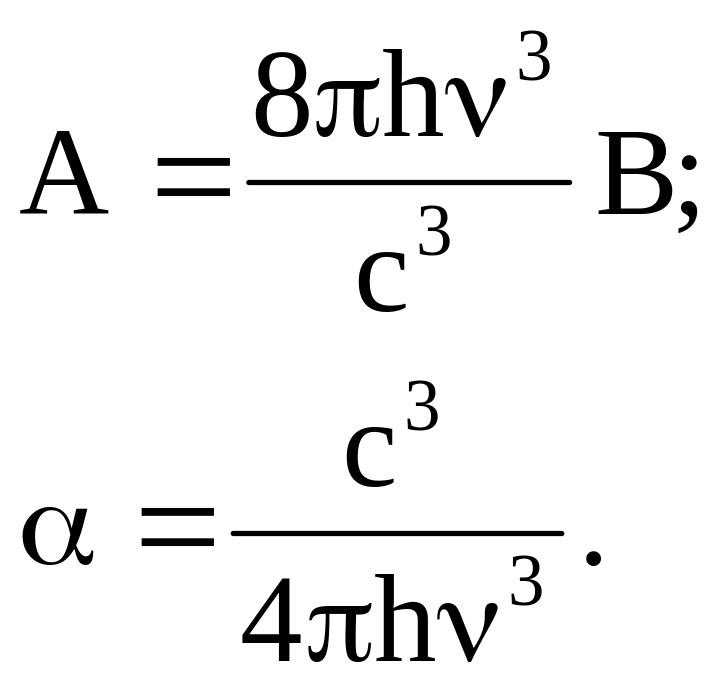
(11)

Для
света видимого диапазона 
= 0,5 10¹⁵
Гц и в принятой простой двухуровневой
модели вещества 
= 2,610¹³
м³/(Дж
сек).

Объемная
плотность излучения Солнца, приходящаяся
на единичный интервал частот U_c
, равна 2 10^-21
Дж сек/м³.
Таким образом, в случае солнечного
излучения U_с
= 5 10^-8
<< 1. Ясно, что никакая фокусировка
солнечного света не позволит наблюдать
нелинейность коэффициента поглощения
для видимого света в случае двухуровневых
поглощающих частиц. Параметр нелинейности
становится существенно больше в далекой
инфракрасной области спектра, однако
там принятая модель вещества не работает,
так как населенности близко расположенных
уровней энергии сильно зависят от
температуры.

В
то же время спектральная плотность
излучения лазерного света (как показано
выше) на много порядков выше, чем у
солнечного света. Следовательно, при
лазерном возбуждении коэффициент
поглощения вещества может сильно
зависеть от световой мощности. Лазерное
возбуждение позволяет создавать сильно
неравновесные состояния вещества со
значительной заселенностью возбужденных
состояний.

В
случае вещества с трехуровневыми
частицами ситуация может быть радикально
другой. Если уровень 2 долгоживущий
(метастабильный), то есть переходы 2 –
1 запрещены и происходят с малой
вероятностью, то при возбуждении системы
светом на нем могут накапливаться
частицы. Это происходит, если вероятность
переходов 3 – 2 значительно больше, чем
3 – 1. Состояние 3 должно обладать большим
числом разнесенных энергетических
подуровней, тогда вещество будет
эффективно поглощать свет с невысокой
спектральной плотностью, характерной
для тепловых источников света.

Именно
такая схема энергетических уровней
реализуется в кристаллических фосфорах,
для которых Вавилов с сотрудниками
наблюдали нарушение закона Бугера в
канале 1 – 3. По этой же схеме возбуждения
работает рубин, на котором был создан
первый лазер.

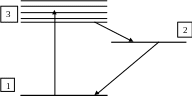
Рис.
12. Схема энергетических уровней
кристаллических фосфоров (стекол,
активированных ураном) и рубина. 2 –
долгоживущий, метастабильный уровень.

Явление квазистационарного просветления
вещества излучением используется для
модуляции добротности резонатора
импульсных лазеров. Соответствующие
устройства назвали просветляющимися
или фототропными затворами.

Просветляющийся, пассивный или
фототропный затвор представляет собой
кювету, заполненную раствором красителя,
или пластинку из цветного стекла или
полупроводникового материала, которые
резонансно поглощают свет на частоте
лазерного перехода. Под действием
интенсивного лазерного излучения
коэффициент поглощения вещества затвора
обратимо уменьшается вследствие
насыщения поглощения. Таким образом,
просветляющийся затвор, помещенный в
лазерный резонатор, осуществляет режим
модуляции добротности без использования
устройств, управляемых внешними
электрическими сигналами.

Использование зависимости коэффициента
поглощения от интенсивности света,
падающего на образец, для модуляции
добротности лазера в 1964 г. было предложено
несколькими группами американских
ученых [31].

Для вещества, содержащего поглощающие
частицы с произвольным числом
энергетических уровней, в стационарном
случае вероятностный подход дает простую
универсальную зависимость коэффициента
поглощения от плотности световой энергии
в единице объема U(x):

, (12)

где k₀
– коэффициент поглощения вещества,
измеряемый при малых плотностях
излучения,  – параметр
нелинейности вещества, зависящий от
особенностей расположения его
энергетических уровней и вероятностей
переходов между ними.

В соответствии с (12) при больших плотностях
излучения U коэффициент
поглощения любого вещества должен
стремиться к нулю, то есть вещества
должны просветляться.

Для экспериментального изучения
насыщения поглощения удобнее пользоваться
не коэффициентом поглощения вещества,
а непосредственно измеряемой величиной
– коэффициентом пропускания затвора
Т, равного отношению интенсивностей
излучения на выходе и входе образца.

К пропусканию образца легко перейти
воспользовавшись законом Бугера в
дифференциальной форме, который
справедлив и в случае зависимости
коэффициента усиления от мощности
возбуждающего излучения:

dU(x) = – k(x)U(x)dx. (13)

Совместное решение уравнений (12) и (13)
дает:

,
(14)

где T₀
– начальное пропускание образца,
измеренное спектрофотометром при малых
мощностях возбуждения.

Справедливость линейного соотношения
(14) была детально проверена экспериментально
[4] путем измерения пропускания различных
резонансно поглощающих веществ излучением
моноимпульсного рубинового лазера.

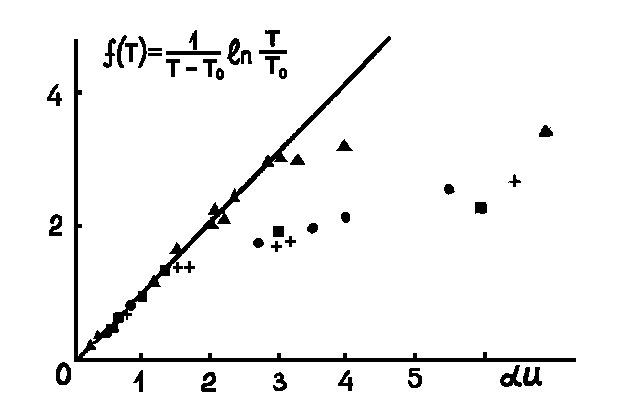
а б

Рис.13. а – Зависимость
функции пропускания некоторых фототропных
затворов для импульсов наносекундной
длительности от мощности падающего
излучения рубинового лазера. 
– фталоцианин галлия в хлорбензоле; ∎
– краситель ПК169 в хлорбензоле; ▲
– фталоцианин ванадила в хлорбензоле;
╋
– криптоцианин в этаноле. б – Зависимость
пропускания фототропного затвора с
раствором фталоцианини ванадила в
хлорбензоле от мощности излучения в
случаях воздействия стоячей (1), ● и
бегущей волны (2), ▲. Сплошные линии –
расчет, пунктир – эксперимент.

Экспериментальная проверка соотношения
(14) [32] показывает, что в наносекундном
диапазоне длительностей возбуждающих
импульсов света оно хорошо выполняется
для сравнительно малых плотностей
излучения. При U
больших, чем 2… 3 линейная зависимость
функции пропускания затвора от плотности
излучения (14) нарушается.

Заметная зависимость пропускания
вещества от мощности излучения наступает,
очевидно, при U
 0,1 (см. (12)). Этому
значению соответствуют плотности
мощности ~ 10⁵ Вт/см² для
раствора фталоцианинов (просветляющихся
по трехуровневой схеме) и ~10⁶
Вт/см² для криптоцианина
(двухуровневая модель вещества). При
повышении мощности быстро наступает
насыщение поглощения, причем, вопреки
теоретическому соотношению (14) максимальное
пропускание стремиться не к единице, а
к меньшему значению. Как видно на рис.
13а пропускание насыщается при значении,
существенно меньшем 1, при U
~ 2…3. То есть просветляющийся затвор
может сокращать длительность наносекундных
импульсов или подавлять мало интенсивные
импульсы при изменении световой мощности
не более, чем в 20 …30 раз.

Просветление затвора стоячей и бегущей
световыми волнами, как кажется, должно
происходить при разных мощностях
излучения. В первом случае вещество
просветляется только в пространственных
областях пучностей волны, поэтому здесь
степень просветления затвора должна
быть выше (кривая 1 рис.13б). Практически,
по-видимому, из-за влияния рефракционной
нелинейности вещества затвора, никакой
разницы между этими двумя случаями не
наблюдается (пунктир рис.13б) для всех
затворов, в том числе и на стекле типа
КС. Затвор в лазерном резонаторе будет
просветляться аналогично тому, как это
происходит при его облучении бегущей
волной вне резонатора [32].

Существенный недостаток просветляющегося
затвора – наличие необратимых потерь
проходящего через него света [4]. Например,
для наиболее оптимального для синхронизации
мод рубинового лазера затвора на основе
этанольного раствора криптоцианина,
начальное пропускание 0,15, максимально
может достичь значения 0,75. При этом
затвор поглощает более 50% падающей на
него мощности наносекундного импульса.
Причины потерь кроются в слабо изученных
процессах рассеяния света за счет
нелинейных и тепловых эффектов возникающих
в веществе затвора при высоких плотностях
излучения.

Литература к разделу 1.4.

Вавилов
С.И.//Собр.соч.: М., 1954. т.1. с 80 –83.
Свешников Б.Я. //
Дан СССР. 1946. т. 31, № 9. с. 675 –678.
Степанов Б.И.,
Грибковский В.П. Изв АН СССР. Сер. Физ.
1960, т. 24 с. 534 – 538.
Пилипович
В. А. Ковалев А.А. Оптические квантовые
генераторы с просветляющимися затворами.
Минск, 1975, 216 с.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Вредители
Микроорганизмы и насекомые
Природные цеолиты
Определение болезней и вредителей
Органическое вещество почвы
Почва, растение, удобрение
Агрохимические методы
Применение удобрений
Сельскохозяйственная радиология
Обезвреживание навоза
Органические удобрения
Микроорганизмы почвы

23.05.2023

22.05.2023

Количественные закономерности поглощения излучения

11.09.2012

Самый простой вариант излучения, т. е. излучение в виде узкого пучка его поглощения при прохождении через вещество, происходит согласно экспоненциальным выражениям

где I0 и I – интенсивности излучений исходного и после прохождения через слой толщиной х; μ – линейный коэффициент поглощения (ослабления излучения); x1/2 – толщина слоя полуослабления (полупоглощения).
Величина линейного коэффициента поглощения зависит от вида и энергии излучения, а также от свойств поглощающею излучение материала. Если толщину материала выражать в см, то размерность коэффициента будет в обратных см, т. е. см-1. Слой полуослабления равен толщине материала, ослабляющей интенсивность излучения в 2 раза (аналогично определению Т1/2). Соотношение этих двух показателей сходное выражением (2.7)

Экспоненциальный закон поглощения выполняется строго для γ-излучения, а для β-излучения только в некотором приближении. Заметные отклонения от закона для β-излучения проявляются при большой толщине поглотителя – примерно 5 слоев полупоглощения и более. Необходимо учитывать то, что для β-излучения всегда имеется предельное значение толщины поглощения, или максимальный пробег (Rmax), соответствующий максимальной энергии β-излучения (Еmax). Для γ-излучений, в строгом соответствии с видом закона поглощения, понятие максимального пробега неприменимо, поглощение в таких случаях оценивается по кратности ослабления излучения

(здесь n обозначает число слоев полуослабления х1/2). Второе из выражений удобно для ориентировочных оценок.
Поглощение γ-излучений типичных энергий происходит большей частью во взаимодействиях с электронами (см. раздел 2.5), поэтому и значение характеристических коэффициентов ослабления μ должно зависеть от электронной плотности среды, которая для разных элементов должна быть пропорциональна отношению Z/A. Как легко убедиться, это отношение остается приблизительно одинаковым (-0.5) в широкой области значений 1 < Z < 40, в которую входят большинство природных макроэлементов (за исключением водорода). Отсюда следует, что поглощение γ-излучения (определяемое величиной коэффициента μ) не должно значительно изменяться в зависимости от химического состава природных материалов (например, почвы).
Поглощение γ-излучения существенно зависит от плотности среды. Для упрощения расчетов было призвано целесообразным преобразовать коэффициент ослабления в виде μ’ = μ/р (т. е. с учетом физической плотности материала р), а толщину поглотителя измерять соответственно не в линейных единицах, а в единицах поверхностной плотности d = x•p с размерностью [мг/см3]. Новый коэффициент μ’ назван массовым коэффициентом ослабления излучения, его размерность – [см2/мг]. С учетом сделанных изменений закон поглощения излучения, а также выражение для кратности ослабления принимают вид

Вышеприведенные зависимости используются для расчета защиты от излучений и для решения множества прикладных задач, в том числе в радиационных методах определения плотности почв и грунтов, запасов воды в снежном покрове и т. п.
1. Внутренняя структура и свойстве атомов определяются содержанием частиц трех видов – протонов и нейтронов (в ядре) и электронов (на оболочках). Электроны, особенно находящееся на внешней оболочке, определяют химические свойства моментов; соотношение протонов и нейтронов в ядре определяет стабильность или нестабильность атомного ядра.
2. Радиоактивность – проявление неустойчивости атомных (точнее, ядерных) структур. Она обусловлена внутриядерными перестройками, которые сопровождаются излучениями элементарных или других микрочастиц.
3. Радиоактивный распад происходит самопроизвольно, какие либо силы физического или химического воздействия на атомы неспособны ни ускорить, ни замедлить, ни тем более остановить его.
4. Радиоактивные превращении различного типа (α-, β-, изомерные переходы, осколочное деление) всегда связаны с переходом ядра из состояния с более высокой внутренней энергией в состояние с меньшей энергией. Полная энергия радиоактивного распада имеет определенное значение, равное разности внутренних энергий ядра до и после распада.
5. Проникающая способность радиоактивных излучений зависит от размера частиц излучений и наличия или отсутствия у них электрического заряда.
6. Ионизирующая способность излучений определяется величиной энергии частиц, которая должна быть достаточной для выбивании электронов на атомов или для перевода их в состояние возбуждения. Способность к ионизации или возбуждению атомов определяет опасность радиоактивных излучений для человека и других живых организмов.
7. Явления, наблюдаемые при поглощении излучений в веществе, используются для обнаружения и количественной оценки интенсивности излучения с помощью детекторов излучения (счетчиков). Идентификация радионуклидного состава естественных или искусственных радионуклидов требует определения энергии излучений, которые выполняются методами спектрометрии или другими способами.
8. Ионизирующая радиация (α-, β-. γ-) после прохождения через вещество не оставляет после себя какой-либо остаточной радиоактивности. Данное утверждение не относится к нейтронному излучению, способному вызывать «наведенную радиоактивность» в результате осуществления ядерных реакций, которые также являются причиной образования на Земле «космогенных радионуклидов».
9. Радиоактивный распад имеет вероятностную природу, его закономерности выполняются достаточно точно только при наличии большого количества радиоактивных атомов.
10. Количество радиоактивного вещества удобнее выражать не в массовых единицах, а в единицах активности, т. е. по количеству распадов в единицу времени. Активность со временем снижается, но доля распадающихся атомов остается постоянной. Период полураспада, т. е. значение времени распада половины от имеющихся радиоактивных атомов, используется в качестве важнейшей характеристики радиоактивного потопа.
11. Заменой концентрационным понятиям в радиологии служит удельная активность (массовая или объемная), т.е. активность радионуклида в пересчете на единицу массы или объема материала.

Активность
Основные закономерности радиоактивного распада
Ядерные реакции наведения радиоактивности
Спектральные характеристики излучений
Основные виды радиоактивного распада
Механизмы взаимодействия излучений с веществом
Проникающая способность излучения
Виды излучений
Радиоактивность
Строение атома и изотопы

Источник

From Wikipedia, the free encyclopedia

Emission lines and absorption lines compared to a continuous spectrum

Einstein coefficients are quantities describing the probability of absorption or emission of a photon by an atom or molecule.^[1] The Einstein A coefficients are related to the rate of spontaneous emission of light, and the Einstein B coefficients are related to the absorption and stimulated emission of light. Throughout this article, “light” refers to any electromagnetic radiation, not necessarily in the visible spectrum.

Spectral lines[edit]

In physics, one thinks of a spectral line from two viewpoints.

An emission line is formed when an atom or molecule makes a transition from a particular discrete energy level E₂ of an atom, to a lower energy level E₁, emitting a photon of a particular energy and wavelength. A spectrum of many such photons will show an emission spike at the wavelength associated with these photons.

An absorption line is formed when an atom or molecule makes a transition from a lower, E₁, to a higher discrete energy state, E₂, with a photon being absorbed in the process. These absorbed photons generally come from background continuum radiation (the full spectrum of electromagnetic radiation) and a spectrum will show a drop in the continuum radiation at the wavelength associated with the absorbed photons.

The two states must be bound states in which the electron is bound to the atom or molecule, so the transition is sometimes referred to as a “bound–bound” transition, as opposed to a transition in which the electron is ejected out of the atom completely (“bound–free” transition) into a continuum state, leaving an ionized atom, and generating continuum radiation.

A photon with an energy equal to the difference E₂ − E₁ between the energy levels is released or absorbed in the process. The frequency ν at which the spectral line occurs is related to the photon energy by Bohr’s frequency condition E₂ − E₁ = hν where h denotes the Planck constant.^[2]^[3]^[4]^[5]^[6]^[7]

Emission and absorption coefficients[edit]

An atomic spectral line refers to emission and absorption events in a gas in which $n_{2}$ is the density of atoms in the upper-energy state for the line, and $n_{1}$ is the density of atoms in the lower-energy state for the line.

The emission of atomic line radiation at frequency ν may be described by an emission coefficient with units of energy/(time × volume × solid angle). ε dt dV dΩ is then the energy emitted by a volume element in time into solid angle dOmega . For atomic line radiation,

${displaystyle varepsilon ={frac {hnu }{4pi }}n_{2}A_{21},}$

where $A_{21}$ is the Einstein coefficient for spontaneous emission, which is fixed by the intrinsic properties of the relevant atom for the two relevant energy levels.

The absorption of atomic line radiation may be described by an absorption coefficient kappa with units of 1/length. The expression κ’ dx gives the fraction of intensity absorbed for a light beam at frequency ν while traveling distance dx. The absorption coefficient is given by

${displaystyle kappa '={frac {hnu }{4pi }}(n_{1}B_{12}-n_{2}B_{21}),}$

where $B_{12}$ and $B_{21}$ are the Einstein coefficients for photon absorption and induced emission respectively. Like the coefficient $A_{21}$ , these are also fixed by the intrinsic properties of the relevant atom for the two relevant energy levels. For thermodynamics and for the application of Kirchhoff’s law, it is necessary that the total absorption be expressed as the algebraic sum of two components, described respectively by $B_{12}$ and $B_{21}$ , which may be regarded as positive and negative absorption, which are, respectively, the direct photon absorption, and what is commonly called stimulated or induced emission.^[8]^[9]^[10]

The above equations have ignored the influence of the spectroscopic line shape. To be accurate, the above equations need to be multiplied by the (normalized) spectral line shape, in which case the units will change to include a 1/Hz term.

Under conditions of thermodynamic equilibrium, the number densities $n_{2}$ and $n_{1}$ , the Einstein coefficients, and the spectral energy density provide sufficient information to determine the absorption and emission rates.

Equilibrium conditions[edit]

The number densities $n_{2}$ and $n_{1}$ are set by the physical state of the gas in which the spectral line occurs, including the local spectral radiance (or, in some presentations, the local spectral radiant energy density). When that state is either one of strict thermodynamic equilibrium, or one of so-called “local thermodynamic equilibrium”,^[11]^[12]^[13] then the distribution of atomic states of excitation (which includes $n_{2}$ and $n_{1}$ ) determines the rates of atomic emissions and absorptions to be such that Kirchhoff’s law of equality of radiative absorptivity and emissivity holds. In strict thermodynamic equilibrium, the radiation field is said to be black-body radiation and is described by Planck’s law. For local thermodynamic equilibrium, the radiation field does not have to be a black-body field, but the rate of interatomic collisions must vastly exceed the rates of absorption and emission of quanta of light, so that the interatomic collisions entirely dominate the distribution of states of atomic excitation. Circumstances occur in which local thermodynamic equilibrium does not prevail, because the strong radiative effects overwhelm the tendency to the Maxwell–Boltzmann distribution of molecular velocities. For example, in the atmosphere of the Sun, the great strength of the radiation dominates. In the upper atmosphere of the Earth, at altitudes over 100 km, the rarity of intermolecular collisions is decisive.

In the cases of thermodynamic equilibrium and of local thermodynamic equilibrium, the number densities of the atoms, both excited and unexcited, may be calculated from the Maxwell–Boltzmann distribution, but for other cases, (e.g. lasers) the calculation is more complicated.

Einstein coefficients[edit]

In 1916, Albert Einstein proposed that there are three processes occurring in the formation of an atomic spectral line. The three processes are referred to as spontaneous emission, stimulated emission, and absorption. With each is associated an Einstein coefficient, which is a measure of the probability of that particular process occurring. Einstein considered the case of isotropic radiation of frequency ν and spectral energy density ρ(ν).^[3]^[14]^[15]^[16]

Various formulations[edit]

Hilborn has compared various formulations for derivations for the Einstein coefficients, by various authors.^[17] For example, Herzberg works with irradiance and wavenumber;^[18] Yariv works with energy per unit volume per unit frequency interval,^[19] as is the case in the more recent (2008) ^[20] formulation. Mihalas & Weibel-Mihalas work with radiance and frequency;^[13] also Chandrasekhar;^[21] also Goody & Yung;^[22] Loudon uses angular frequency and radiance.^[23]

Spontaneous emission[edit]

Schematic diagram of atomic spontaneous emission

Spontaneous emission is the process by which an electron “spontaneously” (i.e. without any outside influence) decays from a higher energy level to a lower one. The process is described by the Einstein coefficient A₂₁ (s⁻¹), which gives the probability per unit time that an electron in state 2 with energy $E_{2}$ will decay spontaneously to state 1 with energy $E_{1}$ , emitting a photon with an energy E₂ − E₁ = hν. Due to the energy-time uncertainty principle, the transition actually produces photons within a narrow range of frequencies called the spectral linewidth. If $n_{i}$ is the number density of atoms in state i , then the change in the number density of atoms in state 2 per unit time due to spontaneous emission will be

${displaystyle left({frac {dn_{2}}{dt}}right)_{text{spontaneous}}=-A_{21}n_{2}.}$

The same process results in increasing of the population of the state 1:

${displaystyle left({frac {dn_{1}}{dt}}right)_{text{spontaneous}}=A_{21}n_{2}.}$

Stimulated emission[edit]

Schematic diagram of atomic stimulated emission

Stimulated emission (also known as induced emission) is the process by which an electron is induced to jump from a higher energy level to a lower one by the presence of electromagnetic radiation at (or near) the frequency of the transition. From the thermodynamic viewpoint, this process must be regarded as negative absorption. The process is described by the Einstein coefficient $B_{21}$ (m³ J⁻¹ s⁻²), which gives the probability per unit time per unit energy density of the radiation field per unit frequency that an electron in state 2 with energy $E_{2}$ will decay to state 1 with energy $E_{1}$ , emitting a photon with an energy E₂ − E₁ = hν. The change in the number density of atoms in state 1 per unit time due to induced emission will be

${displaystyle left({frac {dn_{1}}{dt}}right)_{text{neg. absorb.}}=B_{21}n_{2}rho (nu ),}$

where rho(nu) denotes the spectral energy density of the isotropic radiation field at the frequency of the transition (see Planck’s law).

Stimulated emission is one of the fundamental processes that led to the development of the laser. Laser radiation is, however, very far from the present case of isotropic radiation.

Photon absorption[edit]

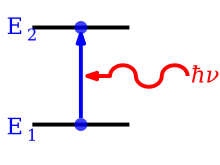
Schematic diagram of atomic absorption

Absorption is the process by which a photon is absorbed by the atom, causing an electron to jump from a lower energy level to a higher one. The process is described by the Einstein coefficient $B_{12}$ (m³ J⁻¹ s⁻²), which gives the probability per unit time per unit energy density of the radiation field per unit frequency that an electron in state 1 with energy $E_{1}$ will absorb a photon with an energy E₂ − E₁ = hν and jump to state 2 with energy $E_{2}$ . The change in the number density of atoms in state 1 per unit time due to absorption will be

${displaystyle left({frac {dn_{1}}{dt}}right)_{text{pos. absorb.}}=-B_{12}n_{1}rho (nu ).}$

Detailed balancing[edit]

The Einstein coefficients are fixed probabilities per time associated with each atom, and do not depend on the state of the gas of which the atoms are a part. Therefore, any relationship that we can derive between the coefficients at, say, thermodynamic equilibrium will be valid universally.

At thermodynamic equilibrium, we will have a simple balancing, in which the net change in the number of any excited atoms is zero, being balanced by loss and gain due to all processes. With respect to bound-bound transitions, we will have detailed balancing as well, which states that the net exchange between any two levels will be balanced. This is because the probabilities of transition cannot be affected by the presence or absence of other excited atoms. Detailed balance (valid only at equilibrium) requires that the change in time of the number of atoms in level 1 due to the above three processes be zero:

${displaystyle 0=A_{21}n_{2}+B_{21}n_{2}rho (nu )-B_{12}n_{1}rho (nu ).}$

Along with detailed balancing, at temperature T we may use our knowledge of the equilibrium energy distribution of the atoms, as stated in the Maxwell–Boltzmann distribution, and the equilibrium distribution of the photons, as stated in Planck’s law of black body radiation to derive universal relationships between the Einstein coefficients.

From Boltzmann distribution we have for the number of excited atomic species i:

${displaystyle {frac {n_{i}}{n}}={frac {g_{i}e^{-E_{i}/kT}}{Z}},}$

where n is the total number density of the atomic species, excited and unexcited, k is Boltzmann’s constant, T is the temperature, $g_{i}$ is the degeneracy (also called the multiplicity) of state i, and Z is the partition function. From Planck’s law of black-body radiation at temperature T we have for the spectral radiance (radiance is energy per unit time per unit solid angle per unit projected area, when integrated over an appropriate spectral interval)^[24] at frequency ν

${displaystyle rho _{nu }(nu ,T)=F(nu ){frac {1}{e^{hnu /kT}-1}},}$

where^[25]

${displaystyle F(nu )={frac {2hnu ^{3}}{c^{2}}},}$

where is the speed of light and is Planck’s constant.

Substituting these expressions into the equation of detailed balancing and remembering that E₂ − E₁ = hν yields

${displaystyle A_{21}g_{2}e^{-hnu /kT}+B_{21}g_{2}e^{-hnu /kT}{frac {F(nu )}{e^{hnu /kT}-1}}=B_{12}g_{1}{frac {F(nu )}{e^{hnu /kT}-1}},}$

${displaystyle A_{21}g_{2}(1-e^{-hnu /kT})+B_{21}g_{2}F(nu )e^{-hnu /kT}=B_{12}g_{1}F(nu ).}$

The above equation must hold at any temperature, so from one gets

${displaystyle B_{21}g_{2}=B_{12}g_{1},}$

and from

${displaystyle A_{21}g_{2}=B_{21}g_{2}F(nu ).}$

Therefore, the three Einstein coefficients are interrelated by

${displaystyle {frac {A_{21}}{B_{21}}}=F(nu )}$

and

${displaystyle {frac {B_{21}}{B_{12}}}={frac {g_{1}}{g_{2}}}.}$

When this relation is inserted into the original equation, one can also find a relation between $A_{21}$ and $B_{12}$ , involving Planck’s law.

Oscillator strengths[edit]

The oscillator strength $f_{12}$ is defined by the following relation to the cross section sigma for absorption:^[17]

${displaystyle sigma ={frac {e^{2}}{4varepsilon _{0}m_{e}c}},f_{12},phi _{nu }={frac {pi e^{2}}{2varepsilon _{0}m_{e}c}},f_{12},phi _{omega },}$

where is the electron charge, $m_{e}$ is the electron mass, and ${displaystyle phi _{nu }}$ and ${displaystyle phi _{omega }}$ are normalized distribution functions in frequency and angular frequency respectively.
This allows all three Einstein coefficients to be expressed in terms of the single oscillator strength associated with the particular atomic spectral line:

${displaystyle B_{12}={frac {e^{2}}{4varepsilon _{0}m_{e}hnu }}f_{12},}$

${displaystyle B_{21}={frac {e^{2}}{4varepsilon _{0}m_{e}hnu }}{frac {g_{1}}{g_{2}}}f_{12},}$

${displaystyle A_{21}={frac {2pi nu ^{2}e^{2}}{varepsilon _{0}m_{e}c^{3}}}{frac {g_{1}}{g_{2}}}f_{12}.}$

References[edit]

^ Hilborn, Robert C. (1982). “Einstein coefficients, cross sections, f values, dipole moments, and all that”. American Journal of Physics. 50 (11): 982–986. arXiv:physics/0202029. Bibcode:1982AmJPh..50..982H. doi:10.1119/1.12937. ISSN 0002-9505. S2CID 119050355.
^ Bohr 1913.
^ ^a ^b Einstein, A. (1916). “Strahlungs-Emission und -Absorption nach der Quantentheorie”. Verhandlungen der Deutschen Physikalischen Gesellschaft. 18: 318–323. Bibcode:1916DPhyG..18..318E. Translated in Alfred Engel. The Berlin Years: Writings, 1914-1917. Vol. 6. pp. 212–216.
^ Sommerfeld 1923, p. 43.
^ Heisenberg 1925, p. 108.
^ Brillouin 1970, p. 31.
^ Jammer 1989, pp. 113, 115.
^ Weinstein, M. A. (1960). “On the validity of Kirchhoff’s law for a freely radiating body”. American Journal of Physics. 28 (2): 123–25. Bibcode:1960AmJPh..28..123W. doi:10.1119/1.1935075.
^ Burkhard, D. G.; Lochhead, J. V. S.; Penchina, C. M. (1972). “On the validity of Kirchhoff’s law in a nonequilibrium environment”. American Journal of Physics. 40 (12): 1794–1798. Bibcode:1972AmJPh..40.1794B. doi:10.1119/1.1987065.
^ Baltes, H. P. (1976). On the validity of Kirchhoff’s law of heat radiation for a body in a nonequilibrium environment, Chapter 1, pages 1–25 of Progress in Optics XIII, edited by E. Wolf, North-Holland, ISSN 0079-6638.
^ Milne, E. A. (1928). “The effect of collisions on monochromatic radiative equilibrium”. Monthly Notices of the Royal Astronomical Society. 88 (6): 493–502. Bibcode:1928MNRAS..88..493M. doi:10.1093/mnras/88.6.493.
^ Chandrasekhar, S. (1950), p. 7.
^ ^a ^b Mihalas, D., Weibel-Mihalas, B. (1984), pp. 329–330.
^ Loudon, R. (2000), Section 1.5, pp. 16–19.
^ Einstein, A. (1916). “Zur Quantentheorie der Strahlung”. Mitteilungen der Physikalischen Gessellschaft Zürich. 18: 47–62.
^ Einstein, A. (1917). “Zur Quantentheorie der Strahlung”. Physikalische Zeitschrift. 18: 121–128. Bibcode:1917PhyZ…18..121E. Translated in ter Haar, D. (1967). The Old Quantum Theory. Pergamon. pp. 167–183. LCCN 66029628. Also in Boorse, H. A., Motz, L. (1966). The world of the atom, edited with commentaries, Basic Books, Inc., New York, pp. 888–901.
^ ^a ^b Hilborn, R. C. (2002). Einstein coefficients, cross sections, f values, dipole moments, and all that.
^ Herzberg, G. (1950).
^ Yariv, A. (1967/1989), pp. 171–173.
^ Garrison, J. C., Chiao, R. Y. (2008), pp. 15–19.
^ Chandrasekhar, S. (1950), p. 354.
^ Goody, R. M., Yung, Y. L. (1989), pp. 33–35.
^ Loudon, R. (1973/2000), pp. 16–19.
^ Robert W. Boyd, Radiometry and the Detection of Optical Radiation, John Wiley and Sons, 1983
^ Hubeny, Ivan; Mihalas, Dimitri (2015). Theory of stellar atmospheres : an introduction to astrophysical non-equilibrium quantitative spectroscopic analysis. Princeton University Press. pp. 116–118. ISBN 9780691163291.

Cited bibliography[edit]

Bohr, N. (1913). “On the constitution of atoms and molecules” (PDF). Philosophical Magazine. 26 (153): 1–25. Bibcode:1913PMag…26..476B. doi:10.1080/14786441308634993.
Brillouin, L. (1970). Relativity Reexamined. Academic Press. ISBN 978-0-12-134945-5.
Chandrasekhar, S. (1950). Radiative Transfer, Oxford University Press, Oxford.
Garrison, J. C., Chiao, R. Y. (2008). Quantum Optics, Oxford University Press, Oxford UK, ISBN 978-019-850-886-1.
Goody, R. M., Yung, Y. L. (1989). Atmospheric Radiation: Theoretical Basis, 2nd edition, Oxford University Press, Oxford, New York, 1989, ISBN 0-19-505134-3.
Heisenberg, W. (1925). “Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen”. Zeitschrift für Physik. 33 (1): 879–893. Bibcode:1925ZPhy…33..879H. doi:10.1007/BF01328377. S2CID 186238950. Translated as “Quantum-theoretical Re-interpretation of kinematic and mechanical relations” in van der Waerden, B. L. (1967). Sources of Quantum Mechanics. North-Holland Publishing. pp. 261–276.
Herzberg, G. (1950). Molecular Spectroscopy and Molecular Structure, vol. 1, Diatomic Molecules, second edition, Van Nostrand, New York.
Jammer, M. (1989). The Conceptual Development of Quantum Mechanics (second ed.). Tomash Publishers American Institute of Physics. ISBN 0-88318-617-9.
Loudon, R. (1973/2000). The Quantum Theory of Light, (first edition 1973), third edition 2000, Oxford University Press, Oxford UK, ISBN 0-19-850177-3.
Mihalas, D., Weibel-Mihalas, B. (1984). Foundations of Radiation Hydrodynamics, Oxford University Press, New York ISBN 0-19-503437-6.
Sommerfeld, A. (1923). Atomic Structure and Spectral Lines. Brose, H. L. (transl.) (from 3rd German ed.). Methuen.
Yariv, A. (1967/1989). Quantum Electronics, third edition, John Wiley & sons, New York, ISBN 0-471-60997-8.
Hubeny, Ivan; Mihalas, Dimitri (2015). Theory of stellar atmospheres : an introduction to astrophysical non-equilibrium quantitative spectroscopic analysis. Princeton University Press. ISBN 9780691163291.

External links[edit]

Emission Spectra from various light sources

Источник

Определения[править | править код]

Коэффициент внутреннего поглощения [править | править код]

См. также[править | править код]

Примечания[править | править код]

Количественные закономерности поглощения излучения

Spectral lines[edit]