Как найти коэффициент полезного действия цикла карно

Термодинамические циклы
Эдвардса Аткинсона Брайтона/Джоуля Гирна Дизеля Калины Карно Ленуара Миллера Отто Ренкина Стирлинга Тринклера Хамфри Эрикссона
Статья является частью серии «Термодинамика»

В термодинамике цикл Карно́ или процесс Карно́ — это идеальный^[1] круговой процесс, состоящий из двух адиабатных и двух изотермических процессов^[2]. В процессе Карно термодинамическая система выполняет механическую работу за счёт обмена теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры. Резервуар с более высокой температурой называется нагревателем, а с более низкой температурой — холодильником^[3].

Цикл Карно назван в честь французского учёного и инженера Сади Карно, который впервые его описал в своём сочинении «О движущей силе огня и о машинах, способных развивать эту силу» в 1824 году^[4][5].

Поскольку идеальные процессы могут осуществляться лишь с бесконечно малой скоростью, мощность тепловой машины в цикле Карно равна нулю. Мощность реальных тепловых машин не может быть равна нулю, поэтому реальные процессы могут приближаться к идеальному процессу Карно только с большей или меньшей степенью точности.

Коэффициент полезного действия (КПД) любой тепловой машины не может превосходить КПД идеальной тепловой машины, работающей по циклу Карно с теми же самыми температурами нагревателя и холодильника^[6]. По этой причине, позволяя оценить верхний предел КПД тепловой машины, цикл Карно важен для теории тепловых машин. В то же время КПД цикла Карно настолько чувствителен к отклонениям от идеальности (потерям на трение), что данный цикл никогда не применяли в реальных тепловых машинах^{[K 1][8]}.

Описание цикла Карно[править | править код]

Пусть тепловая машина состоит из нагревателя с температурой , холодильника с температурой и рабочего тела.

Цикл Карно состоит из четырёх обратимых стадий, две из которых осуществляются при постоянной температуре (изотермически), а две — при постоянной энтропии (адиабатически). Поэтому цикл Карно удобно представить в координатах (температура) и (энтропия).

1. Изотермическое расширение (на рис. 1 — процесс A→B). В начале процесса рабочее тело имеет температуру , то есть температуру нагревателя. При расширении рабочего тела его температура не падает за счет передачи от нагревателя количества теплоты , то есть расширение происходит изотермически (при постоянной температуре) . При этом объём рабочего тела увеличивается, оно совершает механическую работу, а его энтропия возрастает.

2. Адиабатическое расширение (на рис. 1 — процесс B→C). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом температура тела уменьшается до температуры холодильника , тело совершает механическую работу, а энтропия остаётся постоянной.

3. Изотермическое сжатие (на рис. 1 — процесс C→D). Рабочее тело, имеющее температуру , приводится в контакт с холодильником и начинает изотермически сжиматься под действием внешней силы, отдавая холодильнику количество теплоты . Над телом совершается работа, его энтропия уменьшается.

4. Адиабатическое сжатие (на рис. 1 — процесс D→A). Рабочее тело отсоединяется от холодильника и сжимается под действием внешней силы без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя, над телом совершается работа, его энтропия остаётся постоянной.

Обратный цикл Карно[править | править код]

В термодинамике холодильных установок и тепловых насосов рассматривают обратный цикл Карно, состоящий из следующих стадий^[9][10]: адиабатического сжатия за счёт совершения работы (на рис. 1 — процесс C→B); изотермического сжатия с передачей теплоты более нагретому тепловому резервуару (на рис. 1 — процесс B→A); адиабатического расширения (на рис. 1 — процесс A→D); изотермического расширения с отводом теплоты от более холодного теплового резервуара (на рис. 1 — процесс D→C).

Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно

Аналогично, при изотермическом сжатии рабочее тело отдаёт холодильнику

Отсюда коэффициент полезного действия тепловой машины Карно равен

Первая и вторая теоремы Карно[править | править код]

Из последнего выражения следует, что КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела. Этот результат составляет содержание первой теоремы Карно^[11]. Кроме того, из него следует, что КПД может составлять 100 % только в том случае, если температура холодильника равна абсолютному нулю. Это невозможно, но не из-за недостижимости абсолютного нуля (этот вопрос решается только третьим началом термодинамики, учитывать которое здесь нет необходимости), а из-за того, что такой цикл или нельзя замкнуть, или он вырождается в совокупность двух совпадающих адиабат и изотерм.

Поэтому максимальный КПД любой тепловой машины не может превосходить КПД тепловой машины Карно, работающей при тех же температурах нагревателя и холодильника. Это утверждение называется второй теоремой Карно^[12][13]. Оно даёт верхний предел КПД любой тепловой машины и позволяет оценить отклонение реального КПД от максимального, то есть потери энергии вследствие неидеальности тепловых процессов.

Связь между обратимостью цикла и КПД[править | править код]

Для того чтобы цикл был обратимым, в нём должна быть исключена передача теплоты при наличии разности температур, иначе нарушается условие адиабатичности процесса. Поэтому передача теплоты должна осуществляться либо в изотермическом процессе (как в цикле Карно), либо в эквидистантном процессе (обобщённый цикл Карно или, для примера, его частный случай Цикл Брайтона). Для того чтобы менять температуру рабочего тела от температуры нагревателя до температуры холодильника и обратно, необходимо использовать либо адиабатические процессы (они идут без теплообмена и, значит, не влияют на энтропию), либо циклы с регенерацией тепла при которых нет передачи тепла при разности температур. Мы приходим к выводу, что любой обратимый цикл может быть сведён к циклу Карно.

Примером обратимого цикла, не являющегося циклом Карно, но интегрально совпадающим с ним, является идеальный цикл Стирлинга: в двигателе Стирлинга добавлен регенератор, обеспечивающий полное приближение цикла к циклу Карно с достижением обратимости и тех же величин КПД^[14]. Возможны и другие идеальные циклы, в которых коэффициент полезного действия определяется по той же формуле, что и для циклов Карно и Стирлинга, например цикл Эрикссона  (англ.) (рус., состоящий из двух изобар и двух изотерм^[14].

Если же в цикле возникает передача теплоты при наличии разности температур, а таковыми являются все технические реализации термодинамических циклов, то цикл утрачивает свойство обратимости. Иначе говоря, посредством отведённой в цикле механической работы становится невозможным получить исходную теплоту. КПД такого цикла будет всегда меньше, чем КПД цикла Карно.

См. также[править | править код]

• Термодинамические циклы
• Первое начало термодинамики
• Второе начало термодинамики
• Термодинамическая энтропия
• Термодинамические потенциалы

Комментарии[править | править код]

Примечания[править | править код]

Литература[править | править код]

• Carnot S. Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance. — Paris: Gauthier-Villars, Imprimeur-Libraire, 1878. — 102 p. (фр.)
• Бахшиева Л. Т., Кондауров Б. П., Захарова А. А., Салтыкова В. С. Техническая термодинамика и теплотехника / Под ред. проф А. А. Захаровой. — 2-е изд., испр. — М.: Академия, 2008. — 272 с. — (Высшее профессиональное образование). — ISBN 978-5-7695-4999-1.
• Бэр Г. Д. [download1.libgen.io/ads.php?md5=F54DE2B5B715C97EA3375A180801C390 Техническая термодинамика]. — М.: Мир, 1977. — 519 с. (недоступная ссылка)
• Кинан Дж. Термодинамика / Пер с англ. А. Ф. Котина под ред. М. П. Вукаловича. — М.—Л.: Госэнергоиздат, 1963. — 280 с.
• Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1. — Издание 3-е, доп. — М.: Наука, 1976. — 584 с. — («Теоретическая физика», том V).
• Крестовников А. Н., Вигдорович В. Н. Химическая термодинамика. — 2-е изд., испр. и доп. — М.: Металлургия, 1973. — 256 с.
• Николаев Г. П., Лойко А. Э. Техническая термодинамика. — Екатеринбург: УрФУ, 2013. — 227 с.
• Румер Ю. Б., Рывкин М. Ш. Термодинамика, статистическая физика и кинетика. — 2-е изд., испр. и доп. — Новосибирск: Изд-во Носиб. ун-та, 2000. — 608 с. — ISBN 5-7615-0383-2.
• Савельев И. В. Курс общей физики:Молекулярная физика и термодинамика. — М.: Астрель, 2001. — Т. 3. — 208 с. — 7000 экз. — ISBN 5-17-004585-9.
• Кудрявцев П. С. История физики. — М.: Гос. учебно-педагог. изд-во, 1956. — Т. 1. От античной физики до Менделеева. — 564 с. — 25 000 экз.
• Сивухин Д. В. Общий курс физики. — Т. II. Термодинамика и молекулярная физика. — 5 изд., испр.. — М.: ФИЗМАТЛИТ, 2005. — 544 с. — ISBN 5-9221-0601-5.

Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист. Эти сайты могут нарушать авторские права, быть признаны неавторитетными источниками или по другим причинам быть запрещены в Википедии. Редакторам следует заменить такие ссылки ссылками на соответствующие правилам сайты или библиографическими ссылками на печатные источники либо удалить их (возможно, вместе с подтверждаемым ими содержимым). Список проблемных ссылок download1.libgen.io/ads.php?md5=F54DE2B5B715C97EA3375A180801C390

На этой странице вы узнаете

• В чем прелесть фазовых переходов?
• Что лучше выбрать: Mercedes или BMW?

Люди научились летать в космос, покорять недра Земли и погружаться в глубины океана. Эти и другие достижения возможны благодаря способности извлекать максимум пользы из имеющихся ресурсов,а именно получать тепловую энергию различными доступными способами. Сегодня мы разберем задачи, которые заставят тепловые процессы играть на нашей стороне. 

Тепловые машины и их КПД

Рекомендация: перед тем как приступить к выполнению задач неплохо было бы повторить тему «Уравнение состояния идеального газа» . Но ключевую теорию, на которой основано решение задач, сейчас разберем вместе.

Мы не почувствуем, как испарится капелька у нас на руке, потому что это не требует много тепла от нашего тела. Но мы можем наблюдать, как горят дрова в мангале, когда мы жарим шашлык, потому что выделяется огромное количество теплоты. А зачем мы вообще рассматриваем эти фазовые переходы? Все дело в том, что именно фазовые переходы являются ключевым звеном во всех процессах, где нас просят посчитать КПД, от них нашему рабочему телу и подводится теплота нагревателя.

Человечество придумало такие устройства, которые могут переработать тепловую энергию в механическую.

Тепловые двигатели, или тепловые машины, — устройства, способные преобразовывать внутреннюю энергию в механическую. 

Их устройство довольно просто: они на входе получают какую-то энергию (в основном — энергию сгорания топлива), а затем часть этой теплоты расходуется на совершение работы механизмом. Например, в автомобилях часть энергии от сгоревшего бензина идет на движение. Схематично можно изобразить так:

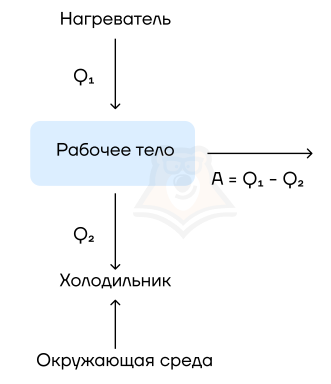
Рабочее тело — то, что совершает работу — принимает от нагревателя количество теплоты Q₁, из которой A уходит на работу механизма. Остаток теплоты Q₂ рабочее тело отдает холодильнику, по сути — это потеря энергии.

Физика не была бы такой загадочной, если б все в ней было идеально. Как и в любом процессе или преобразовании, здесь возможны потери, зачастую очень большие. Поэтому «индикатором качества» машины является КПД, с которым мы уже сталкивались в механике:

Коэффициент полезного действия (КПД) тепловой машины — это отношение полезной работы двигателя к энергии, полученной от нагревателя.

Мы должны понимать, что КПД на практике никогда не получится больше 1, поскольку всегда будут тепловые потери. 

Полезную работу можно расписать как Q₁ — Q₂ (по закону сохранения энергии). Тогда формула примет вид:

(eta = frac{Q_1 — Q_2}{Q_1} = 1 — frac{Q_2}{Q_1})

Цикл Карно

Мы знаем, что потери — это плохо, поэтому должны предотвращать их. Как это сделать? Нам ничего делать не нужно, за нас уже все сделал Сади Карно, французский физик, разработавший цикл, в котором машины достигают наивысшего КПД. Этот цикл носит его имя и состоит из двух изотерм и двух адиабат. Рассмотрим, как этот цикл выглядит в координатах p(V).

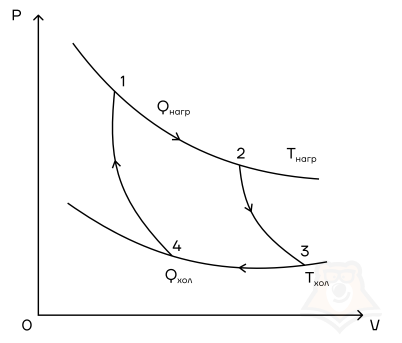
• Температура верхней изотермы 1-2 — температура нагревателя (так как теплота в данном процессе подводится).
• Температура нижней изотермы 3-4 — температура холодильника (так как теплота в данном процессе отводится).
• 2-3 и 4-1 — это адиабатические расширение и сжатие соответственно, в них газ не обменивается теплом с окружающей средой.

Цикл Карно — цикл идеальной тепловой машины, которая достигает наивысшего КПД. 

Формула, по которой можно рассчитать ее КПД выражается через температуры:

Приступим к задачам

Задачи на данную тему достаточно часто встречаются в задании 27 из КИМа ЕГЭ. Давайте разберем некоторые примеры.

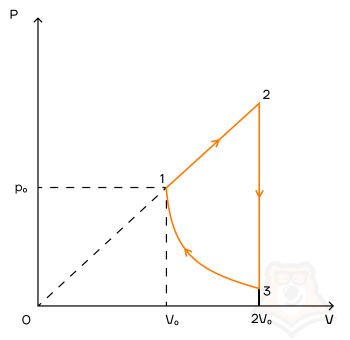
Задание 1. Одноатомный газ совершает циклический процесс, как показано на рисунке. На участке 1–2 газ совершает работу A₁₂ = 1520 Дж. Участок 3–1 представляет собой адиабатный процесс. Количество теплоты, отданное газом за цикл холодильнику, равно |Q_хол| = 4780 Дж. Найдите работу газа |A₁₃| на адиабате, если количество вещества постоянно.

Решение:

Шаг 1. Первое, с чего лучше начинать задачи по термодинамике — исследование процессов. 

Посмотрим на участок 1-2 графика: продолжение прямой проходит через начало координат, поэтому график функционально можно записать, как p = aV, где a — какое-то число, константа. Графиком является не изотерма, поскольку график изотермы в координатах p-V — гипербола. Из уравнения Менделеева-Клапейрона следует: (frac{pV}{T} = const). Отсюда можно сделать вывод, что возрастает температура, так как растут давление и объем.  Температура и объем растут, значит, увеличивается и внутренняя энергия и объем соответственно.

Участок 2-3: процесс изохорный, поскольку объем постоянен, следовательно, работа газом не совершается. Рассмотрим закон Шарля: (frac{p}{T} = const). Давление в этом процессе растет, тогда растет и температура, поскольку дробь не должна менять свое значение. Делаем вывод, что внутренняя энергия тоже увеличивается.

Участок 3-1: адиабата по условию, то есть количество теплоты в этом переходе равна нулю из определения адиабатного процесса. Работа газа отрицательна, так как газ уменьшает объем. 

Оформим все данные в таблицу. 

Определим знаки Q, используя первый закон термодинамики: Q = ΔU + A.

Из этих данных сразу видно, что количество теплоты, отданное холодильнику — это количество теплоты в процессе 2-3.

Шаг 2. Первый закон термодинамики для процесса 1-2 запишется в виде: 

Q₁₂ = ΔU₁₂ + A₁₂. 

Работа A12 — площадь фигуры под графиком процесса, то есть площадь трапеции: 

(A_{12} = frac{p_0 + 2p_0}{2} * V0 =frac{3p_0V_0}{2}). 

Запишем изменение внутренней энергии для этого процесса через давление и объем. Мы выводили эту формулу в статье «Первое начало термодинамики»:

(Delta U_{12} = frac{3}{2}(2p_0 * 2V_0 — p_0V_0) = frac{9p_0V_0}{2}). 

Заметим, что это в 3 раза больше работы газа на этом участке: 

(Delta U_{12} = 3A_{12} rightarrow Q_{12} = 4A_{12}).

Шаг 3. Работа цикла — площадь фигуры, которую замыкает график, тогда . A = A₁₂ — |A₃₁|. С другой стороны, работа цикла вычисляется как разность между энергиями нагревателя и холодильника: A = Q₁₂ — |Q₃₁|.

 Сравним эти формулы:

Q₁₂ -|Q₃₁| = A₁₂ — |A₃₁|,

подставим выражения из предыдущего пункта:

4A₁₂ — |Q₃₁| = A₁₂ — |A₃₁| (rightarrow) |A₃₁| = -3A₁₂ + |Q₃₁| = -31520 + 4780 = 220 Дж.

Ответ: 220 Дж

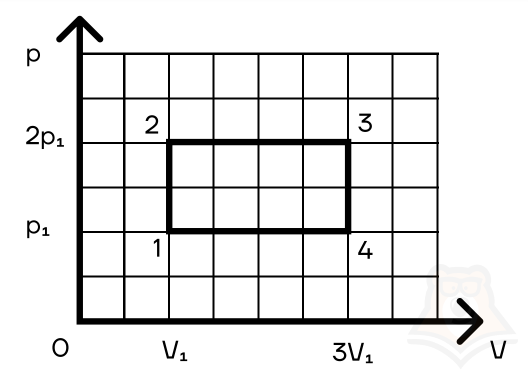
Задание 2. Найти КПД цикла для идеального одноатомного газа.

Решение:

Шаг 1. КПД цикла определим по формуле: (eta = frac{A}{Q}), где Q — количество теплоты от нагревателя, а А — работа газа за цикл. Найдем А как площадь замкнутой фигуры: A = (2p₁ — p₁)(3V₁ — V₁) = 2p₁V₁.

Шаг 2. Найдем процесс, который соответствует получению тепла от нагревателя. Воспользуемся теми же приемами, что и в прошлой задаче:

Посмотрим на участок 1-2 графика: давление растет, объем не меняется. По закону Шарля (frac{p}{T} = const) температура тоже растет. Работа газа равна 0 при изохорном процессе, а изменение внутренней энергии положительное.

2-3: давление не меняется, растет объем, а значит, работа газа положительна. По закону Гей-Люссака (frac{V}{T} = const) температура тоже растет, растет и внутренняя энергия.

3-4: давление уменьшается, следовательно, и температура уменьшается. При этом процесс изохорный и работа газа равна 0.

4-1: давление не меняется, объем и температура уменьшаются — работа газа отрицательна и внутренняя энергия уменьшается.

Оформим данные в таблицу: 

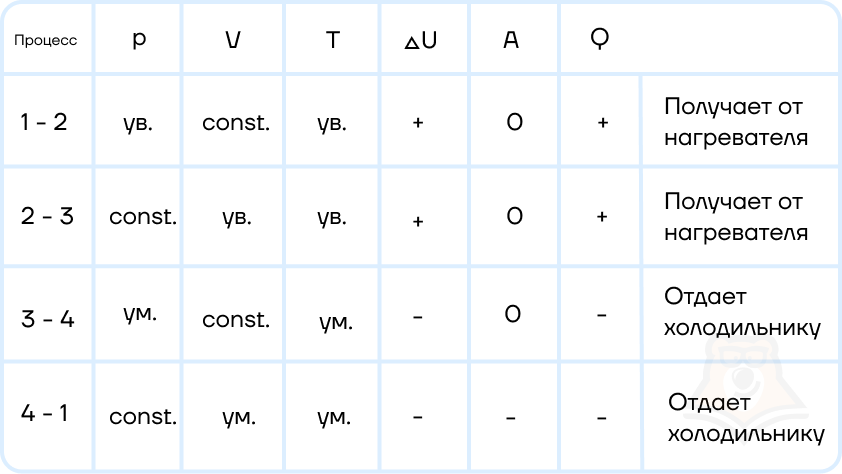
Отметим, что  необходимое Q = Q₁₂ + Q₂₃.

Шаг 3. Запишем первый закон термодинамики для процессов 1-2 и 2-3:

(Q_{12} = U_{12} + A_{12} = Delta U_{12} = frac{3}{2}(2p_1V_1 -p_1V_1) = frac{3}{2}p_1V_1).
(Q_{23} = Delta U_{23} + A_{23}), работу газа найдем как площадь под графиком: A₂₃ = 2p₁(3V₁ — V₁) = 4p₁V₁.
(Delta U_{12} = frac{3}{2}(2p_1 * 3V_1 — 2p_1V_1) = 6p_1V_1).
(Q_{23} = Delta U_{23} + A_{23} = 10p_1V_1).

Шаг 4. Мы готовы считать КПД: (eta = frac{A}{Q} = frac{A}{Q_{12} + Q_{23}} = frac{2p_1V_1}{frac{3}{2}p_1V_1 + 10p_1V_1} = frac{4}{23} approx 0,17).

Ответ: 17%

Теперь вас не должно настораживать наличие графиков в условиях задач на расчет КПД тепловых машин. Продолжить обучение решению задач экзамена вы можете в статьях «Применение законов Ньютона» и «Движение точки по окружности».

Фактчек

• Тепловые двигатели — устройства, способные преобразовывать внутреннюю энергию в механическую. 
• Тепловая машина принимает тепло от нагревателя, отдает холодильнику, а рабочим телом совершает работу.
• Коэффициент полезного действия (КПД) тепловой машины — это отношение полезной работы двигателя к энергии, полученной от нагревателя.
  (eta = frac{A}{Q_1} = frac{Q_1 — Q_2}{Q_1} = 1 — frac{Q_2}{Q_1})  
• Цикл Карно — цикл с максимально возможным КПД: (eta = frac{T_1 — T_2}{T_1} = 1 — frac{T_2}{T_1})
• Не забываем, что работа считается, как площадь фигуры под графиком.

Проверь себя

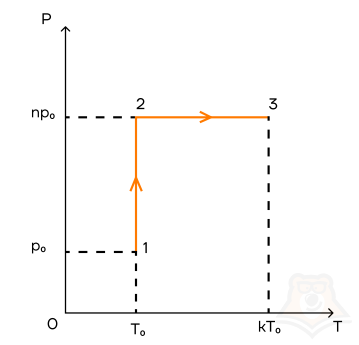
Задание 1. 
1 моль идеального газа переходит из состояния 1 в состояние 2, а потом — в состояние 3 так, как это показано графике. Начальная температура газа равна T₀ = 350 К. Определите работу газа при переходе из состояния 2 в состояние 3, если k = 3, а n = 2.

1. 5672 Дж
2. 4731 Дж
3. 5817 Дж
4. 6393 Дж

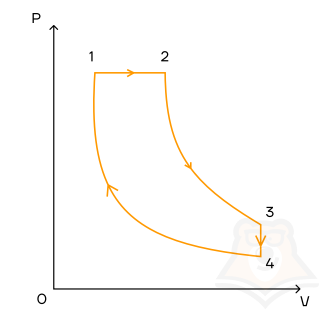
Задание 2. 
1 моль идеального одноатомного газа совершает цикл, который изображен на pV-диаграмме и состоит из двух адиабат, изохоры, изобары. Модуль отношения изменения температуры газа при изобарном процессе ΔT₁₂ к изменению его температуры ΔT₃₄ при изохорном процессе равен 1,5. Определите КПД цикла.

1. 0,6
2. 0,5
3. 0,8
4. 1

Задание 3.
В топке паровой машины сгорело 50 кг каменного угля, удельная теплота сгорания которого равна 30 МДж/кг. При этом машиной была совершена полезная механическая работа 135 МДж. Чему равен КПД этой тепловой машины? Ответ дайте в процентах.

1. 6%
2. 100%
3. 22%
4. 9%

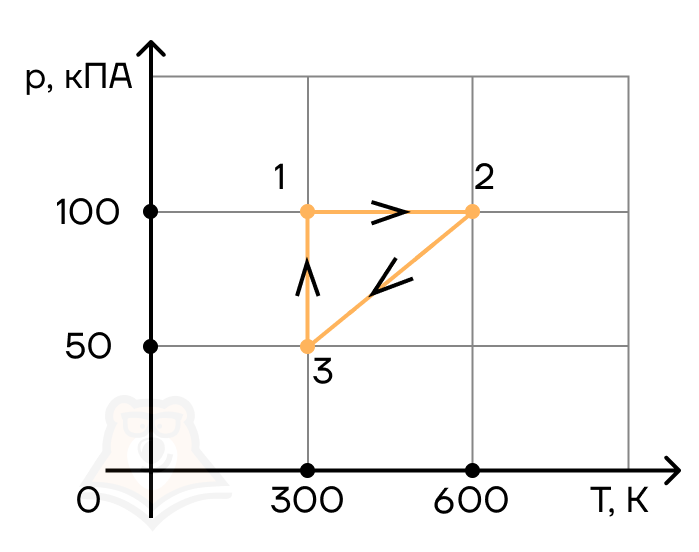
Задание 4.
С двумя молями одноатомного идеального газа совершают циклический процесс 1–2–3–1 (см. рис.). Чему равна работа, совершаемая газом на участке 1–2 в этом циклическом процессе?

1. 4444 Дж
2. 2891 Дж
3. 4986 Дж
4. 9355 Дж

Ответы:1 — 3; 2 — 1; 3 — 4; 4 — 3.

1. Цикл Карно и его кпд

Цикл
Карно́
— идеальный термодинамический
цикл.
Тепловая
машина Карно,
работающая по этому циклу, обладает
максимальным КПД
из всех машин, у которых максимальная
и минимальная температуры осуществляемого
цикла совпадают соответственно с
максимальной и минимальной температурами
цикла Карно. Состоит из 2 адиабатических
и 2 изотермических
процессов.

Одним
из важных свойств цикла Карно является
его обратимость: он может быть проведён
как в прямом, так и в обратном направлении,
при этом энтропия
адиабатически
изолированной (без теплообмена с
окружающей средой) системы не меняется.

Пусть тепловая
машина состоит из нагревателя с
температурой T_H, холодильника
с температурой T_X и рабочего
тела.

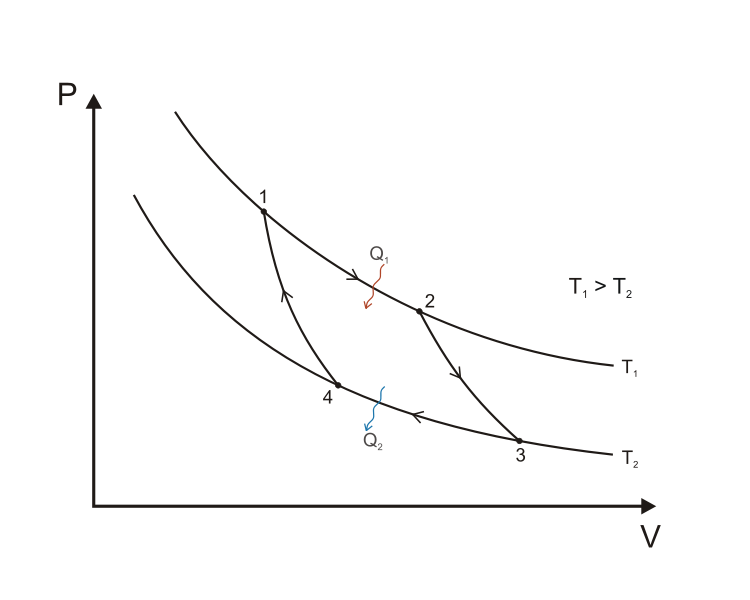
Цикл
Карно состоит из четырёх стадий:

1. Изотермическое расширение (на
   рисунке — процесс A→Б). В начале процесса
   рабочее тело имеет температуру T_H,
   то есть температуру нагревателя. Затем
   тело приводится в контакт с нагревателем,
   который изотермически (при постоянной
   температуре) передаёт ему количество
   теплоты Q_H. При этом
   объём рабочего тела увеличивается.

2. Адиабатическое (изоэнтропическое)
   расширение (на рисунке — процесс
   Б→В). Рабочее тело отсоединяется от
   нагревателя и продолжает расширяться
   без теплообмена с окружающей средой.
   При этом его температура уменьшается
   до температуры холодильника.

3. Изотермическое сжатие (на рисунке
   — процесс В→Г). Рабочее тело, имеющее
   к тому времени температуру T_X,
   приводится в контакт с холодильником
   и начинает изотермически сжиматься,
   отдавая холодильнику количество теплоты
   Q_X.

4. Адиабатическое (изоэнтропическое)
   сжатие (на рисунке — процесс Г→А).
   Рабочее тело отсоединяется от холодильника
   и сжимается без теплообмена с окружающей
   средой. При этом его температура
   увеличивается до температуры нагревателя.

При изотермических процессах температура
остаётся постоянной, при адиабатических
отсутствует теплообмен, а значит,
сохраняется энтропия:

при
δQ = 0.

Количество теплоты, полученное рабочим
телом от нагревателя при изотермическом
расширении, равно

.

Аналогично, при изотермическом сжатии
рабочее тело отдало холодильнику

.

Отсюда коэффициент
полезного действия тепловой машины
Карно равен

.

Из последнего выражения видно, что КПД
тепловой машины Карно зависит только
от температур нагревателя и холодильника.
Кроме того, из него следует, что КПД
может составлять 100 % только в том
случае, если температура холодильника
равна абсолютному
нулю. Это невозможно, но не из-за
недостижимости абсолютного нуля (этот
вопрос решается только третьим началом
термодинамики, учитывать которое здесь
нет необходимости), а из-за того, что
такой цикл или нельзя замкнуть, или он
вырождается в совокупность двух
совпадающих адиабат и изотерм.

Поэтому максимальный КПД любой тепловой
машины, будет меньше или равен КПД
тепловой машины Карно, работающей при
тех же температурах нагревателя и
холодильника. Например, КПД идеального
цикла
Стирлинга равен КПД цикла Карно.

1. 25. Реальные газы. Уравнение Ван-дер-Вальса.

Как мы видели, идеальный газ — это
упрощенная модель реальных газов. В
этой модели не учитываются объем молекул
и силы взаимодействия между ними. Между
тем молекулы реальных газов занимают
определенный объем и взаимодействуют
между собой. При больших давлениях и
низких температурах становится заметным
влияние собственных объемов молекул и
сил взаимодействия между ними. При этих
условиях уравнение Клапейрона—Менделеева
и законы Бойля—Мариотта, Гей-Люссака,
Шарля непригодны для описания состояния
реальных газов.

В 1873 г. голландский физик И. Ван дер-Ваальс
ввел в уравнение Клапейрона—Менделеева
поправки на размер молекул и на действие
сил притяжения между ними. И. Ван-дер-Ваальс
предложил модель реального газа, в
которой молекулы принимаются за твердые
шарики диаметром d и занимают хоть
малый, но некоторый объем. Молекулы не
только отталкиваются при соударениях,
но еще и притягиваются друг к другу
сравнительно слабыми силами на
расстояниях, сравнимых с размерами
молекул.

Запишем уравнение Клапейрона—Менделеева
для одного моля идеального газа (m
= M):

,
где V_M — молярный объем газа.

Учет собственного объема молекул
приводит к тому, что фактический свободный
объем, в котором могут двигаться молекулы
реального газа, будет не V_M, a
(V_M – b), где постоянная b
равна приблизительно учетверенному
собственному объему молекул.

Действие сил притяжения между молекулами
реального газа приводит к появлению
дополнительного давления на газ. При
приближении некоторой молекулы к стенке
сосуда все остальные молекулы оказываются
по одну сторону от нее и равнодействующая
сил притяжения, действующих на эту
молекулу, оказывается направленной от
стенки сосуда внутрь газа. Это приводит
к тому, что уменьшается импульс,
передаваемый молекулой стенке сосуда.
В результате давление газа p на
стенки сосуда уменьшается по сравнению
с тем p_id, каким оно было бы в
отсутствие сил притяжения:

.
Как показывают расчеты, это дополнительное
давление обратно пропорционально
квадрату объема газа, т.е.

где а — постоянная.

Вводя эти поправки, получим уравнение
Ван-дер-Ваальса для одного моля газа
(уравнение состояния реальных газов)

Если газ произвольной массы m занимает
объем V, то его молярный объем

,
где количество газа

.
Подставив значение молярного объема,
получим уравнение Ван-дер-Ваальса для
произвольного числа ν молей газа:

Постоянные для каждого газа поправки
a и b находят экспериментально.

Так как молекулы идеального газа не
имеют объема и не взаимодействуют между
собой, то идеальный газ при любых
изменениях его параметров остается
газом.

Совсем иначе ведут себя реальные газы.
Чтобы убедиться в этом, исследуемый газ
помещают в прозрачный цилиндр с подвижным
поршнем (рис. 1), который помещают в
термостат.

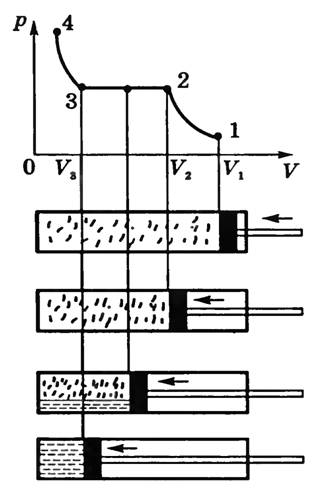
При медленном сжатии газа температура
его не изменяется (процесс изотермический)
и давление газа увеличивается в
соответствии с законом Бойля—Мариотта.
На графике эта стадия опыта изображена
кривой 1-2. Но, начиная с некоторого
объема, дальнейшее уменьшение объема
газа уже не приводит к увеличению
давления, а на стенках цилиндра появляются
капельки жидкости. При этом находящиеся
одновременно газ и жидкость имеют
одинаковую температуру и находятся под
одинаковым давлением, т.е. находятся в
термодинамическом равновесии.

Газ, находящийся в термодинамическом
равновесии со своей жидкостью, называется
насыщенным
паром.

Таким образом, участок изотермы 2-3
соответствует насыщенному пару над
жидкостью (двухфазная среда). Когда весь
газ превратится в жидкость, дальнейшее
уменьшение объема приводит к резкому
возрастанию давления (участок кривой
3-4), поскольку молекулы в жидкости
упакованы достаточно плотно и ее
сжимаемость мала. Вся кривая 1-2-3-4
называется изотермой реального газа.

Таким образом, изотермы реального газа
заметно отличаются от изотерм идеального
газа наличием у них горизонтальных
участков, соответствующих области
существования двухфазной системы.

Следовательно, основное отличие реальных
газов от идеального состоит в том, что
реальный газ может быть превращен в
жидкость.

26. Изотермы Ван-дер-Ваальса.

27. Внутренняя энергия реального
газа

Внутренняя
энергия реального газа складывается
из кинетической энергии теплового
движения его молекул, которая определяет
внутреннюю энергию идеального газа и
потенциальную энергию межмолекулярного
взаимодействия. Потенциальная энергия
реального газа обусловлена только
силами притяжения между молекулами.
Наличие сил притяжения приводит к
возникновению внутреннего давления на
газ

Работа,
которая затрачивается на преодоление
сил притяжения, действующих между
молекулами газа, идет на увеличение
потенциальной энергии системы.

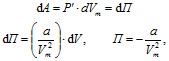
где
постоянная интегрирования принята
равной нулю. Знак «–» означает, что
молекулярные силы, создающие внутреннее
давление P′, являются силами притяжения.
Учитывая оба слагаемых, получим, что
внутренняя энергия моля реального газа

растет
с повышением температуры и увеличением
объема. Если газ расширяется без
теплообмена с окружающей средой, т.е.
dQ = 0, и не совершает внешней работы, т.е.
dA = 0, то на основании первого начала
термодинамики получим, что

U1
= U2  (2).

Следовательно,
при адиабатическом расширении без
совершения внешней работы внутренняя
энергия газа не изменяется. Равенство
(2) формально справедливо как для
идеального, так и для реального газа,
но физический смысл для обоих случаев
совершенно различен.

Для
идеального газа равенство (2) означает
равенство температур, т.е. T1 = T2, и при
адиабатическом расширении идеального
газа в вакуум его температура не
изменяется.

Для
реального газа из равенства (2) для моля
газа

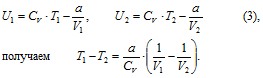
Т.к.
V2 > V1, то T1 > T2, т.е. газ при адиабатическом
расширении в вакуум охлаждается и
наоборот, при адиабатическом сжатии в
вакуум реальный газ нагревается.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Устройство, имеющее способность преобразовывать полученную теплоту в механическую работу носит название теплового двигателя. В таких машинах механическая работа совершается в процессе расширения вещества, называющегося рабочим телом. Его роль обычно исполняют газообразные вещества, вроде паров бензина, воздуха и водяного пара.

Рабочее тело приобретает или отдает тепловую энергию при теплообмене с телами, которые имеют внушительный запас внутренней энергии. Такие тела называют тепловыми резервуарами.

Исходя из первого закона термодинамики, можно сделать вывод, что полученное газом количество теплоты Q полностью преобразуется в работу A в условиях изотермического процесса, при котором внутренняя энергия не претерпевает изменений (ΔU=0): 

A=Q

Однако, подобный однократный акт превращения теплоты в работу для техники не представляет интереса. Существующие тепловые двигатели, такие как паровые машины, двигатели внутреннего сгорания и им подобные, работают циклически. Необходимо периодическое повторение процесса теплопередачи и преобразования полученной теплоты в работу. Чтобы данное условие выполнялось, рабочее тело должно совершать круговой процесс или же термодинамический цикл, при котором исходное состояние с периодически восстанавливается. На рисунке 3.11.1 в виде диаграммы (p, V) газообразного рабочего тела с помощью замкнутых кривых проиллюстрированы круговые. В условиях расширения газ производит положительную работу A1, эквивалентную площади под кривой abc. При сжатии газ совершает отрицательную работу A2, равную по модулю площади под кривой cda. Полная работа за цикл A=A1+A2 на диаграмме (p, V) равняется площади цикла. Работа A положительна, в том случае, если цикл проходит по часовой стрелке, и A отрицательна, когда цикл проходит в противоположном направлении.

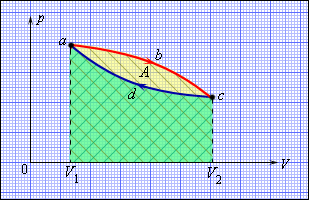
Рисунок 3.11.1. Круговой процесс на диаграмме (p, V). abc – кривая расширения, cda – кривая сжатия. Работа A в круговом процессе равна площади фигуры abcd.

Все круговые процессы обладают общей чертой. Они не могут привестись в действие при контакте рабочего тела только с одним тепловым. Их минимальное число должно быть равным двум.

Тепловой резервуар, обладающий более высоким значением температуры, носит название нагревателя, а с более низким – холодильника.

Рабочее тело при совершении кругового процесса получает от нагревателя некоторую теплоту Q1>0 и теряет, отдавая холодильнику, количество теплоты Q2<0. Для полного полученного рабочим телом за цикл количества теплоты Q справедливо следующее выражение:

Q=Q1+Q2=Q1-Q2.

Совершая цикл, рабочее тело приходит в свое первоначальное состояние, из чего можно сделать вывод, что изменение его внутренней энергии равняется ΔU=0. Основываясь на первом законе термодинамики, запишем: 

∆U=Q-A=0.

Из этого следует: 

A=Q=Q1-Q2.

Работа A, которую рабочее тело совершает за цикл, эквивалентна полученному за этот же цикл количеству теплоты Q.

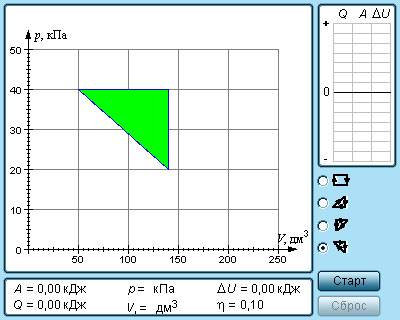
Рисунок 3.11.2. Модель термодинамических циклов.

Коэффициент полезного действия теплового двигателя демонстрирует, какая доля тепловой энергии, которую получило рабочее тело от нагревателя, преобразовалась в полезную работу. Оставшаяся часть (1–η) была без пользы передана холодильнику. Коэффициент полезного действия тепловой машины не может быть больше единицы η<1. На рисунке 3.11.3 проиллюстрирована энергетическая схема тепловой машины.

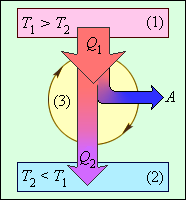
Рисунок 3.11.3. Энергетическая схема тепловой машины: 1 – нагреватель; 2 – холодильник; 3 – рабочее тело, совершающее круговой процесс. Q1>0, A>0, Q2<0; T1>T2.

Виды тепловых двигателей

В технике свое применение находят двигатели, использующие круговые процессы. Рисунок 3.11.3 демонстрирует нам циклы, применяемые в бензиновом карбюраторном и в дизельном двигателях. Они оба в качестве рабочего тела используют смесь паров бензина или дизельного топлива с воздухом. Цикл карбюраторного двигателя внутреннего сгорания включает в себя две изохоры (1–2, 3–4) и две адиабаты (2–3, 4–1), дизельного двигателя -две адиабаты (1–2, 3–4), одну изобару (2–3) и одну изохору (4–1). Реальный КПД (коэффициент полезного действия) у карбюраторного двигателя составляет около 30 %, у дизельного двигателя – приблизительно 40 %.

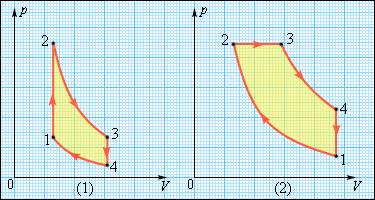
Рисунок 3.11.4. Циклы карбюраторного двигателя внутреннего сгорания (1) и дизельного двигателя (2).

Цикл Карно

Круговой процесс, изображенный на рисунке 3.11.5, состоящий из двух изотерм и двух адиабат был назван циклом Карно в честь открывшего его в 1824 году французского инженера. Данное явление впоследствии оказало колоссальное влияние на развитие учения о тепловых процессах.

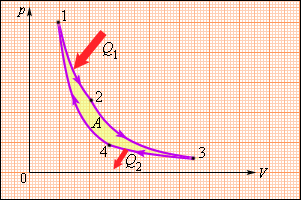
Рисунок 3.11.5. Цикл Карно.

Находящийся в цилиндре, под поршнем, газ совершает цикл Карно. На участке изотермы (1–2) он приводится в тепловой контакт с нагревателем, обладающим некоторой температурой T1. Газ изотермически расширяется, при этом к нему подводится эквивалентное совершенной работе A12 количество теплоты Q1=A12. После этого на участке адиабаты (2–3) газ помещается в адиабатическую оболочку и продолжает процесс расширения при отсутствующем теплообмене. На данной части цикла газ совершает работу A23>0. Его температура при адиабатическом расширении снижается до величины T2. На идущем следующим участке изотермы (3–4) газ приводится в тепловой контакт с холодильником в условиях температуры T2<T1. Производится процесс изотермического сжатия. Газом совершается некоторая работа A34<0 и отдается тепло Q2<0, эквивалентное произведенной им работе A34. Его внутренняя энергия не претерпевает изменений. На последнем оставшемся участке адиабатического сжатия газ снова помещают в адиабатическую оболочку. При сжатии его температура вырастает до величины T1, также совершается работа A41<0. совершаемая газом за цикл полная работа A эквивалентна сумме работ на отдельных участках: 

A=A12+A23+A34+A41.

На диаграмме (p, V) данная работа равняется площади цикла.

Процессы на любом из участков цикла Карно квазистатичны. Например, оба участка 1–2 и 3–4, относящихся к изотермическим, производятся при пренебрежительно малой разности температур рабочего тела, то есть газа, и теплового резервуара, будь то нагреватель или холодильник.

Исходя из первого закона термодинамики, можно заявить, что работа газа в условиях адиабатического расширения или сжатия эквивалентна падению значения ΔU его внутренней энергии. Для 1 моля газа верно следующее выражение:

A=-∆U=-CV(T2-T1),

в котором T1 и T2 представляют собой начальную и конечную температуры рабочего тела.

Из этого следует, что работы, совершаемые газом на двух адиабатических участках цикла Карно, противоположны по знакам и одинаковы по модулю:

A23=-A41.

Коэффициент полезного действия η цикла Карно может рассчитываться с помощью следующих соотношений: 

η=AQ1=A12+A34Q12=Q1-Q2Q1=1-Q2Q1.

С. Карно выразил коэффициент полезного действия цикла через величины температур холодильника T2 и нагревателя T1: 

η=T1-T2T1=1-T2T1.

Цикл Карно примечателен тем, что ни на одном из его участков тела, обладающие различными температурами, не соприкасаются. Любое состояние рабочего тела в цикле является квазиравновесным, что означает его бесконечную близость к состоянию теплового равновесия с окружающими объектами, то есть тепловыми резервуарами или же термостатами. В цикле Карно исключен теплообмен в условиях конечной разности температур рабочего тела и окружающей среды (термостатов), если тепло имеет возможность переходить без совершения работы. По этой причине любые другие возможные круговые процессы проигрывают ему в эффективности при заданных температурах нагревателя и холодильника: 

ηКарно=ηmax

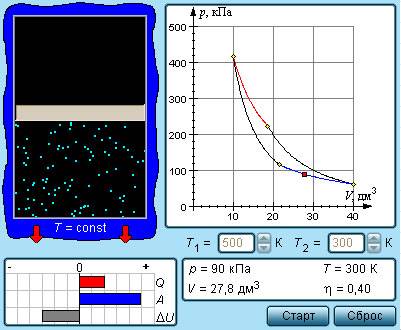
Рисунок 3.11.6. Модель цикла Карно.

Каждый участок цикла Карно и цикл в целом могут проходиться в обоих направлениях.

Обход цикла по часовой стрелке соответствует тепловому двигателю, в котором полученное рабочим телом тепло частично преобразуется в полезную работу. Обход против часовой стрелки соответствует холодильной машине, где некое количество теплоты отходит от холодного резервуара и передается горячему резервуару за счет совершения внешней работы. Именно поэтому идеальное устройство, работающее по циклу Карно, носит название обратимой тепловой машины.

В реально существующих холодильных машинах применяются разные циклические процессы. Любой холодильный цикл на диаграмме (p, V) обходятся против часовой стрелки. На рисунке 3.11.7 проиллюстрирована энергетическая схема холодильной машины.

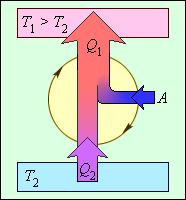
Рисунок 3.11.7. Энергетическая схема холодильной машины. Q1<0, A>0, Q2 > 0, T1>T2.

Работающее по холодильному циклу устройство может обладать двояким предназначением.

Если полезным эффектом является отбор некоторого количества тепла Q2 от охлаждаемых тел, к примеру, от продуктов в камере холодильника, то такое устройство является обычным холодильником.

Эффективность работы холодильника может быть охарактеризована следующим отношением: 

βx=Q2A.

Таким образом, эффективность работы холодильника представляет собой количество тепла, отбираемого от охлаждаемых тел на 1 джоуль затраченной работы. В условиях подобного определения βх может быть, как больше, так и меньше единицы. Для обращенного цикла Карно справедливо выражение:

βx=T2T1-T2.

В случае, когда полезным эффектом является передача некоего количества тепла
|Q1| нагреваемым телам, чьим примером может выступать воздух в помещении, то такое устройство называется тепловым насосом.

Эффективность βТ теплового насоса может быть определена с помощью отношения: 

βт=Q1A.

То есть она может определяться количеством теплоты, передаваемым более теплым телам на 1 джоуль затраченной работы. Из первого закона термодинамики следует: 

Q1>A.

Следовательно, βТ всегда больше единицы. Для обращенного цикла Карно справедливо следующее выражение:

βт=1η=T1T1-T2.

Большинство современных двигателей преобразуют внутреннюю энергию углеводородного топлива в механическую энергию. То есть являются тепловыми машинами. Первым ученым, который задался вопросом о создании самой эффективной тепловой машины стал французский физик Сади Карно. В 1824 в его работе – «Размышления о движущей силе огня и о машинах, способных развивать эту силу», предложен идеальный термодинамический цикл тепловой машины. Цикл, позволяющий получить максимальный теоретический КПД, затем назвали именем Карно. 

Главной характеристикой, на которую обращают внимание при проектировании любого двигателя является коэффициент полезного действия или КПД. Коэффициент КПД показывает, насколько эффективно протекает трансформация тепловой энергии в системе в полезную механическую работу. КПД любого цикла вычисляется путем отношения полезной работы к затраченной энергии (которую передают системе).

• Полезная работа – та, которую получаем на выходе системы в результате выполнения цикла.
• Затраченная энергия – та, что была подведена к системе за цикл.

Термодинамические процессы и циклы.

Цикл Карно состоит из двух изотермических и двух адиабатных процессов. Чтобы понять, что из себя представляют эти процессы, обратимся к первому закону термодинамики:

∆U = A + Q,

где ∆U – внутренняя энергия рабочего тела или системы,

A – совершаемая в цикле работа,

Q – количество теплоты, переданное за цикл, системе.

Формулировка первого закона термодинамики: при переходе системы из одного состояния в другое, изменение внутренней энергии системы равно сумме количества теплоты, переданного системе, и работы внешних сил.

Что такое изотермический и адиабатный процессы?

Изотермический процесс

Изотермический процесс – процесс, перехода рабочего тела из одного состояния в другое без изменения температуры ∆T=0.  

Например, изменение объёма и давления газа при неизменной температуре.

При постоянной температуре изменение внутренней энергии газа ∆U будет равно нулю, так как ∆T = 0.

Тогда, согласно первому закону термодинамики: Q = A.  Это значит:

• получая теплоту, газ будет расширяться, совершая положительную работу. При этом всё количество тепла будет потрачено на совершение работы.
• и наоборот, при отдаче теплоты объем газа будет уменьшаться.

Адиабатный процесс

Адиабатный процесс – такой процесс, который протекает без передачи или получения тепла Q от окружающей среды. То есть, процесс протекает в теплоизолированной системе или с бесконечно большой скоростью, при которой теплообменом можно пренебречь Q = 0.

Согласно первому закону термодинамики: A = -∆U.

Это значит:

• работу газ совершает за счет уменьшения внутренней энергии;
• и наоборот, приложенная к системе работа, затрачивается только на повышение внутренней энергии.

Из каких процессов состоит цикл Карно

Главная особенность всех круговых процессов или циклов состоит в том, что их работа невозможна, если приводить рабочее тело в контакт только с одним источником теплоты. Любой тепловой двигатель устроен таким образом, что за счет теплообмена между двумя источниками теплоты он способен преобразовать тепло в механическую работу. Температуры этих источников должны отличаться, но, при этом, быть постоянными.

Чтобы понять, как работает цикл Карно, нужно представить простой тепловой двигатель, например цилиндр с поршнем, внутри которого находится газ. К газу может подводиться и отводится тепло. Источники тепла, при этом, называются:

• нагреватель – источник, имеющий высокую постоянную температуру T_Н
• холодильник – с постоянной низкой температурой T_Х.

Цикл Карно имеет четыре обратимых процесса – два изотермических, и два – адиабатных.

Изотермические процессы протекают при постоянной температуре T. Адиабатные процессы – при постоянной энтропии S, без теплообмена с окружающей средой.

Для удобства, цикл Карно представляют в:

• T-S координатах – зависимость энтропии S от температуры T.
• p-V координатах – зависимость давления p от удельного объёма V.

Изотермическое расширение

Изотермическое расширение или изотермический подвод тепла – показано процессом AB. В начале рабочее тело находится в точке A. На данном этапе рабочее тело или газ имеет начальную температуру T_Н. Затем, к телу подводится энергия в виде теплоты Q₁. Снижение температуры при расширении отсутствует, так как подводится теплота Q₁, от нагревателя. Увеличения температуры тоже не будет, так как совершается работа A₁=Q₁. Поэтому, при расширении рабочего тела его температура остается постоянной – изотермическое расширение T_Н=const. При этом, энтропия рабочего тела увеличивается, из-за увеличения его объема. Происходит это за счет совершения механической работы.

Адиабатическое расширение

Адиабатическое расширение – показано процессом BC. После окончания изотермического подвода тепла газ находится в состоянии, характеризуемом точкой B. Далее следует адиабатическое расширение рабочего тела. На этом этапе газ в двигателе изолирован от обоих тепловых источником – как от горячего, так и от холодного. Поэтому ни источники, ни рабочее тело получают и не теряют тепло. Такой процесс называется адиабатическим. Из-за отсутствия теплообмена с окружающей средой Q=0 энтропия рабочего тела остается постоянной S=const. Работа осуществляется только за счет внутренней энергии A = -∆U. Поэтому происходит снижение температуры газа.

Рабочее тело, расширяясь, заставляет поршень двигаться вверх. Давление газа под поршнем постепенно снижается. Выталкивая подвижный поршень вверх, рабочее тело совершает механическую работу, в результате чего теряет определенное количество внутренней энергии. Количество этой энергии равно проделанной работе A = -∆U. В процессе расширения рабочего тела его температура уменьшается и становится равной T_Х.

Изотермическое сжатие

Изотермическое сжатие – процесс CD. На данном этапе рабочее передаёт тепло холодному источнику при температуре T_Х. К газу подводится работа сжатия путем перемещения поршня вниз. В результате этого процесса, рабочее тело передает холодильнику количество теплоты равное подводимой работе Q₂=А₂. Изменения внутренней энергии не будет ∆U=0. Поэтому, этот процесс считается изотермическим сжатием T_Х=const. Энтропия газа уменьшается.

Адиабатическое сжатие

Адиабатическое сжатие – процесс DA. После завершения отвода тепла, газ находится в состоянии, характеризуемом точкой D. На последней стадии цикла рабочее тело снова остается изолированным обоих источников Q=0. Предполагается, что поршень движется без трения, а процесс является обратимым. Работа продолжает подводиться и поршень движется вниз, сжимая газ. В результате этого внутренняя энергия газа возрастает A = +∆U. Под давлением поршня температура рабочего тела поднимается до температуры нагревателя T_Н, но энтропия остается неизменной. Итогом этого этапа является то, что рабочее тело возвращается к своему изначальному состоянию в точку А.

Поскольку цикл Карно идеальный, то принято допущение, что температуры рабочего тела в процессах AB и CD равна температуре горячего и холодного источника или отличаются на бесконечно малую величину.

Формула расчета цикла Карно

Коэффициент КПД показывает, насколько совершенен цикл и входящие в него термодинамические процессы. Термический КПД любого термодинамического цикла рассчитывается по формуле:

Где Q₁ – тепло, подведенное к рабочему телу от нагревателя;

Q₂ – тепло, отведенное от рабочего тела к холодильнику.

Применительно для расчета КПД цикла Карно используется формула:

Где T_Н -температура горячего источника;

T_Х -температура холодно источника.

Температура формуле вычисления КПД цикла Карно в кельвинах [К].

Обратный цикл Карно

Описанный выше цикл теплового двигателя Карно полностью обратим. Это значит, что можно пройти все процессы в обратном направлении:

• процесс отвода тепла станет процессом подвода тепла
• процесс сжатия – расширением.

При проходе процессов в обратном направлении получим циклом холодильной машины Карно или теплового насоса. Диаграммы остаются абсолютно такими же, измениться лишь направление процессов.

Единственное отличие обратного цикла Карно — это противоположные направления всех четырёх термодинамических процессов.

Тепло в обратном цикле Карно будет поглощаться из холодильника, и далее отводиться к нагревателю. Чтобы это осуществить, в соответствии со вторым законом термодинамики, необходимо затратить работу. Работа затрачивается на сжатие газа.

В результате того, что к данной системе прикладывается работа, тепло перемещается от холодного источника к горячему.

Подробнее про обратный цикл Карно и холодильные машины рекомендуем прочитать в статье.

Теорема Карно

Теорема Карно – это теорема, выявляющая некоторые ограничения для предела КПД реальных тепловых машин. Описал ее Сади Карно в своем труде о движущей силе огня. Но некоторые из современных авторов считают, что рассуждения Карно позволяют сформулировать сразу две теоремы. Звучат они так:

1. КПД любого обратимого теплового двигателя, работающего по циклу Карно, не зависит от природы рабочего тела и конструкции самой машины, а является лишь функцией температур нагревателя и холодильника:

Из этой теоремы можно сделать вывод, что самую большую роль, определяющую КПД тепловой машины, играет разница температур горячего и холодного источников.

1. КПД любого теплового двигателя, работающего по необратимому циклу, должен быть меньше КПД двигателя с обратимым циклом Карно, при условии равных температур нагревателей и холодильников.

Эта трактовка теоремы дает понять, что реальные двигатели неидеальны, в отличии от теоретической модели Карно. Поэтому, из-за наличия неизбежных потерь энергии, КПД реального двигателя будет снижаться в зависимости от объема этих потерь.

Исходя из этого, уравнение расчета КПД цикла Карно показывает максимальную эффективность работы для любого двигателя, в котором задействованы соответствующие температурные параметры.

Следствие теоремы Карно – все обратимые двигатели, которые работают между идентичными источниками тепла, имеют одинаковую эффективность.

Отсюда можно сделать вывод: понижение температуры холодного резервуара сильнее влияет на максимальный КПД тепловой машины, чем увеличение температуры горячего резервуара на такую же величину. На практике добиться этого довольно сложно, так как чаще всего источником для охлаждения является окружающая среда со своей температурой.

Максимальный КПД достигается только в том случае, когда значение энтропии не изменяется в течение цикла. Например, в течение цикла энтропия может изменяться при наличии трения, в результате которого при механической работе выделяется тепло. В данной ситуации цикл нельзя назвать обратимым.

Обобщенный цикл Карно

Согласно описанной ранее теореме Карно, КПД абсолютно любого реального цикла не может быть выше КПД в цикле Карно при идентичных температурных параметрах. Несмотря на это существуют примеры, термический КПД которых, при определенных условиях, равен циклу Карно. Такие циклы имеют отличия в изображении на T-S диаграмме. В данных циклах используется регенерация теплоты, поэтому они называются регенеративными.

Термодинамический цикл с регенерацией теплоты

Происходит процесс регенерации следующим образом. Доля тепла, отдаваемая рабочим телом холодильнику, переходит обратно к рабочему телу для его нагревания. Такой метод повышает термический КПД рабочего цикла, позволяя сделать расход теплоты более выгодным, и используется в теплосиловых устройствах. Например, в современных тепловых электрических станциях.

Рассмотрим T-S диаграмму регенеративного цикла.

Данный цикл состоит из двух изотермических (1-2) и (3-4) и двух политропных (произвольных) (2-3) и (4-1) обратимых и эквидистантных процессов.

1. Горячий источник (нагреватель), имея начальную температуру T₁, по изотерме (1-2) передает теплоту рабочему телу.
2. В точке 2 начинается расширение рабочего тела в направлении (2-3) – политропный процесс. На данной кривой происходит отвод теплоты регенерации q_рег.
3. Точка 3 на диаграмме находится левее, чем в диаграмме для идеального цикла Карно, поскольку вследствие отвода теплоты регенерации уменьшается энтропия рабочего тела.
4. Далее, на изотермической прямой (3-4) происходит сжатие рабочего тела и отведение теплоты к холодному источнику с температурой T₂ (холодильник).
5. В точке 4 начинается политропный процесс сжатия по кривой (4-1). Одновременно с этим к рабочему телу подводится теплота q_рег.

Рабочее тело принимает и отдает равное количество теплоты q_рег, значит в данном процессе происходит перенос теплоты из одной части цикла в другую, это и называется процессом регенерации.

Термический КПД регенеративного цикла

Термический КПД регенеративного цикла будет равен термическому КПД Карно при идентичных параметрах температуры. Поэтому такой регенеративный цикл так же называют обобщенным циклом Карно (только если он обратим). Подобные явления находят массовое практическое применение на различных промышленных объектах и предприятиях.

К примеру, по принципу регенерации происходит подогрев воды в паровых турбинах и подогрев воздуха в газовых турбинах. 

Говоря об обобщенном цикле Карно, стоит отметить, что его реализация в идеальном виде невозможна. Обусловлено это тем, что в идеале такая система должна содержать бесконечно большое количество промежуточных регенераторов. При этом, для каждого из них температура отводимой и подводимой теплоты должна быть определенной. Любые методы регенерации, которые используются на практике, являются в определенной мере приближенными к идеальному циклу.

Эффективность реальных тепловых двигателей.

Обратимые двигатели в реальности невозможны. Реальные машины имеют еще меньший КПД, чем КПД машины Карно. Помимо этого, реальные двигатели, работающие по принципу Карно, можно встретить крайне редко. Несмотря на это, данное уравнение не теряет своей актуальности для определения максимального КПД, который можно спрогнозировать для определенной пары источников теплоты. Двигатель, работающий по принципу Карно должен рассматриваться как теоретическая модель тепловых двигателей.

Важнейшей технической задачей является повышение КПД тепловых двигателей и приближение этого значение к максимально возможному. Сравним значения термических КПД некоторых тепловых двигателей:

• Паровой двигатель – 8%
• Газотурбинная установка – 25-38%
• Паротурбинная установка – 40-50%

Начальные и конечные температуры пара для паровой турбины имеют такие приблизительные значения: T_н = 800 К, T_х = 300 К. Максимальное теоретическое значение КПД при данных температурах – 62%. Но, вследствие различных потерь энергии, в реальности экономичность достигает 45%.

На сегодня, КПД самых экономичных паротурбинных блоков на сверхперегретом паре с развитой системой регенерации и промежуточным перегревом пара достигает 52%.

Заключение

Модель работы идеального теплового двигателя, предложенная Сади Карно почти 200 лет назад, хоть и нереализуема на практике, но определенно остается актуальной и в нынешнее время.

Цикл Карно – теоретический инструмент, позволяющий рассчитать максимальную эффективность для любого теплового двигателя, что является немаловажной задачей для каждого инженера, занимающегося разработкой и моделированием термодинамических систем.