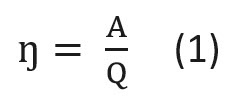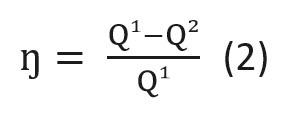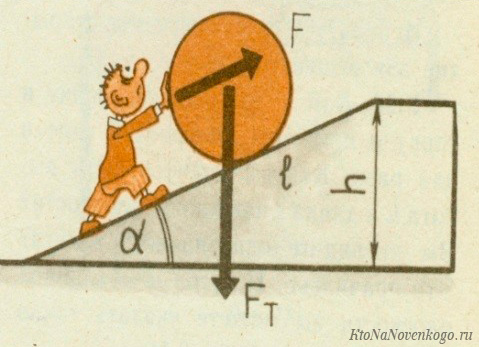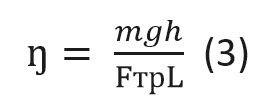Коэффицие́нт поле́зного де́йствия (КПД) — характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии. Определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой; обозначается обычно η («эта»)[1]. КПД является безразмерной величиной и часто выражается в процентах. Часто применяется в переносном смысле как метафора эффективности чего-либо без привязки к расчётам.
Определение[править | править код]
Математически КПД определяется как
где А — полезная работа (энергия), а Q — затраченная энергия.
Если КПД выражается в процентах, эту формулу иногда записывают в виде
.
Здесь умножение на 
не несёт содержательного смысла, поскольку 
. В связи с этим второй вариант записи формулы менее предпочтителен (одна и та же физическая величина может быть выражена в различных единицах независимо от формул, где она участвует).
В силу закона сохранения энергии и в результате неустранимых потерь энергии КПД реальных систем всегда меньше единицы, то есть невозможно получить полезной работы больше или столько, сколько затрачено энергии.
КПД теплово́го дви́гателя — отношение совершённой полезной работы двигателя к энергии, полученной от нагревателя. КПД теплового двигателя может быть вычислен по следующей формуле
- ,
где 
— количество теплоты, полученное от нагревателя, 
— количество теплоты, отданное холодильнику. Наибольшим КПД среди циклических машин, оперирующих при заданных температурах нагревателя T1 и холодильника T2, обладают тепловые двигатели, работающие по циклу Карно; этот предельный КПД равен
- .
Другие похожие показатели[править | править код]
Не все показатели, характеризующие эффективность энергетических процессов, соответствуют вышеприведённому описанию. Даже если они традиционно или ошибочно называются «коэффициент полезного действия», они могут иметь другие свойства, в частности, превышать 100 %.
КПД котлов[править | править код]
КПД котлов на органическом топливе традиционно рассчитывается по низшей теплоте сгорания; при этом предполагается, что влага продуктов сгорания покидает котёл в виде перегретого пара. В конденсационных котлах эта влага конденсируется, теплота конденсации полезно используется. При расчёте КПД по низшей теплоте сгорания он в итоге может получиться больше единицы. В данном случае корректнее было бы считать его по высшей теплоте сгорания, учитывающей теплоту конденсации пара; однако при этом показатели такого котла трудно сравнивать с данными о других установках.
Тепловые насосы и холодильные машины[править | править код]
Достоинством тепловых насосов как нагревательной техники является возможность получать больше теплоты, чем расходуется энергии на их работу. Холодильная машина может отвести от охлаждаемого конца больше теплоты, чем затрачивается энергии на организацию процесса.
Эффективность машин характеризует холодильный коэффициент[en]
- ,
где 
— тепло, отбираемое от холодного конца (в холодильных машинах холодопроизводительность); 
— затрачиваемая на этот процесс работа (или электроэнергия).
Для тепловых насосов используют термин коэффициент трансформации
- ,
где 
— тепло конденсации, передаваемое теплоносителю; — затрачиваемая на этот процесс работа (или электроэнергия).
В идеальной машине 
, отсюда для идеальной машины 
Наилучшими показателями производительности для холодильных машин обладает обратный цикл Карно: в нём холодильный коэффициент
- ,
где 
, 
— температуры горячего и холодного концов, K[2]. Данная величина, очевидно, может быть сколь угодно велика; хотя практически к ней трудно приблизиться, холодильный коэффициент может превосходить единицу. Это не противоречит первому началу термодинамики, поскольку, кроме принимаемой в расчёт энергии A (напр., электрической), в тепло Q идёт и энергия, отбираемая от холодного источника.
Примечания[править | править код]
- ↑ Зубарев Д. Н. Коэффициент полезного действия // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 484—485. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
- ↑ Холодильный коэффициент // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
Литература[править | править код]
- Пёрышкин А. В. Физика. 8 класс. — Дрофа, 2005. — 191 с. — 50 000 экз. — ISBN 5-7107-9459-7..
При использовании механизмов всегда совершается работа, превышающая работу, которая необходима для достижения поставленной цели, поэтому различают полную (или затраченную) работу —
Aз
и полезную работу —
Aп
.
Рассмотрим подъём груза массой (m) на высоту (h.)
Полезная работа заключается в подъёме груза на высоту, а для этого необходимо преодолеть силу тяжести. Если движение равномерное, то полезная работа равна:
Если груз оказывается достаточно тяжёлым и не представляется возможным поднять его вручную, можно использовать механизмы, например блок или наклонную плоскость. В этом случае, кроме действующей на груз силы тяжести, придётся преодолеть ещё и другие силы, например, при движении по наклонной плоскости — силу трения между грузом и плоскостью.
Более того, выигрывая в силе, всегда проигрывают в пути, что также влияет на работу.
Всё это приводит к тому, что совершённая с помощью механизма затрачиваемая (полная) работа всегда несколько больше полезной работы:
или
AпAз<1
.
Отношение полезной работы к полной работе называется коэффициентом полезного действия механизма (КПД):
, где
η
— буквенное обозначение КПД, (A_П) — полезная работа, (A_З) — затраченная работа.
КПД может выражаться и в долевом отношении, и в процентах:
η
(=) (0,35) (=) (35) (%).
При разработке двигателей и механизмов инженеры нацелены уменьшить затраты энергии и повысить коэффициент полезного действия. В процессе научно-технического развития коэффициент полезного действия изменялся. Современные технологии позволяют достичь высокого КПД. Это необходимо для сохранения природы.
- КПД парового двигателя — (1)–(8) (%).
- КПД бензинового двигателя — (20)–(25) (%).
- КПД электрического двигателя — (90)–(95) (%).
Формула КПД (коэффициента полезного действия) в физике
Формула КПД (коэффициента полезного действия)
В реальной действительности работа, совершаемая при помощи какого – либо устройства, всегда больше полезной работы, так как часть работы выполняется против сил трения, которые действуют внутри механизма и при перемещении его отдельных частей. Так, применяя подвижный блок, совершают дополнительную работу, поднимая сам блок и веревку и, преодолевая силы трения в блоке.
Введем следующие обозначения: полезную работу обозначим $A_p$, полную работу – $A_{poln}$. При этом имеем:
[A_p < A_{poln} ; frac{A_p}{A_{poln}}<1left(1right).]
Определение и формула КПД
Определение
Коэффициентом полезного действия (КПД) называют отношение полезной работы к полной. Обозначим КПД буквой $eta $, тогда:
[eta =frac{A_p}{A_{poln}} left(2right).]
Чаще всего коэффициент полезного действия выражают в процентах, тогда его определением является формула:
[eta =frac{A_p}{A_{poln}}cdot 100% left(2right).]
При создании механизмов пытаются увеличить их КПД, но механизмов с коэффициентом полезного действия равным единице (а тем более больше единицы) не существует.
И так, коэффициент полезного действия – это физическая величина, которая показывает долю, которую полезная работа составляет от всей произведенной работы. При помощи КПД оценивают эффективность устройства (механизма, системы), преобразующей или передающей энергию, совершающего работу.
Для увеличения КПД механизмов можно пытаться уменьшать трение в их осях, их массу. Если трением можно пренебречь, масса механизма существенно меньше, чем масса, например, груза, который поднимает механизм, то КПД получается немного меньше единицы. Тогда произведенная работа примерно равна полезной работе:
[A_papprox A_{poln}left(3right).]
Золотое правило механики
Необходимо помнить, что выигрыша в работе, используя простой механизм добиться нельзя.
Выразим каждую из работ в формуле (3) как произведение соответствующей силы на путь, пройденный под воздействием этой силы, тогда формулу (3) преобразуем к виду:
[F_1s_1approx F_2s_2left(4right).]
Выражение (4) показывает, что используя простой механизм, мы выигрываем в силе столько же, сколько проигрываем в пути. Данный закон называют «золотым правилом» механики. Это правило сформулировал в древней Греции Герон Александрийский.
Это правило не учитывает работу по преодолению сил трения, поэтому является приближенным.
КПД при передаче энергии
Коэффициент полезного действия можно определить как отношение полезной работы к затраченной на ее выполнение энергии ($Q$):
[eta =frac{A_p}{Q}cdot 100% left(5right).]
Для вычисления коэффициента полезного действия теплового двигателя применяют следующую формулу:
[eta =frac{Q_n-Q_{ch}}{Q_n}left(6right),]
где $Q_n$ – количество теплоты, полученное от нагревателя; $Q_{ch}$ – количество теплоты переданное холодильнику.
КПД идеальной тепловой машины, которая работает по циклу Карно равно:
[eta =frac{T_n-T_{ch}}{T_n}left(7right),]
где $T_n$ – температура нагревателя; $T_{ch}$ – температура холодильника.
Примеры задач на коэффициент полезного действия
Пример 1
Задание. Двигатель подъемного крана имеет мощность $N$. За отрезок времени равный $Delta t$ он поднял груз массой $m$ на высоту $h$. Каким является КПД крана?textit{}
Решение. Полезная работа в рассматриваемой задаче равна работе по подъему тела на высоту $h$ груза массы $m$, это работа по преодолению силы тяжести. Она равна:
[A_p=mgh left(1.1right).]
Полную работу, которая выполняется при поднятии груза, найдем, используя определение мощности:
[N=frac{A_{poln}}{Delta t}to A_{poln}=NDelta tleft(1.2right).]
Воспользуемся определением коэффициента полезного действия для его нахождения:
[eta =frac{A_p}{A_{poln}}cdot 100%left(1.3right).]
Формулу (1.3) преобразуем, используя выражения (1.1) и (1.2):
[eta =frac{mgh}{NDelta t}cdot 100%.]
Ответ. $eta =frac{mgh}{NDelta t}cdot 100%$
Пример 2
Задание. Идеальный газ выполняет цикл Карно, при этом КПД цикла равно $eta $. Какова работа в цикле сжатия газа при постоянной температуре? Работа газа при расширении равна $A_0$
Решение. Коэффициент полезного действия цикла определим как:
[eta =frac{A_p}{Q}left(2.1right).]
Рассмотрим цикл Карно, определим, в каких процессах тепло подводят (это будет $Q$).
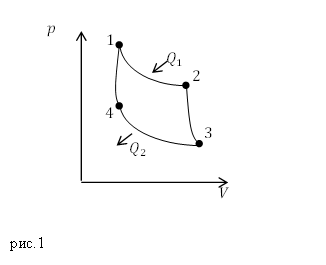
Так как цикл Карно состоит из двух изотерм и двух адиабат, можно сразу сказать, что в адиабатных процессах (процессы 2-3 и 4-1) теплообмена нет. В изотермическом процессе 1-2 тепло подводят (рис.1 $Q_1$), в изотермическом процессе 3-4 тепло отводят ($Q_2$). Получается, что в выражении (2.1) $Q=Q_1$. Мы знаем, что количество теплоты (первое начало термодинамики), подводимое системе при изотермическом процессе идет полностью на выполнение газом работы, значит:
[Q=Q_1=A_{12}left(2.2right).]
Газ совершает полезную работу, которую равна:
[A_p=Q_1-Q_2left(2.3right).]
Количество теплоты, которое отводят в изотермическом процессе 3-4 равно работе сжатия (работа отрицательна) (так как T=const, то $Q_2=-A_{34}$). В результате имеем:
[A_p=A_{12}+A_{34}left(2.4right).]
Преобразуем формулу (2.1) учитывая результаты (2.2) – (2.4):
[eta =frac{A_{12}+A_{34}}{A_{12}}to A_{12}eta =A_{12}+A_{34}to A_{34}=(eta -1)A_{12}left(2.4right).]
Так как по условию $A_{12}=A_0, $окончательно получаем:
[A_{34}=left(eta -1right)A_0.]
Ответ. $A_{34}=left(eta -1right)A_0$
Читать дальше: формула линейной скорости.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Формула КПД и как его вычислить для тепловой машины или механизма
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Эта аббревиатура вряд ли требует расшифровки: она неизвестна разве что тем, у кого в школе был «неуд» по физике.
Но для забывчивых всё же напомним, что под этим сокращением скрывается коэффициент полезного действия. Что же собой представляет эта величина?
Поговорим о ней простым и понятным языком – это может пригодиться даже в повседневной жизни.
Что такое КПД в физике и какова его формула
Для выполнения какой-либо работы необходимо затратить определённое количество энергии. Чтобы ехал велосипед, вы тратите мышечную энергию крутя педали. Чтобы двигался автомобиль, используется энергия сжигаемого топлива (бензина, солярки или газа).
Для горения лампочки требуется энергия электрического тока. Список можно продолжать до бесконечности. Точку можно поставить на солнечной энергии, благодаря которой существует жизнь на Земле.
Далее возникает логичный вопрос: а насколько эффективно расходуется эта энергия? В идеале хотелось бы, чтобы вся она шла «в дело», то есть использовалась только по прямому назначению. Но, к сожалению, на практике такого не бывает.
Затраченная энергия будет всегда больше, чем полезная работа, так как для достижения основной цели (движение, подъём груза, освещение, отопление и т.д.) часть энергии неизбежно уйдёт на неустранимые потери (преодоление силы трения, нагрев электропроводки, выброс продуктов горения в атмосферу и т.д.). Понятно, что чем меньше такие потери, тем лучше.
Критерием того, насколько эффективно работает система (устройство, агрегат, двигатель, машина и т.д.), служит показатель, получивший название коэффициент полезного действия (КПД).
Иными словами, коэффициент полезного действия показывает, какова доля полезной работы в общих энергозатратах. Математически КПД (чаще всего обозначается символом ŋ) определяется по формуле:
где A — полезная энергия (работа);
Q — энергия, затраченная на совершение полезной работы.
Понятно, что ŋ – величина безразмерная и не может быть больше единицы (да и равной единице она может быть чисто теоретически).
Выражается она в виде десятичной дроби либо в процентах (в последнем случае в формулу вставляется множитель х100).
Так, если КПД равен 0,9 (90%), то это значит, что 10% полезной мощности составили безвозвратные потери.
КПД теплового двигателя (машины)
Под тепловым двигателем понимается машина (агрегат), в которой энергия, высвобождающаяся в процессе расширения рабочего тела, преобразуется в механическую работу.
В качестве рабочего тела обычно выступает газ или газообразные вещества (пары бензина, водяной пар и т.п.).
Тепловые машины работают по замкнутому циклу. Это значит, что процесс преобразования энергии и сопутствующей теплопередачи периодически повторяется, а рабочее тело совершает круговой цикл, возвращаясь в исходное состояние.
К тепловым двигателям относятся:
- поршневые (паровые машины, двигатели внутреннего сгорания);
- роторные/турбинные (газовые или паровые турбины АЭС и ТЭЦ);
- реактивные (авиация);
- ракетные (космическая техника).
Используя положения предыдущего параграфа, КПД тепловой машины можно сформулировать как отношение полезной работы, совершённой за один цикл, к энергии (количеству теплоты), поступившей от энергоносителя (нагревателя).
Тогда формулу (1) можно преобразовать следующим образом:
где Q1 — количество теплоты, полученное двигателем от нагревателя за цикл;
Q2 — количество теплоты, отданное двигателем охладителю (холодильнику) за цикл;
Q1 – Q2 – количество теплоты, которое пошло на совершение работы.
Предположим, что Q1 = Q2, то есть на совершение полезной работы ничего не осталось – вся энергия «ушла в трубу». Тогда и КПД будет нулевым. Если же Q2 = 0, то есть вся энергия отдана полезной работе (потери отсутствуют), то коэффициент полезного действия будет равен 1.
Но это теория, на практике ни то ни другое нереалистично. В первом случае двигатель просто бесполезен, во втором – идеален, но недосягаем.
Значения КПД для различных типов тепловых двигателей приведены ниже.
Самым большим КПД обладают тепловые двигатели, работающие на основе цикла Карно (процесс назван в честь французского инженера, открывшего это явление в 1824 г.). В термодинамике оно характеризует круговой цикл, включающий в себя две стадии: расширение и сжатие рабочего тела.
Причём на протяжении обеих стадий попеременно проходят два процесса: изотермический (протекающий при постоянной температуре), и адиабатический (протекающий без теплообмена с окружающей средой). Максимальное значение КПД здесь достигается за счёт того, что тела с разной температурой не контактируют, а значит, без осуществления работы теплопередача исключается.
КПД механизма — по какой формуле вычисляют
Человек придумал разнообразные механизмы, с помощью которых можно поднимать тяжёлые грузы на определённую высоту. Так, для подъёма ведра с водой из колодца изобрели ворот, для подъёма автомобиля – домкрат. При помощи лебёдки и наклонной плоскости египтяне построили свои грандиозные пирамиды.
Пользуясь этими приспособлениями, человек редко вспоминает об их КПД. В качестве примера рассмотрим этот показатель для наклонной плоскости.
Принцип расчёта КПД остаётся неизменным: нужно найти отношение полезной работы ко всей затраченной энергии. То есть опять-таки используем общую формулу (1), сделав соответствующие преобразования.
Предположим, тело массой m нужно поднять (точнее затолкать или затянуть) на высоту h. При постоянной скорости подъёма полезная работа будет равна произведению силы тяжести (mg) на высоту (h).
Затраченная работа определяется произволением силы толчка или тяги F на длину наклонной плоскости L. Заметим, что толчковое (тяговое) усилие идёт на преодоление силы трения Fтр.
Таким образом, КПД такого простейшего механизма можно посчитать по формуле:
Несложный анализ показывает, что коэффициент полезного действия наклонной плоскости обратно пропорционален силе трения и длине аппарели. Последняя, в свою очередь, зависит от угла наклона: чем он больше, тем короче аппарель.
Как можно увеличить КПД
Современная наука постоянно ищет пути повышения коэффициента полезной модности двигателей и отдельных механизмов, внедряя новые технические решения и технологические инновации.
Чем выше будет КПД, тем экономичней будет двигатель, тем больше энергоресурсов удастся сберечь.
Тепловой двигатель
Из формулы (2) следует, что для увеличения КПД есть два пути: а) повышение температуры нагревателя; б) понижение температуры холодильника. Оба пути малоперспективны.
Нагреватель нельзя разогревать до бесконечности, так как любой материал имеет предел жаропрочности. Холодильником почти всегда служит окружающая среда, а внедрение в систему дополнительного теплообменника (например, баллона с жидким азотом) нецелесообразно: это резко увеличит вес, габариты и стоимость двигателя.
Установлено, что на коэффициент полезного действия не влияют характеристики рабочего тела. Что же остаётся?
А остаётся немало практически реализуемых способов, таких как уменьшение трения в механических узлах, минимизация теплопотерь путём достижения максимально полного сгорания топлива, создание обтекаемых форм для снижения лобового сопоставления (воздуха или воды) и т.д.
Учитывая, что в механике хорошим показателем на сегодняшний день считается КПД 30-40%, учёным и практикам есть над чем работать.
Наклонная плоскость
Из формулы (3) следует, что для повышения КПД нужно снижать силу трения (прежде всего, путём создания гладких соприкасающихся поверхностей) и увеличивать угол наклона. Но! При крутом уклоне силёнок для поднятия тяжёлого груза может и не хватить.
В заключение отметим, что в электротехнике ситуация с КПД обстоит гораздо лучше (показатель в 95% для электродвигателя – норма). На то есть объективные причины, объяснение которых выходит за рамки рассматриваемой темы.
Используя тот или иной механизм, мы совершаем работу, всегда превышающую ту, которая необходима для достижения поставленной цели. В соответствии с этим различают полную или затраченную работу Aз и полезную работу Aп. Если, например, наша цель — поднять груз массой m на высоту h, то полезная работа — это та, которая обусловлена лишь преодолением силы тяжести, действующей на груз. При равномерном подъеме груза, когда прикладываемая нами сила равна силе тяжести груза, эта работа может быть найдена следующим образом:
Aп = Fтh = mgh. (24.1)
Если же мы применяем для подъема груза блок или какой-либо другой механизм, то, кроме силы тяжести груза, нам приходится преодолевать еще и силу тяжести частей механизма, а также действующую в механизме силу трения. Например, используя подвижный блок, мы вынуждены будем совершать дополнительную работу по подъему самого блока с тросом и по преодолению силы трения в оси блока. Кроме того, выигрывая в силе, мы всегда проигрываем в пути (об этом подробнее будет рассказано ниже), что также влияет на работу. Все это приводит к тому, что затраченная нами работа оказывается больше полезной:
Aз > Aп
Полезная работа всегда составляет лишь некоторую часть полной работы, которую совершает человек, используя механизм.
Физическая величина, показывающая, какую долю составляет полезная работа от всей затраченной работы, называется коэффициентом полезного действия механизма.
Сокращенное обозначение коэффициента полезного действия — КПД.
Чтобы найти КПД механизма, надо полезную работу разделить на ту, которая была затрачена при использовании данного механизма.
Коэффициент полезного действия часто выражают в процентах и обозначают греческой буквой η (читается «эта»):
η =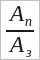
* 100% (24.2)
Поскольку числитель Aп в этой формуле всегда меньше знаменателя Aз, то КПД всегда оказывается меньше 1 (или 100%).
Конструируя механизмы, стремятся увеличить их КПД. Для этого уменьшают трение в осях механизмов и их массу. В тех случаях, когда трение ничтожно мало и используемые механизмы имеют массу, пренебрежимо малую по сравнению с массой поднимаемого груза, коэффициент полезного действия оказывается лишь немного меньше 1. В этом случае затраченную работу можно считать примерно равной полезной работе:
Aз ≈ Aп (24.3)
Следует помнить, что выигрыша в работе с помощью простого механизма получить нельзя.
Поскольку каждую из работ в равенстве (24.3) можно выразить в виде произведения соответствующей силы на пройденный путь, то это равенство можно переписать так:
F1s1 ≈ F2s2 (24.4)
Отсюда следует, что,
выигрывая с помощью механизма в силе, мы во столько же раз проигрываем в пути, и наоборот.
Этот закон называют «золотым правилом» механики. Его автором является древнегреческий ученый Герон Александрийский, живший в I в. н. э.
«Золотое правило» механики является приближенным законом, так как в нем не учитывается работа по преодолению трения и силы тяжести частей используемых приспособлений. Тем не менее оно бывает очень полезным при анализе работы любого простого механизма.
Так, например, благодаря этому правилу мы сразу можем сказать, что рабочему, изображенному на рисунке 47, при двукратном выигрыше в силе для подъема груза на 10 см придется опустить противоположный конец рычага на 20 см. То же самое будет и в случае, изображенном на рисунке 58. Когда рука человека, держащего веревку, опустится на 20 см, груз, прикрепленный к подвижному блоку, поднимется лишь на 10 см.
1. Почему затраченная при использовании механизмов работа оказывается все время больше полезной работы? 2. Что называют коэффициентом полезного действия механизма? 3. Может ли КПД механизма быть равным 1 (или 100%)? Почему? 4. Каким образом увеличивают КПД? 5. В чем заключается «золотое правило» механики? Кто его автор? 6. Приведите примеры проявления «золотого правила» механики при использовании различных простых механизмов.
