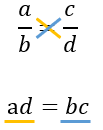Как найти коэффициент пропорции

Была ли эта статья полезной?

Прямая и обратная пропорциональность. Пропорция

ПРЯМАЯ ПРОПОРЦИОНАЛЬНОСТЬ:

Величины называются прямо пропорциональными, когда при увеличении одной из них в какое-то количество раз, в это же количество раз увеличивается и другая. Аналогично при уменьшении одной из величин в какое-то количество раз, вторая уменьшается во столько же.

Например:

(S = vt)

где S – расстояние, v – скорость, t – время.

Представим, что скорость у нас всегда равна 5 км/ч. Тогда будем изменять только расстояние и время:

– Если время равно 1 ч, то расстояние будет равным:

(S = 5 bullet 1 = 5)

– Увеличим время в 3 раза, получим, что время равно 3 ч, а расстояние:

(S = 5 bullet 3 = 15)

Видим, что расстояние тоже увеличилась в 3 раза.

Тогда мы говорим, что в выражении (S = vt) величины S и t – прямо пропорциональные.

Аналогично можем поступить с расстоянием и скоростью, если время будет постоянной величиной. Расстояние и время, расстояние и скорость – прямо пропорциональные между собой, потому что имеют один вид. Такая формула называется – формулой прямой пропорциональности:

(y = kx)

где (x, y) – переменные пропорциональные величины, а (k )– коэффициент пропорциональности

Если выразим k, получим, что:

(k = frac{y}{x})

В таком случае коэффициент k будет одинаков при любых значениях переменных, если они прямо пропорциональны.

ОБРАТНАЯ ПРОПОРЦИОНАЛЬНОСТЬ:

Величины называются обратно пропорциональными, если при увеличении одной из них в какое-то количество раз, вторая в это же количество раз уменьшается. И наоборот, если одна из величин в какое-то количество раз уменьшается, то вторая в это же количество раз увеличивается.

Например:

(S = vt)

где S – расстояние, v – скорость, t – время.

Представим, что расстояние у нас всегда равно 60 км. Тогда будем изменять только скорость и время. Выразим, например, скорость:

(v = frac{S}{t})

– Если время равно 1 ч, то скорость будет равна:

(v = frac{60}{1} = 60)

– Увеличим время в 2 раза, то время будет равно 2 ч, а скорость:

(v = frac{60}{2} = 30)

Видим, что при увеличении времени в 2 раза, скорость в 2 раза уменьшилась. Такие величины, как скорость и время в данном выражении, называются обратно пропорциональными.

Общая формула обратной пропорциональности выглядит так:

(y = frac{k}{x})

А коэффициент обратной пропорциональности находится перемножением обратно пропорциональных величин:

(k = x bullet y)

В таком случае коэффициент k будет одинаков при любых значениях переменных, если они обратно пропорциональны.

ПРОПОРЦИЯ:

Пропорция – это выражение, описывающее равенство отношений двух величин.

То есть, если (frac{a}{b} = k) и (frac{c}{d} = k), то пропорцией будет являться выражение:

(frac{a}{b} = frac{c}{d} = k)

где (k) – коэффициент пропорциональности данной пропорции. Обычно пропорцию записывают без коэффициента в виде:

(frac{a}{b} = frac{c}{d})

Числа a и d – крайние члены пропорции, а b и с – средние

Это легко запомнить, если записать пропорцию в строчку:

(a : b = c : d)

Сразу видно, что a и d находятся по краям, а b и с – посредине

Свойство пропорции:

Если помножить обе части пропорции на (text{bd}), то мы получим:

(frac{a}{b} bullet text{bd} = frac{c}{d} bullet bd)

(ad = cb)

Это и есть свойство пропорции – произведение крайних членов пропорции равно произведение средних членов. Еще такое равенство произведений называют умножением крест-накрест.

Чтобы проверить, является ли выражение пропорцией – используют свойство или коэффициент пропорции.

Пример №1:

Проверим, является ли пропорцией:

(frac{0,1}{0,175} = frac{4}{7})

Используем свойство пропорции, т.к. найти коэффициент пропорции будет затруднительно:

(0,1 bullet 7 = 4 bullet 0,175)

(0,7 = 0,7)

Значит данное выражение является пропорцией.

Пример №2:

Проверим, является ли пропорцией:

(frac{4}{0,2} = frac{95}{5})

Используем коэффициент пропорции. Он должен быть равен для двух дробей, если выражение является пропорцией:

(frac{4}{0,2} = frac{40}{2} = 20)

(frac{95}{5} = 19)

(20 neq 19)

Значит данное выражение НЕ является пропорцией.

Как найти коэффициент пропорциональности

Две взаимозависимые величины являются пропорциональными, если отношение их значений не изменяется. Это неизменное отношение величин называют коэффициентом пропорциональности.

Вам понадобится

• – калькулятор;
• – исходные данные.

Инструкция

Прежде чем найти коэффициент пропорциональности, познакомьтесь поближе со свойствами пропорций. Предположим, что дано четыре отличающихся друг от друга числа, каждое из которых не равно нулю (a, b, c и d), а отношение между этими числами имеет следующий вид: a : b = c : d. В этом случае a и d являются крайними членами пропорции, b и c – средними членами таковой.

Основное свойство, которым обладает пропорция: произведение ее крайних членов равно результату умножения средних членов данной пропорции. Другими словами, ad = bc.

Вместе с тем при перестановке средних (a : c = b : d) и крайних членов пропорции (d : b = c : a) отношение между данными величинами остается справедливым.

Две взаимозависимые величины пропорции соотносятся следующим образом: y = kx, при условии, что k не равен нулю. В этом равенстве k является коэффициентом пропорциональности, а y и x – пропорциональными переменными. О переменной у говорят, что она является пропорциональной переменной х.

При расчете коэффициента пропорциональности обратите внимание на тот факт, что таковая может быть прямой и обратной. Область определения прямой пропорциональности – множество всех чисел. Из отношения пропорциональных переменных следует, что у/х = k.

Чтобы выяснить, является ли данная пропорциональность прямой, сравните частные у/х для всех пар с соответствующими значениями переменных х и у, при условии, что х ≠ 0.

Если сравниваемые вами частные равны одному и тому же k (этот коэффициент пропорциональности не должен равняться нулю), то зависимость у от х является прямо пропорциональной.

Обратная пропорциональная зависимость проявляется в том, что с увеличением (либо уменьшением) одной величины в несколько раз, вторая пропорциональная переменная уменьшается (увеличивается) во столько же раз.

Обратите внимание

Помните: на ноль делить нельзя!

Полезный совет

Коэффициент пропорциональности показывает, сколько единиц пропорциональной переменной у приходится на единицу переменной х.

Источники:

• Пропорциональность

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Прямая и обратная пропорциональность

• Прямая пропорциональность
• Формула прямой пропорциональности
• Обратная пропорциональность
• Формула обратной пропорциональности

Пропорциональность — это зависимость одной величины от другой, при которой изменение одной величины приводит к изменению другой во столько же раз.

Пропорциональность величин может быть прямой и обратной.

Прямая пропорциональность

Прямая пропорциональность — это зависимость двух величин, при которой одна величина зависит от второй величины так, что их отношение остаётся неизменным. Такие величины называются прямо пропорциональными или просто пропорциональными.

Рассмотрим пример прямой пропорциональности на формуле пути:

s = vt,

где  s  — это путь,  v  — скорость, а  t  — время.

При равномерном движении путь пропорционален времени движения. Если взять скорость  v  равной  5 км/ч,  то пройденный путь  s  будет зависеть только от времени движения  t:

Скорость v = 5 км/ч
Время t (ч)	1	2	4	8	16
Путь s (км)	5	10	20	40	80

Из примера видно, что во сколько раз увеличивается время движения  t,  во столько же раз увеличивается пройденное расстояние  s.  В примере мы увеличивали время каждый раз в 2 раза, так как скорость не менялась, то и расстояние увеличивалось тоже в два раза.

В данном случае скорость  (v = 5 км/ч)  является коэффициентом прямой пропорциональности, то есть отношением пути ко времени, которое остаётся неизменным:

следовательно,

5	=	10	=	20	=	40	=	80	= 5.
1	2	4	8	16

Если время движения остаётся неизменным, то при равномерном движении расстояние будет пропорционально скорости:

Время  t = 2 ч
Скорость  v (км/ч)	5	15	45	90
Расстояние  s (км)	10	30	90	180

В этом примере коэффициентом прямой пропорциональности, то есть, отношением пути к скорости, которое остаётся неизменным, является время  (t = 2 ч):

следовательно,

10	=	30	=	90	=	180	= 2.
5	15	45	90

Из данных примеров следует, что две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз другая увеличивается (или уменьшается) во столько же раз.

Формула прямой пропорциональности

Формула прямой пропорциональности:

y = kx,

где  y  и  x  — это переменные величины, а  k  — это постоянная величина, называемая коэффициентом прямой пропорциональности.

Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных  y  и  x  равное одному и тому же числу.

Формула коэффициента прямой пропорциональности:

Обратная пропорциональность

Обратная пропорциональность — это зависимость двух величин, при которой увеличение одной величины приводит к пропорциональному уменьшению другой. Такие величины называются обратно пропорциональными.

Рассмотрим пример обратной пропорциональности на формуле пути:

s = vt,

где  s  — это путь,  v  — скорость, а  t  — время.

При прохождении одного и того же пути с разной скоростью движения время будет обратно пропорционально скорости. Если взять путь  s  равным  120 км,  то потраченное на преодоление этого пути время  t  будет зависеть только от скорости движения  v:

Путь  s = 120 км
Скорость  v (км/ч)	10	20	40	80
Время  t (ч)	12	6	3	1,5

Из примера видно, что во сколько раз увеличивается скорость движения  v,  во столько же раз уменьшается время  t.  В примере мы увеличивали скорость движения каждый раз в 2 раза, а так как расстояние, которое нужно преодолеть, не менялось, то количество времени на преодоление данного расстояния сокращалось тоже в два раза.

В данном случае путь (s = 120 км) является коэффициентом обратной пропорциональности, то есть произведением скорости на время:

s = vt,

следовательно,

10 · 12 = 20 · 6 = 40 · 3 = 80 · 1,5 = 120.

Из данного примера следует, что две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.

Формула обратной пропорциональности

Формула обратной пропорциональности:

где  y  и  x  — это переменные величины, а  k  — это постоянная величина, называемая коэффициентом обратной пропорциональности.

Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных  y  и  x,  равное одному и тому же числу.

Формула коэффициента обратной пропорциональности:

xy = k.

Пропорциональными называются две взаимно зависимые величины, если отношение их значений остаётся неизменным^[1].

Равенство между отношениями двух или нескольких пар чисел или величин в математике называется пропорцией.

Для обозначения пропорциональных величин используется символ (Юникод: U+223C ∼ tilde operator)^[2] подобно тому как используется знак равенства. Например,

означает, что величина постоянна. В англоязычной литературе обычно используется знак (Юникод: U+221D ∝ proportional to):

Пример[править | править код]

Масса керосина пропорциональна его объёму: 2 л керосина имеют массу 1,6 кг, 5 л имеют массу 4 кг, 7 л имеют массу 5,6 кг. Отношение массы к объёму при одинаковых условиях всегда будет равно плотности:

Коэффициент пропорциональности[править | править код]

Неизменное отношение пропорциональных величин называется коэффициентом пропорциональности. Коэффициент пропорциональности показывает, сколько единиц одной величины приходится на единицу другой^[1].

Прямо пропорциональные величины[править | править код]

Две величины называются прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз, другая увеличивается (уменьшается) во столько же раз.
Пример: такие величины, как скорость объекта и пройденное им расстояние являются прямо пропорциональными.

Обратная пропорциональность[править | править код]

Обра́тная пропорциона́льность — это функциональная зависимость, при которой увеличение независимой величины (аргумента) вызывает пропорциональное уменьшение зависимой величины (функции).

Свойства функции:

См. также[править | править код]

• Гипербола
• Линейная функция
• Пропорция
• Подобие
• Корреляция

Источники[править | править код]