Почему медь проводит электричество лучше, чем вода? Прочитав эту статью, вы больше не будете задавать себе больше этот вопрос. Далее мы обсудим электропроводность и рассмотрим формулы, которые описывают это понятие. Наконец, вы можете проверить свои знания на двух примерах.
Простое объяснение.
Электропроводность — это физическая величина, которая описывает насколько хорошо определенный материал проводит электричество.
Формулы
Существует три различных формульных обозначения удельной электропроводности σ (греч. сигма), k (каппа) и γ (гамма). В дальнейшем мы будем использовать σ. Формула электропроводности, также называемой удельной электропроводностью, описывается формулой:
σ = 1 / ρ .
Здесь ρ называется удельным сопротивлением. Вы можете рассчитать электрическое сопротивление R проводника с учетом его параметров следующим образом: R = ( ρ * l ) / S .
Таким образом, сопротивление R равно удельному сопротивлению ρ , умноженному на длину проводника l, деленному на площадь поперечного сечения S. Если теперь вы хотите выразить эту формулу через удельную электропроводность σ = 1 / ρ , полезно знать, что электрическая проводимость G проводника выражается следующим образом: G = 1 / R .
Если в верхнюю формулу подставить удельную электропроводность σ и электрическую проводимость G, то получится следующее: 1 / G = ( 1 / σ ) * ( l / S ) .
Путем дальнейшего преобразования можно получить выражение: G = σ * S / l .
С помощью электропроводности можно также описать важную зависимость между плотностью электрического тока и напряженностью электрического поля с помощью выражения: J = σ * E .
Единица измерения
Единицей удельной электропроводности σ в СИ является: [ σ ] = 1 См/м ( Сименс на метр ).
Эти единицы определяются по формуле G = σ * S / l . Если решить эту формулу в соответствии с σ, то получим σ = G * l / S .
Единица измерения электрической проводимости G задается как: [ G ] = 1 / σ = 1 См ( Сименс, международное обозначение: S ).
Если теперь ввести в формулу все единицы измерения, то получится:
[ σ ] = 1 См * 1 м / м2 = 1 См / м .
Вы также будете чаще использовать единицы измерения См / см , м / Ом * мм2 или См * м / мм2 . Вы можете преобразовать отдельные измеряемые переменные так: См / см = См / 10-2 м и так: м / Ом * мм2 = См * м / мм2 = См * м / 10-3 м * 10-3 м = 106 См / м .
Электропроводность металлов
В зависимости от количества свободно перемещающихся электронов один материал проводит лучше, чем другой. В принципе, любой материал является проводящим, но в изоляторах, например, протекающий электрический ток ничтожно мал, поэтому здесь мы говорим о непроводниках.
В металлических связях валентные электроны, т.е. крайние электроны в атоме, свободно подвижны. Они расположены в так называемой полосе проводимости. Находящиеся там электроны образуют так называемый электронный газ. Соответственно, металлы являются сравнительно хорошими проводниками. Если теперь подать электрическое напряжение на металл, валентные электроны медленно движутся к положительному полюсу, потому что он их притягивает.
На рисунке 1 видно, что некоторые электроны не могут быть притянуты непосредственно к положительному полюсу, потому что на пути стоит, так сказать, твердое атомное ядро. Там они замедляются и в некоторой степени отклоняются. Именно поэтому электроны не могут ускоряться в металле бесконечно, и именно так возникает удельное сопротивление или электропроводность.
Теперь вы также можете измерить удельную электропроводность в металле с помощью следующей формулы: σ = ( n * e2 * τ ) / m .
В этой формуле n означает число электронов, e — заряд электрона, m — массу электрона, а τ — среднее время полета электрона между двумя столкновениями.
Таблица удельной электропроводности
Для большинства веществ уже известны значения удельной электропроводности. Некоторые из них вы можете найти в следующей таблице ниже. Все значения в этой таблице действительны для комнатной температуры, т.е. 25°C.
| Вещество | Удельная электропроводность в См / м |
| Серебро | 62 · 106 |
| Медь | 58 · 106 |
| Золото | 45,2 · 106 |
| Алюминий | 37,7 · 106 |
| Вольфрам | 19 · 106 |
| Латунь | 15,5 · 106 |
| Железо | 9,93 · 106 |
| Нержавеющая сталь (WNr. 1,4301) | 1,36 · 106 |
| Германий (легирование <10-9) | 2 |
| Кремний (легирование <10-12) | 0,5 · 10-3 |
| Морская вода | примерно 5 |
| Водопроводная вода | примерно 0,05 |
| Дистиллированная вода | 5 · 10-6 |
| Изолятор | обычно <10-8 |
Удельная электропроводность сильно зависит от температуры, поэтому указанные значения применимы только при 25°C. При повышении температуры вибрация решетки в веществе становится выше. Это нарушает поток электронов, и поэтому электропроводность уменьшается с ростом температуры.
Из таблицы видно, что медь имеет вторую по величине электропроводность, поэтому медные кабели очень часто используются в электротехнике. Серебро обладает еще более высокой проводимостью, но стоит намного дороже меди.
Интересно также сравнение между морской и дистиллированной водой. Здесь электропроводность возникает благодаря растворенным в воде ионам. Морская вода имеет очень высокую долю соли, которая растворяется в воде. Эти ионы передают электрический ток. В дистиллированной воде нет растворенных ионов, поэтому в ней практически не может протекать электрический ток. Поэтому электропроводность морской воды намного выше, чем дистиллированной.
Примеры задач
Для более детального рассмотрения приведём два примера расчетов.
Задача 1.
В первой задаче представьте, что у вас есть провод длиной 2 м с поперечным сечением 0,5 мм2. Электрическое сопротивление провода при комнатной температуре составляет 106 мОм. Из какого материала изготовлен провод?
Решение.
Решение данной задачи можно найти с помощью формулы: R = ( 1 / σ ) * ( l / S ). Из этой формулы найдём σ = l / ( S * R ) .
Теперь вы можете вставить заданные значения, убедившись, что вы перевели сечение в м2.
σ = l / ( S * R ) = 2 м / ( ( 0,5 * 10-6 м2 ) * ( 1 / 106 * 10-3 Ом ) ) = 37, 7 * 106 См / м .
Наконец, вы ищите в таблице, какой материал имеет удельную электропроводность σ = 37, 7 * 106 См / м и приходите к выводу, что провод сделан из алюминия.
Задача 2.
В задаче 2 вам дано только удельное сопротивление образца с 735 * 10-9 Ом * м. Из какого материла изготовлен образец?
Решение.
Вы можете использовать формулу σ = 1 / ρ для расчёта удельной электропроводности. После подстановки значений в эту формулу вы получите: σ = 1 / ρ = 1 / 735 * 10-9 Ом * м = 1,36 * 106 См / м .
Если вы снова заглянете в таблицу, то обнаружите, что образец должен быть изготовлен из нержавеющей стали.
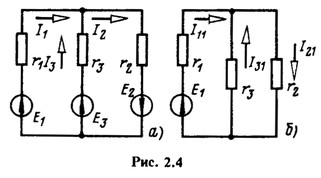Входные и взаимные проводимости можно рассчитать или определить экспериментально. Определение входных и взаимных проводимостей расчетом покажем на примере схемы рис. 2.4, а.
Приравняем ЭДС E2 и E3 нулю (рис. 2.4,6), при этом токи в ветвях
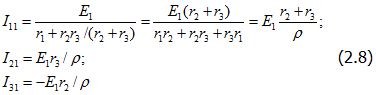
где 
Из (2.8) определим:
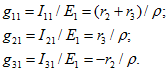
Аналогично рассчитываются входные и взаимные проводимости второй и третьей ветвей:
Если взаимные проводимости найдены, то легко определить токи во всех ветвях при любых значениях ЭДС. Так, для схемы рис. 2.4, а
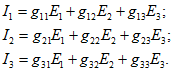
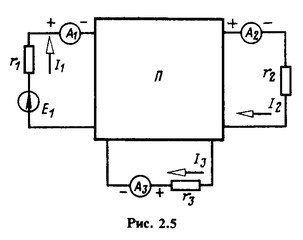Экспериментальное определение входных и взаимных проводимостей и сопротивлений рассмотрим на примере произвольной цепи, из которой предварительно исключены все источники ЭДС и источники тока (рис. 2.5). Три ветви этой цепи выделены, а остальная часть условно показана в виде прямоугольника. В каждую ветвь включен амперметр. Чтобы определить входную проводимость первой ветви g31 и взаимные проводимости второй и первой g21 и третьей и первой g31 ветвей, надо включить в первую ветвь источник ЭДС Е1. Измерив вольтметром напряжение U1 = E1 на выводах источника ЭДС и амперметрами токи I1, I2 и I3 в трех ветвях, нетрудно вычислить входную и взаимные проводимости ветвей по формулам 
Аналогично определяются входные и взаимные проводимости других ветвей.
Пример 2.2.
Определить входные и взаимные проводимости ветвей схемы рис. 2.6, а, если 
Решение.
Для определения входной проводимости 
и взаимных проводимостей между первой и остальными ветвями положим Е3 = E5 = 0 (рис. 2.6, б). Затем можно задаться E1 и найти все токи. Однако для данной схемы проще задать ток в ветви с сопротивлением r4 или r5, например I51 = = 1 А, и найти необходимую ЭДС E1 и токи в остальных ветвях.
Так как r4 = r5, то I41 = I51 и I31 = — (I51 + I41) = — 2 А. На выводах элемента с сопротивлением r2 напряжение 
; токи 
и ЭДС, при действии которой ток I51 = 1 А, а остальные токи равны найденным значениям, 
.
Входная проводимость первой ветви 
.
Взаимные проводимости между первой и остальными ветвями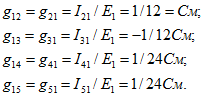
Аналогично определяются входные и взаимные проводимости остальных ветвей:
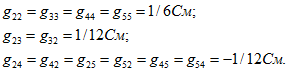
При определении проводимостей 
следует включить ЭДС Е2 в ветвь 2, направленную так же, как и ток I2, а при определении 
ЭДС E4 в ветвь 4.
Пример 2.3.
В условиях предыдущей задачи (см. пример 2.2) определить токи во всех ветвях, если ЭДС Е1 = 24 В, E3 = 12 В и E5 = 24 В.
Решение.
Зная входные и взаимные проводимости ветвей, легко определить в них токи, пользуясь принципом наложения:
и т.д.
Если кроме источников ЭДС схема содержит и источники тока, то по принципу наложения к частичным токам, обусловленным действием источников ЭДС, добавятся частичные токи, обусловленные каждым из источников тока:
При определении входных и взаимных проводимостей все токи следует считать равными нулю (источники тока не действуют), а ветви с источниками тока разорвать (идеальные источники тока). При расчете коэффициентов передачи 
следует считать все ЭДС 
.
Пример 2.4.
Составить зависимость 
при r1 = r2 = r3 = 2 Ом в схеме рис. 2.7, а.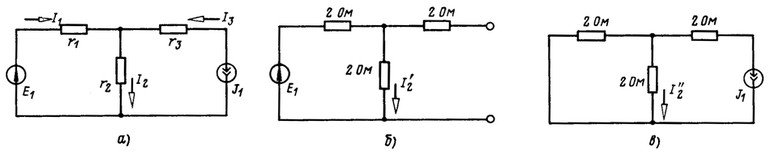
Решение.
Ток 
Проводимость 
определяется расчетом режима в схеме рис. 2.7, б. Ток 
. Коэффициент 
определяется расчетом режима в схеме рис. 2.7, в. Ток 
| Классическая электродинамика |
|---|
 |
| Электричество · Магнетизм |
|
Электростатика Закон Кулона |
|
Магнитостатика Закон Био — Савара — Лапласа |
|
Электродинамика Векторный потенциал |
|
Электрическая цепь Закон Ома |
|
Ковариантная формулировка Тензор электромагнитного поля |
| См. также: Портал:Физика |
Электропрово́дность (электри́ческая проводи́мость, проводимость) — способность тела (среды) проводить электрический ток, свойство тела или среды, определяющее возникновение в них электрического тока под воздействием электрического поля. Также физическая величина, характеризующая эту способность и обратная электрическому сопротивлению[1].
В Международной системе единиц (СИ) единицей измерения электрической проводимости является сименс (русское обозначение: См; международное: S), определяемый как 1 См = 1 Ом−1, то есть как электрическая проводимость участка электрической цепи сопротивлением 1 Ом[2].
Также термин электропроводность (электропроводность среды, вещества) применяется для обозначения удельной электропроводности (см. ниже).
Под электропроводностью подразумевается способность проводить прежде всего постоянный ток (под воздействием постоянного поля), в отличие от способности диэлектриков откликаться на переменное электрическое поле колебаниями связанных зарядов (переменной поляризацией), создающими переменный ток. Ток проводимости практически не зависит от частоты приложенного поля (до определённых пределов, в области низких частот).
Электропроводность среды (вещества) связана со способностью заряженных частиц (электронов, ионов), содержащихся в этой среде, достаточно свободно перемещаться в ней. Величина электропроводности и её механизм зависят от природы (строения) данного вещества, его химического состава, агрегатного состояния, а также от физических условий, прежде всего таких, как температура.
Удельная электропроводность[править | править код]
Удельной электропроводностью (удельной проводимостью) называют меру способности вещества проводить электрический ток. Согласно закону Ома в линейном изотропном веществе удельная проводимость является коэффициентом пропорциональности между плотностью возникающего тока и величиной электрического поля в среде:
- где
— удельная проводимость, - — вектор плотности тока,
- — вектор напряжённости электрического поля.
- Электрическая проводимость G однородного проводника длиной L с постоянным поперечным сечением площадью S может быть выражена через удельную проводимость вещества, из которого сделан проводник:
- В системе СИ удельная электропроводность измеряется в сименсах на метр (См/м) или в Ом−1·м−1. В СГСЭ единицей удельной электропроводности является обратная секунда (с−1).
В неоднородной среде σ может зависеть (и в общем случае зависит) от координат, то есть не совпадает в различных точках проводника.
Удельная проводимость анизотропных (в отличие от изотропных) сред является, вообще говоря, не скаляром, а тензором (симметричным тензором ранга 2), и умножение на него сводится к матричному умножению:
при этом векторы плотности тока и напряжённости поля в общем случае не коллинеарны.
Для любой линейной среды можно выбрать локально (а если среда однородная, то и глобально) т. н. собственный базис — ортогональную систему декартовых координат, в которых матрица 
становится диагональной, то есть приобретает вид, при котором из девяти компонент отличными от нуля являются лишь три: 
, 
и 
. В этом случае, обозначив 
как 
, вместо предыдущей формулы получаем более простую формулу:
Величины называют главными значениями тензора удельной проводимости. В общем случае приведённое соотношение выполняется только в одной системе координат[3].
Величина, обратная удельной проводимости, называется удельным сопротивлением.
Вообще говоря, линейное соотношение, написанное выше (как скалярное, так и тензорное), верно в лучшем случае[4] приближённо, причём приближение это хорошо только для сравнительно малых величин E. Впрочем, и при таких величинах E, когда отклонения от линейности заметны, удельная электропроводность может сохранять свою роль в качестве коэффициента при линейном члене разложения, тогда как другие, старшие, члены разложения дадут поправки, обеспечивающие хорошую точность.
Также в случае нелинейной зависимости J от E (то есть в общем случае) может явно вводиться дифференциальная удельная электропроводность, зависящая от E:
- (для анизотропных сред: ).
Электропроводность и носители тока[править | править код]
Электропроводность всех веществ связана с наличием в них носителей тока (носителей заряда) — подвижных заряженных частиц (электронов, ионов) или квазичастиц (например, дырок в полупроводнике), способных перемещаться в данном веществе на большое расстояние. Упрощённо можно сказать, что такая частица или квазичастица должна быть способна пройти в данном веществе неограниченно большое, по крайней мере макроскопическое, расстояние, хотя в некоторых частных случаях носители могут меняться, рождаясь и уничтожаясь, и переносить ток, сменяя друг друга (возможно, и через очень небольшое расстояние)[5].
Поскольку плотность тока определяется для одного типа носителей формулой:
- где — заряд одного носителя,
- — концентрация носителей,
- — средняя скорость их движения,
или 
для более чем одного вида носителей, нумеруемых индексом 
принимающим значение от 1 до количества типов носителей, у каждого из которых может быть свой заряд (возможно отличающийся величиной и знаком), своя концентрация, своя средняя скорость движения (суммирование в этой формуле подразумевается по всем имеющимся типам носителей), то, учитывая, что (установившаяся) средняя скорость каждого типа частиц при движении в конкретном веществе (среде) пропорциональна приложенному электрическому полю (в том случае, когда движение вызвано именно этим полем, что мы здесь и рассматриваем):
- где — коэффициент пропорциональности, называемый подвижностью и зависящий от вида носителя тока в данной конкретной среде[6].
Отсюда следует, что для электропроводности справедливо выражение:
или:
- — для более чем одного вида носителей.
Механизмы электропроводности и электропроводность различных классов веществ[править | править код]
Электронная проводимость[править | править код]
Подробнее по теме «Электронная проводимость» см. Электронный газ
Дырочная проводимость[править | править код]
Ионная проводимость[править | править код]
Подробнее по теме «Ионная проводимость» см. Электролит
Ионной проводимостью обладают газы, некоторые твердые соединения (ионные кристаллы и стёкла), расплавленные индивидуальные соли и растворы соединений в воде, неводных растворителях и расплавах. Значения удельной проводимости проводников второго рода разных классов колеблются в очень широких пределах.
Электропроводность металлов[править | править код]
Ещё до открытия электронов было обнаружено, что протекание тока в металлах, в отличие от тока в жидких электролитах, не обусловлено переносом вещества металла. Эксперимент, который выполнил немецкий физик Карл Виктор Эдуард Рикке (Riecke Carl Viktor Eduard) в 1901 году, состоял в том, что через контакты различных металлов, — двух медных и одного алюминиевого цилиндра с тщательно отшлифованными торцами, поставленными один на другой, в течение года пропускался постоянный электрический ток. Затем исследовался состав материала вблизи контактов. Оказалось, что переноса вещества металла через границу не происходит и вещество по разные стороны границы раздела имеет тот же состав, что и до пропускания тока. Таким образом было показано, что перенос электрического тока осуществляется не атомами и молекулами металлов, а другими частицами. Однако эти опыты не дали ответа на вопрос о природе носителей заряда в металлах[7].
Связь с коэффициентом теплопроводности[править | править код]
Закон Видемана — Франца, выполняющийся для металлов при высоких температурах, устанавливает однозначную связь удельной электрической проводимости 
с коэффициентом теплопроводности K:
- где k — постоянная Больцмана,
- e — элементарный заряд.
Эта связь основана на том факте, что как электропроводность, так и теплопроводность в металлах обусловлены движением свободных электронов проводимости.
Электропроводность растворов[править | править код]
Скорость движения ионов зависит от напряженности электрического поля, температуры, вязкости раствора, радиуса и заряда иона и межионного взаимодействия.
У растворов сильных электролитов наблюдается характер концентрационной зависимости электрической проводимости объясняется действием двух взаимно противоположных эффектов. С одной стороны, с ростом разбавления уменьшается число ионов в единице объёма раствора. С другой стороны, возрастает их скорость за счет ослабления торможения ионами противоположного знака.
Для растворов слабых электролитов наблюдается характер концентрационной зависимости электрической проводимости можно объяснить тем, что рост разбавления ведёт, с одной стороны, к уменьшению концентрации молекул электролита. В то же время возрастает число ионов за счёт роста степени ионизации.
В отличие от металлов (проводники 1-го рода) электрическая проводимость растворов как слабых, так и сильных электролитов (проводники 2-го рода) при повышении температуры возрастает. Этот факт можно объяснить увеличением подвижности в результате понижения вязкости раствора и ослаблением межъионного взаимодействия
Электрофоретический эффект — возникновение торможения носителей вследствие того, что ионы противоположного знака под действием электрического поля двигаются в направлении, обратном направлению движения рассматриваемого иона
Релаксационный эффект — торможение носителей в связи с тем, что ионы при движении расположены асимметрично по отношению к их ионным атмосферам. Накопление зарядов противоположного знака в пространстве за ионом приводит к торможению его движения.
При больших напряжениях электрического поля скорость движения ионов настолько велика, что ионная атмосфера не успевает образоваться. В результате электрофоретическое и релаксационное торможение не проявляется.
Удельная электропроводность некоторых веществ (таблица)[править | править код]
Удельная проводимость приведена при температуре +20 °C[8]:
| Вещество | См/м | Вещество | См/м | Вещество | См/м | Вещество | См/м | Вещество | См/м |
|---|---|---|---|---|---|---|---|---|---|
| серебро | 62 500 000 | молибден | 18 500 000 | олово | 8 330 000 | ртуть | 1 040 000 | мрамор | 10−8 |
| медь | 59 500 000[9] | вольфрам | 18 200 000 | сталь литая | 7 690 000 | нихром | 893 000 | стекло | 10−11 |
| золото | 45 500 000 | цинк | 16 900 000 | свинец | 4 810 000 | графит | 125 000 | фарфор | 10−14 |
| алюминий | 38 000 000[9] | никель | 11 500 000 | нейзильбер | 3 030 000 | вода морская | 4 | кварцевое стекло | 10−16 |
| магний | 22 700 000 | железо чистое | 10 000 000 | константан | 2 000 000 | земля влажная | 10−2 | янтарь | 10−18 |
| иридий | 21 100 000 | платина | 9 350 000 | манганин | 2 330 000 | вода дистилл. | 10−4 |
См. также[править | править код]
- Адмиттанс
- Зонная теория
- Эффект Холла
- Сверхпроводимость
- Отрицательная абсолютная проводимость
Примечания[править | править код]
- ↑ Электропроводность (физич.) // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978. (см. копию на bse.sci-lib.com/article126142.html)
- ↑ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 105. — 240 с. — ISBN 5-7050-0118-5.
- ↑ В случае совпадения двух из трех собственных чисел , есть произвол в выборе такой системы координат (собственных осей тензора ), а именно довольно очевидно, что можно произвольно повернуть её относительно оси с отличающимся собственным числом, и выражение не изменится. Однако это не слишком меняет картину. В случае же совпадения всех трех собственных чисел мы имеем дело с изотропной проводимостью, и, как легко видеть, умножение на такой тензор сводится к умножению на скаляр.
- ↑ Для многих сред линейное приближение является достаточно хорошим или даже очень хорошим для достаточно широкого диапазона величин электрического поля, однако существуют среды, для которых это совсем не так уже при весьма малых E.
- ↑ Впрочем, если речь идет об однородном веществе, как правило, если что-то подобное имеет место, проще описать коллективное возмущение как квазичастицу.
- ↑ Здесь мы для простоты не рассматриваем анизотропных кристаллов с тензорной подвижностью, считая μ скаляром; впрочем, при желании можно считать его тензором, понимая произведение в матричном смысле.
- ↑ Элементарный учебник физики / Под ред. Г. С. Ландсберга. — М.: Наука, 1985. — Т. II. Электричество и магнетизм. — С. 194. — 479 с.
- ↑ Кухлинг Х. Справочник по физике. Пер. с нем., М.: Мир, 1982, стр. 475 (табл. 39); значения удельной проводимости вычислены из удельного сопротивления и округлены до 3 значащих цифр.
- ↑ 1 2 Герасимов В. Г., Грудинский П. Г., Жуков Л. А. Электротехнический справочник. В 3-х томах. Т.1 Общие вопросы. Электротехнические материалы / Под общей редакцией профессоров МЭИ. — 6-е изд.. — Москва: Энергия, 1980. — С. 353. — 520 с. — ISBN ББК 31.2.
Литература[править | править код]
- Матвеев А. Н. Электричество и магнетизм. (Первое изд. М.: Высшая школа, 1983. 463 с.)
- Ершов Ю. А., Попков В. А., Берлянд А. С. и др. Общая химия. Биофизическая химия. Химия биогенных элементов. — Изд. 8-е, стереотипное. — М.: Высшая школа, 2010. — 559 с. — ISBN 978-5-06-006180-2.
- Блатт Ф. Физика электронной проводимости в твердых телах. — М.: Мир, 1971. — 470 с.
Коэффициент – электрическая проводимость
Cтраница 1
Коэффициент электрической проводимости / Л вносит поправку на межионное взаимодействие в растворах сильных электролитов при прохождении тока. Он уменьшается с повышением концентрации и приближается к Л0 при бесконечном разведении.
[1]
А) / ( к А) называется коэффициентом электрической проводимости.
[3]
При более высоких концентрациях необходимо учитывать кажущуюся степень диссоциации или коэффициент электрической проводимости.
[4]
Величины е, ье последовательно означают электрическую и магнитную проницаемости, а а является коэффициентом электрической проводимости. Постоянные е, ле имеют те же значения, что и в случае, когда тело находится в состоянии покоя. Обозначения divrot и производная по времени относятся к системе со штрихами.
[5]
Для сильных электролитов отношение эквивалентной электрической проводимости при данном разбавлении к эквивалентной проводимости при бесконечном разбавлении дает уже не а, а / л – коэффициент электрической проводимости.
[6]
Кинетические коэффициенты у и х называются соответственно коэффициентом электрической проводимости ( удельной электрической проводимостью) и коэффициентом теплопроводности.
[7]
Применительно к сильным электролитам отношение А / А, , согласно уравнению (10.18), равно коэффициенту электрической проводимости f) и характеризует силу межионного взаимодействия.
[8]
Находят Л как отрезок на ординате. Она отличается от зависимости a. Степень диссоциации изменяется с концентрацией более сильно, чем коэффициент электрической проводимости.
[10]
Принцип его работы основан на измерении сопротивления нагретой платиновой или вольфрамовой нити. Количество теплоты, отводимое от нагретой нити при прочих постоянных условиях, зависит от теплопроводности газа, а теплопроводность смеси газов зависит от ее состава. В последнее время металлические нити успешно заменяются термисторами, имеющими более высокий, чем у металлов, коэффициент электрической проводимости.
[11]
Страницы:
1
4.1. Теоретическая часть
Константа
и степень диссоциации слабого электролита
К
равновесию,
которое устанавливается в растворе
слабого электролита
между
ионами и молекулами можно применить
законы химического
равновесия
и записать выражение константы равновесия.
Например, для
диссоциации
типичного слабого электролита — уксусной
кислоты
CH3COOH
H+
+ CH3COO–
константа
равновесия КС,
выраженная через молярные концентрации
реагентов (
),
имеет вид:
.(4.1)
Константа
равновесия диссоциации слабого
электролита называется
константой
диссоциации (К).
Величина К
зависит от природы электролита и
растворителя,
а также от температуры. Термодинамическая
константа
диссоциации,
выраженная через активность ионов и
молекул, не зависит от
концентрации.
Вычисленная практическая константа
диссоциации (К)
может
изменяться
с изменением концентрации. Поэтому для
сравнения значения практической
константы диссоциации
со
справочным при заданной температуре,
рассчитанные для разных
концентраций,
усредняются.
Константа
диссоциации характеризует способность
данного электролита
распадаться
на ионы в растворе. Чем больше К,
тем
полнее диссоциирует
электролит
в растворе.
Получим
в наиболее общем виде выражение для
константы диссоциации
слабого
электролита (
)
через его начальную концентрацию (С)
и
степень
диссоциации (α), исходя из следующей
схемы диссоциации,
соответствующей
суммарному равновесию:
. (4.2)
Константа
диссоциации этого суммарного процесса
равна:
,(4.3)
где
— равновесные активности компонентов.
Выразим их через соответствующие
коэффициенты активности (
):
;
;
.
(4.4)
Для
разбавленных растворов 
,
,
тогда
,
где
— равновесные концентрации компонентов.
В этом случае для начальной молярной
концентрации электролитаСм
(моль/л) равновесные концентрации
компонентов с учетом степени диссоциации
будут равны:
;
;
.
(4.5)
С
учетом вышеизложенного из (4.3) получим:
.(4.6)
Приведем
примеры.
CH3COOH
H+
+ CH3COO–
;
.
(4.7)
Это
уравнение для константы диссоциации
выражает закон разведения Оствальда.
Слабые
электролиты, для которых ν
> 2, в меньшей степени отвечают
условию
(4.4) вследствие возрастания сил ионного
взаимодействия, кроме того,
в
этих случаях процесс диссоциации может
протекать в несколько стадий,
каждая
из которых имеет свое значение К.
Например,
угольная кислота диссоциирует в две
ступени:
.
Константа
диссоциации (равновесия)
по
1-ой ступени –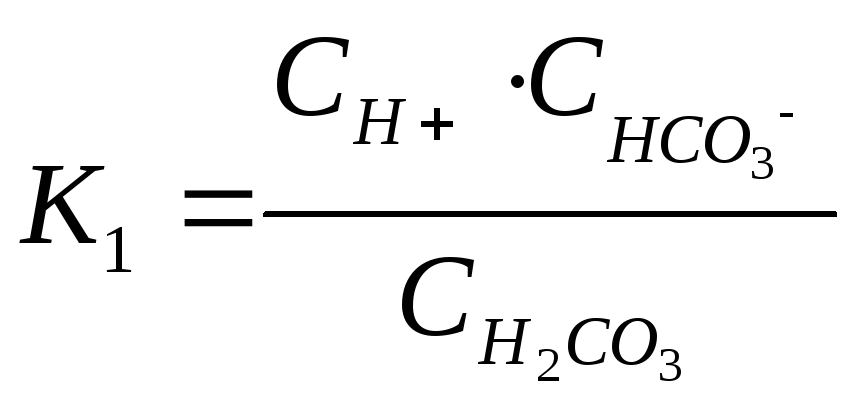 
,
по
2-ой ступени –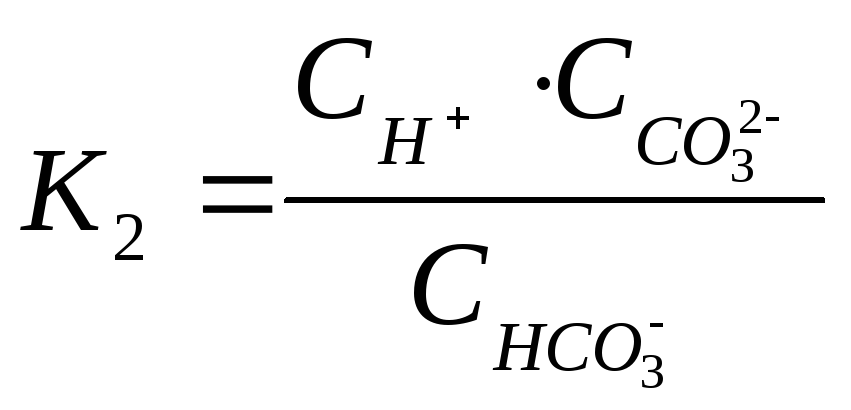 
.
Суммарному
равновесию соответствует константа
–
диссоциации:
.
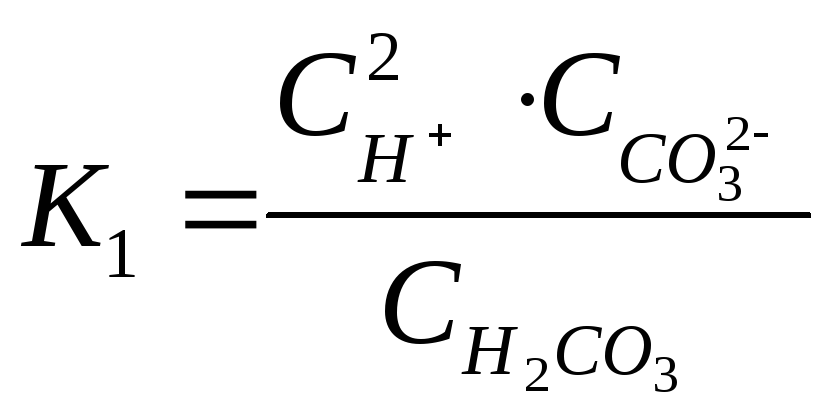При
этом выполняется соотношение 
и, как правило,
.
Из
уравнения (4.5) константа диссоциации
для этого типа электролитов рассчитывается
по уравнению:
;
;
.
(4.8)
Расчет
константы диссоциации электролитов,
для которых ν > 3, из
кондуктометрических
измерений, по причинам, изложенным выше,
приведет
к
значительным ошибкам, поэтому проводить
его в этом случае, на наш взгляд,
нецелесообразно.
Решая
уравнение (4.7) относительно α,
получим:
. (4.9)
Уравнение
(4.8) позволяет рассчитывать степень
диссоциации (α) по
известному
значению константы диссоциации слабого
электролита для
различных
концентраций. Для малых значений α,
когда
,
уравнение (4.7) принимает вид
,
или
.
(4.10)
То
есть степень диссоциации уменьшается
при возрастании концентрации
раствора
слабого электролита. Объясняется это
тем, что разбавление раствора
не
препятствует прямому процессу в
равновесии (распаду молекул), но
затрудняет
обратный процесс образования молекул
из ионов при их
столкновении.
Значения констант диссоциации электролитов
приводятся в
справочниках.
Например, для уксусной кислоты при 298 К
.
Для
процесса диссоциации воды
.
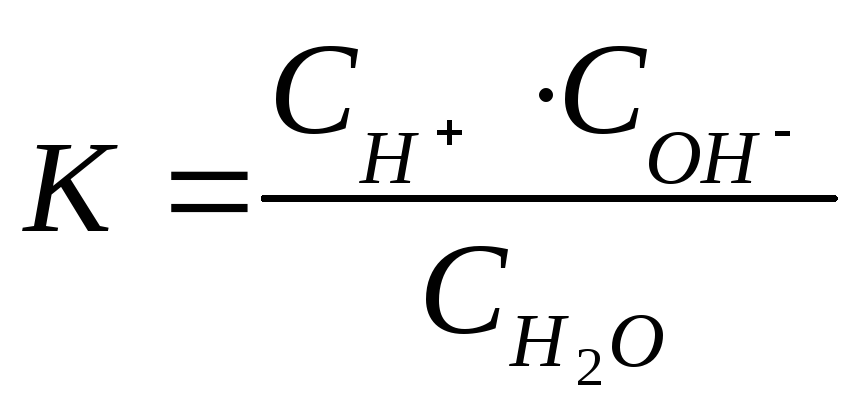(4.11)
Концентрация
воды (
)
в водных растворах остается практически
постоянной, так как вода диссоциирует
на ионы очень слабо.
Из
(4.11) получаем
.(4.12)
Величину
КW
называют
ионным произведением воды. В чистой
воде при 25
C
моль/л,
поэтому
.
При
увеличении температуры
заметно
растет и при 100
С
достигает
=
.
Температурная
зависимость константы диссоциации
выражается уравнением изобары реакции:
Эти
уравнения выражают зависимость константы
равновесия реакции от температуры и в
дифференциальном виде имеют вид:
.(4.13)
Если
тепловой эффект реакции положителен
,
то
.
Это
означает, что с ростом температуры
константа равновесия
эндотермической
реакции всегда увеличивается,
следовательно, увеличивается α
— степень
диссоциации электролитов. Если 
,
то 
.
В этом
случае
с ростом температуры константа диссоциации
уменьшается,
следовательно,
уменьшается и α.
Электрическая
проводимость растворов электролитов
Способность
веществ проводить электрический ток
под действием внешнего электрического
поля называется электрической
проводимостью (L).
Это величина обратная сопротивлению
(R).
Так как
,
то
,
(4.14)
где
ρ
— удельное
сопротивление, Ом/м; S
— площадь поперечного сечения, м2;
l
— длина проводника, м.
Различают
удельную и молярную электрическую
проводимость растворов электролитов.
Удельная
электрическая проводимость
Удельная
электрическая проводимость раствора
электролита (
)
— это
проводимость
объема раствора, заключенного между
двумя параллельными
электродами,
имеющими площадь по одному квадратному
метру и
расположенными
на расстоянии 1 м друг от друга.
Удельная
электрическая проводимость является
величиной обратной
удельному
сопротивлению (ρ).
Тогда из (4.14) получаем:
, (4.15)
,
где φ – постоянная сосуда.
Следовательно,
размерность величины удельной
электрической проводи-
мости
=См/м,
где См (Сименс) — это обозначение единицы
измерения
электропроводности.
В
электрохимии часто пользуются традиционным
определением удельной
электрической
проводимости: это проводимость объема,
раствора, располо-
женного
между параллельными электродами,
расстояние между которыми
составляет
1 м, а площадь каждого из них равна 1 см2.
При этом размерность
.
Удельная
электрическая проводимость
электролитов
определяется количеством и
зарядом
ионов, переносящих электричество, а
также
скоростью их движения в электрическом
поле.
График
зависимости
от концентрации
раствора
для сильных электролитов представ-
ляет
собой кривую с четко выраженным
максимумом,
а для слабых — этот максимум
в
значительной степени размыт и практически
не
проявляется (рис. 4.1). В области малых
концентраций растворов
сильных
и слабых электролитов рост
электрической
проводимости обусловлен
увеличением
количества
ионов
— переносчиков электричества.
При
увеличении
концентрации растет плотность
раствора,
что снижает скорость движения ионов,
при этом у слабых электролитов заметно
снижается степень
диссоциации,
поэтому
для слабых электролитов начинает
уменьшаться в
области
значительно более разбавленных растворов
и роста электропро-
водности
практически не наблюдается, а максимум
на кривой получается
очень
пологим.
Повышение
температуры на 1 К
увеличивает
удельную электропро-
водность
на 2 — 2,5% за счет понижения вязкости
раствора и уплотнения
гидратированных
ионов, а для растворов слабых электролитов
— за счет
увеличения
степени диссоциации в случае эндотермической
реакции
растворения
электролита.
На
величину удельной электрической
проводимости, кроме перечисленных
факторов,
влияет валентность (заряд) иона, так как
чем больше заряд иона,
тем
большее количество электричества он
переносит. Так, двухвалентный
анион
отдает аноду два электрона, в то время
как одновалентный — только
один.
Давление
не оказывает заметного влияния на
удельную электрическую
проводимость.
|
|
Таким |
|
Рис. |
Молярная
электрическая проводимость
Молярная
электрическая проводимость (λ) — это
электрическая
проводимость
объема раствора электролита, содержащего
1 моль раство-
ренного
вещества и находящегося между двумя
параллельными электродами,
расположенными
на расстоянии одного метра друг от
друга.
Эквивалентная
электрическая проводимость относится
к
раствору,
содержащему
1 моль-экв растворенного электролита.
Однако в настоящее
время
не рекомендуется использовать этот
термин. Вместо него применяется
термин
«молярная электрическая проводимость»
с указанием той единицы
электролита,
к которой относится концентрация.
Например,
,
но
очевидно, что
=129
.
Для
ионной электрической проводимости в
случае
необходимости
следует указывать формальную единицу:
или 
.
Молярная
электрическая проводимость связана с
удельной электрической
проводимостью
простым соотношением:
,
(4.16)
где
–
удельная электрическая проводимость,
[C]—
молярная концентрация вещества.
Следовательно,
размерность 
в единицах СИ: =См·моль-1·м2.
В практических расчетах чаще используются
производные единицы СИ:
=
См/см,
(λ)= См ·моль-1
см2,
[C]=моль·
дм-3.
При
этом вместо уравнения (4.16) получаем:
.
(4.17)
Зависимость
λ от скорости движения для 1—1 валентных
ионов выражается уравнением:
,
(4.18)
где
и
—
абсолютные
скорости движения положительных и
отрицатель-
ных
ионов, соответственно.
Для
сильных электролитов α
= 1,
поэтому
.
(4.19)
Произведения
и
называются подвижностями ионов. Тогда:
.
(4.20)
Для
предельно разбавленных растворов 
,(4.21)
,
(4.22)
где
и 
–
подвижности ионов при предельном
разведении.
Уравнение
(4.21) справедливо как для сильных, так и
для слабых разбавленных электролитов
и называется законом Кольрауша (законом
аддитивности электропроводности), а
также законом независимого движения
ионов.
Численные
значения подвижностей ионов 
и 
в настоящее время
практически
найдены для всех ионов и для Т=
298
К приводятся в справоч-
никах.
Пользуясь этими данными, электропроводность
предельно разбав-
ленного
электролита (
)
можно определить простым расчетом по
уравнению
(4.21).
Например,
для уксусной кислоты:
=35+315=350
См· моль-1·
см2.
Сопоставление
данных показывает, что аномально высокими
величинами
электропроводностей в водном растворе
обладают ионы
гидроксония
и гидроксила. Это объясняется эстафетным
механизмом
перемещения
указанных ионов в растворе. Поэтому
растворы кислот и
щелочей
по сравнению с растворами солей при
одинаковых концентрациях
обладают
большей электрической проводимостью.
Из
уравнений (4.19 и 4.22) получаем:
.(4.23)
Откуда
,
(4.24)
,
(4.25)
где
— коэффициент электропроводности,
который характеризует степень
элек-
тростатического
взаимодействия между ионами в растворе.
В
разбавленных растворах слабых электролитов
электростатическое
взаимодействие
между ионами мало 
,поэтому
.
Для
таких
растворов из (4.24) получаем
.(4.26)
То
есть степень диссоциации можно определить
по значениям электропро-
водности,
а так как для электролита постоянна,
то изменение электропро-
водности
разбавленных растворов слабого
электролита при изменении его
концентрации
определяется только зависимостью от
концентрации раствора.
Экспериментальные
данные зависимости электропроводности
разбав-
ленного
слабого 1—1 валентного электролита от
его концентрации позволяют
графически
определить величины , К.
Для этого уравнение (4.6) с использованием
(4.26) приводят к
линейному
виду в координатах (1/ λ – λC):
1/λ=
.(4.27)
П
(22)
остроив график в указанных
координатах
и продолжив прямую
линию
графика до пересечения с осью
ординат,
находят значение , как
величину
обратную величине отрезка
ординаты,
отсекаемой линией графика.
К
определяют из треугольника как отношение
противолежащего катета к прилежащему
катету в масштабах осей графика (
— острый угол наклона линии графикак
оси
абсцисс).
.(4.28)
В
тех случаях, когда, вследствие особенности
распределения точек экспериментальных
данных, экстраполяцию графика на ось
ординат с необходимой точностью провести
не удается, значение , для исследуемого
раствора электролита берут из справочника.
В
концентрированных растворах слабых
электролитов нужно учитывать коэффициент
электрической проводимости () и
коэффициенты активности ионов электролита.
Для
сильных электролитов α
= 1, тогда из (4.24):
.(4.29)
Таким
образом, в растворах сильных электролитов
изменение молярной
электрической
проводимости с концентрацией раствора
обусловлено
изменением
коэффициента электрической проводимости
(), то есть,
влиянием
электростатического взаимодействия
ионов на скорость их движения.
Опыт
показывает, что 
слабых
электролитов изменяется с концентрацией
значительно
сильнее, чем сильных электролитов.
Поэтому кривая графика
зависимости
молярной электропроводности от
концентрации раствора для
слабых
электролитов падает значительно круче
при увеличении концентрации,
чем
кривая этой же зависимости для сильных
электролитов (рис. 4.3).
Н
аиболее
известно эмпирическое уравнение
Кольрауша для разбавленных растворов
называемого законом квадратного корня:
.(4.30)
где
h
— эмпирический коэффициент.
Э
Рис.
4.3.
Зависимость
молярной элек-
трической проводимости
растворов
слабых (1) и сильных (2)
электроли-
тов от их концентрации
та зависимость подтверждена
многочисленными
экспериментами и
теоретически
обоснована в теории Дебая –
Гюккеля – Онзагера, в которой
снижение
молярной электропроводности
разбавленных
растворов сильных
электролитов
при увеличении
концентрации
электролита объясняется
уменьшением
скорости движения ионов
за
счет электростатического взаимодей-
ствия
ионов, окруженных их ионными
атмосферами
при движении таких ионов
в
электрическом поле.
Зависимость
электрической проводимости растворов
электролитов от
температуры
В
большинстве случаев повышение температуры
раствора сопровождается увеличением
его электропроводности. Зависимость
электропроводности от температуры
можно представить эмпирическими
уравнениями:
,
(4.31)
,
(4.32)
где
и
и
– электропроводности соответственно
при температуре t
и
25°С;
— температурный коэффициент
электропроводности.
Уравнения
(4.31)
и (4.32) справедливы для узкого интервала
температур. Значения для раз-
личных
ионов, за исключением ионов водорода и
гидроксила, колеблются в
пределах
от 0.016 до 0.025 в зависимости от типа
электролита и выражаются
уравнением:
.(4.33)
Из
уравнения (4.33) следует, что температурные
коэффициенты удельной и
молярной
электропроводности одинаковы.
Экспериментально установлено,
что
кривая зависимости удельной
электропроводности от температуры в
широком
интервале температур проходит через
максимум, который
определяется
концентрацией и типом электролита, чем
выше концентрация и
заряд
иона, тем при более низких температурах
появляется максимум.
Для
водных
и органических растворителей на
температурную зависимость
электропроводности
влияют вязкость, диэлектрическая
проницаемость,
степень
диссоциации, сольватация ионов. Для
водных растворов с
повышением
температуры
уменьшается вязкость, возрастает
подвижность ионов, что
увеличивает
электропроводность. Но с другой стороны
увеличение
температуры
уменьшает диэлектрическую проницаемость
растворителя, что
приводит
к понижению степени диссоциации и
электропроводности. Однако
влияние
этого явления оказывается незначительно,
если ограничиться
температурами
около 25
С.
Необходимо учитывать также, что для
органических
растворителей температурный коэффициент
диэлектрической
проницаемости
может быть положительным и отрицательным.
Кондуктометрия
и ее
практическое
применение
Методы
исследования, основанные на измерении
электрической
проводимости
растворов, называются кондуктометрическими.
Эти методы
просты,
практически удобны, достаточно точны
и позволяют решить ряд
важных
научно-исследовательских и производственных
задач, не поддающихся
решению
другими методами. Измеряя электрическую
проводимость
растворов,
можно определить основность органических
кислот, растворимость
и
произведение растворимости малорастворимых
соединений, степень
минерализации
почв, вод и грунтов. Широко используется
кондуктометрическое
титрование различных (особенно мутных)
растворов.
Измерение
электрической проводимости растворов
электролитов
Традиционное
экспериментальное определение
электрической
проводимости
раствора основано на измерении
сопротивления раствора при
прохождении
электрического тока методом компенсации.
Для этого
используется
простейшая мостовая схема.
Перемещая
контакт С, добиваются отсутствия тока
или его минимума в
цепи
CD.
При этом справедливо соотношение
,
(4.34)
Р
ис.
4.4. Схема установки для измерения
электрического сопротивления раствора:
АВ – реохорд с фиксированными значениями
сопротивлений в различных положениях
скользящего контактаC;
–
магазин сопротивлений;
– сосуд с исследуемым раствором,
сопротивление которого следует
определить; Г– нуль инструмент
(гальванометр или осциллограф);
–
генератор тока высокой частоты.
Переменный
ток высокой частоты в схеме измерения
используется для
того,
чтобы избежать последствий электролиза
на электродах в сосуде с
исследуемым
раствором и для уменьшения емкостного
сопротивления.
Обязательные
условия проведения измерений:
1.
Объем раствора во всех измерениях должен
быть постоянным.
2.
Электроды должны занимать фиксированное
положение в сосуде, рассто-
яние
между ними не должно изменяться.
3.
Материал электродов должен быть
электрохимически инертным. Площадь
электродов должна быть по возможности
большой и не изменяться.
Следовательно,
все условия измерения должны поддерживаться
постоянными
при всех повторных измерениях.
Измерив,
сопротивление исследуемого раствора
(R),
электрическую
проводимость
его, рассчитывают по формулам приведенным
выше.
В
заключение отметим, что измерение
сопротивления растворов
электролитов
является довольно сложной задачей, что
обусловлено
невозможностью
полного разделения фарадеевской и
нефарадеевской
составляющих
тока, а также неоднородностью поверхности
электрода. Все
это
серьезно осложняет интерпретацию
экспериментальных данных. Так, опыт
показывает,
что такая физически однозначная величина,
как постоянная сосуда,
определяемая
кодуктометрически, изменяет свое
значение в растворах разной
концентрации,
кроме того, она зависит и от частоты
переменного тока.
Поэтому
результаты расчета физико-химических
характеристик раствора на
основе
кондуктометрических измерений можно
считать достоверными только
для
конкретных условий проведения опыта,
а несовпадение рассчитанных
констант
со справочными данными может быть
обусловлено различными
условиями
проведения эксперимента.
