Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 3 апреля 2020 года; проверки требуют 13 правок.
| коэффициент Пуассона | |
|---|---|
| Размерность | 1 |
| Единицы измерения | |
| СИ | безразмерная |
| СГС | безразмерная |
Эта статья — о параметре, характеризующем упругие свойства материала. О понятии в термодинамике см. Показатель адиабаты.
Коэффициент Пуассона (обозначается как 


Детальное определение[править | править код]
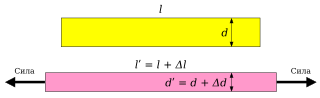
Однородный стержень до и после приложения к нему растягивающих сил.
Приложим к однородному стержню растягивающие его силы. В результате воздействия таких сил стержень в общем случае окажется деформирован как в продольном, так и в поперечном направлениях.
Пусть 












Обычно при приложении к стержню растягивающих усилий он удлиняется в продольном направлении и сокращается в поперечных направлениях. Таким образом, в подобных случаях выполнятся 

Для абсолютно хрупких материалов коэффициент Пуассона равен 0, для абсолютно несжимаемых — 0,5. Для большинства сталей этот коэффициент лежит в районе 0,3, для резины он равен приблизительно 0,5[3]. Для большинства сплавов, металлов, горных пород значение коэффициента Пуассона лежит в пределах 0,25-0,35, в бетоне 0,16-0,18[1].
Связь с другими упругими константами[править | править код]
1) Через модуль сдвига 
2) Через отношение скоростей продольных и поперечных упругих волн волн[4]:
Ауксетики[править | править код]
Существуют также материалы (преимущественно полимеры), у которых коэффициент Пуассона отрицателен, такие материалы называют ауксетиками. Это значит, что при приложении растягивающего усилия поперечное сечение тела увеличивается.
К примеру, бумага из однослойных нанотрубок имеет положительный коэффициент Пуассона, а по мере увеличения доли многослойных нанотрубок наблюдается резкий переход к отрицательному значению −0,20.
Отрицательным коэффициентом Пуассона обладают многие анизотропные кристаллы[5], так как коэффициент Пуассона для таких материалов зависит от угла ориентации кристаллической структуры относительно оси растяжения. Отрицательный коэффициент обнаруживается у таких материалов, как литий (минимальное значение равно −0,54), натрий (−0,44), калий (−0,42), кальций (−0,27), медь (−0,13) и других. 67 % кубических кристаллов из таблицы Менделеева имеют отрицательный коэффициент Пуассона.
Значения коэффициента Пуассона[править | править код]
Грунты[править | править код]
Коэффициент Пуассона (коэффицент бокового расширения) для грунтов[6]:
| Грунты | Коэффициент поперечной
деформации ν |
|---|---|
| Крупнообломочные грунты |
|
| Пески и супеси |
|
| Суглинки |
|
| Глины при показателе текучести IL | |
|
|
| Примечание. Меньшие значения ν применяют при большей плотности грунта. |
В бентонитовом растворе Коэффициент Пуассона≈0,5 т.к. в жидкости жесткости E там нет.
Изотропные материалы[править | править код]
| Материал | Коэффициент Пуассона μ |
|---|---|
| Бетон | 0,2 по СНиП, в расчётах возможно снижение до 0,15—0,17 |
| Алюминий | 0,34 |
| Вольфрам | 0,29 |
| Германий | 0,31 |
| Дюралюминий | 0,34 |
| Иридий | 0,26 |
| Кварцевое стекло | 0,17 |
| Константан | 0,33 |
| Латунь | 0,35 |
| Манганин | 0,33 |
| Медь | 0,35 |
| Органическое стекло | 0,35 |
| Полистирол | 0,35 |
| Свинец | 0,44 |
| Олово | 0,44 |
| Серебро | 0,37 |
| Серый чугун | 0,22 |
| Сталь | 0,25 |
| Стекло | 0,25 |
| Фарфор | 0,23 |
Примечания[править | править код]
- ↑ 1 2 Владимир Атапин, Александр Пель, Анатолий Темников. Сопротивление материалов. Базовый курс. Дополнительные главы. — Litres, 2021-03-16. — 507 с. — ISBN 978-5-04-112997-2. Архивировано 30 декабря 2021 года.
- ↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит, 2005. — Т. I. Механика. — С. 414. — 560 с. — ISBN 5-9221-0225-7.
- ↑ Владимир Черняк, Паригорий Суетин. Механика сплошных сред. — Litres, 2018-12-20. — 353 с. — ISBN 978-5-457-96786-1. Архивировано 30 декабря 2021 года.
- ↑ Виталий Щербинин, Анатолий Зацепин. Акустические измерения. Учебное пособие для вузов. — Litres, 2021-12-02. — 210 с. — ISBN 978-5-04-041588-5. Архивировано 30 декабря 2021 года.
- ↑ Гольдштейн Р. В., Городцов, В. А., Лисовенко Д. С. «Ауксетическая механика кристаллических материалов». Известия РАН, МТТ, 2010 г., № 4, С. 43—62.
- ↑ Таблица 5.10, СП 22.13330.2016 Основания зданий и сооружений.
См. также[править | править код]
- Модуль упругости
- Модуль Юнга

Коэффициент Пуассона (коэффициент поперечной деформации) одна из механических характеристик материалов, показывает зависимость между продольными и поперечными деформациями элемента, характеризует упругие свойства материала.
Обозначается строчными греческими буквами ν или μ и не имеет размерности.
Определяется отношением относительных поперечных εпоп и продольных εпр деформаций бруса (элемента):
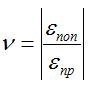
Порядок определения коэффициента поперечной деформации:
Рассмотрим деформацию элемента цилиндрической формы (рис. 1) который до нагружения имеет следующие размеры:

Рис. 1. Размеры бруса до нагружения
здесь
h0 — начальный продольный размер;
d0 — начальный поперечный размер (в данном случае — диаметр).
После нагружения некоторой продольной системой сил (например сжимающей) брус изменит свои размеры, продольный размер уменьшится (т.к. сжатие) а поперечный наоборот увеличится (рис. 2).
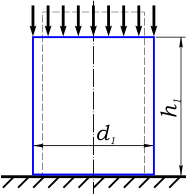
Рис. 2. Размеры бруса после деформации
Полученные в результате деформации размеры обозначим соответственно h1 и d1, где:
h1=h0 — Δh
d1=d0 + Δd
здесь Δh и Δd соответственно абсолютные продольные и поперечные деформации.
Отношение абсолютных деформаций к соответствующим начальным размерам покажет относительные деформации:
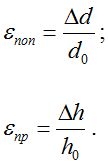
а их отношение в свою очередь определяет коэффициент Пуассона материала бруса.
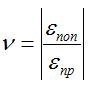
Значение коэффициента принимается по модулю, т.к. продольная и поперечная деформации всегда имеют противоположные знаки (удлинение бруса приводит к его сужению и наоборот).
Лабораторная работа по определению коэффициента поперечной деформации.
В таблице 1 приведены сравнительные значения коэффициента для некоторых материалов.
Таблица 1
|
Материал |
Коэффициент Пуассона, ν |
|
Сталь |
0,3 |
|
Чугун |
0,25 |
|
Медь |
0,32 |
|
Титан |
0,3 |
|
Алюминий |
0,3 |
|
Бетон |
0,16 |
Для всех существующих материалов его значение находится в пределах от 0 до 0,5.
Минимальное значение коэффициента свойственно хрупким материалам, максимальное — эластичным.
Для сталей в зависимости от марки, коэффициент Пуассона принимает значения от 0,27 до 0,32.
Модуль упругости I рода (модуль Юнга) >
Лабораторные работы >
Примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
When a rubber band is stretched, it becomes considerably thinner, which is a familiar observation. The strain and stress that we utilize in the direction of the stretching force make up Poisson’s Ratio. In addition, it has to do with an object’s tensile strength. In the direction of the stretching force, Poisson’s ratio relates to the transverse or lateral shrinkage strain to longitudinal extension strain. The tensile deformation is considered to be positive and compressive deformation to be negative.
Poisson’s ratio is the inverse of the ratio of transverse strain to lateral or axial strain. It is the ratio of the amount of transversal expansion to the amount of axial compression for small values of these changes, and it is named after Siméon Poisson and denoted by the Greek symbol ‘nu.’
Poisson’s Ratio
Poisson’s ratio is the proportion of a material’s change in width per unit width to its change in length per unit length as a result of strain.
Furthermore, the Poisson’s Ratio consists of a negative sign, resulting in a positive ratio for normal materials. It’s also known as Poisson Ratio or Poisson Coefficient. In addition, the lower case Greek letter nu, ν, is commonly used to represent the ratio.
This is where the strain is defined in its basic form. It is the ratio of change in dimension to the original dimension. For a rectangular section of rubber having length L and breadth B, the following strains are:
- Lateral Strain (εt) is defined as,
εt = -ΔB / B
- While the longitudinal Strain (εl) is defined as,
εl = ΔL / L
Here, Δ is the change in dimensions.

The Poisson’s Ratio formula is as follows:
ν = –εt / εl
where, εt is the lateral or transverse strain, εl is longitudinal or axial strain & ν is the Poisson’s ratio.
The negative sign in the formula gives the positive value of the ratio.
Poisson Effect
The Poisson effect is a phenomenon in which a material expands in directions perpendicular to the direction of compression. Poisson’s ratio is a measure of this phenomenon. When a material is stretched rather than crushed, it tends to contract in directions that are transverse to the stretching direction.
Poisson’s ratio values for different materials
With the application of force on a body, stress and strain relationship can be formed.
- It is a scalar and unit less quantity.
- It is positive for tensile deformation or anisotropic materials.
- It is negative for compressive deformation or isometric materials.
Even though the longitudinal strain is positive, the negative Poisson ratio indicates that the material will exhibit positive strain in the transverse direction.
The range of its value lies between -1.0 to +0.5. However, the value of Poisson’s ratio for most materials is between 0 and 0.5.
For plastics, the Poisson’s Ratio is in the range of 0 to 0.5. When the Poisson’s Ratio is 0, there is no reduction in diameter or, to put it another way, no lateral contraction occurs when the material is elongated, but the density decreases.
When the diameter of the material drops during the elongation process or when the material is elastomeric, a value of 0.5 implies that the volume of the material or item will remain the same or constant.
The following table shows the various Poisson’s Ratios for various materials.
|
Material |
Poisson’s Ratio |
|---|---|
|
Rubber |
0.49 |
|
Gold |
0.43 |
|
Clay |
0.37 |
|
Copper |
0.33 |
|
Aluminum |
0.32 |
|
Cast Iron |
0.24 |
|
Concrete |
0.2 |
|
Cork |
0 |
Poisson’s Ratio is usually positive since most common materials get narrower in the opposite or cross direction when stretched. Most materials resist changes in volume, as defined by the bulk modulus K or also known as B, more than changes in shape, as determined by the shear modulus G. The shape distortion also causes the interatomic connections to realign.
Sample Problems
Problem 1: The longitudinal strain for a wire is 0.02 and its Poisson ratio is 0.6. Find the lateral strain in the wire.
Solution:
Given:
Longitudinal strain of wire = 0.02
Poisson ratio = 0.6
The Poisson’s Ratio formula is as follows:
ν = lateral strain/longitudinal strain
Substitute the given values to find the lateral strain.
0.6 = Lateral strain / 0.02
Lateral strain = 0.012
Hence, the lateral strain in the wire is 0.012.
Problem 2: What is the maximum and minimum values of Poisson’s ratio for a metal?
Solution:
The Poisson’s Ratio formula is as follows:
ν = Lateral strain/longitudinal strain
It is always positive because if we apply force in longitudinal strain, lateral strain always decreases for metals. It lies between 0 to 0.5.
Problem 3: Is Poisson’s ratio affected by temperature?
Solution:
In general, lower temperatures reduce both horizontal and vertical strain, while higher temperatures increase both horizontal and vertical strain. As a result, the net effect on Poisson’s Ratio is negligible because both horizontal and vertical strain change by the same amount.
Problem 4: A 2.0 m long metal wire is loaded, resulting in a 4 mm elongation. Find the change in diameter of wire when elongated if the diameter of wire is 1.5 mm and the Poisson’s ratio of wire is 0.24.
Solution:
Given:
Length of wire, L is 2.0 m.
Change in length, ΔL is 4 mm = 0.004 m
Diameter of wire, D is 1.5 mm.
Poisson’s ratio, ν is 0.24.
The longitudinal strain in the wire is given as:
Longitudinal strain = ΔL/L
= 0.004/2.0
= 0.002
The Poisson’s Ratio formula is as follows:
ν = Lateral strain/longitudinal strain
Substitute the given values to find the lateral strain.
0.24 = lateral strain / 0.002
Lateral strain = 0.00048
The lateral strain in a wire is given as:
Lateral strain = ΔD / D
0.00048 = ΔD / 1.5 mm
ΔD = 0.00072 mm
Hence, the change in diameter of the wire is 0.00072 mm.
Problem 5: What if a material’s Poisson’s ratio is zero?
Solution:
A Poisson’s ratio of 0 indicates that the material does not deform in either the lateral or axial directions in response to the application of force. Cork is an example of a material with a Poisson’s ratio of nearly 0 and no deformation under stress. Cork is applied as a seal in bottle stoppers because it expands and contracts under stress, protecting the substance inside.
Last Updated :
26 May, 2021
Like Article
Save Article

Содержание
- Формула коэффициента Пуассона
- Связь с модулем упругости и модулем жесткости
- Значение коэффициента Пуассона для материалов
- Примеры расчетов
- Пример 1
- Решение для
- Решение б
- Решение c
- Решение d
- Решение e
- Пример 2
- Решение
- Расчет деформации проволоки
- Расчет поперечной деформации
- Расчет абсолютного натяжения кабеля
- Расчет уменьшения диаметра
- Ссылки
В Коэффициент Пуассона это безразмерная величина, характерная для каждого материала. Это показатель деформации куска материала перед приложением определенных сил.
Когда кусок материала, который подвергается растяжению или сжатию, подвергается деформации, соотношение между поперечной деформацией и продольной деформацией является в точности коэффициентом Пуассона.

Например, резиновый цилиндр, испытывающий напряжение на концах, растягивается в продольном направлении, но сужается в поперечном направлении. На рисунке 1 показан стержень, исходные размеры которого: длина L и диаметр D.
Брус подвергается растяжению Т на своих концах, и как следствие этого натяжения он подвергается растяжению, так что новая длина L ‘> L. Но при растяжении его диаметр также сужается до нового значения: D ‘<D.
Частное между растяжением (положительным) и сужением (отрицательным), умноженное на (-1), является положительным числом от 0 до 0,5. Это число называется коэффициентом Пуассона ν (греческая буква ню).
Формула коэффициента Пуассона
Для расчета коэффициента Пуассона необходимо определить продольную и поперечную деформации.
Продольная деформация εL деление растяжки на исходную длину:
εL = (L ’- L) / L
Аналогично поперечная деформация εТ это радиальный конус, деленный на исходный диаметр:
εТ = (D ‘- D) / D
Следовательно, коэффициент Пуассона рассчитывается по следующей формуле:
ν = – εТ / εL
Связь с модулем упругости и модулем жесткости
Коэффициент Пуассона ν связан с модулем А ТАКЖЕ упругость (или модуль Юнга) и с модулем жесткости ГРАММ, по следующей формуле:
ν = E / (2G) – 1
Значение коэффициента Пуассона для материалов


Примеры расчетов
Пример 1
Брусок из определенного пластика имеет длину 150 мм и круглое сечение диаметром 20 мм. При воздействии силы сжатия F, равной 612,25 кгс, наблюдается сокращение на 14 мм и одновременное увеличение диаметра стержня на 0,85 мм.
Рассчитать:
а) Продольная деформация.
б) Поперечная деформация.
c) Коэффициент Пуассона этого материала.
г) модуль упругости Юнга, соответствующий материалу.
д) Модуль жесткости этого пластика.
Решение для
Напомним, что продольная деформация εL – это растяжение, деленное на исходную длину:
εL = (L ’- L) / L
εL = (-14 мм) / 150 мм = -0,0933
Отметим, что продольная деформация безразмерна, и в этом случае она была отрицательной, поскольку произошло уменьшение ее продольного размера.
Решение б
Точно так же поперечная деформация εT – это радиальный конус, деленный на исходный диаметр:
εT = (D ‘- D) / D
εT = (+0,85 мм) / 20 мм = 0,0425
Поперечная деформация была положительной, поскольку диаметр стержня увеличился.
Решение c
Для расчета коэффициента Пуассона мы должны помнить, что он определяется как отрицательное значение отношения между поперечной деформацией и продольной деформацией:
ν = – εT / εL
ν = – 0,0425 / (-0,0933) = 0,4554
Следует помнить, что коэффициент Пуассона является положительным безразмерным числом и для большинства материалов находится в пределах от 0 до 0,5.
Решение d
Модуль упругости Юнга, обозначаемый буквой E, является константой пропорциональности в законе Гука. Согласно E нормальное напряжение σL связано с деформацией εL следующим образом:
σL = E εL
Нормальное напряжение определяется как отношение нормальной силы (в данном случае параллельной оси стержня) и площади поперечного сечения:
σL = F / A = F / (π / 4 * D ^ 2)
В этом упражнении сила F равна 612,25 кгс, которую необходимо преобразовать в ньютоны, что является единицей силы в системе СИ:
F = 612,25 кг-f = 612,25 * 9,8 Н = 6000 Н = 6 кН
Со своей стороны, поперечное сечение площади A составляет:
A = (π / 4 * D ^ 2) = (3,1416 / 4) * (20 * 10 ^ -3 м) ^ 2 = 3,1416 * 10 ^ -4 м ^ 2
Наконец, нормальное напряжение, приложенное к стержню, составляет:
σL = F / A = 6000 Н / 3,1416 * 10 ^ -4 м ^ 2 = 19,098,593 Па = 19,098 МПа
Чтобы вычислить модуль упругости Юнга, мы решаем для E из закона Гука σL = E εL:
E = σL / εL = 19 098 593 Па / 0,0933 = 204,7 МПа
Решение e
Модуль жесткости G связан с модулем Юнга E и коэффициентом Пуассона ν следующей формулой:
E / (2 G) = 1 + ν
Оттуда мы можем решить для G:
G = E / (2 (1 + ν)) = 204,7 МПа / (2 (1 + 0,4554)) = 70,33 МПа
Пример 2
Имеет медный кабель диаметром 4 мм и длиной 1 м. Зная, что модуль Юнга меди составляет 110000 МПа, а коэффициент Пуассона равен 0,34, оцените растяжение и сужение в диаметре, которым подвергается проволока, когда на нее подвешивают груз весом 100 кгс.
Решение
Во-первых, необходимо рассчитать нормальное растягивающее напряжение, которое вес оказывает на проволоку, по следующей формуле:
σL = F / A = F / (π / 4 * D ^ 2)
Сила F составляет 980 Н, а площадь поперечного сечения составляет:
A = (π / 4 * D ^ 2) = (3,1416 / 4) * (4 * 10 ^ -3 м) ^ 2 = 1,2566 * 10 ^ -5 м ^ 2
Тогда растягивающее напряжение равно:
σL = 980 Н / 1,2566 * 10 ^ -5 м ^ 2 = 77,986,000 Па
Расчет деформации проволоки
Модуль упругости Юнга, обозначаемый буквой E, является константой пропорциональности в законе Гука, которая связывает нормальное напряжение σL с деформацией εL:
σL = E εL
Отсюда можно решить проблему продольной деформации медного провода:
εL = σL / E = 77,986 МПа / 110000 МПа = 7,09 * 10 ^ -4
Расчет поперечной деформации
С другой стороны, чтобы узнать поперечную деформацию, применяется коэффициент Пуассона:
ν = – εT / εL
Наконец, поперечная деформация равна:
εT = –ν εL = – 0,34 * 7,09 * 10 ^ -4 = -2,41 * 10 ^ -4
Расчет абсолютного натяжения кабеля
Наконец, чтобы узнать абсолютное натяжение кабеля, необходимо применить следующее соотношение:
ΔL = εL * L = 7,09 * 10 ^ -4 * 1 м = 7,09 * 10 ^ -4 м = 0,709 мм
То есть при таком весе кабель едва растягивается на 0,709 миллиметра.
Расчет уменьшения диаметра
Чтобы получить абсолютную усадку по диаметру, воспользуемся следующей формулой:
ΔD = εT * D = -2,41 * 10 ^ -4 * 4 мм = -9,64 * 10 ^ -4 мм = -0,000964 миллиметра.
Это сужение в диаметре настолько мало, что его трудно увидеть невооруженным глазом, даже для его измерения требуется высокоточный инструмент.
Ссылки
- Бир Ф .. Механика материалов. 5-е. Издание. 2010. Мак Гроу Хилл. 1-130.
- Хиббелер Р. Механика материалов. Издание восьмое. Прентис Холл. 2011. 3-60.
- Гир Дж. Механика материалов. Издание восьмое. Cengage Learning. 4-220.
- Джанколи, Д. 2006. Физика: принципы с приложениями. 6-е изд. Прентис Холл. 238-242.
- Валера Негрете, Дж. 2005. Заметки по общей физике. UNAM. 87-98.
Инженеры часто должны наблюдать, как различные объекты реагируют на силы или давления в реальных ситуациях. Одним из таких наблюдений является то, как длина объекта увеличивается или сжимается под действием силы.
Это физическое явление известно как деформация и определяется как изменение длины, деленное на общую длину. Коэффициент Пуассона количественно определяет изменение длины в двух ортогональных направлениях при приложении силы. Эта величина может быть рассчитана по простой формуле.
Формула коэффициента Пуассона
Коэффициент Пуассона – это отношение относительной деформации сжатия (то есть поперечной, поперечной или радиальной деформации), перпендикулярной приложенной нагрузке, к относительной деформации растяжения (то есть осевой деформации) в направлении приложенной нагрузки. Коэффициент Пуассона можно выразить как
μ = –ε t / ε l.
где μ = коэффициент Пуассона, ε t = поперечная деформация (м / м или фут / фут) и ε l = продольная или осевая деформация (опять-таки м / м или фут / фут).
Модуль Юнга и коэффициент Пуассона являются одними из наиболее важных величин в области техники напряжений и деформаций.
-
Коэффициент прочности Пуассона материалов
-
Продольное напряжение
-
Поперечное напряжение
-
Вывод формулы
Подумайте о том, как сила оказывает напряжение вдоль двух ортогональных направлений объекта. Когда сила применяется к объекту, она становится короче в направлении силы (продольной), но удлиняется в ортогональном (поперечном) направлении. Например, когда автомобиль проезжает по мосту, он прикладывает усилие к вертикальным несущим стальным балкам моста. Это означает, что балки становятся немного короче, так как они сжимаются в вертикальном направлении, но становятся немного толще в горизонтальном направлении.
Рассчитайте продольную деформацию, ε l, по формуле ε l = – dL / L, где dL – это изменение длины в направлении силы, а L – исходная длина в направлении силы. Следуя примеру моста, если стальная балка, поддерживающая мост, имеет высоту приблизительно 100 метров, а изменение длины составляет 0, 01 метра, то продольная деформация составляет ε l = –0, 01 / 100 = –0, 0001.
Поскольку деформация – это длина, деленная на длину, величина безразмерна и не имеет единиц измерения. Обратите внимание, что в этом изменении длины используется знак минус, поскольку луч становится короче на 0, 01 метра.
Вычислите поперечную деформацию, ε t, используя формулу ε t = dLt / Lt, где dLt – изменение длины в направлении, ортогональном силе, а Lt – исходная длина, ортогональная силе. Следуя примеру моста, если стальная балка расширяется приблизительно на 0, 0000025 метров в поперечном направлении и ее первоначальная ширина составляла 0, 1 метра, то поперечная деформация составляет ε t = 0, 0000025 / 0, 1 = 0, 000025.
Запишите формулу для коэффициента Пуассона: μ = –ε t / ε l. Опять же, обратите внимание, что коэффициент Пуассона делит две безразмерные величины, и, следовательно, результат безразмерен и не имеет единиц измерения. Продолжая на примере автомобиля, проезжающего по мосту, и воздействия на несущие стальные балки, коэффициент Пуассона в этом случае равен μ = – (0, 000025 / –0, 0001) = 0, 25.
Это близко к табличному значению 0, 265 для литой стали.
Коэффициент Пуассона для общих материалов
Большинство бытовых строительных материалов имеют μ в диапазоне от 0 до 0, 50. Резина близка к верхнему уровню; свинец и глина оба более 0, 40. Сталь имеет тенденцию быть ближе к 0, 30, а производные железа еще ниже, в диапазоне от 0, 20 до 0, 30. Чем меньше число, тем менее подвержены «растяжению» силы, о которых идет речь.





