Как найти коэффициент расхода жидкости

Истечение жидкости
через отверстие может происходить при
постоянном и переменном напоре. Если
истечение жидкости через отверстие
происходит в атмосферу или другую
газовую среду, то такое отверстие
называется незатопленным.
Если же истечение идет под уровень, а
не в атмосферу –
затопленным.

Сжатие называется
неполным,
если при подходе к отверстию поток с
одной или нескольких сторон не испытывает
сжатия.

Сжатие называется
полным
(совершенным),
если расстояние от любой стороны контура
до свободной поверхности жидкости или
края стенки, в которой расположено
отверстие, не будет меньше утроенного
поперечного размера отверстия.

Истечение
жидкости через отверстия и насадки
является одной из основных задач
гидродинамики. Задача гидравлического
расчета отверстий и насадков состоит
в определении скорости истечения и
расхода жидкости, вытекающей через
отверстие
или насадок.

Отверстие
в тонкой стенке – это отверстие, диаметр
которого минимум в 3 раза больше толщины
стенки, т.е. d_o>
3δ_.

Насадком
называется
короткая труба длиной от 3 до 5 его
диаметров, присоединенная к отверстию.
При расчете насадков потерями напора
по длине обычно пренебрегают.

Скорость
истечения и вытекающий расход
рассчитываются по общим формулам для
отверстия и насадка, выведенным на
основе уравнения Бернулли. Общими
являются гидравлические характеристики:
коэффициенты расхода, скорости, сжатия,
сопротивления. Однако коэффициенты
расхода для отверстия и насадка различны
по величине, что связано с различной
картиной движения жидкости в них (рисунок
28).

а	б
Рисунок 28 – Истечение жидкости через а) отверстие, б) насадок

При истечении
жидкости, через отверстие в тонкой
стенке на некотором расстоянии от
стенки, происходит сжатие струи. Площадь
живого сечения струи будет меньше
площади отверстия (рисунок 27 а).
Сжатие струи обусловлено необходимостью
плавного перехода от различных направлений
движения жидкости в резервуаре, в том
числе от радиального движения по стенке,
к осевому движению струи (т.е. частицы
жидкости при входе в отверстие имеют
скорости различных направлений).

При истечении
жидкости через насадок после входа в
насадок жидкость сжимается примерно
так же, как и при истечении через отверстие
в тонкой стенке, а затем струя постепенно
расширяется до размеров отверстия и из
насадка выходит полным сечением (рисунок
27 б).

Сжатие струи
характеризуется коэффициентом
сжатия –
отношение площади сечения струи в месте
наибольшего сжатия к площади сечения
отверстия.

,

где S_c–
площадь живого сечения струи
;

S₀
– площадь
отверстия,
.

Коэффициент сжатия
ε
для круглых отверстий равен 0,64, а для
цилиндрических насадков равен 1.

4.8.1. Истечение жидкости через отверстие (или насадок) при постоянном уровне

Для вывода уравнений
расхода и скорости истечения через
отверстие и насадок при постоянном
уровне запишем уравнение Бернулли для
идеальной жидкости для двух живых
сечений 1–1
(на
свободной поверхности жидкости в сосуде)
и 2–2,
за плоскость сравнения примем сечение
2–2,
(рисунок 29):

Рисунок 29 – К выводу уравнений расхода и скорости истечения жидкости через отверстие

,

Тогда
z₁=
H
, z₂=0.

Скоростью в сечении
1-1
,
скорость в сечении 2-2(– теоретическая скорость истечения
жидкости).

,

Тогда

и.

Пусть
у поверхности жидкости в резервуаре,
давление равно атмосферному и истечение
через отверстие происходит в пространство
с атмосферным давлением, то есть
p₁
= p₂
= p_атм
.

И теоретическая
скорость истечения в этом случае
рассчитывается:

.

Эта
формула была получена Эванджелиста
Торричелли,
в 1643 году.

Для реальной
жидкости учитываются потери напора в
сечении 2-2.
Они обусловлены потерей напора h_п
на местном
сопротивлении и
определяются по формуле:

,

где ζ -коэффициент
местного сопротивления (для входа в
трубу без закругленных кромок ζ= 0,5, а с
закругленными кромками ζ= 0,1).

Тогда формула для
расчета действительной скорости
истечения через отверстие будет выглядеть
следующим образом:

,

Величина

называется коэффициентом
скорости и обозначается через φ.

Коэффициент
скорости φ
представляет собой отношение действительной
скорости истечения к теоретической,
определяется опытным путем.

Таким образом,
действительная скорость истечения
реальной жидкости:

,

Зная скорость
истечения жидкости можно определить
расход жидкости через отверстие:

,

где

Подставляя значения,
для скорости и коэффициента сжатия
получаем:

,

где ε
– коэффициент сжатия струи,

S₀
– площадь отверстия,

φ
– коэффициент скорости,

Произведение
коэффициента сжатия струи на коэффициент
скорости называется коэффициентом
расхода и обозначается μ_р.
Следовательно:

,

Коэффициентом
расхода μ_р
называется
отношение действительного расхода к
теоретическому:

,

Тогда

,

,

При
истечении через малое отверстие в тонкой
стенке коэффициент скорости φ
с увеличением Re
возрастает, что связано с уменьшение
сил вязкости, что в свою очередь
сказывается на уменьшении коэффициента
сопротивления ξ.

Коэффициент сжатия
струи на выходе из насадка ε=1,
что приводит к повышению значения
коэффициента расхода μ_р
и соответственно
расхода жидкости.

Средние значения
коэффициентов истечения ε,
φ, μ_р,
ξ для малых
отверстий в тонкой стенке и насадка при
числах Re
больше 10⁵
приведены в таблице 2.

Таблица 2 – Основные
гидравлические характеристики для
малых отверстий и насадка при числах
Re>10⁵

Тип насадка или отверстия	Коэффициенты
ε	φ	μр	ξ
Отверстие в тонкой стенке	0,62÷0,64	0,97	0,6÷0,62	0,06
Внешний цилиндрический насадок	1,0	0,82	0,82	0,5

В случаях, когда
число Re
меньше 10⁵,
коэффициенты истечения находят из
графика А.Д. Альтшуля (рисунок 30),
составленного на основании опытов
разных авторов.

Рисунок 30 –
Зависимость коэффициента расхода от
значения критерия Рейнольдса для
круглого отверстия

Из графика следует,
что с увеличением числа Re
коэффициент расхода μ_р
сначала увеличивается, а затем, достигнув
максимального значения μ_р = 0,69
при Re
= 350, уменьшается и стабилизируется на
значении, близком к μ_р
= 0,62. Таким образом, коэффициенты истечения
при достаточно больших числах Re
зависят только от формы отверстий и
насадков [2-4,10].

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #

  15.05.2015135.17 Кб18генетическая карта русских.doc
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Истечение жидкости через насадки и отверстия

• gidroadmin
• 13155

Отверстие принято считать малым, если его диаметр d (для круглых отверстий)
или высота а (для прямоугольных отверстий) весьма малы по сравнению с напором Н.
При этом условии скорости во всех точках сечения струи в плоскости отверстия
практически одинаковы.

Под термином «тонкая» стенка следует понимать такую ее толщину, при которой она
не оказывает влияния на характер истечения. Опытами установлено, что толщина
стенки в этом случае не должна превышать 1—1,5 диаметра отверстия.

На расстоянии L~(0,5—l,0)d от плоскости отверстия образуется так называемое сжатое
сечение струи с—с (рис. 1), в котором течение можно считать параллельно-струйным. Площадь сжатого
сечения S_c = ε·S,
где S — площадь отверстия; ε — коэффициент сжатия.

Сжатие струи может быть совершенным, несовершенным, полным и неполным. Совершенным сжатие будет в
том случае, если боковые стенки и днище сосуда достаточно удалены от ближайшей точки контура
отверстия и не влияют на характер истечения. Можно считать, что этот случай имеет место при
неравенствах
L₁≥3а и L₂≥3b (рис.2. I).

Если же это условие не соблюдается (рис. 5.2, II), то сжатие называют несовершенным. Полное
сжатие струи — сжатие всестороннее, когда отверстие в достаточной мере удалено от боковых стенок
и днища сосуда. Если же часть периметра отверстия совпадает с боковой стенкой или днищем сосуда
(рис. 5.2, III), то сжатие струи называется неполным.

Скорость и расход жидкости при истечении

Скорость υ в сжатом сечении струи и расход жидкости Q определяются формулами:

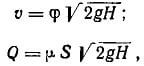
где φ — коэффициент скорости, характеризующий уменьшение действительной скорости υ по
сравнению с теоретической скоростью υ_т:

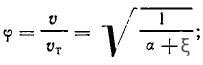
где ξ – коэффициент потери напора (сопротивления);
α – коэффициент Кориолиса, α = 1;
μ -коэффициент расхода: μ = εφ

Расчетный напор H

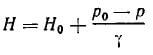
Скорость жидкости в резервуарах обычно принимается равной нулю. H₀ — напор над
центром отверстия; p ₀ и p — соответственно давления на поверхности жидкости в
резервуаре и в среде, куда вытекает жидкость через отверстие.
Если истечение происходит из закрытого резервуара в атмосферу,
числитель второго слагаемого представляет избыточное давление;
при истечении в атмосферу из открытого резервуара второе слагаемое обращается в нуль.

Коэффициент расхода μ, коэффициент скорости φ, и коэффициент сжатия ε

Численные значения φ, ξ, ε и μ обычно определяются опытным путем и зависят от
расположения отверстия относительно стенок резервуара, а также от критериев подобия,
основным из которых является число Рейнольдса Re.

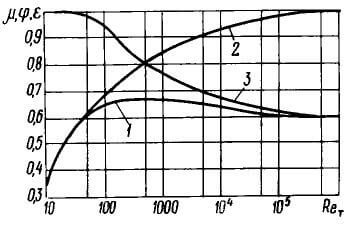
На рисунке 3 приведены графики зависимости μ, φ и ε и от Re_т для круглого
отверстия при совершенном и полном сжатии, построенные А. Д. Альтшулем.
Кривая 1 — μ = f₁(Re_т); кривая 2 — φ =
f₂(Re_т);
кривая 3 — ε = f₃(Re_т).

Число Рейнольдса Re_т подсчитано по теоретической скорости истечения:

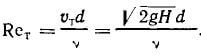
Как видно из графика, при Re_т → ∞ φ → 1, а ε →
μ → 0,605.

Для маловязких жидкостей (вода, бензин, керосин), истечение которых обычно происходит при
достаточно больших числах Рейнольдса (Re> 10⁵), коэффициенты истечения меняются в
сравнительно небольших пределах, поэтому в расчетах для случая совершенного сжатия можно
принимать следующие их усредненные значения: ε = 0,64; ξ = 0,06; φ = 0,97; μ
= 0,62.

Коэффициенты истечения практически не зависят от формы отверстия
(круглое, прямоугольное и т. д.), но изменяются при закруглении входной кромки
отверстия. При увеличении радиуса кривизны μ и ε увеличиваются.

Истечение жидкости из резервуаров может происходить также через различные типы насадков, например, цилиндрические и конические. В этом случае коэффициенты расхода и истечения можно определить по таблице.

Подробное видео по теме “Истечение жидкости через насадки и отверстия” приведено ниже.

Вильнер Я.М. Справочное пособие по гидравлике, гидромашинам и гидроприводам.

Верности творцу вам. Станьте верны творцу, создавшему вас и весь мир, чтобы жить в истине и доброте, во благо себе и всему окружающему. Если вы женского пола, то не выделяйте штанами женские ноги, не обнажайте ноги, грудь, плечи перед мужской частью населения, но носите длинное платье, длинную юбку, скрывая их. Если вы мужского пола, то не сбривайте бороду – не уподобляйте мужское лицо женскому; волосы можно подстригать, укорачивая их длину, но сохраняя видимое и осязаемое наличие на лице, на теле.И не ешьте мясо, яйца, как и не пользуйтесь вещами из кожи и меха, потому что это убийство, это зло – лишать жизни тех, кому мы её не дали. Питайтесь многообразной растительной пищей, съедобными грибами, мёдом, молочными продуктами – этим вы утолите голод, укрепите здоровье, но никому не нанесёте вред и не совершите убийство. Творец, действительно создавший вас и мир, – это не вымышленные религиозные бог, боги, которых нет. Творец не создавал никаких религий и не писал никаких религиозных книг, которые искусственно созданы людьми, отвергающими своего творца. Если вы хотите задать вопрос, я постараюсь вам ответить. Верности творцу вам. a.m_gurin@mail.ru 8-903-121-93-27 Андрей.

Спасибо за статью! Познавательно!

8. Истечение жидкости через отверстия и насадки при постоянном напоре.

8.1. Истечение через отверстия при постоянном напоре.

8.2. Истечение при совершенном сжатии. Скорость истечения реальной жидкости при совершенном сжатии.

8. 3. Коэффициенты: ξ, φ, μ

8.3. Истечение при несовершенном сжатии

8.4. Истечение под уровень

8.5. Истечение через насадки при постоянном напоре.

8.5.1.Первый режим течения.

8.5.2 Второй режим истечения

Рекомендуемые материалы

Отверстия и насадки, из которых происходит истечение,  могут иметь  различное конструктивное исполнение и назначение.

Перелив жидкости из бака в бак производится через отверстия между баками, которые закрываются запорными элементами.

Насадки применяются в моечных устройствах и двигателях, где с их помощью производится распыление жидкости. Такие насадки являются сложным изделием,  имеют  предкамеру высокого давления, запирающую иглу, которой открывается отверстие вначале впрыска на неполное сечение и открывается полностью к концу сжатия, чтобы обеспечить нормальный режим сгорания топлива в цилиндре.

Компактная и сильная струя для брандспойта или гидромонитора  формируется при помощи насадков.

В устройствах гидроавтоматики: золотниках и  элементах типа  “сопло-заслонка” применяются соотношения, полученные в теории истечения.   

При переходе потенциальной энергии  жидкости в резервуаре в кинетическую энергию струи,  часть энергии теряется на трение и завихрение частиц жидкости.

Задачей изучения истечения является определение скоростей истечения,  расхода и давления жидкости в  отверстиях и насадках и  их техническое применение.

8.1. Истечение через отверстия  при постоянном напоре .

Истечение из резервуара при постоянном напоре и  под  давлением Р₁ над свободной поверхностью через круглое отверстие с острой кромкой.

Через отверстие струя жидкости вытекает в воздушное пространство с атмосферным давлением Р₂ =Рат.

Глубина расположения отверстия в дне или на стенке резервуара во много раз больше диаметра отверстия  Н₀ >> d_о (рис.8.1).

К отверстию жидкость подтекает со всех сторон, поэтому в плоскости отверстия  частицы движутся по криволинейным траекториям, поэтому за отверстием  площадь сечения струи оказывается меньше площади отверстия, происходит сжатие струи. В дальнейшем струя сохраняет свою форму на некотором расстоянии от отверстия.

1. Сжатие струи называется совершенным,  если стенки резервуара удалены от центра отверстия на расстояние l > 3d   и не оказывают влияния на сжатие струи. В этом случае сечение струи получается наименьшим.

2.Сжатие струи называется несовершенным при l < 3d. в этом случае влияние стенок резервуара на сжатие струи значительно меньше и сечение струи оказывается   больше, чем при совершенном сжатии. 

8.2. Истечение при совершенном сжатии. Скорость истечения реальной жидкости.

Сжатие струи оценивается коэффициентом сжатия ε, равным отношению площади поперечного сечения струи к площади отверстия

ε = Sc/S₀ = (dc/d₀)².     (8.1)

Коэффициент сжатия зависит от 1)формы отверстия; 2)положения отверстия относительно стенок резервуара, например,  в центре симметрии дна или смещенное от центра и  от 3) числа Рейнольдса                    .

Влияние числа Рейнольдса на коэффициент сжатия показывает график Альтшуля.

Для определения скорости в сжатом сечении запишем уравнение Бернулли для живого сечения,  соответствующего свободной поверхности жидкости в резервуаре “1-1” и сжатого сечения струи «2 –2», плоскость сравнения выберем по сечению “2-2”.

 

Определим напоры, входящие в уравнение Бернулли.

1. Рассматривается установившееся движение, уровень жидкости не меняется, истечение происходит под постоянным напором: следовательно:  геометрический напор z₁ =H.

2. Давление Р₁   на поверхности “1-1” может быть равно атмосферному, больше или меньше атмосферного, поэтому пьезометрический напор равен Р₁/ρg.

3. Поскольку уровень жидкости в сечении “1-1” не меняется,  скорость V₁ = 0 равна нулю.

4. По сечению “2-2” выбрана плоскость сравнения, поэтому геометрический напор равен z₂=0.

5. Истечение происходит в атмосферу, поэтому избыточное давление в сечении 2-2″ Р₂ = Ратм = Рс = 0, пьезометрический напор равен Р₂/ρg = 0.

6. Скорость в сжатом сечении V₂  = Vc.

7. При ламинарном режиме движения эпюра скоростей близка к параболической, коэффициент Кариолиса принимается равным двум α_л ≈2, при турбулентном режиме движении эпюра близка к трапециидальной α_т ≈ 1-1,1 приниманется в расчетах равным единице.

С учетом этих допущений и исходных данных для  турбулентного режим течения  уравнение Бернулли для сечений “1-1” и “2-2”,принимает вид

где ζ — коэффициент  сопротивления отверстия,  α  – коэффициент Кориолиса, 

Н = Н₁ + Р₁ / ρg  – напор истечения,  сумма геометрического и пьезометрического напора,  – коэффициент  скорости для сжатого сечения. Скорость истечения реальной жидкости в сжатом сечении при совершенном сжатии

                                 

Коэффициент скорости при совершенном сжатии  

8.3. Коэффициенты:ε, ζ, φ, μ

В уравнении Бернулли для идеальной жидкости из-за отсутствия вязкости нет потерь на трение, и   коэффициенты сопротивления равен  ξ = 0, при α = 1, φ = 1.  Скорость истечения идеальной жидкости из отверстия с острой кромкой

                                                    .

Коэффициент скорости φ для реальной вязкой жидкости можно определить, поделив скорость истечения реальной жидкости в сжатом сечении  на скорость истечения идеальной жидкости .

,              (8.5)

Коэффициент φ   равен отношению скорости истечения реальной жидкости к скорости истечения идеальной жидкости.  Коэффициент  φ < 1     из-за наличия вязкости у реальной жидкости.

Умножив  площадь сечения сжатой струи  Sc = εSо на скорость струи  в сжатом сечении , получим выражение для расхода жидкости через отверстие с острой кромкой при совершенном сжатии

                    (8.6)

Коэффициентом расхода при истечении из отверстия μ  называется произведение коэффициента сжатия  ε на коэффициент  скорости φ

μ = ε * φ.                   (8.7)

Расхода через отверстие с острой кромкой при совершенном сжатии

 (8.8)  или     (8.9)

где Н- напор истечения или расчетный напор, а ΔР=(р1-Р2)/ρg — расчетная разность давлений, под действием которой происходит истечение.

По этим формулам определяется расход истечения из отверстия  с острой кромкой и через насадки различных форм.

На рис. 8.4 показаны составленные А.Д. Альтшулем  зависимости для  коэффициентов ε,   φ  и  μ  для круглого отверстия в функции  числа Rе.

1.Увеличение числа    означает уменьшение сил вязкости, влияние трения становится меньше,  поэтому коэффициент сопротивления  ζ уменьшается,  и коэффициент скорости  возрастает. 

2. Коэффициент ε  уменьшается из-за уменьшения торможения жидкости у кромки отверстия и увеличения радиусов кривизны струи на входе в цилиндрическую часть. При Rе →∞  значения коэффициентов приближаются к φ→1 и ε→0,6.

3 Коэффициент расхода равный произведению μ = ε * φ  с увеличением Re сначала растет, что связано с ростом φ, а затем уменьшается в связи  со значительным падением  ε, при больших Rе_и равен μ = 0,60÷0,62.

4. В области малых Re (Rе_и < 25) роль вязкости велика, торможение жидкости у кромки значительно,  сжатие струи почти отсутствует и  ε = 1, φ = μ. 

При числах Re <23 для определения μ можно пользоваться формулой:

                    (8.11)

5.При увеличении скорости и числах Рейнольдса  Re> 10⁵ , Re почти не влияет на ко­эффициенты истечения (квадратичная зона истечения), для рас­четов можно пользоваться средними значениями:    φ = 0,97; ε= 0,62; μ = 0,60.

При турбулентном режиме движения неравномерность средних скоростей в сжатом сечении струи  невелика,  α_т = 1,  при φ = 0,97 можно принимать в среднем для  круглого отверстия с  острой кромкой при несовершенном сжатии

                        (8.12)

6.Коэффициент полезного действия отверстия – отношение удельной кинетической энергии струи к напору истечения:

  где    (8.13)

7. При больших Re α=1,  КПД равен                           (8.14)

8. Для малых отверстий некруглой  формы при больших Re значения коэффициента расхода в формуле для определения расхода можно принимать равны­ми  μ= 0,6.

8.4. Истечение при несовершенном сжатии

Сжатие струи называется несовершенным, когда на формирование струи оказывает влияние близость боковых стенок резервуара, то есть расстояние от оси отверстия до стенки l < 3d. Сечение резервуара соизмеримо с сечением отверстия.

Боковые стенки успевают сформировать поток жидкости при подходе к отверстию, и струя   сжимается в меньшей степени, чем при истечении из резервуара неограниченных размеров при совершенном сжатии. Увеличивается  коэффициент сжатия  и коэффициент расхода.

1. При несовершенном сжатии и больших числах Re коэффициент сжатия ε₁ определяется по  формуле

ε₁ = 0,62 +0,38/(S₀/S₁)               (8.15)

где   S₀/S₁ отношение площади отверстия S₀ к площади S₁ поперечного сечения резервуара.

2. Коэффициент скорости при несовершенном сжатии  φ находят по графику  Альтшуля на рис.8.3 по числу Re.

3. Коэффициент сопротивления отверстия ζ  можно найти из формулы, связывающей , где α = 1

4. Коэффициент расхода при несовершенном сжатии равен μ₁ = ε₁ φ .

Используем уравнение Бернулли для определения коэффициентов истечения при несовершенном сжатии.

 где  – потеря напора.

За плоскость сравнения возьмем сечение 2. Исходные данные по сечению “1-1”: z₁=h, P/ρg, V₁.  Исходные данные по сечению “2-2”:  z₂=0, P₂=Pатм =0,  V₁=Vс-скорость в сжатом сечении,  S₂ = Sc = ε₁S₀.  Напор истечения равен :

Выразим V₁ через V₂ :  ,    Р₂=Р₀, и получим

                             

4.Cкорость в сжатом сечении при несовершенном сжатии струи 

                (8.16)

5.Расход для несовершенного сжатия струи 

              (8.17)

8.5. Истечение под уровень

Истечением жидкости в пространство, заполненное этой же жидкостью, называется истечением под уровень (рис. 8.6). Кинетическая энергия струи теряется на вихреобразование.

Определим скорость и расход, используя уравнение Бернулли для поверхности “1- 1” и  сечения “2 – 2”, за плоскость сравнения принято – сечение “1-1”.

Исходные данные: z₁=h₁, P₁ > Ратм, V₁ = 0 , в сечении “2-2” : z₂=0, Р_2в< Ратм,

P₂ =- Р_2в+ρgh₂, скорость в сжатом сечении V₂ →?, ξ ≈0,06 – коэффициент сопротивления отверстия принимают таким же, как  при истечении в атмосферу, коффициента  Кориолиса α.

Исходное уравнение 

 

после подстановки исходных данных:  ,

где Н –напор истечения: разность  гидростатических напоров по обе стороны стенки. Скорость и расход не зависят от  высоты расположения отверстия.

               ,

где S_c – площадь сжатого сечения струи, S₀ – площадь отверстия. Скорость и расход в этом случае определяются,   как при истечении в атмосферу.

  Значения коэффициентов истечения для затопленного отверстия можно принимать такими же, как при истечении свободной струи в атмосферу.

8.5. Истечение через насадки при постоянном напоре.

Внешним цилиндрическим насадком называется короткая трубка длиной, равной l = (1÷5)d с острой входной  кромкой (рис.8.7).  Истечение через такой насадок в атмосферу может происходить  в двух режимах.

а) Безотрывной режим течения называется режим истечения, при котором  струя после входа в насадок сначала сжимается, потом  затем сжатая часть струи расширяется до размеров выходного диаметра и  выходит сечением равным сечению насадка.

При истечении жидкости из больших резервуаров через на­садки  скорость ис­течения на выходе из насадка и расход определяются по форму­лам. 

В формуле (6.6) F₀ заменяется выходной площа­дью насадка F_н.

Для коноидального (плавно сужающегося насадка без сжатия струи на выходе) 

ε = 1 можно принимать в квадратичной зоне сопротивления μ = φ = 0,97.

Коэффициенты истечения могут быть приближенно определены  путем суммирования потерь на отдельных участках потока.

Так, например, для внешнего цилиндрического насадка (рис. 6.8) потерю напора можно представить в виде суммы:

где hп(1+x) потеря при входе в насадок на участке до сжатого сечения струи (х)’,hп(х+2) – потеря при расширении потока на участ­ке между сжатым и выходным сечениями.

Предполагая турбулентный режим течения, и выра­жая эти потери по формулам

получим

где ζ₀ – коэффициент сопротивления отверстия с острой кромкой; v_x – скорость в сжатом сечении струи. По уравнению расхода

.

где F_x– площадь сжатого сечения; ε –  коэффициент сжатия струи при входе в насадок.

Значение ε зависит от соотношения площадей насадка Fн  и резервуара F₁ и может быть определено по формуле          ε₁ = 0,62 +0,38/(S₀/S₁)²              (6.12).

Подставляя в выражение суммы потерь значение V_х, находим коэффициент сопротивления насадка

 (6.15)

при помощи которого определяются скорость истечения и расход  (сжатие струи на выходе из насадка отсутствует);

При истечении из большого резервуара (рис. 6.9) сжатие струи в сечении х является совершенным, и расчет дает в этом случае для средних значений ζ₀ =0,06 и ε_x  ζ=0,5. Скорость и расход опре­деляются по формулам (6.1) и (6.6), в которых

Наглядное представление об изменениях напора потока и его составляющих при истечении жидкости через насадок дается гра­фиком напоров (см. рис. 6.9). Линия напора и пьезометрическая линия на этом графике качественно изображают ход изменения полного и гидростатического напоров по длине насадка от началь­ного сечения перед входом в насадок до его выходного сечения.

Пьезометрический напор р_н /(ρg) в любом сечении насадка опреде­ляется расстоянием по вертикали от оси насадка до пьезометриче­ской линии, скоростной напор v² /(2g) – расстоянием по вертика­ли между пьезометрической линией и линией напора.

8. Если в промежуточных сечениях насадка скорости имеют большие значения, чем скорость выхода из насадка, то в этих се­чениях при истечении в атмосферу возникает вакуум (пьезомет­рическая линия проходит здесь ниже оси насадка).

Так, например, наибольший вакуум р_в, возникающий внутри цилиндрического насадка в сжатом сечении струи, определяется из выражения

 6.16)

Истечение через насадок в атмосферу с заполнением выходно­го сечения насадка возможно только при напорах, меньших пре­дельного H_пр, который соответствует падению абсолютного дав­ления в сжатом сечении до давления насыщенных паров жидко­сти (р_x = рн_п):

                             (6.7)

При Н ≥ Нпр происходит срыв режима работы насадка: струя отрывается от стенок, и процесс сменяется истечением через от­верстие с острой кромкой.

При истечении через затопленный насадок его работа под бо­лее высоким напором, чем некоторое предельное значение (зави­сящее от заглубления насадка), сопровождается кавитацией.

Если истечение жидкости происходит под действием давления Р₀ в среду газа с давлением Р₂, расчетный напор в этом случае равен

H = (P₀ – Р₂)/(ρg)

В струе на выходе из насадка давление равно Р₂, в суженном месте струи внутри насадка, где скорость увеличена, давление Р₁ меньше, чем Р₂. Чем больше напор, под которым происходит истечение и расход через насадок, тем меньше абсолютное давление  Р₁. Разность давлений Р₂ – Р₁   растет пропорционально напору Н.

Составим уравнение Бернулли для сечений 1 – 1 и 2 – 2 (см. рис.8.7),

Последний член уравнения представляет собой потерю напора на расширение потока, которое происходит примерно, как при внезапном расширении трубы.

Сжатие струи внутри насадка можно оценить коэффициентом сжатия ε, как и в случае отверстия, поэтому на основании уравнения расхода

       (8.18)

Заменив скорость V₁  в уравнении Бернулли на скорость V_2,  и,  использовав формулу , найдем падение давления внутри насадка:

  (8.19)

   Подставляя сюда φ = 0,8 и ε=0.63, получаем

(Р₂ – Р₁  ) ≈ 0,75ρgH (8.20)

Если истечение происходит в среду, где давление Р₂ постоянно и равно  атмосферному, увеличение   напора приводит к уменьшению Р₁ –  абсолютное давление в сжатом сечении «1 – 1»  внутри насадка может уменьшиться до  давления насыщенных паров. Поэтому существует величина напора, называемая  критическим напором

Hкр ≈ Р₂ /(0,75ρg).    (8.21)

Следовательно, при Н > Hкр и постоянном Р₂  давление Р₁  должно стать отрицательным, но отрицательных давлений в жидкости не бывает, поэтому режим безотрывного истечения при  Н > Hкр делается невозможным. При Н ≈ Hкр происходит изменение режима истечения и  переход к отрывному режиму.

Если через насадок происходит истечение воды в атмосферу, то

Hкр ≈ Р_а /(0,75ρg) = 10,33/0,75 ≈ 14 м.

Когда давление  Р_н.п. насыщенных паров истекающей жидкости соизмеримо с давлением Р₂ среды, в которую происходит истечение,  пренебречь величиной Р_н.п.  нельзя, в формуле (8.20) следует принять Р₁ = Р_н.п. 

Hкр = (Р_а ^– Р_н.п.) /(0,75ρg)     (8.22)

б) Отрывной  режим истечения характеризуется тем, что струя после сжатия уже не расширяется, сохраняя цилиндрическую форму, и внутри насадка  не соприкасается с его стенками. Течение становится таким же, как из отверстия в тонкой стенке, с теми же значениями коэффициентов. Следовательно, при переходе от безотрывного к отрывному скорость возрастает,  а расход уменьшается, благодаря сжатию струи.

Если после перехода от первого режима истечения ко второму уменьшить напор Н, то второй режим будет сохраняться вплоть до самых малых Н. Это значит, что второй режим истечения возможен при любых напорах,  следовательно, при Н < Нкр возможны оба режима.

При истечении через цилиндрический насадок под уровень безотрывной режим истечения будет таким же. Когда абсолютное давление внутри насадка благодаря увеличению Н падает до давления насыщенных паров и перехода к отрывному течению не происходит, а начинается кавитационный режим, при котором расход перестает зависеть от противодавления Р₂, и получается эффект стабилизации расхода.  При этом чем меньше относительное противодавление Р₂/Р₀ = Р_вых/Р_вх =, которое является критерием кавитации, тем шире область кавитации внутри насадка и тем меньше коэффициент расхода μ.

Информация в лекции “27. Концентрация капитала во французской прессе” поможет Вам.

Коноидальный насадок (рис.8.8) выполняется по форме естественно сжимающейся струи и  обеспечивает безотрывность течения внутри насадка и параллельность струй в выходном сечении. Этот насадок имеет коэффициент расхода, близкий к единице, и очень малые потери (коэффициент сжатия ε = 1),   устойчивый режим течения без кавитации.

Значения коэффициента сопротивления ξ= 0,03 ÷ 0,1 (большим Re соответствуют малые ξ ‚ и наоборот). В соответствии с этим μ =φ= 0,99÷0,96.

Диффузорный насадок представляет собой комбинацию сопла и диффузора (рис. 8.8).

Приставка диффузора к соплу влечет за собой снижение давления в узком месте насадка, увеличение скорости и расхода жидкости через него. При том же диаметре узкого сечения, что и у сопла, и том же напоре диффузорный насадок может дать значительно больший расход (увеличение до 2,5 раза), чем сопло.

Такие насадки применяют, когда заданы диаметр узкого сечения и напор и требуется получить возможно больший расход. Однако, используют диффузорные насадки при небольших  напорах Н = 1 ÷4 м, так как иначе в узком месте насадка возникает кавитация.  Следствием кавитации являются увеличение сопротивления и уменьшение пропускной способности насадка.

12-я лекция, 2010

8. ИСТЕЧЕНИЕ ЖИДКОСТИ
ЧЕРЕЗ ОТВЕРСТИЯ И НАСАДКИ

8.1 Истечение через отверстия в тонкой стенке и насадки (короткие трубки)
 при постоянном напоре.

8.2. Истечение при совершенном сжатии.

8.3 Скорость истечения при совершенном сжатии. Коэффициенты:ε, ξ, φ, μ

8.4 Истечение при несовершенном сжатии

8.5. Истечение под уровень

8.6. Истечение через насадки при постоянном напоре.

8.7 Первый режим течения.

8.8 Второй режим истечения

8.1. Истечение через
отверстия и насадки (короткие трубки)

 при постоянном напоре.

Рассматривается
процесс истечение жидкости из резервуаров через отверстия и насадки в атмосферу
и в пространство, заполненное жидкостью.

При истечении запас
потенциальной энергии  жидкости в
резервуаре, переходит в кинетическую энергию свободной струи, при переходе есть
 потери энергии на трение и завихрение
частиц жидкости.

Задачей изучения
процесса истечения является определение скорости истечения и расхода жидкости.

Истечение
производится из резервуара с жидкостью под давлением Р₀ на
свободной поверхности через круглое отверстие в тонкой стенке на глубине (во
много раз большей диаметра отверстия) Н₀ >> d_от (рис. 12.1).

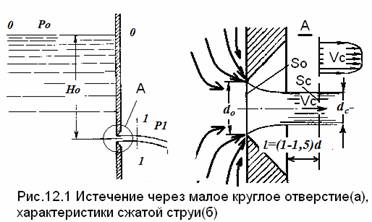
Через отверстие
жидкость вытекает в воздушное пространство с давлением Р₁.

Отверстие в стенке
имеет острую кромку. Частицы жидкости приближаются к отверстию из всего
прилежащего объема, двигаясь ускоренно по различным плавным траекториям (см.
рис.12.1б). Струя отрывается от стенки у кромки отверстия и затем сжимается. Формирование
сжатого сечения  струи происходит на расстоянии
примерно одного диаметра отверстия.

Сжатие струи происходит
при плавном переходе от различных направлений движения жидкости в резервуаре.

12.2. Истечение при
совершенном сжатии.

Совершенным сжатием называется наибольшее
сжатие струи, когда  диаметр отверстия во
много раз меньше  напора Н₀.

Н₀ >> d_от

В этом случае боковые
стенки и свободная поверхность жидкости не влияют на поток жидкости к отверстию.

Сжатие струи оценивается
коэффициентом сжатия ε, равным отношению площади
поперечного сечения струи к площади отверстия

ε = Sc/S₀ = (dc/d₀)².                             (12.1)

Для определения
скорости истечения и расхода из отверстия запишем уравнение Бернулли для движения
жидкости от свободной поверхности «0 – 0»  в резервуаре   и сечением
струи «1 – 1» (на рис.12.1а).

В рассматриваемом
случае уравнение Бернулли записывается для установившейся скорости,  истечение происходит под постоянным напором,
над свободной поверхностью  «0 – 0» давление
равно Р_0,   скорость
также равна нулю.

В сечении   «1 – 1», струя примет  цилиндрическую форму, давление  Р₁,    скорость V₁ предстоит определить из уравнения Бернулли для
потока реальной жидкости.

где ξ—
коэффициент, характеризующий  сопротивление отверстия,   -коэффициент Кориолиса из уравнения Бернулли
для потока вязкой жидкости, характеризующий неравномерность распределения
скоростей в потоке.

Если умножить
числитель и знаменатель выражения для  α  на ρ/2, можно убедиться, что α
является отношением действительной кинетической энергии потока в данном сечении
к кинетической энергии этого потока в этом сечения  при равномерном распределении скоростей.

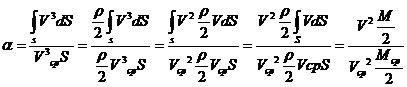
Выделив сумму
геометрического и пьезометрического напора Н = Н₀ + (Р₀ – Р₁)/(ρg), получаем выражение,
связывающее скорость истечения и скоростной напор.

12.3 Скорость истечения
реальной жидкости при совершенном сжатии.

Коэффициенты:ε, ξ, φ, μ

Из выражения для
гидростатического напора, получим формулу для определения скорости истечения из
отверстия с острой кромкой для реальной жидкости

,                             (12.2)

где φ —
коэффициент скорости

   .                                                        (12.3)

Для идеальной
жидкости, так как у нее отсутствует вязкость, трения и потерь на трение
нет  ξ = 0, α = 1, следовательно,
φ
= 1. 

Скорость
истечения идеальной жидкости из отверстия с острой кромкой

                   (12.4)

Из  формулы (12.2) можно заключить, что коэффициент
скорости φ есть отношение скорости истечения реальной жидкости к скорости истечения
идеальной жидкости.

,              (12.5)

Скорость
истечения реальной жидкости меньше  идеальной
из-за вязкости и трения, поэтому коэффициент скорости φ  всегда меньше единицы.

Измерения
показывают, что в средней части сечения струи эпюра скоростей является
равномерной,  поэтому  скорость в средней части  струи близка к идеальной , наружный слой жидкости притормаживается при трении о края
стенки отверстия.  Коэффициент φ
рассматривается, как коэффициент по средней скорости.

Умножив  скорость истечения на площадь сечения струи, получим
выражение для расхода жидкости через отверстие с острой кромкой при совершенном
сжатии

.                     (12.6)

Коэффициентом
расхода μ  называют произведение
значений коэффициентов сжатия  ε и скорости
φ

μ = ε * φ.

Формула для
расхода через отверстие с острой кромкой с учетом выражения для μ

 (12.7)  или

   (12.8)

где ΔР
— расчетная разность давлений, под действием которой происходит истечение.

По этим формулам
определяется расход для всех случаев связанных с истечением из отверстия  с острой кромкой и через насадки различных
форм.

Из уравнения (12.7)
следует, что

        (12.9)

Коэффициент
расхода есть отношение  действительного
расхода Q к  расходу идеальной
жидкости Q_и,
определенному по ее скорости .  Действительный
расход всегда меньше расхода идеальной жидкости, следовательно, коэффициент
расхода всегда меньше единицы из-за сжатия струи и трения.

Коэффициенты
сжатия струи  ε,  сопротивления  ξ, скорости φ,  расхода μ = ε * φ зависят от
типа отверстия и насадка  и от  числа Рейнольдса.

На рис. 12.2
показаны составленные Альтшулем  зависимости
для  коэффициентов ε,   φ  и  μ
 для круглого отверстия в функции
 числа Rе_и, подсчитанного по
скорости истечения идеальной жидкости

Rе_и=V_иd/ν = .

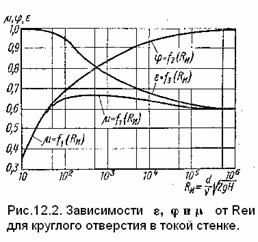
Увеличение числа Re означает
уменьшение сил вязкости, поэтому коэффициент φ возрастает в связи
с уменьшением коэффициента сопротивления ξ 
(влияние трения становится меньше),  коэффициент ε  уменьшается из-за уменьшения торможения жидкости
у кромки отверстия и увеличения радиусов кривизны струи на входе в цилиндрическую
часть. При Rе_и
→∞  значения коэффициентов приближаются к φ→1
и ε→0,6
и соответствуют истечению идеальной жидкости.  

Коэффициент
расхода μ,  определяемый
произведением ε на φ  с увеличением Re сначала растет, что связано с сростом
φ,
а затем уменьшается в связи  со
значительным падением  ε
и при больших Rе_и
равен μ = 0,60÷061.

В области малых Re (Rе_и < 25) роль
вязкости велика, торможение жидкости у кромки значительно так,  что сжатие струи отсутствует ε
= 1, φ = μ.  В этом
случае можно пользоваться формулой:

                    (12.10)

12.3. Истечение при
несовершенном сжатии

Несовершенным
сжатием струи тогда, когда на формирование струи оказывает влияние близость боковых
стенок резервуара.

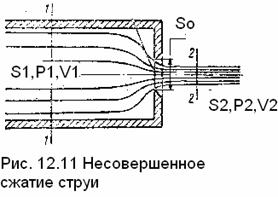
Боковые стенки успевают
направлять жидкость при подходе к отверстию, и струя   сжимается в меньшей степени, чем при истечении
из резервуара неограниченных размеров при совершенном сжатии. Увеличивается  коэффициент сжатия  и коэффициент расхода.

При истечении из
цилиндрического резервуара через круглое отверстие, расположенное в центре торцевой
стенки  при больших числах Re,  коэффициент сжатия ε₁ можно
находить по формуле Жуковского для идеальной жидкости

ε₁ = 0,57 +0,043/(1,1 – n)  
                              (12.11)

где n = S₀/S₁ отношение площади
отверстия S₀ к
площади S₁ поперечного
сечения резервуара.

Коэффициент
скорости φ при несовершенном сжатии мало зависит от отношения n и его
находят по графику на рис.12.2, коэффициент сопротивления отверстия ξ  можно найти из формулы, связывающей

Коэффициент
расхода μ₁ = ε₁ φ
, уравнение Бернулли записывается для сечения «1-1» в резервуаре и сечения в
наиболее сжатой части струи, где давление равно Р₀ –атмосферному.

Выразим V₁ через V₂  V₁S₁=V₂ ε₁S₀;
      V₁=V₂ ε₁S₀/S₁;
             V₁=V₂ ε₁n

.                            
 (12.12)

Откуда получаем:  

скорость для несовершенного
сжатия струи 

;       (12.13)

расход для несовершенного
сжатия струи 

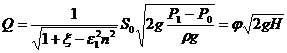         (12.14)

12.5. Истечение под
уровень

Истечением под
уровень называется истечение жидкости в пространство, заполненное этой же жидкостью
(рис. 12.12).

Вся кинетическая
энергия струи теряется на вихреобразование, как при внезапном расширении.

Составляя уравнение
Бернулли относительно свободных поверхностей «0 – 0» и   «2 –
2»   скорости считаем равными нулю, а приравнивая к
первой и второй части члены уранения для сжатого сечения получим с учетом
коффициента  α :

 или

1-я сумма, 2-я сумма, 3- сжатое сечение

где Н – обозначен
расчетный напор, ξ – коэффициент сопротивления отверстия, имеющий примерно
то же значение, что и при истечении в атмосферу, V – скорость истечения в сжатом сечении
струи.

Скорость в этом
случае

  (12.15)

Расход

,   (12.16)

где S_c – площадь
сжатого сечения струи, S₀
– площадь отверстия.

  Получились такие же  расчетные формулы, что и при истечении в
воздух, только расчетный напор Н в данном
случае представляет собой разность 
гидростатических напоров по обе стороны стенки, т.е. скорость и расход
не зависят от  высоты расположения
отверстия.

Коэффициенты
сжатия и расхода при истечении под уровень можно принимать  те же, что и при истечении в воздушную среду.

12.6.
Истечение через насадки при постоянном напоре.

Внешним
цилиндрическим насадком называется короткая трубка длиной, равной l = (2÷6)d без
закругления входной  кромки (рис.12.4а).  Истечение через такой насадок в атмосферу может
происходить  в двух режимах.

12.5.1.Первый режим течения- безотрывный:
 струя после входа в насадок сжимается
примерно как  при истечении через
отверстие в тонкой стенке.

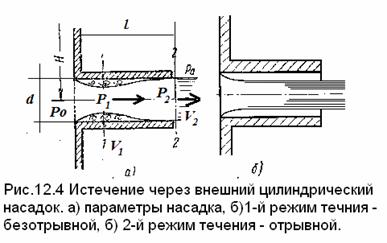
Затем сжатая часть
струи расширяется до размеров отверстия, и из насадка выходит полным сечением. Такой
режим истечения называют безотрывным. На выходе диаметр струи равен диаметру отверстия.

Для маловязких
жидкостей  средние значения коэффициентов
для этого режима при больших числах Re равны: μ=φ = 0,8, ξ = 0,5-0,63.

Коэффициент μ
расхода такого насадка при этом режиме истечения жидкости зависит от относительной
длины насадка l/d и числа Re. Однако и при достаточном значении
l/d не всегда возможен
этот режим.

Пусть
истечение жидкости происходит под действием давления Р₀ в среду
газа с давлением Р₂. Расчетный напор в этом случае

H = (P₀ – Р₂)/(ρg)

В
струе на выходе из насадка давление равно Р₂, в суженном месте
струи внутри насадка, где скорость увеличена, давление Р₁ меньше, чем
Р₂.
Чем больше напор, под которым происходит истечение и расход через насадок, тем
меньше абсолютное давление  Р₁.
Разность давлений Р₂ – Р₁  
растет пропорционально напору Н.

Покажем
это, составив уравнение Бернулли для сечений 1 – 1 и 2 – 2,α = 1 (см. рис.12.4а):

Последний
член уравнения представляет собой потерю напора на расширение потока, которое в
данном случае происходит примерно так же, как и при внезапном расширении трубы (формула
Борда). Сжатие струи внутри насадка можно оценить коэффициентом сжатия ε,
как и в случае отверстия, поэтому на основании уравнения расхода

ε=S₁/S₂; V₁S₁=V₂S₂;
V₁/V₂=S₂/S₁=1/ ε;

  V₁=V₂/ε.                 (12.17)

Заменив
с помощью этого соотношения скорость V₁  в уравнении
Бернулли на скорость V_2, а  ее скорость V₂ выражением через , найдем падение давления внутри насадка:

  (12.18)

   Подставляя сюда φ = 0,8 и
ε=0.63, получаем

(Р₂ – Р₁  ) ≈ 0,75ρgH (12.19)

Если
истечение происходит в среду, где Р₂ равно постоянному ,
например, атмосферному давлению, увеличение 
 напора до критической величины Нкр приводит
к уменьшению Р₁ –  абсолютное давление в сжатом сечение «1 – 1»  внутри насадка может уменьшиться до  давления насыщенных паров. Поэтому существует
величина напора, называемая  критическим
напором

Hкр ≈ Р₂ /(0,75ρg).    (12.20)

Следовательно,
при Н
> Hкр
давление Р₁  должно
стать отрицательным, но отрицательных давлений в жидкости не бывает, поэтому
первый режим истечения при

Н
> Hкр
делается невозможным. При Н ≈ Hкр происходит внезапное
изменение режима истечения, переход от первого режима ко второму (см. рис.12.4в).

12.5.2. Второй режим истечения
характеризуется тем, что струя после сжатия уже не расширяется, сохраня
цилиндрическую форму, и перемещается внутри насадка, не соприкасаясь с его
стенками. Течение становится таким же, как из отверстия в тонкой стенке, с теми
же значениями коэффициентов. Следовательно, при переходе от первого режима ко
второму скорость возрастает,  расход
уменьшается, благодаря сжатию струи.

Если
через насадок происходит истечение воды в атмосферу, то

Hкр ≈ Р_а /(0,75ρg) = 10,33/0,75 ≈ 14 м.

Когда
давление  Р_н.п.
насыщенных паров истекающей жидкости соизмеримо с давлением Р₂
среды, в которую происходит истечение, 
пренебречь величиной Р_н.п.  нельзя, в формуле (12.19) следует принять Р₁
= Р_н.п. 

Hкр = (Р_а ^– Р_н.п.)
/(0,75ρg)     (12.21)

Если
после перехода от первого режима истечения ко второму уменьшить напор Н,
то второй режим будет сохраняться вплоть до самых малых Н. Это значит, что второй
режим истечения возможен при любых напорах,  следовательно, при Н < Нкр возможны оба
режима.

При
истечении через цилиндрический насадок под уровень первый режим истечения не
будет отличаться от описанного выше. Но когда абсолютное давление внутри
насадка благодаря увеличению Н падает до давления насыщенных
паров перехода ко второму режиму не происходит, а начинается кавитационный
режим, при котором расход перестает зависеть от противодавления Р₂,
 получается эффект стабилизации расхода.  При этом чем меньше относительное противодавление
Р₂/Р₀
= Р_вых/Р_вх =, которое является критерием кавитации, тем шире
область кавитации внутри насадка и тем меньше коэффициент расхода μ.

Таким
образом, при истечении жидкости через внешний цилиндрический насадок под
уровень коэффициент является функцией трех безразмерных критериев, а именно

μ = f (l/d, Re,  ).

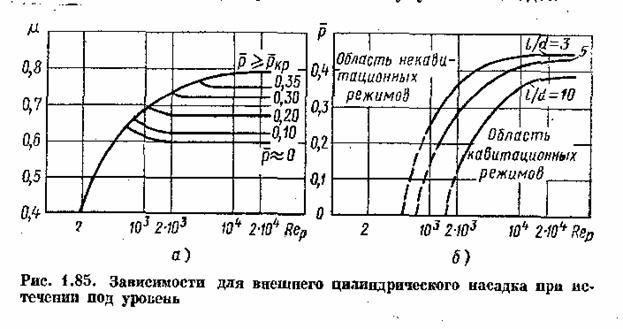
Результаты
новых экспериментальных исследований этого случаи истечения представлены в
безразмерных координатах на рис. 1.85. На рис.1.85а даны зависимости от Re при l/d = 3
для ряда значений , начиная от = 0 и до > , где –  критическое
значение , соответствующее началу кавитации и, следовательно,
критерию ηкр(см. п. 1.23). На рис. 1.85б показаны области кавитационных и
безкавитационных режимов истечения через насадки с l/d = 3; 5 и 10. Увеличениепри возрастании Re объясняется уменьшением коэффициента ε сжатия струи
внутри насадка, т. е. увеличением степени сжатия, а уменьшение при увеличении l/d происходит из-за возрастания давления в сжатом сечении вследствие
увеличения потерь на трение по длине насадка.

Таким
образом, внешний цилиндрический насадок имеет существенные недостатки: на
первом режиме – большое сопротивление и недостаточно высокий коэффициент расхода,
а на втором – очень низкий коэффициент расхода. Недостатком является также двойст-венность
режима истечения в газовую среду при Н < Нкр, а следовательно двузначность
расхода при данном Н и возможность кавитации при истечении под уровень.

При
использовании цилиндрического насадка (сверления в толстой стенке), например в
качество жиклеров, дросселей или форсунок эти недостатки следует учитывать или
улучшать насадок.

Внешний
цилиндрический насадок может быть значительно улучшен путем закругления входной
кромки (см. штриховые линии на рис. 1.83) или устройства конического входа с
углом конусности около 60° (см. жиклер на рис. 1.75).

Чем
больше радиус закругления, тем выше коэффициент расхода и ниже коэффициент
сопротивления. В пределе при радиусе кривизны, равном толщине стенки, цилиндрический
насадок приближается к коноидальному насадку, или соплу.

Коноидальный
насадок (рис. 1.86) очерчивается приблизительно по форме естественно сжимающейся
струи и, благодаря этому, обеспечивает безотрывность течения внутри насадка в
параллельноструйность в выходном сечении. Это весьма распространеный насадок, так
как он имеет коэффициент расхода, близкий к единице, и очень малые потери
(коэффициент сжатия ε = 1), а также устойчивый режим течения без кавитации.

Значения
коэффициента сопротивления те же, что и при плавном сужении (см. п. 1.32), т.
е. ξ= 0,03 ÷ 0,1 (большим Re соответствуют малые ξ ‚ и наоборот). В соответствии с этим
μ =φ= 0,99÷0,96.

Диффузорный
насадок представляет собой комбинацию сопла и диффузора (рис. 1.87).

Приставка
диффузора к соплу влечет за собой снижение давления в узком месте насадка, а
следовательно, увеличение скорости и расхода жидкости через него. При том жедиаметре
узкого сечения, что и у сопла, и том же напоре диффузорный насадок может дать
значительно больший расход (увеличение до 2,5 раза), чем сопло.

Такие насадки
применяют в том случае, когда заданы диаметр узкого сечения и напор и требуется
получить возможно больший расход. Однако, использовать диффузорных насадков
можно лишь при небольших  напорах Н = 1 ÷4
м, так как иначе в узком месте насадка возникает кавитация.  Следствием кавитации являются увеличение
сопротивления и уменьшение пропускной способности насадка.

На рис.1.88
показано падение коэффициента расхода диффузорного насадка с увеличением напора
вследствие кавитации, возникающей в узком месте насадка при истечении воды в атмосферу.

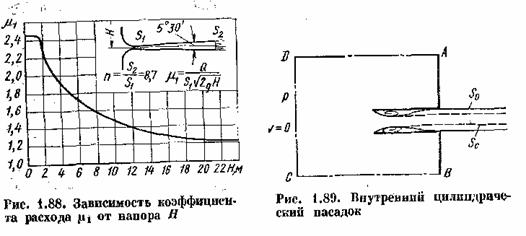
Коэффициент
расхода отнесен к площади узкого сечения, т. е. . Приведенная кривая получена в результате испытания диффузорного
насадка, обладающего наивыгоднейшим углом и степенью расширения, которые
обеспечивают наибольший коэффициент расхода.

Внутренний
цилиндрический насадок или насадок Борда, изображен на рис.1.89. Там же
схематически показаны два режима истечения , аналогичные режимам истечения
через внешний цилиндрический насадок. Очертания струи при первом режиме
показаны сплошными линиями, а при втором – штриховыми. Так как частицы жидкости
приближаются  к входному отверстию
насадка из всего прилежащего объема, а некоторые из них, попадающие на
периферию струи, изменяют направление своего движения на 180°, то степень
сжатия струи в данном насадке больше, а коэффициент ε меньше, чем во внешнем
цилиндрическом насадке. Значение ε в этом случае при истечении идеальной
жидкости  может быть получено на основании
теоремы Эйлера об изменения количества движения (см. п. 1.15). Применим эту
теорему к фиксированному объему в виде кругового цилиндра ABCD соосного с насадком, и с основанием
 CD, достаточно удаленным от насадка, где V=0. Пренебрегая толщиной стенки
насадка на основании указанной теоремы при втором режиме истечения получим

PS₀ = ρS_с*V²,

где
P— давление в центре
основания CD, S₀ и S_с —
площади отверстия насадка и сечения струи (силы давления жидкости на кольцевые
площади оснований цилиндра ABCD  уравновешиваются, а избыточное
давление по площади S₀ в
 плоскости АВ равно нулю.

С
другой стороны, для скорости истечения имеем

1 .

IIосле
подстановки второго уравнения в первое и сокращения на Р и ρ получим

ε = S_с / S₀ = ½.

Этому
значению ε соответствуют значения коэффициентов расхода μ = 0,71 и потерь
ξ =1, что подтверждается опытами при первом режиме истечения и больших
числах Рейнольдса.

Истечение жидкости через отверстия, насадки и водосливы

Задача 6.1.

Определить коэффициенты расхода, скорости, сжатия и сопротивления при истечении воды в атмосферу через отверстие диаметром d = 10 мм под напором H = 2 м, если расход Q = 0.294 л/с, а координаты центра одного из сечений струи x = 3 м и y = 1.2 м.

Задача 6.3.

Для насадка, составленного из двух цилиндрических патрубков диаметрами d = 70 мм и D = 100 мм, определить коэффициенты сопротивления и расхода. Найти предельный напор H_пр в случае истечения воды в атмосферу, принимая, что при H = H_пр вакууметрическая высота в наименьшем сечении потока достигает 10 м.

Задача 6.4.

Для увеличения пропускной способности плавно сходящегося насадка, выходной диаметр которого d = 80 мм и коэффициент сопротивления ξ = 0.04, к нему присоединен цилиндрический патрубок. Определить диаметр патрубка, при котором пропускная способность полученного таким образом составного насадка будет наибольшей. Для этого же насадка определить в случае истечения воды в атмосферу предельный напор, при котором вакуум в узком сечении насадка достигает 0.1 МПа.

Задача 6.5.

Определить, до какого наибольшего избыточного давления p_u сжатого воздуха над поверхностью бензина в баке истечение через цилиндрический насадок будет происходить с заполнением его выходного сечения. Каков при этом будет массовый расход m бензина, если диаметр d = 50 мм? Уровень бензина в баке h = 1.5 м. Плотность бензина ρ = 750 кг/м³, давление насыщенных паров p_н.п = 26.5 кПа. Атмосферное давление равно 97 кПа. Принять коэффициент расхода насадка μ = 0.81 и коэффициент сжатия струи при входе в насадок ε = 0.62.

Задача 6.6.

Определить расход воды Q через отверстие с острой кромкой диаметром d = 120 мм, выполненное в торце трубы диаметром D = 200 мм, если показание манометра перед отверстием M = 0.1 МПа и высота расположения манометра над осью трубы h = 1.3 м. Как изменится расход, если к отверстию присоединить цилиндрический насадок (штриховая линия)? Для насадка найти показание манометра, при котором произойдет срыв режима работы, принимая, что срыву соответствует абсолютное давление в сжатом сечении струи, равное нулю. Атмосферное давление на выходе из насадка 0.1 МПа. Коэффициент сопротивления отверстия принять ξ = 0.04, коэффициент сжатия струи определить по формуле (6.12).