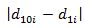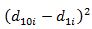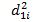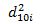Как найти коэффициент различия

Как найти коэффициент различия

From Wikipedia, the free encyclopedia

In single-variable calculus, the difference quotient is usually the name for the expression

{frac {f(x+h)-f(x)}{h}}

which when taken to the limit as h approaches 0 gives the derivative of the function f.[1][2][3][4] The name of the expression stems from the fact that it is the quotient of the difference of values of the function by the difference of the corresponding values of its argument (the latter is (x + h) – x = h in this case).[5][6] The difference quotient is a measure of the average rate of change of the function over an interval (in this case, an interval of length h).[7][8]: 237 [9] The limit of the difference quotient (i.e., the derivative) is thus the instantaneous rate of change.[9]

By a slight change in notation (and viewpoint), for an interval [a, b], the difference quotient

{frac {f(b)-f(a)}{b-a}}

is called[5] the mean (or average) value of the derivative of f over the interval [a, b]. This name is justified by the mean value theorem, which states that for a differentiable function f, its derivative f′ reaches its mean value at some point in the interval.[5] Geometrically, this difference quotient measures the slope of the secant line passing through the points with coordinates (a, f(a)) and (b, f(b)).[10]

Difference quotients are used as approximations in numerical differentiation,[8] but they have also been subject of criticism in this application.[11]

Difference quotients may also find relevance in applications involving Time discretization, where the width of the time step is used for the value of h.

The difference quotient is sometimes also called the Newton quotient[10][12][13][14] (after Isaac Newton) or Fermat’s difference quotient (after Pierre de Fermat).[15]

Overview[edit]

The typical notion of the difference quotient discussed above is a particular case of a more general concept. The primary vehicle of calculus and other higher mathematics is the function. Its “input value” is its argument, usually a point (“P”) expressible on a graph. The difference between two points, themselves, is known as their Delta (ΔP), as is the difference in their function result, the particular notation being determined by the direction of formation:

  • Forward difference:  ΔF(P) = F(P + ΔP) − F(P);
  • Central difference:  δF(P) = F(P + ½ΔP) − F(P − ½ΔP);
  • Backward difference: ∇F(P) = F(P) − F(P − ΔP).

The general preference is the forward orientation, as F(P) is the base, to which differences (i.e., “ΔP”s) are added to it. Furthermore,

The function difference divided by the point difference is known as “difference quotient”:

{frac {Delta F(P)}{Delta P}}={frac {F(P+Delta P)-F(P)}{Delta P}}={frac {nabla F(P+Delta P)}{Delta P}}.,!

If ΔP is infinitesimal, then the difference quotient is a derivative, otherwise it is a divided difference:

{text{If }}|Delta P|={mathit {iota }}:quad {frac {Delta F(P)}{Delta P}}={frac {dF(P)}{dP}}=F'(P)=G(P);,!
{text{If }}|Delta P|>{mathit {iota }}:quad {frac {Delta F(P)}{Delta P}}={frac {DF(P)}{DP}}=F[P,P+Delta P].,!

Defining the point range[edit]

Regardless if ΔP is infinitesimal or finite, there is (at least—in the case of the derivative—theoretically) a point range, where the boundaries are P ± (0.5) ΔP (depending on the orientation—ΔF(P), δF(P) or ∇F(P)):

LB = Lower Boundary;   UB = Upper Boundary;

Derivatives can be regarded as functions themselves, harboring their own derivatives. Thus each function is home to sequential degrees (“higher orders”) of derivation, or differentiation. This property can be generalized to all difference quotients.
As this sequencing requires a corresponding boundary splintering, it is practical to break up the point range into smaller, equi-sized sections, with each section being marked by an intermediary point (Pi), where LB = P0 and UB = Pń, the nth point, equaling the degree/order: 

  LB =  P0  = P0 + 0Δ1P     = Pń − (Ń-0)Δ1P;
        P1  = P0 + 1Δ1P     = Pń − (Ń-1)Δ1P;
        P2  = P0 + 2Δ1P     = Pń − (Ń-2)Δ1P;
        P3  = P0 + 3Δ1P     = Pń − (Ń-3)Δ1P;
            ↓      ↓        ↓       ↓
       Pń-3 = P0 + (Ń-3)Δ1P = Pń − 3Δ1P;
       Pń-2 = P0 + (Ń-2)Δ1P = Pń − 2Δ1P;
       Pń-1 = P0 + (Ń-1)Δ1P = Pń − 1Δ1P;
  UB = Pń-0 = P0 + (Ń-0)Δ1P = Pń − 0Δ1P = Pń;

  ΔP = Δ1P = P1 − P0 = P2 − P1 = P3 − P2 = ... = Pń − Pń-1;

  ΔB = UB − LB = Pń − P0 = ΔńP = ŃΔ1P.

The primary difference quotient (Ń = 1)[edit]

{frac {Delta F(P_{0})}{Delta P}}={frac {F(P_{{{acute {n}}}})-F(P_{0})}{Delta _{{{acute {n}}}}P}}={frac {F(P_{1})-F(P_{0})}{Delta _{1}P}}={frac {F(P_{1})-F(P_{0})}{P_{1}-P_{0}}}.,!

As a derivative[edit]

The difference quotient as a derivative needs no explanation, other than to point out that, since P0 essentially equals P1 = P2 = … = Pń (as the differences are infinitesimal), the Leibniz notation and derivative expressions do not distinguish P to P0 or Pń:
{frac {dF(P)}{dP}}={frac {F(P_{1})-F(P_{0})}{dP}}=F'(P)=G(P).,!

There are other derivative notations, but these are the most recognized, standard designations.

As a divided difference[edit]

A divided difference, however, does require further elucidation, as it equals the average derivative between and including LB and UB:
{begin{aligned}P_{{(tn)}}&=LB+{frac {TN-1}{UT-1}}Delta B =UB-{frac {UT-TN}{UT-1}}Delta B;\[10pt]&{}qquad {color {white}.}(P_{{(1)}}=LB, P_{{(ut)}}=UB){color {white}.}\[10pt]F'(P_{{tilde {a}}})&=F'(LB<P<UB)=sum _{{TN=1}}^{{UT=infty }}{frac {F'(P_{{(tn)}})}{UT}}.end{aligned}}
In this interpretation, Pã represents a function extracted, average value of P (midrange, but usually not exactly midpoint), the particular valuation depending on the function averaging it is extracted from. More formally, Pã is found in the mean value theorem of calculus, which says:
For any function that is continuous on [LB,UB] and differentiable on (LB,UB) there exists some Pã in the interval (LB,UB) such that the secant joining the endpoints of the interval [LB,UB] is parallel to the tangent at Pã.
Essentially, Pã denotes some value of P between LB and UB—hence,
P_{{tilde {a}}}:=LB<P<UB=P_{0}<P<P_{{acute {n}}},!
which links the mean value result with the divided difference:
{begin{aligned}{frac {DF(P_{0})}{DP}}&=F[P_{0},P_{1}]={frac {F(P_{1})-F(P_{0})}{P_{1}-P_{0}}}=F'(P_{0}<P<P_{1})=sum _{{TN=1}}^{{UT=infty }}{frac {F'(P_{{(tn)}})}{UT}},\[8pt]&={frac {DF(LB)}{DB}}={frac {Delta F(LB)}{Delta B}}={frac {nabla F(UB)}{Delta B}},\[8pt]&=F[LB,UB]={frac {F(UB)-F(LB)}{UB-LB}},\[8pt]&=F'(LB<P<UB)=G(LB<P<UB).end{aligned}}
As there is, by its very definition, a tangible difference between LB/P0 and UB/Pń, the Leibniz and derivative expressions do require divarication of the function argument.

Higher-order difference quotients[edit]

Second order[edit]

{begin{aligned}{frac {Delta ^{2}F(P_{0})}{Delta _{1}P^{2}}}&={frac {Delta F'(P_{0})}{Delta _{1}P}}={frac {{frac {Delta F(P_{1})}{Delta _{1}P}}-{frac {Delta F(P_{0})}{Delta _{1}P}}}{Delta _{1}P}},\[10pt]&={frac {{frac {F(P_{2})-F(P_{1})}{Delta _{1}P}}-{frac {F(P_{1})-F(P_{0})}{Delta _{1}P}}}{Delta _{1}P}},\[10pt]&={frac {F(P_{2})-2F(P_{1})+F(P_{0})}{Delta _{1}P^{2}}};end{aligned}}
{begin{aligned}{frac {d^{2}F(P)}{dP^{2}}}&={frac {dF'(P)}{dP}}={frac {F'(P_{1})-F'(P_{0})}{dP}},\[10pt]&= {frac {dG(P)}{dP}}={frac {G(P_{1})-G(P_{0})}{dP}},\[10pt]&={frac {F(P_{2})-2F(P_{1})+F(P_{0})}{dP^{2}}},\[10pt]&=F''(P)=G'(P)=H(P)end{aligned}}
{begin{aligned}{frac {D^{2}F(P_{0})}{DP^{2}}}&={frac {DF'(P_{0})}{DP}}={frac {F'(P_{1}<P<P_{2})-F'(P_{0}<P<P_{1})}{P_{1}-P_{0}}},\[10pt]&{color {white}.}qquad neq {frac {F'(P_{1})-F'(P_{0})}{P_{1}-P_{0}}},\[10pt]&=F[P_{0},P_{1},P_{2}]={frac {F(P_{2})-2F(P_{1})+F(P_{0})}{(P_{1}-P_{0})^{2}}},\[10pt]&=F''(P_{0}<P<P_{2})=sum _{{TN=1}}^{infty }{frac {F''(P_{{(tn)}})}{UT}},\[10pt]&=G'(P_{0}<P<P_{2})=H(P_{0}<P<P_{2}).end{aligned}}

Third order[edit]

{begin{aligned}{frac {Delta ^{3}F(P_{0})}{Delta _{1}P^{3}}}&={frac {Delta ^{2}F'(P_{0})}{Delta _{1}P^{2}}}={frac {Delta F''(P_{0})}{Delta _{1}P}}={frac {{frac {Delta F'(P_{1})}{Delta _{1}P}}-{frac {Delta F'(P_{0})}{Delta _{1}P}}}{Delta _{1}P}},\[10pt]&={frac {{frac {{frac {Delta F(P_{2})}{Delta _{1}P}}-{frac {Delta F'(P_{1})}{Delta _{1}P}}}{Delta _{1}P}}-{frac {{frac {Delta F'(P_{1})}{Delta _{1}P}}-{frac {Delta F'(P_{0})}{Delta _{1}P}}}{Delta _{1}P}}}{Delta _{1}P}},\[10pt]&={frac {{frac {F(P_{3})-2F(P_{2})+F(P_{1})}{Delta _{1}P^{2}}}-{frac {F(P_{2})-2F(P_{1})+F(P_{0})}{Delta _{1}P^{2}}}}{Delta _{1}P}},\[10pt]&={frac {F(P_{3})-3F(P_{2})+3F(P_{1})-F(P_{0})}{Delta _{1}P^{3}}};end{aligned}}
{begin{aligned}{frac {d^{3}F(P)}{dP^{3}}}&={frac {d^{2}F'(P)}{dP^{2}}}={frac {dF''(P)}{dP}}={frac {F''(P_{1})-F''(P_{0})}{dP}},\[10pt]&={frac {d^{2}G(P)}{dP^{2}}} ={frac {dG'(P)}{dP}} ={frac {G'(P_{1})-G'(P_{0})}{dP}},\[10pt]&{color {white}.}qquad qquad ={frac {dH(P)}{dP}} ={frac {H(P_{1})-H(P_{0})}{dP}},\[10pt]&={frac {G(P_{2})-2G(P_{1})+G(P_{0})}{dP^{2}}},\[10pt]&={frac {F(P_{3})-3F(P_{2})+3F(P_{1})-F(P_{0})}{dP^{3}}},\[10pt]&=F'''(P)=G''(P)=H'(P)=I(P);end{aligned}}
{begin{aligned}{frac {D^{3}F(P_{0})}{DP^{3}}}&={frac {D^{2}F'(P_{0})}{DP^{2}}}={frac {DF''(P_{0})}{DP}}={frac {F''(P_{1}<P<P_{3})-F''(P_{0}<P<P_{2})}{P_{1}-P_{0}}},\[10pt]&{color {white}.}qquad qquad qquad qquad qquad neq {frac {F''(P_{1})-F''(P_{0})}{P_{1}-P_{0}}},\[10pt]&={frac {{frac {F'(P_{2}<P<P_{3})-F'(P_{1}<P<P_{2})}{P_{1}-P_{0}}}-{frac {F'(P_{1}<P<P_{2})-F'(P_{0}<P<P_{1})}{P_{1}-P_{0}}}}{P_{1}-P_{0}}},\[10pt]&={frac {F'(P_{2}<P<P_{3})-2F'(P_{1}<P<P_{2})+F'(P_{0}<P<P_{1})}{(P_{1}-P_{0})^{2}}},\[10pt]&=F[P_{0},P_{1},P_{2},P_{3}]={frac {F(P_{3})-3F(P_{2})+3F(P_{1})-F(P_{0})}{(P_{1}-P_{0})^{3}}},\[10pt]&=F'''(P_{0}<P<P_{3})=sum _{{TN=1}}^{{UT=infty }}{frac {F'''(P_{{(tn)}})}{UT}},\[10pt]&=G''(P_{0}<P<P_{3}) =H'(P_{0}<P<P_{3})=I(P_{0}<P<P_{3}).end{aligned}}

Nth order[edit]

{begin{aligned}Delta ^{{acute {n}}}F(P_{0})&=F^{{({acute {n}}-1)}}(P_{1})-F^{{({acute {n}}-1)}}(P_{0}),\[10pt]&={frac {F^{{({acute {n}}-2)}}(P_{2})-F^{{({acute {n}}-2)}}(P_{1})}{Delta _{1}P}}-{frac {F^{{({acute {n}}-2)}}(P_{1})-F^{{({acute {n}}-2)}}(P_{0})}{Delta _{1}P}},\[10pt]&={frac {{frac {F^{{({acute {n}}-3)}}(P_{3})-F^{{({acute {n}}-3)}}(P_{2})}{Delta _{1}P}}-{frac {F^{{({acute {n}}-3)}}(P_{2})-F^{{({acute {n}}-3)}}(P_{1})}{Delta _{1}P}}}{Delta _{1}P}}\[10pt]&{color {white}.}qquad -{frac {{frac {F^{{({acute {n}}-3)}}(P_{2})-F^{{({acute {n}}-3)}}(P_{1})}{Delta _{1}P}}-{frac {F^{{({acute {n}}-3)}}(P_{1})-F^{{({acute {n}}-3)}}(P_{0})}{Delta _{1}P}}}{Delta _{1}P}},\[10pt]&=cdots end{aligned}}
{begin{aligned}{frac {Delta ^{{acute {n}}}F(P_{0})}{Delta _{1}P^{{acute {n}}}}}&={frac {sum _{{I=0}}^{{{acute {N}}}}{-1 choose {acute {N}}-I}{{acute {N}} choose I}F(P_{0}+IDelta _{1}P)}{Delta _{1}P^{{acute {n}}}}};\[10pt]&{frac {nabla ^{{acute {n}}}F(P_{{acute {n}}})}{Delta _{1}P^{{acute {n}}}}}\[10pt]&={frac {sum _{{I=0}}^{{{acute {N}}}}{-1 choose I}{{acute {N}} choose I}F(P_{{acute {n}}}-IDelta _{1}P)}{Delta _{1}P^{{acute {n}}}}};end{aligned}}
{begin{aligned}{frac {d^{{acute {n}}}F(P_{0})}{dP^{{acute {n}}}}}&={frac {d^{{{acute {n}}-1}}F'(P_{0})}{dP^{{{acute {n}}-1}}}}={frac {d^{{{acute {n}}-2}}F''(P_{0})}{dP^{{{acute {n}}-2}}}}={frac {d^{{{acute {n}}-3}}F'''(P_{0})}{dP^{{{acute {n}}-3}}}}=cdots ={frac {d^{{{acute {n}}-r}}F^{{(r)}}(P_{0})}{dP^{{{acute {n}}-r}}}},\[10pt]&={frac {d^{{{acute {n}}-1}}G(P_{0})}{dP^{{{acute {n}}-1}}}}\[10pt]&={frac {d^{{{acute {n}}-2}}G'(P_{0})}{dP^{{{acute {n}}-2}}}}= {frac {d^{{{acute {n}}-3}}G''(P_{0})}{dP^{{{acute {n}}-3}}}}=cdots ={frac {d^{{{acute {n}}-r}}G^{{(r-1)}}(P_{0})}{dP^{{{acute {n}}-r}}}},\[10pt]&{color {white}.}qquad qquad qquad ={frac {d^{{{acute {n}}-2}}H(P_{0})}{dP^{{{acute {n}}-2}}}}= {frac {d^{{{acute {n}}-3}}H'(P_{0})}{dP^{{{acute {n}}-3}}}}=cdots ={frac {d^{{{acute {n}}-r}}H^{{(r-2)}}(P_{0})}{dP^{{{acute {n}}-r}}}},\&{color {white}.}qquad qquad qquad qquad qquad qquad = {frac {d^{{{acute {n}}-3}}I(P_{0})}{dP^{{{acute {n}}-3}}}}=cdots ={frac {d^{{{acute {n}}-r}}I^{{(r-3)}}(P_{0})}{dP^{{{acute {n}}-r}}}},\[10pt]&=F^{{({acute {n}})}}(P)=G^{{({acute {n}}-1)}}(P)=H^{{({acute {n}}-2)}}(P)=I^{{({acute {n}}-3)}}(P)=cdots end{aligned}}
{begin{aligned}{frac {D^{{acute {n}}}F(P_{0})}{DP^{{acute {n}}}}}&=F[P_{0},P_{1},P_{2},P_{3},ldots ,P_{{{acute {n}}-3}},P_{{{acute {n}}-2}},P_{{{acute {n}}-1}},P_{{acute {n}}}],\[10pt]&=F^{{({acute {n}})}}(P_{0}<P<P_{{acute {n}}})=sum _{{TN=1}}^{{UT=infty }}{frac {F^{{({acute {n}})}}(P_{{(tn)}})}{UT}}\[10pt]&=F^{{({acute {n}})}}(LB<P<UB)=G^{{({acute {n}}-1)}}(LB<P<UB)=cdots end{aligned}}

Applying the divided difference[edit]

The quintessential application of the divided difference is in the presentation of the definite integral, which is nothing more than a finite difference:

{begin{aligned}int _{{LB}}^{{UB}}G(p),dp&=int _{{LB}}^{{UB}}F'(p),dp=F(UB)-F(LB),\[10pt]&=F[LB,UB]Delta B,\[10pt]&=F'(LB<P<UB)Delta B,\[10pt]&= G(LB<P<UB)Delta B.end{aligned}}

Given that the mean value, derivative expression form provides all of the same information as the classical integral notation, the mean value form may be the preferable expression, such as in writing venues that only support/accept standard ASCII text, or in cases that only require the average derivative (such as when finding the average radius in an elliptic integral).
This is especially true for definite integrals that technically have (e.g.) 0 and either pi,! or 2pi ,! as boundaries, with the same divided difference found as that with boundaries of 0 and begin{matrix}frac{pi}{2}end{matrix} (thus requiring less averaging effort):

{begin{aligned}int _{0}^{{2pi }}F'(p),dp&=4int _{0}^{{{frac {pi }{2}}}}F'(p),dp=F(2pi )-F(0)=4(F({begin{matrix}{frac {pi }{2}}end{matrix}})-F(0)),\[10pt]&=2pi F[0,2pi ]=2pi F'(0<P<2pi ),\[10pt]&=2pi F[0,{begin{matrix}{frac {pi }{2}}end{matrix}}]=2pi F'(0<P<{begin{matrix}{frac {pi }{2}}end{matrix}}).end{aligned}}

This also becomes particularly useful when dealing with iterated and multiple integrals (ΔA = AU − AL, ΔB = BU − BL, ΔC = CU − CL):

{begin{aligned}&{}qquad int _{{CL}}^{{CU}}int _{{BL}}^{{BU}}int _{{AL}}^{{AU}}F'(r,q,p),dp,dq,dr\[10pt]&=sum _{{T!C=1}}^{{U!C=infty }}left(sum _{{T!B=1}}^{{U!B=infty }}left(sum _{{T!A=1}}^{{U!A=infty }}F^{{'}}(R_{{(tc)}}:Q_{{(tb)}}:P_{{(ta)}}){frac {Delta A}{U!A}}right){frac {Delta B}{U!B}}right){frac {Delta C}{U!C}},\[10pt]&=F'(C!L<R<CU:BL<Q<BU:AL<P<!AU)Delta A,Delta B,Delta C.end{aligned}}

Hence,

F'(R,Q:AL<P<AU)=sum _{{T!A=1}}^{{U!A=infty }}{frac {F'(R,Q:P_{{(ta)}})}{U!A}};,!

and

F'(R:BL<Q<BU:AL<P<AU)=sum _{{T!B=1}}^{{U!B=infty }}left(sum _{{T!A=1}}^{{U!A=infty }}{frac {F'(R:Q_{{(tb)}}:P_{{(ta)}})}{U!A}}right){frac {1}{U!B}}.,!

See also[edit]

  • Divided differences
  • Fermat theory
  • Newton polynomial
  • Rectangle method
  • Quotient rule
  • Symmetric difference quotient

References[edit]

  1. ^ Peter D. Lax; Maria Shea Terrell (2013). Calculus With Applications. Springer. p. 119. ISBN 978-1-4614-7946-8.
  2. ^ Shirley O. Hockett; David Bock (2005). Barron’s how to Prepare for the AP Calculus. Barron’s Educational Series. p. 44. ISBN 978-0-7641-2382-5.
  3. ^ Mark Ryan (2010). Calculus Essentials For Dummies. John Wiley & Sons. pp. 41–47. ISBN 978-0-470-64269-6.
  4. ^ Karla Neal; R. Gustafson; Jeff Hughes (2012). Precalculus. Cengage Learning. p. 133. ISBN 978-0-495-82662-0.
  5. ^ a b c Michael Comenetz (2002). Calculus: The Elements. World Scientific. pp. 71–76 and 151–161. ISBN 978-981-02-4904-5.
  6. ^ Moritz Pasch (2010). Essays on the Foundations of Mathematics by Moritz Pasch. Springer. p. 157. ISBN 978-90-481-9416-2.
  7. ^ Frank C. Wilson; Scott Adamson (2008). Applied Calculus. Cengage Learning. p. 177. ISBN 978-0-618-61104-1.
  8. ^ a b Tamara Lefcourt Ruby; James Sellers; Lisa Korf; Jeremy Van Horn; Mike Munn (2014). Kaplan AP Calculus AB & BC 2015. Kaplan Publishing. p. 299. ISBN 978-1-61865-686-5.
  9. ^ a b Thomas Hungerford; Douglas Shaw (2008). Contemporary Precalculus: A Graphing Approach. Cengage Learning. pp. 211–212. ISBN 978-0-495-10833-7.
  10. ^ a b Steven G. Krantz (2014). Foundations of Analysis. CRC Press. p. 127. ISBN 978-1-4822-2075-9.
  11. ^ Andreas Griewank; Andrea Walther (2008). Evaluating Derivatives: Principles and Techniques of Algorithmic Differentiation, Second Edition. SIAM. pp. 2–. ISBN 978-0-89871-659-7.
  12. ^ Serge Lang (1968). Analysis 1. Addison-Wesley Publishing Company. p. 56.
  13. ^ Brian D. Hahn (1994). Fortran 90 for Scientists and Engineers. Elsevier. p. 276. ISBN 978-0-340-60034-4.
  14. ^ Christopher Clapham; James Nicholson (2009). The Concise Oxford Dictionary of Mathematics. Oxford University Press. p. 313. ISBN 978-0-19-157976-9.
  15. ^ Donald C. Benson, A Smoother Pebble: Mathematical Explorations, Oxford University Press, 2003, p. 176.

External links[edit]

  • Saint Vincent College: Br. David Carlson, O.S.B.—MA109 The Difference Quotient Archived 2005-09-12 at the Wayback Machine
  • University of Birmingham: Dirk Hermans—Divided Differences
  • Mathworld:
    • Divided Difference
    • Mean-Value Theorem
  • University of Wisconsin: Thomas W. Reps and Louis B. Rall — Computational Divided Differencing and Divided-Difference Arithmetics
  • Interactive simulator on difference quotient to explain the derivative
Источник

Калькулятор разницы в процентах между двумя числами онлайн

Разница в процентах относительно первого числа (a) равна:

0.00%

Разница в процентах относительно второго числа (b) равна:

0.00%

0.00

Как определить разницу в процентах?

Определить можно по простой формуле:

Разница относительно первого числа (a) равна:

c=(b—a)/a*100, где

  • с— разница в процентах
  • a — первое число
  • b — второе число

Данная разница обозначает на сколько процентов второе число (b) больше (или меньше, если знак «-«) относительно первого числа (a).

Разница относительно второго числа (b) равна:

c=(a—b)/b*100, где

  • с— разница в процентах
  • a — первое число
  • b — второе число

Данная разница обозначает на сколько процентов первое число (a) больше (или меньше, если знак «-«) относительно второго числа (b).

Источник

Задача

Имеются данные выборочного обследования домашних хозяйств:

Показатель

Домохозяйства по 10%-ым группам населения

Первая
(с наименьшими доходами)

Десятая
(с наибольшими доходами)

Среднедушевой денежный доход в месяц, руб.

112,4

608,9

Удельный вес денежных доходов, %

Оплата труда, доход от предпринимательской деятельности и пр.

69,4

78,5

Социальные трансферты

19,5

8,7

Поступления от продажи сельхозпродуктов и прочие поступления

11,1

12,8

Определите:

  1. коэффициент фондов;
  2. коэффициенты структурных различий (линейный, квадратический, коэффициент Гатева, индекс Салаи).

Решение

Коэффициент фондов применяется для количественной оценки дифференциации доходов населения и определяется как соотношение между средними доходами в первой и десятой децильных группах населения.

Для расчета этого показателя население подразделяется на 10 групп по уровню доходов. Первая децильная группа – 10% населения с минимальными доходами, десятая – 10% населения с максимальными доходами. Коэффициент фондов рассчитывается по формуле:

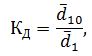
где: 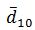 – среднедушевой доход 10% населения с наименьшими доходами;
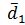 – среднедушевой доход 10% населения с самыми высокими доходами.

Коэффициент фондов равен:

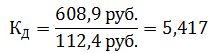
Для оценки структурный различий используются следующие показатели: линейный коэффициент структурных различий, квадратический коэффициент структурных различий, а также индексы Гатева и Салаи.

Линейный коэффициент структурных различий определяется как отношение суммы модулей абсолютных изменений долей к числу наблюдений:

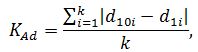
где: d10i, d1i  – i-тое значение удельного веса в доходах соответственно в 10-й и первой децильных группах населения;
k – количество статей денежных доходов.

Расчет показателей структурных различий

№

d1

d10

1

69,40

78,50

0,0910

0,0083

0,4816

0,6162

0,0038

2

19,50

8,70

0,1080

0,0117

0,0380

0,0076

0,1467

3

11,10

12,80

0,0170

0,0003

0,0123

0,0164

0,0051

Итого:

0.2160

0.0202

0.5320

0.6402

0.1555

Линейный коэффициент структурных различий равен:

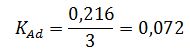
Если вместо модулей изменений применить квадраты, можно получить квадратический коэффициент структурных изменений:

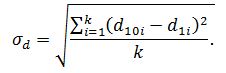
Квадратический коэффициент структурных изменений равен:

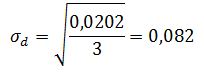
Индекс К. Гатева является интегральным показателем изменения структуры и изменяется в пределах от 0 до 1. Чем ближе значение показателя к 1, тем сильнее различия в структуре. Индекс определяется по формуле:

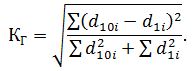
Индекс Гатева составил:

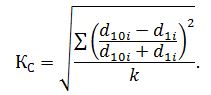
Индекс Салаи был введен при исследовании различий в структуре использования бюджета времени у различных групп населения. Он определяется по формуле:

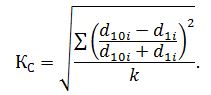
Индекс Салаи для доходов населения равен:

Источник

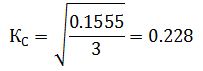
Есть два примера ряда натуральных чисел:

1) 4 5 5 5 4 5 4 5 5 5
2) 3 10 25 4 15 40 32 9 14 19

И там и там по 10 числел.

В первом случае максимальный разброс между числами очевидно мал. Все числа в ряде между собой практически равны, то есть если каждое число сравнить с каждым другим, то средняя разница между числами будет не больше единицы. Можно так же представить эти числа как линию на графике – будет практически идеальная прямая.

Во втором случае разброс очевидно больше и я не знаю как посчитать этот среднее число, на которое каждое число в ряде отличается от другого. Сразу представляется сильно ломанный график и вообще все это наглядно если в голове представлять, но нужно как-то математически это выразить. Есть какие-то варианты/формулы, чтобы получить этот коэффициент, кроме как буквально каждое число сравнивать с каждым другим и потом считать среднее арифметическое?

Спасибо 🙂

Источник

Показатели структурных различий и сдвигов

Простейшими
показателями структурных различий
/сдвигов/ являются:

1. Линейный
коэффициент структурных различий
/сдвигов/.

, где

и
– сравниваемые признаки;n
– количество строк или элементов в
структуре.

2. Квадратический
коэффициент структурных различий
/сдвигов/.

.

Эти показатели
находятся в интервале от 0 до 1 или 100 %,
в зависимости от единиц измерения
исходных данных. Для них используется
следующий критерий: если по значению
они до 0,03 или 3 %, то структурные различия
или сдвиги не наблюдаются; если больше
либо равны 0,03, то структурные различия
или сдвиги наблюдаются.

3. Интегральный
коэффициент (индекс).

.

4. Индекс Салаи.

.

Два последних
показателя могут принимать значения
от 0 до 1, здесь могут быть применены
общие количественные критерии оценки
наличия структурных различий /сдвигов/.
Интегральный коэффициент характеризует
значимость структурных различий
/сдвигов/ по отношению к типу сравниваемых
структур. Например, если в структуре
преобладают крупные элементы, то значение
индексов при прочих равных условиях
будет меньше. Индекс Салаи характеризует
изменение каких элементов в структуре
произошло. Т.е. если изменился /различается/
удельный вес крупных элементов, то
значение индекса Салаи при прочих равных
условиях будет меньше, по сравнению с
изменениями /различиями/ небольших по
удельному весу структур.

Примеры решения типовых заданий

Пример 1.

Оцените
связь между уровнем успеваемости
студентов и отношением к получению
второго высшего образования с помощью
соответствующих показателей:

Считаете ли
Вы необходимым получение второго
высшего образования?

Всего

опрошено

Уровень
успеваемости

«Отличники»

«Хорошисты»

«Троечники»

Да

105

25

50

30

Затрудняюсь
ответить

70

10

20

40

Нет

75

15

30

30

ИТОГО:

250

50

100

100

Решение:

В
данном случае принимаются гипотезы Н0
– уровень успеваемости не влияет на
отношение студентов к получению второго
высшего образования, и Н1
– влияние есть.

Рассчитаем
значение непараметрического критерия
χ2:

.

При уровне значимости
0,05 и числе степеней свободы
ν= 4 табличное
значение составляет 9,488, отсюда вывод
– уровень успеваемости студентов влияет
на их отношение к необходимости получить
второе высшее образование.

Рассчитаем
коэффициенты Пирсона и Чупрова:

,

.

Поскольку оба
коэффициента меньше 0,3, значит, гипотеза
Н1 не
подтверждается. Уровень успеваемости
студентов не влияет на отношение к
получению второго высшего образования.

Пример 2.

Исследовалась
социально-демографическая характеристика
занятого населения в зависимости от их
семейного положения в Российской
Федерации в 2006 г. (млн. чел.).

Занятое население

по наличию
дополнительной работы

Семейное
положение

Всего

Состоят в
браке

Не состоят
в браке

Имеют одну
работу

44,2

22,6

66,8

Имеют две и
более работ

1,7

0,6

2,3

Итого

45,9

23,2

69,1

Решение:

Коэффициент
ассоциации:
;

коэффициент
контингенции:
.

Можно сделать
вывод, что семейное положение занятого
населения не влияет на наличие
дополнительной работы. Отрицательные
значения коэффициентов можно
интерпретировать так: семейное положение
стимулирует занятых иметь две и более
работ.

Пример 3.

С помощью
соответствующих коэффициентов определить,
имеется ли связь между ответами на
вопрос «Кому Вы скорее доверите свои
тайны?» молодежи разного пола:

Варианты
ответов

Доля ответов,
в %

Девушки

Юноши

Лучшей подруге
(другу)

20,0

24,0

Родителям

18,0

12,0

Уважаемому для Вас
человеку

18,0

8,0

Братьям, сестрам

14,0

20,0

Случайному попутчику

12,0

4,0

Любимому человеку

9,0

16,0

Никому

3,0

12,0

Другие варианты
ответа

6,0

4,0

Решение:

Принимаем
гипотезы Н0
– связи между ответами на вопрос девушек
и юношей нет, и Н1
– связь есть

Для
расчета коэффициентов представим
промежуточные результаты в таблице:

Варианты ответов

Девушки

Юноши

R1

R2

di

d

Лучшей подруге
(другу)

20,0

24,0

1

1

0

0

Родителям

18,0

12,0

2,5

4,5

2

4

Уважаемому для Вас
человеку

18,0

8,0

2,5

6

3,5

12,25

Братьям, сестрам

14,0

20,0

4

2

2

4

Случайному попутчику

12,0

4,0

5

7,5

2,5

6,25

Любимому человеку

9,0

16,0

6

3

3

9

Никому

3,0

12,0

8

4,5

3,5

12,25

Другие варианты
ответа

6,0

4,0

7

7,5

0,5

0,25

Сумма

48,0

Коэффициент
ранговой корреляции Спирмена:

.

Для расчета
коэффициента ранговой корреляции
Кенделла проводим следующие действия:

Варианты ответов

R1

R2

X

Y

R–

R+

Лучшей подруге
(другу)

1

1

1

1

0

7

Родителям

2,5

4,5

2,5

4,5

0

3

Уважаемому для Вас
человеку

2,5

6

2,5

6

0

2

Братьям, сестрам

4

2

4

2

2

4

Случайному попутчику

5

7,5

5

7,5

0

0

Любимому человеку

6

3

6

3

3

2

Никому

8

4,5

7

7,5

0

0

Другие варианты
ответа

7

7,5

8

4,5

4

0

Сумма

9

18

Столбец Х –
переранжируем столбец R1
по возрастанию.

Столбец Y
– восстанавливаем значение строк, т.е.
проставляем ранги, которые первоначально
соответствовали рангам колонки R1
для колонки
R2.

R–
– число рангов, предшествующее i-му
рангу в колонке Y
и больших его по значению.

R+
– число рангов, последующих i-му
рангу в колонке Y
и больших его по значению.

S
= 18 – 9 = 9.

.

Оба коэффициента
подтверждают наличие связи между
ответами на поставленный вопрос девушек
и юношей, но слабую. Результаты опроса
показывают, что в первую очередь молодежь
доверяет тайны своим друзьям (подругам),
но затем девушки предпочитают доверять
родителям и уважаемым ими людям, а юноши
– близким родственникам и любимым.

Источник

Добавить комментарий